A Generalized Maximum Entropy Stochastic Frontier Measuring Productivity Accounting for Spatial Dependency
Abstract
:1. Introduction
2. The Empirical Model
3. Data and the Estimation
| Variables | Units | Avg | Min | Max | Std |
|---|---|---|---|---|---|
| Agr. Output | ×103 I$ | 8281701.2 | 53350.0 | 38125640.0 | 9950171.2 |
| Land | ×103 Ha | 8335.2 | 9.0 | 41223.0 | 10174.4 |
| Machinery | ×103 No | 349.1 | 0.5 | 1900.0 | 458.2 |
| Labour | ×103 Pe | 875.9 | 2.0 | 10454.0 | 1854.0 |
| Fertilizer | ×103 Mt | 740.6 | 0.9 | 5064.0 | 1019.5 |
| Livestock | ×103 SE | 42007.8 | 236.8 | 191956.0 | 50067.3 |
4. Empirical Results and Discussion
| Coef | GME1 | Support1 | GME2 | Support2 | GME3 | Support3 |
|---|---|---|---|---|---|---|
| β1 | 0.2005 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.2005 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.2005 | m = (0, 0.1, 0.2, 0.3, 0.4) |
| β2 | 0.1996 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.1996 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.1996 | m = (0, 0.1, 0.2, 0.3, 0.4) |
| β3 | 0.1999 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.1999 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.1999 | m = (0, 0.1, 0.2, 0.3, 0.4) |
| β4 | 0.1991 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.1991 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.1991 | m = (0, 0.1, 0.2, 0.3, 0.4) |
| β5 | 0.2008 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.2008 | m = (0, 0.1, 0.2, 0.3, 0.4) | 0.2008 | m = (0, 0.1, 0.2, 0.3, 0.4) |
| βt | 0.0126 | m = (−1000, −500, 0, 500, 1000) | 0.0126 | m = (−500, −250, 0, 250, 500) | 0.0126 | m = (−250, −125, 0, 125, 250) |
| β11 | 0.2159 | m = (−1000, −500, 0, 500, 1000) | 0.2159 | m = (−500, −250, 0, 250, 500) | 0.2158 | m = (−250, −125, 0, 125, 250) |
| β12 | −0.1479 | m = (−1000, −500, 0, 500, 1000) | −0.1478 | m = (−500, −250, 0, 250, 500) | −0.1477 | m = (−250, −125, 0, 125, 250) |
| β13 | −0.0098 | m = (−1000, −500, 0, 500, 1000) | −0.0098 | m = (−500, −250, 0, 250, 500) | −0.0097 | m = (−250, −125, 0, 125, 250) |
| β14 | −0.0272 | m = (−1000, −500, 0, 500, 1000) | −0.0272 | m = (−500, −250, 0, 250, 500) | −0.0271 | m = (−250, −125, 0, 125, 250) |
| β15 | 0.1382 | m = (−1000, −500, 0, 500, 1000) | 0.1382 | m = (−500, −250, 0, 250, 500) | 0.1381 | m = (−250, −125, 0, 125, 250) |
| β1t | 0.0108 | m = (−1000, −500, 0, 500, 1000) | 0.0108 | m = (−500, −250, 0, 250, 500) | 0.0108 | m = (−250, −125, 0, 125, 250) |
| β22 | 0.1058 | m = (−1000, −500, 0, 500, 1000) | 0.1058 | m = (−500, −250, 0, 250, 500) | 0.1058 | m = (−250, −125, 0, 125, 250) |
| β23 | 0.1171 | m = (−1000, −500, 0, 500, 1000) | 0.1171 | m = (−500, −250, 0, 250, 500) | 0.1170 | m = (−250, −125, 0, 125, 250) |
| β24 | −0.0419 | m = (−1000, −500, 0, 500, 1000) | −0.0419 | m = (−500, −250, 0, 250, 500) | −0.0419 | m = (−250, −125, 0, 125, 250) |
| β25 | 0.0661 | m = (−1000, −500, 0, 500, 1000) | 0.0661 | m = (−500, −250, 0, 250, 500) | 0.0660 | m = (−250, −125, 0, 125, 250) |
| β2t | 0.0066 | m = (−1000, −500, 0, 500, 1000) | 0.0066 | m = (−500, −250, 0, 250, 500) | 0.0066 | m = (−250, −125, 0, 125, 250) |
| β33 | 0.0185 | m = (−1000, −500, 0, 500, 1000) | 0.0184 | m = (−500, −250, 0, 250, 500) | 0.0184 | m = (−250, −125, 0, 125, 250) |
| β34 | −0.0539 | m = (−1000, −500, 0, 500, 1000) | −0.0539 | m = (−500, −250, 0, 250, 500) | −0.0539 | m = (−250, −125, 0, 125, 250) |
| β35 | −0.0667 | m = (−1000, −500, 0, 500, 1000) | −0.0667 | m = (−500, −250, 0, 250, 500) | −0.0667 | m = (−250, −125, 0, 125, 250) |
| β3t | −0.0100 | m = (−1000, −500, 0, 500, 1000) | −0.0100 | m = (−500, −250, 0, 250, 500) | −0.0100 | m = (−250, −125, 0, 125, 250) |
| β44 | 0.0228 | m = (−1000, −500, 0, 500, 1000) | 0.0228 | m = (−500, −250, 0, 250, 500) | 0.0229 | m = (−250, −125, 0, 125, 250) |
| β45 | 0.1690 | m = (−1000, −500, 0, 500, 1000) | 0.1689 | m = (−500, −250, 0, 250, 500) | 0.1688 | m = (−250, −125, 0, 125, 250) |
| β4t | −0.0064 | m = (−1000, −500, 0, 500, 1000) | −0.0064 | m = (−500, −250, 0, 250, 500) | −0.0064 | m = (−250, −125, 0, 125, 250) |
| β55 | −0.4092 | m = (−1000, −500, 0, 500, 1000) | −0.4091 | m = (−500, −250, 0, 250, 500) | −0.4087 | m = (−250, −125, 0, 125, 250) |
| β5t | −0.0012 | m = (−1000, −500, 0, 500, 1000) | −0.0012 | m = (−500, −250, 0, 250, 500) | −0.0012 | m = (−250, −125, 0, 125, 250) |
| βtt | −0.0017 | m = (−1000, −500, 0, 500, 1000) | −0.0017 | m = (−500, −250, 0, 250, 500) | −0.0017 | m = (−250, −125, 0, 125, 250) |
| ρ | 0.5001 | m = (0, 0.25, 0.5, 0.75, 1) | 0.5001 | m = (0, 0.25, 0.5, 0.75, 1) | 0.5001 | m = (0, 0.25, 0.5, 0.75, 1) |
| Countries | GME1A | Support1 | Countries | GME1B | Support2 |
|---|---|---|---|---|---|
| Austria | 0.80499 | w = (0. 0.005. 0.010. 0.015. 1) | Austria | 0.86293 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Denmark | 0.80447 | w = (0. 0.005. 0.010. 0.015. 1) | Denmark | 0.86261 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Greece | 0.80180 | w = (0. 0.005. 0.010. 0.015. 1) | Greece | 0.86062 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Germany | 0.80153 | w = (0. 0.005. 0.010. 0.015. 1) | Germany | 0.86052 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Finland | 0.79926 | w = (0. 0.005. 0.010. 0.015. 1) | Finland | 0.85875 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Sweden | 0.79923 | w = (0. 0.005. 0.010. 0.015. 1) | Sweden | 0.85874 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| France | 0.79763 | w = (0. 0.005. 0.010. 0.015. 1) | France | 0.85758 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Italy | 0.79735 | w = (0. 0.005. 0.010. 0.015. 1) | Italy | 0.85736 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Netherlands | 0.79659 | w = (0. 0.005. 0.010. 0.015. 1) | Netherlands | 0.85682 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Belgium | 0.79392 | w = (0. 0.005. 0.010. 0.015. 1) | Belgium | 0.85504 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Ireland | 0.75978 | w = (0. 0.005. 0.010. 0.015. 1) | Ireland | 0.82970 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Portugal | 0.75977 | w = (0. 0.005. 0.010. 0.015. 1) | Portugal | 0.82970 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Spain | 0.75973 | w = (0. 0.005. 0.010. 0.015. 1) | Spain | 0.82968 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| United Kingdom | 0.75968 | w = (0. 0.005. 0.010. 0.015. 1) | United Kingdom | 0.82966 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Slovakia | 0.80520 | w = (0. 0.005. 0.010. 0.015. 1) | Slovakia | 0.86310 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Poland | 0.80483 | w = (0. 0.005. 0.010. 0.015. 1) | Poland | 0.86283 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Hungary | 0.80473 | w = (0. 0.005. 0.010. 0.015. 1) | Hungary | 0.86275 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Czech Republic | 0.80462 | w = (0. 0.005. 0.010. 0.015. 1) | Czech Republic | 0.86268 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Slovenia | 0.80454 | w = (0. 0.005. 0.010. 0.015. 1) | Romania | 0.86265 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Romania | 0.80454 | w = (0. 0.005. 0.010. 0.015. 1) | Slovenia | 0.86261 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Malta | 0.80235 | w = (0. 0.005. 0.010. 0.015. 1) | Malta | 0.86102 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Bulgaria | 0.80212 | w = (0. 0.005. 0.010. 0.015. 1) | Bulgaria | 0.86084 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Lithuania | 0.80070 | w = (0. 0.005. 0.010. 0.015. 1) | Lithuania | 0.85981 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Latvia | 0.80002 | w = (0. 0.005. 0.010. 0.015. 1) | Latvia | 0.85932 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Estonia | 0.79925 | w = (0. 0.005. 0.010. 0.015. 1) | Estonia | 0.85875 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Cyprus | 0.79803 | w = (0. 0.005. 0.010. 0.015. 1) | Cyprus | 0.85785 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Croatia | 0.80490 | w = (0. 0.005. 0.010. 0.015. 1) | Croatia | 0.86287 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| FYROM | 0.80440 | w = (0. 0.005. 0.010. 0.015. 1) | FYROM | 0.86256 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Turkey | 0.79041 | w = (0. 0.005. 0.010. 0.015. 1) | Turkey | 0.85228 | w = (0. 0.005. 0.010. 0.015. 0.67) |
| Standard Deviation | 0.01496 | Standard Deviation | 0.01100 |
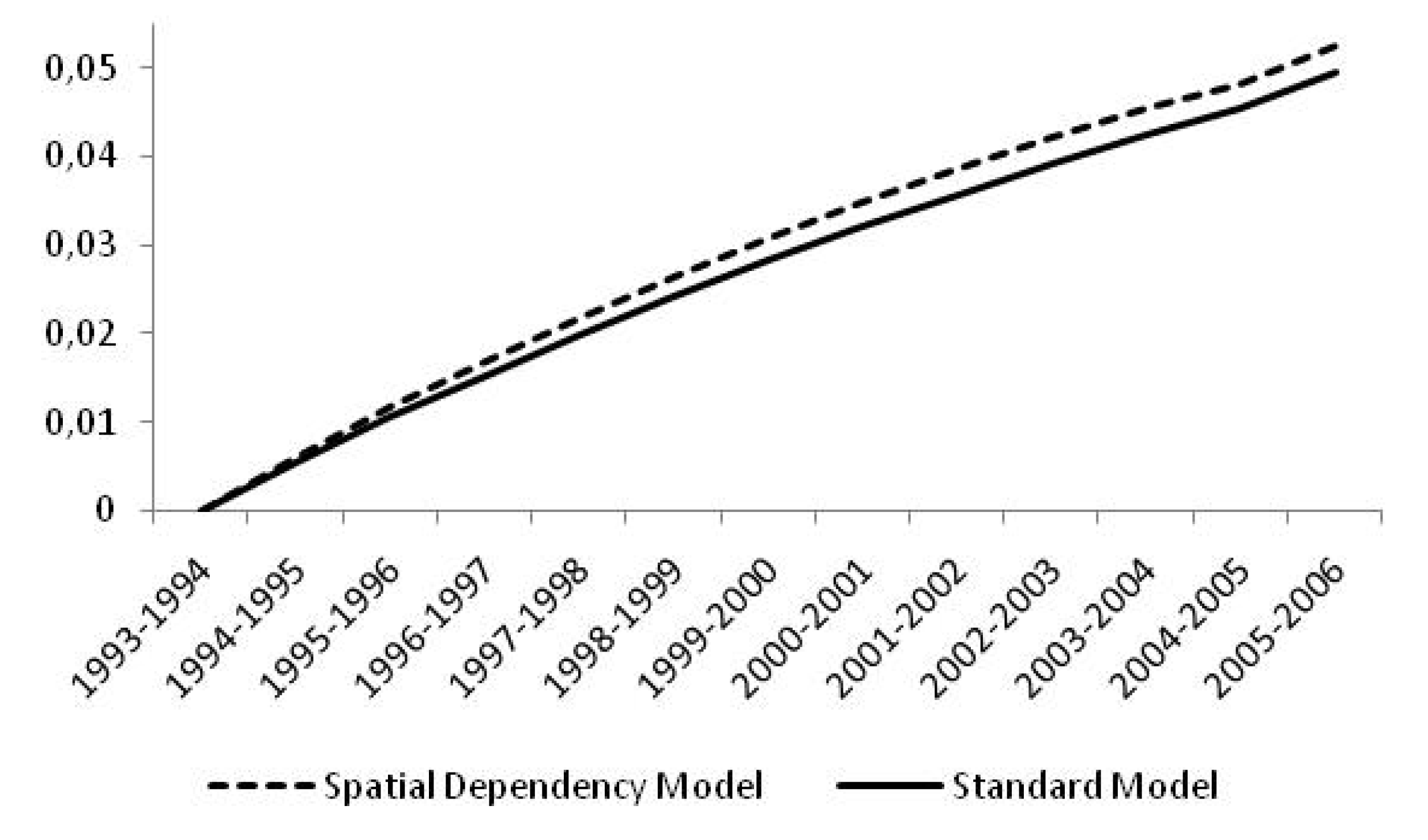
| Countries | Efficiency Change | Technical Change | Scale Change | TFP Change |
|---|---|---|---|---|
| Austria | 0.0150 | 2.1045 | −0.1027 | 2.0168 |
| Denmark | 0.1108 | 1.5095 | 0.1393 | 1.7595 |
| Sweden | −0.0479 | 1.8101 | −0.0362 | 1.7259 |
| Spain | 0.0773 | 1.6065 | 0.0086 | 1.6924 |
| Finland | −0.0097 | 1.6997 | −0.0104 | 1.6796 |
| Ireland | 0.0073 | 1.3844 | 0.0069 | 1.3986 |
| United Kingdom | −0.0991 | 1.5839 | −0.2259 | 1.2589 |
| Belgium | −0.1952 | 1.1707 | 0.1765 | 1.1519 |
| France | 0.0504 | 1.7017 | −0.6795 | 1.0725 |
| Italy | −0.0086 | 1.5461 | −0.4885 | 1.0490 |
| Greece | −0.0597 | 1.1068 | −0.0547 | 0.9365 |
| Germany | 0.1686 | 1.2156 | −0.6197 | 0.7645 |
| Portugal | 0.0338 | 0.7013 | −0.0142 | 0.7209 |
| Netherlands | 0.0604 | 0.3225 | 0.2351 | 0.6180 |
| EU-15 average | 0.0074 | 1.3902 | −0.1190 | 1.2747 |
| Slovenia | 0.0345 | 2.4905 | 0.9645 | 3.4894 |
| Estonia | −0.0128 | 1.7539 | 1.2814 | 3.0225 |
| Malta | 0.0565 | −0.0044 | 2.8695 | 2.9216 |
| Latvia | −0.0486 | 1.7321 | 0.7246 | 2.4081 |
| Cyprus | −0.0103 | 0.4935 | 1.2080 | 1.6912 |
| Lithuania | −0.0458 | 1.5618 | 0.0213 | 1.5373 |
| Bulgaria | −0.0289 | 1.3112 | 0.0368 | 1.3192 |
| Slovakia | −0.0666 | 0.4443 | 0.4215 | 0.7992 |
| Hungary | 0.0465 | 0.8790 | −0.1343 | 0.7912 |
| Romania | 0.1022 | 0.8323 | −0.3632 | 0.5714 |
| Poland | −0.0564 | 0.5874 | 0.0009 | 0.5319 |
| Czech Republic | −0.0620 | 0.5649 | −0.0184 | 0.4846 |
| EU-12 average | −0.0076 | 1.0539 | 0.5844 | 1.6306 |
| Fyrom | 0.1146 | 1.8425 | 0.3255 | 2.2826 |
| Croatia | 0.0089 | −0.3494 | 1.3851 | 1.0446 |
| Turkey | −0.0187 | 0.1320 | 0.3707 | 0.4841 |
| CC average | 0.0349 | 0.5417 | 0.6937 | 1.2704 |
5. Conclusions
References
- Aigner, D.J.; Lovell, C.A.K.; Schmidt, P.J. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; van den Broeck, J. Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Battese, G.E.; Corra, G. Estimation of a production frontier model with application to the pastoral zone of Easter Australia. Aust. J. Agric. Econ. 1977, 21, 167–179. [Google Scholar]
- Coelli, T.J.; Prasada Rao, D.S.; O’Donnell, C.G.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis, 2nd ed.; Kluwer Academic: Boston, MA, USA, 2005; p. 367. [Google Scholar]
- Cuesta, R. A production model with firm specific temporal variation in technical efficiency: With application to Spanish dairy farms. J. Prod. Anal. 2000, 13, 139–158. [Google Scholar] [CrossRef]
- Monchuk, D.C.; Miranovski, J.A. Spatial Labor Market and Technology Spillovers—Analysis from US Midwest, No. 22250. In Proceedings of the 2003 Annual Meeting, Montreal, Canada, 27–30 July 2003.
- Druska, V.; Horrace, W.C. Generalized moment estimation for spatial panel data: Indonesian rice farming. Am. J. Agric. Econ. 2004, 86, 185–198. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models, 1st ed.; Kluver: London, UK, 1988; p. 304. [Google Scholar]
- Golan, A.; Judge, J.; Miller, D. Maximum Entropy Econometrics: Robust Estimation with Limited Data, 1st ed.; John Wiley and Sons: Chichester, UK, 1996; p. 324. [Google Scholar]
- Schmidt, P.; Sickles, R.C. Production frontier and panel data. J. Bus. Econ. Stat. 1984, 2, 299–326. [Google Scholar]
- Macedo, P.; Silva, E. A stochastic production frontier model with a translog specification using the generalized maximum entropy estimator. Econ. Bull. 2010, 1, 587–596. [Google Scholar]
- Greene, W.H. Distinguishing between heterogeneity and inefficiency: Stochastic frontier analysis of the World Health Organization’s panel data on national health care systems. Health Econ. 2004, 13, 959–980. [Google Scholar] [CrossRef] [PubMed]
- Greene, W.H. Fixed and random effects in stochastic frontier models. J. Prod. Anal. 2005, 23, 7–32. [Google Scholar] [CrossRef]
- Terrell, D. Incorporating monotonicity and concavity conditions in flexible functional forms? J. Appl. Econ. 1996, 11, 179–194. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Prod. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Bell, K.P.; Bockstael, N.E. Applying the generalized-moments estimation approach to spatial problems involving micro-level data. Rev. Econ. Statictics 2000, 82, 72–82. [Google Scholar] [CrossRef]
- Caves, D.W.; Christensen, L.R.; Diewert, W.E. The economic theory of index numbers and the measurement of input, output and productivity. Econometrica 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- Orea, L. Parametric decomposition of a generalized Malmquist index. J. Prod. Anal. 2002, 18, 5–22. [Google Scholar] [CrossRef]
- Mittelhammer, R.C.; Judge, G.G.; Douglas, J.M. Econometric Foundations, 1st ed.; Cambridge University Press: Cambridge, UK, 2000; p. 784. [Google Scholar]
- Perloff, J.M.; Karp, L.S.; Golan, A. Estimating Market Power and Strategies, 1st ed.; Cambridge University Press: Cambridge, UK, 2007; p. 352. [Google Scholar]
- Golan, A.; Perloff, J.M.; Shen, E.Z. Estimating a demand system with non-negativity constraints: Mexican meat demand. Rev. Econ. Statistics 2001, 83, 541–550. [Google Scholar] [CrossRef]
- Golan, A. Information theoretic approach for estimating nonlinear dynamic models. Stud. Nonlinear Dyn. E 2003, 7, 1–24. [Google Scholar] [CrossRef]
- Campbell, R.; Rogers, K.; Rezek, J. Efficient frontier estimation: A maximum entropy approach. J. Prod. Anal. 2008, 30, 213–221. [Google Scholar] [CrossRef]
- Pukelsheim, F. The three sigma rule. Am. Stat. 1994, 48, 88–91. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tonini, A.; Pede, V. A Generalized Maximum Entropy Stochastic Frontier Measuring Productivity Accounting for Spatial Dependency. Entropy 2011, 13, 1916-1927. https://doi.org/10.3390/e13111916
Tonini A, Pede V. A Generalized Maximum Entropy Stochastic Frontier Measuring Productivity Accounting for Spatial Dependency. Entropy. 2011; 13(11):1916-1927. https://doi.org/10.3390/e13111916
Chicago/Turabian StyleTonini, Axel, and Valerien Pede. 2011. "A Generalized Maximum Entropy Stochastic Frontier Measuring Productivity Accounting for Spatial Dependency" Entropy 13, no. 11: 1916-1927. https://doi.org/10.3390/e13111916
APA StyleTonini, A., & Pede, V. (2011). A Generalized Maximum Entropy Stochastic Frontier Measuring Productivity Accounting for Spatial Dependency. Entropy, 13(11), 1916-1927. https://doi.org/10.3390/e13111916




