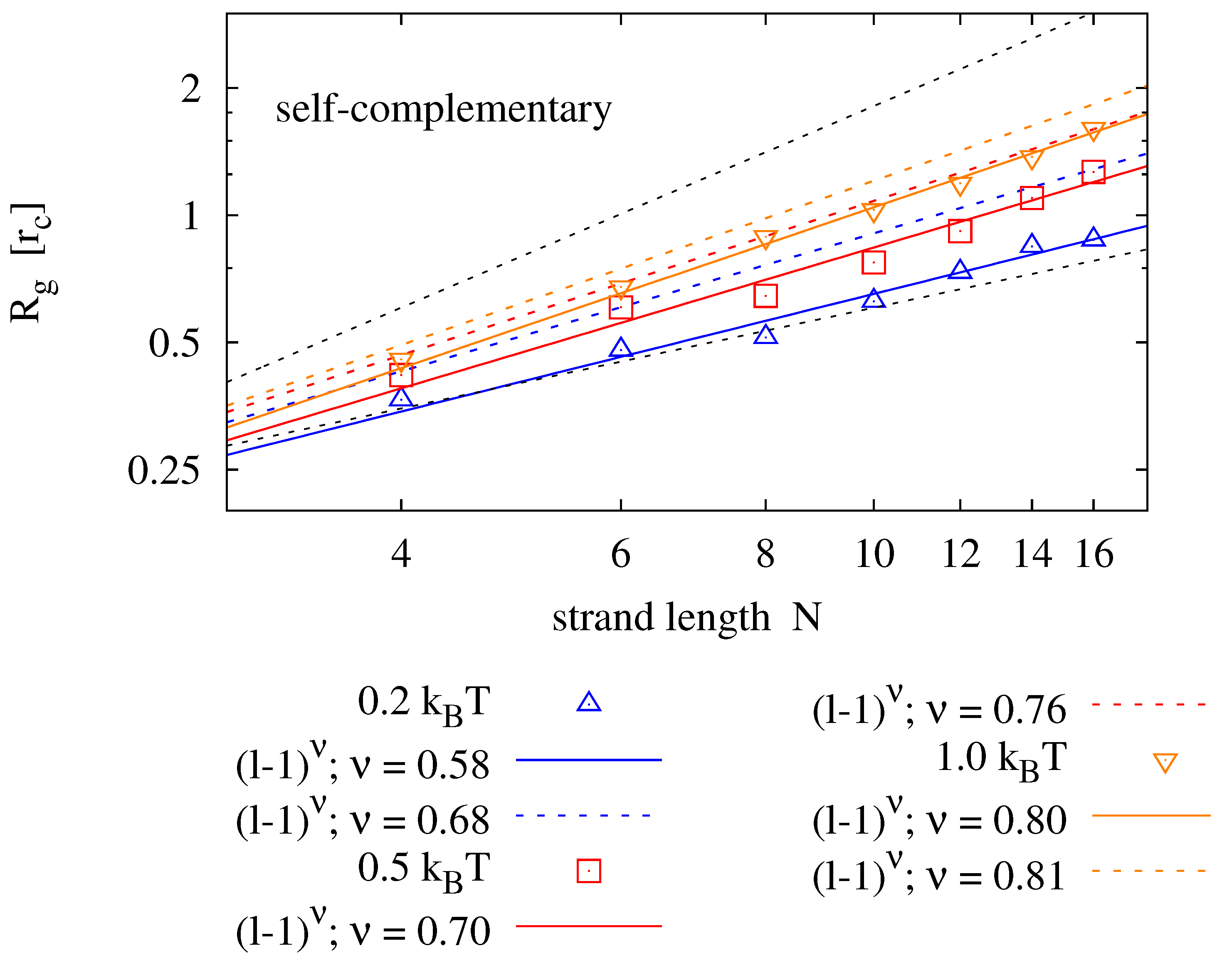1. Introduction
Optimizing the yield of non-enzymatically self-replicating biopolymers is of great interest for many basic science and application areas. Clearly, early organisms could not emerge with a fully developed enzymatic gene replication machinery, so it is plausible that the first organisms had to rely on non-enzymatic replication [
1,
2,
3]. Most bottom-up protocell models also rely on non-enzymatic biopolymer replication [
4,
5,
6,
7,
8,
9], which is also true for a variety of prospective molecular computing and manufacturing applications (for example, see [
10,
11]). Common for all of these research areas is the interest to obtain an optimal replication yield in the absence of modern enzymes. Depending on the details the biopolymer can be deoxyribonucleic acid (DNA), ribonucleic acid (RNA), peptide nucleic acid (PNA),
etc. In the following we’ll refer to them as XNA. In this study we investigate the detailed replication kinetics of well defined and relatively short XNA oligomers of interest to laboratory assembly of protocells as well as molecular computing and manufacturing applications.
Conceptually, XNA replication proceeds in three basic steps: (a) association, or
hybridization, of
n nucleotide monomers or oligomers with a single stranded, complementary template; (b) formation of covalent bonds in a condensation reaction, called
polymerization in case of monomer condensation and
ligation in case of oligomers; and finally (c) dissociation, or
dehybridization, of the newly formed complementary strand:
Here,
X and
denote the template strand and its complement,
O denotes monomers/oligomers,
W is the leaving group of the condensation reaction, and
are the equilibrium constants of the three reactions. Note that the left hand transition of reaction scheme (
1) is an abbreviation of a multi-step process that accounts for all
n individual oligomer hybridizations and dehybridizations, which is only partly captured by the net reaction process.
The covalent condensation reaction is entirely activation limited. For nucleotide monophosphates, the leaving group corresponds to water which (due to its high concentration in aqueous solution) pushes the equilibrium to the hydrolyzed state. Product yields are significantly increased when using activated nucleotides, such as nucleotide triphosphate or imidazole.
Due to its complex reaction mechanism, non-enzymatic XNA replication from monomers suffers from various complications, namely inefficient extension of sequences containing consecutive adenine and thymine nucleotides [
12,
13], as well as side reactions such as partial replication and random strand elongation [
14]. Consequently, experiments with activated nucleotides typically show little yield in aqueous solution, although results can be enhanced by employing surfaces (e.g., clay) or up-concentration in water-ice [
2,
15].
Replication from short activated oligomers, on the other hand, does produce high yields for both RNA and DNA [
16,
17,
18,
19,
20] (and references therein). In particular, this observation has lead to the development of
minimal replicator systems, in which ligation of two oligomers is sufficient to form the complementary replica (see
Figure 1). One of the reasons why these systems outperform replicators that draw from monomers is that the above side reactions expectedly occur, if at all, only to a negligible extent.
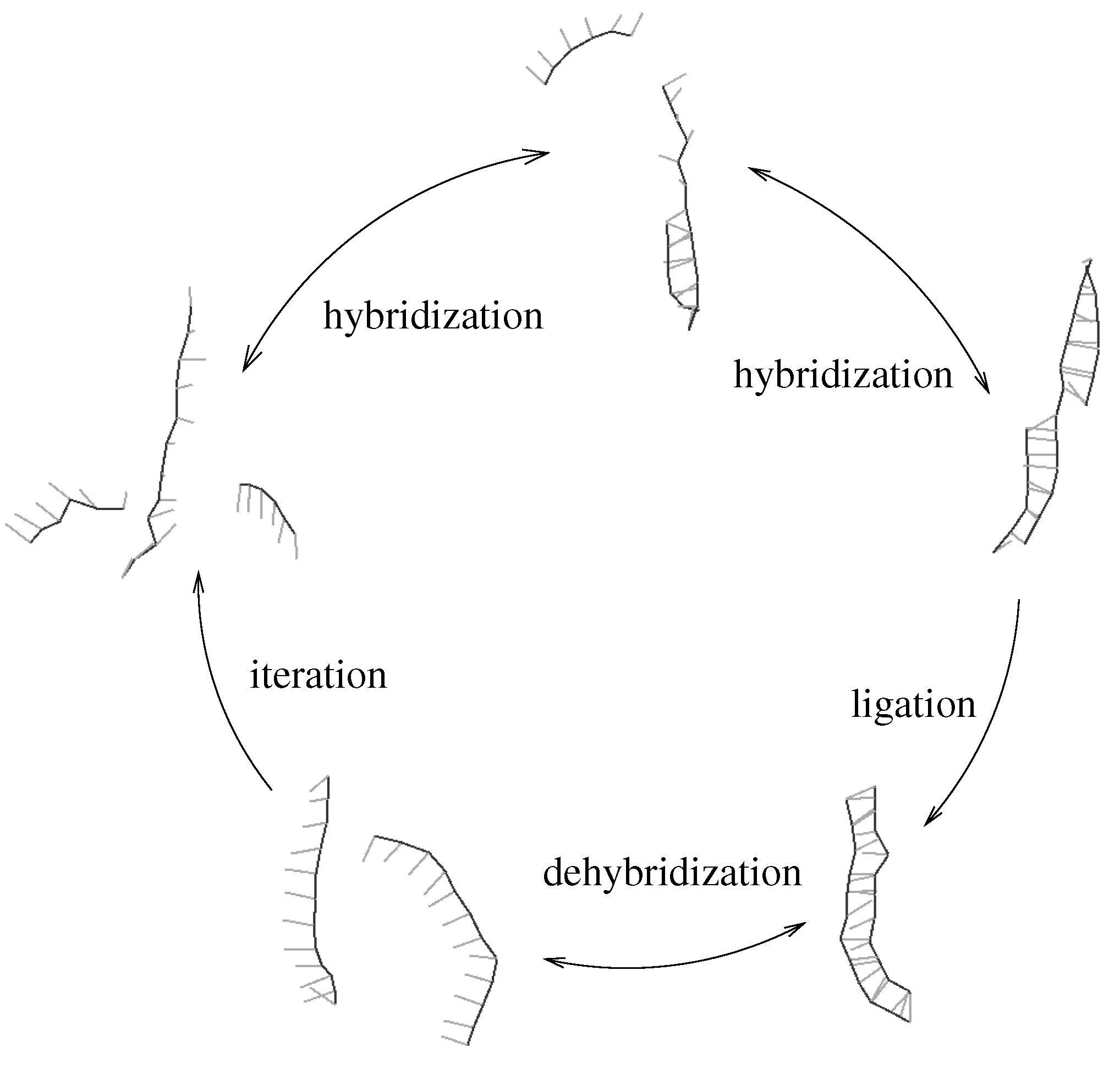
Figure 1.
Minimal template directed replicator: two complementary oligomers hybridize to a template strand (upper part). An irreversible ligation reaction transforms the oligomers into the complementary copy of the template. The newly obtained double strand can dehybridize (lower part) thus allowing for iteration of the process. We assume that ligation is rate limiting, which implies that hybridization and dehybridization are in local equilibrium.
Figure 1.
Minimal template directed replicator: two complementary oligomers hybridize to a template strand (upper part). An irreversible ligation reaction transforms the oligomers into the complementary copy of the template. The newly obtained double strand can dehybridize (lower part) thus allowing for iteration of the process. We assume that ligation is rate limiting, which implies that hybridization and dehybridization are in local equilibrium.
Neglecting both the production of waste as well as the hydrolysis of the ligation product, but explicitly taking into account the individual oligomer associations, minimal replicator systems (here for the case of a self-complementary template) can be written as
where we have introduced the shorthand notation
.
In this article, we first develop a theoretical expression for the template directed replication rate of minimal replicator systems as a function of strand length and temperature. This analytical model provides transparent physical relations for how temperature, strand length and composition impact the overall replication rate. We then present a 3D, implicit solvent, constrained Brownian Dynamics model for short nucleotide strands, i.e., strands with negligible secondary structures. The model does not attempt to be (quantitatively) predictive. In particular, we do not attempt to calibrate interaction parameters to experimental data, which prevents any sequence prediction. On the contrary, it is our aim to demonstrate that many of the replication properties of oligonucleotides arise from rather general statistical physics. The simulation is used to measure diffusion coefficients, effective reaction radii, and hybridization rates and their dependence on temperature, strand length, and, to some extent, sequence information. This allows us to qualitatively obtain equilibrium constants and and to qualitatively sketch the effective replication rate k as a function of strand length and temperature. Our analysis focuses on minimal replicator systems in the context of chemical replication experiments as employed in protocell research and manufacturing applications, where the researcher controls reactant concentrations as well as most experimental parameters. However, we also discuss the impact of our findings in the context of origin of life research, were possible side reactions cannot be neglected.
2. Parabolic Growth and Replication Rate
Following and extending the derivation of [
21,
22], we assume that ligation is the rate limiting step. This translates into the following conditions for the rate constants:
One can then assume a steady state of the hybridization/dehybridization reactions and express the total template concentration
in terms of equilibrium constants as
When solved for
, this gives
Template directed replication typically suffers from product inhibition, where most templates are in double strand configuration, i.e., . Over the course of the reaction, this is tantamount of saying that . This allows us to approximate
and simplify (
6) to
This is a lower bound of the single strand concentration, which is approached in the limit of vanishing oligomer concentration. By combining (
3) and (
7), we get
with
This well-established parabolic growth law is known to qualitatively alter evolutionary dynamics of XNA based minimal replicators and to promote coexistence of replicators rather than selection of the fittest [
23,
24,
25].
Consequently, several strategies have been designed to overcome product inhibition in order to reestablish Darwinian evolution and survival of
only the fittest [
20,
22,
26,
27]. Most of these approaches hinge on a mechanism to lower the hybridization tendency of the product to the template. In this article, however, we accept parabolic growth and instead focus on the effective growth rate.
The key observation of Equation (
9) is that, due to the steady state assumption, the overall growth rate is independent of the individual association and dissociation rates
, but only depends on the equilibrium constants
and
. Expressed in free energy changes, Equation (
9) becomes
where
A and
are the pre-exponential factor and activation energy of the ligation reaction, respectively, and we have used the Arrhenius equation
We further observe that any potential optimum of (
9) must obey
where the prime indicates derivation with respect to any variable. Note that derivatives of
, and
can be taken with respect to parameters such as temperature and template length, whereas the notion of a derivative in sequence space is ill-defined. Therefore, Equation (
12) can only give us partial information about an optimal growth rate.
It is well-known that the equilibrium constants
and
depend on various parameters such as temperature, salt concentration, strand length, and sequence information—all being relevant control parameters when designing replication experiments or delimiting origin of life conditions [
28,
29]. Furthermore, the two rates are interdependent as one expects
to rise with increasing
.
Qualitatively, the free energy of XNA hybridization obeys a form given by
where
N signifies the strand length,
is the (maximal) energy change per base,
is the initiation energy and
are negative, whereas
are positive. The right hand side of the equation expresses a saturation in the free energy per base as a function of the strand length; the free energy gain for each base pairing asymptotically becomes constant for long strands [
30]. Inserting (
13) into (
10) and separating out the rate constant for the ligation reaction
, we obtain:
which, when differentiated for
T, yields a positive dependence on temperature, iff
Since , and , this critical strand length is truly positive. It might surprise that can increase with decreasing temperature—the regime where templates are primarily inhibited by the product. The results become understandable when considering that oligomers, with their lower hybridization rate, barely associate with the template if the temperature is raised.
Reintroducing the ligation reaction, this relation gets refined to
with the critical strand length
In words: we can identify a critical strand length
above which the overall replication rate
k increases with decreasing temperature. This critical strand length is determined by the hybridization enthalpies
, and activation enthalpy change
of ligation.
Figure 2 depicts the graph of the replication rate landscape (
15) that clearly identifies the optimum of Equation (
12) as a saddle point. The corresponding temperature
where
k changes its scaling with respect to strand length is—independent of the ligation reaction—given by
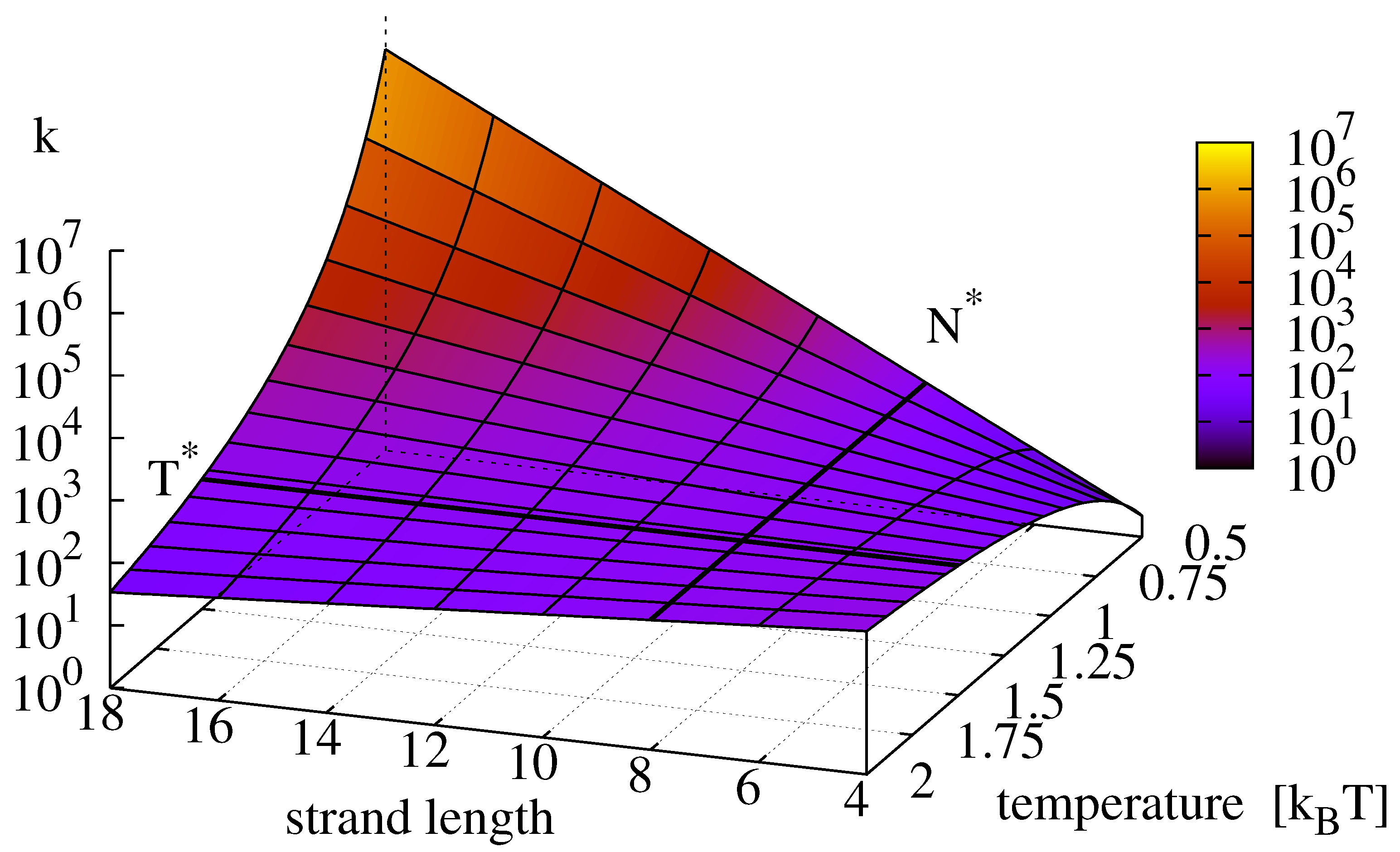
Figure 2.
Effective replication rate
k (given by Equation
15) as a function of strand length and temperature. For strands below a critical length
(here 10) the rate increases with temperature, for strands longer than
, the replication rate grows with decreasing temperature. The value of
is determined through Equation (
16). Note the saddle point of the surface where
and
intersect (Equation (
12) (
,
,
,
,
,
).
Figure 2.
Effective replication rate
k (given by Equation
15) as a function of strand length and temperature. For strands below a critical length
(here 10) the rate increases with temperature, for strands longer than
, the replication rate grows with decreasing temperature. The value of
is determined through Equation (
16). Note the saddle point of the surface where
and
intersect (Equation (
12) (
,
,
,
,
,
).
Can we obtain a higher replication rate by using non-symmetric oligomers? The rational behind this strategy is to increase the binding affinity of one oligomer to maybe decrease product inhibition. A simple refinement of Equation (
14) allows us to capture this approach with our model:
where
denote the lengths of oligomer strands
and
. Thus, according to our simple thermodynamic considerations, non-symmetric variants of the replication process do not show more yield than the corresponding symmetric system: the binding affinity gained for the long oligomer strand is paid to hybridize the short oligomer strand.
Figure 2 seemingly implies that replication rates grow beyond any limit for long templates, which is unphysical. To resolve this inconsistency, it is important to remember that our findings are only valid in the regime where ligation is rate limiting. For very long XNA strands, however, double strands are so stable that dehybridization of the ligation product is expected to become the rate limiting step. Independent of the exact shape of the growth law, the dominant factor of the effective growth rate is given by
where
summarizes both pathways of either product rehybridization or hybridization of oligomers followed by ligation. As
is composed of hybridization (
i.e., diffusion plus orientational alignment) and ligation events, it varies only slightly with sequence length when compared to dehybridization rates for the case of large
N. Therefore, the effective replication rate will be governed by the scaling
with the limit
since
. As a consequence, we expect a full non-equilibrium study of the replication process to show a proper maximum in the replication rate as a function of strand length.
3. Spatially Resolved Replicator Model
Spatially resolved template-directed replicators have been previously simulated in the Artificial Life community using two-dimensional cellular automata and continuous virtual physics [
14,
31,
32]. The model we present here is conceptually similar to, but simpler than other coarse-grained DNA models, e.g., [
33,
34,
35]. Compared to our earlier work on hybridization and ligation [
36], the model presented here is less computationally expensive while simultaneously being broader in its range of application.
We model nucleic acid strands as chains of hard spheres that are connected by rigid bonds. Each sphere has mass
m, radius
r, position and velocity
, as well as moment of inertia
θ, orientation and angular momentum
representing the spatial orientation of the respective nucleotide. Further, each sphere has a type
, and we define A and B (C and D) to be complementary. The model is implicit in the sense that solvent molecules are not represented explicitly, but only through their effect on the nucleotide strands. We model the (translational and rotational) motion of each sphere by a
Langevin equation Here,
γ is the friction coefficient, and
are zero mean random variables accounting for thermal fluctuations. Together, friction and thermal noise act as a thermostat: they equilibrate the kinetic energy with an external heat bath whose temperature is given by the following
fluctuation-dissipation-theorem [
37]:
Hence, a temperature change directly translates into a change of the Brownian noise amplitude. We use the moment of inertia for solid spheres
—noting that one could, in principle, use moment of inertia tensors to reflect the geometry of the individual nucleobases.
Equations (
21)–(
24) are solved under the constraints
to account for rigid bonds (
27) and hard spheres (
28). By setting
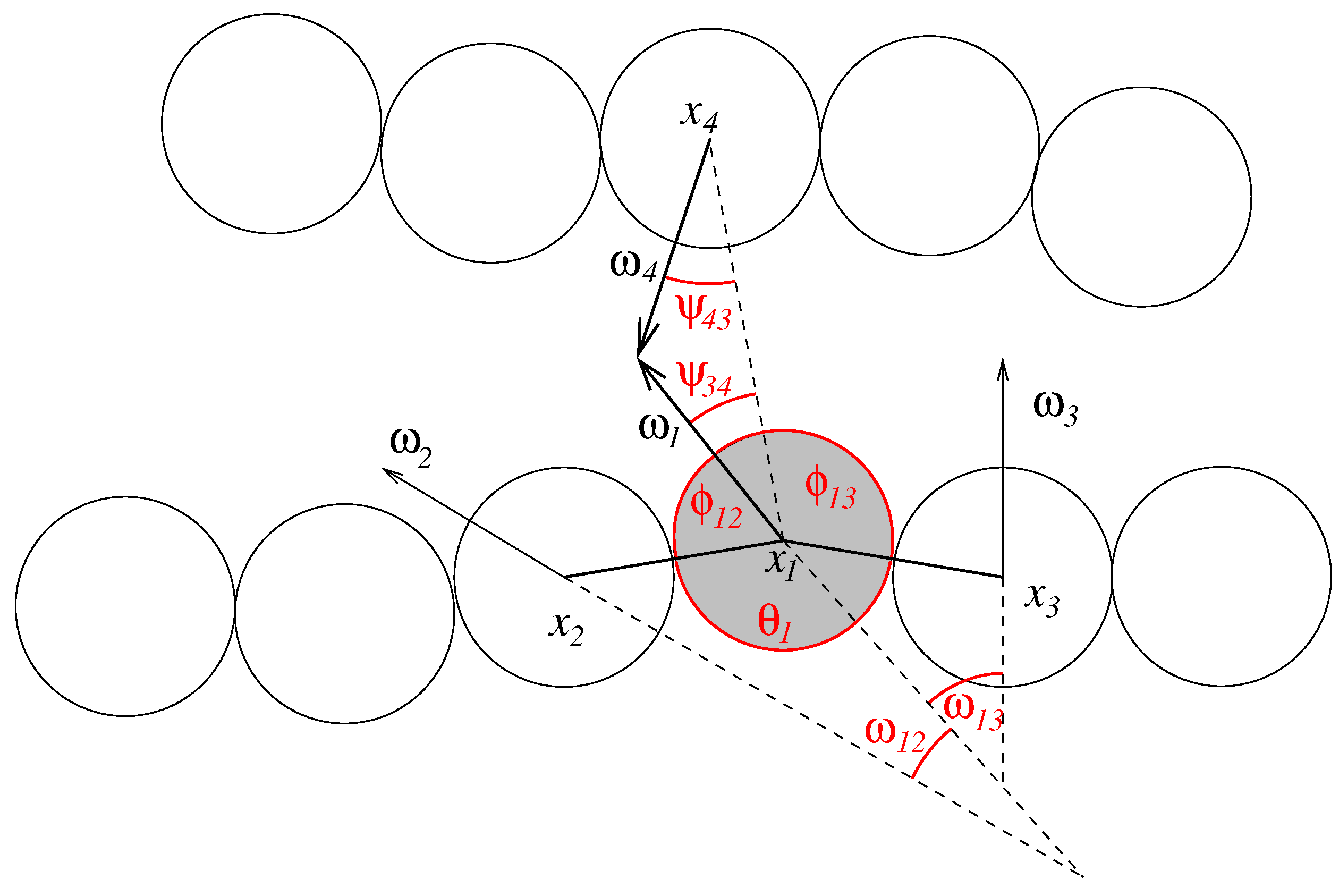
, we can assert that strands do not penetrate each other. We define the following angles (see
Figure 3):
As much of the molecular geometry is already determined through the constraints, the innermolecular potentials
U and
only need to account for strand stiffness (
30), base orientation (
31), and
π-stacking (
32). We set:
The minimum energy state of these definitions are stretched out nucleotide strands with orientations perpendicular to the strand and parallel to each other.
Figure 3.
Geometry of the nucleotide strands. The figure shows the angles that define inner- and intermolecular interactions for one nucleobase (shaded in grey).
Figure 3.
Geometry of the nucleotide strands. The figure shows the angles that define inner- and intermolecular interactions for one nucleobase (shaded in grey).
In addition, we define the following intermolecular potentials between non-bonded complementary nucleobases
i and
j:
The shift and weighing function
asserts that the potentials take on a minimum at particle contact and level out to zero at the force cutoff radius
. Equation (
33) allows for a nucleobase
i to attract its complement
j along the direction of
, while (
34) orients
toward the complement.
Taking the above potentials together, we define
Equations (
21) to (
29) are numerically integrated using a Velocity Verlet algorithm that, in each iteration, first computes unconstrained coordinates which are afterwards corrected with a
Shake algorithm to satisfy the constraints [
38,
39]. Typical system configurations are shown in
Figure 1.
4. Simulation Results
In the subsequent analyses, we will employ reduced units,
i.e.,
,
, and
define the units of mass, length, and energy. From this, the natural unit of time follows as
The parameters
r and
are chosen to prevent crossing of strands (
). The ratio
determines the double strand geometry which is modeled more sparse than in actual nucleic acid strands in order to compensate for the relatively shallow potentials of the coarse-grained model. The ratio
determines the distance at which complementary bases “feel each other” and has been set to two times the bead diameter.
Assuming a reference temperature
, we set
to loosely match the persistence length of about
for single stranded DNA [
29,
40]:
The parameters
,
of the potential functions are chosen in order to promote stacking of single strands for temperatures up to at least
[
29]. The parameter
is on the order of magnitude of base pair interactions averaged from the interaction parameters in nearest-neighbor models [
41]:
We point out that our model utilizes a high value
in order to promote fast hybridization. A list of all model parameters (unless otherwise noted) is given in
Table 1.
Table 1.
Model parameters in reduced units (unless otherwise noted).
Table 1.
Model parameters in reduced units (unless otherwise noted).
| Parameter | Value | Comment | Equations |
|---|
| m | 1 | particle mass | (22)–(24) |
| γ | 3 | friction coefficient | (22), (24) |
| 1 | equilibrium temperature | (25), (26) |
| | numerical time step | |
| r | | particle radius | (28) |
| | bond length | (27) |
| 1 | force cutoff radius | (33)–(34) |
| 5 | strand stiffness | (30) |
| | angular stretching | (31) |
| 1 | angular alignment | (32) |
| 10 | angular hybridization | (34) |
| 1 | complementary attraction | (33) |
Note that it is not mandatory to relate one bead of the model to one physical nucleotide. Instead, each bead could also represent a short XNA subsequence (e.g., 2–4 nucleotides). While this would result in a closer match of the ratio , the amplitudes of the potential functions would need to be adapted to reflect the changed representation.
4.1. Diffusion
In dilute solution, DNA diffusion depends primarily on temperature and strand length, as opposed to primary or secondary structure. In the limit of low Reynolds numbers, the diffusion coefficient of a sphere is given by the
Einstein-Stokes equation where
η is the viscosity of the medium and
r the radius of the sphere. For the Rouse chains implemented by our model, theory predicts a linear scaling of the effective Stokes radius with polymer length [
42].
In order to compare our model polymer diffusion to (
37), we perform simulations of single homopolymers (e.g., poly-C) and determine the diffusion coefficient from its measured mean square displacement
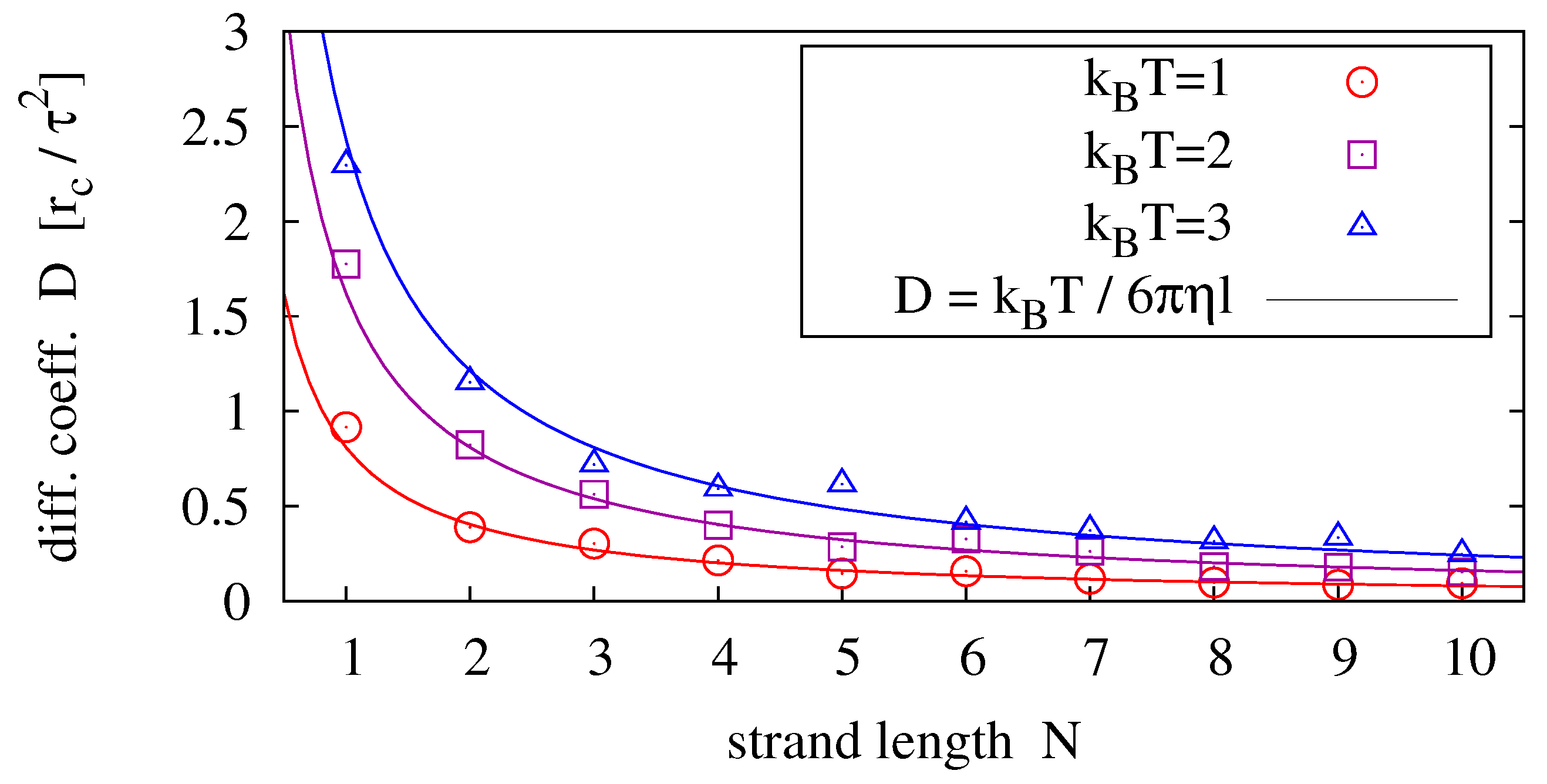
Figure 4 shows results for strands of lengths
and temperatures
.
Figure 4.
Diffusion coefficients measured for different strand lengths and temperatures (symbols) fitted to the prediction of the Einstein-Stokes relation (solid lines). For each parameter pair, 40 simulation runs over have been averaged.
Figure 4.
Diffusion coefficients measured for different strand lengths and temperatures (symbols) fitted to the prediction of the Einstein-Stokes relation (solid lines). For each parameter pair, 40 simulation runs over have been averaged.
For the general scaling relation
we obtain the most likely exponent from data fitting via
ν and
η as
. By setting
, and equivalently
, we obtain the best agreement between measurement and theory (by fitting via
η only) for
(see solid lines in
Figure 4).
4.2. Radius of Gyration
Again in dilute solution, the radius of gyration
with
being the center of gravity of the chain, is expected to depend on chain length and temperature (or equally the backbone stiffness
). As opposed to diffusion, we do expect the radius of gyration to change with sequence information, as it affects the secondary structure of the molecule. For homopolymers, we expect
to be well described by the Flory mean field model [
42]
We perform simulations of single homopolymers and self-complementary nucleotide strands and determine the radius of gyration.
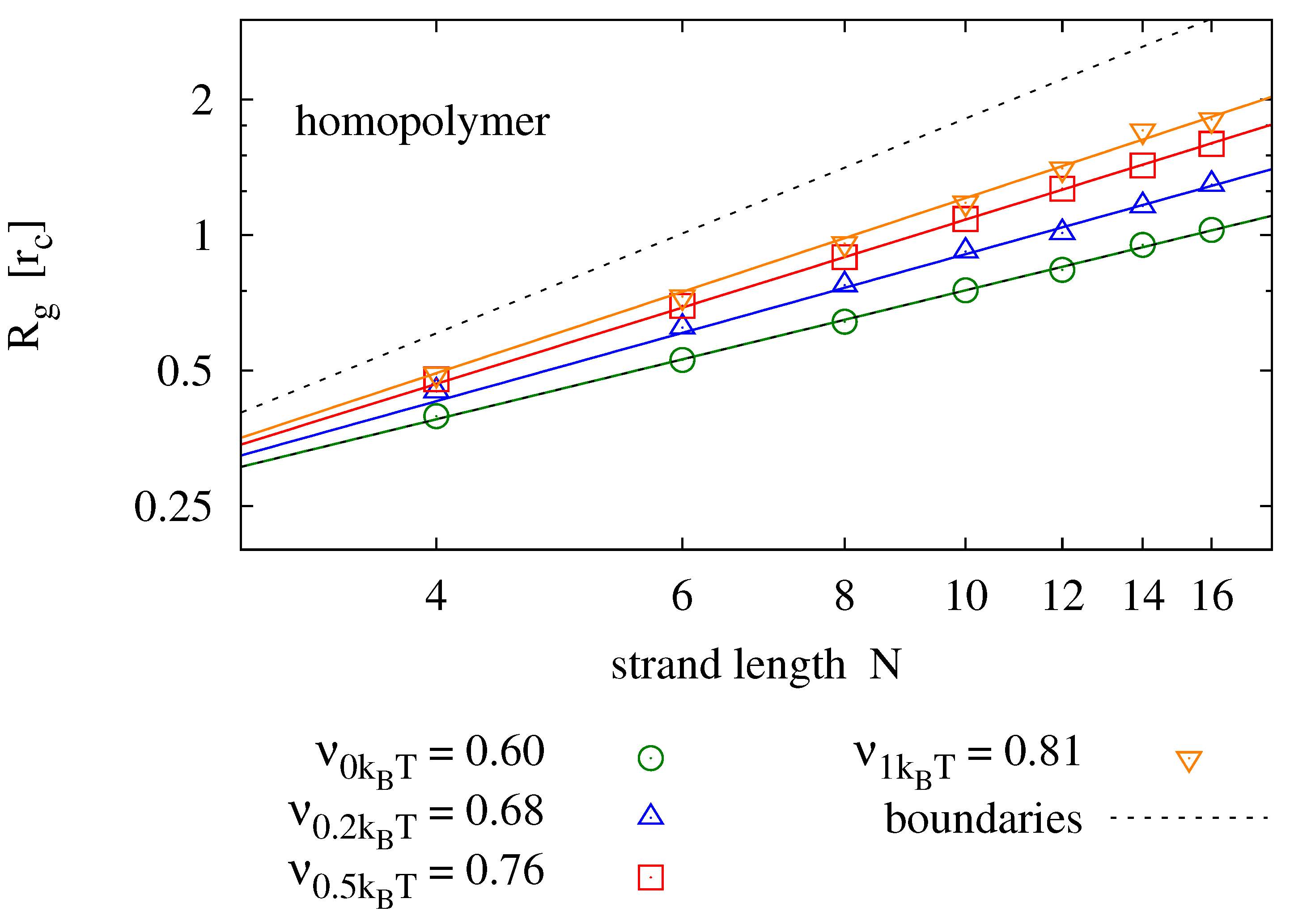
Figure 5 shows results for strands of lengths
and various backbone stiffness values. It is found that the Flory model is a good prediction, not only for homopolymers, but also for self-complementary strands. Expectedly, the radius of gyration is smaller for self-complementary strands. For
, we find the radius of gyration of self-complementary strands to be slightly longer than the radius of gyration of a homopolymer with half the length—implying that the self-complementary strand is almost always in a hairpin configuration. For stronger backbone stiffness values, the effect is reduced.
Figure 5.
Radius of gyration measured for different strand lengths and bending potentials (symbols) fitted to the prediction of the Flory mean field theory (solid lines). For each parameter pair, 40 simulation runs over have been averaged. The upper panel shows results for homopolymers (e.g., poly-C), the lower panel compares those to radii of self-complementary strands. The plots also show the boundaries for maximally stretched chains (—upper dotted line) and the expectation value of an ideal chain (—lower dotted line).
Figure 5.
Radius of gyration measured for different strand lengths and bending potentials (symbols) fitted to the prediction of the Flory mean field theory (solid lines). For each parameter pair, 40 simulation runs over have been averaged. The upper panel shows results for homopolymers (e.g., poly-C), the lower panel compares those to radii of self-complementary strands. The plots also show the boundaries for maximally stretched chains (—upper dotted line) and the expectation value of an ideal chain (—lower dotted line).
4.3. Melting Behavior
We analyze the melting behaviour
of complementary nucleotide strands as a function of temperature for various strand lengths and sequences. We consider a base to be hybridized if there is a complementary base of another strand within a maximal distance of
. Denoting the fraction of hybridized nucleobases with
, we can compare the melting curves to the theoretical prediction
where
are constants depending on template length, sequence, and concentration.
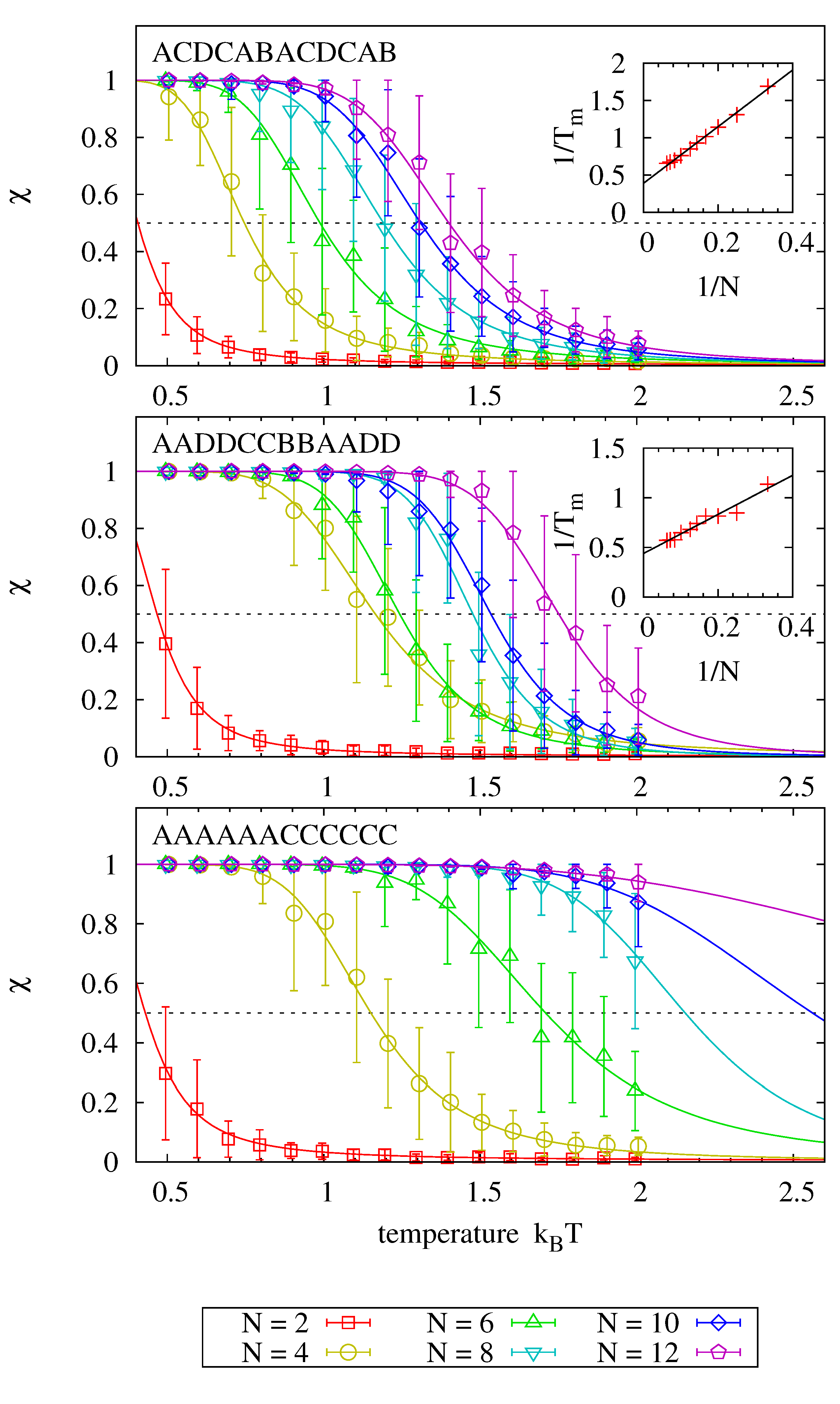
Figure 6 shows melting curves for 18 different sequences and fits (via
) to the theoretical prediction, where each panel analyzes sequences that are subsequences of a common master sequence denoted in each panel. The graphs clearly show how the average hybridization increases with strand length for each master sequence. Inlays, where present, emphasize that the inverse of the melting point, at which
, scales linearly with the inverse of the strand length.
Comparing the individual panels to each other, we find that melting temperatures for strands of equal length are higher for sequences with identical adjacent bases. In fact, the melting behavior is dominated by the presence of identical adjacent bases: adding a single nucleobase to a strand that consists otherwise only of identical pairs (i.e., moving from length 4 to 6 and from length 8 to 10 in panel two) has no significant impact on the observed melting temperature. We assume that this behavior is due to the fact that dehybridized nucleotides of a partly molten strand find more potential binding partners to enforce the stability of the partly molten strand, thereby promoting recombination of products.
Figure 6.
Systems of size are initialized with two complementary strands of length N. The sequence information is taken from the N central nucleotides of the master sequence denoted in each panel (e.g., implies sequence CABACD in the first panel). Each system is simulated over , and the average fraction χ of hybridized nucleobases is determined. Error bars show the average and standard deviation of 40 measurements. Solid lines show the theoretical prediction fitted individually to each data set via and . Melting temperatures are obtained from the relation , and their scaling as a function of strand length is depicted in the inlays for the cases where enough melting points had been observed.
Figure 6.
Systems of size are initialized with two complementary strands of length N. The sequence information is taken from the N central nucleotides of the master sequence denoted in each panel (e.g., implies sequence CABACD in the first panel). Each system is simulated over , and the average fraction χ of hybridized nucleobases is determined. Error bars show the average and standard deviation of 40 measurements. Solid lines show the theoretical prediction fitted individually to each data set via and . Melting temperatures are obtained from the relation , and their scaling as a function of strand length is depicted in the inlays for the cases where enough melting points had been observed.
Experimentally obtained nearest neighbor interactions show indeed that there is a 40%–70% increase in the hybridization energy for AA and TT bases as compared to AT and TA pairs. However, adjacent CC/GG bases lower the melting energy by 15%–20% when compared to CG/GC pairs [
41]. We suspect that this difference is rooted in a difference in stacking energies which is not sufficiently resolved in our parametrization model.
Up to now, we have analyzed hybridization of two complementary strands of equal length. How is the stability of the hybridization complex affected if one of the strands is replaced by two oligomers of half the length? We analyze the master sequence CBACBADDDDDD. Its left half is similar to the first sequence of
Figure 6 with respect to non-identical neighboring bases. The right half has been chosen for its strong hybridization tendency. We run experiments as before and measure the hybridization of the left oligomer. By comparing its equilibrium rate to the one for two templates of half the length, we can determine how the dangling right hand side affects the equilibrium rate (e.g., we compare the hybridization of a 4-mer to an 8-mer template to the hybridization of two 4-mers.)
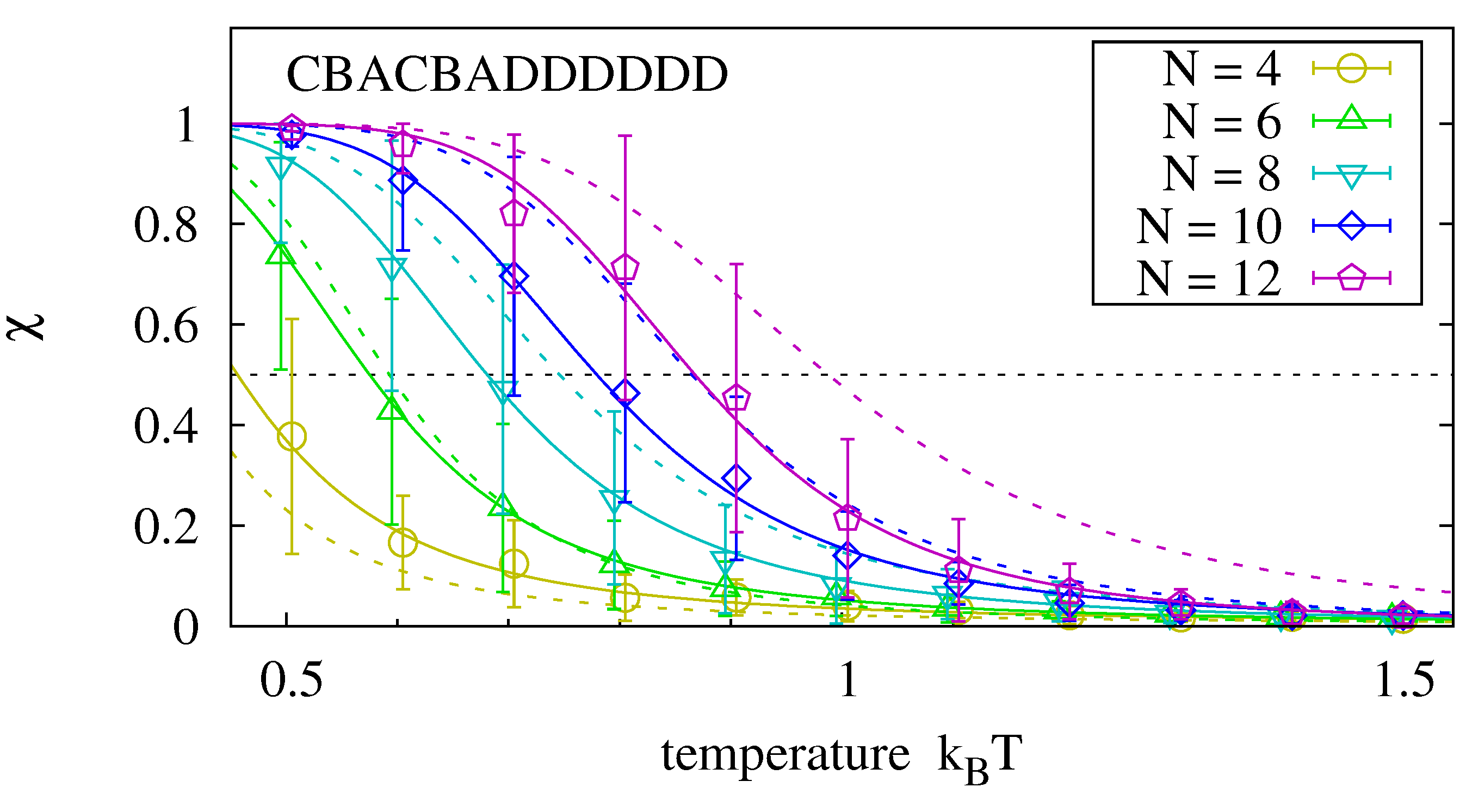
Figure 7 shows that the hybridization fractions
and
are comparable for the analyzed sequence. We expect, however, that
decreases when the two oligomers have more interaction possibilities than in the selected master sequence.
Figure 7.
Melting curves for an oligomer that hybridizes to the left hand side of the master sequence in the presence of the right hand side oligomer. Data is obtained with the procedure described in
Figure 6. For the analyzed master sequence, the results are comparable to those of two complementary strands of length
(dotted lines).
Figure 7.
Melting curves for an oligomer that hybridizes to the left hand side of the master sequence in the presence of the right hand side oligomer. Data is obtained with the procedure described in
Figure 6. For the analyzed master sequence, the results are comparable to those of two complementary strands of length
(dotted lines).
4.4. Effective Replication Rate
We can roughly equate
and obtain an estimate for the equilibrium constant
from the measurements. This equation has to be taken with some caution because the measured hybridization times reflect a non-trivial relation between diffusing reactants and rehybridization of partly molten complexes—both scaling differently with concentration. To truly obtain
K, one is advised to repeat the simulations with varying concentrations,
i.e., box size. By means of Equation (
39), we convert the melting data from
Section 4.3 to obtain hybridization energy changes
In the latter equation,
denotes the translational entropy for a box of size
, while
accounts for the configurational entropy of a single strand. We combine both entropy terms,
, and fit
which allows for better comparison to the melting temperature plots, as
.
Determining hybridization energies is difficult because hybridization is very stable at low temperatures, particularly for long XNA strands. Dehybridization then becomes a rare event, which requires unfeasibly long simulation runs in order to sample equilibrium distributions. Consequently, data for low temperatures and long strands is overshadowed by noise and we have excluded such data from the analysis. For the regime that is accessible to simulation,
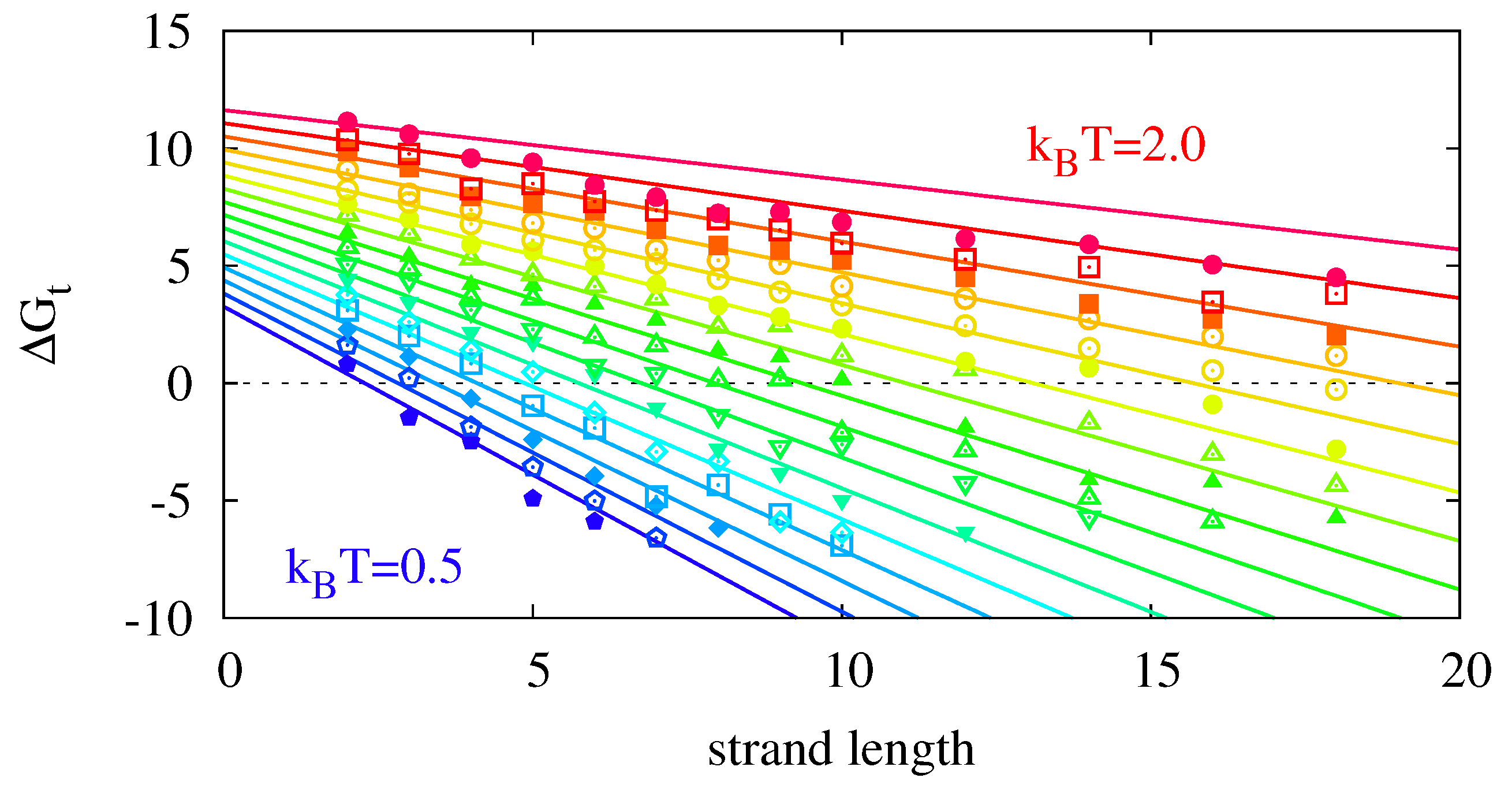
Figure 8 shows the measured hybridization energies fitted to the theoretical model of Equation (
13)—see figure caption for details. The data follows the linear trend of the model and can recover the proper temperature scaling. However, we also observe deviations from the analytical prediction for
. The plot confirms that hybridization energy changes are close to zero at the melting temperature of each double strand. For the simulation, where
, we obtain
, which confirms that
is primarily entropic.
Figure 8.
Hybridization energy changes
obtained from the measurements of
Section 4.3, sequence ACDCABACDCABACDCABAC (symbols), fitted to the analytical model of Equation (
13) via the parameters
,
,
, and
. Since
, we can estimate
.
Figure 8.
Hybridization energy changes
obtained from the measurements of
Section 4.3, sequence ACDCABACDCABACDCABAC (symbols), fitted to the analytical model of Equation (
13) via the parameters
,
,
, and
. Since
, we can estimate
.
Unfortunately, the removal of noisy simulation results implies that we do not have measurements for the regime where the analytical model predicts the most features. To nevertheless obtain estimates for these points, we perform the same simulations as before but start with a perfectly hybridized complex. For short strands, the difference in initial conditions is negligible, as hybridization and dehybridization equilibrate within the simulated time span. For long strands / strands at low temperatures, the sampled χ values progressively overestimate the equilibrium time fraction of hybridization.
The rational behind these dehybridization measurements is the following: for long strands and low temperatures dehybridization of the ligation product becomes the rate limiting step and we are in the regime of Equation (
20). Here, the effective replication rate is primarily governed by the rate of product dehybridization which in turn gives us an upper bound for the replication rate. By combining the results of the two scenarios, we implicitly relate the simulated time span with an assumed ligation rate.
Plugging the measured constants
and
into Equation (
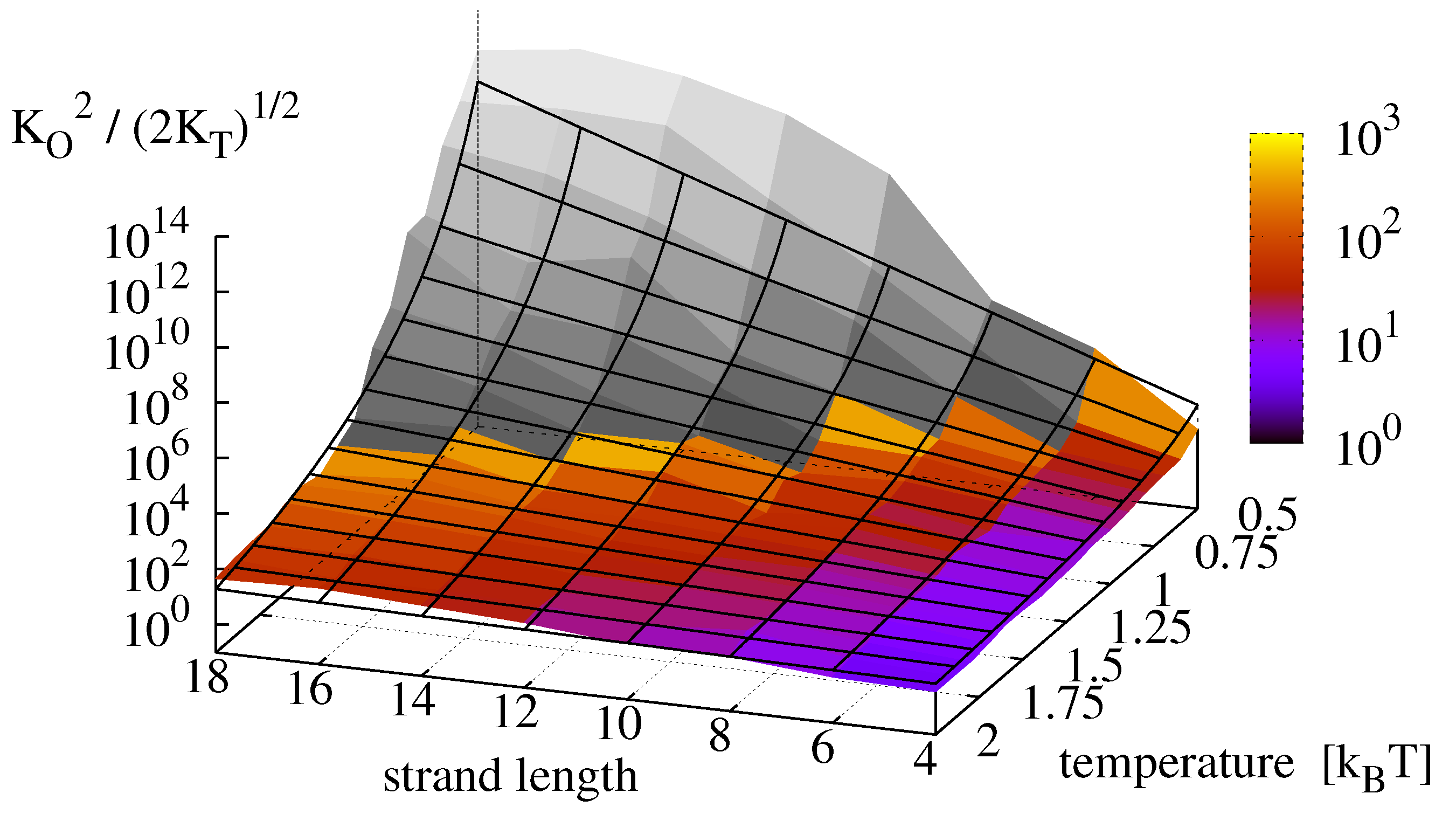
9), we obtain a replication rate landscape for minimal replicators which is depicted in
Figure 9. The colored surface shows the effective equilibrium constant
, obtained from the original measurements. The grey surface shows the results from the dehybridization experiments. Finally, the replication rate landscape obtained via Equation (
13) is shown as a mesh. For the analyzed master sequence and range of observation, the effective oligomer complex concentration
varies over 13 orders of magnitude with highest rates for long strands (
) and low temperatures (
).
Figure 9.
Effective equilibrium constant
, obtained from the measurements of
Figure 8 (colored) compared to the theoretical prediction of Equation (
13) (mesh). Data shaded in gray is extrapolated from dehybridization experiments.
Figure 9.
Effective equilibrium constant
, obtained from the measurements of
Figure 8 (colored) compared to the theoretical prediction of Equation (
13) (mesh). Data shaded in gray is extrapolated from dehybridization experiments.
Contrary to the analytical derivations, the numerical results of the dehybridization experiments indicate a saturation and possibly a decrease of the replication rate for long strands at low temperatures, thereby supporting our hypothesis that the effective rate indeed possesses an optimum when dehybridization and ligation occur on comparable time scales.
The numerical simulations do not incorporate the ligation reaction. To include its temperature dependence, we superpose the Arrhenius Equation (
11) with parameters as in
Figure 2 onto
Figure 9 and obtain the replication rate landscape shown in
Figure 10. The resulting figure features a critical strand length
at which the temperature scaling inverts. With the parameters obtained from the data fits, the critical temperature
lies outside the analyzed area.
Figure 10.
Final replication rate
k as a function of template length and temperature. The figure is produced by superposing the data from
Figure 9 with the Arrhenius equation for the ligation reaction following Equation (
15) with
. For this parametrization, the critical strand length
above which the temperature dependence of the reaction inverts is 8.
Figure 10.
Final replication rate
k as a function of template length and temperature. The figure is produced by superposing the data from
Figure 9 with the Arrhenius equation for the ligation reaction following Equation (
15) with
. For this parametrization, the critical strand length
above which the temperature dependence of the reaction inverts is 8.
5. Discussion
The common strategy to increase the yield in template directed replication experiments is to increase the concentration of oligomers. This is certainly viable, and the fact that the growth rate
k is proportional to the square of the oligomer concentration encourages this approach. Our investigation, however, indicates that oligomer concentration can be outweighed drastically by factors such as temperature, template length, as well as sequence information, which all influence the replication rate at least exponentially and thus over many orders of magnitude. These findings are consistent for the simple analytical expressions (
Figure 2), for the simulations (
Figure 8) as well as for the combined analysis (
Figure 9 and
Figure 10).
Perhaps contrary to intuition, we find the highest growth rates for long replicators and low temperatures. This finding can be explained by the fact that the effective growth rate of minimal replicators features a critical strand length
at which the temperature dependence of the overall replication reaction inverts: below
the replication rate is dominated by the ligation reaction and its positive temperature scaling, whereas above
, the negative temperature scaling of the hybridization reactions becomes dominant, recall
Figure 10.
We observe that hybridization rates are highly sequence dependent. In particular, our spatially resolved simulations reveal that adjacent identical nucleobases can drastically stabilize the hybridization complex. We expect that the overall replication process is primarily sequence specific near to the ligation sites, as it is known that mismatches near the ligation site effect the ligation the most [
29].
We also find that there is no difference in the replication rates of symmetric versus asymmetric replicators. We see that from equation 18, where only the sum of the oligomer lengths appears: while the longer oligomer of an asymmetric replicator has a high binding affinity to the template and therefore promotes the formation of a hybridization complex, the short oligomer has a smaller binding affinity, such that the total asymmetric hybridization complex is as stable as its symmetric counterpart.
We emphasize that our approach hinges on the assumption that ligation is the rate limiting step of the replication reaction. Due to the temperature scaling of the diffusion, hybridization, and ligation processes, our approach breaks down for very low temperatures or very long template strands. As discussed in
Section 2, Equation (
20), for long strands and low temperatures the dehybridization of the templates becomes the rate limiting step. Exactly what happens in the transition region between these two limits requires a more detailed non-equilibrium analysis and is outside the scope of this investigation. The grey shaded area in
Figure 9 and
Figure 10 depicts the expected landscape for the replication rate as we approach this transition zone from the regime where ligation is rate limiting, and it is clearly seen how the replication rate levels off as temperature decreases and the sequence length increases. In any event, we would expect the existence of a true optimal temperature for a given strand length, and equally a true optimal strand length for a given temperature, such that replication rates are maximized.
In the context of origin of life research, we cannot expect the presence of “clean" oligomer systems, as the ones we have used in current investigations. However, our findings clearly indicate that lower temperatures and longer strands have favorable replication rates under restricted conditions such as ligation limiting rate as well as single ligation events. Lower temperatures provide a qualitative mechanism for the preferred replication of longer information molecules, which may have implications for the “Snowball Earth" hypothesis.
Most importantly, in the context of minimal replicator experiments and applications, e.g., in protocell as well as molecular computing and fabrication research, our findings suggest a qualitative recipe for optimizing replication yields, as they relate experimentally accessible data such as melting temperatures and ligation rate to critical strand length (Equation
16) and temperature (Equation
17).