Information Storage in Liquids with Ordered Molecular Assemblies
Abstract
:1. Introduction
2. Negative Entropy Residing in Molecular Assemblies
3. Information Capacity in Fluids
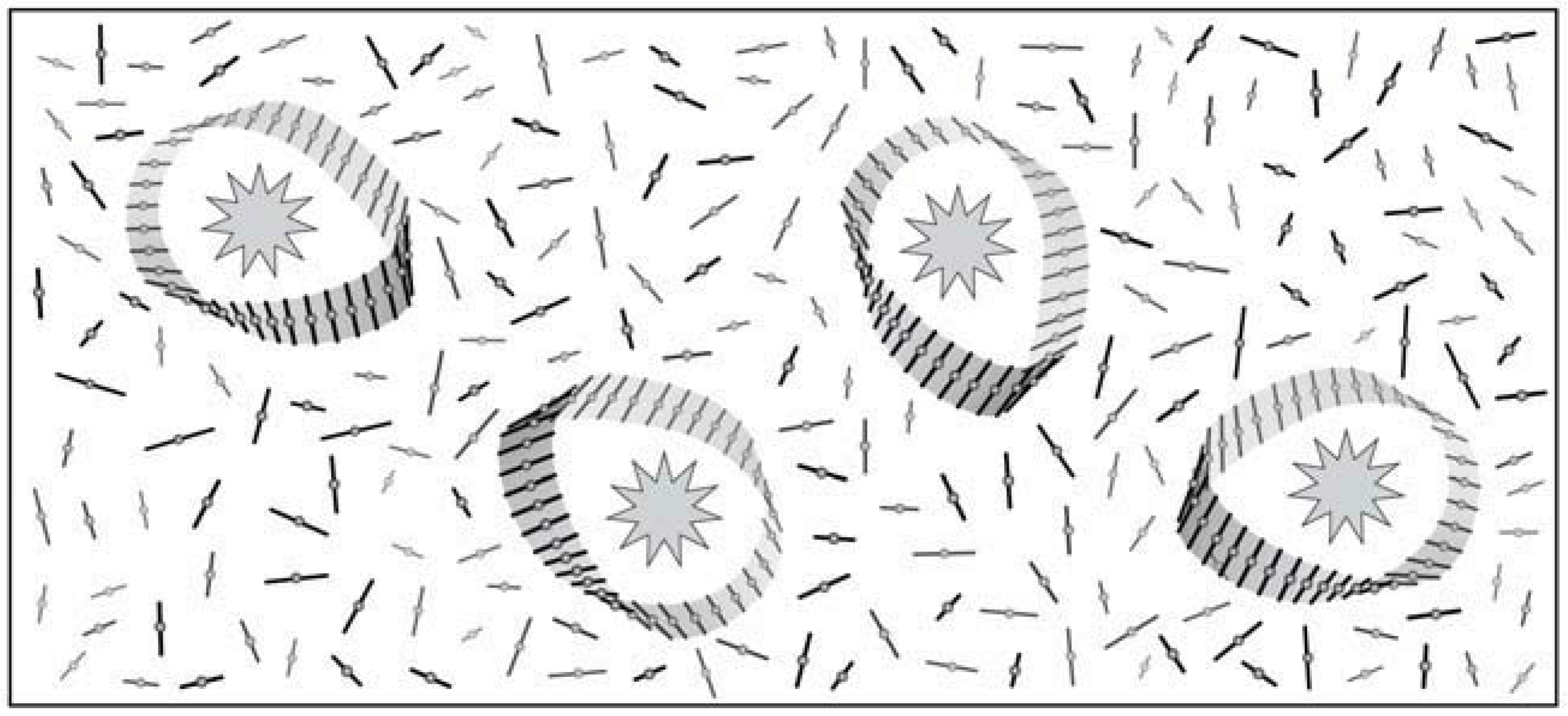
4. Information Storage in Solvent Envelopes
5. Chiral Solutions
| Resident solute | Liberated heat upon point racemization, Q, (J·mole−1) | IfRT (J·mole−1 ·optdeg−1) | If (optdeg−1) | Information capacity, RT α/αmax, estimated (kJ·mole−1) |
|---|---|---|---|---|
| L-Proline | 19.2 | 18.0 | 7.1·10−3 | 0.3 |
| D-Proline | 26.4 | 22.6 | 9.0·10−3 | 0.3 |
| L-Alanine | 2.5 | 104.7 | 4.2·10−2 | 1.2 |
| D-Alanine | 2.6 | 108.9 | 4.3·10−2 | 1.2 |
6. Neat Chiral Liquids
7. Micellar Aggregates
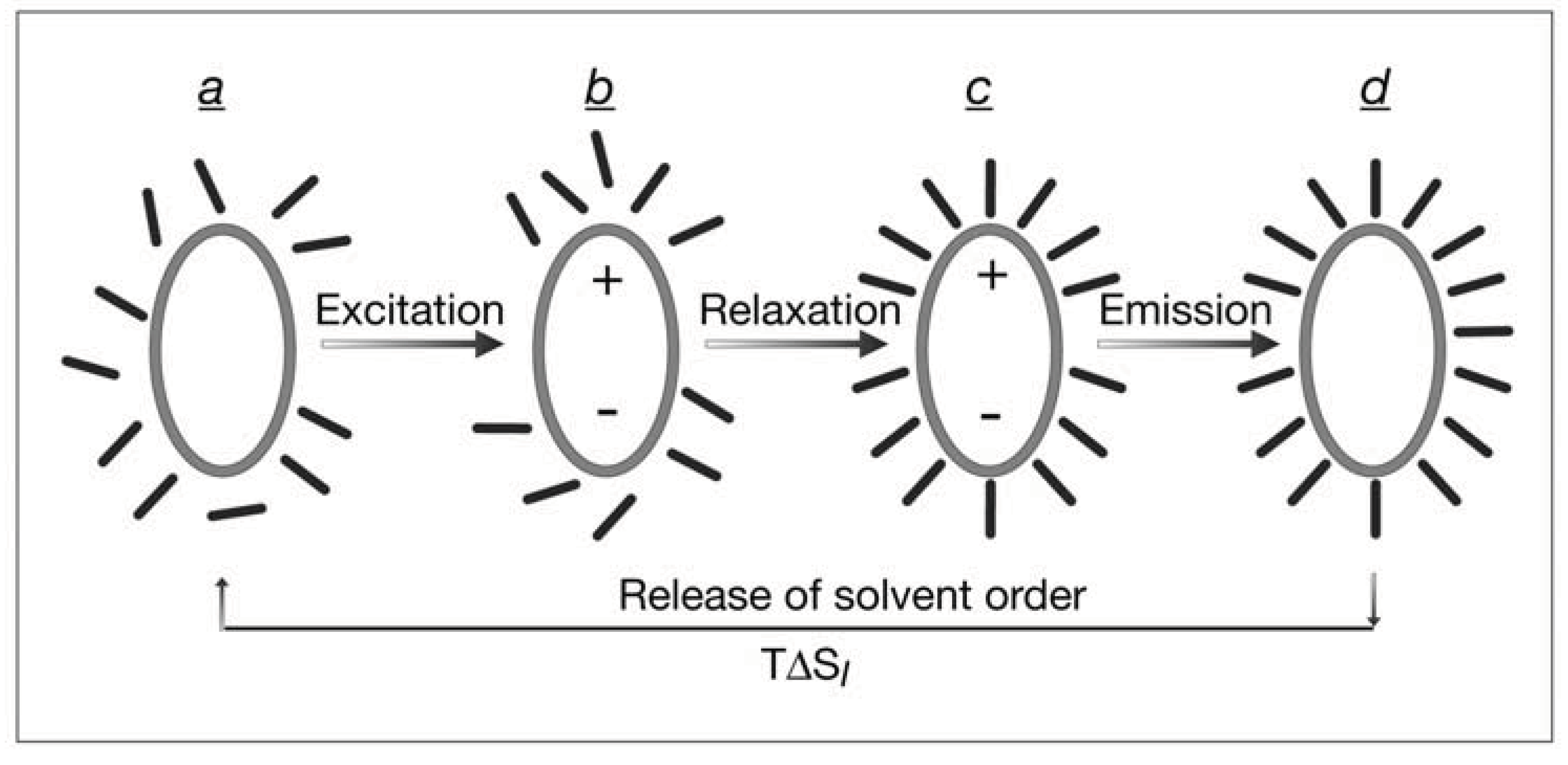
8. Transient Information Acquired by Fluorescent Solutes
9. Chiral Conductivity
10. Information Processing
11. Conclusions
References
- Shannon, C.E.; Weaver, D.W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Brillouin, L. Science and Information Theory; Academic Press: New York, NY, USA, 1962. [Google Scholar]
- Brillouin, L. Negentropy principle of information. J. Appl. Phys. 1953, 24, 1152–1163. [Google Scholar] [CrossRef]
- Schrodinger, E. What Is Life? The Physical Aspect of Living Cell; Cambridge University Press: Cambridge, UK, 1945. [Google Scholar]
- Kondepudi, D. Non-equilibrium polymers, entropy and algorithmic information. In Complexity, Entropy and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley: Redwood City, CA, USA, 1990; pp. 199–206. [Google Scholar]
- Mahulikar, S.P.; Herwig, H. Exact thermodynamic principles for dynamic order existence and evolution in chaos. Chaos Sol. Frac. 2009, 41, 1939–1948. [Google Scholar] [CrossRef]
- Shinitzky, M.; Shvalb, A.; Elitzur, A.C.; Mastai, Y. Entrapped energy in chiral solutions: Quantification and information capacity. J. Phys. Chem. B. 2007, 111, 11004–11008. [Google Scholar] [CrossRef] [PubMed]
- Shinitzky, M. Configurational entropy in chiral solutions-Negative entropy of solvent envelopes. Entropy 2009, 11, 667–674. [Google Scholar] [CrossRef]
- Scolnik, Y.; Portnaya, I.; Cogan, U.; Tal, S.; Haimovitz, R.; Fridkin, M.; Elitzur, A.C.; Deamer, D.W.; Shinitzky, M. Subtle differences in structural transitions between poly L- and poly D-amino acids of equal length in water. Phys. Chem. Chem. Phys. 2006, 8, 333–339. [Google Scholar] [CrossRef] [PubMed]
- Cogan, U.; Shpigelman, A.; Portnyana, I.; Rutenberg, A.; Scolnik, Y.; Shinitzky, M. Intermolecular chiral assemblies in R(−) and S(+) 2-butanol detected by microcalorimetry measurements. Chirality 2010, in press. [Google Scholar]
- Shvalb, A.; Mastai, Y.; Shinitzky, M. Chiral configuration of the hydration layers of D- and L-alanine in water implied from dilution calorimetry. Chirality 2010, 22, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Cooper, A.; Johnson, C.M.; Lackely, J.H.; Nollmann, M. Heat does not come in different colours: Entropy-enthalpy compensation, free energy windows, quantum confinement, pressure perturbation calorimetry, solvation and the multiple causes of heat capacity effects in biomolecular interactions. Biophys. Chem. 2001, 93, 215–230. [Google Scholar] [CrossRef]
- Clementi, E.; Cavallon, F.; Scordamaglia, R. Analytical potentials fromab initio computation for the interaction between biomolecules. 1. Water with amino acids. J. Am. Chem. Soc. 1977, 99, 5531–5545. [Google Scholar] [CrossRef] [PubMed]
- Run-Shen, C.; Xiang-Shan, N.; Xiu-Fan, S. Computer simulation of structuralorganization of water around biomolecules. In Water and Ions in Biological Systems; Pullman, A., Vasilescu, V., Packer, L., Eds.; Plenum: New York, NY, USA, 1983; pp. 137–149. [Google Scholar]
- Jelesarov, I.; Bosshard, H.R. Isothermal titration calorimetry and differential scanning calorimetry, as complementary tools to investigate the energetics of biomolecular recognition. J. Mol. Recog. 1999, 12, 3–18. [Google Scholar] [CrossRef]
- Weber, P.C.; Salemme, F.R. Applications of calorimetric methods to drug discovery and the study of protein interactions. Curr. Opin. Struc. Biol. 2003, 13, 115–121. [Google Scholar] [CrossRef]
- Shinitzky, M.; Haimovitz, R. Chiral surfaces in micelles of N-palmitoyl or N-stearoyl L-(or D-) serine. J. Am. Chem. Soc. 1993, 115, 12545–12549. [Google Scholar] [CrossRef]
- Deamer, D.A.; Dick, K.; Thiemann, W.; Shinitzky, M. Intrinsic asymmetries of amino acid enantiomers and their peptides: A possible role in the origin of biochirality. Chirality 2007, 19, 751–764. [Google Scholar] [CrossRef] [PubMed]
- Ellizur, A.C.; Shinitzky, M. P-violation manifested at the molecular level—A simple means for an absolute definition of “left” vs. “right”. arXiv Chem. Phys. 2006. arXiv:physics/0601010v1. [Google Scholar]
- Kimura, T.; Khan, M.A.; Ishii, M.; Kamiyama, T. Enthalpy change on mixing a couple of S- and R- enantiomers of some chiral compounds at 298.15 K. Chirality 2006, 18, 581–586. [Google Scholar] [CrossRef] [PubMed]
- Kimura, T.; Matsushita, T.; Ueda, K.; Aktar, F.; Matsuda, T.; Kamiyama, T.; Fujisawa, M. Enthalpic changes on mixing two couples of S- and R-enantiomers of heptane-2-ol, octane-2-ol, nonane-2-ol, 3-chloro-propane-1,2-diol, 2-methyl-1,4-butanediol at 298.15 K. Thermochim. Acta 2004, 414, 209–214. [Google Scholar] [CrossRef]
- Weber, G.; Teale, F.W.J. Ultraviolet fluorescence of the aromatic amino acids. Biochem J. 1957, 65, 476–482. [Google Scholar]
- Richter, P.H.; Eigen, M. Diffusion controlled reaction rates in spheroidal geometry. Application to repressor-operator association and membrane bound enzymes. Biophys. Chem. 1974, 2, 255–263. [Google Scholar] [CrossRef]
- Shinitzky, M. Symmetry, entropy and information capacity in chiral solutions. Symmetry Cult. Sci. 2010, 21, 17–26. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shinitzky, M. Information Storage in Liquids with Ordered Molecular Assemblies. Entropy 2011, 13, 1-10. https://doi.org/10.3390/e13010001
Shinitzky M. Information Storage in Liquids with Ordered Molecular Assemblies. Entropy. 2011; 13(1):1-10. https://doi.org/10.3390/e13010001
Chicago/Turabian StyleShinitzky, Meir. 2011. "Information Storage in Liquids with Ordered Molecular Assemblies" Entropy 13, no. 1: 1-10. https://doi.org/10.3390/e13010001
APA StyleShinitzky, M. (2011). Information Storage in Liquids with Ordered Molecular Assemblies. Entropy, 13(1), 1-10. https://doi.org/10.3390/e13010001




