Entropy and Information Approaches to Genetic Diversity and its Expression: Genomic Geography
Abstract
:1. Introduction
1.1. Mathematical Approaches to Predictive Biological Science
1.2. Entropy, Information, and Related Approaches in Genetics
- (a)
- (b)
- (c)
- incorporability into a model-fitting or statistical testing framework.
2. Ability to Express Diversity in a Way That Makes Intuitive Sense
2.1. Diversity Measures and Partitioning Diversity in Genetics and Ecology
- Variety–“the number of categories into which system elements can be apportioned” [40]. This is also called “richness” in biology, e.g., the number of different allelic types or the number of different species, termed S in this article.
- Balance–“a function of the pattern of apportionment of elements across categories” [40]. This is based on pi–e.g., the proportions of each different type of allele.
- Disparity–“the manner and degree in which the elements may be distinguished” [40]. This has been given a large number of names in biology, some of which will be introduced later.
- DNA sequence diversity and linkages along DNA in the genome;
- Sequence diversity between different alleles within one individual, for organisms with more than one genome (e.g., diploids such as humans);
- Diversity of alleles within one population;
- Diversity of allele proportions in different populations of the same species;
- Diversity of interactions between genes and environmental factors;
- Diversity of genetics, morphology, etc., between species;
- Diversity of types of species within a community;
2.2. “One-part” Diversity Measures
| Location | Allele | Marginal Total | |
|---|---|---|---|
| Allele Xa | Allele Xb | ||
| 1 | fa1 = N1pa1 | fb1 = N1pb1 | N1 = r1 Ntot |
| 2 | fa2 = N2pa2 | fb2 = N2pb2 | N2 = r2 Ntot |
| Summed Populations, or Marginal Total | Na = N1pa1 + N2p a2 | Nb = N1p b1 + N2p b2 | Ntot = N1 + N2 |
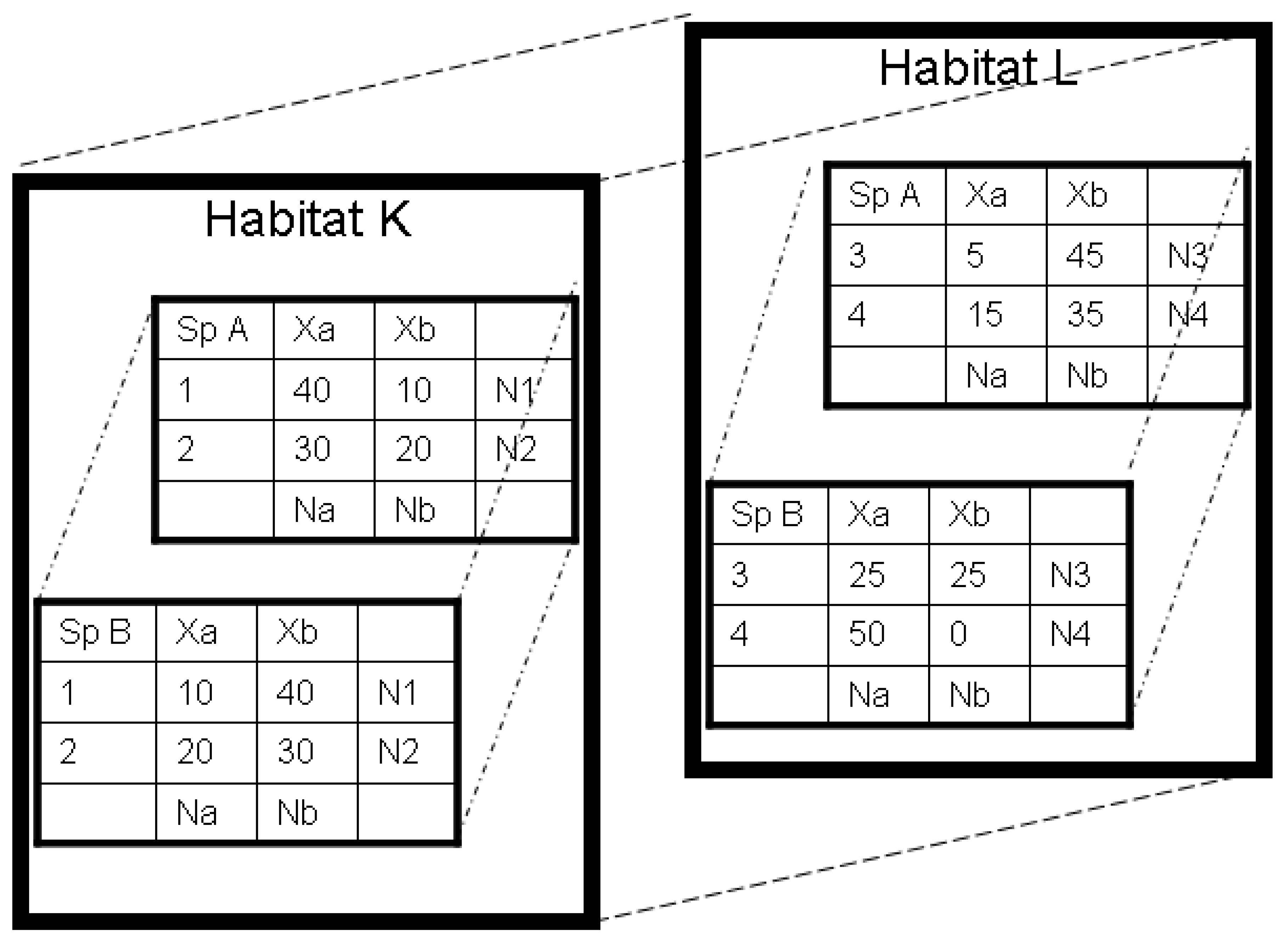
2.3. Two-part Approaches to Diversity
3. Integrating Genetic Diversity Measures with Natural Processes such as Selection and Dispersal
3.1. Subdivision
3.2. Gene Interactions
| SNP 1 | ||||
| AA | AC | CC | ||
| SNP 2 | GG | g1 | g2 | g3 |
| C-diseased | B ENVIRONMENT–temperature | ||||
| low | mid | high | |||
| A the SNP | GG | 12 | 43 | 18 | |
| C-non-diseased | B ENVIRONMENT–temperature | ||||
| low | mid | high | |||
| A the SNP | GG | 12 | 13 | 18 | |
3.3. Selection
4. Ability to be Incorporated into an Inclusive Statistical Framework
5. Future Directions
6. Summary
Acknowledgements
References and Notes
- Sherwin, W.B.; Jabot, F.; Rush, R.; Rossetto, M. Measurement of biological information with applications from genes to landscapes. Molec. Ecol. 2006, 15, 2857–2869. [Google Scholar] [CrossRef] [PubMed]
- Zar, J.H. Biostatistical analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Banavar, J.R.; Maritan, A.; Volkov, I. Applications of the principle of maximum entropy: from physics to ecology. J. Phys.: Condens. Matter 2010, 22, 063101. [Google Scholar] [CrossRef] [PubMed]
- Dewar, R.C.; Porté, A. Statistical mechanics unifies different ecological patterns. J. Theoret. Biol. 2008, 251, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Dewar, R.C. Maximum entropy production as an inference algorithm that translates physical assumptions into macroscopic predictions: Don’t shoot the messenger. Entropy 2009, 11, 931–944. [Google Scholar]
- Barton, N.H.; Coe, J.B. On the application of statistical physics to evolutionary biology. J. Theoret. Biol. 2009, 259, 317–324. [Google Scholar]
- Lande, R. Statistics and partitioning of species diversity and similarity among multiple communities. Oikos 1996, 76, 5–13. [Google Scholar]
- Zhang, J. Modeling multi-species interacting ecosystem by a simple equation. Int. Joint Conf. Comp. Sci. Opt. 2009, 1, 1003–1007. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. On generalized entropy measures and pathways. Phys. A 2007, 385, 493–500. [Google Scholar] [CrossRef]
- Kimura, M. Stochastic processes and distribution of gene frequencies under natural selection. Cold Spring Harbor Symp. Quant. Biol. 1955, 20, 33–53. [Google Scholar] [CrossRef] [PubMed]
- Ewens, W.J. The sampling theory of selectively neutral alleles. Theoret. Pop. Biol. 1972, 3, 87–112. [Google Scholar] [CrossRef]
- Ewens, W.J. Mathematical Population Genetics; Springer-Verlag: New York, NY, USA, 1979. [Google Scholar]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Friedman, W.F. The Index of Coincidence and its Applications in Cryptology; Riverbank Laboratories, Department of Ciphers: Geneva, IL, USA, 1922. [Google Scholar]
- Index of coincidence. http://en.wikipedia.org/wiki/Index_of_coincidence (accessed on 8 July 2010).
- Kimura, M.; Crow, J. The number of alleles that can be maintained in a finite population. Genetics 1964, 49, 725–738. [Google Scholar] [PubMed]
- Rao, C.R. Diversity and dissimilarity coefficients: a unified approach. Theoret. Pop. Biol. 1982, 21, 24–43. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379-423, 623-656. [Google Scholar] [CrossRef]
- Bell, D. Information Theory; Pitman: London, UK, 1968. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Csiszár, I.; Shields, P. Information theory and statistics: A tutorial. Found. Tr. Commun. Inform. Theor. 2004, 1, 417–528. [Google Scholar]
- Buddle, C.M.; Beguin, J.; Bolduc, E.; Mercado, A.; Sackett, T.E.; Selby, R.D; Varady-Szabo, H.; Zeran, R.M. The importance and use of taxon sampling curves for comparative biodiversity research with forest arthropod assemblages. Can. Entomol. 2004, 137, 120–127. [Google Scholar] [CrossRef]
- Bulit, C.; Diaz-Avalos, C.; Montagnes, D.J.S. Scaling patterns of plankton diversity: a study of ciliates in a tropical coastal lagoon. Hydrobiologia 2009, 624, 29–44. [Google Scholar] [CrossRef]
- Lewontin, R.C. The apportionment of human diversity. Evol. Biol. 1972, 6, 381–398. [Google Scholar]
- Smouse, P.E.; Ward, R.H. A comparison of the genetic infra-structure of the Ye'cuana and Yanomama: A likelihood analysis of genotypic variation among populations. Genetics 1978, 88, 611–631. [Google Scholar] [PubMed]
- Hartl, G.B.; Willing, R.; Nadlinger, K. Allozymes in mammalian population genetics and systematics: Indicative function of a marker system reconsidered. Exp. Suppl. 1994, 69, 299–310. [Google Scholar]
- Lacerda, D.R.; Acedo, M.D.P.; Lemos Filho, J.P.; Lovato, M.B. Genetic diversity and structure of natural populations of Plathymenia reticulata (Mimosoideae), a Tropical Tree from the Brazilian Cerrado. Molec.Ecol. 2001, 10, 1143–1152. [Google Scholar] [CrossRef]
- Wang, T.; Su, Y.J.; Li, X.Y. Genetic Structure and Variation in the Relict Populations of Alsophila spinulosa from Southern China based on RAPD Markers and cpDNA atpB-rbcL Sequence Data. Hereditas 2004, 140, 8–17. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Krauss, S.L.; Lamont, B.B.; Miller, B.P.; Enright, N.J. Long-distance seed dispersal in a metapopulation of Banksia hookeriana inferred from a population allocation analysis of amplified fragment length polymorphism data. Mol. Ecol. 2004, 13, 1099–1109. [Google Scholar] [CrossRef] [PubMed]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Jost, L. Partitioning diversity into independent alpha and beta components. Ecology 2007, 88, 2427–2439. [Google Scholar] [CrossRef]
- Jost, L. Gst and its relatives do not measure differentiation. Mol. Ecol. 2008, 17, 4015–4026. [Google Scholar] [CrossRef] [PubMed]
- Jost, L. D vs. GST: Response to Heller and Siegismund (2009) and Ryman and Leimar (2009). Mol. Ecol. 2009, 18, 2088–2091. [Google Scholar] [CrossRef]
- Jost, L.; DeVries, P.; Walla, T.; Greeney, H.; Chao, A.; Ricotta, C. Partitioning diversity for conservation analyses. Divers. Distrib. 2010, 16, 65–76. [Google Scholar] [CrossRef]
- Adami, C. Information theory in molecular biology. Phys. Life Rev. 2004, 1, 3–22. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Frieden, B.R. Information theory in living systems, methods, applications, and challenges. Bull. Mathemat. Biol. 2007, 69, 635–657. [Google Scholar] [CrossRef] [PubMed]
- Polley, H.W.; Wilsey, B.J.; Derner, J.D.; Johnson, H.B.; Sanabria, J. Early-successional plants regulate grassland productivity and species composition: a removal experiment. Oikos 2006, 113, 287–295. [Google Scholar] [CrossRef]
- Boyero, L.; Pearson, R.G.; Bastian, M. How biological diversity influences ecosystem function: a test with a tropical stream detritivore guild. Ecol. Res. 2007, 22, 551–558. [Google Scholar] [CrossRef]
- Westermeier, R.L.; Brawn, J.D.; Simpson, S.A.; Esker, T.L.; Jansen, R.W.; Walk, J.W.; Kershner, E.L.; Bouzat, J.L.; Paige, K.N. Tracking the long-term decline and recovery of an isolated population. Science 1998, 282, 1695–1698. [Google Scholar] [CrossRef]
- Stirling, A. A general framework for analysing diversity in science, technology and society. J. Roy. Soc. Interface. 2007, 4, 707–719. [Google Scholar] [CrossRef] [PubMed]
- Keylock, C.J. Simpson diversity and the Shannon /wiener index as special cases of a generalized entropy. Oikos 2005, 109, 203–207. [Google Scholar] [CrossRef]
- Hill, M.O. Diversity and evenness: a unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- A similar equation to Tsallis [43] can be found in Havrda, M.; Charvat, F. Quantification method of classification processes: concept of structural a-entropy. Kybernetik 1967, 3, 30–35. [Google Scholar], cited in [61].
- Jost, L. The relationship between eveness and diversity. Diversity 2010, 2, 207–232. [Google Scholar] [CrossRef]
- Gosselin, F. An assessment of the dependence of evenness indices on species richness. J. Theor. Biol. 2006, 242, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Wright, S. The genetical structure of populations. Ann. Eugen. 1951, 16, 323–354. [Google Scholar]
- Heller, R.; Siegismund, H. Relationship between three measures of genetic differentiation GST DEST and G’ST: how wrong have we been? Mol. Ecol. 2009, 18, 2080–2083. [Google Scholar] [CrossRef] [PubMed]
- Ricotta, C.; Marignani, M. Computing β-diversity with Rao’s Quadratic Entropy: a Change of Perspective. Divers. Distrib. 2007, 13, 237–241. [Google Scholar] [CrossRef]
- SPSS. http://www.spss.com/ (Accessed on 8 July 2010).
- Log-Linear Analysis for an AxBxC Contingency Table. http://faculty.vassar.edu/lowry/abc.html (Accessed on 8 July 2010).
- Pavoine, S.; Bonsall, M.B. Biological diversity: distinct distributions can lead to the maximization of Rao’s quadratic entropy. Theoret. Pop. Biol. 2009, 75, 153–163. [Google Scholar] [CrossRef] [PubMed]
- Welsh, A. Mathematics, Australian National University; (in prep, pers comm.).
- Everitt, B.S. The Analysis of Contingency Tables; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Chao, A.; Jost, L.; Chiang, S.C.; Jiang, Y.H.; Chazdon, R.L. A two-stage probabilistic approach to multiple-community similarity indices. Biometrics 2008, 64, 1178–1186. [Google Scholar] [CrossRef] [PubMed]
- Sarrazin, C.; Bruckner, M.; Herrmann, E; Ruster, B.; Bruch, K.; Roth, W.K.; Zeuzem, S. Quasispecies heterogeneity of the carboxy-terminal part of the E2 gene including the PePHD and sensitivity of Hepatitis C virus 1b isolates to antiviral therapy. Virology 2001, 289, 150–163. [Google Scholar] [CrossRef] [PubMed]
- De Bello, F.; Thuiller, W.; Leps, J.; Choler, P.; Clement, J.C.; Macek, P.; Sebastia, M.T.; Lavorel, S. Partitioning of functional diversity reveals the scale and extent of trait convergence and divergence. J. Veget. Sci. 2009, 20, 475–486. [Google Scholar] [CrossRef]
- Excoffier, L.; Smouse, P.E.; Quattro, J.M. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 1992, 131, 479–491. [Google Scholar] [PubMed]
- Page, R.D.M.; Holmes, E.C. Molecular Evolution: a Phylogenetic Approach; Blackwell Science: Malden, MA, USA, 1998. [Google Scholar]
- Hardy, O.J.; Jost, L. Interpreting and estimating measures of community phylogenetic structuring. J. Ecology. 2008, 96, 849–852. [Google Scholar] [CrossRef]
- Ricotta, C.; Szeidl, L. Towards a unifying approach to diversity measures: bridging the gap between the Shannon entropy and Rao’s quadratic index. Theoret. Pop. Biol. 2006, 70, 237–243. [Google Scholar] [CrossRef] [PubMed]
- Allen, B.; Kon, M.; Bar-Yam, Y. A new phylogenetic diversity measure generalizing the Shannon index and its application to phyllostomid bats. Amer. Natur. 2009, 174, 236–243. [Google Scholar]
- Guiaşu, S. Weighted entropy. Rep. Mathl. Phys. 1971, 2, 165–171. [Google Scholar] [CrossRef]
- Pavoine, S.; Love, M.S.; Bonsall, M.B. Hierarchical partitioning of evolutionary and ecological patterns in the organization of phylogenetically-structured species assemblages: application to rockfish (genus: Sebastes) in the Southern California Bight. Ecol. Lett. 2009, 12, 898–908. [Google Scholar] [CrossRef] [PubMed]
- Crozier, R.H. Preserving the information content of species: genetic diversity, phylogeny and conservation worth. Ann. Rev Ecol Syst. 1997, 28, 243–268. [Google Scholar] [CrossRef]
- Faith, D. P. Conservation evaluation and phylogenetic diversity. Biol. Conserv. 1992, 61, 1–10. [Google Scholar] [CrossRef]
- Cadotte, M.W.; Davies, J.; Regetz, J.; Kembel, S.W.; Cleland, E.; Oakley, T.H. Phylogenetic diversity metrics for ecological communities: integrating species richness, abundance and evolutionary history. Ecol. Lett. 2010, 13, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Hohl, M.; Ragan, M.A. Is multiple-sequence alignment required for accurate inference of phylogeny? Syst. Biol. 2007, 56, 206–221. [Google Scholar] [CrossRef] [PubMed]
- Daskalakis, C.; Roch, S. Alignment-Free Phylogenetic Reconstruction. In Research in Computational Molecular Biology, 14th Annual International Conference, RECOMB 2010, Lisbon, Portugal; Berger, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 123–137. [Google Scholar]
- Otu, H.H.; Sayood, K. A new sequence distance measure for phylogenetic tree construction. Bioinformatics 2003, 19, 2122–2130. [Google Scholar] [CrossRef] [PubMed]
- Ané, C.; Sanderson, M.J. Missing the forest for the trees: phylogenetic compression and Its implications for inferring complex evolutionary histories. Syst. Biol. 2005, 54, 146–157. [Google Scholar] [CrossRef] [PubMed]
- Utilsky, I.; Burstein, D.; Tuller, T.; Chor, B. The average common substring approach to phylogenomic reconstruction. J. Comput. Biol. 2006, 13, 336–350. [Google Scholar]
- Wu, G.A.; Jun, S.R.; Sims, G.E.; Kim, S.H. Whole-proteome phylogeny of large dsDNA virus families by an alignment-free method. Proc. Natl. Acad. Sci. USA. 2009, 106, 12826–12831. [Google Scholar] [CrossRef] [PubMed]
- Cantor, R. M.; Lange, K.; Sinsheimer, J.S. Prioritizing GWAS results: a review of statistical methods and recommendations for their application amer. J. Hum. Genet. 2010, 86, 6–22. [Google Scholar] [CrossRef] [PubMed]
- Kimura, M.; Ohta, T. Distribution of allele frequencies in a finite population under stepwise production of neutral alleles. Proc. Natl. Acad. Sci. USA. 1975, 72, 2761–2764. [Google Scholar] [CrossRef] [PubMed]
- Etienne, R.S.; Olff, H. A novel genealogical approach to neutral biodiversity theory. Ecol. Lett. 2004, 7, 170–175. [Google Scholar] [CrossRef]
- Vellend, M. Species diversity and genetic diversity: parallel processes and correlated patterns. Amer. Natur. 2005, 166, 199–215. [Google Scholar] [CrossRef] [PubMed]
- Halliburton, R. Introduction to Population Genetics; Pearson Education: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Rossetto, M.; Kooyman, R.; Sherwin, W.B.; Jones, R. Dispersal limitations, rather than bottlenecks or habitat specificity, can restrict the distribution of rare and endemic rainforest trees. Amer. J. Bot. 2008, 95, 321–329. [Google Scholar] [CrossRef] [PubMed]
- Ryman, N.; Leimar, O. GST is still a useful measure of differentiation: a comment on Jost’s D. Mol. Ecol. 2009, 18, 2084–2087. [Google Scholar] [CrossRef] [PubMed]
- Kosman, E.; Leonard, K.J. Conceptual analysis of methods applied to assessment of diversity within and distance between populations with asexual or mixed mode of reproduction. New Phytol. 2007, 174, 683–696. [Google Scholar] [CrossRef] [PubMed]
- Wienberg, R. Point: hypotheses first. Nature 2010, 464, 678. [Google Scholar] [CrossRef] [PubMed]
- Golub, T. Counterpoint: data first. Nature 2010, 464, 679. [Google Scholar] [CrossRef] [PubMed]
- Kang, G.; Yue, W.; Zhang, J.; Huebner, M.; Zhang, H.; Ruan, Y.; Lu, T.; Ling, Y.; Zuo, Y.; Zhang, D. Two-stage designs to identify the effects of SNP combinations on complex diseases. J. Hum. Genet. 2008, 53, 739–746. [Google Scholar] [CrossRef] [PubMed]
- Cordell, H.J. Detecting gene-gene interactions that underlie human diseases. Nat. Rev. Genet. 2009, 10, 393–404. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Chu, X.; Wang, Y.; Wang, Y.; Jin, L.; Shi, T.; Huang, W.; Li, Y. Exploration of gene-gene interaction effects using entropy-based methods. Eur. J. Hum. Genet. 2008, 16, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Chanda, P.; Sucheston, L.; Zhang, A.; Brazeau, D.; Freudenheim, J.L.; Ambrosone, C.; Ramanathan, M. Ambience: A novel approach and efficient algorithm for identifying informative genetic and environmental associations with complex phenotypes. Genetics 2008, 180, 1191–1210. [Google Scholar] [CrossRef] [PubMed]
- Chanda, P.; Sucheston, L.; Liu, S.; Zhang, A.; Ramanathan, M. Information-theoretic gene-gene and gene-environment interaction analysis of quantitative traits. BMC Genom. 2009, 10, 509. [Google Scholar] [CrossRef] [PubMed]
- Volkov, I.; Banavara, J.R.; Hubbell, S.P.; Maritane, A. Inferring species interactions in tropical forests. Proc. Natl. Acad. Sci. USA 2009, 106, 13854–13859. [Google Scholar] [CrossRef] [PubMed]
- Greenspan, G.; Geiger, D. Model-based inference of haplotype block variation. J. Computat. Biol. 2004, 11, 495–506. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Kang, G.; Sun, K.; Qian, M.; Romero, R.; Fu, W. Gene-Centric genomewide association study via entropy. Genetics 2008, 179, 637–650. [Google Scholar] [CrossRef] [PubMed]
- Laurie, C.C.; Nickerson, D.A.; Anderson, A.D.; Weir, B.S.; Livingston, R.J.; Dean, M.D.; Smith, K.; Schadt, E.E.; Nachman, M.W. Linkage disequilibrium in wild mice. PLoS Genet. 2007, 3, e144. [Google Scholar] [CrossRef] [PubMed]
- Padhukasaharsam, B.; Wall, J.D.; Marjoram, P.; Nordborg, M. Estimating recombination rates from single-nucleotide polymorphisms using summary statistics. Genetics 2006, 174, 1517–1528. [Google Scholar] [CrossRef] [PubMed]
- Siegmund, D.; Yakir, B. The Statistics of Gene Mapping; Springer: New York, NY, USA, 2007. [Google Scholar]
- Stephan, W.; Song, Y.S.; Langley, C.H. The hitchhiking effect on linkage disequilibrium between linked neutral loci. Genetics 2006, 172, 2647–2663. [Google Scholar] [CrossRef] [PubMed]
- Voight, B.F.; Kudaravalli, S.; Wen, X.; Pritchard, J.K. A map of recent positive selection in the human genome. PLoS. Biol. 2006, 4, e72. [Google Scholar] [CrossRef] [PubMed]
- McVean, G. The structure of linkage disequilibrium around a selective sweep. Genetics 2007, 175, 1395–1406. [Google Scholar] [CrossRef] [PubMed]
- Clarke, C.A.; Sheppard, P.M. Further studies on the genetics of the mimetic butterfly Papilio memnon L. Phil. Trans. Roy. Soc. London. B, Biol. Sci. 1971, 263, 35–70. [Google Scholar] [CrossRef]
- Slatkin, M.; Excoffier, L. Maximum likelihood estimation of haplotype frequencies in a diploid population. Mol. Biol. Evol. 1995, 12, 921–927. [Google Scholar]
- Slatkin, M. Linkage disequilibrium–understanding the evolutionary past and mapping the medical future. Nat. Rev. Genet. 2008, 9, 477–485. [Google Scholar] [CrossRef] [PubMed]
- Weir, B.S.; Hill, W.G.; Cardon, L.R. Allelic association patterns for a dense SNP map. Genet. Epidemiol. 2004, 27, 442–450. [Google Scholar] [CrossRef] [PubMed]
- Sved, J.A. Linkage disequilibrium and its expectation in human populations. Twin Res. Hum. Genet. 2008, 12, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, J.; Deng, H.W. A multilocus linkage disequilibrium measure based on mutual information theory and its applications. Genetica 2009, 137, 355–364. [Google Scholar] [CrossRef] [PubMed]
- Hampe, J.; Schreiber, S.; Krawczak, M. Entropy-based SNP selection for genetic association studies. Hum. Genet. 2003, 114, 36–43. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Valdes, M.H.; Williams, C.G. An entropy-based measure of founder informativeness. Genet. Res. 2005, 85, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Frankham, R.; Ballou, J.; Briscoe, D.A. Introduction to Conservation Genetics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Madsen, T.; Stille, B. Inbreeding depression in an isolated population of adders. Vipera brevis Biol. Conserv. 1996, 75, 113–118. [Google Scholar] [CrossRef]
- Hedrick, P.W. Gene flow and genetic restoration: the Florida panther as a case study. Conserv. Biol. 1995, 9, 996–1007. [Google Scholar] [CrossRef]
- Sommer, S. The importance of immune gene variability (MHC) in evolutionary ecology and conservation. Front. Zool. 2005, 2, 16. [Google Scholar] [CrossRef] [PubMed]
- Saakian, D.B.; Fontanari, J.F. Evolutionary dynamics on rugged fitness landscapes: exact dynamics and information theoretical aspects. Phys. Rev. E 2009, 80, 041903. [Google Scholar] [CrossRef]
- Sella, G.; Hirsh, A.E. The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. 2005, 102, 9541–9546. [Google Scholar] [CrossRef] [PubMed]
- Iwasa, Y. Free fitness that always increases in evolution. J. Theor. Biol. 1988, 135, 265–281. [Google Scholar] [CrossRef]
- Barton, N.H.; De Vladar, H.P. Statistical mechanics and the evolution of polygenic quantitative traits. Genetics 2009, 181, 997–1011. [Google Scholar] [CrossRef] [PubMed]
- Mustonen, V.; Lässig, M. Fitness flux and ubiquity of adaptive evolution. Proc. Natl. Acad. Sci. USA 2010, 107, 4248–4253. [Google Scholar] [CrossRef] [PubMed]
- Schwanz, L.E.; Proulx, S.R. Mutual information reveals variation in temperature-dependent sex determination in response to environmental fluctuation, lifespan and selection. Proc. R. Soc. B. 2008, 275, 2441–2448. [Google Scholar] [CrossRef] [PubMed]
- Ohta, T. Linkage disequilibrium due to random genetic drift in subdivided populations. Proc. Natl. Acad. Sci. USA. 1982, 79, 1940–1944. [Google Scholar] [CrossRef] [PubMed]
- Black, W.C.IV.; Krafsur, E.S. A fortran program for the calculation and analysis of two-locus linkage disequilibrium coefficients. Theoret. Appl. Genet. 1985, 70, 491–496. [Google Scholar] [CrossRef] [PubMed]
- Smouse, P.E. Likelihood analysis of recombinational disequilibrium in multiple locus gametic frequencies. Genetics 1974, 76, 557–565. [Google Scholar] [PubMed]
- Smouse, P.E. Likelihood analysis of geographic variation in allelic frequencies. II. The logit model and an extension to multiple loci. Theoret. Appl. Genet. 1974, 45, 52–58. [Google Scholar] [CrossRef] [PubMed]
- von Kodolitsch, Y.; Berger, J.; Rogan, P.K. Predicting severity of haemophilia A and B splicing mutations by information analysis. Haemophilia 2006, 12, 258–262. [Google Scholar] [CrossRef] [PubMed]
- Pielou, E.C. Mathematical Ecology, 2nd ed.; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Gregorius, H.R. A diversity-independent measure of evenness. Amer. Natur. 1990, 136, 701–711. [Google Scholar] [CrossRef]
- Neilsen, R.; Tarpy, D.R.; Reeve, H.K. Estimating effective paternity number in social insects and the effective number of alleles in a population. Mol. Ecol. 2003, 12, 3157–3164. [Google Scholar] [CrossRef]
- Schneider, T.D.; Stormo, G.D.; Gold, L.; Ehrenfreucht, A. Information content of binding sites on nucleotide sequences. J. Molec. Biol. 1986, 188, 415–431. [Google Scholar] [CrossRef]
- Chao, A.; Shen, T.J. Nonparametric estimators of Shannon's index of diversity when there are unseen species in sample. Envir. Ecol. Statistics. 2003, 10, 429–443. [Google Scholar] [CrossRef]
- Shervais, S.; Zwick, M. Ordering genetic algorithm genomes with reconstructability analysis. Intl. J. Gen. Syst. 2003, 32, 491–502. [Google Scholar] [CrossRef]
- Zeeberg, B. Shannon information theoretic computation of synonymous codon usage biases in coding regions of human and mouse genomes. Genom. Res. 2002, 12, 944–955. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.M.; Ray, S.C.; Laeyendecker, O.; Ticehurst, J.R.; Thomas, D.L. Assessment of hepatitis C virus sequence complexity by electrophoretic mobilities of both single- and double-stranded DNAs. J. Clin. Microbiol. 1998, 36, 2982–2989. [Google Scholar] [PubMed]
- Schneider, T.D. Evolution of biological information. Nucl. Acids Res. 2000, 28, 2794–2799. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, R.; Grau, R. A genetic code Boolean structure. II. The Genetic Information system as a Boolean Information System. Bull. Math. Biol. 2005, 67, 1017–1029. [Google Scholar] [CrossRef] [PubMed]
- Gilchrist, M.A.; Shah, P.; Zaretzki, R. Measuring and detecting molecular adaptation in codon usage against nonsense errors during protein translation. Genetics 2009, 183, 1493–1505. [Google Scholar] [CrossRef] [PubMed]
- Loewenstern, D.; Yianilos, P. Significantly lower entropy estimates for natural DNA sequences. J. Comput. Biol. 1999, 6, 125–142. [Google Scholar] [CrossRef] [PubMed]
- Díaz, J.; Alvarez-Buylla, E.R. Information flow during gene activation by signaling molecules: ethylene transduction in Arabidopsis cells as a study system. BMC Syst. Biol. 2009, 3, 48. [Google Scholar] [CrossRef] [PubMed]
- Adami, C.; Hintze, A. Evolution of complex modular biological networks. PLoS Comput. Biol. 2008, 4, e23. [Google Scholar]
- Lezon, T.R.; Banavar, J.R.; Cieplak, M.; Maritan, A.; Fedoroff, N.V. Using the principle of entropy maximization to infer genetic interaction networks from gene expression patterns. Proc. Natl. Acad. Sci. 2006, 103, 19033–19038. [Google Scholar] [CrossRef] [PubMed]
- Peakall, R.; Smouse, P.E. GenALEx 6: Genetic analysis in excel. Population genetic software for teaching and research. Mol. Ecol. N. 2006, 6, 288–295. [Google Scholar] [CrossRef]
- msBayes. http://msbayes.sourceforge.net/ (Accessed on 8 July 2010).
- Microsatellite Analyzer. http://i122server.vu-wien.ac.at/MSA/MSA_download.html (Accessed on 8 July 2010).
- Refoufi, A.; Esnault, M.A. Population genetic diversity in the polyploid complex of wheatgrasses using isoenzyme and RAPD data. Biol. Plant. 2008, 52, 543–547. [Google Scholar] [CrossRef]
- Markwith, S.H.; Stewart, D.J.; and Dyer, J.L. TETRASAT: A program for the population analysis of allotetraploid microsatellite data. Mol. Ecol. N. 2006, 6, 586–589. [Google Scholar] [CrossRef]
- Pielou, E.C. The measurement of diversity in different types of biological collections. J. Theoret. Biol. 1966, 13, 131–144. [Google Scholar] [CrossRef]
- Horn, H.S. Measurement of “overlap” in comparative ecological studies. Amer. Natur. 1966, 100, 419–424. [Google Scholar] [CrossRef]
Appendix: Glossary
| Allele | alternative versions of the DNA sequence at a locus; see pi. |
| Balance | “a function of the pattern of apportionment of elements across categories”. This is based on what is called in this article. |
| Balancing selection | various types of selection which tend to maintain variants. Also called stabilizing selection in multilocus cases. |
| Base | a component of DNA, also (somewhat loosely) called a nucleotide. There are four possible bases, A C T and G. The sequence of bases in DNA spells out the code. In the case of portions that code for amino acids, the code is read in triplets of bases. |
represents some estimate of difference between the types (e.g., difference of morphology of species, or number of non-shared bases between alleles). See disparity. | |
| Diploid | This is when cells contain two genomes, one from each parent individual, so that each gene might be represented by two different alleles in the one individual. Much of the information in humans is diploid. Where there is only one genome, as for the Y-chromosome or mitochondrial or chloroplast DNA, this is called haploidy (not mono- or uni-ploidy, as one might expect!). Polyploidy is when there are more than two genomes in each cell. |
| Differential entropy h | A continuous version of Shannon entropy. See Equation 17. |
| DNA | carries the genetic code. Composed of bases. Some parts of the code are in triplets. |
| Disparity | the manner and degree in which the elements of a group (e.g., the different allele types) may be distinguished. See . |
| Directional selection | selection which eliminates one genetic variant in favour of another. Also called positive selection when the focus is on the favoured variant, or negative when the focus is on the disadvantageous variant. |
| Disruptive or divergent selection | when phenotypically intermediate genotypes are at a disadvantage. |
| Dominant | in heterozygotes, where the two different alleles from each parent are not the same type, sometimes it is only possible to detect the phenotypic effect of one allele–the dominant allele. The other allele is said to be recessive. |
| Drift | random processes in transmission of genes from one generation to the next. |
| Effective number of alleles (entropic) neS | neS is the number of equi-frequent alleles that would be required to provide the same value as the actual sample–see Equation 4. This is the entropic analogue of neH. |
| Effective number of alleles (heterozygosity) neH | neH is the number of equi-frequent alleles that would be needed to give the same heterozygosity as the actual sample–see Equation 2. Also see neS. |
| Effective population size | see Ne. |
| Epistasis | interaction between the effects of two different loci, in production of the phenotype. |
| Evenness | a transform of one of the diversity indices (usually Shannon’s) to make explicit the departure from the most diverse case: equal numbers of each type of allele–see Equations 5 and 6. |
| Fitness | a function of the survival and reproduction of carriers of a certain genotype. Genotypes with higher fitness will tend to become more numerous over the generations. See also “selection”. |
| Gametic disequilibrium | see “linkage”. |
| Gene | this word is used variously to mean locus or allele. In the present review, it is restricted to meaning a protein-coding locus. The word should probably be abandoned, due to its sloppy use. |
| Genome | a complete set of genetic information, coded as base sequence of DNA. Some of this code is in triplets which each specify an amino acid in a protein. Other parts of the genome have other functions, such as regulating the expression of parts of the genome. |
| Genotype | the alleles contained in an individual for one or more loci. |
see Shannon entropy. | |
see heterozygosity. | |
| h | see differential entropy. |
| Haploid | see diploid. |
| Haplotype | a block of DNA containing multiple SNPs, and coding for one or more genes and their regulatory regions. Haplotypes are an example of genetic linkage. |
| Haplotype diversity | see Heterozygosity. |
| Heterozygote | an individual whose genotype has one copy of each of two different alleles, at a diploid locus. |
| Heterozygosity, | the chance of drawing two different alleles at random (with replacement) from a population: see Equation 1. Note that in this review, I do not also discuss the observed heterozygosity–the actual occurrence of heterozygous individuals. See supplement of Sherwin et al. 06 [1] for more discussion of this, as well as its information- theoretic applications. Heterozygosity is also called “Simpson index” when applied to species in ecological communities, “Haplotype Diversity” when it is the chance of drawing two different haplotypes at random, or “Nucleotide Diversity” when it is the chance of drawing two different nucleotides at random. |
| Homozygote | an individual whose genotype has two copies of the same allele at a diploid locus. |
| Indel | an insertion or deletion which appears in one sequence when compared to another sequence. These occur naturally during evolution of DNA. During reconstruction of phylogenies, the size and relative positions of indels must be estimated in a trade-off with the number of mismatched bases at other positions [59]. |
| Infinite alleles model (IAM) | see mutation. |
| Information gain | see Kullback-Liebler. |
| Kullback-Liebler divergence | for a given set of observed proportions of different types this is a comparison of the entropy based on an underlying distribution which really is given by versus the entropy if the underlying proportions follow some other distribution, . Also called relative entropy or information gain.
|
| Linkage | Linkage of two different genetic loci in the genome is when the inheritance of allelic variants at one locus is not statistically independent of alleles at another. Apparent linkage between two loci is called “linkage disequilibrium” or a more correct term “gametic disequilibrium” which recognizes that apparent linkage can be due to causes other than actual physical linkage. |
| Linkage disequilibrium | see “linkage”. |
| Locus | a position in the genome. Sometimes restricted to a protein-coding region, other times applied to any region of DNA at a fixed location in the genome, such as a SNP. |
| μ | see “mutation”. |
| Mutation | a change to the genetic code. Note that this is best called a change, not an error–all current codes, advantageous and deleterious, were derived via multiple mutations. Various different types of mutation occur. Two contrasting types that are commonly modeled are infinite allele model (IAM), and stepwise mutation model (SMM). In IAM, every mutation makes a novel allele, which is a reasonable approximation of the evolution of a coding region made up of thousands of bases, each with four alternatives, A C G T, and a per-base mutation rate such as μ = 10-9 per generation. SMM or similar is seen in repetitive regions such as CACACACACACA, where repeats (CA) are added or subtracted, so that alleles of the same length are re-created regularly. |
| Mutual information | For two variables, the mutual information between them is the reduction in uncertainty of the level of one variable, when there is information about the level of the other variable. Or, roughly stated, this is the ability of one type of information to enlighten us about another. For example, if two populations have no shared genetic variants, then knowing the genotype of an individual would give a perfectly accurate guide to the individual’s population membership, so there is said to be high mutual information between the genes and the population membership. Conversely, if the two populations have exactly the same arrays of genetic variants, then knowledge of the genes gives no indication of population membership, so mutual information is zero. See Equation 9. |
| Ne | effective population size: This depends not only upon actual population size, but also on any other factor that alters the rate at which random processes affect genetic quantities such as the heterozygosity [78] |
| , | see effective number of alleles. |
| Negative selection | see directional selection. |
| Nucleotide | see base. |
| Nucleotide diversity | see heterozygosity. |
the proportion of entities of type i in some group (e.g., numbers of different allelic variants encountered in a population, or numbers of different species encountered in an ecological community). See balance. | |
| Phenotype | the detectable effect of genetic and environmental information. This might be shape, chemistry, or colour of the organism carrying a certain genotype, or the survival and reproduction of that individual. |
| Phylogeny | a reconstruction of the evolutionary history of a number of separate groups, usually based only upon present-day data from those groups [59]. |
| Polymorphism | the occurrence of more than one variant within a population, e.g., two different alleles at the same locus. |
| Polyploid | see diploid. |
| Positive selection | see directional selection. |
| Q, or Quadratic Entropy | a generalization of Simpson’s index/Heterozygosity:
|
| r1,r2 | the proportion of a species that is in each of two populations 1 and 2. This may sometimes also be used as the relative sizes of the samples form the two populations, when performing significance testing. Note that these symbols are not to be confused with the correlation between uniting gametes, r2, used in linkage analysis. |
| Reaction norm | a measure of the interaction between genotypes and environmental conditions, in production of phenotypes. |
| Recessive | see dominant. |
| Recombination | this occurs when two haplotypes from different genomes break and rejoin to make new combinations of the alleles at the different loci, ie new haplotypes. |
| Relative entropy | see Kullback-Liebler. |
| Richness | see variety. |
| RNA | a molecule similar to DNA, e.g., messenger RNA which carries the DNA code to the cell to be converted to an amino acid sequence in a protein. |
| S | see variety. |
| s | see selection. |
see Shannon’s diversity or entropy. | |
| Selection | the consequence of fitness differences. Genotypes with higher fitness will tend to become more numerous over the generations. See also directional, balancing and disruptive selection. Relative fitness of different genotypes is often expressed by selection coefficents s, where one genotype is arbitrarily assigned maximum fitness of 1, and other genotypes are given fitnesses reduced by a selection coefficient s, so their fitness is 1-s (). |
| Shannon’s diversity or entropy | (Equation 3) |
| Simpson index | see heterozygosity. |
| Single-nucleotide-polymorphism | Where there is variation at one base position, this is called a “single-nucleotide-polymorphism” or SNP. Thus the alleles of a SNP locus are alternative bases A C G or T. |
| SNP | see “single-nucleotide-polymorphism”. |
| Splicing | after RNA code is transcribed from the DNA code, often portions of the code are removed, between two splice sites, before the code is used to direct the production of proteins. |
| Stepwise mutation (SMM) | see mutation. |
| Variety | “the number of categories into which system elements can be apportioned”. Also called “richness” in biology, e.g., the number of different allelic types or the number of different species, termed S in this article. |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sherwin, W.B. Entropy and Information Approaches to Genetic Diversity and its Expression: Genomic Geography. Entropy 2010, 12, 1765-1798. https://doi.org/10.3390/e12071765
Sherwin WB. Entropy and Information Approaches to Genetic Diversity and its Expression: Genomic Geography. Entropy. 2010; 12(7):1765-1798. https://doi.org/10.3390/e12071765
Chicago/Turabian StyleSherwin, William B. 2010. "Entropy and Information Approaches to Genetic Diversity and its Expression: Genomic Geography" Entropy 12, no. 7: 1765-1798. https://doi.org/10.3390/e12071765
APA StyleSherwin, W. B. (2010). Entropy and Information Approaches to Genetic Diversity and its Expression: Genomic Geography. Entropy, 12(7), 1765-1798. https://doi.org/10.3390/e12071765




