1. Introduction
The question about the structure and organization of scientific knowledge is one of the fundamental questions in educational and cognitive sciences [
1,
2,
3], as well as in the field of philosophy of science [
4]. The conceptions of the structure of scientific knowledge also deeply affect the ways such knowledge is taught, thus having practical educational consequences [
5,
6,
7].
Many of the studies concerned with the structure of scientific knowledge in learning—in particular in learning physics—have perpetuated an understanding that the structure of physics knowledge is hierarchically arranged [
5,
8]. This conception is maintained also within the logical empiricist views on science [
9,
10] and also inherited in semantic views on theories [
10,
11]. It is more or less evident that in the strongly reconstructed form of finalized theories, the physics knowledge structures are indeed hierarchical. However, in addition to hierarchical organization within the physics knowledge there is also a type of order originating from the “genealogy” of conceptual systems; concepts, laws and principles are based on precedents, which affect how the conceptualization proceeds and how new knowledge becomes justified and annexed into an existing body of knowledge. In this case, the knowledge system is naturally seen as an interconnected network or web of concepts and laws [
4,
12], but where also the hierarchical skeletal structure fundamentally affects the way the knowledge is ordered. The concepts of such networked conceptual systems are far from being independent; instead, they are fundamentally entangled and can be used only with an understanding of their interdependency. The overall coordination between concepts also has epistemological significance. The justification of knowledge—although based on empirical results—becomes fundamentally affected by the structure; the truth value of pieces of knowledge which fit well into the existing structures is increased [
12,
13]. Understanding the interconnected and networked nature of knowledge is not only to understand the structure of science but also to understand the way in which scientific knowledge is produced, justified and accepted;
i.e., how knowledge acquires its epistemological credentials [
4,
12,
13]. Many of these structural aspects of epistemological importance are quite naturally captured by notions of
connectivity and
cohesion of knowledge structures [
6,
7,
14].
In learning and education these notions are echoed by constructivistic views of learning, where interconnectedness and cohesion are seen as features that allow the learner to proceed through different paths in the conceptual space where the learning actually takes place [
15]. The interconnected network also naturally displays the manner in which nearby concepts are functionally related
i.e., how changes in one concept affect the changes in other concepts and how concepts can be used together for providing explanations and making predictions [
6,
14]. These kinds of structural aspects of knowledge are quite naturally displayed by concept maps and networks, which are node-link-node representations of the relational structure of concepts [
1,
2,
5,
6,
14,
15].
The concept maps are known to be effective learning tools encouraging reflective thinking and students’ metacognitive skills. It has been suggested that concept maps are effective because they reduce the effort of handling, ordering and retrieving knowledge in learning [
1,
2,
16,
17]. This kind of reduction of effort is referred to as the reduction of cognitive load [
16,
17], a term borrowed from cognitive load theory (CLT) [
17,
18]. Although cognitive load has very different and diverse meanings within the CLT, the common idea is that cognitive processing of knowledge requires mental effort, thus causing cognitive load. The concept maps function as scaffoldings which reduce this kind of cognitive load. Construction of concept maps is a rather complex cognitive task. In the initial stage the linking of concepts can be done by processing small parts or patterns, which then can be recombined back. The cognitive load associated with this type of process is called intrinsic. The
intrinsic cognitive load is apparently reduced in the construction of concept maps. However, it is common to find that in constructing maps the ordering becomes more difficult when a certain stage of organization is reached. This increasing difficulty can be quite naturally associated with the so-called
germane cognitive load, related to further processing of patterns and structures on the larger scale (closely related to the schema construction in CLT) [
18]. Therefore, the germane cognitive load almost certainly increases when maps become more and more organized. The reduction of intrinsic load and the increase of cognitive load suggests that there is an optimum balance between these two different types of cognitive loads and in this zone learning might also be optimal. Finding and recognizing the characteristic features of this zone on the basis of structural analysis of concept maps is clearly an important task.
Although the role of maps in reducing the cognitive load has been recognized, it has been difficult to study in more detail, as to how the reduction happens, what the characteristic features are that serve to reduce of the cognitive load, what the important discernible structural features are that we should pay attention to and how to make these features measurable. These problems of characterization are actually closely related to the basic problems concerning the structure of complex networks and measurements of their properties, and many of the methods developed for the study of complex networks can be carried over to study the properties of the concept maps [
19,
20]. The theory of complex networks provides the basic topological measures and methods of measurements we need to explore the structure of concept maps. However, the measured values of topological properties like the connectivity and clustering produces much data, where dependencies of interest and interpretability in terms of the learning process are not yet visible. Therefore, in order to make the regularities in the data visible, the data needs to be modelled. The first problem is to find a set of variables which is descriptive enough and which have resolving power in regard to the properties of interest. This approach parallels the so-called structural equation modelling, with the goal of finding the simplest set of variables and their mutual dependencies describing the data adequately [
21,
22]. When the variables and their possible correlations are known, the next step is to find out how the measured values of the variables are distributed. If such distribution can be established, it opens up the possibility of classifying the graphs on the basis of the probability distribution of the structural variables. Finding the appropriate probability distribution is in fact at the core of the statistical theory (or statistical mechanics) of graphs [
19,
20,
23].
Very often–and in particular in the case encountered here—the pool of data is not rich enough to decide unambiguously the form of probability density function. However, in addition to actual measured values of the data we often have other relevant information, e.g., about the possible range of values of the variables or of other constraints posed on the measured values. In this situation, the Maximum Entropy (MaxEnt) method [
24] is an invaluable approach for finding the distribution which best corresponds with our knowledge about the distribution of the values. Moreover, the MaxEnt approach quite naturally lends itself to macro-level interpretation of the properties of networks and provides knowledge of the “free energy”, “entropy” and “response functions” of the networks [
23,
25]. The MaxEnt description leads also naturally to probability distributions, which are in accordance with the exponential-family used widely in exponential random graph models (ERGM) [
26,
27].
In this study we examine the structure and organization of concept maps made by physics students, and representing the relations between concepts of electromagnetism. First, the student-made concept maps are represented as undirected spring-embedded graphs. The property of connectedness in local scale is measured in terms of clustering coefficient and the connectedness in global scale—the cohesion—is measured through the subgraph centrality. Second, by using the MaxEnt approach it is shown that the clustering and the cohesion are distributed according to the beta-distribution. The beta-distribution is then used as a basis upon which to define the free energy and entropy associated with the networks.
The major advantage of the approach proposed here is that it provides a macroscopic concepts for the characterization of the topology of concept maps so that it becomes possible to establish a close contact with the concepts of CLT used to discuss the effectiveness of concept maps in learning. The approach allows for identifying the intrinsic energy of making connections, naturally recognized to be related to the intrinsic cognitive load, and stress energy, associated with the germane cognitive load. Individual variations in students’ capabilities producing organization are, on the other hand, represented in terms of the entropy. The possibility to describe the structure of concept maps in terms of the energy and entropy thus makes these powerful concepts available for description of knowledge organization process and cognitive processes related to it.
2. Concept Maps and Their Structure
The concept maps are network-like node-link-node representations of the relations between concepts. For different types of representations there are different ways of establishing the relations and different rules with regard to linking the concepts, but the skeletal structure of the concept map is always a network of nodes (
i.e., concepts) connected by links. The advantage of making maps and networks is that such representations emphasize the relational structure of knowledge, where the concepts and principles are interconnected and where the principles of making the connections can be explicated [
1,
5,
8]. It is expected that the rules for making the connections have a very central role in determining the structure of the maps. However, the recognition of the structural features of interest is inherently connected to the question, as to the kinds of relations the map are thought to represent. Recently it has been suggested that procedures of knowledge construction and processing may be simple ones, reducible to basic patterns, even in those cases where the resulting structures are complex. Of particular importance seems to be different types of hierarchies, cliques, transitive patterns and cycles [
28,
29]. These notions have encouraged the idea that such patterns may help in understanding the cognitive processes behind knowledge construction and may lead also to the development of computational models for cognitive processes [
28,
29,
30]. In what follows we discuss these kinds of patterns related to the procedures of experiments and modelling as they are involved in connecting physics concepts.
2.1. Experiments and Models as Procedures
In physics as well as in the teaching of physics, experiments and modelling are central procedures connected to the construction and use of knowledge. It is natural to assume that the procedures of the experiments and modelling play an important role in conferring the structure of the concept maps. In what follows, we discuss how operationalizing the concept through experiments and the use and definition of concepts through models have been used as the design principles of the maps studied here. We have discussed elsewhere in more detail such design principles of concepts maps and shown that it is possible to recognize certain basic patterns of knowledge construction [
7].
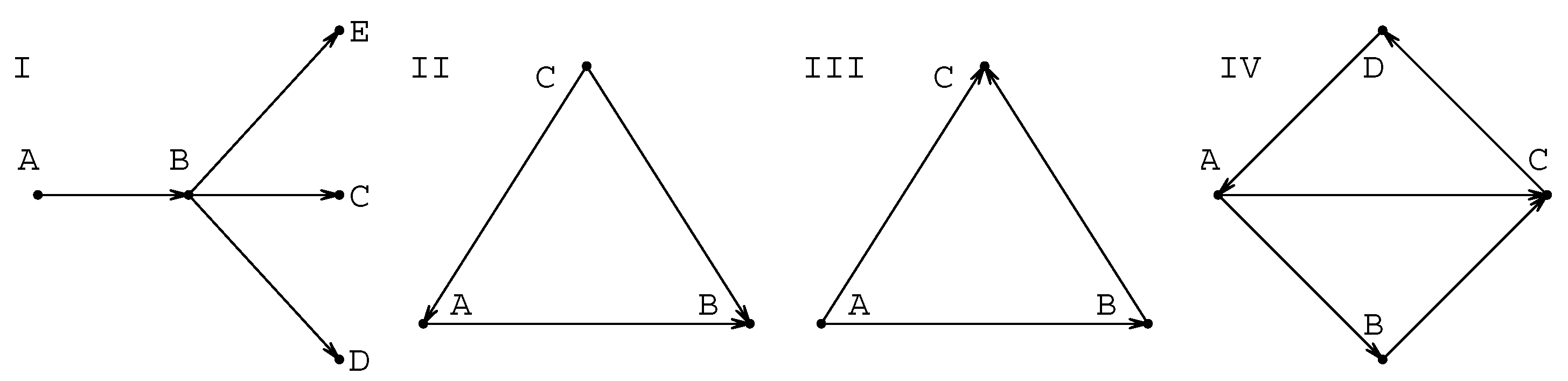
In the operationalizing experiment the concept is operationalized i.e., made measurable through the pre-existing concepts. The new concept or law is constructed sequentially, starting from the already existing ones, which provide the basis for an experiment’s design and interpretation. This process then creates the basic triangular covariation pattern. In its most idealized (but still sufficiently truthful) form the new concept (or law) C is formed on the basis of two pre-existing concepts A and B so that the operationalization creates C on the basis of the relations and , but which also requires that A and B can be related as . There is then a triangular mutual dependence . The modeling procedures, which in the simplest cases are often deductive procedures, produce very similar covariation patterns. The modeling procedure sequentially uses existing concepts to produce a better understanding of the use of a concept or to define it better. In this case concept or principle A is used to model a certain situation (e.g., through idealization) so that new concepts, laws or principles B and C become hypothesized, and then become connected to A through the modelling procedure. The triangular pattern generated by this procedure is then structurally very similar to a triangular pattern found in the case of operationalizing experiments. Another type of modelling procedure is in use when a concept A is generalized so that the new concept B can be used as a basis to form several new concepts, laws or principles. This kind of deductive pattern has a tree-like backbone, which starts with a directed connection and continues then to a set of concepts as a directed spoke .
The basic covariation patterns of concepts originating from the procedures of experiments and models (for details, see refs. [
6,
7] and references therein) are summarized graphically in
Figure 1. The importance of triangular (or transitive) connections like those shown in
Figure 1 have been recognized in the case of the functional structures of knowledge, in the context of giving explanations or predictions. To this kind of functional relatedness three properties can be assigned: 1) change in one variable affects another, 2) there are more than two variables connected, and 3) explanation for the behaviour of any of the components is done in the context of all other components [
6,
7,
14]. In fact, the essence of the “dynamic relationship” is that there is such a dependence between quantities which is also the basic structure of a physical law, where two or more quantities (variables) are related and together define their possible covariation. As we have discussed in detail elsewhere [
7], it is possible to trace the triangular covariation to the basic methodological procedures in use in knowledge production and acquisition; to the procedures of modelling and experiments [
7]. The triangular patterns may also be combined to give rise to 4-cycles of the form shown also in
Figure 1. It is interesting to note that triangular patterns like those in
Figure 1 have been recognized as an essential feature not only in the case of functional knowledge [
6,
14] but also in information acquisition and in the evolution of knowledge [
31] as well as information processing [
28,
29,
32].
2.2. Measuring the Structural Features of Interest
The concept maps are graph-like node-link-node structures, which means that they can be quite naturally analyzed as network structures. The qualitative structural features of primary interest are the clustering of concepts around other concepts, and cyclical paths connecting the concept. The clustering provides the connectivity locally, cyclical paths globally. The shortest cycle is a triangle or the 3-cycle. The ratio of the number of 3-cycles to the triply connected nodes is called the clustering coefficient of the node [
19,
23]. The role of longer cycles, on the other hand, is to hold the network together and prevent it from break-down in bi-partite structures,
i.e., the role of longer cycles is to provide the cohesion of the whole network. The different types of clustering and cyclicity of graphs can be gauged by many different measures for centrality of the node, e.g., by clustering centrality, betweenness centrality and subgraph centrality [
19,
20,
23,
33]. In what follows we use the clustering centrality [
19,
23] and in addition define a new subgraph centrality type measure to gauge the local and global clustering, respectively.
Pattern I in
Figure 1 is directly related to the number of links connected to the node, i.e to the degree
of the node, and is thus the basic structural feature of the map. In principle, all other properties can be expected to depend on
. The type of connectedness in local scale that we are interested in is related to the role of the triangular patterns II and III and to their role in forming longer cycles. The property of clustering can be simply characterized by
the clustering coefficient C of the network [
19,
23] measuring the relative number of triangles to the triply connected nodes so that
C obtains values between 0 and 1. As is well known, clustering measures the importance of the smallest cliques consisting of three interconnected nodes [
20,
23,
33]. The role of larger cycles that we are interested in here is related to the question of how large cycles connect the nodes and hold the network together. In principle, the basic quantity related to this property is the subgraph centrality
, which is a weighted sum of all cycles or subgraphs passing through a given node [
19,
34]. However, instead of subgraph centrality as such we are interested in knowing how triangles of types II and III provide larger cycles. It is known that a large relative number of cycles with an even number of steps is closely related to the network bipartivity
B [
19,
34]. In particular, the larger the fraction of the number of cycles with an even number of nodes, the larger the bipartivity of the networks tends to be,
i.e., the larger the probability that the network can be divided into two subsets of nodes where nodes in the given subset are not connected [
19,
34]. This motivates us to define a new complementary quantity measuring the relative number of odd-cycles
, which will be called
the cohesion coefficient in what follows. The cohesion then directly relates to the overall connectedness of the network. Of course, as all quantities characterizing the clustering and connectedness, also the clustering coefficient and the cohesion coefficient are expected to be appreciably correlated although they are related to different types of structural properties.
All information of the structure of maps is contained in the adjacency matrix
with elements
between nodes; if the nodes
i and
j are connected
and if they are not
. From the adjacency matrix all three quantities the degree
, the clustering
and and the cohesion
can be calculated for each node
k. The detailed mathematical definitions of these quantities are summarized in
Table I.
The analysis based on the distribution of values , and for each concept map produces a great amount of detailed data, and is quite impracticable for characterizing the ensembles of maps. Therefore, the pool of data needs to be reduced for the practical purposes of classification and comparison of different concept maps. In what follows, only the quantities D,C and Ω averaged over the nodes of concept map are discussed. Of these the average degree D is the basic variable related to the connectivity and the number of the links (richness of content), C is related to the clustering (interconnectedness) locally, while Ω relates to the role of cyclicity (interconnectedness in large scale and navigation) in providing cohesion. It is clear that in the structurally good concept maps all the quantities D, C and Ω need to have large enough values. However, it can be expected that intermediate values and could be optimal, because too large values of C and Ω are indicative of too tightly connected network, which clearly is not useful for purposes of knowledge representation and for navigation from one concept to another.
3. The Sample of Concept Maps
The concept maps to be analysed here were designed by physics teacher students (in their third or fourth year of studies) for purposes of representing knowledge structures in physics. The maps represent 34 concepts of electromagnetism, which were given to the students in advance. Two different sets of maps are discussed here. The first set, called here the designed maps, consists of maps constructed by following the design principles where links represent either modelling procedures or procedures of quantitative experiments, as explained in the previous section. The second set, called the associative maps, consists of maps constructed without the design principles. In this set students linked the nodes on the basis of association and without seeking any justification for the links in terms of procedures. In both cases the set of nodes in the maps are similar, consisting of the same set of basic concepts and laws of electromagnetism. Only the principles making the connections,
i.e., the rules of organization, are different. One example of the designed maps is shown in
Figure 2. In this map the different types of basic patterns shown in
Figure 1 can easily be recognized.
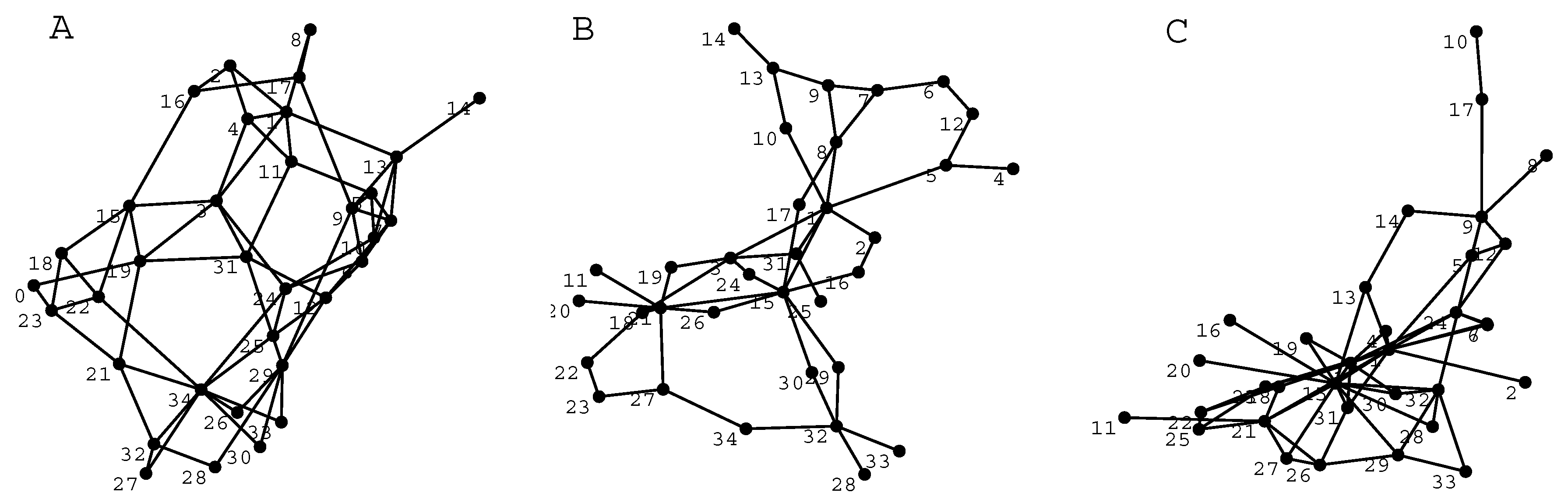
The original maps made by students have very different layouts, which usually makes it difficult to discern the important structural features simply on the basis of visual inspection. Therefore, to get an idea of the visual outlook of the maps it is useful to make the visual appearance of maps comparable by removing the ambiguity associated with different styles of doing the graphical layout. This can be done by redrawing the maps so that the same rules for ordering the nodes are used in all cases. In graph theory this is called embedding of the graph (here the map) and for the embeddings there are several well-defined methods [
20,
35]. We have here used the spring-embedding, which is obtained when each link is assumed to behave like a spring and then the total energy of the spring system is minimized. The energy minimization is done iteratively until a stable structure is achieved [
35]. Usually some tens of iterative steps are needed to reach the stable configuration. Spring-embedding reveals how tightly certain concepts are tied together and it is therefore suitable for visual inspection of the triangular and cyclical patterns. Examples of the designed and associative maps in the spring-embedded form are shown in
Figure 3.
From
Figure 3, it can be seen that both types of maps have a substantial number of 3-cycles but the associative maps have more “hub”-like structures than designed maps, but otherwise the maps are very similar. It is evident that the properties of the maps are not radically different, but still different enough to motivate classification in different classes. However, the classification on the basis of measurements of topological features poses challenges in case the pool of data is limited and when differences are not very clear [
19].
4. Results
The variables D, C and Ω forms the basis of discerning the topological features of clustering and cohesion. However, in order to discern interesting regularities, the measured data needs to be processed further. First, the data-model describing the systematic regularities within the data is introduced. Second, the properties of the distribution of the measured values are examined and the model describing the random variations is introduced.
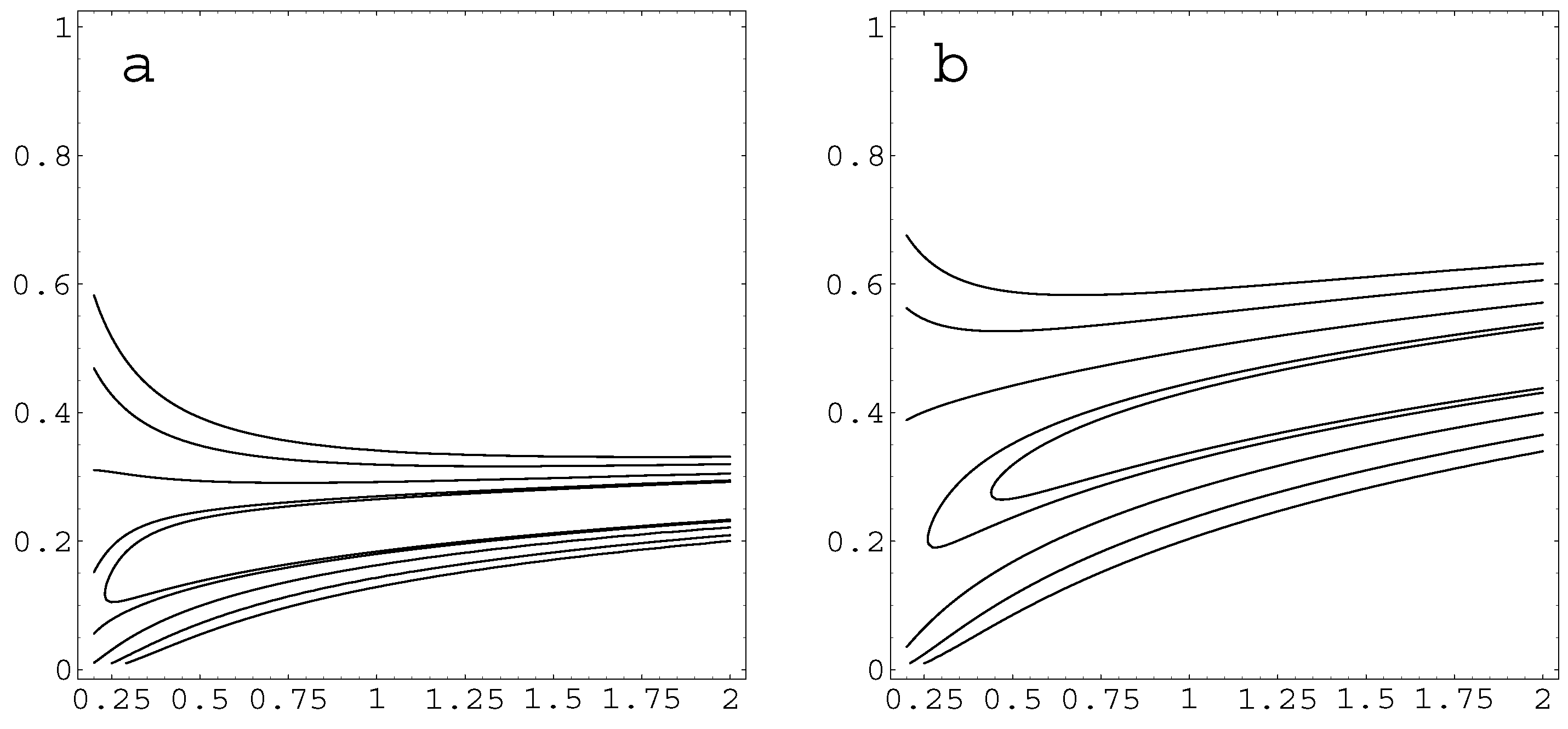
We can expect that
C and Ω depend on
D in some regular manner. Although the data does not allow for unambiguously deciding on the nature of this dependence, we can still make estimates of the expected dependence. We can expect that in region
there is a sharp transition from structures without 3-cycles to structures with 3-cycles, so we can define a threshold value
locating this transition point. In this case it is convenient to use a scaled degree
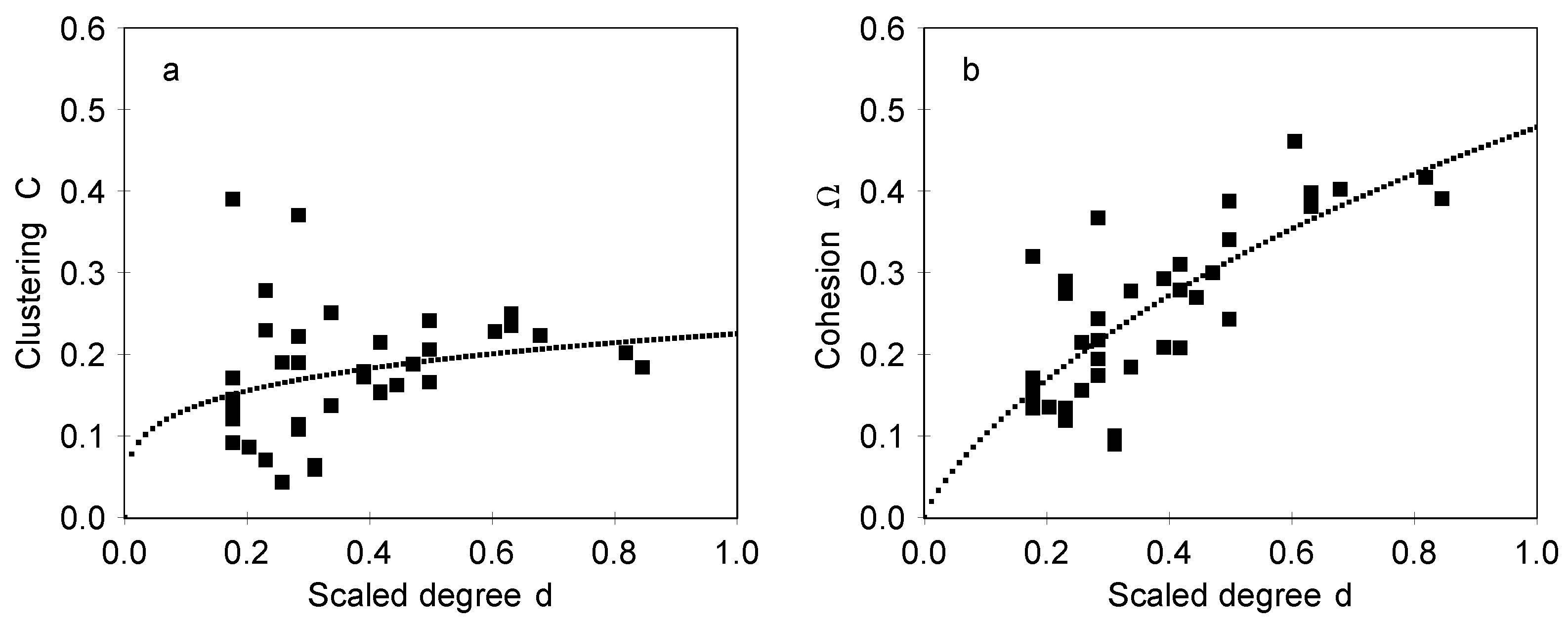
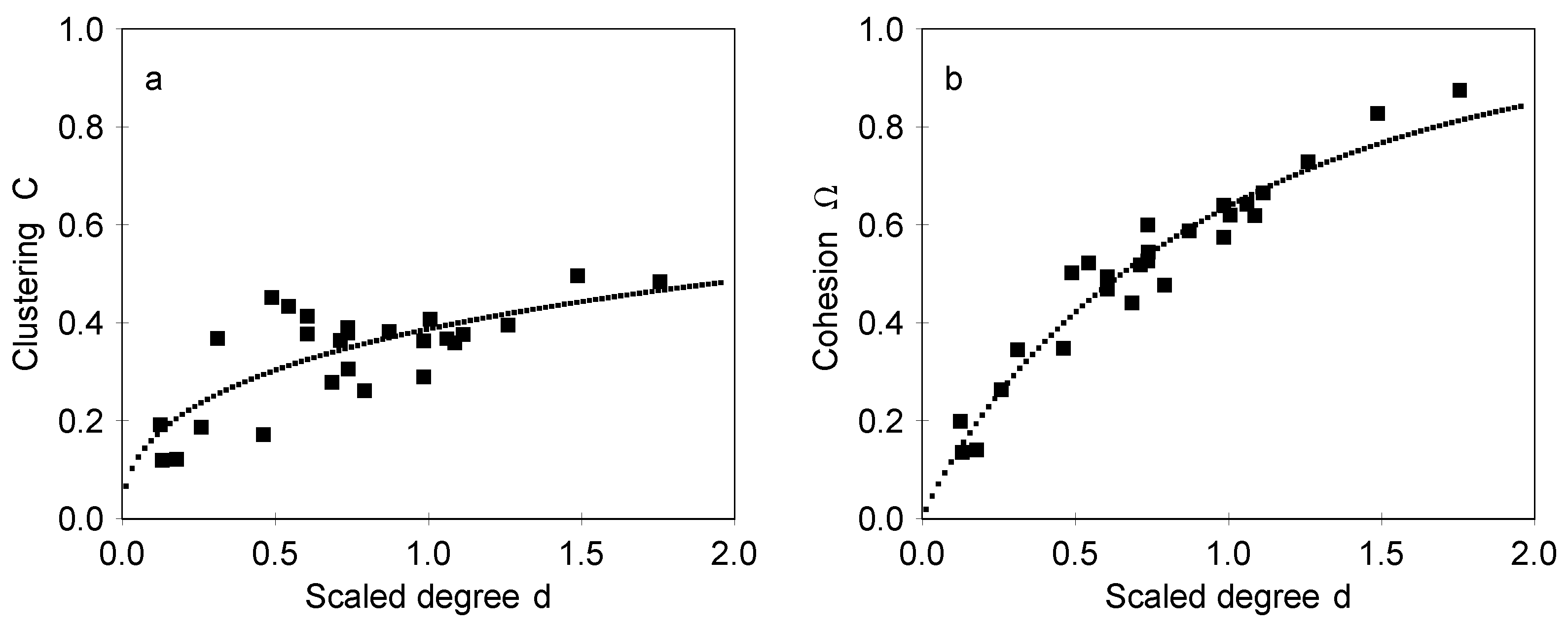
as an independent variable. The measured values of
C and Ω as they depend on
d are shown in
Figure 4 in the case of designed maps and in
Figure 5 in the case of associative maps. The results for
C in
Figure 4a and
Figure 5a show that clustering is appreciable and has a moderate dependence on
d, which indicates high interconnectedness of the neighboring concept. The relative number of cycles with an odd number of steps is given by the cohesion coefficient Ω, shown in
Figure 4b and
Figure 5b. It should be noted that the dependencies shown in
Figure 4 and
Figure 5 are very different from dependencies expected for maps which have a similar distribution of degrees but where links are made at random. We have generated such random configurations, with the distribution of degrees of nodes identical to the designed and associative maps (the so-called configuration model) and measured the clustering and the cohesion of such maps. In a set of 500 examples the clustering is always within the range 0.02
0.1, and the cohesion is 0.05
0.2. Therefore, the designed maps are essentially different from random configurations.
The fact that Ω increases with degree
D indicates that the 3-cycles and larger cycles obtained as their combinations are important also in providing the overall cohesion of the network. Such a cohesion involving 3-cycles is also closely related to the ability to pass information in the concept map (network),
i.e., to the communicability of nodes. Analysis of correlations shows that the values of
C and Ω have correlation coefficients ranging in 0.80–0.89. Such a strong correlation is as expected in the case of centrality measures [
19,
34].
4.1. The Model of Data
In order to pin down the interesting and important regularities in the data we introduce a
structural model describing the dependence of variables
on the scaled degree
d, which is now the basic independent (predictive) variable. The most important feature of the variable
X that the structural model needs to capture is the fact that
X is limited to a range from 0 to 1, increases slowly as
d increases but must eventually level off to 1 (completely connected networks). Furthermore, for small values of
d the dependence is of the power-law type. These notions suggest looking for a stretched exponential type behavior of average values
where parameters
and
are found by least squares fit. The fits thus obtained are shown in
Figure 4 and
Figure 5 for designed and associative maps, respectively.
The appropriateness and adequacy of Equation 1 in describing the data can be decided on the basis of an analysis of residuals
. From
Figure 4 and
Figure 5 it is evident that at least in the case of designed maps the residuals increase as
d decrease, while for associative maps they remain more or less constant. In order to obtain in both cases the residuals, which are amenable for statistical analysis, the residuals are scaled by a factor
. The scaled residuals will then be independently and identically distributed (with no dependence on
d) with zero mean and constant standard deviation
whereby the homoscedasticity condition is fulfilled [
22,
36]. The standard deviation of the original residuals is then given by
The parameter
is selected so that the scaled residuals
become homoscedastic. The Equations 1 and 2 together specify the structural model of the data, where Equation 1 contains the knowledge of the causal dependence of variables
x on
d and Equation 2 contains the knowledge of the fluctuations of the variables
X around the mean value
. The Equation 1 gives now the prediction of the systematic dependence of
X on
d, while the standard deviation in Equation 2 already tells already much about the expected deviations from the mean. However, in order to answer the question, of how probable is the given value
X, we need to know more about the
distribution of the residuals.
4.2. The Distribution of Measured Values
The variables
can be thought of as random variables constrained in the range
and having the mean value and standard deviation given by Equations 1 and 2. In this case a good candidate for description of the probability density function (pdf)
is the beta-distribution
where
and
with
x and
are as defined in Equations (1)-(2). The normalization of the pdf is given by the beta-function
[
37]. The values of the parameters
κ,
α,
and
τ specifying the distributions for designed and associative maps are given in
Table 2.
The examination of the residuals shows that the beta-distribution gives fits with p-value of the goodness of fit ranging from 0.93 to 0.98, depending on the case. Therefore, the beta-distribution is an appropriate fit on the basis of the information (mean and standard deviation) we have about the distribution. It should be noted that it is possible to obtain better goodness of fit values using normal distribution, but then the condition
is violated. Because this latter condition must not be violated, it excludes the normal distribution as a possible fit. As is well known, the goodness of fit is a desirable property but must not be used as a primary guide in selecting the statistically appropriate and adequate fit [
22,
38].
The contour plots of the distributions given by Equation 3 for the clustering
C are shown in
Figure 6 in the case of designed and associative maps. From the contour plots in
Figure 6 it is seen that the standard deviation in the case of designed maps is much reduced when
d increases, while for the associative maps the standard deviation remains large for all
d. Essentially similar behaviour is also obtained for
, because the values of
C and Ω are strongly correlated with correlation coefficients 0.89 and 0.80 in designed and associative maps, respectively.
The results show that a model of the data defined by Equation 1–3 is capable of resolving the properties of designed and associative concept maps. The associative maps has appreciably large clustering and cohesion, indicating good structural coherence. However, the standard deviation is quite large, indicating large individual variations. The designed maps have smaller values of clustering and cohesion, indicating more parsimonious interrelatedness of concepts represented in them. This of course is a consequence of the design principle, which requires justification for each link, thus forcing on the structure a more austere organization than pure association.
5. Energy and Entropy of Knowledge Organization
Networks and the distribution of their properties can be described in terms of exponential-family of probability distributions. This description is widely used in the form of the so-called Exponential Random Graph Models (ERGM) [
26,
27] and can be extended also to more complex networks [
23,
25]. The ensembles of graphs can then be described in a similar way as ensembles of physical systems in the statistical thermodynamics (or mechanics), with a distribution
where function
H characterizing the ensemble can be interpreted as total energy. The quantity
is the partition function and
β is the parameter conjugated to
H and has the role of a state variable defining the state of the system. The advantage of this kind of a statistical ensemble theory is that the information needed to describe the system can be made quite parsimonious. However, the problem is that we do not usually know the total energy (or Hamiltonian) of the graphs of interest.
5.1. Obtaining the Probability Distribution from the MaxEnt Method
In order to deduce the Hamiltonian
, which could be used to describe the system, we need to approach the problem indirectly and try to find the distribution by maximizing the information entropy when certain constraints (e.g., mean value, variance or some other constraints) on the distribution are known. This approach is often called Maximum Entropy (MaxEnt) principle and it is based on Jaynes’s information theoretic approach on statistical mechanics [
40,
41]. In the MaxEnt approach the probability distribution
of statistical variable
is inferred on the basis of the partial information of expectation values (observables)
of weight functions
corresponding to the observables. In the MaxEnt method the probability distribution, which is the least biased estimate of probability distribution assigned to random variables
, is obtained by maximization of information theoretic entropy [
40,
41]
where
K is a constant defining the system of units for entropy and is set to
in what follows the
is the probability of state
s. The information entropy in Equation 5 is a fundamental measure of the uniformity of probability distribution with expectation values
[
40,
41].
In the MaxEnt method the basic questions is, what the physically relevant constraints are. There are three notions, which guide our selection of the constraints. First, the support of the variables of interest is
. Second, in the case of complex networks the energies of nodes can be assumed to depend logarithmically on the degree of the node [
42], which suggests that energies may equally well depend logarithmically on clustering and cohesion. Third, the cognitive load theory strongly suggests that in the case of concept maps the energetics associated with nodes is interpretable in terms of cognitive or mental effort in making the connections. Because many physiological responses are known to be logarithmically dependent on the external stimuli, e.g., responses in vision, hearing and sensory experience [
43], this supports the choice of logarithmic forms of constraints [
42,
43]. Therefore, the constraints which we set on the maximization of the entropy are chosen to be
where
and
are ensemble averages of quantities which suggest themselves as types of “energies” and which are constrained to remain unchanged.
The information entropy in Equation
5 can now be maximized so that the constraints in Equations
6–
7 are fulfilled. This is done by choosing multipliers
β and
λ to correspond with the constraints and then maximizing the quantity [
40,
41]
Requiring that
we get
which can be solved for
in the form of canonical distribution in Equation
4 provided that the Hamiltonian (representing the total energy of cluster states) is given by
The resulting distribution is then the beta-distribution given by Equation 1. In the Hamiltonian
now has the role of energy gained by ordering the node as 3-cycles, while
slows down ordering when
C increases.
5.2. Macroscopic Thermodynamics of Concept Maps
The macroscopic thermodynamic behaviour of the system follows entirely from the partition function, which is now given by [
37]
Next we need to identify the physical meaning of the parameters
β and
λ within the thermodynamic description. It was already noted that
ϵ suggests itself as the energy related to the organization by forming 3-cycles (in what follows the subscript
x referring to the chosen variable is dropped, because both cases
C and Ω are essentially similar). Therefore, this energy is referred to as
intrinsic energy of ordering. We can now relate the average value of energy
and its fluctuations
to the partition function through the basic relations [
39]
Because
this means that
and thus
and
need to be conjugated and related to each other as the energy and the temperature in thermodynamics. This motivates their interpretation as the energy and the temperature
in the case of the present system (see e.g., [
39] for justification of this kind of identification). Similarly, by noting that average values of
and its fluctuations are given by
and that
and
are thus conjugated. We can then interpret Λ as a kind of “strain field” and
as a stress-like system response, which prevents further ordering. This of course is a consequence of the fact that triply connected nodes, which are not already 3-cycles, become more rare with increasing ordering and that it is not meaningful to connect all triples to 3-cycles. Therefore,
ϕ is referred to as
stress energy and it is connected with field Λ.
The remaining thermodynamic quantities are now readily formulated when the meaning of the parameters has been identified. From the definition of entropy in Equation
5 it immediately follows that
where we have defined
and
and where
F represent the free energy (or the thermodynamic potential) of the system. The above identification in Equation
14 is of course the standard result of statistical thermodynamics, but we have now established its validity on the basis of MaxEnt method in the case of an ensemble of networks. Finally, we note that with the identifications in Equations
12–
14 the heat capacity (the thermal susceptibility ) is given by
Because the partition function can be evaluated now in a closed analytical form, we obtain results for thermodynamic functions in the analytical form with results summarized in
Table 3.
The state variables have Θ and Λ can both be expressed as functions of
d, which means that the system’s free energy
F, entropy
S, and heat capacity
C are also unique functions of
d as shown in
Figure 7. The results in
Figure 7 show that the free energy
F is monotonously decreasing function of
d, indicating that ordering is energetically favourable.
5.3. Interpretation of the Energetics Within the CLT
The energetics derived on the basis of the macroscopic thermodynamics yields readily to interpretation by using the terms of the cognitive load theory (CLT). As was discussed in the introduction, according to the CLT the cognitive load can be intrinsic or germane [
18], and both of these cognitive loads are involved in the construction process of concept maps [
16,
17]. The intrinsic energy associated with the creation of the links is reduced when the density of the links (measured by
d) is increased; it behaves in a similar way as the intrinsic cognitive load is expected to behave. Therefore, the intrinsic energy can be directly interpreted as a reduction of intrinsic cognitive load in adding new knowledge to well-ordered structures (cf. refs. [
3,
5,
6,
8,
14,
15]). The stress energy, on the other hand, increases with the increasing content of the map (
i.e., increasing
d). This behaviour is similar to what could be expected from the germane cognitive load, when the task becomes more complex. Therefore, the stress energy suggests itself as a measure for the germane cognitive load. The energetics of the concept maps due to ordering is qualitatively similar in the case of designed and associative maps, but energies are systematically larger for the associative maps.
Entropy, on the other hand, differs more in the case of designed and associative maps. In designed maps entropy decreases with increasing d , while in associative maps it is considerably higher. However, with decreasing d the difference becomes smaller between the associative and designed maps. This suggests that in designed maps better order ensues with increasing connections. The entropy is quite naturally associated with the variations of students capabilities in processing the knowledge.
The free energy of the concept maps is the difference between the sum of energies of intrinsics and germane cognitive loads and the entropic contribution. A very central notion is that free energy is a monotonously decreasing function of the density of links. This result may explain the common notion that concept maps are nearly always beneficial for knowledge processing, even in cases when they become very extensive and complex. This behaviour owes to the fact that the increase of effort or the increased germane cognitive load is always compensated by the intrinsic variation measured in terms of entropy.
Finally, there is a substantial difference in “heat capacities”, i.e., in energetic response of the system on perturbations. In designed maps the heat capacity is large, indicating that the system can efficiently store “energy”, i.e., ordered knowledge and that such a system is robust to perturbations (a small change in energy does not affect the temperature much). In the case of associative maps the capacity to store knowledge is low and the robustness of the system to changes is substantially low.
These interpretations are of course only speculative, based on the structural similarity of the description of thermodynamic systems and concept maps. Nevertheless, the interpretation makes astonishingly close contact with the ideas contained in the CLT. Therefore, the interpretation in terms of the energy and entropy is meaningful and embodies the qualitative notions of “cognitive load” and “robustness of ordered knowledge” and opens up interesting possibilities to bring these kinds of ideas within the limits of mathematical description and modelling.
6. Discussion and Conclusions
High clustering in concept networks is somewhat similar to clustering found in the so-called “small world” networks, in particular in the case of sociological systems [
19,
20,
23]. As in small worlds and in sociological networks, the large clustering is related to transitive “family” or “friendship” ties between concepts, a feature related to the genealogy of concept formation; concepts are not isolated, logically defined entities, instead they have precedents on which they are based. This kind of relatedness also provides overall cohesion of the concept networks and maps in the form of larger cycles, a property suggested to be of great importance for learning and for knowledge representations useful for the learning process. We have here suggested how these central topological features can be measured from concept maps and how a quantitative description of connectedness and cohesion can be formulated. In particular, we have introduced a structural model for systematic regularities found for the clustering and cohesion in concept maps. This allows for the formulation of a statistical theory concerning the fluctuations around the deterministic average values and aids in answering the question, as to which features are characteristic of the well-organized maps. On this basis we have shown that the important quantities of clustering
C and cohesion Ω can be modelled with beta-distribution.
The fact that C and Ω can be represented by beta-distribution opens up the possibility to model the networks with the exponential family of probability distributions . This result is here supported by deriving the distribution on the basis of the Maximum Entropy (MaxEnt) method. In addition, the MaxEnt method allows for constructing a meaningful macro-level description of the concept maps and for basing the interpretation of their structural properties on concepts of energy and entropy. These powerful macro-level concepts open up an entirely different type of insight on the knowledge ordering process and on the cognitive process behind it.
The MaxEnt approach allows for assigning to the basic quantities the corresponding energies and , where can be interpreted as the energy gained by increasing order, while is energy related to the increasing difficulty of ordering the structure by creating 3-cycles by increasing X. In both cases and this difficulty is naturally related to the fact that triply connected nodes, which are not already 3-cycles, become more rare with increasing C and that it is not meaningful to connect all triples to 3-cycles. The intrinsic energy and the stress energy can be associated with the intrinsic cognitive load and germane cognitive load, respectively, associated with the construction of the concept maps. To the variables parameters and are conjugated so that they can be interpreted as the “inverse temperature” and ordering field . These parameters have actually the role of state variable characterizing the state of the system. Furthermore, they can be expressed in terms of scaled degree d, thus greatly simplifying the description of the system.
In addition to the energy, entropy plays a central role in the description of the concept maps. The entropy of the maps is a measure for the fluctuations around the mean values, thus gaining immediately the intuitively attractive interpretation as the measure for the variations in the individual capabilities of organizing knowledge. As expected, in designed maps the entropy is lower than in the associative maps, and in both cases it becomes lower with increasing d, indicating that with more connections the structure also becomes more ordered. This suggests that students that are able to provide more connection (having more knowledge at their command) are also better at organizing that knowledge.
The energetic and entropic description of the properties of concept maps based on the MaxEnt approach is, of course, only another way of representing systematic regularities and fluctuations around them, all that is contained already in the Equations 1–3. Interestingly, the description based on the MaxEnt approach is readily amenable to very persuasive interpretation and provides insight on modelling the cognitive processes during learning and in representing complex knowledge structures. Such a description also makes close contact to the more intuitive and qualitative description of the cognitive process behind knowledge organization, where the idea of “reduction of cognitive load” by knowledge organization is central. The lowering of free energy can be interpreted as a lowering of the total cognitive load (comprising of intrinsic and germane loads) through ordering the knowledge as triangular patterns, expected to be stable patterns in knowledge organization [
31]. In summary, the model we have suggested here points out that some important and central features of organized knowledge representations may be quite simple, like the organization of knowledge around stable and easily tractable patterns of triangular cycles. In particular we can recognize how creation of connected triangular cycles and larger cycles lowers the “cognitive load” in organizing the knowledge. Although this notion is still a speculative one it is a suggestive one that deserves closer attention and may eventually open up new directions for interdisciplinary research related to education and cognitive processes in learning.