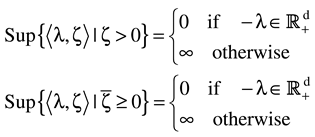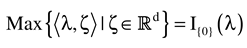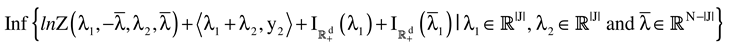1. Introduction and Basic Model
The sample selection problem appears often in empirical studies of labor supply, individuals' wages and other topics. For small sample sizes the existing parametric [
1] and semi-parametric estimators [
2,
3,
4,
5] have difficulties. Recently, [
6], henceforth GMP, developed a semi-parametric, Information-Theoretic (IT) estimator for the sample-selection problem that performs well when the sample is small. This estimator is based on the IT generalized maximum entropy (GME) approach of [
7] and [
8]. GMP used a large number of sampling experiments to investigate and compare the small-sample behavior of their estimator relative to other estimators. GMP concluded that their IT estimator is the most stable estimator while the likelihood estimators predicted better within the sample for large enough samples. Their IT estimator outperformed the AP estimator in most cases and in all small samples. Another set of experiments within the nonlinear framework appear in [
9].
GMP specified their IT-GME model with bounds on the parameters and with finite and discrete support. Though, their IT-GME estimator performs relatively well, it still has some of the basic shortcomings of that estimator. It has finite and bounded supports for both signal and noise, it is not flexible enough to incorporate infinitely large bounds and continuous support spaces, and it is constructed as a constrained optimization estimator. The objective here is to extend the estimator discussed in GMP in three directions. First, we allow unbounded support spaces for all parameters. Second, we accommodate for a whole class of (discrete and continuous) priors. Third, we construct our estimator as an unconstrained concentrated model.
1.1. The Basic Sample Selection Model
For simplicity, we follow a common labor model discussed in [
10]. Suppose individual
h (
h=1,…,
N) values staying (working) at home at wage
and can earn
in the marketplace. If
, the individual works in the marketplace,
y1h = 1, and we observe the market value,
. Otherwise,
y1h = 0 and
y2h = 0.
The individual's value at home or in the marketplace depends (linearly) on demographic characteristics (
x):
where
x1h and
x2h are K
1 and K
2-dimensional vectors,
β1 and
β2 are K
1 and K
2-dimensional vectors of unknowns and “
t” stands for “transpose”. This model can be expressed as
Our objective is to estimate β1 and β2. Typically the researcher is interested primarily in β2.
Unlike the more traditional models, GMP constructed their model as a solution to a constrained optimization problem such that the information represented by the set of censored equations (3)-(4) enters the estimation as inequalities:
In our formulation, we use inequalities as well to represent all available information in the set of censored equations.
2. The Information-Theoretic Estimator
Rewrite equations (1)-(2) as finding γ1 and γ2 in and , where the dependent variable is censored and where , . We formulate the censored model (5)-(7) in the following way.
Let the constraint sets
For each
i,
Ci,s is an auxiliary closed, convex set used to model the a-priori constraints on the
β’s. Similarly, the closed convex set
Ci,n is part of the specification of the “physical” nature of the noise and contains all possible realizations of
ε . We view the coordinates
and
as values of random variables distributed according to some probability measure
such that their expectations (E) are
We note that the qualifier “prior” assigned to the Q probability measures is not the traditional Bayesian view. Rather, the Qs is just a mathematical construct to transform the estimation problem into a variational problem. The Qn, however, could be viewed as the probability measure describing the statistical nature of the noise. The process of estimation of the noise involves a tilting of the prior measure.
Given some (any) prior measures we search for densities such that satisfies the system (3)-(4). This yields the parameter estimator and the estimated residuals .
Next, let
denotes the differential entropy divergence measure between the priors,
Qi, and the post-data (posteriors)
Pi. This is just the continuous version of the Kullback-Liebler information divergence measure, also known as relative entropy (see [
11,
12,
13]). Since the data are naturally divided into observed and unobserved parts, we divide the data into two subsets:
J and
Jc of {1,2,…,
N}. Next, rewrite the data (3)-(4)
and
as
where the matrices
B1 and
B2 correspond to the rows of the matrices
Ai (
i=1, 2) labeled by the indices for which observations are available. For the indices in
J the values
y2 are observed and
, whereas for the values in
Jc all we know is that
.
Our “
Basic (Primal) Problem” is the solution to
where the inequalities between vectors are taken to be component wise.
Next, we formulate the problem as a concentrated (unconstrained) entropy problem. To do so, we view the basic primal problem as a two stage problem, call it an “equivalent primal problem.” In the equivalent model the first stage consists of the standard Generalized Entropy problem (the equality portion of the model) for which a dual can be easily formulated.
The Equivalent primal problem is a solution to the two stage optimization problem:
Theorem 2.1. The
equivalent primal problem (11) is equivalent to the following (dual) problem
where
denotes the Euclidean scalar (inner) product of the vectors
a and
b,
and
are the four sets of Lagrange multipliers associated with (11). To carry out the procedure specified in (12) first set
, and then carry out the minimization.
To confirm the uniqueness of the solution to problem (12), observe that the function
is strictly convex on its domain
, and if
as
, then problem (12) has a unique solution, where “
” is the boundary of the set
Ψ. This is always true in the cases we consider here. A simple example in which it does not hold is
with
as domain. This has no minimum for a positive
y.
Solving (12) yields
, which in turn yields the optimal maximum entropy (posterior) density.
This density is naturally factored into a product of the maximum entropy densities of the two sets of equations. Therefore,
are independent with respect to the reconstructed density
, and with respect to the original priors. Once
is solved, we follow (8), or (9), to get
With that generic formulation, we show below three analytic examples that cover a wide range of possible priors and support spaces for β and ε.
3. Large Sample Properties
Denote by
the estimator of the true
when the sample size is
N. Throughout this section we add a subscript
N to all quantities introduced in
Section 2 to remind us that the size of the data set is
N. We show that
and
as
in some appropriate way. The proof is similar in logic to Proposition 3.2 in [
14]. We assume:
Assumption 3.1. For every sample size N, the minimizers of (12) are all in the interior of their domains: where “int” stands for interior.
Assumption 3.2. Let . Then, assume there exists such that (i) and such that and (ii) assume that there exists two matrices and such that and .
Note that .
Proposition 3.1. (Convergence in distribution.) Under Assumptions 3.1 and 3.2
- a)
as , for i=1, 2.
- b)
as
where
stands for convergence in distribution and
, where
is the covariance matrix of
with respect to
.
The approximate finite sample variance is for i = 1, 2 and as is shown in (8) or similarly in (12).
4. Analytic Examples
We discuss three examples, corresponding to assuming that the β’s are either unbounded (Normal), bounded below (Gamma) and bounded below and above (Bernoulli). Under the normal priors, the minimum described in (12) can be explicitly computed. In the other cases, a numerical computation is necessary.
4.1. Normal Priors
Let the constraint space be . Using the traditional view and centering the support spaces at zero, the prior—a product of two normal distributions—is . The covariance has two diagonal blocks: and . Without loss of generality, we assume that these two matrices are respectively. Our basic model holds for the general covariance structure .
Formulating these priors within our model yields
where
is a diagonal (K + N) × (K + N) matrix, the first block being a
K × K matrix with entries equal to
and the second block is a
N × N matrix with entries equal to
. That is, the priors on signal and noise spaces are iid normal random variables. Thus, problem (12) consists of finding the minimum of
over the set described in (12).
To verify that the minimizer of (12) occurs in the interior of the constraint set, we look at the first order conditions
A feasible solution to (12) may lie inside the domain of the constraints and provides a solution.
Once the system is solved for
, the estimated densities are
which, as expected, are normally distributed. Defining
(recall that
due to the constraints) we use (13) to get
for
i = 1, 2 and where
and
are matrices.
4.2. Gamma Priors
Let β’s be bounded below by 0. This can be easily generalized by an appropriate shifting of the support of the distributions. To show the generality of our model, we let the prior on the noise be normal thereby showing that one can use different priors for the signal and the noise.
The signal and noise constraint spaces respectively are
and
. The prior is
Before specifying the concentrated entropy function, we study the matrix A
1 defined as
. Note that
splits
X1 and
splits the
N × N identity matrix to match the splitting of X. The concentrated entropy function is
(Note that
and
.) A similar expression exists for
.
The problem (12) consists of minimizing
Once
are found, the optimal density is
The estimated parameters are
The realized residuals are
4.3. Bernoulli Priors
This example represents another extreme case where it is assumed that the β’s are bounded. For simplicity, assume that we know that all β’s lie in the interval [a, b], which makes the choice for all of the constraints on the signal space . For the noise component, we follow the previous formulation of normal priors.
With this background, the prior measure used is
The concentrated entropies are
where
and
. Recall that
. In this case, the function to be minimized is
which is minimized over the region described in (12). Again, the optimal solutions (minimizing
) is to be found numerically. The estimated post-data is
for i = 1,2 and where
from which the estimated parameters and residuals are given by
5. Empirical Example
We illustrate the applicability of our approach using an empirical application consisting of a small data set. The objective here is to demonstrate that our IT estimator is easy to apply and can be used for many different priors. The small sample performance of the IT-GME version of that estimator (uniform discrete priors) and detailed comparisons with other competing estimators is already shown in GMP and it falls outside the objectives of this note. The empirical example is based on one of the examples analyzed in GMP with data drawn from the March 1996 Current Population Survey. We estimated the wage-participation model for the subset of respondents in the labor market. Workers who are self-employed are excluded from the sample. Since the normal maximum likelihood estimator did not converge for that data [
15], only results for the OLS, Heckman two-step, a semi-parametric estimator with a nonparametric selection mechanism due to [
5], AP, and the different IT models developed here are reported [
16]. To make our results comparable across the IT estimators, we use the empirical standard deviations in all three cases and use supports between –100 and 100 for the IT-GME (uniform discrete priors) and the IT-Bernoulli case. In both the IT-Normal and IT-Bernoulli the priors used for the noise components are normal (as is shown in
Section 4). Under these very similar specifications, we would expect all three IT examples to yield comparable estimates. Naturally, there are many other priors to choose from, but the objective here is just to show the flexibility and applicability of our approach.
We analyze a sample of 151 Native American females, of whom 65 are in the labor force. The wage equation covariates include years of education, a dummy for currently enrolled in school, potential experience (age - education - 6) and potential experience squared, a dummy for rural location, and a dummy for central city location. The covariates in the selection equation include all the variables in the wage equation and the amount of welfare payments received in the previous year, a dummy equal one for married, and the number of children. We use the three exclusion restrictions to identify the wage equation in the parametric and nonparametric two-step approaches.
Table 1.
Estimates of the Native American wage equation (151 individuals; 65 in labor force).
Table 1.
Estimates of the Native American wage equation (151 individuals; 65 in labor force).
| | OLS | 2-Step | AP | IT-GME | IT-Normal | IT-Bernoulli |
|---|
| Constant | 1.073 | 1.771 | NA | 1.038 | 1.049 | 1.068 |
| Education | 0.055 | 0.043 | 0.044 | 0.054 | 0.056 | 0.055 |
| Experience | 0.038 | 0.023 | 0.038 | 0.038 | 0.038 | 0.038 |
| Experience Squared | –0.001 | –0.0005 | –0.001 | –0.001 | –0.001 | –0.001 |
| Rural | 0.214 | 0.268 | 0.332 | 0.210 | 0.215 | 0.214 |
| Central City | –0.170 | –0.091 | –0.171 | –0.186 | –0.166 | –0.169 |
| Enrolled in School | –0.290 | –0.471 | –0.190 | –0.301 | –0.283 | –0.288 |
| λ | | –0.461 | | | | |
| R2 | 0.355 | 0.376 | NA | 0.343 | 0.355 | 0.354 |
| MSPE | 0.157 | 0.135 | NA | 0.147 | 0.144 | 0.144 |
Table 1 presents the estimated coefficients for the wage equation. The R
2 and Mean Squared Prediction Error (MSPE) for each model are presented as well. All IT estimators outperform the other estimators in terms of predicting selection [
17]. The estimated return to education is about 5% across all estimation methods, but only statistically significantly different from 0 for the OLS and the IT estimators. Though, all estimators have estimated parameters of the same magnitude and sign, only the OLS and the three reported IT estimates are statistically significantly different from zero in most cases.
6. Conclusion
In this short paper we develop a simple to apply, information-theoretic, method for analyzing nonlinear data with sample selection problem. Rather than using a likelihood approach or a semi-parametric approach we generalized further the IT-GME model of Golan, Moretti and Perloff (2004). Our model (i) allows for bounded and unbounded supports on all the unknown parameters, (ii) allows us to use a whole class of priors (continuous or discrete), (iii) is specified as a nonlinear concentrated entropy model, and (iv) is easy to apply. Like GMP our model works well even with small data. This is shown in our empirical example. The extensions developed here mark a significant improvement on the GMP model and other IT, generalized entropy models.
A detailed set of sampling experiments comparing our IT method with all other competitors, under different data processes, will be done in future work.