As mentioned, there are different measures of fairness such as maximin, proportional, Gini coefficient, Theil index, etc. What then would be the appropriate measure of fairness in an ideal free market environment? In other words, what measure captures the kind of fairness promoted by the ideal, self-organizing, free market dynamics as discussed in the previous section. Recall that in the ideal free market environment there is no central authority to enforce those fairness policies which require the presence of such an authority to compute and enforce the chosen fairness measure. This right away would eliminate measures such as maximin, proportional, Gini coefficient and others which require such a presence.
3.1. Entropy as a Measure of Fairness: Statistical Thermodynamics Approach
In statistical thermodynamics, one analyzes the evolution of many-particle systems by using the concept of
phase space [
9,
10]. The phase space is an abstract multi-dimensional space of positions and momenta. For instance, the phase space of
N mono-atomic gas molecules in a closed container is the
6N dimensional space specifying the three positions and three momenta for each molecule. A point in this space specifies the positions and momenta of all the molecules, thus representing the state of the system at some time
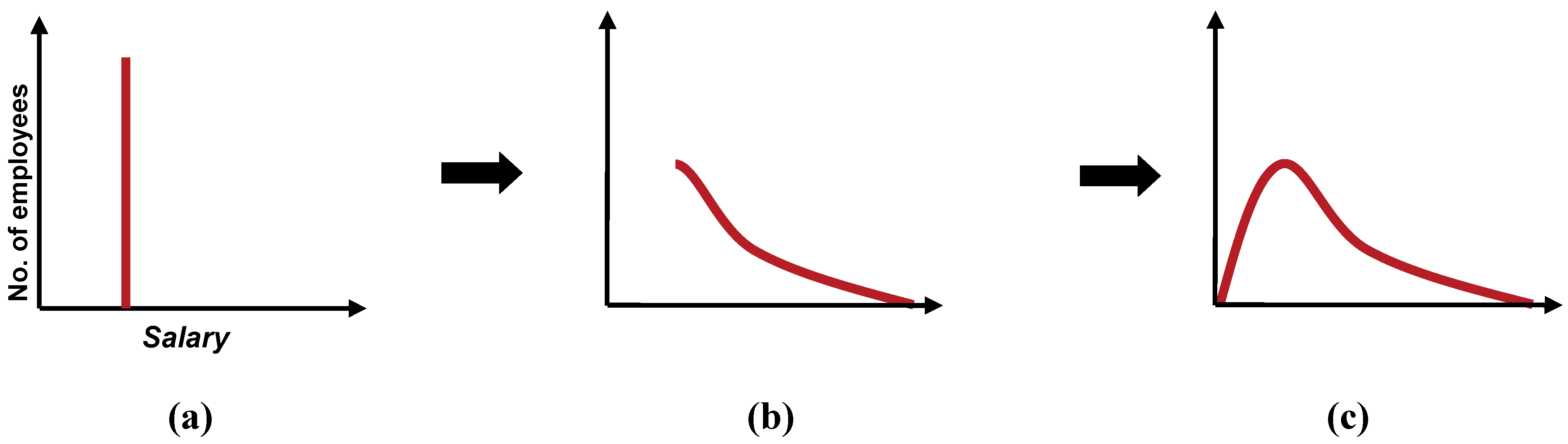
t.Consider an isolated thermodynamic system of N gas molecules and a total energy of E, with an average energy of Eave = E/N. In such an isolated system, both N and E are conserved. Now imagine starting this system at t=0 in the initial state where all molecules are assigned to have exactly the same energy Eave. In time, the system will evolve from this initial state of a Kronecker delta distribution in energy to one where the energy distribution is more spread out as a result of intermolecular collisions which cause varied energy exchanges among the molecules.
Similarly, we can define the economic phase space of the company A as an N-dimensional space with each dimension representing the salary Si of an employee i. In reality, this space will be more complicated with additional dimensions that capture other features such as titles, awards, education, experience, etc., but let us restrict ourselves to salary as it is the dominant feature. A point in this ideal phase space represents the state of the company at some time t by specifying the salaries of all the employees. Company A is an isolated system, in the thermodynamic sense, with respect N and M (i.e., these are conserved) but an open system with respect to information exchanges regarding salaries and job openings elsewhere in the free market economic environment.
The role of information exchanges is an important distinction between thermodynamic systems and economic systems. In thermodynamics, we have three classes of systems: isolated (both total energy E and number of molecules N are fixed), closed (only number of molecules N is constant, E can vary due to exchanges with the surrounding environment), and open (both N and E vary due to exchanges with the environment). Thus, there are only two kinds of exchanges: energy and matter. However, in our free market environment, we have an additional possibility due to information exchange. We can have a situation where a system is isolated with respect to money and employees (i.e., these are fixed as it is in our case) but open with respect to information exchanges. Note, however, that information exchange is not subject to conservation laws like those of energy and matter.
As the salaries of the employees increase and decrease, as discussed in
Section 2, the company adapts, evolves, and wanders stochastically through the phase space. This process is essentially the same as how
N molecules of a gas in an isolated system get distributed in their phase space of
6N dimensions of positions and momenta. Of course, the mechanistic details of the evolution of the two systems are quite different. For molecules, the system evolves through molecular collisions governed by Newton’s laws of motion and conservation laws. For employees, it is through the exchange of information between
A and the free market environment driven by the needs of the rational agents to maximize utility and profit. Information exchanges are the “collisions” in this regard.
We shall now present an intuitive analysis of the dynamics of our ideal free market. To illustrate the key conceptual insights, let us stipulate some numbers for the situation of company
A discussed in
Section 2. Let
N = 1,000 and
M = $60 million. Let us now define the
microstate and the
macrostate of this system. Specifying the salaries for each employee,
i.e., {
S1, S2, …,S1000}, at any given time
t corresponds to defining the
microstate of
A. Specifying how many employees are in
each of the
k salary categories, at any given time, corresponds to defining the
macrostate of
A. Generally, for a large
N, there will be an extremely large number of macrostates. Most macrostates, in turn, would contain an unimaginably large number of different microstates. This property is known as
multiplicity (W) in statistical mechanics. The Kronecker delta function configuration presented above is a unique exception, a macrostate that has only one microstate. As the company adapts and evolves over time, it will wander from one microstate to another. This does not mean, however, it will necessarily move from one macrostate to another as many different microstates could correspond to the same macrostate due to multiplicity.
Let us now consider a free market environment consisting of a large number of companies (
A, B, C, etc.), each one with the same
N and
M as
A. They are all identical replicas of
A, except that each one is in a
different microstate. This is the equivalent of the
microcanonical (NVE) ensemble in
statistical thermodynamics for a free market environment. As noted, many of the microstates may correspond to the same macrostate. In this ensemble, consider two companies
A and
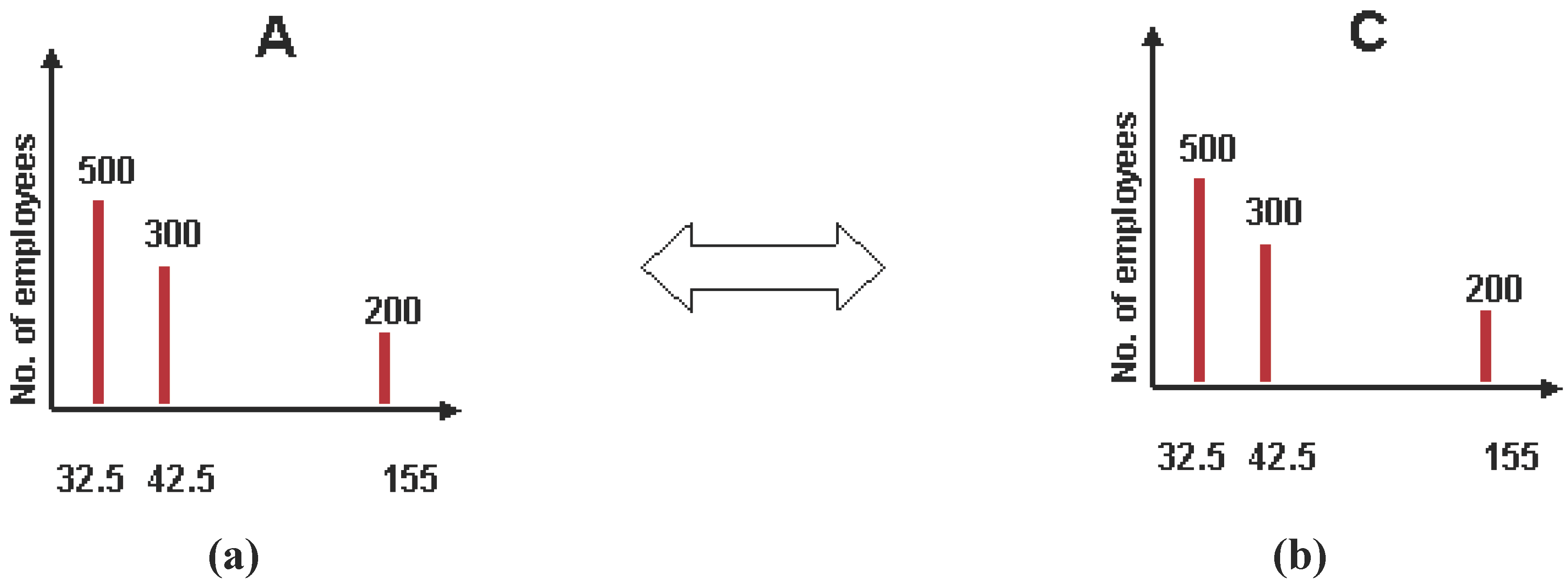
B, shown in
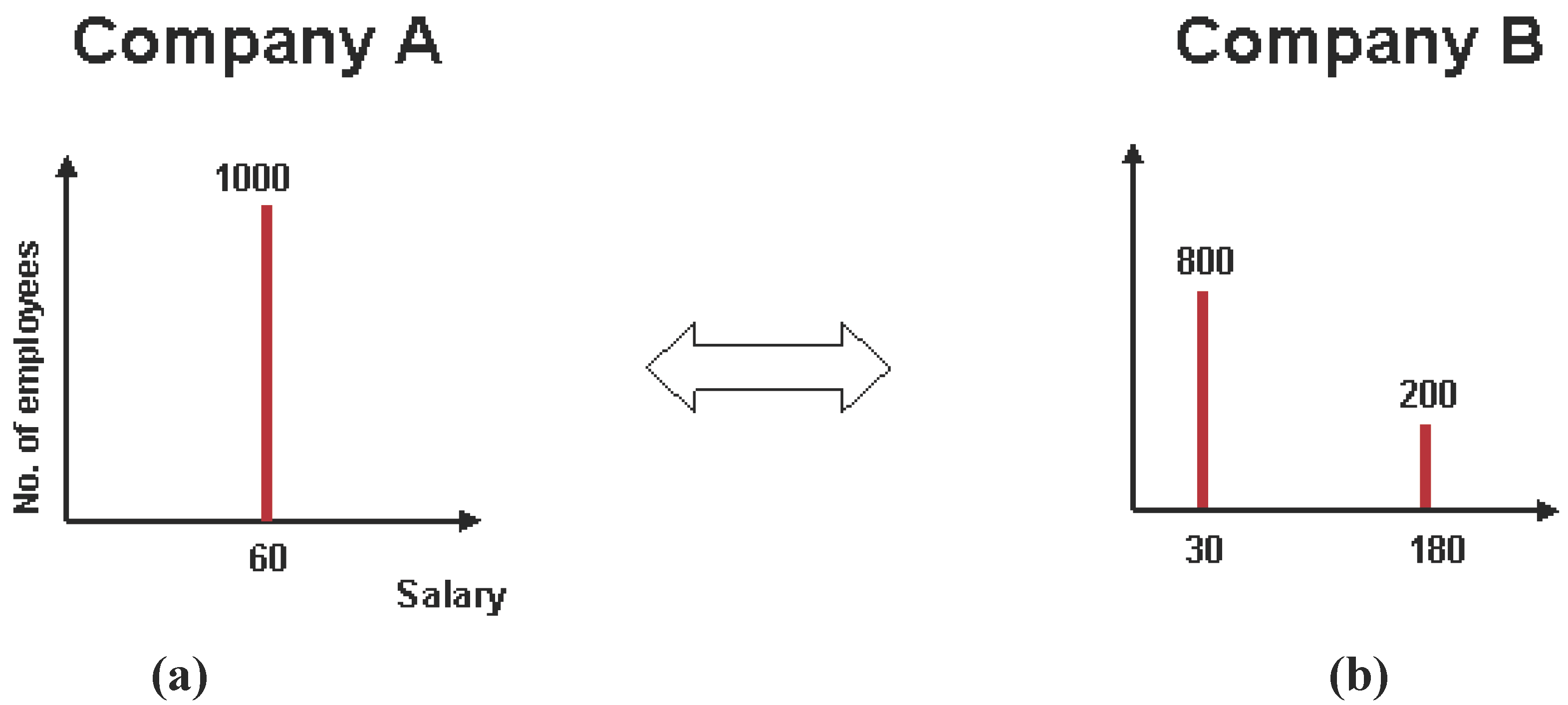
Figure 2(a) and
Figure 2(b) (the figures are not drawn to scale, as it is not important for our discussion).
A is in the macrostate of all 1,000 employees making the same salary of $60,000/year.
B is in the macrostate of 800 employees making $30,000/year and the remaining 200 at $180,000/year. Both satisfy the
N = 1,000 and
M = $60 million constraints. In 2(a) only one category has employees with none in all other categories. This macrostate can be realized in only one way (
W = 1) and, therefore, this macrostate has only one microstate. In 2(b) two categories are active. This macrostate can be realized in 10
220 ways, through the various permutations of the employees, thus resulting in a multiplicity of 10
220 microstates (we show below how multiplicity is calculated). Let us further assume that there are three classes of employees: low skilled (contributing value
Vlow), medium skilled (
Vmed), and high skilled (
Vhigh), such that
Vlow < Vmed < Vhigh, implying that
Slow < Smed < Shigh. Let us further stipulate that the number of low skilled employees is 500, medium skilled 300, and high skilled 200.
Figure 2.
Free market interaction between A and B: Initial macrostate.
Figure 2.
Free market interaction between A and B: Initial macrostate.
As these two companies interact, as shown by the double headed arrow, in the free market environment, the 200 high skilled employees in A (call it A-high), making $60K each, will be motivated to increase their utilities and consider a move to B for the higher salary ($180K). Similarly, B sees an opportunity to reduce its costs by firing all of its 200 high skilled employees (B-high) and hiring the A-high group at a lower salary. But in order to attract A-high B has to offer a salary that is more than what A-high makes currently (i.e., $60K each) as an incentive. However, to maximize its profit, B will offer A-high the smallest incentive possible, say, $60K+ε, where ε is some small amount arbitrarily close to zero (say, $1). Likewise, in order to motivate B to hire A-high it will offer to work for a salary that is less than what B-high makes as an incentive. But, as before, in order to maximize its utility, A-high will offer the smallest incentive possible, and propose a salary of $180K-ε. If both parties don’t budge from their respective initial offers no further action takes place and we reach a stalemate.
But let us suppose that they negotiate, as it typically happens in a real free market environment, and agree to split the difference 50:50. Thus, they agree on a salary of $120K/year.
B decides to fire
B-high and hire
A-high at $120K/yr each.
A-high also decides to leave
A for
B. But the
B-high group do not want to lose their jobs and agree to continue to work at
B for less salary at $120K/yr. At the same time, to avoid losing the
A-high group of employees and go out of business,
A decides to match
B’s offer and agrees to pay them $120K/yr. Thus, a new category, at $120K, appears in
A as well as in
B as seen in
Figure 3(a) and
Figure 3(b).
In a similar fashion, the 300 medium skilled workers in
B (
B-med) making $30K/yr, will try to move to
A, and, likewise,
A will try to fire the 300
A-med employees and hire
B-med for a lower salary. As in the previous case, this will lead to the creation of a new category at $45K for 300 employees in both
A and
B, as shown in
Figure 3(a) and
Figure 3(b).
Figure 3.
Free market interaction between A and B: Evolution of a new macrostate.
Figure 3.
Free market interaction between A and B: Evolution of a new macrostate.
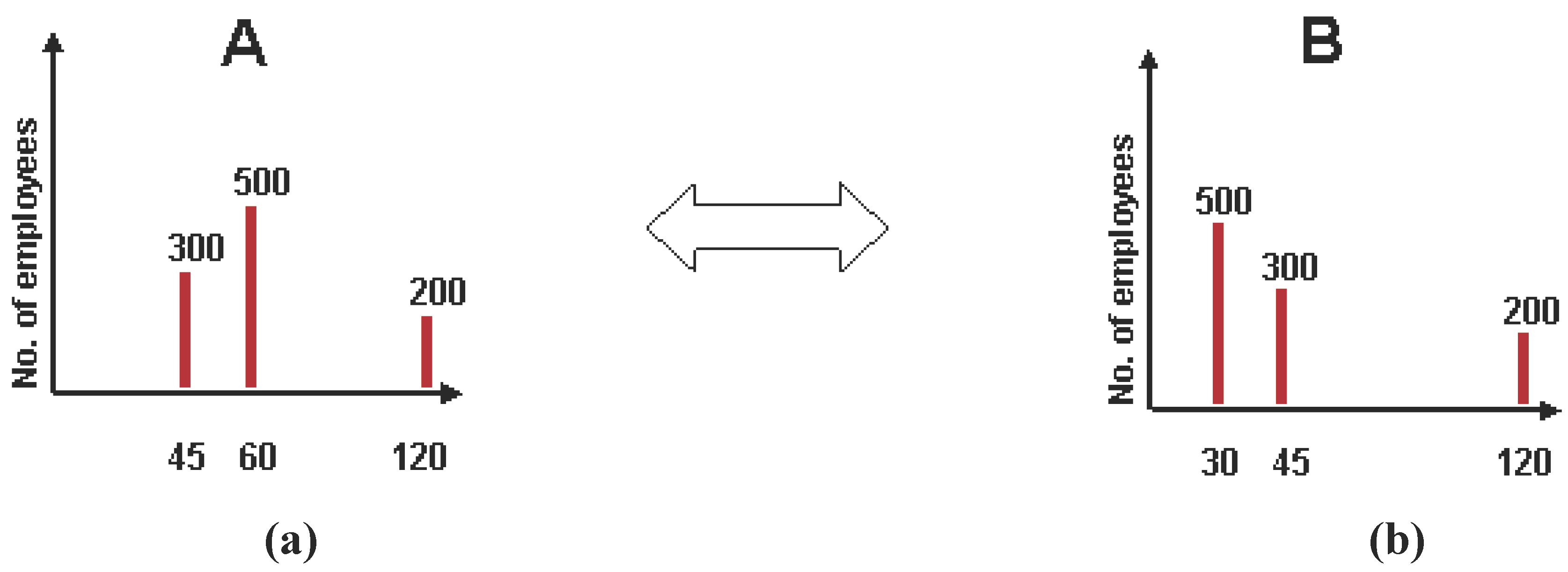
Finally, the 500 low skilled employees in
B (
B-low) making $30K/yr will try to move to
A in order to make more. This will result in the addition of another 500 employees to the $45K category and the elimination of the $30K and $60K categories, leading to the final distributions seen in
Figure 4(a) and
Figure 4(b). These are the final macrostates of
A and
B in this context.
Note that these adjustments and alignments do not happen sequentially but simultaneously. Thus, we see that the initial delta function distribution in
Figure 2(a) has finally led to the emergence of a bimodal distribution through the free market dynamics. Note that not only
A changed but
B also adapted in order to survive. Now, both
A and
B are in equilibrium with each other and no further adjustment takes place between them.
Figure 4.
Free market interaction between A and B: New equilibrium macrostate.
Figure 4.
Free market interaction between A and B: New equilibrium macrostate.
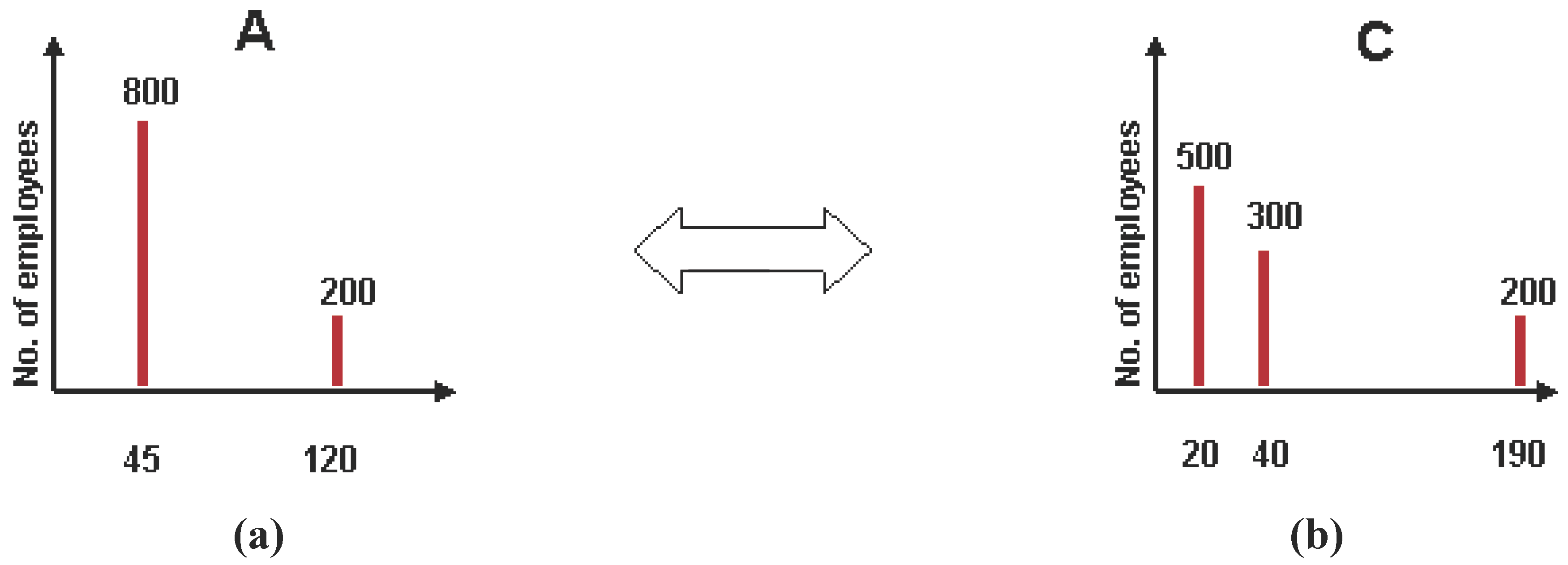
Now, let us examine the situation when this new
A comes in contact with another company
C in the ensemble as shown in
Figure 5(a) and
Figure 5(b). Carrying out the aforementioned analysis, we see that this leads to the final distributions seen in
Figure 6(a) and
Figure 6(c), which are the new final macrostate.
Figure 5.
Free market interaction between A and C: Initial macrostate.
Figure 5.
Free market interaction between A and C: Initial macrostate.
Figure 6.
Free market interaction between A and C: New equilibrium macrostate.
Figure 6.
Free market interaction between A and C: New equilibrium macrostate.
Thus, we see that through such interactions in the free market ensemble companies will evolve, create some new categories, eliminate some other categories, adapt the salaries for the categories, and finally settle in some equilibrium macrostate that naturally emerges as the final resting state. The key insight here is that if a particular value (
i.e., salary) category contains employees making varying value contributions (e.g., as in
Figure 2(a), where three different types of employees,
A-low,
A-med, and
A-high, are all classified as one salary category), the poorly paid “higher-value” employees will be motivated to seek opportunities elsewhere. This will force all the interacting companies to suitably adapt as we saw in our example above. These self corrections will continue to happen until each category, under the
N and
M constraints, finally ends up with a
homogenous subset of employees (meaning that they are all contributing the same value) all of whom receive the same salary appropriate for that category. Thus, the ideal free market ensures that all employees are treated fairly within their respective value categories (which is the same as salary categories as salaries are proxies of the values contributed by the employees)–
i.e.,
intra-category fairness emerges as a natural consequence of the free market dynamics.
But how about inter-category fairness? To gain insights about this let us consider another scenario where company A starts with a uniform distribution of employees over all the possible k categories. Let N = 1,000 and k= 10, and, therefore, we have 100 employees in each category. We have 100 CEOs (corresponding to the k = 10 category), 100 vice presidents (k=9), 100 engineers (say, k=5), etc. What this distribution assumes is that the total value to be created by A, in terms of its products and services, would require such a uniform assignment of employee resources. Obviously, A only needs one CEO, perhaps three or four vice presidents, and many more engineers and other personnel. Let us say that the k = 5 category really needs 200 engineers because of the amount of work needed to be executed at that level, but was assigned only 100.
Since the amount of work to be done, and hence the value created, in the CEO or vice president categories are already specified and limited (as they are in the other categories), one of several work patterns would emerge: all 100 CEOs slack off and contribute 1% each for the total value created by the CEO category, or one CEO creates all the value and the others contribute nothing, or some other combination some contributing and some not. At any rate, not everyone is contributing 100% of the value each, but all of them are getting paid 100% of the CEO salary each.
On the other hand, in k = 5 category, the 100 engineers work twice as hard to create value that nominally requires the output of 200 engineers. However, they are all paid the salary that is specified for the k=5 category and not more. While there is no intra-category unfairness in the k = 5 category (since all these employees are contributing the same value and getting paid the same salary), there is inter-category unfairness felt by the k = 5 category engineers. These employees will resent the unfairness of what the CEOs and VPs are getting away with and hence will leave for other companies where there is no such glaring inter-category disparity. Obviously, this can happen at all categories, not just at k = 5. As a result, A will not survive unless it adapts and reallocates its employee resources more sensibly. We see that when employee resources are not properly allocated across the different categories issues of fairness automatically creep up and the free market tries to correct such imbalances. Since all the companies in the free market will be self correcting in this manner, the distribution will become more and more fair, iteratively, and will eventually reach an equilibrium macrostate where the salary distribution is maximally fair with respect to both intra-category and inter-category under the given constraints.
Thus, we see how the different employee classes, based on their value contributions (which depend on their talents, education, experience, skills,
etc.), naturally emerge and self organize to reach the equilibrium macrostate, guided by Adam Smith’s invisible hands, through the dynamics of the free market environment, such that every employee feels he or she is fairly compensated for the value contribution he or she has made. When all companies in the free market reach such a classification of their employees
equilibrium is reached as there is no incentive left for any employee (or company) to switch jobs (or employees) as we see in
Figure 4 or
Figure 6. Thus, the equilibrium distribution is maximally fair. As the companies evolve, adapt, and stochastically search for this equilibrium macrostate that is the optimal compromise under the given constraints, they will settle into a macrostate that can be arrived at in most number of ways–
i.e., one with the maximum multiplicity,
W, subject to the
N and
M constraints. This is given by the well known result in statistical mechanics and information theory [
9,
10,
11,
15]:
where
ni is the number of employees in the value category
i , subject to the constraints:
Using Stirling’s approximation, for large
N:
it is easy to show that [
15] maximizing ln
W is the same as maximizing entropy
H, subject to the
N and
M constraints, where
H is given by:
Thus, in essence, the evolution of an economic system of rational agents (
i.e., employees and companies) in the abstract phase space is the same as that of a thermodynamic system of molecules. Our claim is that once one transforms the dynamics of a free market process as the wanderings in the
economic phase space, then the formal and powerful mathematical and conceptual machinery of statistical mechanics can be unleashed to prove the maximum entropy outcome at equilibrium. Thus, we conclude that the evolution of our company
A in an ideal free market system will also be governed by the maximum entropy principle with the important distinction that entropy here is a
measure of fairness. We discuss this interpretation and its implications in greater detail in
Section 4.
Even though, for the sake of simplicity of analysis, we made some assumptions regarding the number of different employee classes, the number of employees in a class, the 50:50 compromise in negotiations, etc., these are not necessary to arrive at the conclusions we described above. It is easy to see that one could have started with a different number of classes, different number of employees, and a different kind of compromise, and would still have arrived at the same general conclusions.