1. Introduction
Research on socio-economic problems in general, and economic modeling in particular, often has to deal with information about the flows contained in a matrix of interaction between agents. Just to mention a couple of examples, international economists frequently analyze the flows of bilateral trade between a group of countries in order to measure the level of integration and demographers take data from matrices of international or interregional migration flows and sociologists. The problem is that the compilation of the information required to build this type of matrices is often extremely expensive and time-consuming for the statistical agencies or research institutes. In this context, the use of estimation methods for recovering the cells of these matrices is becoming more and more popular; especially the estimation techniques based on information measures (see Golan
et al., [
2] or Kapur and Kesavan [
3]).
Basically, these techniques take as point of departure an initial matrix (the prior), which is assumed to be similar to the one we want to estimate, together with some limited information of the actual matrix, usually aggregated data -row and column margins-. The basic idea of the estimation process is to choose as solution the matrix that, fulfilling the constraints imposed by the known information, is the closest to the prior according to some divergence criterion. One of the most used adjusting procedures is the Cross-Entropy (CE) technique, which is based on the Kullback-Leibler divergence criterion.
This paper explores from a new viewpoint the role played by the initial information in an estimation process based on information measures. Traditionally, the estimation problem takes as point of departure one single prior; for example, a previous matrix from a past period or a contemporaneous matrix for other geographical area. The novelty of our proposal is that it considers the possibility of including several initial matrices in the estimation process, instead of choosing only one of them. By means of a numerical simulation, we illustrate that the proposed technique that uses a composite of two priors obtain comparative better results than an adjustment from only one of them, provided that none of them is preferable to the other for all the probability distributions contained in the target matrix.
The paper is organized in the following sections.
Section 2 presents the basis of the CE solution to the estimation problem of a matrix with unknown cells but with information on its margins. In
Section 3, the details of the composite CE technique proposed in this paper is introduced.
Section 4 shows a numerical Monte Carlo experiment where the performance of the proposed method is compared with other competing techniques. In
Section 5 an empirical application with a real-world example is included, where a matrix of interregional trade for the Spanish regions is estimated. Finally,
Section 6 concludes the paper.
2. The Ce Solution for the Matrix Balancing Problem
We will base our explanations on the matrix-balancing problem depicted in Golan ([
4], page 105), where the goal is to fill the (unknown) cells of a matrix of dimension
using the information that is contained in the aggregate data of the row and column sums. This is a familiar situation in the context of economics, where the cells of some matrices containing information on flows between several agents are usually not observable directly. Instead, the researchers often limit to observe aggregate information (total sales or purchases per agent, for example), because these aggregates are much quicker and easier to obtain.
The
cells of the matrix are the unknown quantities we would like to estimate, where the aggregate
,
, and
are known. Note that the
elements can be expressed as sets of (column) probability distributions, simply dividing the quantities of the matrix by the corresponding column sums
. In such a case, the previous matrix can be rewritten in terms of a new matrix
that is composed by a set of
M probability distributions (
Table 1).
Table 1.
The matrix balancing problem.
Table 1.
The matrix balancing problem.
| … | | … | | |
| … | | … | | … | … |
| … | | … | | |
| … | | … | | … | … |
| … | | … | | |
| … | | … | | |
Where the
(shaded in grey) are defined as the proportions
, and the new row and column margins as
and
respectively. Consequently, the followings equalities are fulfilled by the
elements:
These two sets of equations reflect all we know about the elements of matrix
. Equation (2) shows the cross-relationship between the (unknown)
in the matrix and the (known) sums of each row and column. Additionally, equation (1) indicates that the
can be viewed as (column) probability distributions. Note that we have only
pieces of information to estimate the
elements of matrix
, which makes the problem ill-posed. The solution to this type of problems can be obtained by minimizing a divergence measure with a prior probability matrix
subject to the set of constraints (1) and (2). This is called a Cross-Entropy (CE) problem, which can be written in the following terms:
Subject to the same restrictions given by the set of equations (1) and (2). The divergence measure
is the Kullback-Liebler entropy divergence between the posterior and prior distributions. The Lagrangian function for the CE problem is:
And the solutions are:
where
are the Lagrangian multipliers associated with the constraints (2). The CE estimation procedure can be seen as an extension of the Maximum Entropy (ME) principle, given that the solutions of both approaches are the same when the
a priori probability distribution contained in
are all uniform. The accuracy of the solution obtained for this matrix adjusting problem will depend on the choice made when specifying
(see, for example, Hewings [
5] for a detailed discussion on the role played by the prior information in such estimation problems in a socio-economic context). In some cases there is no room for this choice, simply because only one possible prior is available. But it may well be that for some cases we have the possibility of using two alternative matrices
or
as prior. For example, if the objective was to estimate inter-industry trade flows for a country in a specific year, it would be possible to take as prior the observed flows for the same country in a past year or, alternatively, to take as prior the distribution of inter-industry flows for a simultaneous year but in a different country. The next section of the paper deals with situations where we include both priors at the same time to the estimation process.
3. A Composite Ce Method: The Dwp Estimation Technique
The above sketched CE procedure can be extended in order to develop a more flexible estimator that allows for including in the estimation process both prior matrices
and
. Related to the Bayesian Method of Moments (see Zellner, [
6,
7]), the technique has been proposed in Golan [
8] as a data-based method of estimation that uses both sample and non-sample information in determining a basis for coefficient reduction and extraneous variable identification in regression linear models. Another recent empirical application of this method to the field of empirical economic analysis can also be found in Bernadini [
9]. The point of departure of the estimation technique proposed in Golan [
8] it is to consider two alternative priors for each coefficient in a linear model. One of the prior is a uniform distribution centered on zero and the other is a spike distribution with a unit mass prior on zero. When the spike prior takes over the uniform one, the coefficient is shrunk and the corresponding variable is classified as extraneous.
This idea will be adapted to a matrix balancing problem of a target matrix
from two possible priors
and
and our objective in this context will be twofold: a) to identify which of the two priors would be preferable for each column of the matrix and, simultaneously, b) to estimate the target matrix. If we denote with
and
the two options we have for the
a priori (column) distributions respectively, the objective proposed can be achieved by modifying the previous CE program in the following way:
The parameters are estimated simultaneously with the unknown probabilities of the matrix. Each measures the weight given to the prior for each column and it is defined as , where and are respectively the lower and upper bound defined as the support of these parameters (note that this implies that ). The a priori probability distributions fixed for them are uniform . This means that the a priori value for each parameter is 0.5, but the sample information contained in constraint (7) allows for estimates that deviate from this initial point.
To understand the logic of this data-weighted prior (DWP) estimator some further explanations on the objective function of the previous minimization program is required. Note that equation (6) is divided in three terms. The first term quantifies the divergence between the recovered probabilities and the a priori probabilities where matrix is chosen as prior, being this divergence weighted by for each column. On the contrary, the second element of (6) measures the divergence with the prior and it is weighted by . The third element in (6) quantifies the Kullback divergence for the weighting parameters .
The solutions of this minimization program are:
where:
and
are the Lagrangian multipliers associated with restrictions (7). The properties of this DWP estimator in the context of classical linear regression models have been tested in Golan [
8] (under some mild assumptions, see Golan [
8], page 177, the consistency and asymptotic normality of the DWP estimates can be ensured. Additionally, these assumptions also guarantee that the approximate variances of the DWP estimator is lower than the approximate variance of the generalized CE estimator, which in turn is lower than the approximate variance of a ML-LS estimator (see Golan, [
8], page 179).
Simultaneously to the estimation of the
cells of the matrix, the DWP estimator discriminates for each column j between the two priors considered. The proposed estimation strategy provides estimates of the weighting parameters
, obtained as:
which can be used as a tool for this purpose. Without any sample information [
i.e., without the set of constraints (7) the estimates of these parameters would be
for each and every column. The more informative the constrains (7), the larger the deviation with this initial value of the parameter. Note that as
the prior
gains weight for column j and the estimates approach those of the CE updating process from
. On the contrary, large values of
, the CE estimation from prior
takes over. Consequently, relatively large values of
(
) will be an indication of a column j characterized by a high weight of prior
. In other words, in this specific column j it would be preferable to use an adjustment from the a
priori matrix
rather than updating
. On the contrary, comparatively small values of
(when
) are a signal of an column j where the updating process should be preferred.
4. Testing the Dwp Estimation Technique with a Numerical Experiment
In order to test the performance of the proposed estimation technique, we have carried out a numerical simulation exercise where the DWP estimation is compared with a more traditional adjusting process where only one prior matrix is considered.
For the sake of simplicity, let us assume that we want to estimate a symmetric matrix (
). In the experiment we have fixed a target matrix
with dimensions
where the only known information is the column and row margins. This matrix has been fixed as the actual matrix of annual interregional trade (in millions of €) for the 15 Spanish inland regions in 2006. The matrix was constructed by the Lawrence Klein Institute (from the Autonomous University of Madrid) inside the C-Intereg project (for more details, visit
http://www.c-intereg.es). Such a matrix is normally quite difficult to construct, given the huge amount of information that it requires, being available matrices only for the short period from 2002 to 2006 constructed annually. This matrix
has been transformed into a matrix of column coefficients
to be estimated from the information contained in vectors
and
y. The information contained in the margin vectors of the matrix (total imports and export per region) is much more accessible, given that it can be obtained from the Regional Accounts regularly published by the Spanish Statistical Institute (see
http://www.ine.es/en/inebmenu/mnu_cuentas_en.htm for more details on the Spanish Regional Accounts).
We also defined several a priori matrices to be used in the estimation of . Firstly, we have generated a possible a priori matrix , being the values of this matrix obtained as where is a perturbation term that distributes as and . Note that the value of scalar reflects the level of deviation between the prior and the posterior: the smaller its value, the more similar the a priori and the target matrix.
Additionally to this
a priori matrix, we have also generated a matrix
whose elements have been obtained as:
In other words, this new a priori matrix is characterized by having ten of their columns (from column number 1 to number 10) more dissimilar to the target matrix than the competing prior ; which means that in these cases it is not a very informative prior and consequently would be preferable taking as initial matrix for the adjusting process of these specific columns. However, for the remaining five columns (number 11 to 15) it happens the opposite, given that the distribution is closer to the target matrix than the prior .
Under these conditions we have estimated matrix
by three different ways: updating the
a priori matrix
, updating the
a priori matrix
and using the proposed DWP estimation technique that construct a composite of both matrices as possible priors. These three estimation strategies correspond respectively with the minimization of the three following divergence measures:
subject to the same type of constraints explained before.
To evaluate the performance of these alternative estimation approaches, 1,000 trials have been carried out and we have computed the average of three measures of overall deviation between the target matrix and the estimates. Specifically, we obtained the total absolute error (TAE), the total squared error (TSE) and the total Kullback divergence (TKL), being respectively defined as:
where the
elements denote the estimated probabilities under the three different approaches.
Table 2 summarizes the average results obtained:
Table 2.
Deviation measures between the target and estimated matrices in the numerical experiments.
Table 2.
Deviation measures between the target and estimated matrices in the numerical experiments.
| Technique (prior used) | Deviation measures |
|---|
| TSE | TAE | TKL |
|---|
| Adjusting from | 0.014 | 0.936 | 0.052 |
| Adjusting from | 0.037 | 1.425 | 0.142 |
| DWP (mixture of , ) | 0.013 | 0.882 | 0.049 |
The deviation measures shown on
Table 2 provide some interesting results. Firstly, we can see the estimation of matrix
taking
as point of departure presents a comparatively worse performance than an adjustment from
. Not surprisingly, the comparatively more dissimilar distributions from matrix
we specified for ten out of the fifteen columns contained in
cause this result. But this does not necessarily mean that all the information contained in this matrix should be neglected. Note that in the remaining columns the elements of
distribute closer to the target matrix than their counterparts in the competing prior
. Therefore, matrix
contains also valuable
a priori information that could be useful in the estimation problem. If we incorporate both matrices of
a priori information in the adjusting process by using the DWP estimation, we let the data speak for themselves and choose the most appropriate prior for each column, which in the end obtains smaller deviation measures.
The average results obtained for the weighting parameters
also show how the DWP estimation works. Under the conditions described in the experiment, the DWP estimation technique identifies the columns where the distribution of the coefficients should be taken from one specific prior of the two initial matrices considered. Without any sample information the a priori expected value is = 0.5, but the information included into the estimation process leads the DWP technique to give on average smaller weights to the first group of columns (column from 1 to 10) in matrix . The weights estimated for this first group are in all the cases not larger than 0.5; which means that in this case the priors contained in take over. On the contrary, for the second group of columns (from 11 to 15) the estimates of are in all the cases equal or larger than 0.5, pointing out that for these columns prior should be preferred.
The relative performance of the DWP technique depends to a great extent on the degree of comparative similarity of the auxiliary prior
with the target matrix
. If the prior
is closer for every column than the prior
, there would not be gains from using the composite prior between both because it would be always better to use as prior
than the competing
and it would be also preferable to any possible combination of
and
(unless that the estimate of
for every column equals exactly one). A similar conclusion would be obtained in a symmetric case when for each column
is more similar to
than
It is on intermediate situations when the DWP estimator outperforms the adjustment form one single prior, given that takes the specific columns for each one that should be selected. In other words, when the number of column that behave like j1 (more dissimilar to
than their counterparts in
) in the numerical experiment takes intermediate values between 0 and 15.
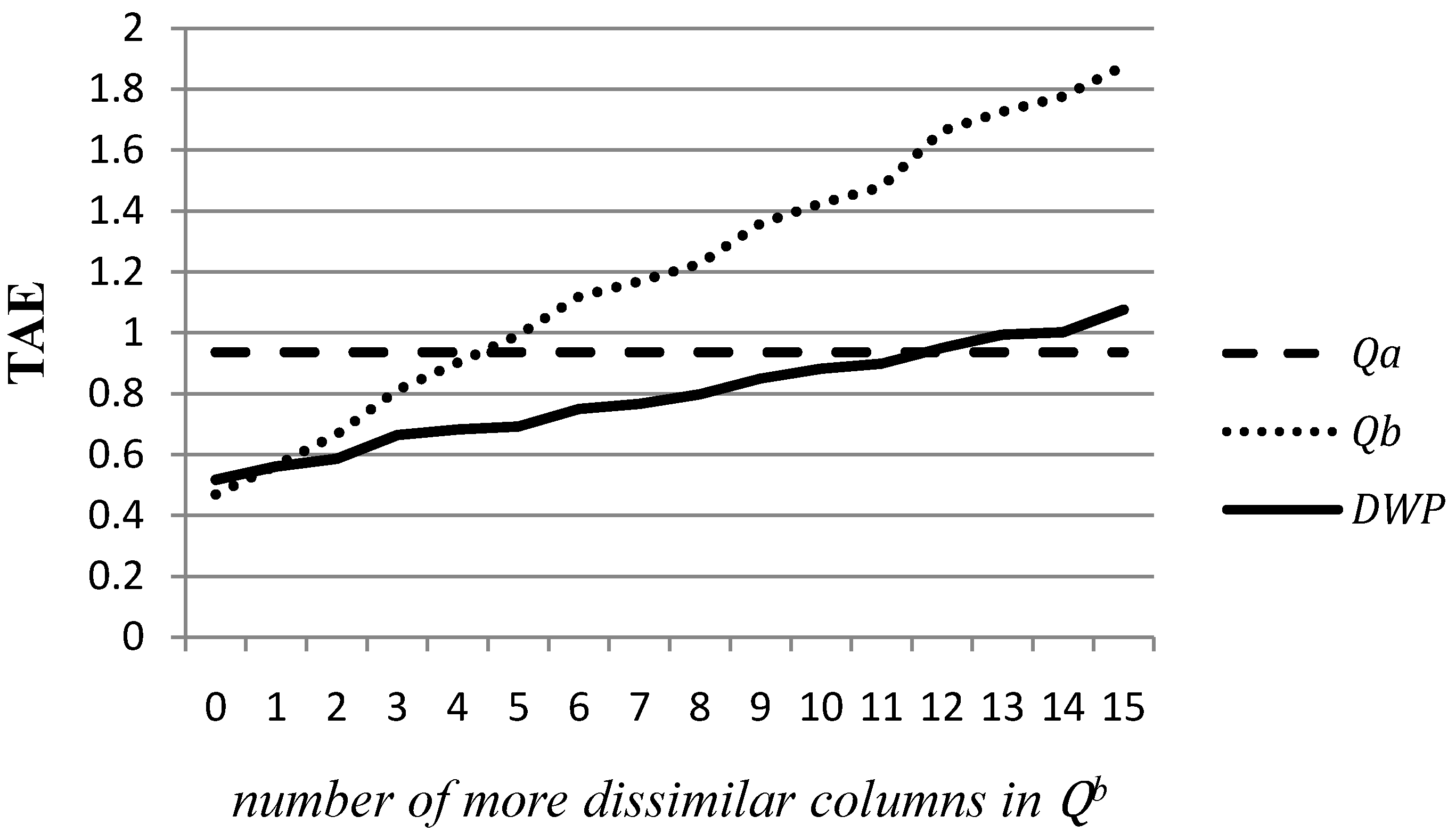
Figure 1 illustrates this idea extending the definition of the column of matrix
to all the possible cases in the terms of the previous numerical simulation.
The horizontal axis of the figure contains different numbers of columns that behave like in the prior . The vertical axis shows the mean of the absolute errors of the three competing adjusting technique that have been obtained along 1,000 simulations. The discontinuous line shows the average absolute deviation between the target matrix and the estimates when they are obtained by and adjustment from . Obviously, this deviation does not depend on the characteristics of , so it is a constant value. The dotted line represents the absolute deviations between the cells of and the estimates obtained from prior . Not surprisingly, it takes very low values when all the columns are more similar to than the other prior and it grows as long as the number of more dissimilar columns also increases.
The solid line represents the deviation measures for the estimates obtained by the DWP technique. When the prior has very few columns (less than two) more dissimilar to than , the estimation with the DWP yields worse result than an adjustment from . Conversely, if has many columns (twelve or more) more dissimilar to than , although the DWP technique outperforms a CE estimation from , it yields comparative higher deviations than and adjustment from . It is on intermediate situations where the DWP approach obtains better results than the CE estimation from only one of the priors, given that in such situations taking a composite of both priors allows for choosing the most valuable information contained in each one.
Figure 1.
Absolute deviations between the target and estimates matrices under different levels of similarity between and .
Figure 1.
Absolute deviations between the target and estimates matrices under different levels of similarity between and .
5. An Empirical Application: Estimating the Interregional Trade Matrix in Spain, 2006
As a complement to the numerical simulation made in the previous section, this section presents an empirical application of the DWP technique and compares the results obtained with other competing techniques. For this purpose, we took again the matrix of interregional trade for fifteen Spanish regions in 2006. Let us assume that the only known information of this matrix are the row and column margins (total sales and purchases per region respectively), and from this partial information we want to estimate the inter-industry flows matrix Z. For this purpose, we will apply an adjusting process to obtain the column-coefficients matrix P from two different initial matrices. Moreover, we also assume that we have some information on the expected structure of this matrix, obtained from the observed matrices of interregional trade column coefficients for two consecutive years in the past, specifically 2004 and 2005 ( and respectively).
Although intuitively one could think that taking the closest matrix (i.e., the 2005 matrix) as prior would be always preferable, it might also happen that for some uncontrolled reasons the structure of interregional trade in 2006 was more similar to a more distant a priori matrix in time. For example, it could happen that some unnoticed phenomenon happened in 2005 that disrupted the usual configuration of the matrix for some of the columns – for example, a massive strike in one region, a natural disaster that spoils the crops in a specific place, etc. - but the normality returns in 2006. In such a case, taking all the columns of this matrix as point of departure could be not the best option, and alternative previous matrix could be preferable as initial distribution in the estimation of the coefficients for some regions.
Consequently, we include as alternative prior in the estimation problem the matrix for 2004 and again we compare the performance of three estimation techniques of the target matrix
P: an adjustment considering from
, from the prior
and the DWP estimator that takes both possible priors.
Table 3 summarizes the results obtained in this study case, applying the same criteria as before for comparing the estimated and the target matrix:
Table 3.
Deviation measures between the target and estimated matrices in the empirical application.
Table 3.
Deviation measures between the target and estimated matrices in the empirical application.
| Technique (prior used) | Deviation measures |
|---|
| TSE | TAE | TKL |
|---|
| Adjusting from | 0.063 | 2.424 | 1.096 |
| Adjusting from | 0.083 | 2.428 | 0.783 |
| DWP (mixture of , ) | 0.047 | 1.999 | 0.672 |
In the estimation problem studied here, the results seem to be in line with the results obtained in the numerical experiment. Firstly, we can see that there is not an a priori matrix always superior to the other, but it depends on the deviation criterion applied: an adjustment from would be preferred to an estimation from under the Kulback divergence, but the opposite decision would be concluded if we pay attention to the squared or absolute divergence criterion. However, the results obtained applying the DWP estimation yields the smallest deviations under the three. The comparatively better performance of the DWP estimation is a consequence of a situation like the explained above: matrix contains a priori information that should be preferred to the prior contained in for some regions, but the contrary situation happens in the remaining cases. In such a case, if we incorporate both matrices by using the DWP estimation, we let the data speak for themselves and choose the most appropriate prior for each column, which in the end obtains smaller deviation measures (the use of the DWP estimator does not imply a significant difference in terms of time cost. Using an average personal computer and the CONOPT solver of the GAMS 2.0 software, the estimations made in this section took less than five seconds).
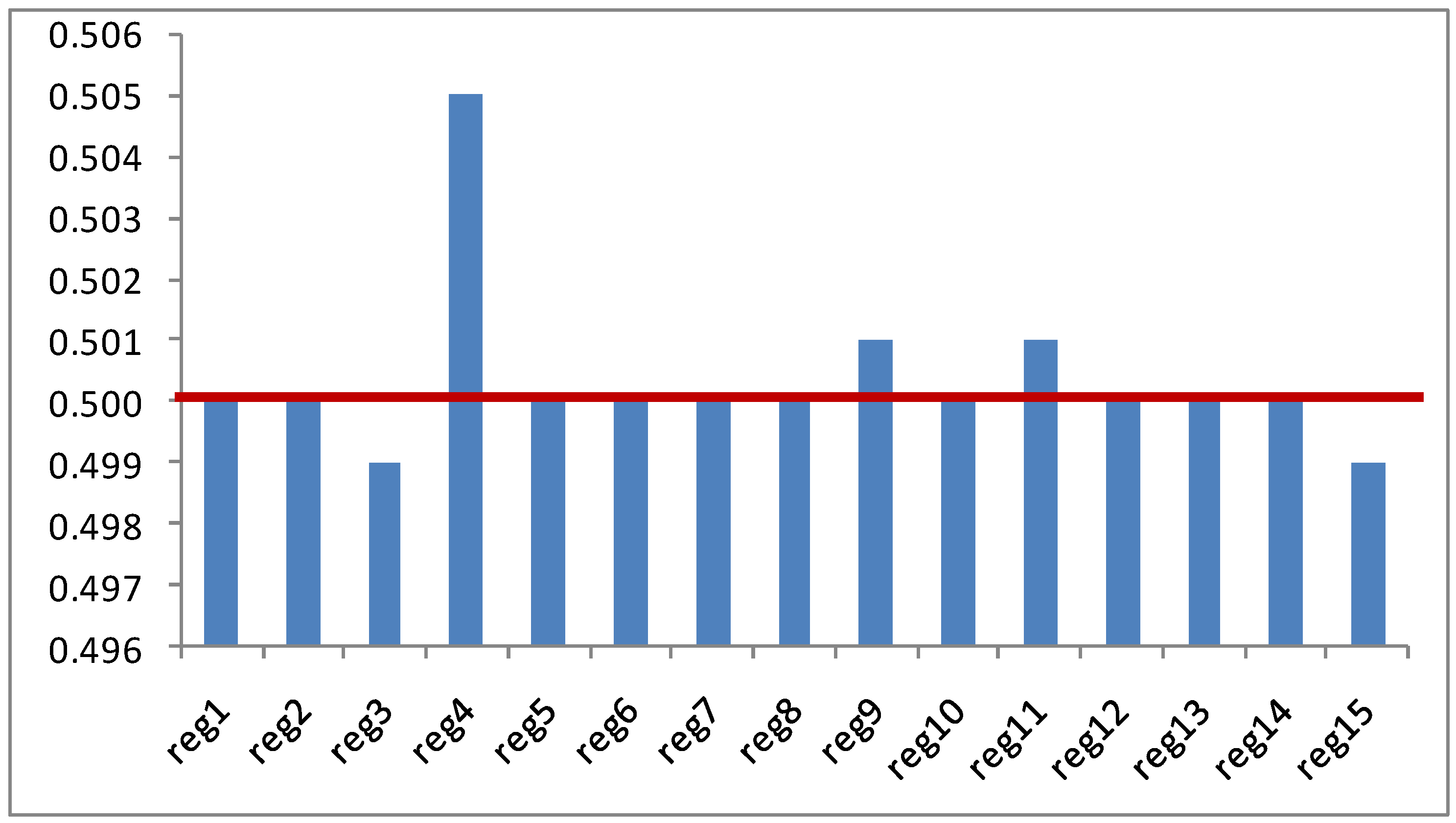
The estimates of the parameters in this empirical application measures the respective weights given to the columns of prior , and their graphical representation can be useful to understand how the DWP discriminates between the two priors in this problem.
Figure 2 shows how the DWP estimator discriminates between the two priors: for all the regions (columns) in the matrix the initial guess of parameter
is 0.5. From this a priori value, the technique manages to identify some regions where the prior contained in the respective column of the matrix
(region 4, Cantabria; region 9, Extremadura; and region 11, Madrid) where this prior is more strongly weighted in the estimation process. Oppositely, there are other regions where the
a priori matrix
is clearly preferred and the estimated value of the corresponding weighting parameter
is smaller than 0.5 (region 3, Asturias; and region 15, La Rioja). This discrimination between priors allows for optimizing the use of the two priors and yields smaller deviations between the estimated matrix and the actual values of interregional trade.
Figure 2.
Estimates of the weighting parameters .
Figure 2.
Estimates of the weighting parameters .