Estimation of Seismic Wavelets Based on the Multivariate Scale Mixture of Gaussians Model
Abstract
:1. Introduction
2. Wavelet Model and the General CM Methods
2.1. Estimating the Phase
2.2. Estimating the Scale and Frequency of the Seismic Wavelet
3. MSMG (Multivariate Scale Mixture of Gaussians) Model
4. Estimating the HOS of Recorded Seismic Trace Based on MSMG Model
4.1. Calculating the HOS of Recorded Seismic Trace
| 0 | |
| 0 | |
4.2. One-dimensional Cumulant Rate
4.3. Estimating ODCR
4.4. The Behavior of ODCR with Different Orders
| Error | The summation of error |
|---|---|
| SNR | |||||
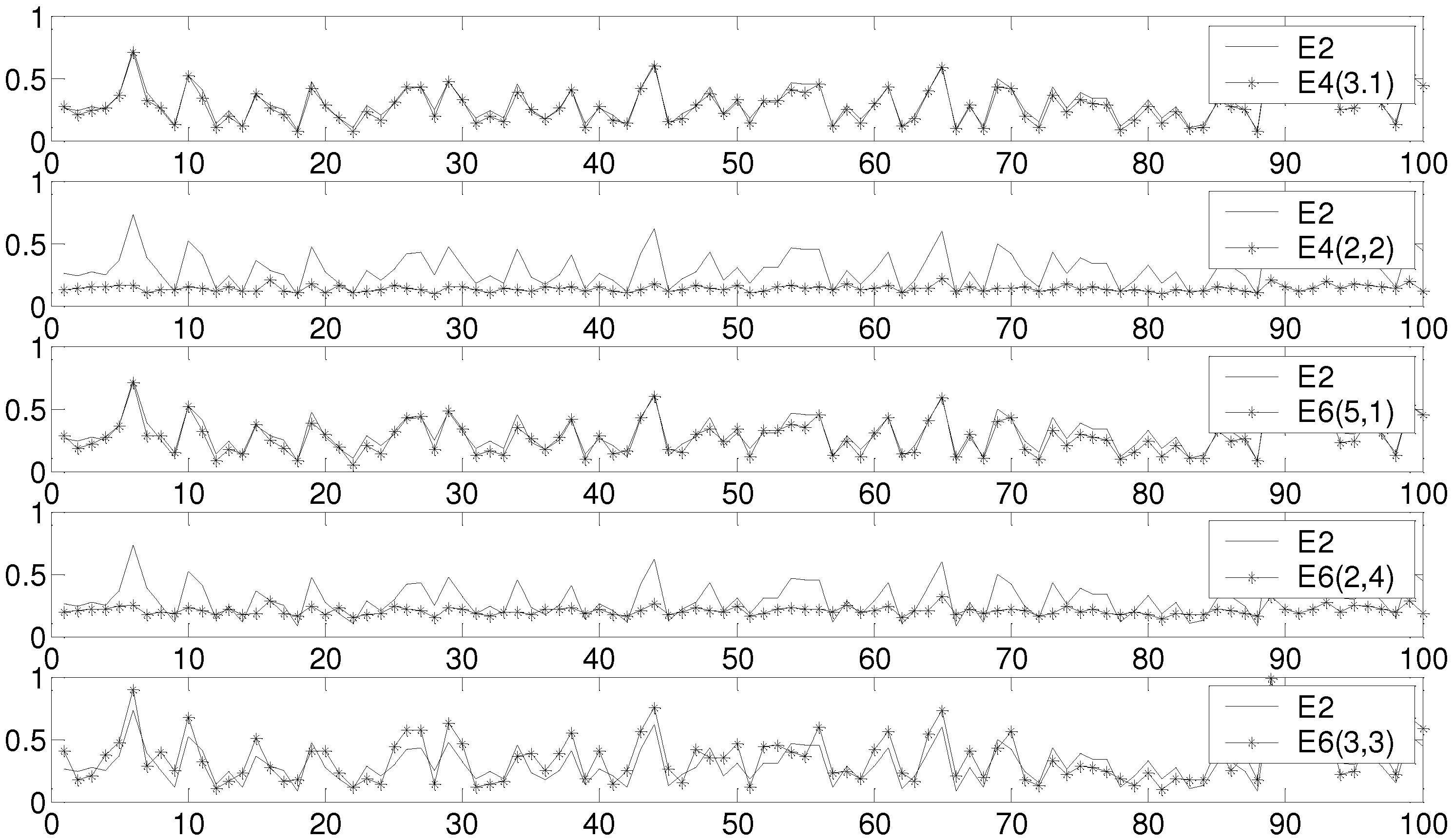
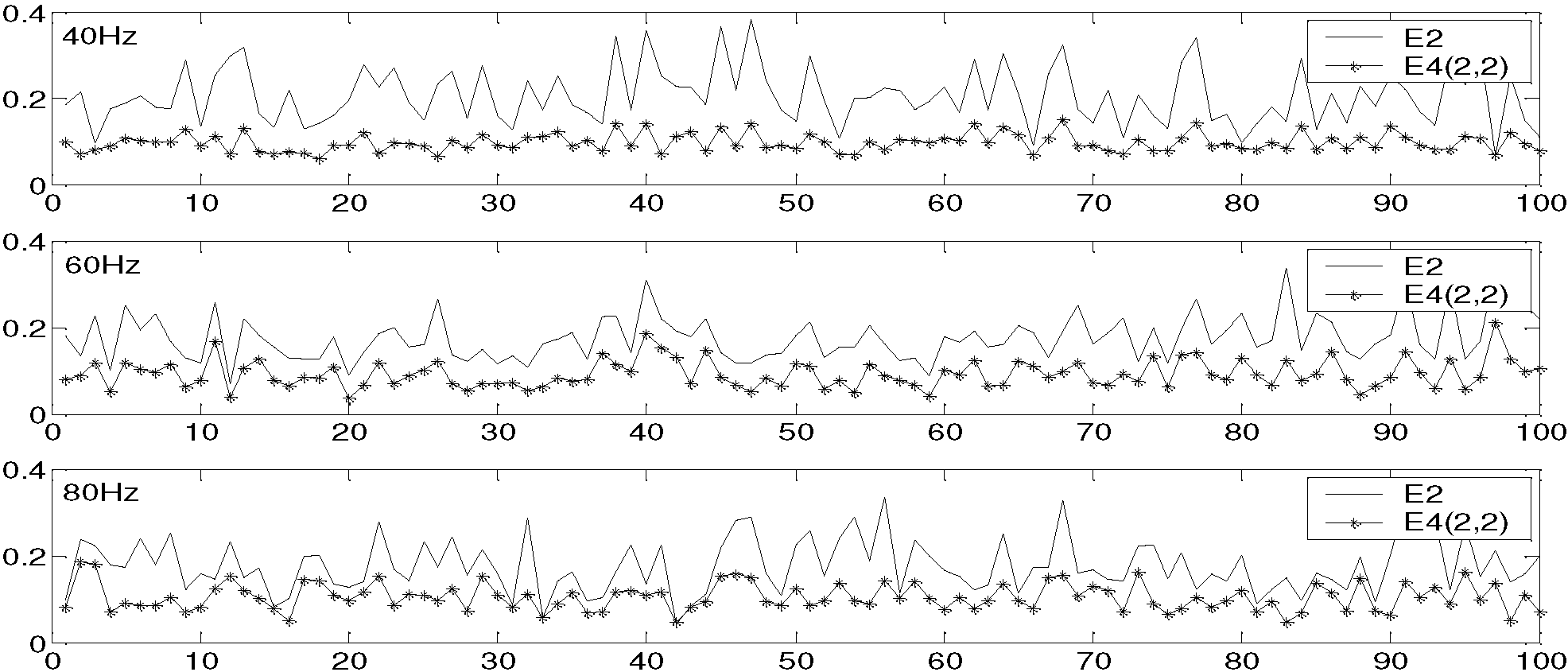
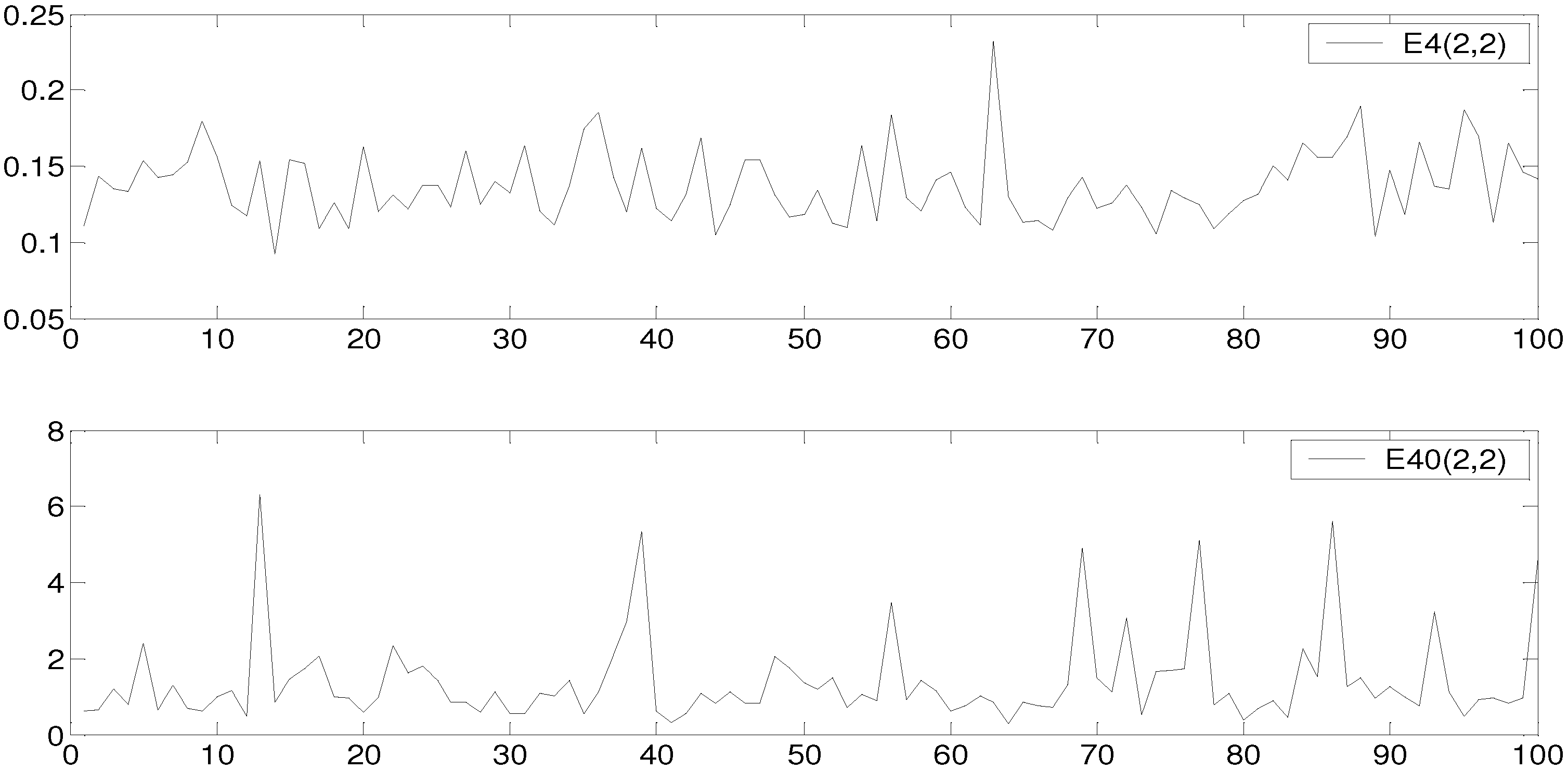
5. Estimating the Wavelet
- Use constant-phase rotation method to obtain the wavelet phase.
- Estimate the correlation coefficient of the recorded seismic trace, and compute 4(yn(2), yn+m(2)).
- Compute (m) corresponding to the different values of the scale, frequency and lags.
- Minimize cost function to get the scale and frequency parameters.
6. Results
6.1. Simulation Results
| SNR | |||||||
| True parameter | |||||||
| Estimated parameter |
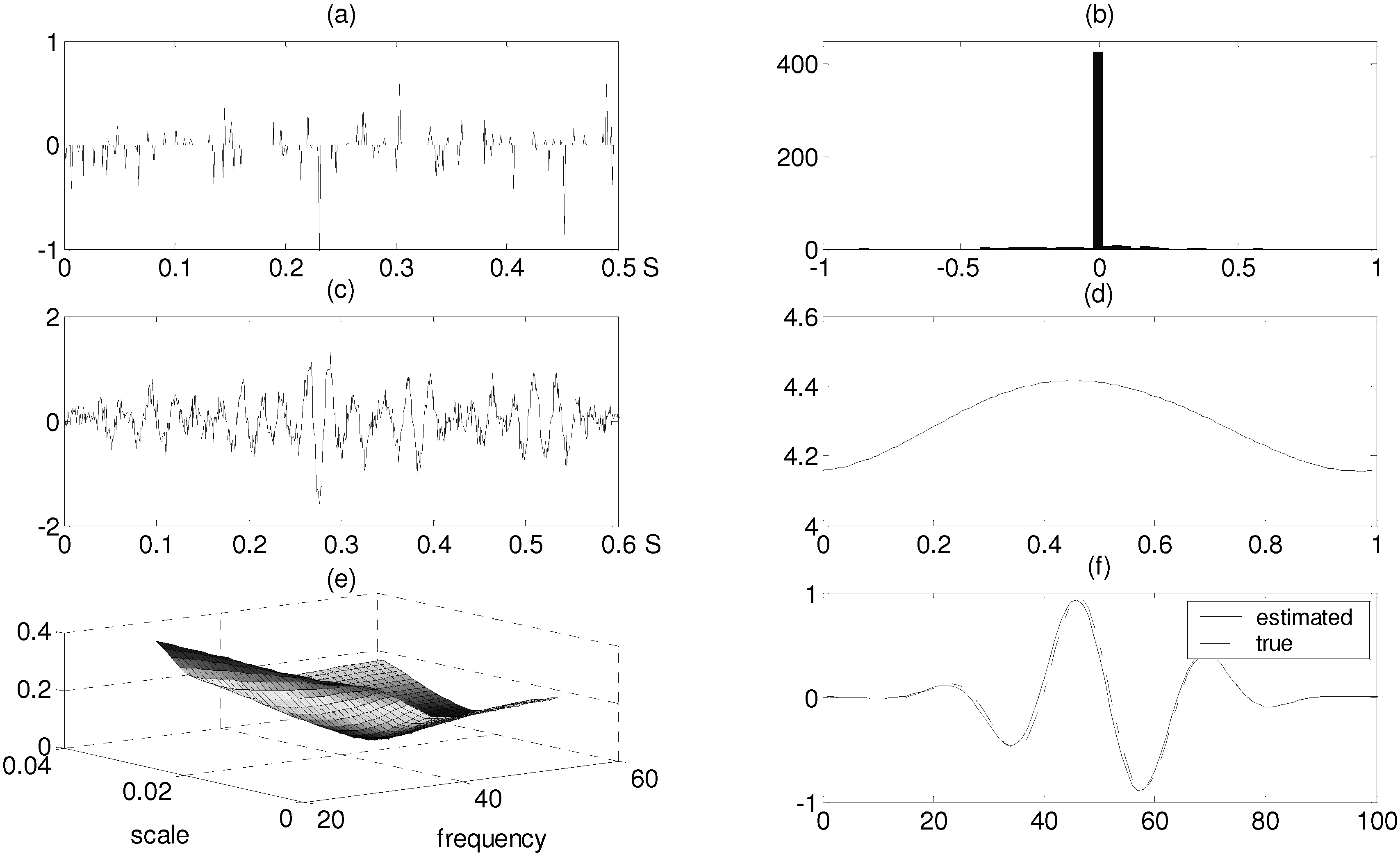
6.2. Real-data Experiment
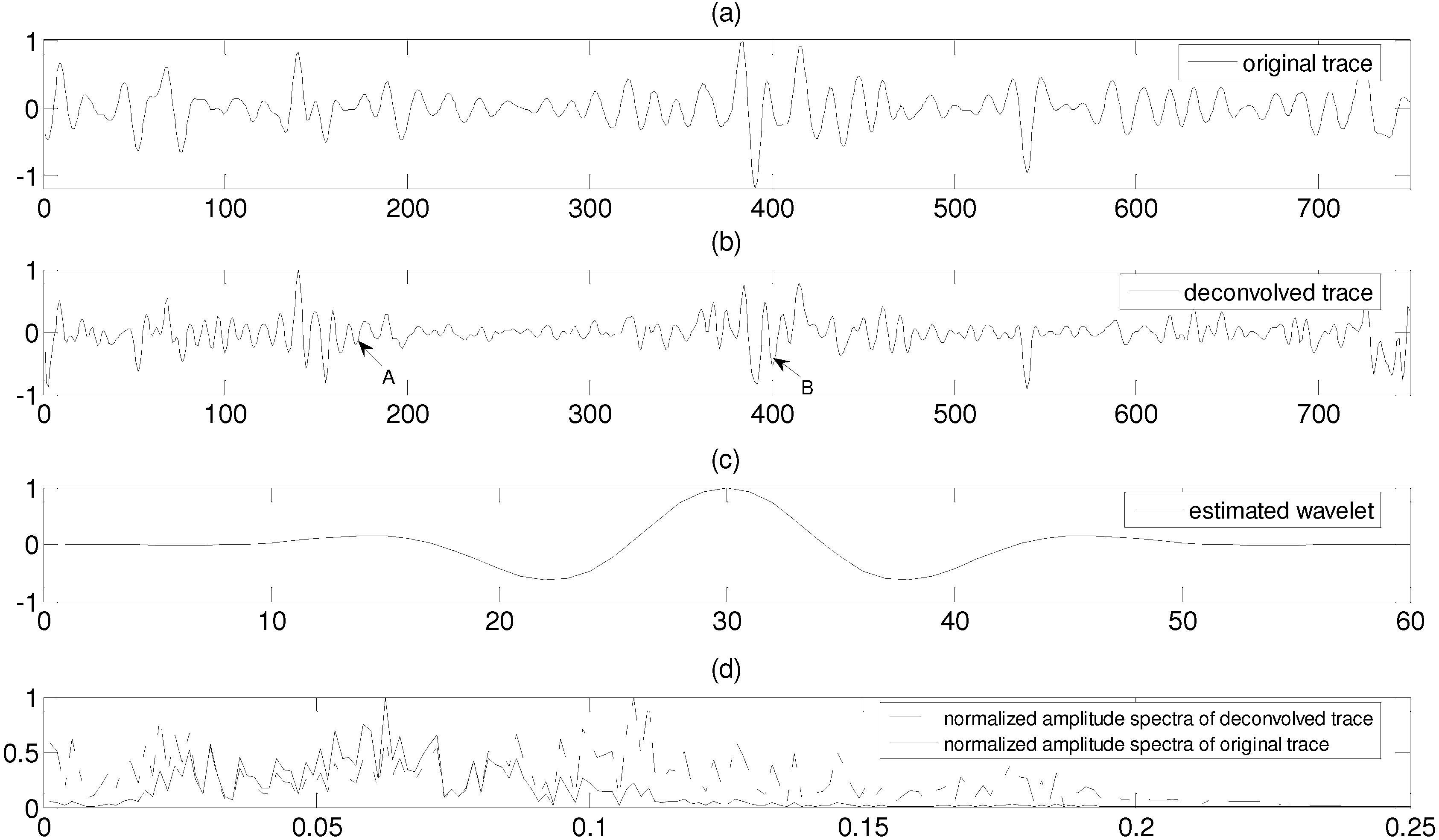
7. Conclusions
Acknowledgements
References
- Robinson, E.A.; Treitel, S. Geophysical Signal Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1980; pp. 152–161. [Google Scholar]
- Peacock, K.I.; Treitel, S. Predictive deconvolution: theory and practice. Geophysics 1969, 43, 155–169. [Google Scholar] [Green Version]
- Larue, A.; Mars, J.I.; Jutten, C. Frequency-domain blind deconvolution based on mutual information rate. IEEE T. Signal Proces. 2006, 54, 1771–1781. [Google Scholar] [CrossRef]
- Larue, A.; Pham, D.T. Comparison of Supergaussianity and Whiteness Assumptions for Blind Deconvolution in Noisy Context. In Proceedings of the EUSIPCO 2006 Conference, Florence, Italy, September 4–9, 2006.
- Pham, D.T. Generalized mutual information approach to multi-channel blind deconvolution. Signal Process. 2007, 87, 2045–2060. [Google Scholar] [CrossRef]
- van der Baan, M.; Pham, D.T. Robust wavelet estimation and blind deconvolution of noisy surface seismics. Geophysics 2008, 73, 37–46. [Google Scholar]
- Nsiri, B.; Chonavel, T.; Boucher, J.-M.; Nouzé, H. Blind submarine seismic deconvolution for long source wavelets. IEEE J. Oceanic Eng. 2007, 32, 729–743. [Google Scholar] [CrossRef]
- Rosec, O.; Boucher, J.-M.; Nsiri, B.; Chonavel, T. Blind marine seismic deconvolution using statistical MCMC methods. IEEE J. Oceanic Eng. 2003, 28, 502–512. [Google Scholar] [CrossRef]
- Cheng, Q.; Chen, R.; Li, T.-H. Simultaneous wavelet estimation and deconvolution of reflection seismic signals. IEEE T. Geosci. Remote 1996, 34, 377–384. [Google Scholar] [CrossRef]
- Veils, D.R.; Ulrych, T.J. Simulated annealing wavelet estimation via fourth-order cumulant matching. Geophysics 1996, 61, 1939–1948. [Google Scholar] [CrossRef]
- Gao, J.-H.; Yang, S.-L.; Wang, D.-X. Q Factor Estimation Using Instantaneous Frequency at Envelope Peak of Seismic Signal. In Presented at the 79th Annual Meeting and International Exposition of the Society of Exploration Geophysicists, Houston, TX, USA, October 25–30, 2009.
- van der Baan, M. Time-varying wavelet estimation and deconvolution by Kurtosis maximization. Geophysics 2008, 73, v11–v18. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; John Wiley & Sons Inc: New York, NY, USA, 2001. [Google Scholar]
- Bartlett, S.M. An Introduction to Stochastic Processes; Cambridge University Press: London, UK, 1955. [Google Scholar]
- Brillinger, D.R.; Rosenblatt, M. Computation and Interpretation of kth-order Spectra; Hams, B., Ed.; Spectral Analysis of Time Series; Wiley: New York, NY, USA, 1967; pp. 189–232. [Google Scholar]
- Øigard, T.A.; Hanssen, A.; Hansen, R.E.; Godtliebsen, F. EM-estimation and modeling of heavy-tailed processes with the multivariate normal inverse gaussian distribution. Signal Process. 2005, 85, 1655–1673. [Google Scholar] [CrossRef]
- Øigard, T.A.; Hanssen, A. The Multivariate Normal Inverse Gaussian Heavy-Tailed Distribution: Simulation and Estimation. Int. Conf. Acoust. Spee. 2002, 2, 1489–1492. [Google Scholar]
- Alecu, T.I.; Voloshynovskiy, S.; Pun, T. The gaussian transform of distributions: Definition, computation and application. IEEE T. Signal Proces. 2006, 54, 2976–2985. [Google Scholar] [CrossRef]
- Shiryayev, A.N. Probability; Springer-Verlag: New York, NY, USA, 1984. [Google Scholar]
Appendix
A. Calculating the Cumulant
B. Calculating the Ratios of cy(k)(τ1, τ2, …, τk-1) to cyk for Fourth-order and Sixth-order
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, J.-H.; Zhang, B. Estimation of Seismic Wavelets Based on the Multivariate Scale Mixture of Gaussians Model. Entropy 2010, 12, 14-33. https://doi.org/10.3390/e12010014
Gao J-H, Zhang B. Estimation of Seismic Wavelets Based on the Multivariate Scale Mixture of Gaussians Model. Entropy. 2010; 12(1):14-33. https://doi.org/10.3390/e12010014
Chicago/Turabian StyleGao, Jing-Huai, and Bing Zhang. 2010. "Estimation of Seismic Wavelets Based on the Multivariate Scale Mixture of Gaussians Model" Entropy 12, no. 1: 14-33. https://doi.org/10.3390/e12010014
APA StyleGao, J.-H., & Zhang, B. (2010). Estimation of Seismic Wavelets Based on the Multivariate Scale Mixture of Gaussians Model. Entropy, 12(1), 14-33. https://doi.org/10.3390/e12010014




