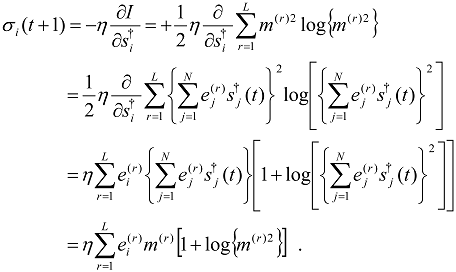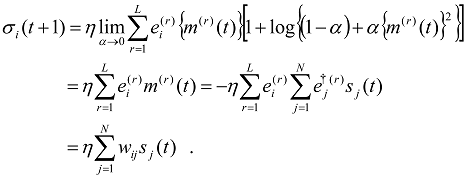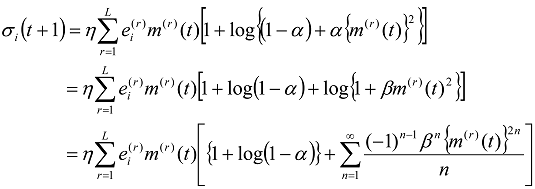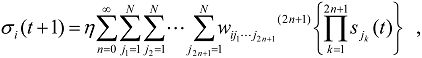1. Introduction
During the past quarter century, a large number of autoassociative models have been extensively investigated on the basis of the autocorrelation dynamics characterized by the quadratic Lyapunov functional to be minimized. Since the proposals of the pioneering retrieval models by Anderson [
1], Kohonen [
2], and Nakano [
3], some works related to such an autoassociation model of the inter-connected neurons through an autocorrelation matrix were theoretically analyzed by Amari [
4], Amit
et al. [
5] and Gardner [
6]. So far it has been well appreciated that the storage capacity of the autocorrelation model, or the number of stored pattern vectors,
L , to be completely associated
vs. the number of neurons
N, which is called the relative storage capacity or loading rate and denoted as
αc = L/N , is evaluated as
αc~0.14 at most for the autocorrelation learning model with the activation function as the signum one (sgn(
x ) for the abbreviation) [
7,
8].
In contrast to the above-mentioned models with monotonous activation functions, neuro-dynamics with a nonmonotonous mapping was recently proposed by Morita [
9], Yanai and Amari [
10], Shiino and Fukai [
11]. They clarified that the nonmonotonous mapping in a neuro-dynamics model possesses a remarkable advantage in the storage capacity,
αc~0.27-0.4, superior than the conventional association models with monotonous activation functions, e.g., the signum or sigmoidal function. Therefore activation functions have been considered to be worthwhile of investigation, not only the associative memory models but also learning models in relation with chaos dynamics [
12].
In the above-mentioned association models, the dynamics have been restricted to the updating rule on the basis of the quadratic form of the Lyapunov functionals to be minimized through the retrieval process. That is, the nonlinearity of the dynamics results from the nonlinear characteristics of the activation function rather than the updating rule of the internal states derived from the quadratic Lyapunov, or energy, functional form.
From the above-mentioned viewpoint, we shall propose a novel approach based on the entropy defined in terms of the overlaps, which are defined by the inner products between the state vector and the embedded vectors. That is, in the present model the functional to be minimized is defined in terms of the entropy instead of the conventional quadratic functionals. Then it will be found that the higher order dynamics is to be involved in a self-contained manner in the present entropy-based approach. In
Section 2 a theoretical framework based on the entropy approach will be described to present the relationship between the present proposal and the conventional model with a quadratic Lyapunov functional to be minimized. Some numerical results will be given in
Section 3 and then
Section 4 will be devoted to concluding remarks.
2. Theory
Let us consider an associative model with the embedded binary vector
= ±1 (1 ≤
i ≤
N,1 ≤
r ≤
L), where
N and
L are the number of neurons and the number of embedded vectors, respectively, to be retrieved. The states of the neural network are to be characterized in terms of the vector
si (1 ≤
i ≤
N) and the internal states
σi (1 ≤
i ≤
N) which are related each other in terms of:
where
f (•) is the activation function of the neuron.
Then we introduce the following entropy which is to be related to the overlaps:
where the overlaps
m(r) (
r = 1,2,...,
L) are defined by:
where the covariant vector
is defined in terms of the following orthogonal relation:
where
ω−1 denotes the inverse matrix of
ω.
Then the entropy defined by Equation (2) can be minimized by the following condition:
and:
That is, regarding
as the probability distribution in Equation (2), a target pattern may be retrieved by minimizing the entropy I with respect to
m(r) or the state vector
si to achieve the retrieval of a target pattern in which the Equation (8) and Equation (9) are to be satisfied. Therefore the entropy function may be considered to be a functional to be minimized during the retrieval process of the auto-association model instead of the conventional quadratic Lyapunov,
i.e. energy functional,
E:
where
is the covariant vector defined by:
and the connection matrix
wij is defined in terms of:
Substituting Equation (12) into Equation (10), one may readily find:
According to the steepest descent approach in the discrete time model, the updating rule of the internal states
may be defined by:
where
η ( > 0) is a coefficient. Substituting Equation (2) and Equation (3) into Equation (14) and noting the following relation with the aid of Equation (11):
one may readily derive the following relation:
Generalizing somewhat the above dynamics, we propose the following dynamic rule for the internal states in order to unify the conventional quadratic dynamics as well as the presently proposed entropy approach as mentioned below:
In the above expression
α (0 < α < 1) is considered to be a control parameter of the present model as follows. First, in the limit of α→0, the above dynamics will be reduced to the conventional autocorrelation dynamics:
On the other hand, Equation (17) results in Equation (16) in the case of α→1. Therefore one may control the dynamics between the autocorrelation (α→0) and the entropy based approach ( α→1) on the basis of the presently proposed generalized approach defined by Equation (17).
Now it seems to be worthwhile to see the higher-order correlation in Equation (17) expanding the right-hand-side of Equation (17) as follows.
where
β is defined by:
Substituting Equation (3) into Equation (19), one may eventually derive the following up-dating rule for the internal state,
i.e.:
where
(0 ≤
n < ∞) are the connection weight tensors between neurons involving such higher-order correlations as n ≥ 1 and are to be expressed by means of
and
comparing Equation (19) and Equation (21). Of course the lowest order connection weight
in Equation (21) corresponds to
in Equation (12),
i.e.:
Thus the lowest correlation is reduced to the conventional quadratic framework expressed in terms of Equation (10) and Equation (12) as
. Furthermore, for the higher-order connection tensors appearing in Equation (10c), one may readily obtain the following results:
It should be borne in mind here that all of the connection tensors, i.e. (0 ≤n <∞) are to be uniquely determined in terms of the embedding vectors and , which may be related to each other according to Equation (5) to Equation (7). Thus the present approach substantially includes the higher-order correlations beyond the conventional approach defined by Equation (11), in which the correlation between neurons is restricted up to the second-order contribution corresponding to the quadratic Lyapunov functional given by Equation (10). For practical association of the stored patterns, the connection tensors (1 ≤ n < ∞) defined by Equation (21) have to be utilised instead of the embedded vectors, i.e. and (1 ≤r ≤L).
3. Results
The embedded vectors are set to the binary random vectors as follows:
where
where (1 ≤
i ≤
N , 1 ≤
r ≤
L ) are the zero-mean pseudo-random numbers between -1 and +1. For simplicity, the activation function , Equation (1), is set to:
where sgn (•) denotes the signum function defined by:
The initial vector
si (0) (1 ≤
i ≤
N) is set to:
where
is a target pattern to be retrieved and
Hd is the Hamming distance between the initial vector
si (0) and the target vector
. The retrieval is successful if:
results in 1 for
, in which the system may be in a steady state such that:
To see the retrieval ability of the present model, the success rate
Sr is defined as the rate of the success for 1,000 trials with the different embedded vector sets
(1 ≤
i ≤
N, 1 ≤
r ≤
L). To control from the autocorrelation dynamics after the initial state (
t~1) to the entropy based dynamics (
t~
Tmax) , the parameter
α in Equation (17) was simply controlled by:
where
Tmax and
αmax are the maximum values of the iterations of the updating according to Equation (17) and
α, respectively.
Choosing
N = 200,
η = 1,
Tmax = 25,
L/
N = 0.5 and
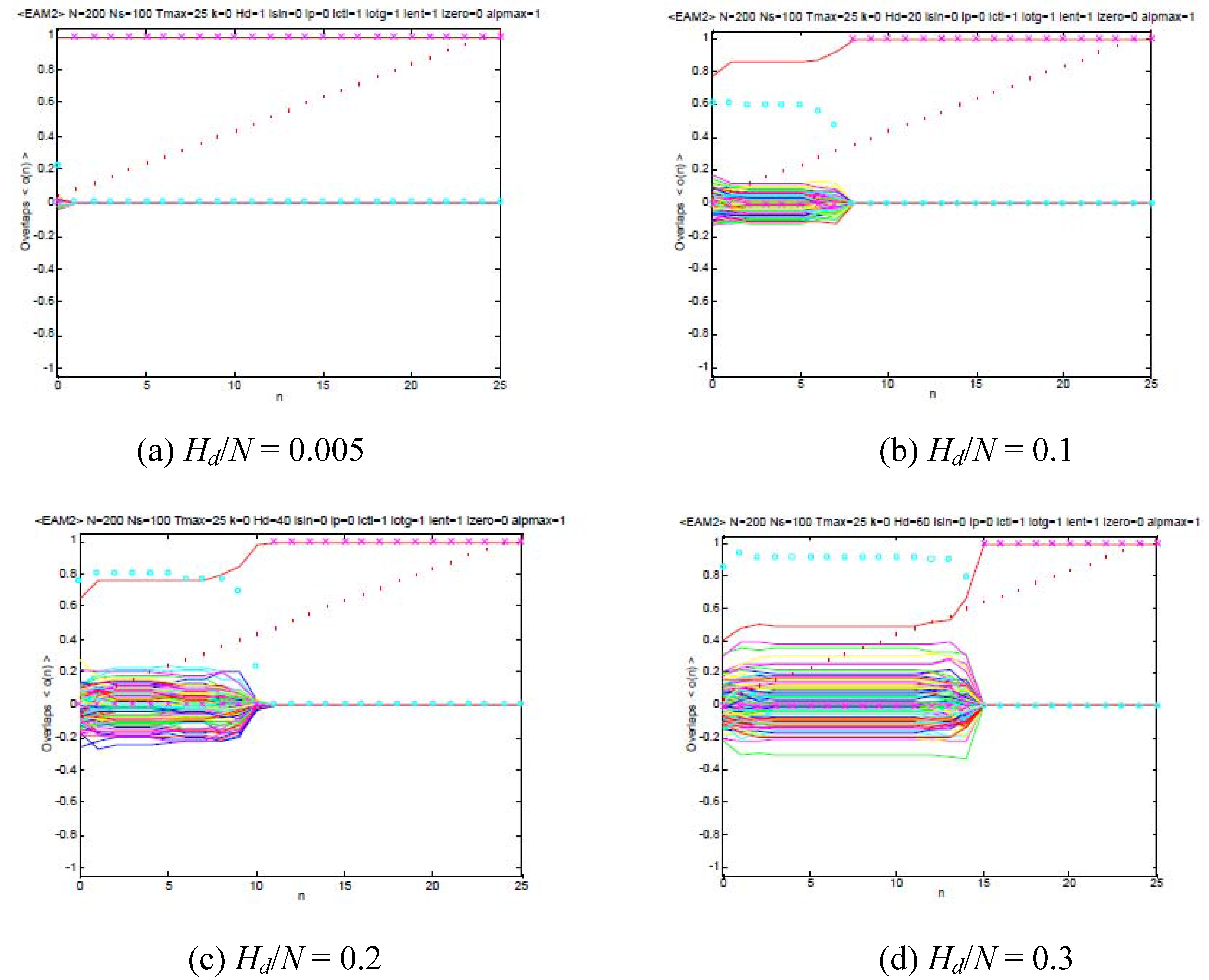
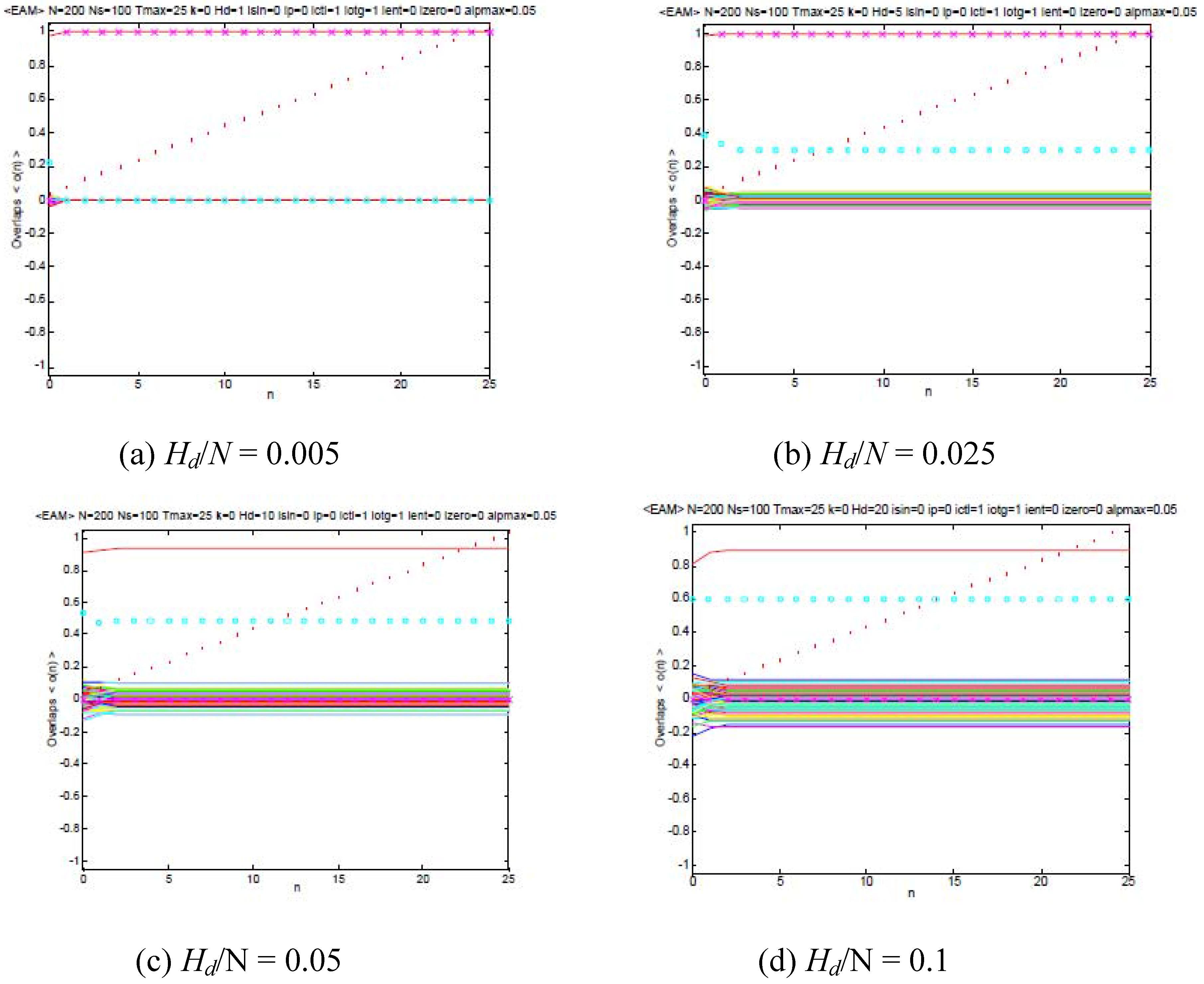
αmax = 1, we first present an example of the dynamics of the overlaps in
Figures 1(a)−(d) (entropy based approach) and
Figures 2(a)–(d) (associatron), in which the abscissa and the ordinate are for the retrieval steps after the initial states and the overlaps derived from Equation (16), respectively. Therein the cross symbols (×) and the open circles (o) represent the success of retrievals, in which Equation (8) and Equation (9) are satisfied, and the entropy defined by Equation (2), respectively, for a retrieval process. In addition the time dependence of the parameter α/α
max defined by Equation (31) is depicted as dots (.). In
Figures 1(a)−(d) after a transient state, it may be confirmed that the complete association corresponding to the conditions, Equation (8) and Equation (9), can be achieved, even for such a relatively large Hamming distance of the initial vector from a target vector as
Hd/
N = 0.1-0.15. On the other hand, in
Figures 2(a)–(d), a trapping in a local minimum is found to be inevitable for
L/
N = 0.5 (>>0.14 which is the relative storage capacity for the autocorrelation model as discussed by Amari and Maginu [
8] (see Concluding remarks), in which Equation (8) and Equation (9) cannot be achieved even for
Hd/
N→0 with
L/
N > 0.5. In addition one may sees that the retrieval cannot be achieved beyond
Hd/
N = 0.05 as in
Figures 2(c) and (d). From these results one may certainly confirm the advantage of our approach beyond the conventional models based on the quadratic Lyapunov (energy) functionals.
Figure 1.
The time dependence of overlaps of the present entropy based model defined by Equation (17).
Figure 1.
The time dependence of overlaps of the present entropy based model defined by Equation (17).
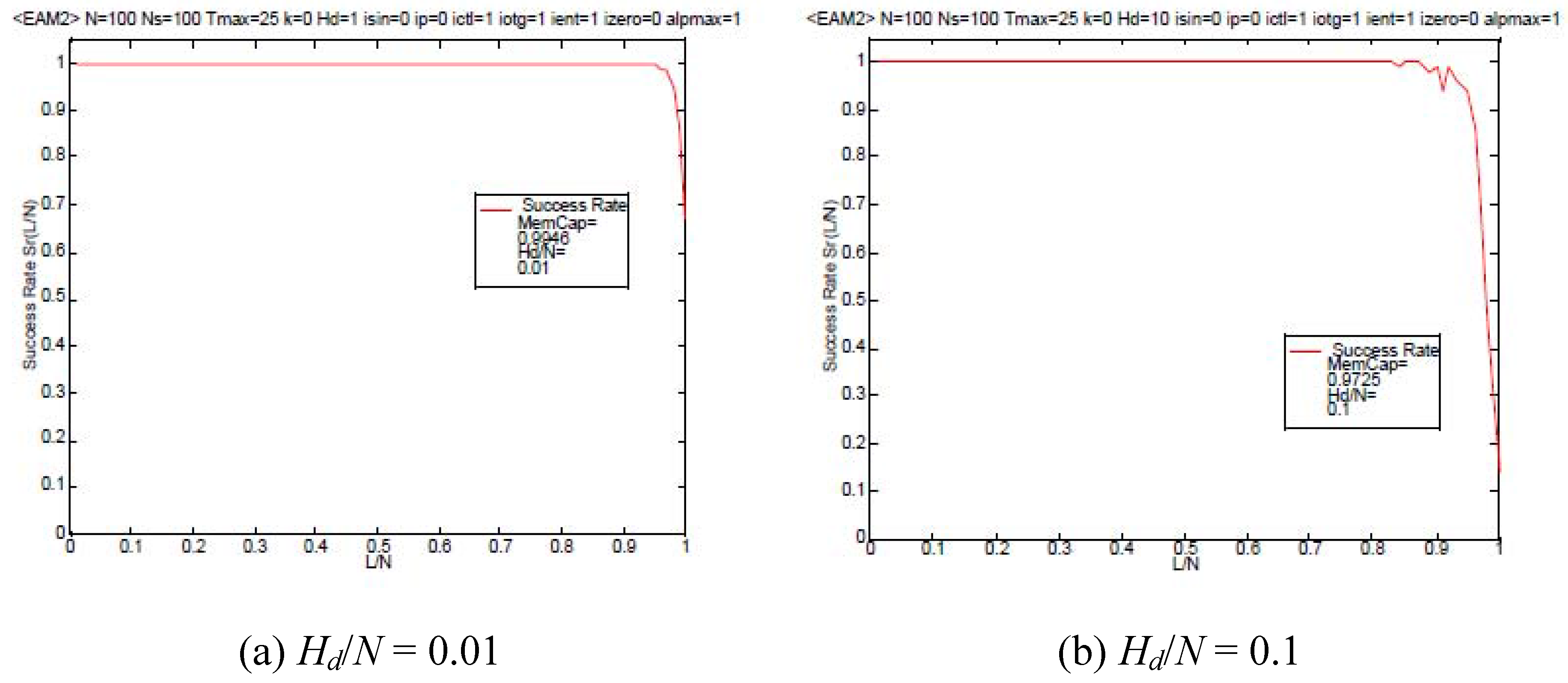
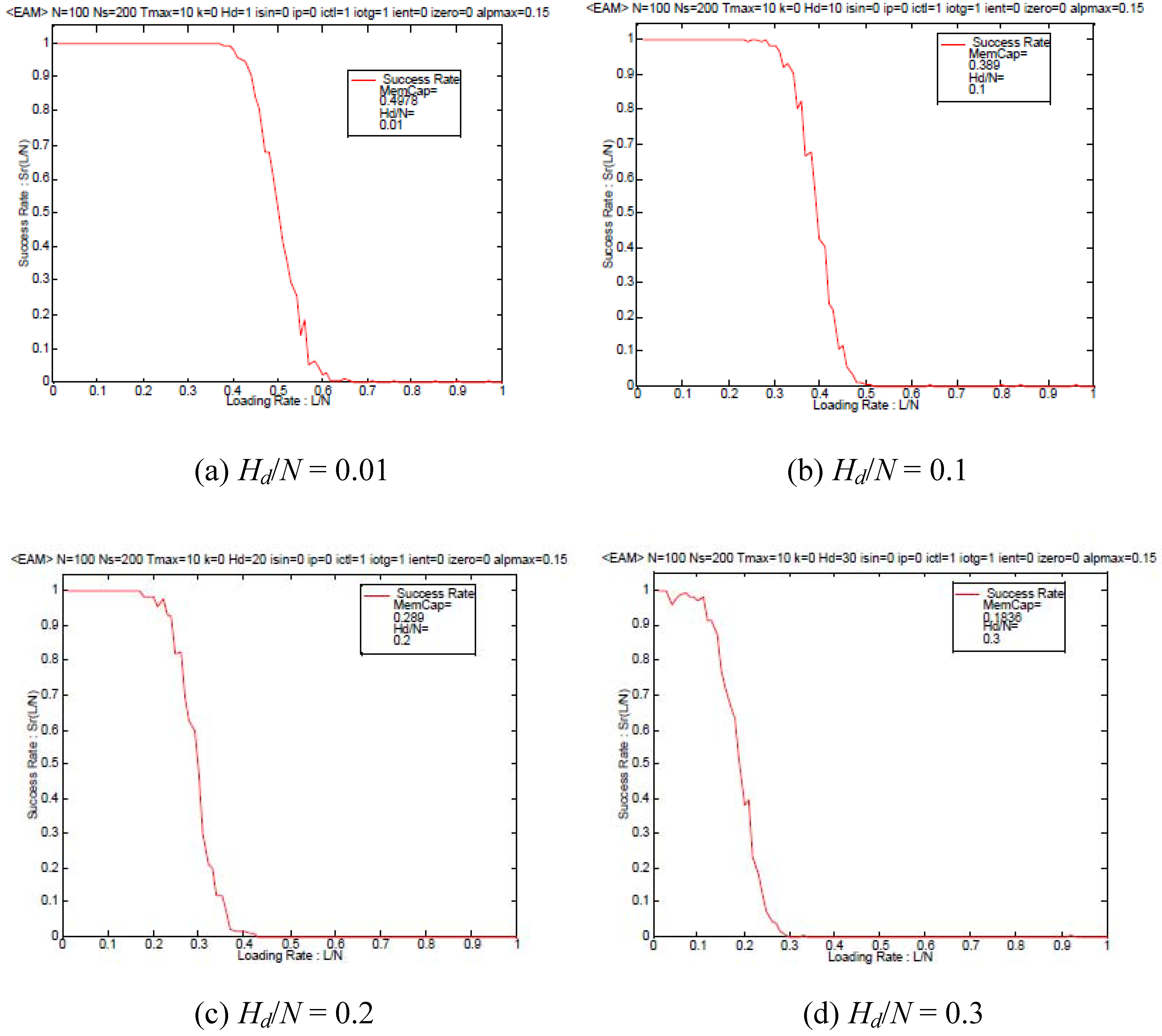
Then we shall present the dependence of the success rate
Sr on the loading rate
L/
N are depicted in
Figure 3 for various Hamming distances
Ηd with
N = 100. For comparison, the corresponding results of the associatron model with
α~0,
i.e. Equation (11), are shown in
Figure 4. Comparing between
Figure 3 and
Figure 4, it is found that the present approach may achieve a relatively larger memory capacity beyond the conventional autocorrelation strategy. Therefore the presently proposed nonlinear dynamics with the higher-order correlations involved in Equation (17) or Equation (21) based on the entropy functional to be minimized has a great advantage for the storage capacity beyond the conventional one based on Equation (10) and Equation (18).
Figure 2.
The time dependence of overlaps of the associatron defined by Equation (18).
Figure 2.
The time dependence of overlaps of the associatron defined by Equation (18).
Figure 3.
The dependence of the success rate on the loading rate α = L/N of autoassociation model based on Equation (17) (entropy based approach).
Figure 3.
The dependence of the success rate on the loading rate α = L/N of autoassociation model based on Equation (17) (entropy based approach).
Figure 4.
The dependence of the success rate on the loading rate α = L/N of autoassociation model based on Equation (18) (associatron).
Figure 4.
The dependence of the success rate on the loading rate α = L/N of autoassociation model based on Equation (18) (associatron).
The depression of the success rate at
L/
N~1 in
Figure 3 may be considered to result from the fact such that:
where Equation (18) reads:
Thus, noting that
si(
t) = sgn(
σi (
t)) and
η> 0, one has:
4. Concluding Remarks
In the present paper, we have proposed an entropy based association model instead of the conventional autocorrelation dynamics. From numerical results, it was found that a large memory capacity may be achieved on the basis of the entropy approach. This advantage of the association property of the present model is considered to result from the fact such that the present dynamics to update the internal state Equation (17) assures that the entropy, Equation (2) is minimized under the conditions, Equation (8) and Equation (9), which corresponds to the successful retrieval of a target pattern.
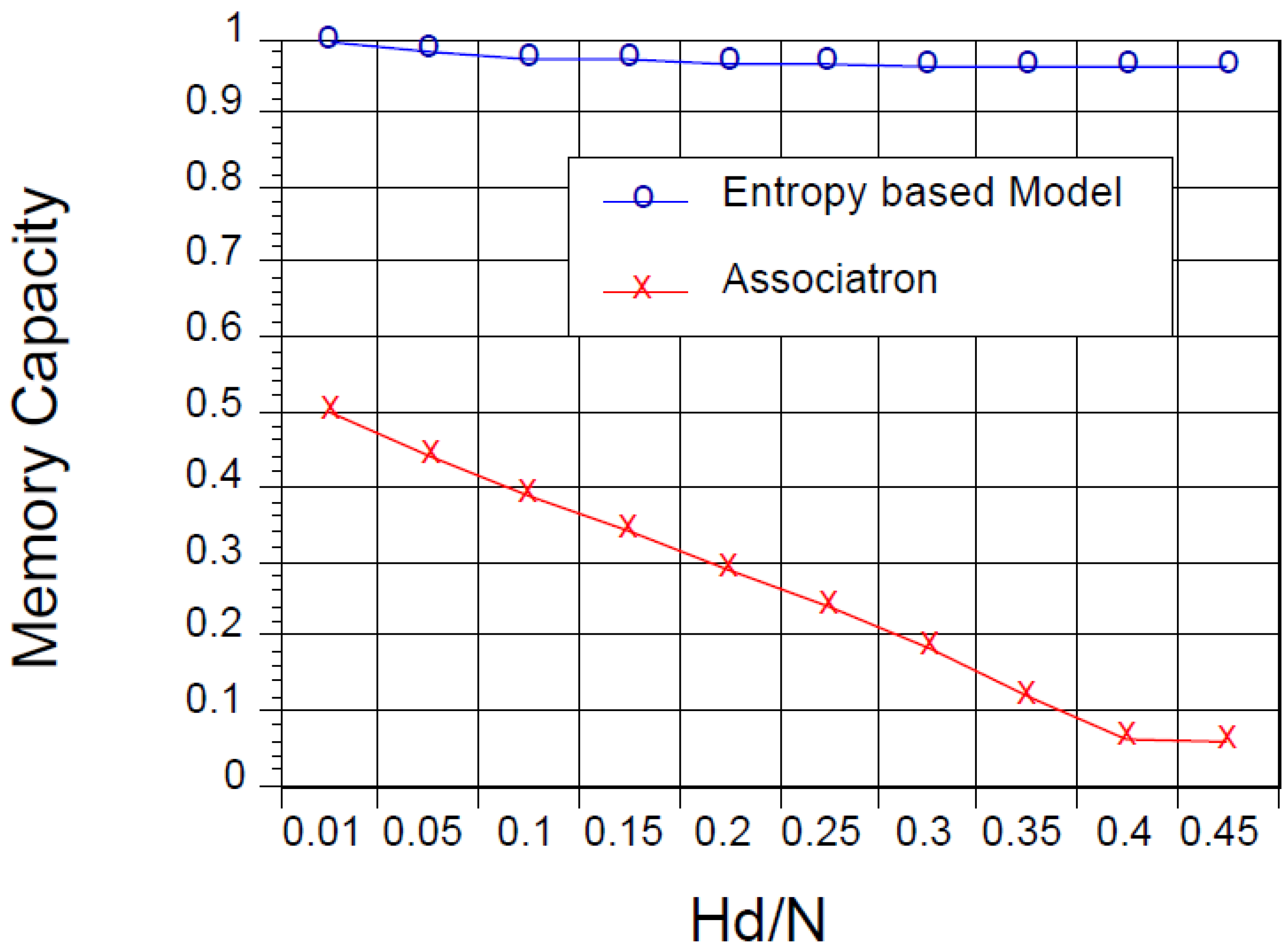
To conclude this work, we shall show the dependence of the storage capacity, which is defined as the area covered in terms of the success rate curves as shown in
Figures 3 and
Figure 4, on the Hamming distance in
Figure 5. Therein one may see again the great advantage of the present model based on the entropy functional to be minimized beyond the conventional quadratic form. In fact one may realize the considerably larger storage capacity in the present model in comparison with the associatron over
Hd/
N~0-0.5. The memory retrievals for the associatron become troublesome near
Hd/
N = 0.5 as seen in
Figure 5 since the directional cosine between the initial vector and a target pattern eventually vanishes therein. Remarkably, even in such a case, the present model attains a remarkably large memory capacity because of the higher-order correlations involved in Equation (17) or Equation (21), as expected from
Figure 3.
As a future problem, it seems to be worthwhile to involve a chaotic dynamics in the present model introducing a periodic activation function such as sinusoidal one and to extend the autocorrelation model replacing
by
/
N in the present approach, in which the connection matrix
wij and the overlaps
m(r) read:
and:
respectively, corresponding to Equation (12) and Equation (15). The entropy based approach with Equation (20),
i.e. autocorrelation dynamics, is now in progress in the relation with chaos dynamics [
12] and will be reported elsewhere as a separated paper and to be compared with the previous works [
13,
14] in the near future. Furthermore it seems to be worthwhile to examine the truncation effects of the expansion tensors as in Equation (21), which was not directly derived in our previous work [
15], for practical applications related to the hardware implementation.
Figure 5.
The dependence of the storage capacity on the Hamming distance. Here symbols o and x are for the entropy based approach and the associatron, respectively.
Figure 5.
The dependence of the storage capacity on the Hamming distance. Here symbols o and x are for the entropy based approach and the associatron, respectively.