The Quantum Noise of Ferromagnetic π-Bloch Domain Walls

Abstract

We quantify the probability per unit Euclidean-time of reversing the magnetization of a π-Bloch vector, which describes the Ferromagnetic Domain Walls of a Ferromagnetic Nanowire at finite-temperatures. Our approach, based on Langer’s Theory, treats the double sine-Gordon model that defines the π-Bloch vectors via a procedure of nonperturbative renormalization, and uses importance sampling methods to minimise the free energy of the system and identify the saddlepoint solution corresponding to the reversal probability. We identify that whilst the general solution for the free energy minima cannot be expressed in closed form, we can obtain a closed expression for the saddlepoint by maximizing the entanglement entropy of the system as a polynomial ring. We use this approach to quantify the geometric and non-geometric contributions to the entanglement entropy of the Ferromagnetic Nanowire, defined between entangled Ferromagnetic Domain Walls, and evaluate the Euclidean-time dependence of the domain wall width and angular momentum transfer at the domain walls, which has been recently proposed as a mechanism for Quantum Memory Storage.

1. Introduction

Spin Polarised Scanning Tunneling Microscopy (SP-STM) measurements of the differential conductance profile of Ferromagnetic Nanowires, such as samples of Fe on W(110) [1, 2], highlight the importance of understanding the effective polarization of the surface-probing tip subsystem, and its contribution to the measured anisotropy of a Ferromagnetic surface. This is because the response of the surface to the magnetic field of the applied probing tip is dependent on the local projection of the surface magnetization onto the probing tip, via the torque that is induced by the spin-polarized tunneling current. Hence, this mechanism is being actively considered for practical Quantum Memory Storage, via the transfer of angular momentum into Ferromagnetic Domain Walls [3,4,5,6]. Although the corresponding changes in the measured resistivity are not large, it is relatively straight forward to understand the scattering mechanism induced by this torque in the two limits that the domain walls are either very narrow or very broad [7, 8]. In the first case, spin magnons will be specularly reflected without the transfer of angular momentum, whilst in the second case, spins adiabatically realign around the local magnetization, whilst precessing with a characteristic Larmor frequency, and transfer angular momentum into the domain wall. A simple (but effective) picture of the local projection of the spins can be parameterized by defining a Bloch vector between neighbouring Ferromagnetic Domain (π-Bloch) Walls,

$$\sin \left(\phi \left(x\right)\right)=\tanh [(x-x_0)/(w/2)]$$

(1)

where $x_0$ is the position of the first domain wall, and w is the domain wall width. This relation is obtained by assuming that nonlocal surface effects can be neglected, and by minimising the free energy, where the free energy of this system is expressed via the generic double sine-Gordon model,

$$S=\int dxA{\left(\frac{\partial \phi }{\partial x}\right)}^2+MB\cos \phi +K{\sin }^2\phi$$

(2)

where A is the exchange interaction stiffness, K the effective anisotropy of the surface, M the saturation value of the local magnetization vector, and B the magnitude of the applied field which generates Zeeman splitting [9]. The domain wall width, w, is then obtained explicitly by assuming that the dissipative dynamics of the spins obeys the Landau-Lifshitz-Gilbert equations, giving,

$$w=\sqrt{\frac{A}{K+MB/2}}{\sinh }^{-1}\left(\sqrt{\frac{2K}{MB}}\right)$$

(3)

However, whilst several experiments have confirmed that this locally planar magnon picture is essentially correct [1, 2, 5, 6], this does mean that the domain wall width of the Ferromagnetic Nanowire is parameterised in (3) via the non-universal effective anisotropy value K. This parameterisation therefore limits the accurate calibration of the angular momentum transfer of a Ferromagnetic Nanowire for a practical Quantum Memory Storage device, and more detailed treatments have stressed the importance of also considering noncollinear magnetization effects [3, 10].

To renormalize this effective anisotropy value, K, we now treat the more general problem of minimising nonadiabatic dynamics in (2), and consider the entanglement between Ferromagnetic Domain Walls that is induced by rapid changes in the tunneling current. We perform a path integral over Euclidean-time for (2) to do this, which is made equivalent to Imaginary-time in our formalism via an exact Wick-rotation [11,12,13]. Physically, this treatment corresponds to the situation where if the system is heated, Stoner excitations eventually destroy the ferromagnetic order by overcoming local energy barriers, however, rapid recooling is not then guaranteed restore the system to the same initial local valley states and so the free energy minima of (2) is not unique [14]. A similar approach to the one we present has been developed in [14,15,16] to treat the Euclidean-time dependence of the nucleation of the Ferromagnetic Domain Walls by applying Langer’s Theory. The approach is to find the minima of the free energy in (2), parameterized as a dilute gas of soliton and anti-soliton states, and to determine the effect of small perturbations to this system obtained by adding a single soliton to the grand canonical partition function of the system . This gives a probability per unit time of reversing the magnetization of the Bloch vector described by the Van’t Hoff-Arrehenius law,

$$\Gamma =\Omega e^{-\beta E_s}$$

(4)

$$\Omega =\kappa \sqrt{\frac{2\beta }{{\pi }^3}}\sqrt{E_s}L\sqrt{\frac{{\prod }_{i=1}{\Lambda }_i^{\left(0\right)}}{|{\Lambda }_1^{\left(\varphi \right)}|{\prod }_{j>1}{\Lambda }_j^{\left(\varphi \right)}}}\sqrt{\frac{{\prod }_i{\Lambda }_i^{\left(0\right)}}{{\prod }_{j>1}{\Lambda }_j^{\left(p\right)}}}$$

(5)

where $E_s$ is the saddlepoint solution for the free energy, β is Euclidean-time, κ is the growth rate of unstable deviations, L is the system length, and $\{\Lambda \}$ are the eigenvalues of the Hamiltonians describing the zero mode, $\left(0\right)$, in-plane, $\left(\varphi \right)$, and out-of-plane fluctuations, $\left(p\right)$, of the Ferromagnetic Domain Wall Bloch vectors [14]. In order to treat perturbations of arbitrary size, in our approach, however, we formulate a fugacity expansion for the full grand canonical partition function, which consists of N soliton and anti-soliton states [18, 19]. Minimizing the free energy of this full partition function enables us to normalize the probability per unit time in (4) via an additional nonanalytic factor, which corresponds to the entropy of adding an additional $(N-1)$ solitons into the system. We then calibrate this contribution as a phase factor, via the Wick-rotation of the operators of our formalism [11,12,13], and use this value to quantify the change in the physical scale of the Bloch vector in (1) and (3) due to the nonanalytic entanglement contributions (quantum noise) arising from magnetization-reversal tunneling transitions between different Ferromagnetic Domains across the surface of the Nanowire.

2. Mixed Quantum Spin Chain

Spin-wave theory can be used to provide a simple description of the propagation of angular momentum at the ferromagnetic domain walls in the limit that the domain walls are either very narrow or very broad [7, 8]. To a first approximation, the angular momentum transfer is described by the magnons that are defined by representing the Bloch vectors of the ferromagnetic domain walls by elements of the $S=1/2$ representation of $SU\left(2\right)$. Therefore, summed over the length of the nanowire, each pair of anti-aligned ferromagnetic domain walls also forms an elementary version of the antiferromagnetic bipartite Heisenberg model in one dimension [17],

$$H=J\sum _{j=0}^{N-1}{\mathit{S}}_j.{\mathit{S}}_{j+1}$$

(6)

Whilst this modeling is clearly an over-simplification of the physical system, it does form an accurate description of the angular momentum transfer in each of the two separate limits where the Grand Canonical Partition Function of Langer’s method disentangles into N separately interacting soliton and anti-soliton pairs [14,15,16]. What makes the problem of accurately describing the angular momentum transfer of the physical system more than simply developing a more effective version of perturbation theory from either of these two separate spin-wave theories is that, in these two limits, the complete specular reflection and complete diffuse reflection results of the two magnon descriptions is exactly π out of phase. There is, therefore, no analytical way to perturb the relevant fluctuations of these two separate limits into each other in order to describe general inter-domain interactions, and to construct a picture of the noncollinear magnetization effects at the domain walls from either separate limit [3, 10]. Much is known about the spin-wave theory of these two separate limits [20]. The spin-wave theory of the diffusive reflection limit corresponds to a triplet of massive $O\left(3\right)$ states, whereas the specular reflection limit corresponds to a spectrum of massless states described by the $SU{\left(2\right)}_1$ Wess-Zumino-Witten model. Although both limits correspond to completely different physical systems, the irreducible $SU\left(2\right)$ representations of both sets of magnons ${\prod }_{{\mathit{S}}_j}$ and ${\prod }_{{{\mathit{S}}^{\prime }}_j}$ are straight-forwardly related via Clebsch-Gordon coefficients,

$$\prod _{{\mathit{S}}_j}\otimes \prod _{{\mathit{S}}_k}=\underset{{{\mathit{S}}^{\prime }}_j}{⨁}{\lambda }_{{\mathit{S}}_j{\mathit{S}}_k}^{{{\mathit{S}}^{\prime }}_j}\prod _{{{\mathit{S}}^{\prime }}_j}$$

(7)

where the magnons correspond to the fundamental and adjoint representations of $SU\left(2\right)$, with $\mathbf{2}\otimes \mathbf{2}=\mathbf{1}\oplus \mathbf{3}$. As this notation implies, however, a more general theory of finite domain wall width can be constructed by making these Clebsch-Gordon coefficients a scale dependent function of the lattice sites in (6). This generalises the definition of the magnons from elements of the fundamental group $SU\left(2\right)$, to elements of $PS{L}_2\left(\mathbb{R}\right)$ - the fundamental group of linear transformations between the Bloch spheres [21]. The identity in (7) preserves the analytic relationship between the magnons of the two separate limits (at the operator level) as we construct this general theory, which we do by generalising the unphysical antiferromagnetic bipartite Heisenberg model in one dimension, in (6), to a Heisenberg model which is defined on a curved background. Identifying the expansion coefficients of the interactions of this antiferromagnetic bipartite Heisenberg model on a curved background thus exactly corresponds to forming the Grand Canonical Partition Function of Langer’s method for N interacting solitons and anti-solitons. Through this approach, we can precisely define the relationship between the in-plane and out-of-plane fluctuations of the domain walls, order-by-order.

A one dimensional antiferromagnetic Heisenberg model on a curved background can be generated in a simple way by constructing an antiferromagnetic chain which has a mixture of different spins of integer and half-integer magnitude. This approach is motivated by the fact that the antisymmetric quantum states of a quantum spin chain are known to undergo destructive interference due to quantum fluctuations. More specifically, the unstable renormalization group flow of the $SU{\left(2\right)}_1$ Wess-Zumino-Witten model is related to the emergence of a gapless groundstate in all half-integer spin chain models (doublets), whereas gapped groundstates states are realised by all quantum spin chain models with integer spin values (triplets) [20, 21]. Hence, if a mixed-spin model is constructed with different exchange couplings defined between the integer/integer, half-integer/half-integer and integer/half-integer spin operators then this one dimensional antiferromagnetic Heisenberg model can be tuned between gapless and gapped groundstates, corresponding to a varying curvature in (7). In this article, following [18], we treat the model which consists of an antiferromagnetic periodic mixed-spin chain of the form $1-1-3/2-3/2$, where 1 and $3/2$ represent the spin magnitudes, and the period of the alternation of this pattern is four lattice sites. The Hamiltonian of this model is given by,

$$H=\sum _{j=0}^{N/4-1}{J}_{1,1}{\mathit{S}}_{4j}^{\left(1\right)}.{\mathit{S}}_{4j+1}^{\left(1\right)}+J_{1,3/2}{\mathit{S}}_{4j+1}^{\left(1\right)}.{\mathit{S}}_{4j+2}^{(3/2)}+J_{3/2,3/2}{\mathit{S}}_{4j+2}^{(3/2)}.{\mathit{S}}_{4j+3}^{(3/2)}+J_{3/2,1}{\mathit{S}}_{4j+3}^{(3/2)}.{\mathit{S}}_{4j+4}^{\left(1\right)}$$

(8)

where j is the lattice site index of the cell along the spin chain, $J_{a,b}$ is the nearest neighbour spin interaction coupling between the neighbouring spins of magnitude a and b, and ${\mathit{S}}^{\left(a\right)}$ is the spin operator of magnitude a. We keep the ratio between like-like and like-dislike spin operators fixed such that $J_{1,1}=J_{3/2,3/2}=J$ and $J_{1,3/2}=J_{3/2,1}=\alpha J$, such that the tunable parameter for varying the groundstate is α. From (7), there are three symmetric Young tableaux for the spin-$3/2$ operator of this Hamiltonian, and hence, there are three distinct realizations of the gapped groundstate of the above mixed-spin model [22]. Consequently, there are three spatially inhomogeneous Bloch vectors defined in the regions between the zero temperature transitions of this system, which we can use to represent a Ferromagnetic Nanowire consisting of four anti-aligned π-Bloch domain walls of arbitrary width.

We can define the precise relationship between the in-plane and out-of-plane fluctuations of the domain walls in this approach, order-by-order, by evaluating the Grand Canonical Partition Function of the above Heisenberg model. This Grand Canonical Partition Function describes the precise combination of both in-plane and out-of-plane fluctuations which collectively minimise the free energy of this system. It is constructed by using the curvature of the above model to define an expansion in the Canonical Partition Functions of the operators in (7). Thus, the geodesic for a given background curvature is given by the scale dependence of the Clebsch-Gordon coefficients in (7). The curvature of the lattice model is precisely defined via the following Clebsch-Gordon coefficients,

$$A_{\mathit{n}}\equiv \sum _{i,\tau }^{N\otimes T}\sum _{\mathit{S}}{\lambda }_{\mathit{n}}^{i\tau \mathit{S}}\frac{\langle \mathit{n}\oplus {\mathbf{1}}_{i\mathit{S}}\oplus {\mathbf{1}}_{\tau \mathit{S}}|\theta \rangle }{\langle \mathit{n}|\theta \rangle },V_{\mathit{n}}\equiv \sum _{i,\tau }^{N\otimes T}\sum _{\mathit{S}}{\left({\lambda }_{\mathit{n}}^{i\tau \mathit{S}}\right)}^{\prime }\frac{\langle \mathit{n}\oplus {\mathbf{1}}_{i\mathit{S}}\oplus {\mathbf{1}}_{\tau \mathit{S}}|\mathit{n}\rangle }{\langle \mathit{n}|\mathit{n}\rangle }$$

(9)

where $A_{\mathit{n}}$ and $V_{\mathit{n}}$ are defined as the compact and noncompact portions of the spin operators in (6) as determined through the Clebsch-Gordon coefficients ${\lambda }_{\mathit{n}}^{i\tau \mathit{S}}$ and ${\lambda }_{\mathit{n}}^{i\tau {\mathit{S}}^{\prime }}$, n is an arbitrary quantum state of the system, and i and τ are respectively the space and Euclidean-time lattice indices [11, 12]. Viewed pictorially, only a subset of the quantum states on the lattice (corresponding to the first operator, $A_{\mathit{n}}$) can be taken smoothly round the phase space of the system. This corresponds to the case when only one type of magnon is needed to describe the angular momentum transfer. In general, however, two different types of magnons are needed (in-plane and out-of-plane) which are not related analytically, and we require a second term, $V_{\mathit{n}}$. The Grand Canonical Partition Function for this approach, $\mathcal{Z}$, is defined by summing over all values of the vacuum angle θ,

$$\mathcal{Z}=\int \mathcal{D}\theta \exp \left[{\int }_0^{\beta }d\tau H\right]\equiv \int \mathcal{D}\theta \exp \left[{\int }_0^{\beta }d\tau A_{\mathit{n}}i\varphi -V_{\mathit{n}}\right]$$

(10)

Note that since the Grand Canonical Partition Function does not have to be in equilibrium the phase factor in the exponent, ϕ, will generally differ from θ. The effective action of the double sine-Gordon model in (2) can be derived from this operator formalism via a simple two-loop expansion of the following form,

$$S_{eff}={\int }_0^{\beta }{\int }_{-\pi }^{\pi }{d}^{2}x{a}_{\tau }{\partial }_x^2{A}_{\mathit{n}}-a_i{\partial }_x^2{V}_{\mathit{n}}-a_i\wedge a_{\tau }$$

(11)

where the first order fluctuations in the Euclidean-time and spatial lattice spacings are defined via,

$$\theta a_i\equiv A_{\mathit{n}\left(i\right)}-{\langle A_{\mathit{n}}\rangle }_{N,T},\beta a_{\tau }\equiv A_{\mathit{n}\left(\tau \right)}-{\langle A_{\mathit{n}}\rangle }_{N,T}$$

(12)

Therefore, the inverse problem, of starting with the double sine-Gordon model in (2), and then expanding this action perturbatively to treat both sets of in-plane and out-of-plane fluctuations, only strictly recovers the expansion terms in both sets of in-plane and out-of-plane fluctuations to first-order in the expansion. This is because the operators in (11) do not represent simple magnons [14], and their proper definition requires knowledge of all inter-valley tunneling processes. In general, therefore, it is not possible to make further progress with defining this expansion for both sets of fluctuations without first determining the full spectrum of the Grand Canonical Partition Function.

3. Renormalized Entanglement Entropy

We evaluate the path integral in (7) via importance sampling using the conventional continuous-time Quantum Monte Carlo scheme. Practical details of this approach are given in [18]. This numerical procedure generates the set of the nonperturbative matrix elements ${\lambda }_{\mathit{n}}^{i\tau \mathit{S}}$ and ${\lambda }_{\mathit{n}}^{i\tau {\mathit{S}}^{\prime }}$ in (9), for the Heisenberg model defined in (8). Constructing these matrix elements allows us to define a geodesic for this system from which we can construct an analogous saddlepoint solution for the Grand Canonical Partition Function to the one in (5). Whilst, the important quantities for this calculation in (5) are the eigenvalues $\left\{{\Lambda }^{\left(0\right)}\right\}$, $\left\{{\Lambda }^{\left(\varphi \right)}\right\}$ and $\left\{{\Lambda }^{\left(p\right)}\right\}$ (which describe the spectrum of zero mode, in-plane and out-of-plane fluctuations of the Bloch vectors), in our calculation, through the identity (7), all of these contributions are included into the nonperturbative matrix elements ${\lambda }_{\mathit{n}}^{i\tau \mathit{S}}$ and ${\lambda }_{\mathit{n}}^{i\tau {\mathit{S}}^{\prime }}$. Hence, to evaluate the saddlepoint solution of (10), we construct the determinant of the following operator P,

$$\det P=\prod _{i=1}^N{\Lambda }_i,\mathcal{Z}=\int \mathcal{D}\theta P$$

(13)

where ${\Lambda }_i=1-{\lambda }_{i,\mathit{n},\tau }^2$ are the eigenvalues of the operator P.

The practical reason why the addition of only one extra soliton is considered for (5), is that, in general, the support of the eigenvalues in (13) cannot be expressed in closed analytic form. However, it is possible to locally regularize (13) via the ζ-function renormalization prescription [13]. Following this prescription, the logarithm of $\det P$ in the limit $N\to \infty$ can be defined by analytically continuing the following function,

$$\sum _{i=1}^N{\Lambda }_i^{-s}\ln {\Lambda }_i,$$

(14)

from large s to $s=0$. Introducing the ζ-function, ${\zeta }_P\left(s\right)={\sum }_{i=1}^N{\Lambda }_i^{-s}$, the logarithm of the determinant of P is then completely defined by the first derivative of this ζ-function at $s=0$. Writing this ζ-function in the usual form of a Mellin transform,

$$\begin{array}{ccc}\hfill {\zeta }_P\left(s\right)& =& \frac{1}{\Gamma \left(s\right)}{\int }_0^{\infty }\mathrm{Tr}\left(e^{-\theta P}\right){\theta }^{s-1}d\theta \hfill \end{array}$$

(15)

$$\begin{array}{ccc}& \equiv & {\int }_0^{\infty }\Lambda \left(\theta \right){\theta }^{s-1}d\theta \hfill \end{array}$$

(16)

$$\Rightarrow \ln \det P=-{\int }_0^{\infty }\Lambda \left(\theta \right)\ln \left(\theta \right)d\theta$$

(17)

However, although (17) completely defines the local limit of the free energy of the Grand Canonical Partition Function in (10), and its saddlepoint solution, because of the rotational symmetry of the Bloch vectors defined through (9), this minima is not unique, and there are several different realizations of the system which are degenerate. Not only can the local minima in (17) be finite, but also a number of the higher moments corresponding to the tunneling from two-, three- and (and more) soliton states. Therefore, to determine the saddlepoint solution of (10), we have to evaluate the ζ-function prescription at a different point on the fundamental strip, at $s=1$, for each of these moments,

$$\frac{d^j{\zeta }_P\left(s\right)}{d{s}^j}{\mid }_{s=1}={\int }_0^{\infty }\Lambda \left(\theta \right){\ln }^j\left(\theta \right)d\theta ,j=0...N$$

(18)

which allows us to address the choices of branch cuts for all of these higher moments that relates to the degeneracy of the minima in (17). Collectively minimising these moments, at $s=1$, then becomes equivalent to analytically continuing the following function via the ζ-function prescription,

$$H={\int }_0^{\infty }\Lambda \left(\theta \right)\ln \Lambda \left(\theta \right)d\theta$$

(19)

and defines the familiar Von Neumann form of the entropy of a quantum spin system. To find the saddlepoint solution of the full grand canonical partition function in (10), it is therefore analytically more well-defined to maximize the entanglement entropy in (19), rather than minimize the free energy in (17), since this resolves the issue of the degeneracy of the free-energy minima. Formally, the structure of the structure of these degenerate singularities corresponds to a polynomial ring. In essence, in order to construct a well-defined spin-wave theory for the in-plane fluctuations (to arbitrary order) which also simultaneously a well-defined spin-wave theory for the out-of plane fluctuations (to arbitrary order), we have constructed a regularized theory which is defined the boundary surface in phase space where these excitations become degenerate. This allows to treat inter-valley tunneling from multiple soliton sectors, and to go beyond the first order expansion of the in-plane and out-of-plane fluctuations of the domain walls that is defined by perturbatively expanding the double sine-Gordon model to finite order.

4. Entangled Domain Wall Width

In Figure 1 we plot the quantity $\ln {\Lambda }_i$ as a function of ϕ, from our definitions in (10) and (13) for the mixed-spin antiferromagnetic Heisenberg model defined in (8). This quantity corresponds to the entanglement entropy in (17), and defines the normalized density of the logarithm of the eigenvalues resolved at $s=1$. A more detailed discussion of the finite lattice size of this treatment is presented in [18], but the general trends evident in Figure 1 (for $N=256$) are that there is both a ϕ-independent component to $\ln {\Lambda }_i$, which is relatively flat and centered on $\ln {\Lambda }_i\sim 1.9$, and two ϕ-dependent components to $\ln {\Lambda }_i$, which asymptotically approach $\varphi \sim 0$ and $\varphi \sim 0.9$. This indicates that the spectral density of the eigenvalues of the Grand Canonical Partition Function in (17) follows two separate scaling patterns, as we would expect from (19). Firstly, the locally-divergent simple spin-wave component of this system diverges at two specific values of ϕ, following the standard scaling pattern for fluctuations about a second order fixed point for spin-wave theories [11, 20], corresponding to the singlet and the triplet states of the system. Secondly, the flat plateau corresponds to the resolution of the branch cuts of these two singular points, at $s=1$, on the curved background. Effectively, the physical scale at which the singlet and triplet states become degenerate. We can, therefore, use the above numerical value of the flat plateau to quantify the nonanalytic contribution to the Bloch vectors due to entanglement between the Ferromagnetic Domain Walls in the ferromagnetic nanowire system, which sets the physical scale for the domain wall width. The distinct separation in the scaling behaviour of the eigenvalue spectrum of the Grand Canonical Partition Function in Figure 1 gives good numerical evidence that two meaningful spin-wave theories can be modeled via this approach, that are separated in this analysis by a specific set of nonlocal expansion coefficients determined via the physical scale corresponding to the flat plateau.

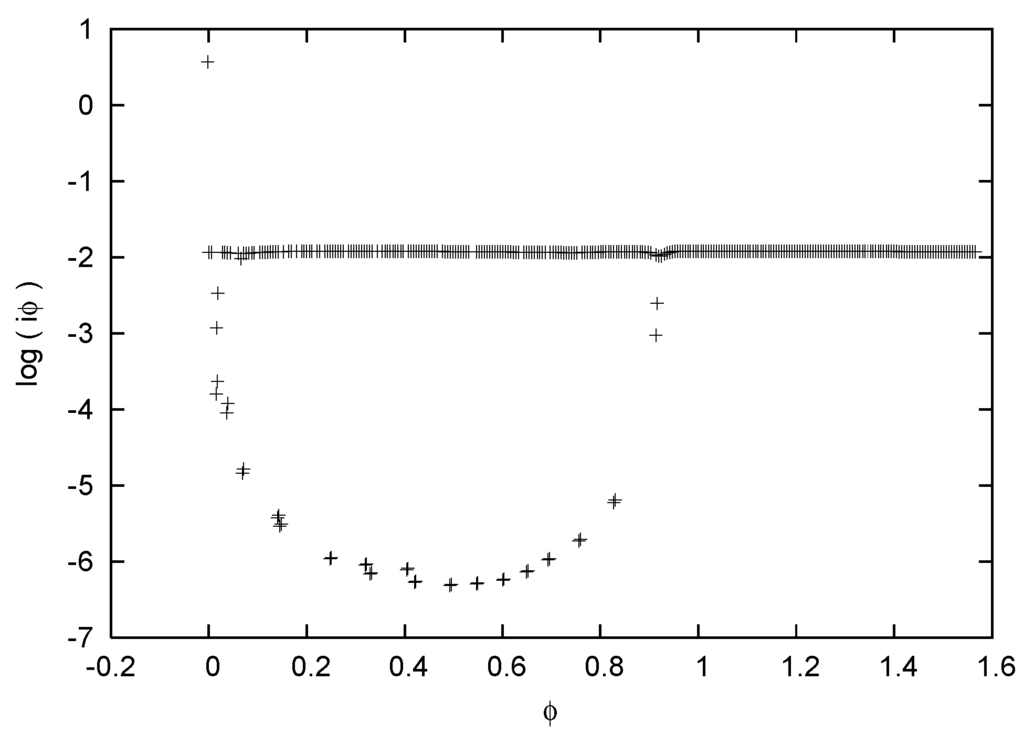
Figure 1. The density of the logarithm of the eigenvalues of P in (13), $\ln {\Lambda }_i$, plotted as a function of the Bloch vector angle ϕ, defined in (10).

Figure 1. The density of the logarithm of the eigenvalues of P in (13), $\ln {\Lambda }_i$, plotted as a function of the Bloch vector angle ϕ, defined in (10).

When the double sine-Gordon model is used to describe the magnons associated with the differential conductance profile of Ferromagnetic Nanowires in [2, 9], or more formally when this model is used (equivalently) to describe the (infrared) singularities associated with topological changes in the ground states of quantum spin chains (where these domain walls are viewed as solitons) [20, 23], in both cases, ϕ, is used to parameterise the angle that describes the orientation of magnetization vectors as they cross the domain walls. The two interaction terms in the double sine-Gordon model in (2) therefore have specific generic meanings - the first interaction term describes the massless singlet state of this magnetization vector, whilst the second interaction term describes the massive triplet state found by the Zeeman splitting of this magnetization vector. In our analysis, this relationship is made explicit by our definition of the Clebsch-Gordon coefficients in (7). Crucially, when long-ranged dynamical fluctuations are neglected (in the limits of either very narrow or very broad domain walls), the only physical process that can generate Zeeman splitting in the ferromagnetic nanowire is an applied external field. However, when these long-ranged dynamical fluctuations are included, this splitting can also be generated dynamically by inter-valley tunneling processes. Thus, to go beyond a simple magnon picture for the angular momentum transfer of the Bloch vectors in the double sine-Gordon model in (2) requires a treatment of the (nonlocal) dependence of the couplings of the two interaction terms. This long-ranged dynamical cutoff scale corresponds to physical scale set by the flat plateau in our analysis in Figure 1.

The surprising result of our analysis for real experimental data is that the measured coupling of the first interaction term, $MB$, in fits of the data to the simple double sine-Gordon model can always be smoothly deformed into the measured couplings of the second interaction term, K, up to the scale at which the two sets of fluctuations become entangled through inter-valley tunneling. From our analysis, this mapping applies regardless of how involved the actual spin-wave theories for the in-plane and out-of-plane fluctuations of the domain walls are, and how many additional interaction terms are included to perturbatively improve the double sine-Gordon model. This hypothesis for the Lorentz covariance of the couplings can also be tested directly in the experimental data for the domain walls in Ferromagnetic Nanowires. In (10), ϕ traces out the surface of the Bloch sphere in Euclidean time, therefore, the smooth deformation of (7) maps this Bloch sphere into an ellipsoid. The eccentricity of this ellipsoid e can therefore be defined from couplings in (2) by,

$$e=\sqrt{1-{(\eta /2\gamma +1)}^2}$$

(20)

where $\gamma =K$ and $\eta =MB/2B_{max}$ and the entanglement entropy is defined in units of $ln\mathrm{B}=ln\left(B/B_{max}\right)$. Viewed physically, as the elementary magnons of either the in-plane or out-of-plane domain walls pass through the domain wall they become effectively oblate through entanglement via inter-domain tunneling. In the limit that the triplet state coupling in the double sine-Gordon model is larger than the singlet state coupling in (2), the above eccentricity parameter then becomes purely imaginary - corresponding to a completely entangled state. A similar elliptical parameterisation of the Bloch vectors is given in [24], to quantify the Pauli cloning of quantum bits.

Figure 2. The Lorentz scaling of the effective anisotropy, K, in (1) defined as a function of the logarithm of the applied field B using the experimental Ferromagnetic Domain Wall data from [2]. The curve indicates the zero entanglement boundary of magnons passing through the domain wall, and is obtained from the preceding numerical analysis.

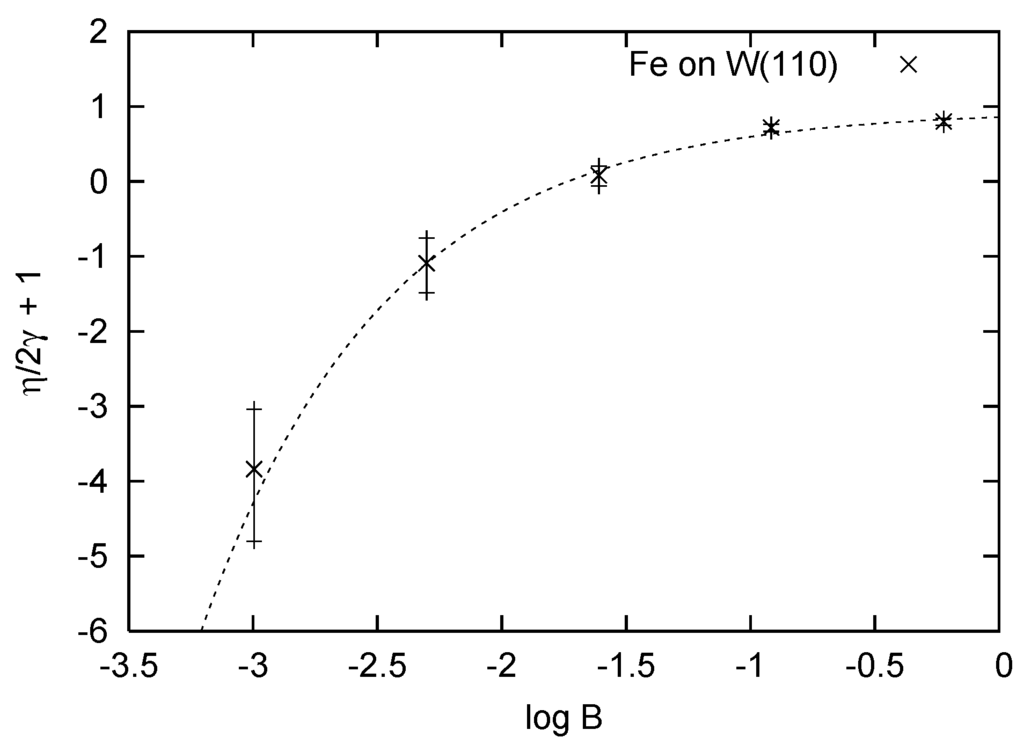
Figure 2. The Lorentz scaling of the effective anisotropy, K, in (1) defined as a function of the logarithm of the applied field B using the experimental Ferromagnetic Domain Wall data from [2]. The curve indicates the zero entanglement boundary of magnons passing through the domain wall, and is obtained from the preceding numerical analysis.

In Figure 2 we plot $\eta /2\gamma +1$ versus $\log \mathrm{B}$ from the domain wall differential conductance profile data obtained experimentally in [2]. To rescale the effective anisotropy data values (which were obtained from fits of the experimental data to the ansatz in (3)) we follow the relatively simple prescription of rescaling e, via the graph. We firstly substitute the data values of η and γ into (18) to calculate the eccentricity, e, of the corresponding Bloch vector. We then recalibrate the magnon couplings by defining the new effective anisotropy value to be ${\gamma }^{\prime }=e$, and set the eccentricity of this new Bloch vector to unity by reading the corresponding ${\eta }^{\prime }$ off the graph. Finally, we calculate the rescaled eccentricity value $e^{\prime }$, by putting ${\gamma }^{\prime }$ and ${\eta }^{\prime }$ in (18). Thus, the ratio $e^{\prime }/e$ quantifies the entanglement contribution to the effective anisotropy value-as distinct from the Zeeman splitting. From this (renormalization) analysis, the effective anisotropy value differs from the renormalized effective anisotropy value by 11% at 200 mT, which implies that the level of quantum noise and loss in angular momentum transfer at the domain walls is 11% at 200 mT. However, this contribution increases dramatically as the field strength is decreased, and magnetic ordering is replaced by quantum-mechanical mixing. The fitted line in Figure 2 corresponds to the scale-independent numerical value for e we obtained from our numerics, which shows good agreement with the data, despite the fact that we have only considered a three domain model.

5. Summary

In this article, we have derived a nonperturbative scaling relation (20) for the angular momentum transfer of magnons at ferromagnetic nanowire domain walls from a rigorous treatment of the singularities associated with the Grand Canonical Partition Function of interacting Ferromagnetic and Anti-Ferromagnetic Domain Walls. Our scaling relation in (20) is defined by finding the infrared cutoff dependence of the couplings in the leading order magnon description of changes in resistivity of the domain wall [18], and we have used a ζ-function renormalization prescription to parameterise the inter-valley tunneling contributions to the magnon couplings via the construction of an exact polynomial ring [13]. The advantage of this approach, over existing calculations for the Grand Canonical Partition function of interacting Ferromagnetic Domain Walls [14,15,16], is that the residual degeneracy of the couplings in this polynomial ring means that we do not need to mathematically separate the planar and non-planar contributions to the domain wall in order to define the magnons, (8). Hence, we are able to quantify the relative changes in the level of quantum noise and loss of angular momentum transfer at the domain wall due to the (inter-valley) mixing of the magnons.

Although no approximations are made in this nonperturbative renormalization calculation, our analysis rests on the simple magnon picture that is used to parameterise the differential conductance profile at the domain wall. We have good evidence in Figure 1 to believe that the leading order contribution to the saddlepoint solution of our system is at most logarithmically divergent, which is in agreement with the general assumptions of the Mermin-Wagner theorem for the condensation of magnons [11, 12] and the experimental successes of the magnon approach [3, 6, 7]. However, although we have explicitly evaluated a Grand Canonical Partition Function for the interacting Ferromagnetic Domain Walls consisting of 256 interacting pairs using importance sampling, the topology of the soliton model we have used only contains interaction terms up to third order. Hence, the numerical results we have presented may not be consistent with much longer Ferromagnetic Nanowires, consisting of a larger number of domains. Nevertheless, our numerical predictions do show good agreement with the scaling of the domain wall data in [2], and our general approach is consistent with the experimental findings of the leading order (planar and non-planar) magnon behaviour of the angular momentum transfer at the domain walls [3,5,6,7,8], which we are now able to renormalize nonperturbatively.