Thermoeconomic Optimum Operation Conditions of a Solar-driven Heat Engine Model
Abstract
:1. Introduction
2. Theoretical Model
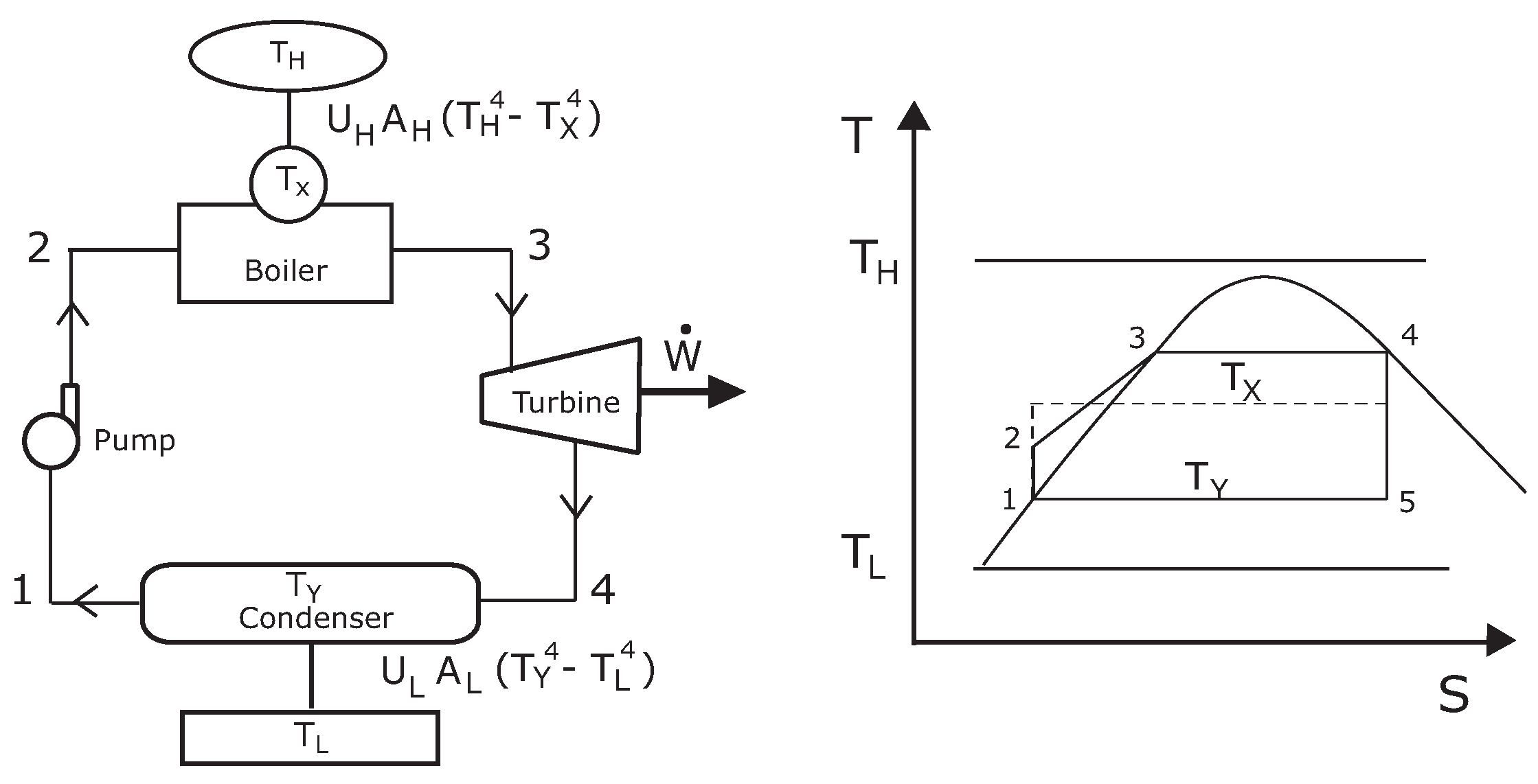
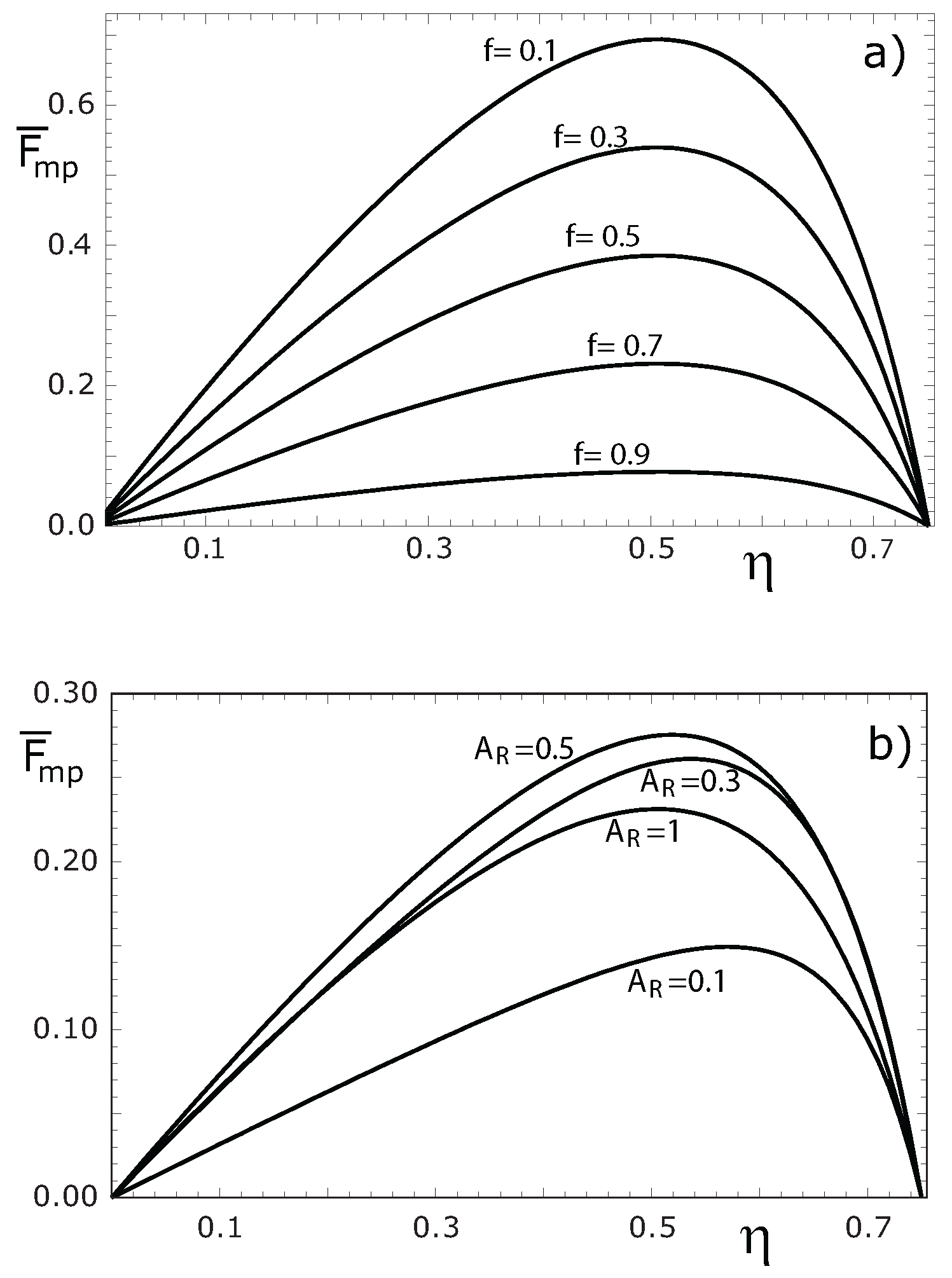

3. Numerical Results and Discussion
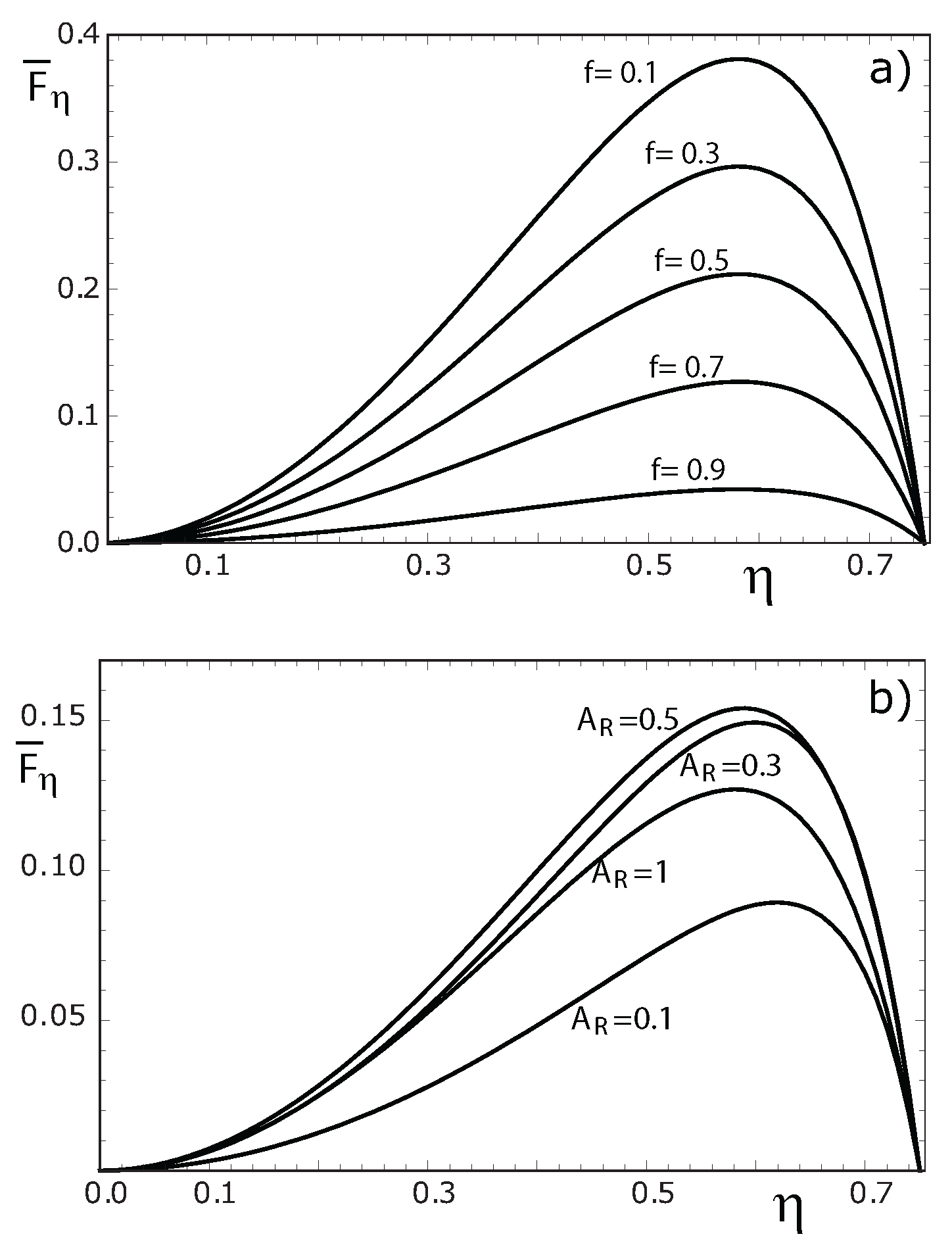
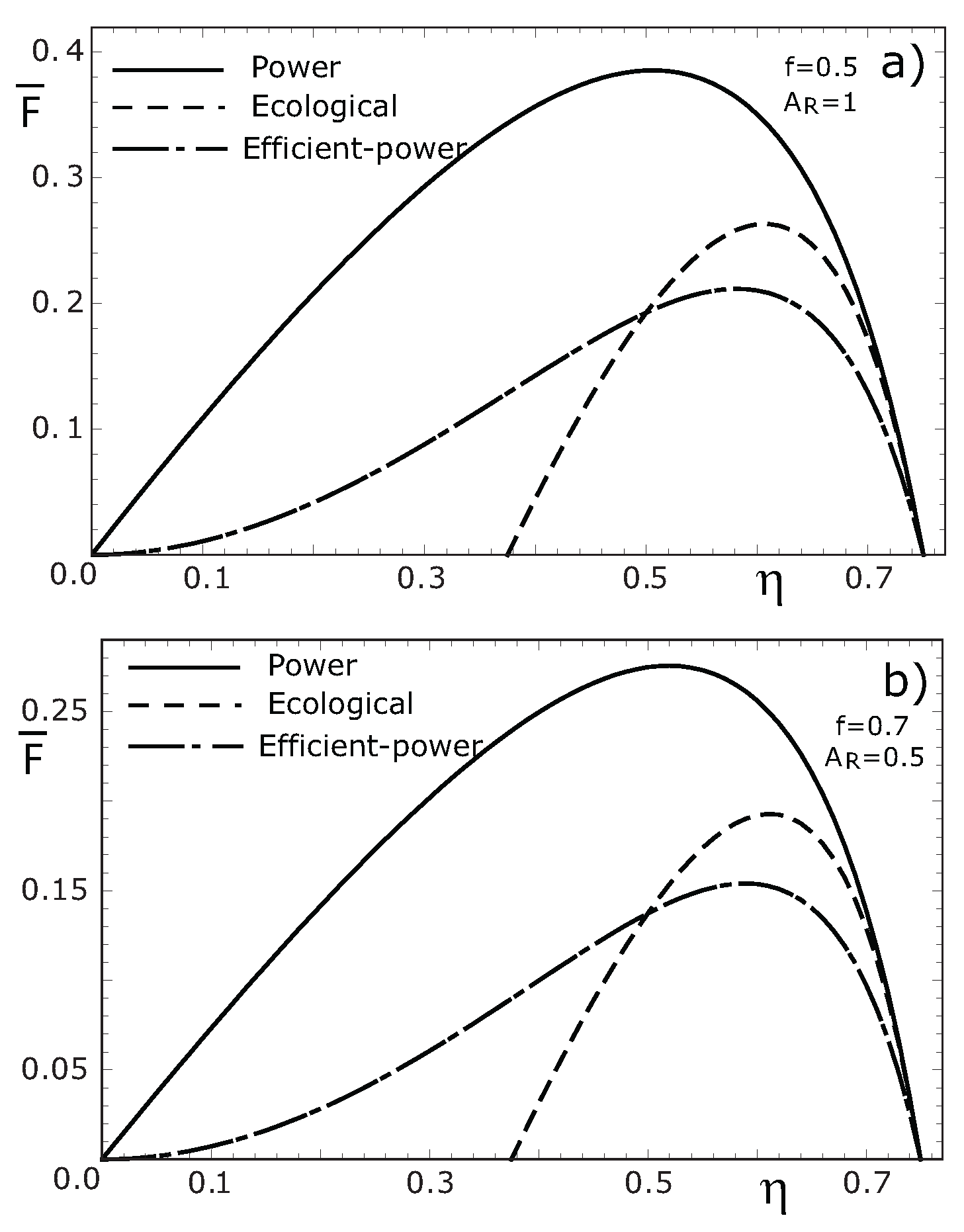
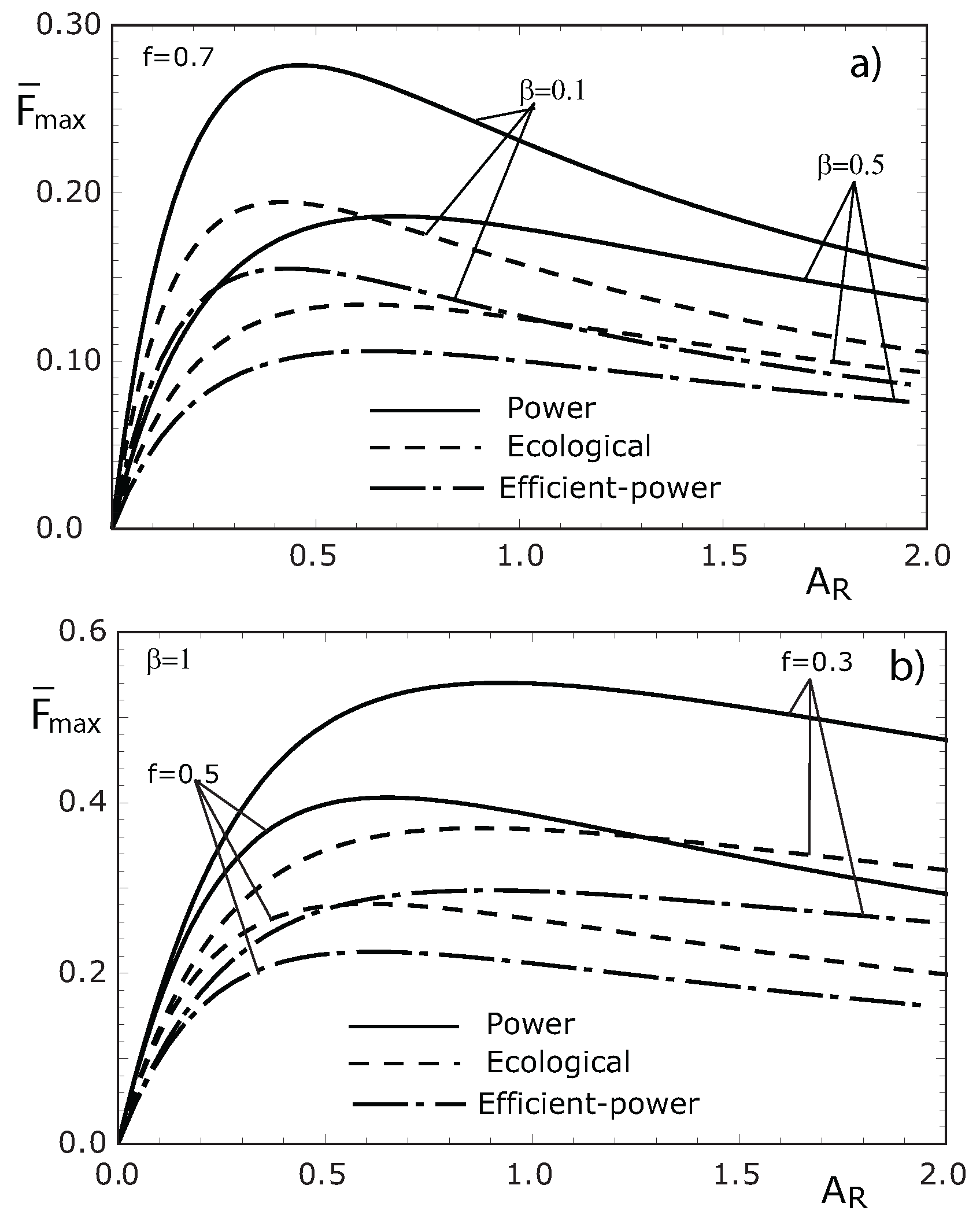
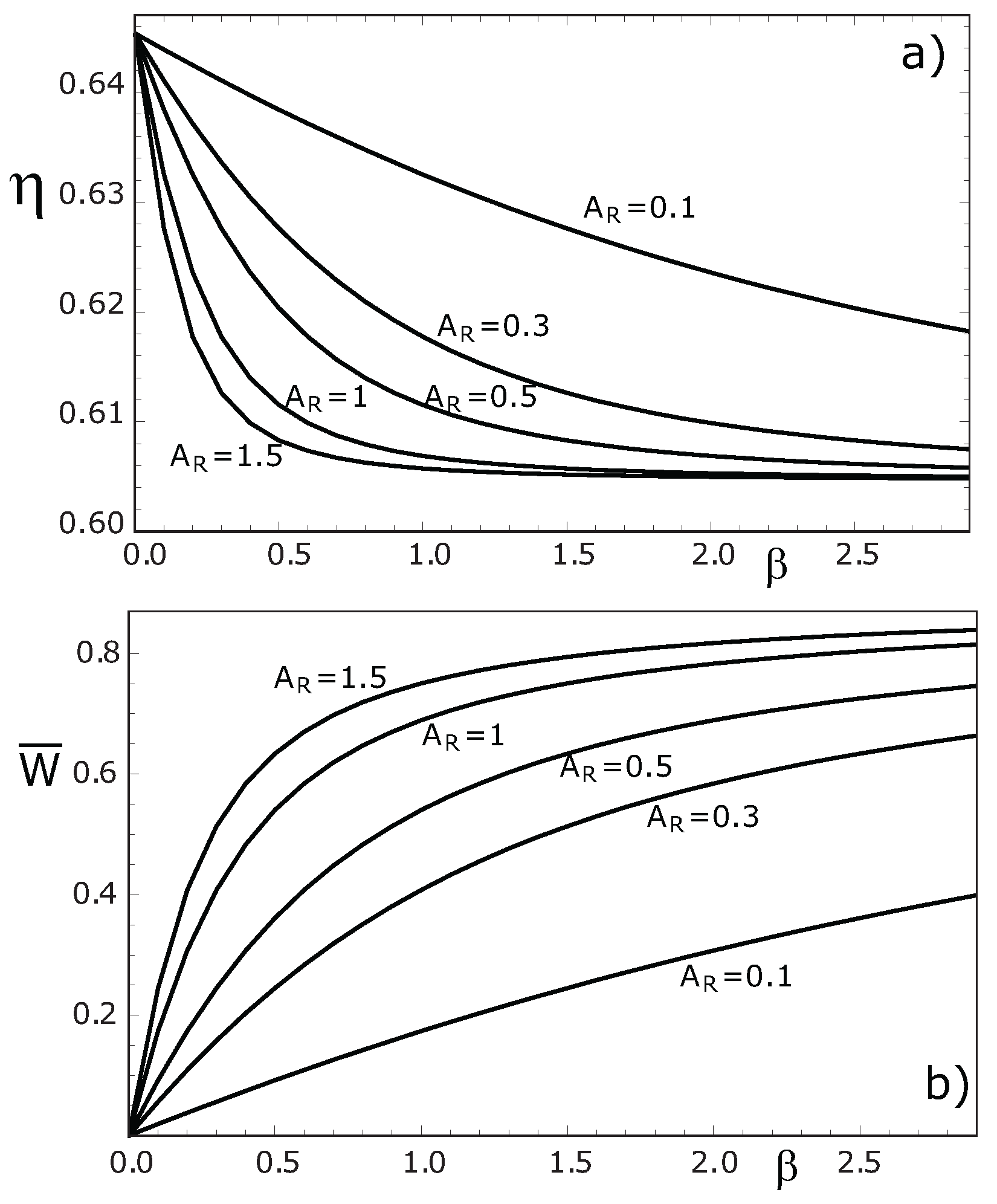
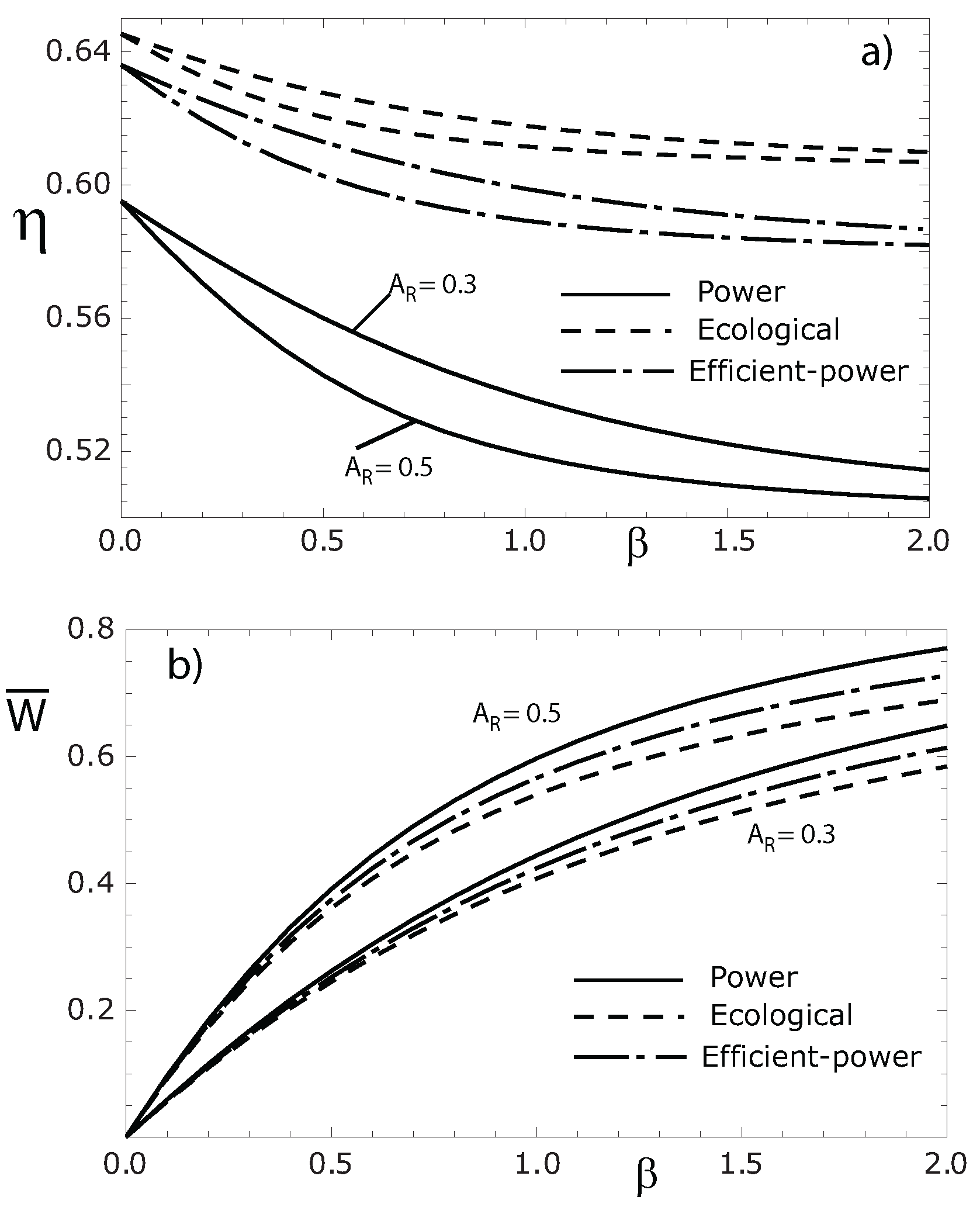
4. Concluding Remarks
Acknowledgements
References
- Bejan, A. Advanced Engineering Thermodynamics; Addison Wiley: New York, NY, USA, 1988. [Google Scholar]
- De Vos, A.; Pauwels, H. On the thermodynamic limit of photovoltaic energy conversion. Appl. Phys. A 1981, 25, 119–125. [Google Scholar] [CrossRef]
- Jeter, S.M. Maximum Conversion efficiency for the utilization of direct solar radiation. Solar Energy 1981, 26, 231–236. [Google Scholar] [CrossRef]
- Gordon, J.M. On optimized solar-driven heat engines. Solar Energy 1988, 40, 457–461. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, X.; Sun, F.; Wu, C. Exergy-based ecological optimization of linear phenomenological heat-transfer law irreversible Carnot-engines. Applied Energy 2006, 83, 573–582. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, L.; Sun, F.; Wu, C. Exergy-based ecological optimization for a generalized irreversible Carnot refrigerator. J. Energy Inst. 2006, 79, 42–46. [Google Scholar] [CrossRef]
- Sahin, A.Z. Optimum operating conditions of solar driven heat engines. Energ. Conv. Manage. 2000, 41, 1335–1343. [Google Scholar] [CrossRef]
- Sahin, A.Z. Finite-time thermodynamic analysis of a solar driven heat engine. Exergy, An International Journal 2001, 01, 122–126. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A. Performance analysis of an endoreversible heat engine based on a new thermoeconomic optimization criterion. Energ. Conv. Manage. 2001, 42, 1085–1093. [Google Scholar] [CrossRef]
- Sahin, B.; Ust, Y.; Tamer, Y.; Akcay, I.H. Thermoeconomic analysis of a solar driven heat engine. Renewable Energy 2006, 31, 1033–1042. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Sánchez-Salas, N.; Angulo-Brown, F. On the optimum operation conditions of an endoreversible heat engine with different heat transfer laws in the thermal couplings. Revista Mexicana de Física 2008, 54, 284–292. [Google Scholar]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermoeconomic optimisation of Novikov power plant model under maximum ecological conditions. J. Energy Inst. 2007, 80, 96–104. [Google Scholar] [CrossRef]
- Yilmaz, T. A new performance criterion for heat engines: efficient power. J. Energy Inst. 2006, 79, 38–41. [Google Scholar] [CrossRef]
- Khaliq, A. Finite-time heat-transfer analysis and generalized power-optimization of an endoreversible Rankine heat-engine. Applied Energy 2004, 79, 27–40. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible thermoeconomics. Energ. Conv. Manage. 1995, 36, 1–5. [Google Scholar] [CrossRef]
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Amer. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible Thermodynamics of Solar Energy Conversion; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
© 2009 by the authors. Licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Barranco-Jiménez, M.A.; Sánchez-Salas, N.; Rosales, M.A. Thermoeconomic Optimum Operation Conditions of a Solar-driven Heat Engine Model. Entropy 2009, 11, 443-453. https://doi.org/10.3390/e11030443
Barranco-Jiménez MA, Sánchez-Salas N, Rosales MA. Thermoeconomic Optimum Operation Conditions of a Solar-driven Heat Engine Model. Entropy. 2009; 11(3):443-453. https://doi.org/10.3390/e11030443
Chicago/Turabian StyleBarranco-Jiménez, Marco A., Norma Sánchez-Salas, and Marco A. Rosales. 2009. "Thermoeconomic Optimum Operation Conditions of a Solar-driven Heat Engine Model" Entropy 11, no. 3: 443-453. https://doi.org/10.3390/e11030443
APA StyleBarranco-Jiménez, M. A., Sánchez-Salas, N., & Rosales, M. A. (2009). Thermoeconomic Optimum Operation Conditions of a Solar-driven Heat Engine Model. Entropy, 11(3), 443-453. https://doi.org/10.3390/e11030443



