Quantification of Information in a One-Way Plant-to-Animal Communication System
Abstract
:1. Introduction
2. Information Entropy Measures and the Zipf Statistic
3. The Zipf Statistic
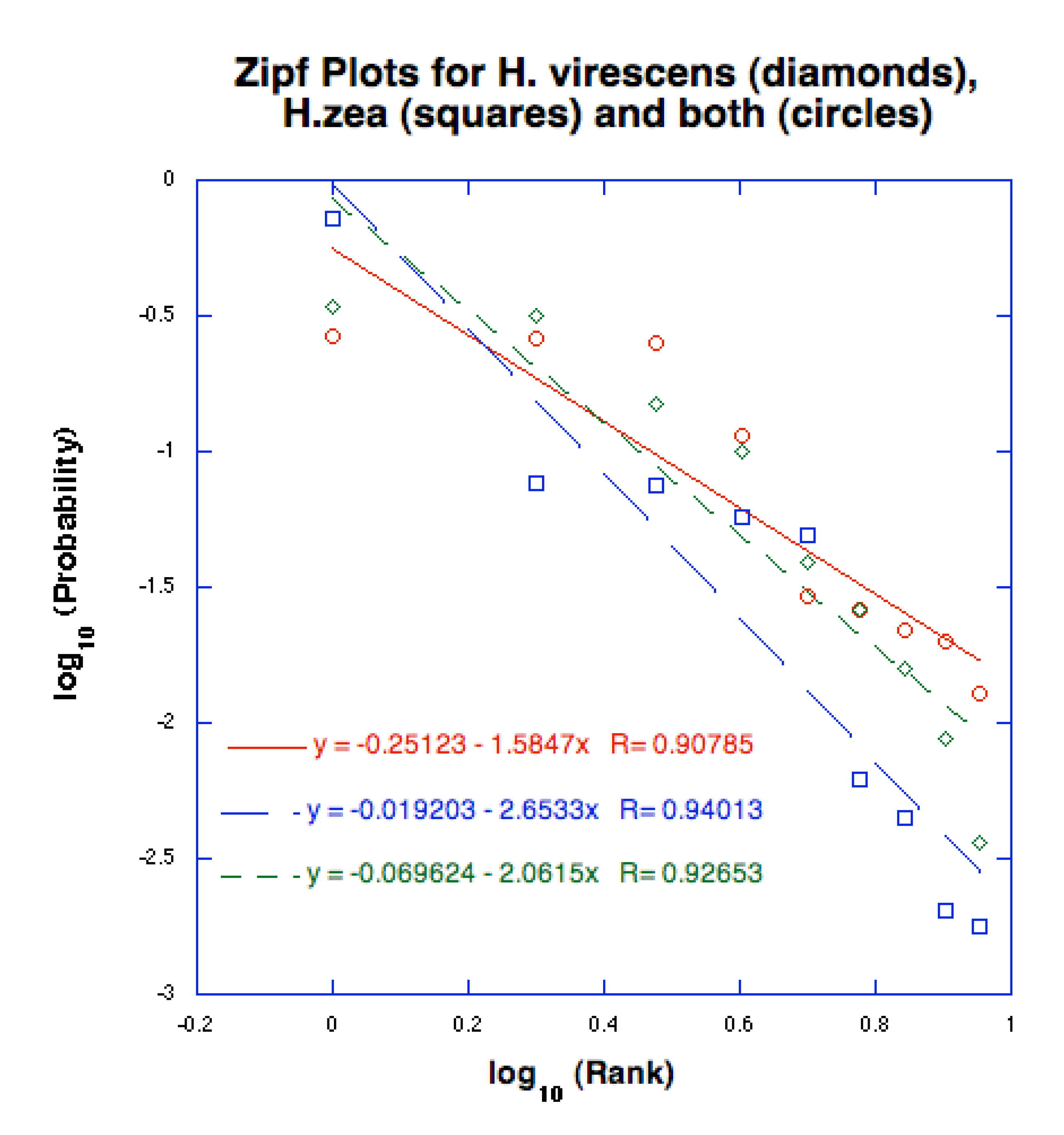
4. Information in the Chemical Signals
4.1. Information in the Transmitted Message
| Chemical Signals | H. virescens (ng) | p(i) | H. zea (ng) | p(j) | p(i, j) |
|---|---|---|---|---|---|
| (Z)-3-Hexen-1-ol | 13,738 | 0.0389 | 215 | 0.0018 | 0.0294 |
| α-Pinene | 53,310 | 0.1509 | 748 | 0.0062 | 0.1140 |
| (Z)-3-Hexenyl acetate | 111,350 | 0.3151 | 6,922 | 0.0572 | 0.2493 |
| (E)-β-Ocimene | 120,257 | 0.3403 | 5,919 | 0.0489 | 0.2660 |
| (E)-4-8-Dimethyl-1,3,7-nonatriene | 35,612 | 0.1008 | 88,000 | 0.7274 | 0.2606 |
| β-Caryophyllene | 5,591 | 0.0158 | 546 | 0.0045 | 0.0129 |
| (E)- β-farnesene | 9,177 | 0.0260 | 247 | 0.0020 | 0.0199 |
| (E,E)- α-farnesene | 1,273 | 0.0036 | 9,073 | 0.0750 | 0.0218 |
| (E,E)-4,8,12-trimethyl-1,3,7-tridecatetnaene | 3,075 | 0.0087 | 9,317 | 0.0770 | 0.0261 |
4.2. Information in the Received Message
5. Interpretation of Results
6. Summary and Conclusions
Acknowledgements
References
- DeMoraes, C.M.; Lewis, W.J.; Paré, P.W.; Alborn, H.T.; Tumlinson, J.H. Herbivore-Infested Plants Selectively Attract Parasitoids. Nature 1998, 393, 570–573. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell. Syst. Tech. J. 2001, 5, 3–55. [Google Scholar]
- Quastler, H. A Primer on Information Theory. In Information Theory in Biology; Yockey, H.P., Platzman, R.L., Quastler, H., Eds.; Pergamon Press: New York, NY, USA, 1958; pp. 3–49. [Google Scholar]
- Pierce, J.R. An Introduction to Information Theory: Symbols, Signals, and Noise; Dover Publications: New York, NY, USA, 1980. [Google Scholar]
- Yaglom, A.M.; Yaglom, I.M. Probability and Information; Reidel Publishers: Boston, MA, USA, 1983. [Google Scholar]
- McCowan, B.; Hanser, S.F.; Doyle, L.R. Quantitative Tools for Comparing Animal Communication Systems: Information Theory Applied to Bottlenose Dolphin Whistle Repertoires. Anim. Behav. 1999, 57, 409–419. [Google Scholar] [PubMed]
- McCowan, B.; Doyle, L.R.; Kaufman, A.B.; Hanser, S.; Burgess, C. Detection and Estimation of Complexity and Contextual Flexibility in Nonhuman Animal Communication. In Evolution of Communicative Flexibility; Complexity, Creativity, and Adaptability in Human and Animal Communication; Oller, D.K., Griebel, U., Eds.; MIT Press: Cambridge, MA, USA, 2008; pp. 281–303. [Google Scholar]
- Yockey, H.P. Information Theory, Evolution, and the Origin of Life; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Zipf, G.K. Human Behaviour and the Principle of Least Effort; Addison-Wesley Press: Cambridge, UK, 1949. [Google Scholar]
- Cancho, R.F.; Solé, R.V. Least Effort and the Origins of Scaling in Human Language. Proc. Natl. Acad. Sci. USA 2003, 100, 788–791. [Google Scholar]
- McCowan, B.; Doyle, L.R.; Jenkins, J.M.; Hanser, S.F. The Appropriate Use of Zipf's Law in Animal Communication Studies. Anim. Behav. 2005, 69, F1–F7. [Google Scholar]
- McCowan, B.; Doyle, L.R.; Hanser, S. Using Information Theory to Assess the Diversity, Complexity, and Development of Communicative Repertoires. J. Comp. Psychol. 2002, 116, 166–172. [Google Scholar] [PubMed]
- Steinberg, J.B. Information Theory as an Ethological Tool. In Quantitative Methods in the Study of Animal Behavior; Hazlett, A., Ed.; Academic Press: New York, NY, USA, 1977; pp. 47–74. [Google Scholar]
- Doyle, L.R.; McCowan, B.; Hanser, S.F.; Bucci, T.; Chyba, C.; Blue, J.E. Applicability of Information Theory to the Quantification of Responses to Anthropogenic Noise by Southeast Alaskan Humpback Whales. Entropy 2008, 10, 33–46. [Google Scholar] [CrossRef]
- Hanser, S.F.T. Toward the Social and Acoustic Ecology of Social Foraging Humpback Whales (megaptera novaelngliae) in Southeast Alaska, Dissertation; University of California: Davis, CA, USA, 2009. [Google Scholar]
- Wilson, E.O. Chemical Communication Among Workers of the Fire Ant Solenopsis Saevissima 2. An Information Analysis of the Odour Trail. Anim. Behav. 1962, 10, 148–158. [Google Scholar]
- Haldane, J.; Spurway, H. A Statistical Analysis of Communication in Apis Mellifera and a Comparison with Communication in Other Animals. Insectes Soc. 1954, 1, 247–283. [Google Scholar] [CrossRef]
- Preston, J. Communication Systems and Social Interactions in a Goby-Shrimp Symbiosis. Anim. Behav. 1978, 26, 791–802. [Google Scholar] [CrossRef]
- Pest of cutton. http://ipm.ncsu.edu/AG271/cotton/cotton.html (accessed August 19, 2009).
© 2009 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Doyle, L.R. Quantification of Information in a One-Way Plant-to-Animal Communication System. Entropy 2009, 11, 431-442. https://doi.org/10.3390/e110300431
Doyle LR. Quantification of Information in a One-Way Plant-to-Animal Communication System. Entropy. 2009; 11(3):431-442. https://doi.org/10.3390/e110300431
Chicago/Turabian StyleDoyle, Laurance R. 2009. "Quantification of Information in a One-Way Plant-to-Animal Communication System" Entropy 11, no. 3: 431-442. https://doi.org/10.3390/e110300431
APA StyleDoyle, L. R. (2009). Quantification of Information in a One-Way Plant-to-Animal Communication System. Entropy, 11(3), 431-442. https://doi.org/10.3390/e110300431




