Structural Entropy to Characterize Small Proteins (70 aa) and Their Interactions
Abstract
:1. Introduction
2. Results and discussion
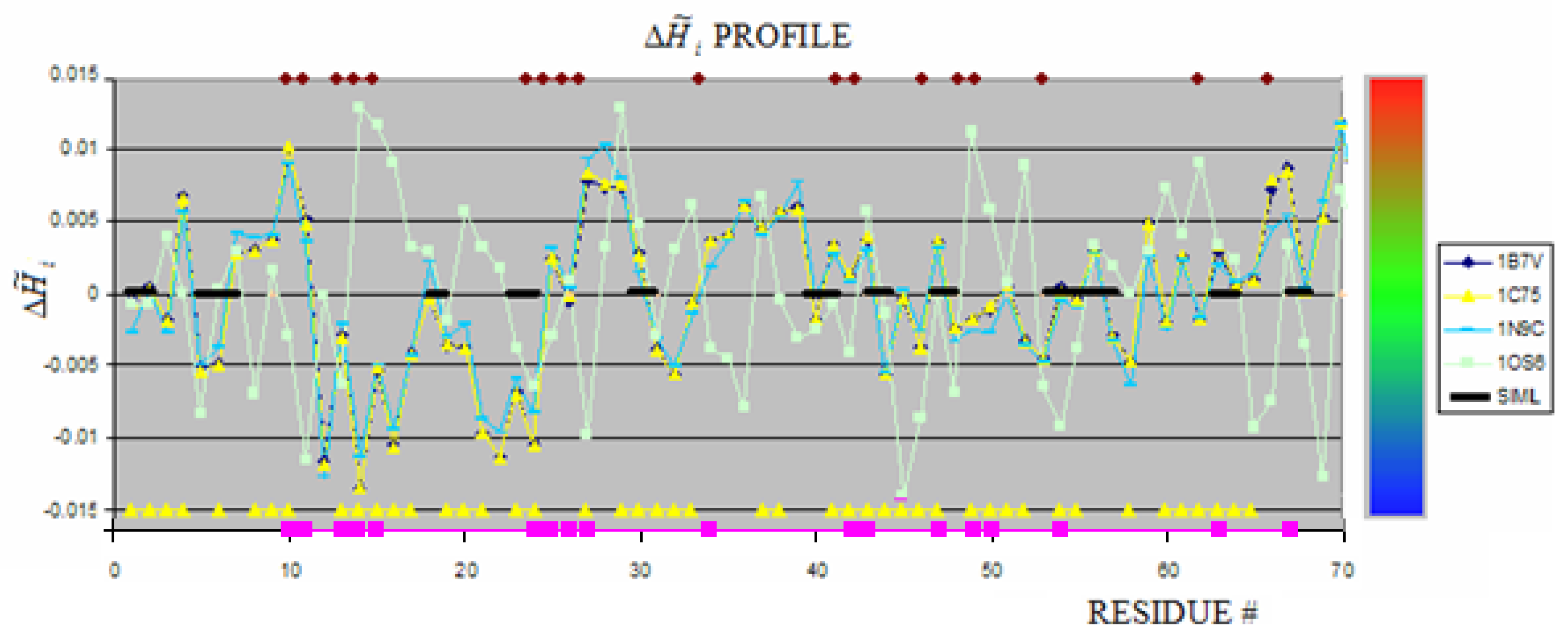
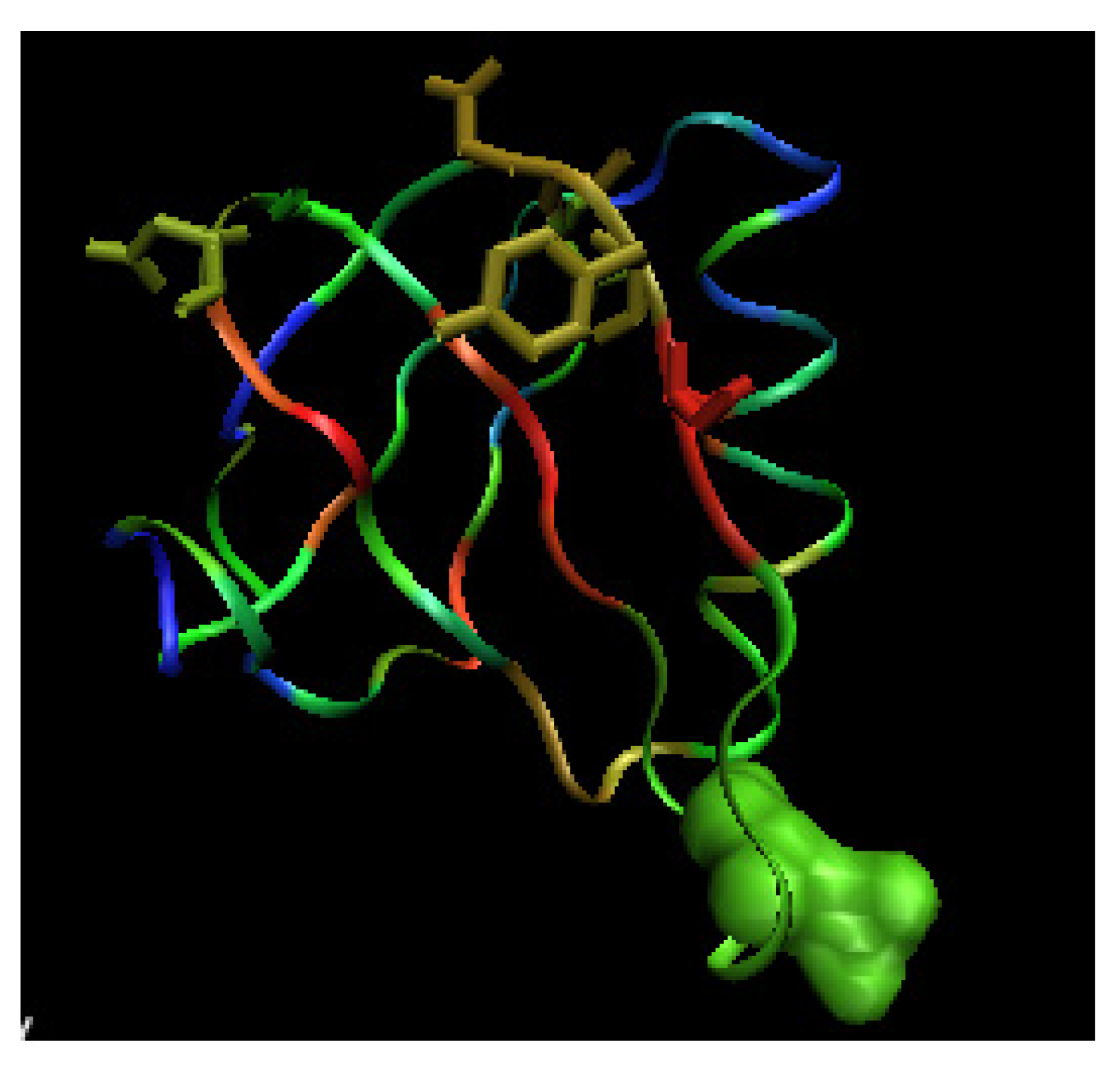
2.1. Hem binding in c-type cytochromes
| PROTEIN | LIGAND | average Residues engaged in interaction with ligand * | average Residues not engaged in interaction with ligand* |
|---|---|---|---|
| 1B7V | Hem | 1.25 | -0.26 |
| 1C75 | Hem | 0.63 | -0.20 |
| 1N96 | Hem | 0.29 | -0.11 |
| 1OS6 | Hem1 | -3.15 | -1.22 |
| Hem2 | 1.44 | ||
| SO4 | 0.83 | ||
| DXC | 3.72 |
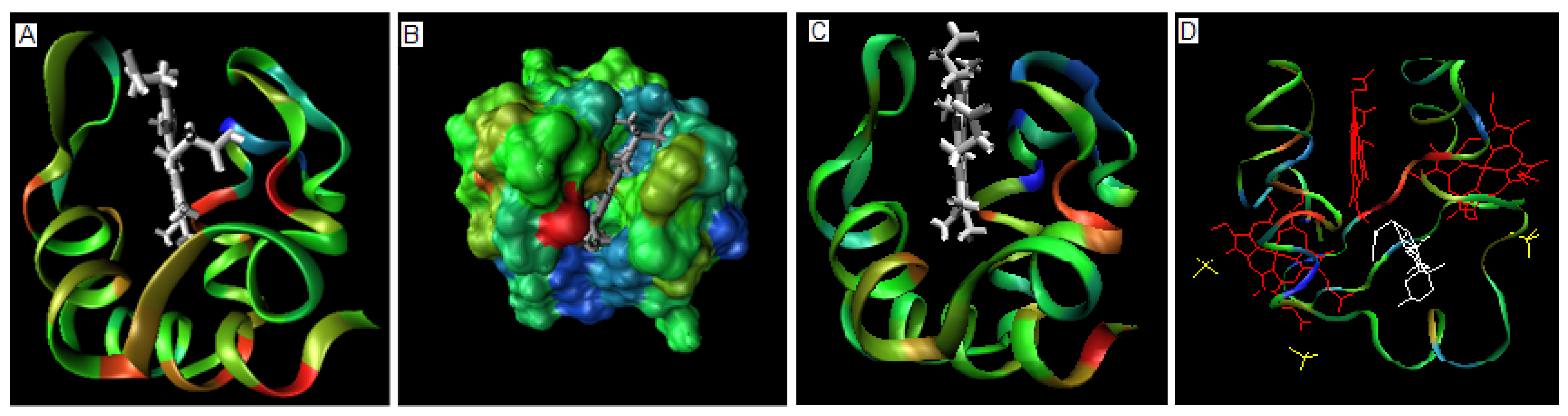
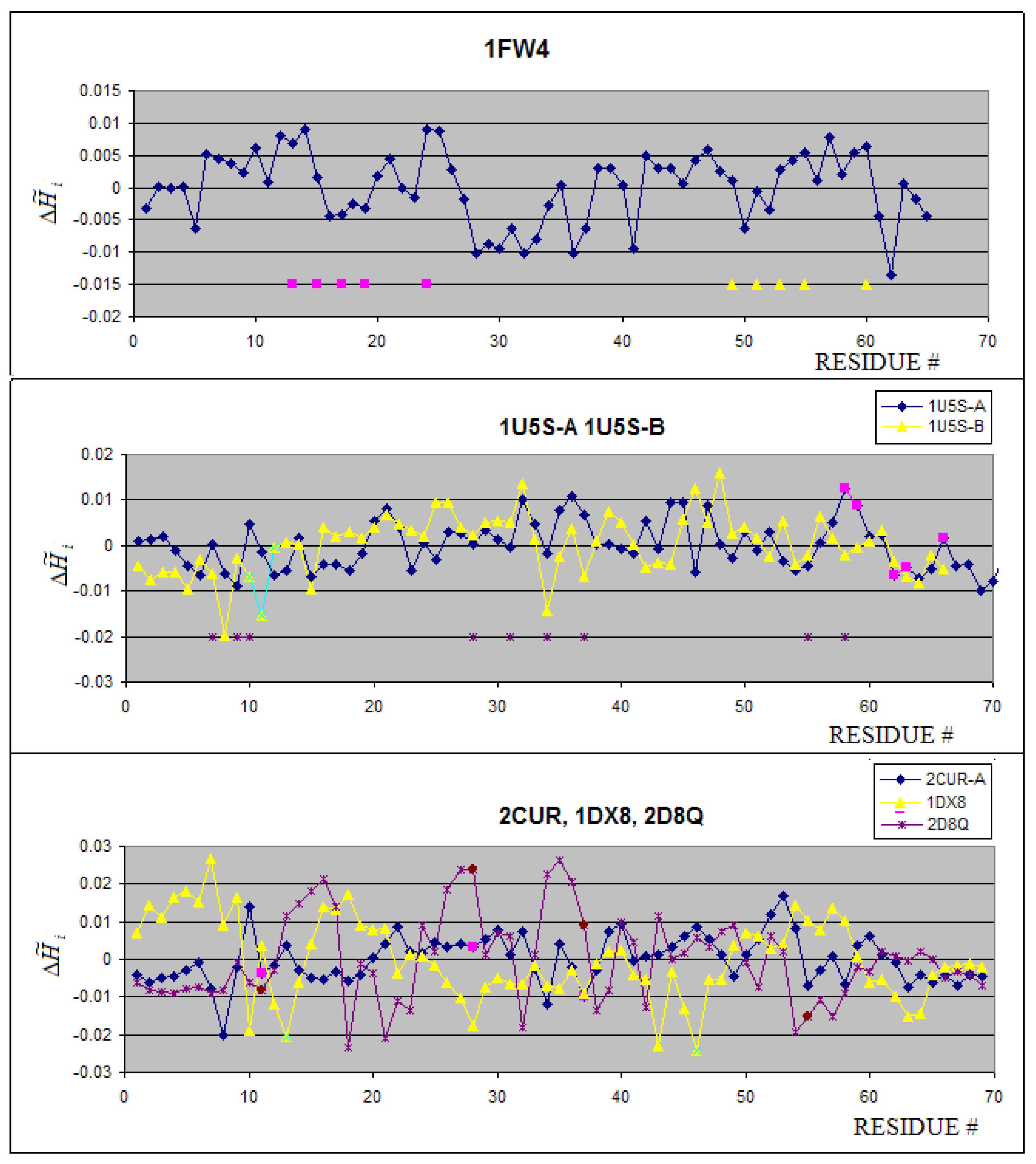
2.2. Metal binding proteins
| PROTEIN | ION | average Residues engaged in interaction with ion * | average Residues not engaged in interaction with ion* |
|---|---|---|---|
| FW4 | Ca2+ | 1.95 | -0.035 |
| 1U5S-B | Zn2+ | -6.40 | 0.41 |
| 2CUR | Zn2+ | -6.83 | 0.90 |
| 2D8Q | Zn2+ | -8.20 | 1.06 |
| 1DX8 | Zn2+ | -21.58 | 1.31 |
2.3. Antibiotics
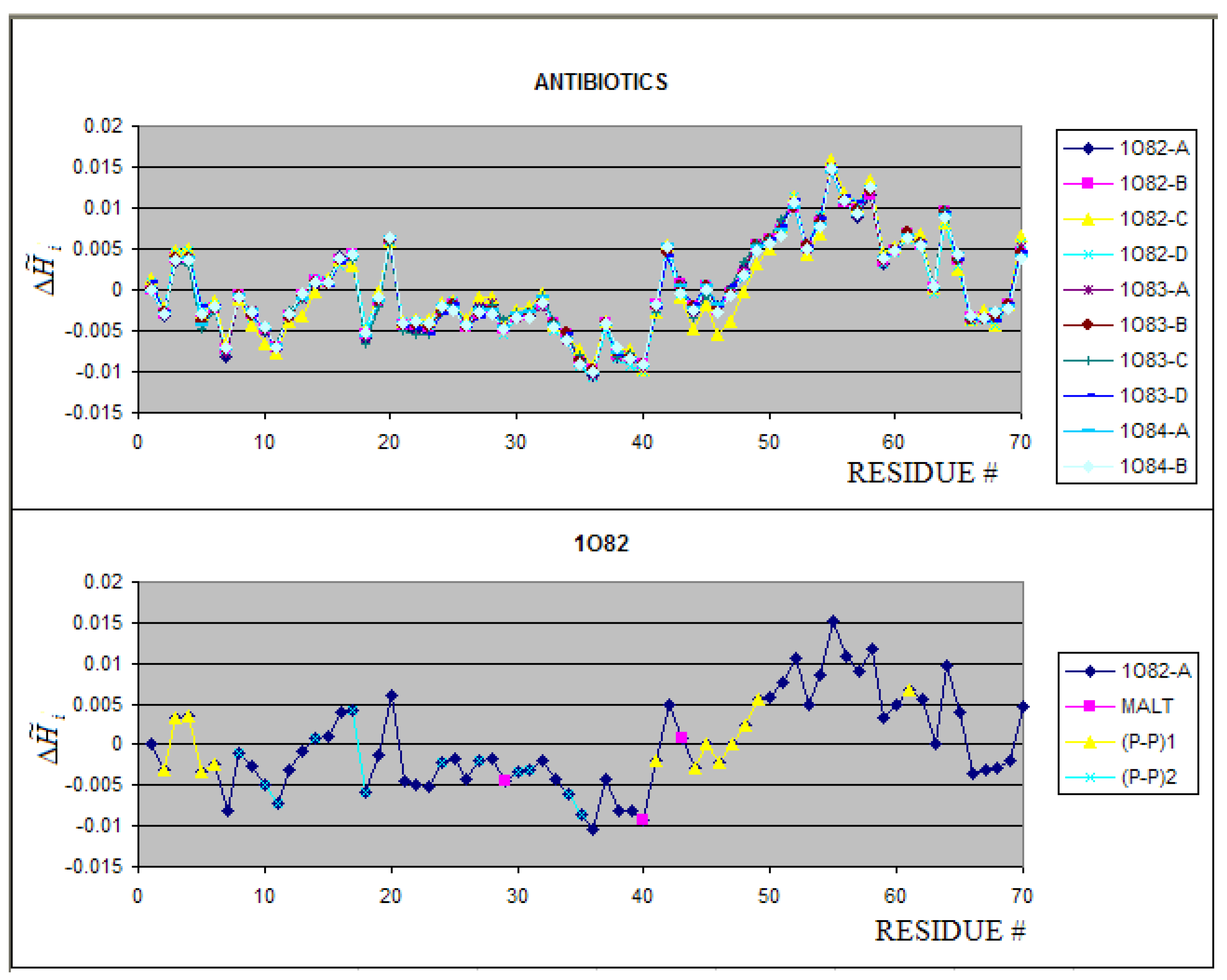
| PROTEIN | CHAIN | average Residues engaged in interaction with protein * | average Residues not engaged in interaction with protein* |
|---|---|---|---|
| 1O82 | A | -3.47 | 0.65 |
| B | -0.94 | 0.37 | |
| C | -3.33 | 0.62 | |
| D | -0.62 | 0.25 | |
| 1O83 | A | -3.40 | 0.65 |
| B | -1.20 | 0.51 | |
| C | -3.55 | 0.60 | |
| D | -0.28 | 0.11 | |
| 1O84 | A | -0.90 | 0.22 |
| B | 0.58 | -0.12 |
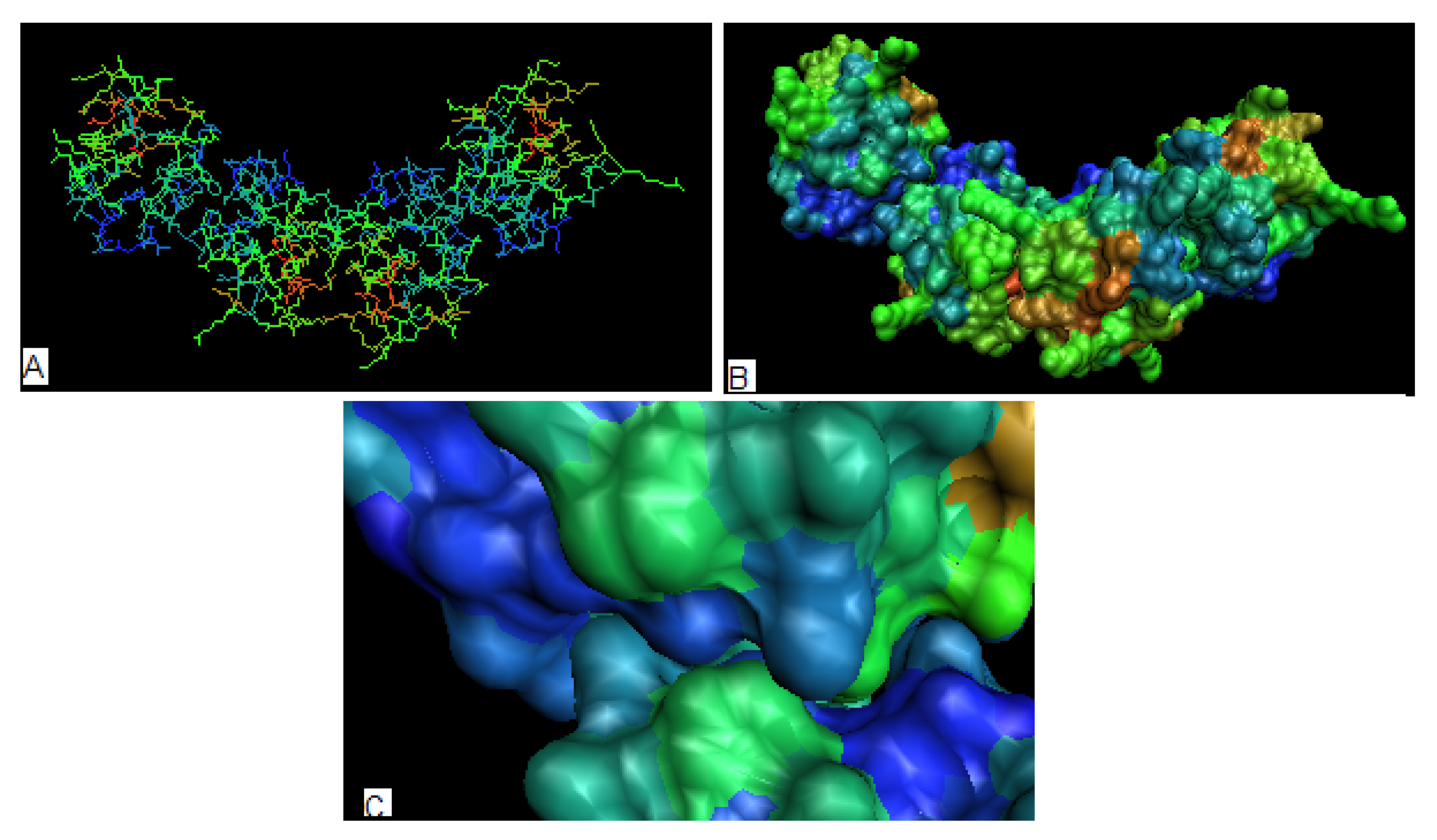
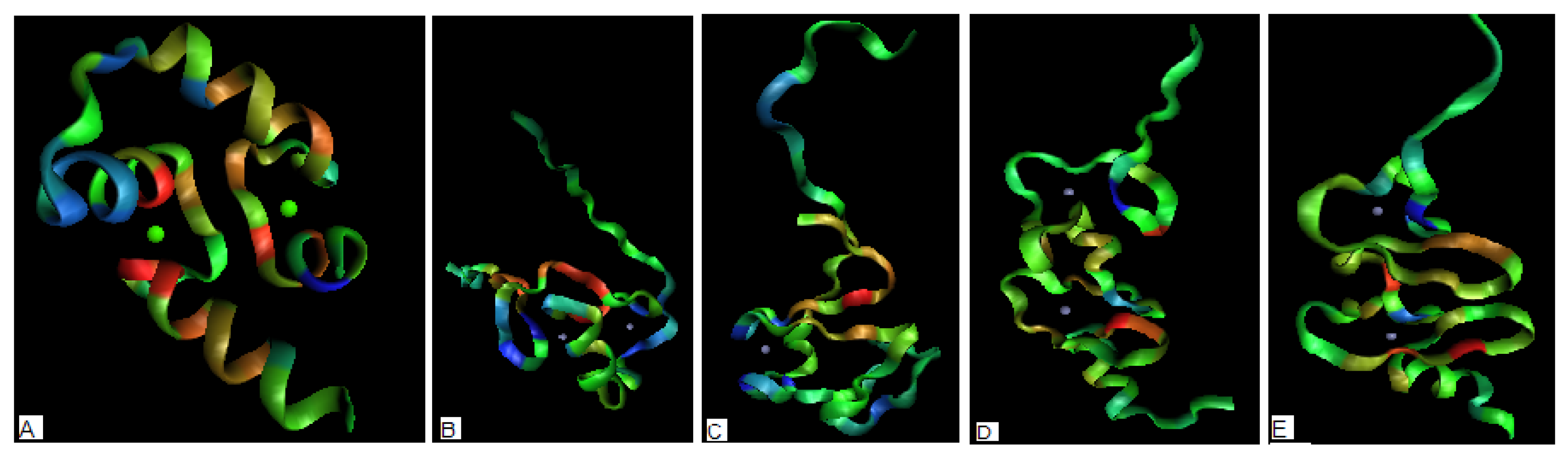
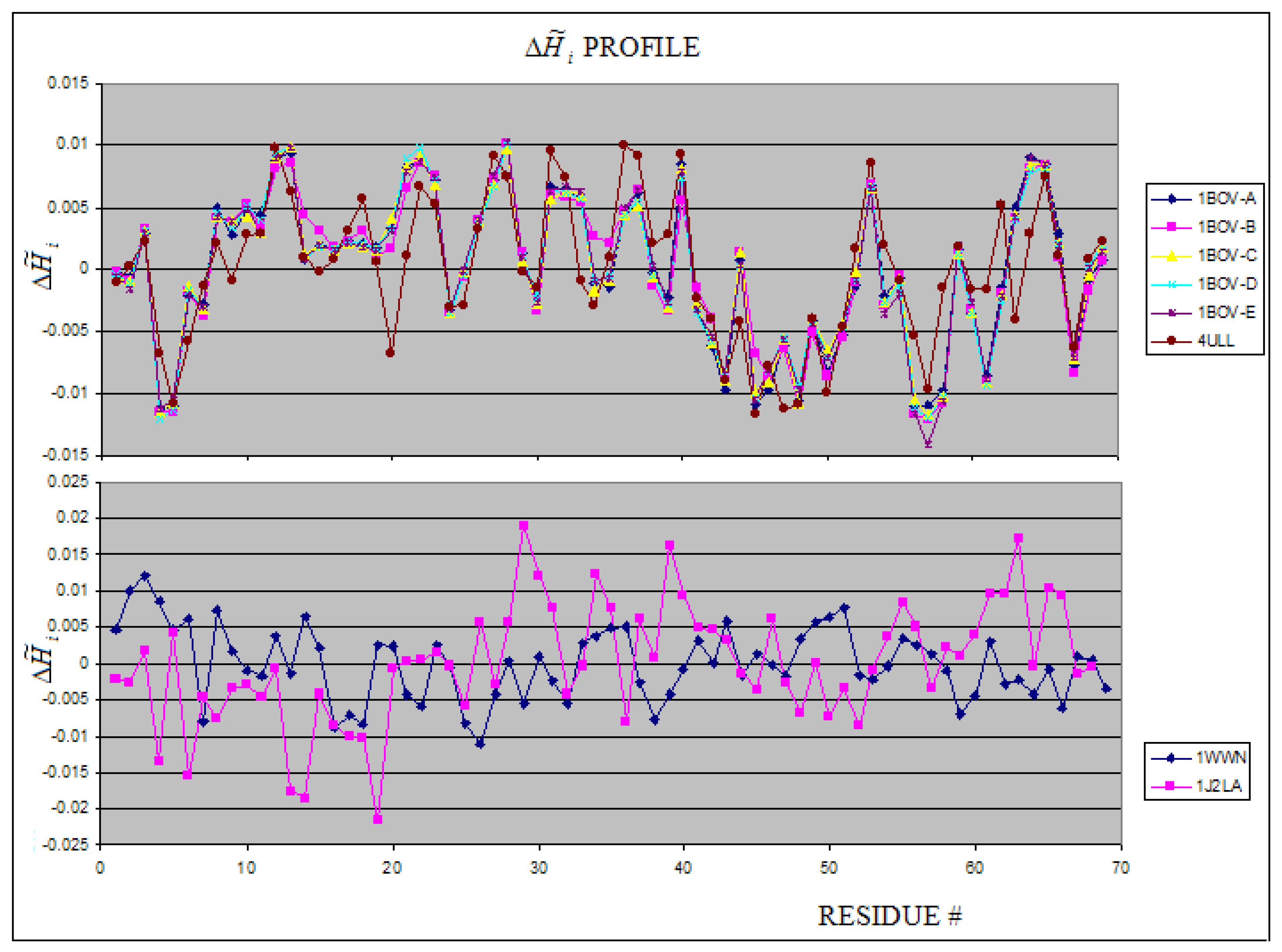
2.4. Toxins
| PROTEIN | average Residues engaged in interaction with protein* | average Residues not engaged in interaction with protein* | average Residues engaged in interaction with ligand* |
|---|---|---|---|
| 1BOV : A | 2.8 | -0.74 | |
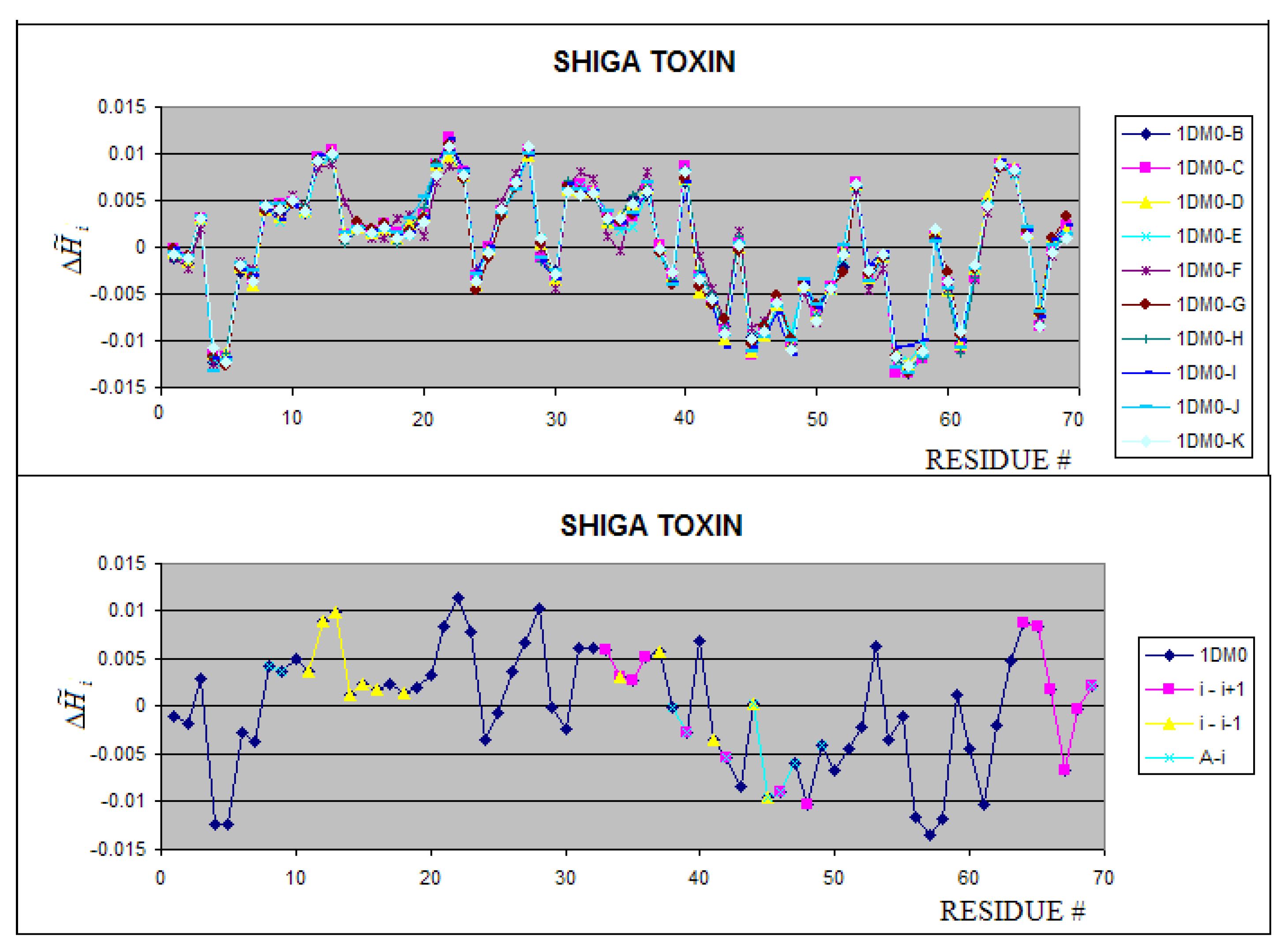
| 1DM0 | 0.96 | -0.55 | |
| 1R4Q – B | -1.08 | 0.30 | |
| 1C48 – A | 0.70 | -0.42 | |
| 1CQF – A | 1.26 | -0.71 | |
| 1CZG – A | 1.30 | -0.85 | |
| 1CZW – A | 0.78 | -0.40 | |
| 1D1I – A | 0.55 | -1.28 | 1.71 |
| 1C4Q | 1.50 | -0.94 | |
| 1D1K | 0.65 | -0.60 | 2.15 |
| 1R4P | 0.86 | -0.57 | |
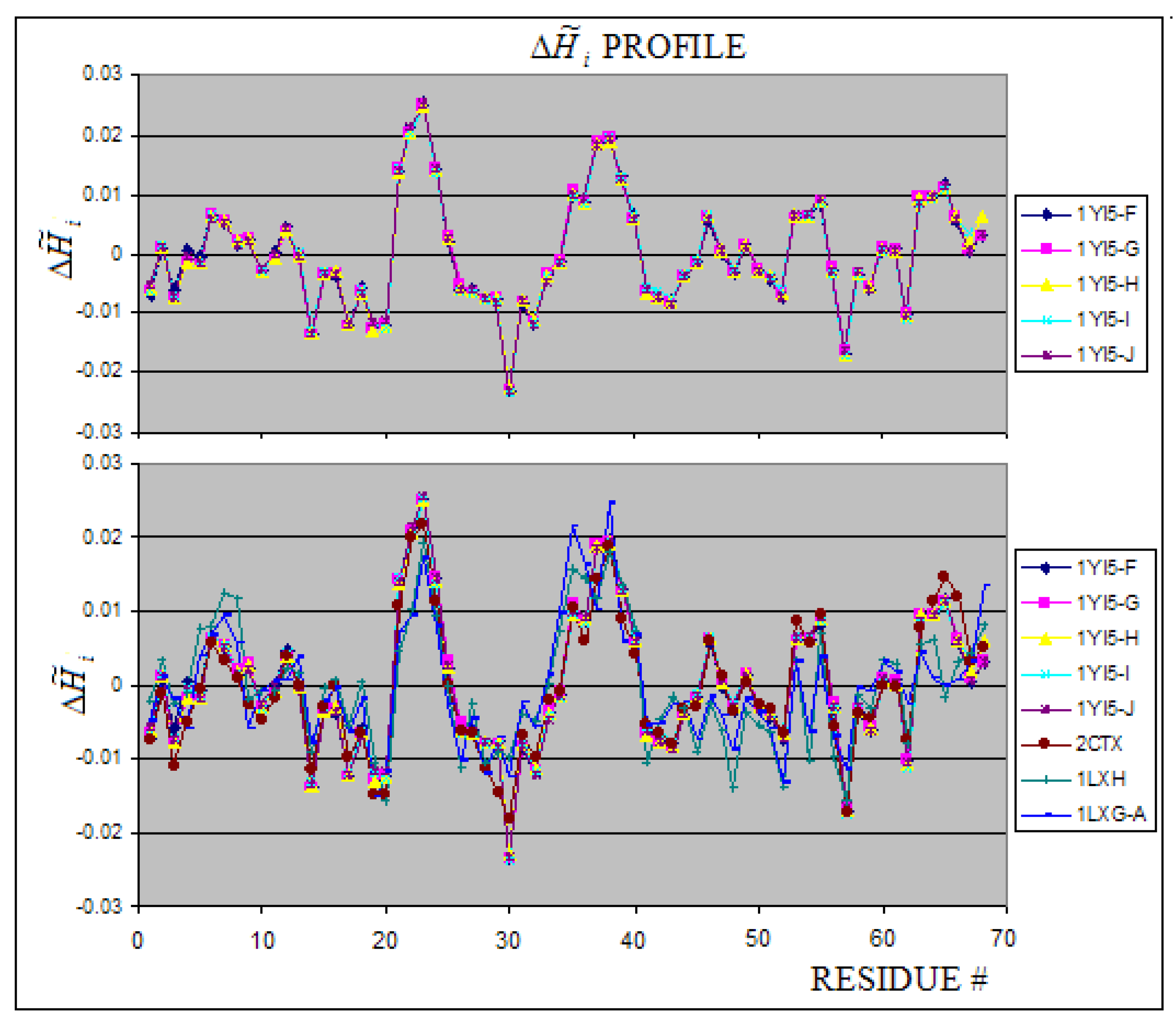
| 1YI5:F | 1.10 | -0.30 | |
| 1LXG | 6.60 | -1.20 |
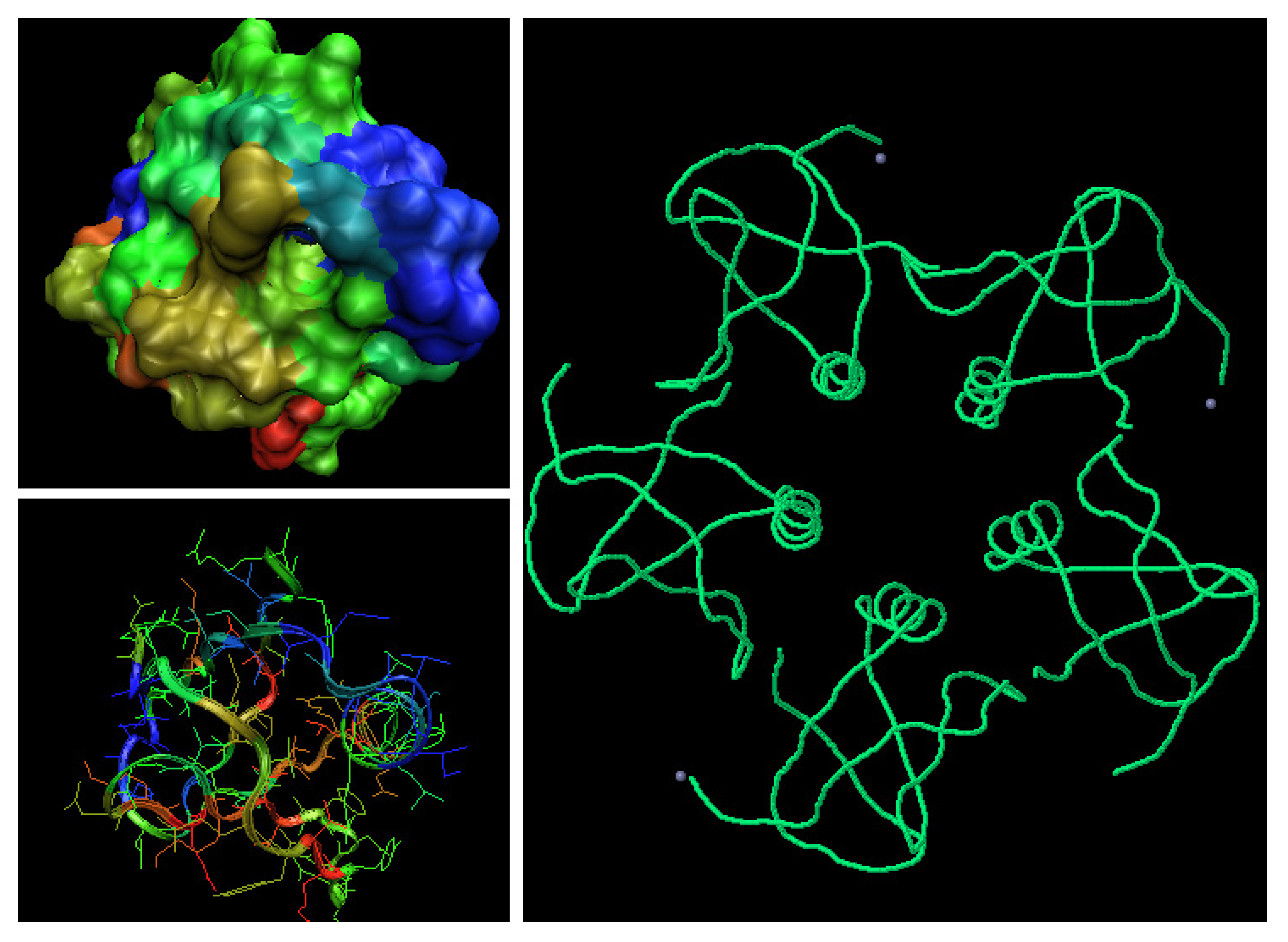
| Description | PDB IDa | Ligand(s)/ Othersb | SE+ | SE+max | SE+ | I+ | SE- | SE-max | SE- | I- |
| Electron transport | 1B7V:A | hem | 2.908 | 3.807 | 0.236 | 46.25 | 2.185 | 3.807 | 0.426 | 51.63 |
| 1C75:A | hem | 2.880 | 3.807 | 0.243 | 46.19 | 2.180 | 3.807 | 0.427 | 51.58 | |
| 1N9C:A | hem | 2.780 | 3.700 | 0.248 | 47.58 | 2.844 | 3.700 | 0.231 | 53.09 | |
| 1OS6:A | 3xhem, DXCc | 3.307 | 3.907 | 0.153 | 54.80 | 3.502 | 3.907 | 0.104 | 52.45 | |
| Metal binding | 1FW4:A | Ca(II) | 2.344 | 3.322 | 0.294 | 17.86 | 2.649 | 3.459 | 0.234 | 40.68 |
| 1U5S:A | - | 3.360 | 4.000 | 0.160 | 61.51 | 3.431 | 4.000 | 0.142 | 54.44 | |
| 1U5S:B | Zn(II) | 1.960 | 3.000 | 0.347 | 26.71 | 2.290 | 3.170 | 0.275 | 36.41 | |
| 2CUR:A | Zn(II) | 2.382 | 3.170 | 0.185 | 28.42 | 2.742 | 3.322 | 0.174 | 32.95 | |
| 2D8Q:A | Zn(II) | 2.437 | 3.170 | 0.231 | 23.83 | 2.605 | 3.322 | 0.216 | 27.72 | |
| 1DX8:A | Zn(II) | 1.751 | 2.585 | 0.322 | 17.47 | 2.220 | 2.585 | 0.141 | 19.10 | |
| Peptide antibiotics | 1O82:A-D | pH 4.5 | 1.229 | 3.000 | 0.590 | 23.45 | 1.666 | 2.807 | 0.406 | 28.96 |
| 1O83:A-D | pH 7.5 | |||||||||
| 1O84:A-B | MALd | |||||||||
| Toxins | 1DM0:B-K | wild type | 2.37 | 3.32 | 0.28 | 29.49 | 2.64 | 3.32 | 0.21 | 36.90 |
| 1BOV:A-E | wild type | 2.539 | 3.459 | 0.266 | 29.04 | 2.711 | 3.459 | 0.216 | 41.24 | |
| 1R4Q:B-K | wild type | 2.356 | 3.322 | 0.291 | 30.85 | 2.678 | 3.320 | 0.194 | 34.75 | |
| 4ULL | wild type | 3.268 | 3.700 | 0.117 | 55.22 | 2.389 | 3.700 | 0.354 | 43.42 | |
| 1C48:A-E | G62T | 2.711 | 3.459 | 0.262 | 35.26 | 2.720 | 3.459 | 0.213 | 34.66 | |
| 1CQF:A-E | G62T | 2.383 | 3.459 | 0.311 | 30.98 | 2.660 | 3.322 | 0.199 | 34.39 | |
| 1CZG:A-E | G62T | 2.395 | 3.170 | 0.294 | 30.28 | 2.326 | 3.170 | 0.266 | 30.93 | |
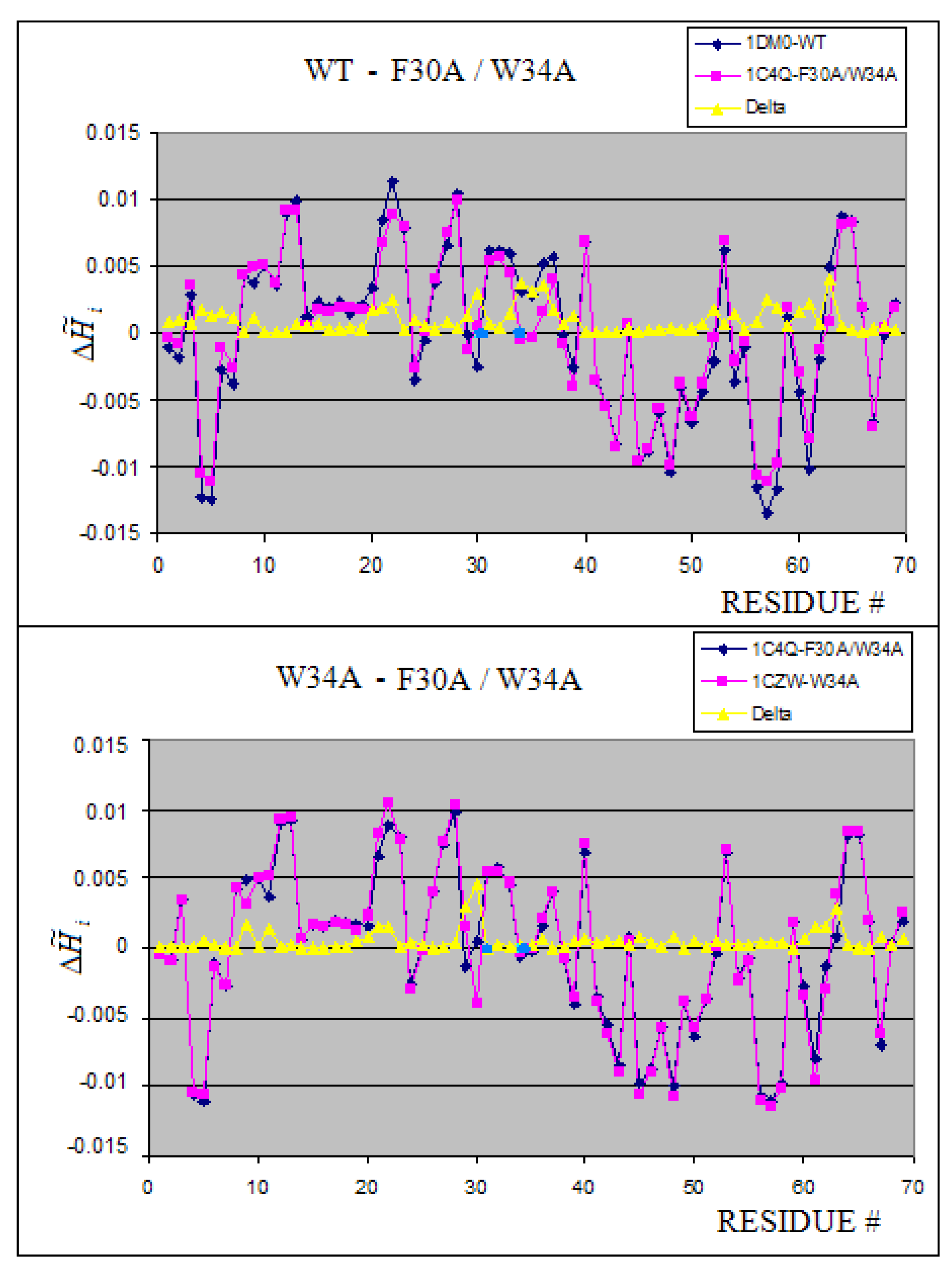
| 1CZW:A-J | W34A | 2.519 | 3.460 | 0.272 | 42.02 | 2.740 | 3.459 | 0.208 | 34.18 | |
| 1D1I:A-E | W34A | 2.520 | 3.460 | 0.272 | 42.03 | 2.741 | 3.460 | 0.208 | 34.17 | |
| 1C4Q:A-E | F30A, W34A | 2.516 | 3.459 | 0.272 | 42.06 | 2.687 | 3.459 | 0.223 | 28.71 | |
| 1D1K:A-E | D17E, W34A | 2.477 | 3.459 | 0.284 | 36.04 | 2.729 | 3.459 | 0.211 | 34.49 | |
| 1R4P:B-F | homologouse | 3.023 | 3.700 | 0.181 | 44.85 | 2.513 | 3.700 | 0.320 | 30.36 | |
| 1YI5:F-J | - | 2.393 | 3.459 | 0.308 | 24.57 | 2.663 | 3.459 | 0.230 | 41.29 | |
| 2CTX | - | 2.287 | 3.000 | 0.237 | 24.85 | 2.576 | 3.000 | 0.141 | 28.35 | |
| 1LXG:A | - | 2.331 | 3.322 | 0.298 | 37.79 | 2.510 | 3.322 | 0.244 | 35.94 | |
| 1J2L:A | - | 2.960 | 3.585 | 0.191 | 39.58 | 2.154 | 3.700 | 0.417 | 50.91 | |
| 1WWN:A | - | 3.061 | 3.907 | 0.216 | 51.20 | 3.453 | 3.907 | 0.116 | 66.87 | |
| a – additionally chain ids are given; b – pH for antibiotics or mutation variant for toxins c – deoxycholic acid d – N-decyl-_-D-maltose e – 65% sequence identity to wild type | ||||||||||
2.5. The structural changes generated by mutation
2.6. Correlation between SE and RSA (relative solvent accessibility)
3. Conclusion
4. Data and Methods
4.1. Data
| Description | Protein name | Source Organism | PDB entries a |
| Electron transport | cytochrome c553 | Bacillus pasteurii | 1B7V, 1C75, 1N9C |
| cytochrome c7 | Geobacter sulfurreducens | 1OS6 | |
| Metal binding | calmodulin | Bos taurus | 1FW4 |
| cytoplasmic protein NCK2 | Homo sapiens | 1U5S | |
| Skeletal muscle LIM-protein 1 | Homo sapiens | 2CUR | |
| BLu protein | Homo sapiens | 2D8Q | |
| rubredoxin | Homo sapiens | 1DX8 | |
| Peptide antibiotic | AS-48 protein | Enterococcus faecalis | 1O82, 1O83, 1O84 |
| Toxin | Shiga toxin subunit B | Shigella dysenteriae | 1DM0*, 1R4Q* |
| Escherichia coli | 1CQF*, 1D1I* | ||
| Bacteriophage H30 | 1CZG*, 1CZW* | ||
| Shiga-like toxin 1 subunit B | Escherichia coli | 1BOV, 1D1K*, 1C4Q* | |
| Bacteriophage H30 | 1C48*, 4ULL* | ||
| Shiga-like toxin 2 subunit B | Escherichia coli | 1R4P* | |
| Alpha-cobratoxin | Naja kaouthia | 1LXG* | |
| Naja naja | 2CTX* | ||
| Naja siamensis | 1YI5* | ||
| BmKIT1 | Mesobuthus martensii | 1WWN* | |
| disintegrin triflavin | Trimeresurus flavoviridis | 1J2L* |
4.2. The protein-ligand contacts analysis
4.3. The structural/functional characteristics
4.4. Relative solvent accessibility
Acknowledgments
References
- Ladner, R.C. Constrained peptides as binding entities. Trends Biotechnol 1995, 13, 426–430. [Google Scholar] [CrossRef] [PubMed]
- Ladner, R.C. Phage display and pharmacogenomics. Pharmacogenomics 2000, 1, 99–202. [Google Scholar] [CrossRef]
- Neri, D.; Petrul, H.; Roncucci, G. Engineering recombinant antibodies for immunotherapy. Cell Biophys 1995, 27, 47–61. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.L. Research and clinical applications of antibody phage display in transfusion medicine. Transfus Med. Rev. 2001, 15, 35–52. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, A.D. Production of human antibodies using bacteriophage. Curr. Opin. Immunol 1993, 5, 263–267. [Google Scholar] [CrossRef]
- Winter, G.; Grifiths, A.D.; Hawkins, R.E.; Hoogenboom, H.R. Making antibodies by phage display technology. Annu Rev Immunol 1994, 12, 433–455. [Google Scholar] [CrossRef] [PubMed]
- Hoogenboom, H.R.; de Bruïne, A.P.; Hufton, S.E.; Hoet, R.M.; Arends, J.W.; Roovers, R.C. Antibody phage display technology and its applications. Immunotechnology 1998, 4, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, H.; Wolynes, P.G. Biomolecules: Where the physics of complexity and simplicity meet. Phys. Today 1994, 47, 58–64. [Google Scholar] [CrossRef]
- Chan, H.S. Dill, K.A. The protein folding problem. Phys. Today 1993, 46, 24–42. [Google Scholar] [CrossRef]
- Karplus, M.; Shakhnovich, E.I. Protein Folding. W. H. Freeman & Co.: New York, 1992. [Google Scholar]
- Covell, D.G.; Jernigan, R.L. Conformations of folded proteins in restricted spaces. Biochemistry 1990, 29, 3287–3294. [Google Scholar] [CrossRef]
- Shakhnovich, E.I.; Gutin, A.M. Implications of thermodynamics of protein folding for evolution of primary sequences. Nature 1990, 346, 773–775. [Google Scholar] [CrossRef] [PubMed]
- Skolnick, J.; Kolinski, A. Simulations of the folding of a globular protein. Science 1990, 250, 1121–1125. [Google Scholar] [CrossRef] [PubMed]
- Lau, K.F.; Dill, K.A. A lattice statistical mechanics model of conformational and sequence spaces of proteins. Macromolecules 1989, 22, 3986–3997. [Google Scholar] [CrossRef]
- Taketomi, H.; Ueda, Y.; Gofi, N. Studies on protein folding, unfolding and fluctuations by computer simulation. I. The effect of specific amino acid sequence represented by specific inter-unit interactions. Int J Pept Protein Res 1975, 7, 445–459. [Google Scholar] [CrossRef] [PubMed]
- Rode, B.M. Peptides and the origin of life. Peptides 1999, 20, 773–786. [Google Scholar] [CrossRef]
- Orgel, L.E. The origin of life - how long did it take? Orig Life Evol Biosph 1998, 28, 91–96. [Google Scholar] [CrossRef]
- Schwartz, A.W. The Molecular Origins of Life: Assembling Pieces of the Puzzle. Cambridge University Press: Cambridge, 1998. [Google Scholar]
- Ferris, J.P.; Hill, A.R.; Liu, R.; Orgel, L.E. Synthesis of long prebiotic oligomers on mineral surfaces. Nature 1996, 381, 59–61. [Google Scholar] [CrossRef]
- Radzicka, A.; Wolfenden, R. Rates of uncatalyzed peptide bond hydrolysis in neutral solution and the transition state a_nities of proteases. Journal of the American Chemical Society 1996, 118, 6105–6109. [Google Scholar] [CrossRef]
- Luisi, P.L. The Emergence of Life. From Chemical Origins to Synthetic Biology. Cambridge University Press: London, 2006. [Google Scholar]
- Lingen, B.; Grötzinger, J.; Kolter, D.; Kula, M.R.; Pohl, M. Improving the carboligase activity of benzoylformate decarboxylase from Pseudomonas putida by a combination of directed evolution and site-directed mutagenesis. Protein Eng 2002, 15, 585–593. [Google Scholar] [CrossRef]
- Meyer, A.; Schmid, A.; Held, M.; Westphal, A.H.; Rothlisberger, M.; Kohler, H.P.E.; van Berkel, W.J.H.; Witholt, B. Changing the substrate reactivity of 2-hydroxybiphenyl 3-monooxygenase from pseudomonas azelaica hbp1 by directed evolution. J Biol Chem 2002, 277, 5575–5582. [Google Scholar] [CrossRef]
- Otten, L.G.; Sio, C.F.; Vrielink, J.; Cool, R.H.; Quax, W.J. Altering the substrate specificity of cephalosporin acylase by directed evolution of the beta-subunit. J Biol Chem 2002, 277, 42121–42127. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, I.; Ellington, A.D. In vitro evolution of beta-glucuronidase into a beta-galactosidase proceeds through non-specific intermediates. J Mol Biol 2001, 305, 331–339. [Google Scholar] [CrossRef] [PubMed]
- Persson, E.; Kjalke, M.; Olsen, O.H. Rational design of coagulation factor via variants with substantially increased intrinsic activity. Proc Natl Acad Sci U S A 2001, 98, 3583–13588. [Google Scholar] [CrossRef] [PubMed]
- Rellos, P.; Ma, J.; Scopes, R.K. Alteration of substrate specificity of zymomonas mobilis alcohol dehydrogenase-2 using in vitro random mutagenesis. Protein Expr Purif 1997, 9, 83–90. [Google Scholar] [CrossRef]
- Neylon, C. Chemical and biochemical strategies for the randomization of protein encoding dna sequences: library construction methods for directed evolution. Nucleic Acids Res 2004, 32, 1448–1459. [Google Scholar] [CrossRef]
- Cirino, P.C.; Mayer, K. M.; Umeno, D. Generating mutant libraries using error-prone PCR. Methods Mol Biol 2003, 231, 3–9. [Google Scholar]
- Murakami, H.; Hohsaka, T.; Sisido, M. . Random insertion and deletion of arbitrary number of bases for codon-based random mutation of DNA’s. Nat Biotechnol 2002, 20, 76–81. [Google Scholar] [CrossRef]
- Murakami, H.; Hohsaka, T.; Sisido, M. Random insertion and deletion mutagenesis. Methods Mol Biol 2003, 231, 53–64. [Google Scholar]
- Shao, Z.; Zhao, H.; Giver, L.; Arnold, F.H. Random-priming in vitro recombination: an effective tool for directed evolution. Nucleic Acids Res 1998, 26, 681–683. [Google Scholar] [CrossRef]
- Cadwell, R.C.; Joyce, G.F. Mutagenic pcr. PCR Methods Appl 1994, 3, S136–S140. [Google Scholar] [CrossRef]
- Aguinaldo, A.M.; Arnold, F.H. Staggered extension process (step) in vitro recombination. Methods Mol Biol 2003, 231, 105–110. [Google Scholar]
- Coco, W.M. RACHITT: Gene family shuffling by Random Chimera genesis on Transient Templates. Methods Mol Biol 2003, 231, 111–127. [Google Scholar] [PubMed]
- Lutz, S.; Ostermeier, M. Preparation of scratchy hybrid protein libraries: size- and in-frame selection of nucleic acid sequences. Methods Mol Biol 2003, 231, 143–151. [Google Scholar] [PubMed]
- Ostermeier, M.; Lutz, S. The creation of ITCHY hybrid protein libraries. Methods Mol Biol 2003, 231, 129–141. [Google Scholar]
- O'Maille, P.E.; Bakhtina, M.; Tsai, M.D. Structure-based combinatorial protein engineering (scope). J Mol Biol 2002, 321, 677–691. [Google Scholar] [CrossRef]
- Joern, J.M. DNA shuffing. Methods Mol Biol 2003, 231, 85–89. [Google Scholar] [PubMed]
- Chiarabelli, C.; Vrijbloed, J.W.; Lucrezia, D.D.; Thomas, R.M.; Stano, P.; Polticelli, F.; Ottone, T.; Papa, E.; Luisi, P.L. Investigation of de novo totally random biosequences, Part II: On the folding frequency in a totally random library of de novo proteins obtained by phage display. Chem Biodivers 2006, 3, 840–859. [Google Scholar] [CrossRef]
- Chiarabelli, C.; Vrijbloed, J.W.; Thomas, R.M.; Luisi, P.L. Investigation of de novo totally random biosequences, Part I: A general method for in vitro selection of folded domains from a random polypeptide library displayed on phage. Chem Biodivers 2006, 3, 827–839. [Google Scholar] [CrossRef]
- Berman, H.M.; Battistuz., T.; Bhat, T.N.; Bluhm, W.F.; Bourne, P.E.; Burkhardt, K.; Feng, Z.; Gilliland, G.L.; Iype, L.; Jain, S.; Fagan, P.; Marvin, J.; Padilla, D.; Ravichandran, V.; Schneider, B.; Thanki, N.; Weissig, H. Westbrook JD, Zardecki C. The Protein Data Bank. Acta Crystallogr D Biol Crystallogr 2002, 58, 899–907. [Google Scholar] [CrossRef]
- Bartalesi, I.; Bertini, I.; Rosato, A. Structure and dynamics of reduced bacillus pasteurii cytochrome c: oxidation state dependent properties and implications for electron transfer processes. Biochemistry 2003, 42, 739–745. [Google Scholar] [CrossRef]
- Brylinski, M.; Konieczny, L.; Roterman, I. Ligation site in proteins recognized in silico. Bioinformation 2006, 1, 127–129. [Google Scholar] [CrossRef] [PubMed]
- Brylinski, M.; Konieczny, L.; Roterman, I. Is the protein folding an aim-oriented process? Human haemoglobin as example. Int J Bioinform Res Appl 2007, 3, 234–260. [Google Scholar] [CrossRef]
- Kauzmann, W. Some factors in the interpretation of protein denaturation. Adv Protein Chem 1959, 14, 1–63. [Google Scholar] [PubMed]
- Simons, K.T.; Ruczinski, I.; Kooperberg, C.; Fox, B.A.; Bystroff, C.; Baker, D. Improved recognition of native-like protein structures using a combination of sequence-dependent and sequence-independent features of proteins. Proteins 1999, 34, 82–95. [Google Scholar] [CrossRef]
- Prymula, K.; Roterman, I. Functional Characteristics of Small Proteins (70 amino acid residues) Forming Protein-Nucleic Acid Complexes. J. Biomol. Struct Dynam. – in press. [CrossRef]
- Laskowski, R.A.; Chistyakov, V.V. Thornton JM. PDBsum more: new summaries and analyses of the known 3d structures of proteins and nucleic acids. Nucleic Acids Res 2005, 33, D266–D268. [Google Scholar] [CrossRef]
- Levitt, M. A simplified representation of protein conformations for rapid simulation of protein folding. J Mol Biol 1976, 104, 59–107. [Google Scholar] [CrossRef]
- Kyte, J.; Doolittle, R.F. A simple method for displaying the hydropathic character of a protein. J Mol Biol 1982, 157, 105–132. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. The Bell System Technical Journal 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Ahmad, S.; Gromiha, M.M.; Fawareh, H.; Sarai, A. ASAView: Solvent Accessibility Graphics for proteins. BMC Bioinformatics 2004, 5, 51. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2009 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prymula, K.; Roterman, I. Structural Entropy to Characterize Small Proteins (70 aa) and Their Interactions. Entropy 2009, 11, 62-84. https://doi.org/10.3390/e11010062
Prymula K, Roterman I. Structural Entropy to Characterize Small Proteins (70 aa) and Their Interactions. Entropy. 2009; 11(1):62-84. https://doi.org/10.3390/e11010062
Chicago/Turabian StylePrymula, Katarzyna, and Irena Roterman. 2009. "Structural Entropy to Characterize Small Proteins (70 aa) and Their Interactions" Entropy 11, no. 1: 62-84. https://doi.org/10.3390/e11010062
APA StylePrymula, K., & Roterman, I. (2009). Structural Entropy to Characterize Small Proteins (70 aa) and Their Interactions. Entropy, 11(1), 62-84. https://doi.org/10.3390/e11010062