Generalized Complexity and Classical-Quantum Transition
Abstract
:1. Introduction
2. A semi-classical model and the CLQM
2.1. Previous q-entropy Results
3. Present results
3.1. Introducing the q-statistical complexity
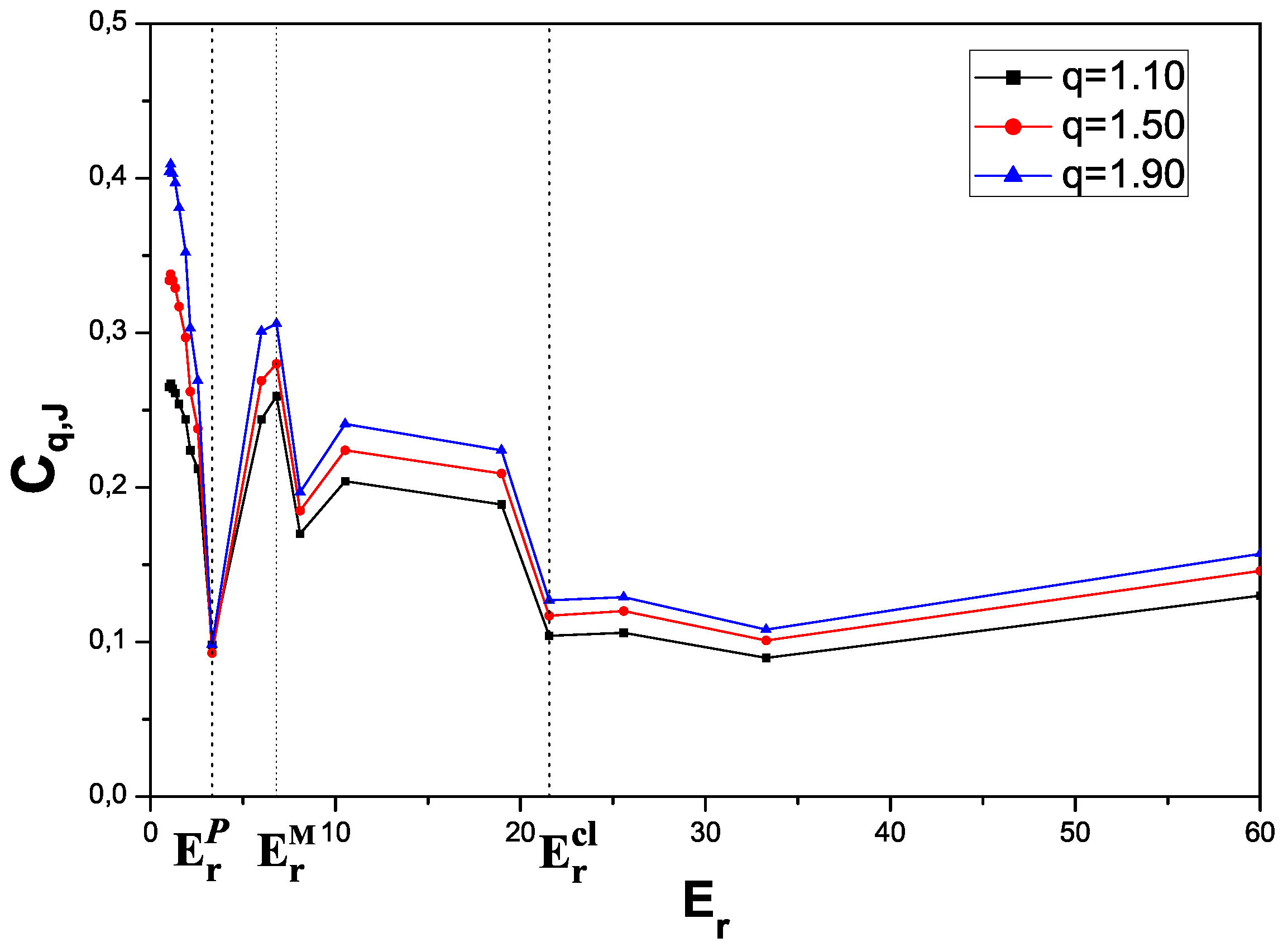
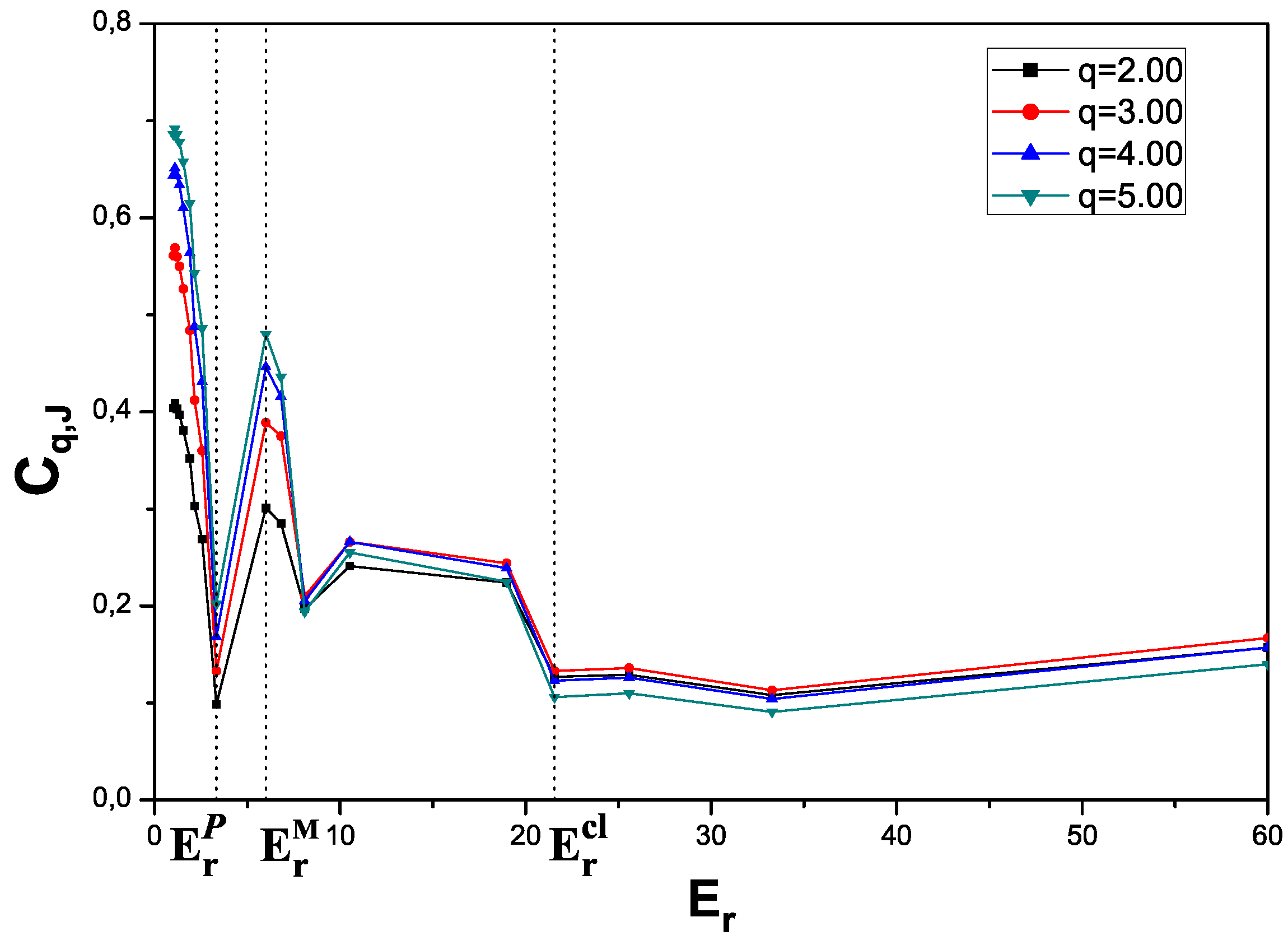
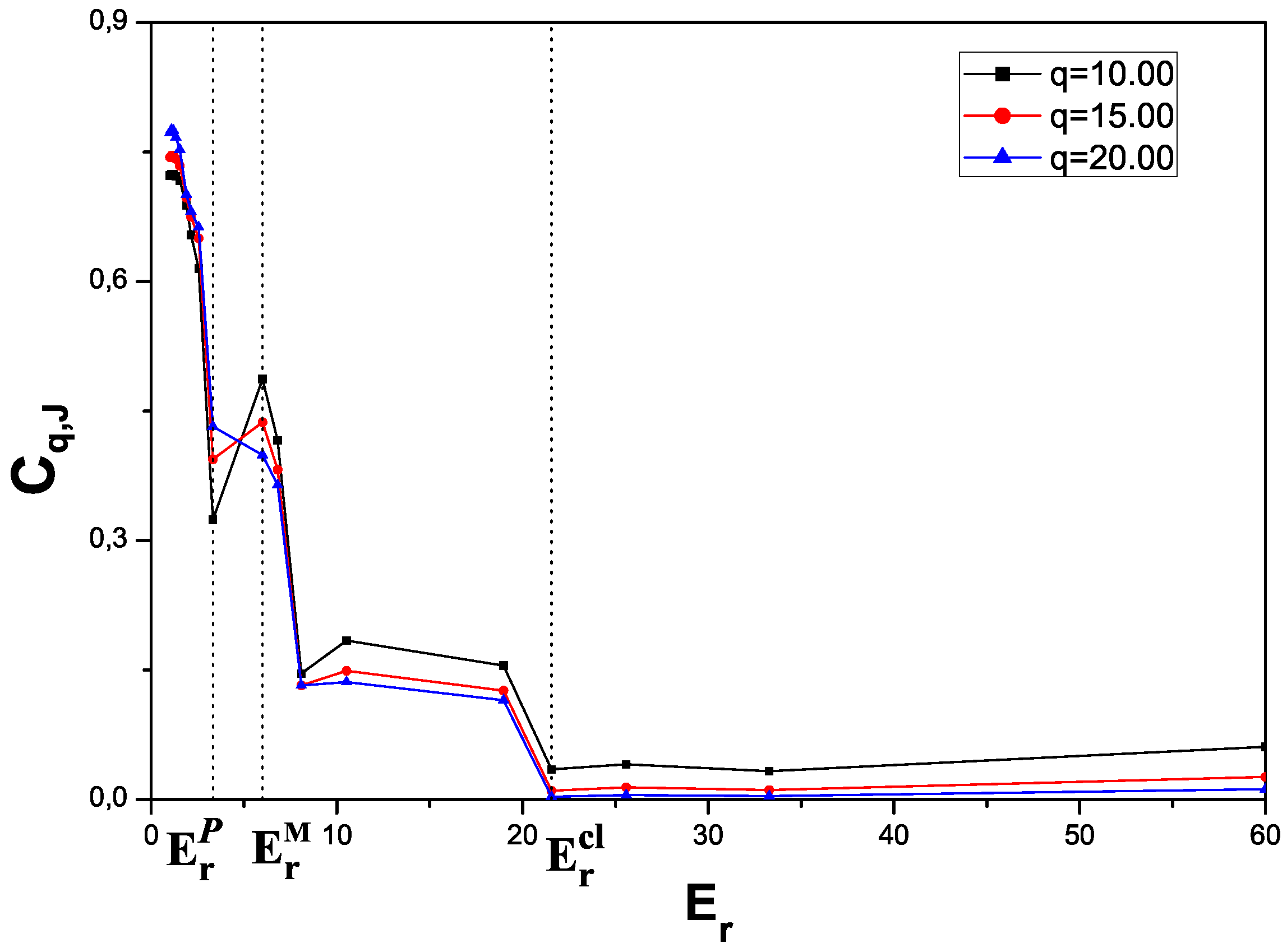
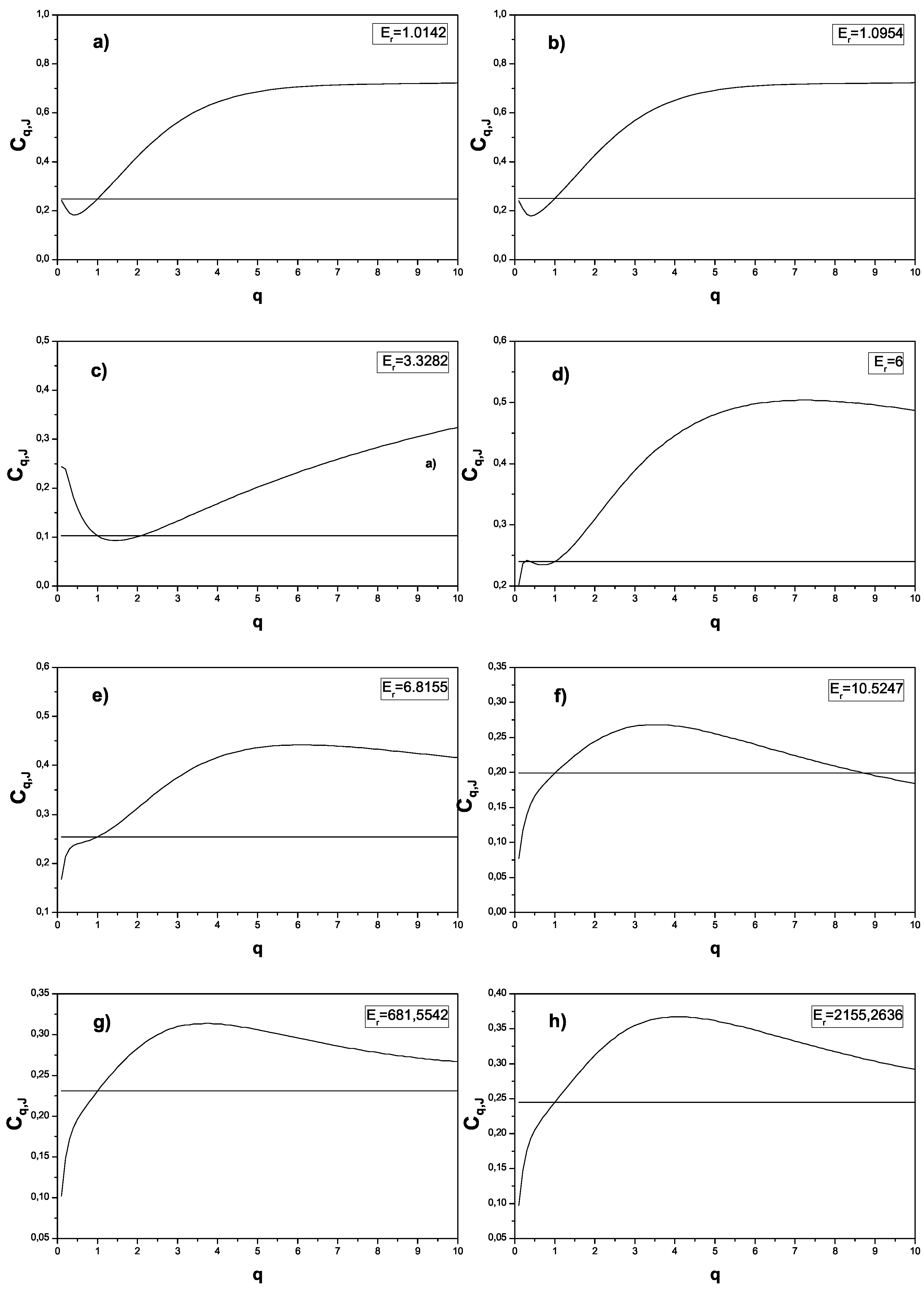
4. Numerical results
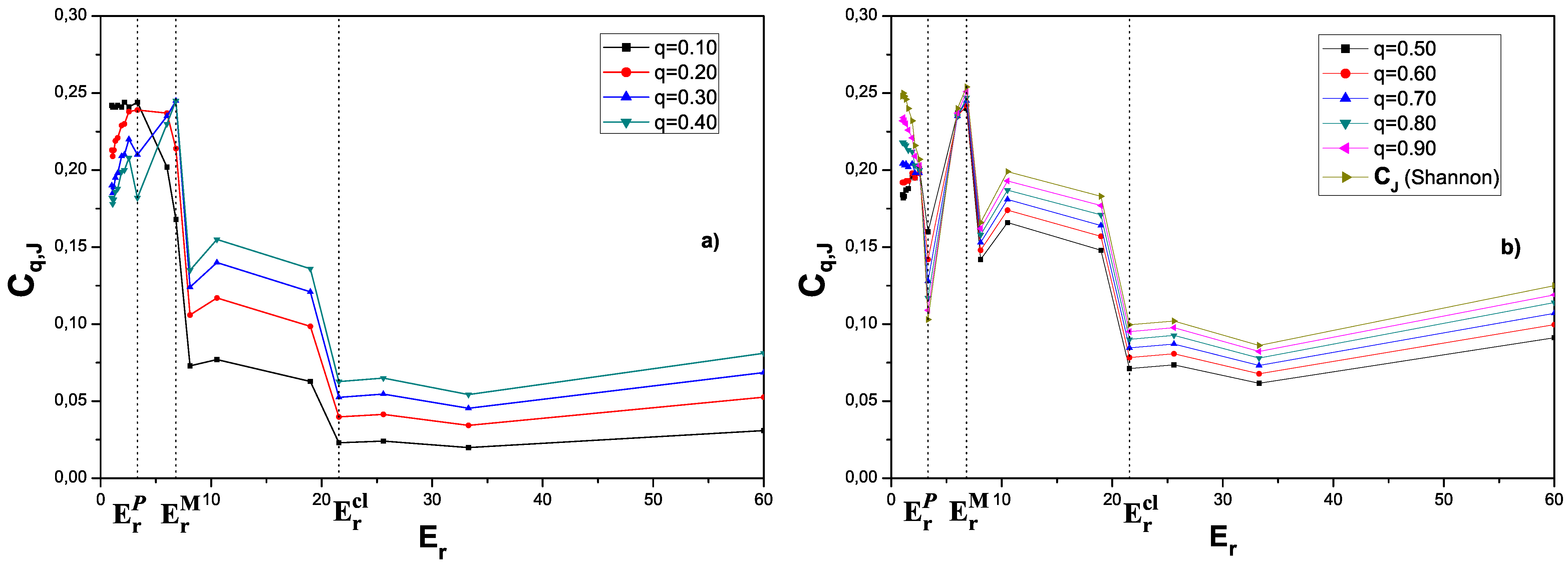
5. Conclusions
Acknowledgments
A Normalized Tsallis wavelet entropy
References and Notes
- Shannon, C.E. A mathematical theory of communication. Bell System Technol. J. 1948, 27, 379–390. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Simple measure for complexity. Phys. Rev. E 1999, 59, 1459–1464. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Lamberti, P.W.; Martin, M.T.; Plastino, A.; Rosso, O.A. Instensive entropic non-triviality measure. Physica A 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A new metric invariant of transitive dynamic system and automorphysms in Lebesgue spaces. Dokl. Akad. Nauk SSSR 1958, 119, 861–864. [Google Scholar]
- Sinai, Y.G. On the concept of entropy of dynamical system. Dokl. Akad. Nauk SSSR 1959, 124, 768–771. [Google Scholar]
- Mischaikow, K.; Mrozek, M.; Reiss, J.; Szymczak, A. Construction of Symbolic Dynamics from Experimental Time Series. Phys. Rev. Lett. 1999, 82, 1144–1147. [Google Scholar] [CrossRef]
- Powell, G.E.; Percival, I.C. A spectral entropy method for distinguishing regular and irregular motion of hamiltonian systems. J. Phys A: Math. Gen. 1979, 12, 2053–2071. [Google Scholar] [CrossRef]
- Rosso, O.A.; Mairal, M.L. Characterization of time dynamical evolution of electroencephalographic records. Physica A 2002, 312, 469–504. [Google Scholar] [CrossRef]
- Martín, M.T.; Plastino, A.; Rosso, O. A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. Generalized Boltzmann Factors and the Maximum Entropy Principle: Entropies for Complex Systems. Physica A 2007, 380, 109–114. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Alemany, P.A.; Zanette, D.H. Fractal random walks from a variational formalism for Tsallis entropies. Phys. Rev. E 1994, 49, R956–R958. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Nonextensive thermostatistics and fractals. Fractals 1995, 3, 541–547. [Google Scholar] [CrossRef]
- Tsallis, C. Generalized entropy-based criterion for consistent testing. Phys. Rev. E 1998, 58, 1442–1445. [Google Scholar] [CrossRef]
- Kalimeri, M.; Papadimitriou, C.; Balasis, G.; Eftaxias, K. Dynamical complexity detection in pre-seismic emissions using nonadditive Tsallis entropy. Physica A 2008, 387, 1161–1172. [Google Scholar] [CrossRef]
- Paz, J.P.; Zurek, W.H. Quantum Limit of Decoherence: Environment Induced Superselection of Energy Eigenstates. Phys. Rev. Lett. 1999, 82, 5181–5185. [Google Scholar] [CrossRef]
- Emerson, J.; Ballentine, L.E. Quantum-classical correspondence for the equilibrium distributions of two interacting spins. Phys. Rev. E 2001, 64, 026217:1–026217:11. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martin, M.T.; Plastino, A.; Proto, A.N. Classical Limit and Chaotic Regime in a Semi-Quantum Hamiltonian. Int. J. Bifurcation Chaos 2003, 13, 2315–2325. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martin, M.T.; Plastino, A.; Proto, A.N.; Rosso, O.A. Wavelet statistical complexity analysis of the classical limit. Phys. Lett. A 2003, 311, 180–191. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martin, M.T.; Plastino, A.; Rosso, O.A. Entropic Non-Triviality, the Classical Limit, and Geometry-Dynamics Correlations. Int. J. Mod. Phys. B 2005, 14, 2273–2285. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: geometrical and analytical properties. Physica A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Bloch, F. Nuclear Induction. Phys. Rev. 1946, 70, 460–474. [Google Scholar] [CrossRef]
- Meystre, P.; Sargent, M., III. Elements of Quantum Optics; Springer-Verlag: New York/Berlin, 1991. [Google Scholar]
- Bulgac, A. Configurational quasidegeneracy and the liquid drop model. Phys. Rev. C 1989, 40, 1073–1076. [Google Scholar] [CrossRef]
- Milonni, P.W.; Shih, M.L.; Ackerhalt, J. R. Chaos in Laser-Matter Interactions; World Scientific Publishing: Singapore, 1987. [Google Scholar]
- Kociuba, G.; Heckenberg, N. R. Controlling the complex Lorenz equations by modulation. Phys. Rev. E 2002, 66, 026205:1–026205:5. [Google Scholar] [CrossRef] [PubMed]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer-Verlag: New York/Berlin, 1980. [Google Scholar]
- Bonilla, L. L.; Guinea, F. Collapse of the wave packet and chaos in a model with classical and quantum degrees of freedom. Phys. Rev. A 1992, 45, 7718–7728. [Google Scholar] [CrossRef] [PubMed]
- Cooper, F.; Habib, S.; Kluger, Y.; Mottola, E. Nonequilibrium dynamics of symmetry breaking in λϕ4 theory. Phys. Rev. D 1997, 55, 6471–6503. [Google Scholar] [CrossRef]
- Cooper, F.; Dawson, J.; Habib, S.; Ryne, R.D. Chaos in time-dependent variational approximations to quantum dynamics. Phys. Rev. E 1998, 57, 1489–1498. [Google Scholar] [CrossRef]
- Chung, D.J.H. Classical inflaton field induced creation of superheavy dark matter. Phys. Rev. D 2003, 67, 083514:1–083514:14. [Google Scholar] [CrossRef]
- Kowalski, A. M.; Martin, M. T.; Nuñez, J.; Plastino, A.; Proto, A. N. A quantitative indicator for semi-quantum chaos. Phys. Rev. A 1998, 58, 2596–2599. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Plastino, A.; Proto, A.N. Classical limits. Phys. Lett. A 2002, 297, 162–172. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martin, M.T.; Plastino, A.; Proto, A.N.; Rosso, O.A. Bandt-Pompe approach to the classical-quantum transition. Physica D 2007, 233, 21–31. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martin, M.T.; Plastino, A.; Zunino, L. Tsallis’ deformation parameter q quantifies the classical-quantum transition. [arXiv:0812.4221v1], 2008. Physica A 2009. (in Press). [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kowalski, A.M.; Plastino, A.; Casas, M. Generalized Complexity and Classical-Quantum Transition. Entropy 2009, 11, 111-123. https://doi.org/10.3390/e11010111
Kowalski AM, Plastino A, Casas M. Generalized Complexity and Classical-Quantum Transition. Entropy. 2009; 11(1):111-123. https://doi.org/10.3390/e11010111
Chicago/Turabian StyleKowalski, A. M., Angelo Plastino, and Montserrat Casas. 2009. "Generalized Complexity and Classical-Quantum Transition" Entropy 11, no. 1: 111-123. https://doi.org/10.3390/e11010111
APA StyleKowalski, A. M., Plastino, A., & Casas, M. (2009). Generalized Complexity and Classical-Quantum Transition. Entropy, 11(1), 111-123. https://doi.org/10.3390/e11010111




