Entropy Generation and Human Aging: Lifespan Entropy and Effect of Physical Activity Level
Abstract
:1. Introduction
2. Literature Review
2.1 Allometry
- a)
- Metabolic rates: Metabolism involves oxidation of glucose, fats and proteins in the nutrients, which require oxygen for oxidation. The O2 consumption rate is given by the above general law [8] with:
- y= O2 consumption rate in mL/hr, x= mass of body in g
- a= 4 - 4.2, b = 0.68
- a = 0.064, b = 0.734 with y = mL O2/min and x = body mass in g
- y= specific metabolic rate (W/kg), x= mass of body in kg
- a= 3.55, b = -0.26
- b)
- Mass of brain: Same equation (1) with:
- y = brain mass in g, x = body mass in g
- a = 0.043, b = 2/3 to 0.73
- c)
- Body surface area (BSA) [http://ajpendo.physiology.org/cgi/content/full/281/3/E586]
- y, BSA in m2, x, body mass in kg
- a= 0.1173, b = 0.6466, R2 = 0.9914
- y = lifespan, days
- x = body mass in g
- z = brain mass in g
2.2 Lifespan
3. Rationale and Objective
- Accounting for the metabolic efficiency (production of ATP) in the BS. We will start with the basic chemical reactions typical of metabolism to determine the efficiency of ATP production, or MWE, for each of the three main nutrient groups. In the BS, energy not converted to ATP is disposed of as heat, thus, increasing entropy.
- Accounting for the effects of age, body mass, physical activity level and diet composition on entropy generation.
- Using the maximum allowable entropy generation per unit mass as a criteria in defining life span. As long as the organism performs its life functions, entropy continues to be generated. If we calculate the maximum lifespan entropy, then we can study the effect of the different factors on the time needed to reach lifespan entropy.
3.1 Hypothesis:
4. Analysis
4.1 Phenomenological Analysis
4.2 Rigorous Analysis
a) Overview on present methodology
b) Assumptions
- ○
- The essential nutrients are Carbohydrates (CH), fats (F) and proteins (P).
- ○
- CH, F and P will be modeled using glucose, palmitic acid, and average amino acids composition respectively.
- ○
- The time span of interest is much longer compared to metabolic reaction time scales; thus, quasi-steady approach is valid.
- ○
- The MWE for conversion of CH, F and P energy into ATP is different for every nutrient but remains constant over the whole life span. Thus, a child who is physically active requires more metabolic rate to produce necessary ATP rather than increased MWE.
- ○
- Metabolic rate and MWE are the same throughout the body including all body organs. It is known that oxidation near heart cells require more ATP, requiring increased MWE or increased metabolic rate.
- ○
- Actual energy requirements are used instead of basal metabolism in order to include the entropy generated by physical activity.
- ○
- Functioning normally, human beings and other large organisms cannot tolerate changes of body temperature of more than a few degrees16, and can be considered isothermal. One may assume that biochemical reactions in humans proceed at constant temperatures and pressures.
- ○
- It is presumed that entropy generated for the metabolic part of the body determines the life span of BS since they produce ATP which enables the body to perform life sustaining functions and the metabolic mass of the body is proportional to body total mass.
- ○
- The nutrient consumption data are based on normal gravity environment.
- ○
- It will be assumed that a low-active physical activity level is the best representation of the healthy average individual activity.
- ○
- In order to keep the physics simple, we assume all of ATP is converted into work and there is no dissipative heat produced by ATP.
- ○
- All the processes within BS occur isothermally.
- ○
- For warm blood invertebrate, only 10% of the feed is converted into body substance called efficiency of conversion of ingested food (ECI). Note that for cold blooded vertebrate the ECI could be as high as 44 % (e.g. German Cockroaches). Thus the analysis is essentially for warm blooded vertebrate only; hence it is assumed that the feed ration is essentially used for conversion to ATP and dissipative heat.
4.3 Governing Equations
a) Energy Conservation:
b) Availability Balance:
4.4 Simplifications
a) Gibbs free energy and Isothermal Chemical Reactions:
b) Metabolism, Work in Biological Systems and Bioenergetics:
4.5 Entropy Generation
5. Input data and procedure
5.1 Fuel Data
5.2 Statistical Databases
| Glucose | C6H12O6 | 180 | 15630 | 14665 | -1260 | 212.0 | 38.2 |
| Protein | C4.57H9.03N1.27O2.25S0.046 | 119 | 22790 | 14705 | -385 | 10.4 | |
| Fat | C16H32O2 | 256 | 39125 | 13635 | -835 | 452.4 | 32.2 |
| PAL category | PAL value | (m/d at 2-4 mph) (*) | |
| Sedentary | 1.0 – 1.39 | ||
| Low Active | 1.4 – 1.59 | 1.5, 2.2, 2.9 for PAL=1.5 | |
| Active | 1.6 – 1.89 | 3.0, 4.4, 5.8 for PAL=1.6 | |
| 5.3, 7.3, 9.9 for PAL=1.75 | |||
| Very Active | 1.9 – 2.5 | 7.5, 10.3, 14.0 for PAL=1.9 | |
| 12.3, 16.7, 22.5 for PAL=2.2 | |||
| 17.0, 23.0, 31.0 for PAL=2.5 |
5.3 Adequate Macronutrients Distribution Range (AMDR) / Adequate Intake (AI)
5.4 Calculation Procedure
- ○
- Use of 0.25-year increments (trimesters, 91.5 days) within the age range from 0 to 90 years.
- ○
- Use of growth data from CDC to obtain body size and weight as function of age for both genders and 50th percentile.
- ○
- ○
- ○
- Apply Eq. (27) to obtain entropy generated.
- ○
- Generate tables and charts for entropy generation per trimester and calculate cumulative entropy generated.
- ○
- Express all data as per unit total body mass.
- ○
- Though calculations are made for different activity levels, it is assumed that the Low Active (LA) PAL represents the best average of the healthy individual.
| 0-3 months (89 x weight of infant[kg] -100) + 175 | ||||||
| 4-6 months (89 x weight of infant[kg] -100) + 56 | ||||||
| 7-12 months (89 x weight of infant[kg] -100) + 22 | ||||||
| 13-35 months (89 x weight of child[kg] -100) + 20 | ||||||
| EER for Boys 3 through 8 years, EER = TEE + Energy Deposition | ||||||
| EER = 88.5 - 61.9 x Age[y] + PA x (26.7 x Weight[kg] + 903 x Height[m]) + 20 | ||||||
| Where PA is the physical activity coefficient: | ||||||
| PA = 1.00 if PAL is estimated to be > 1.0 < 1.4 (Sedentary) | ||||||
| PA = 1.13 if PAL is estimated to be > 1.4 < 1.6 (Low Active) | ||||||
| PA = 1.26 if PAL is estimated to be > 1.6 < 1.9 (Active) | ||||||
| PA = 1.42 if PAL is estimated to be > 1.9 < 2.5 (Very Active) | ||||||
| EER for Boys 9 through 18 Years, EER = TEE + Energy Deposition | ||||||
| EER = 88.5 - 61.9 x Age[y] + PA x (26.7 x Weight[kg] + 903 x Height[m]) + 25 | ||||||
| Where PA is the physical activity coefficient, equal to the 3-8 years range. | ||||||
| EER for Total Energy Expenditure (TEE) for Men 19 years and older | ||||||
| EER = 662 - 9.53 x Age [y] + PA x (15.91 x Weight [kg] + 539.6 x Height [m]) | ||||||
| Where PA is the physical activity coefficient: | ||||||
| PA = 1.00 if PAL is estimated to be > 1.0 < 1.4 (Sedentary) | ||||||
| PA = 1.11 if PAL is estimated to be > 1.4 < 1.6 (Low Active) | ||||||
| PA = 1.25 if PAL is estimated to be > 1.6 < 1.9 (Active) | ||||||
| PA = 1.48 if PAL is estimated to be > 1.9 < 2.5 (Very Active) | ||||||
| Carbohydrates | Total Fats | Protein | |||||
| RDA/AI | AMDR | RDA/AI | AMDR | RDA/AI | AMDR | ||
| Years | (g/d) | (%) | (g/d) | (%) | (g/d) | (%) | |
| Infants | |||||||
| 0 | 0.5 | 60 | 31 | 9.1 | |||
| 0.5 | 1 | 95 | 30 | 13.5 | |||
| Children | |||||||
| 1 | 3 | 130 | 45-65 | 30-40 | 13 | 5-20 | |
| 4 | 8 | 130 | 45-65 | 25-35 | 19 | 10-30 | |
| Male | |||||||
| 9 | 13 | 130 | 45-65 | 25-35 | 34 | 10-30 | |
| 14 | 18 | 130 | 45-65 | 25-35 | 52 | 10-30 | |
| 19 | 30 | 130 | 45-65 | 20-35 | 56 | 10-35 | |
| 31 | 50 | 130 | 45-65 | 20-35 | 56 | 10-35 | |
| 50 | 70 | 130 | 45-65 | 20-35 | 56 | 10-35 | |
| >70 | 130 | 45-65 | 20-35 | 56 | 10-35 | ||
| Female | |||||||
| 9 | 13 | 130 | 45-65 | 25-35 | 34 | 10-30 | |
| 14 | 18 | 130 | 45-65 | 25-35 | 46 | 10-30 | |
| 19 | 30 | 130 | 45-65 | 20-35 | 46 | 10-35 | |
| 31 | 50 | 130 | 45-65 | 20-35 | 46 | 10-35 | |
| 50 | 70 | 130 | 45-65 | 20-35 | 46 | 10-35 | |
| >70 | 130 | 45-65 | 20-35 | 46 | 10-35 | ||
| Pregnancy | |||||||
| ≤18 | 175 | 45-65 | 20-35 | 71 | 10-35 | ||
| 19 | 30 | 175 | 45-65 | 20-35 | 71 | 10-35 | |
| 31 | 50 | 45-65 | 20-35 | 71 | 10-35 | ||
| Lactation | |||||||
| ≤18 | 210 | 45-65 | 20-35 | 71 | 10-35 | ||
| 19 | 30 | 210 | 45-65 | 20-35 | 71 | 10-35 | |
| 31 | 50 | 210 | 45-65 | 20-35 | 71 | 10-35 | |
6. Results
6.1 Base case
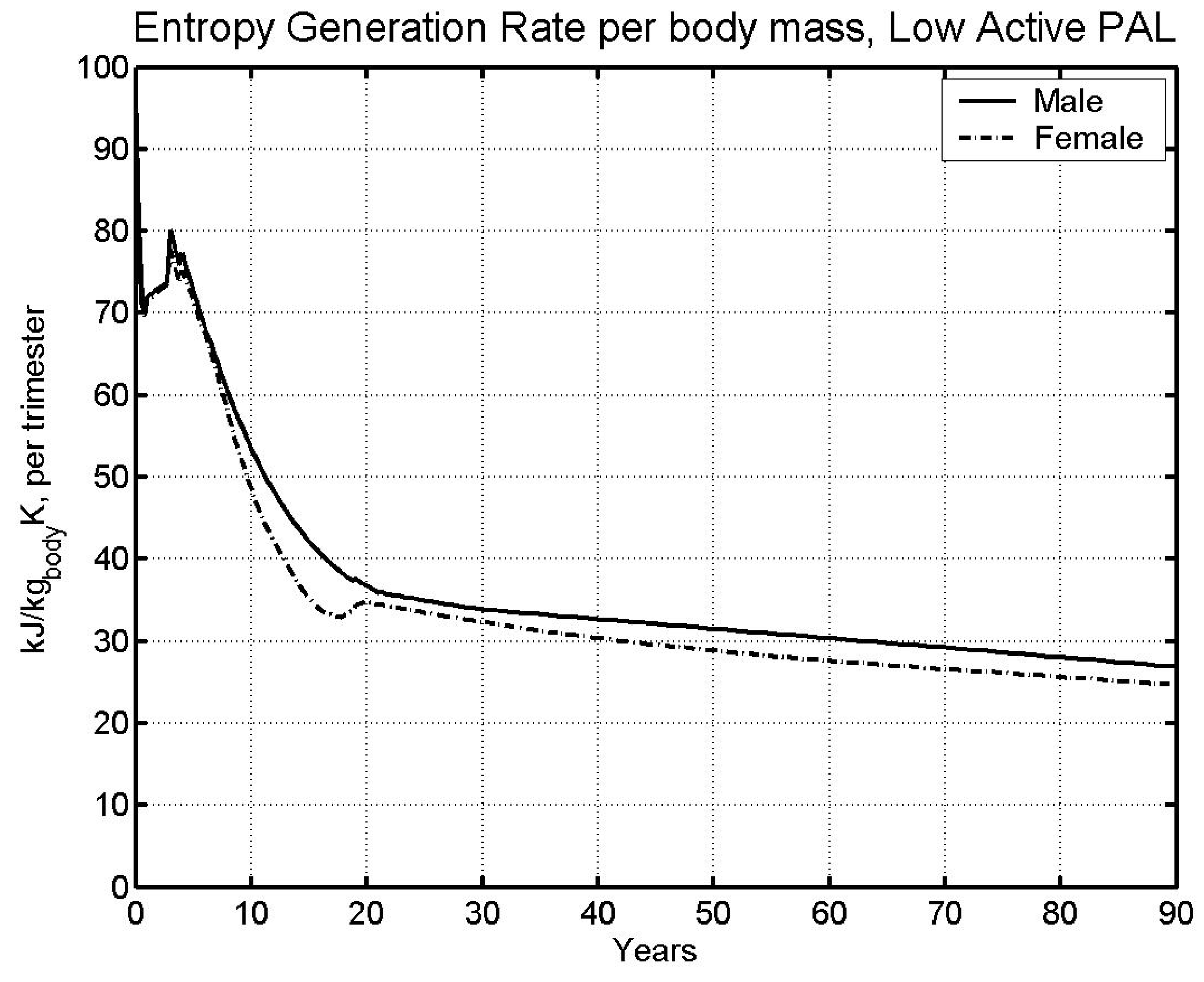
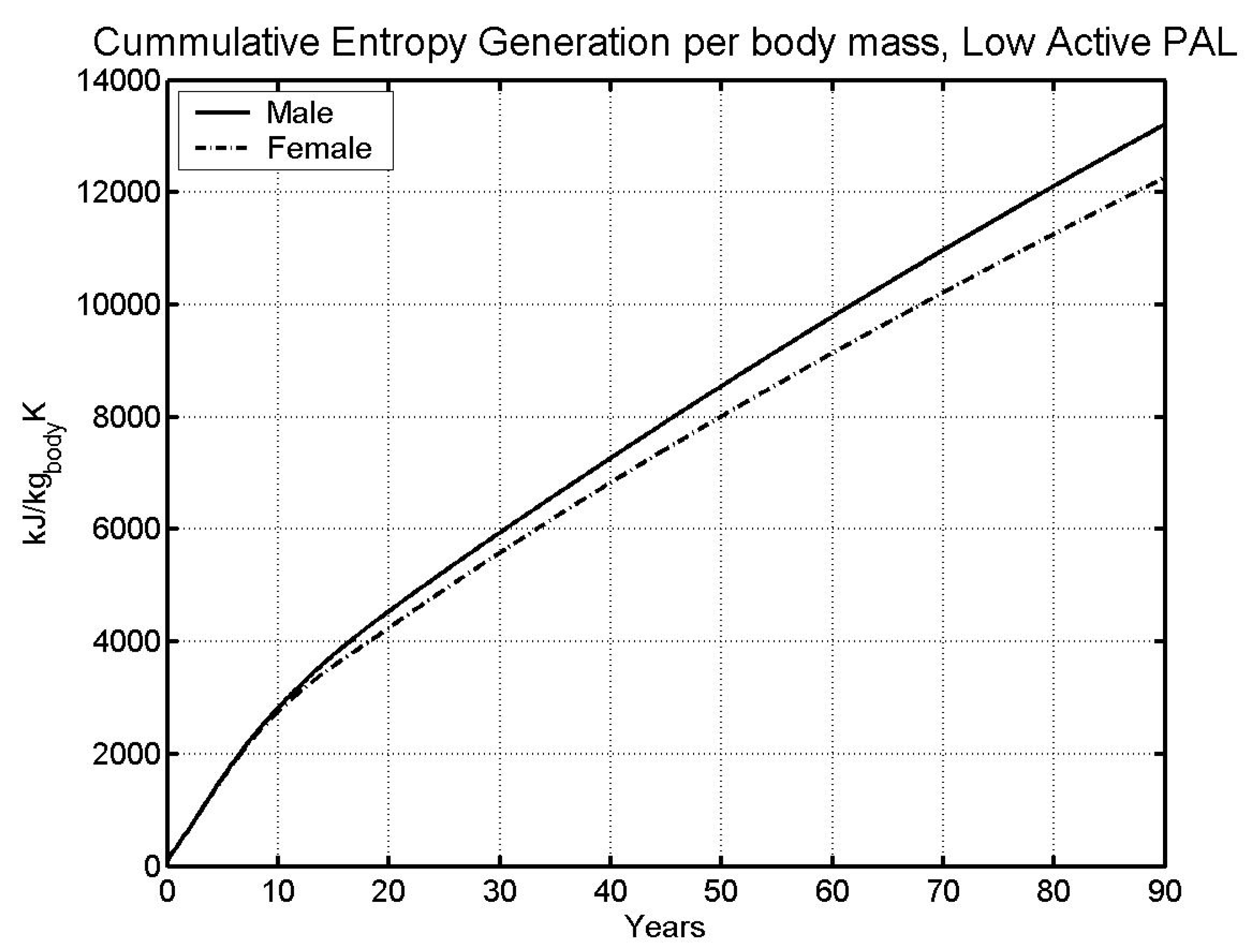
| Av. Lifespan [5] | 74.63 | 80.36 |
6.2 Effect of physical activity level
| Case | Male | Female | ||
| Sedentary | 85.05 | 95.75 | ||
| LA - | Low Active (base) | 73.78 | 81.61 | |
| A - | Active | 63.78 | 69.53 | |
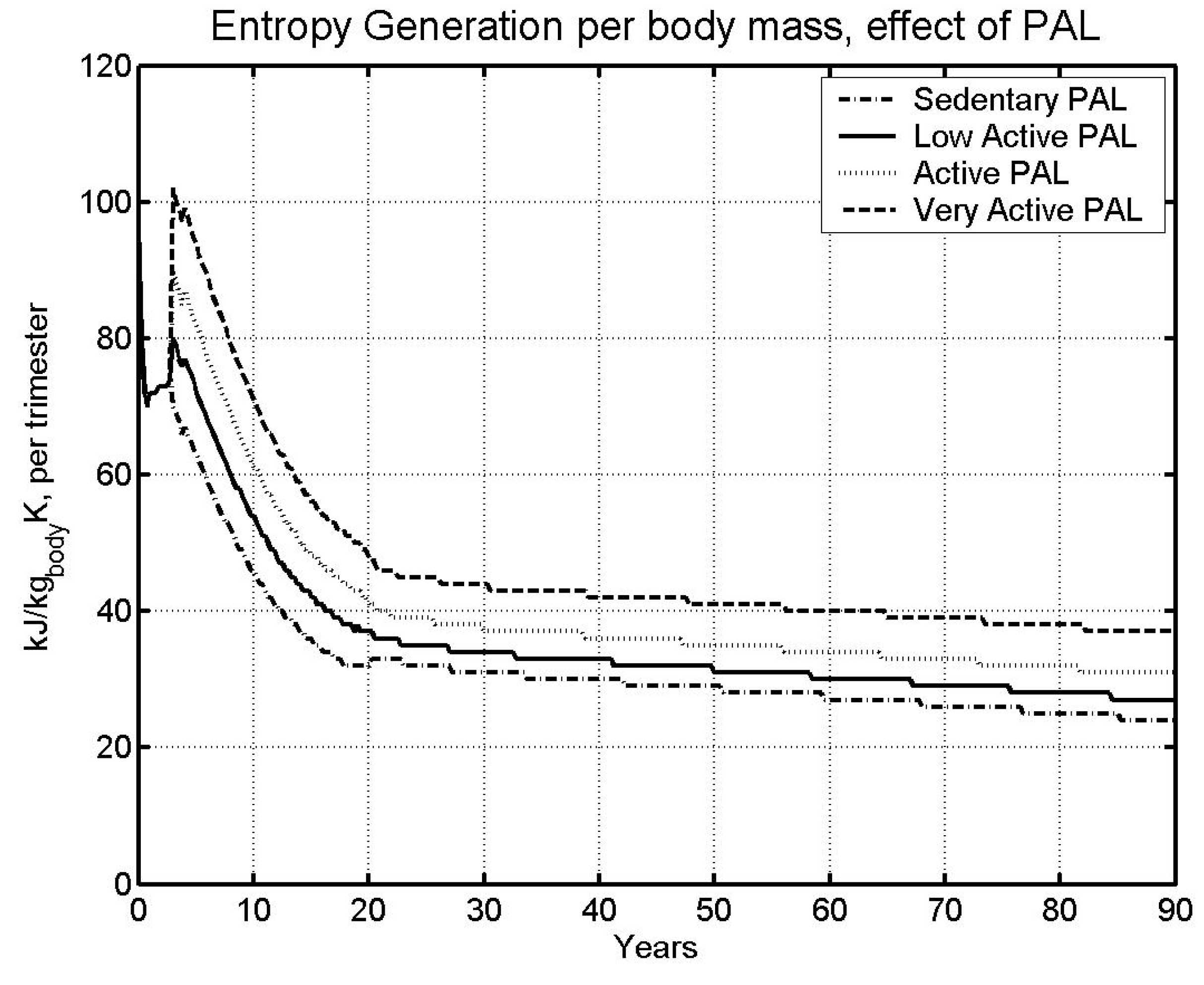
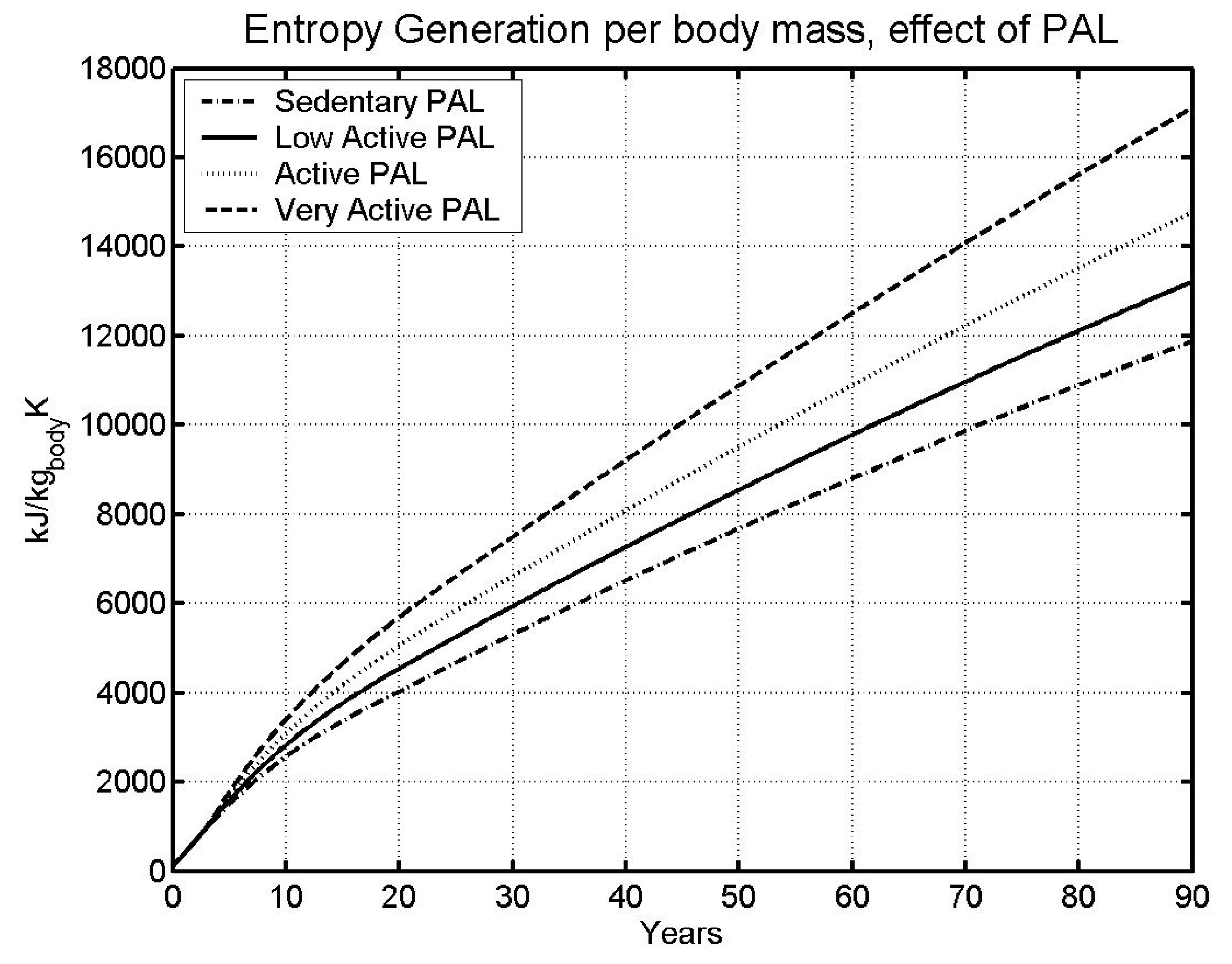
6.3 Gravitational Effects
7. Conclusions
- ○
- The basic laws of thermodynamics were applied to biological systems, using a combination of laws of thermodynamics and available information from biochemistry literature and updated CDC databases. Entropy generated was determined for metabolism of the typical components of the human diet, and total entropy generation was estimated through numerical integration for the average population.
- ○
- Data on average lifespan was used to obtain lifetime limit entropy, which was found equal to 11,404 kJ/kg-K. This value of entropy predicts life span within 1.5% of the life span from literature (predicted: 73.78 and 81.61 years; Literature: 74.63 and 80.36 years; males and females respectively).
- ○
- ○
- The higher the specific metabolic rate (kW/kg), the higher the specific entropy generation rate (kW/kg), and the faster we approach the specific entropy generation limit over a lifetime (kJ/kg K).
- ○
- The entropy generation rate depends upon the type of ration fed to BS.
- ○
- When a non-zero gravity environment is approximated as a change from low active to sedentary PAL, it is possible to predict changes on the lifespan of astronauts based on the exposition time to the weightless condition. It was found that a male astronaut will extend his life span 1 year for every 9.5 years he spent in space. For a female astronaut, this time was estimated as 7.5 years.
- ○
- The present approach presumes that the ATP acts as work currency, generating no entropy.
- ○
- While the present analysis for entropy generation is conducted considering the human as a whole system, the analysis can be extended to determine the entropy generation for each organ of the system (heart, kidney, liver etc) and to determine which degenerates rapidly as long as metabolic rates and metabolic efficiencies of the organ are known.
Acknowledgments
Appendix A - Terminology
Basal Metabolic Rate (BMR)
Total Energy Expenditure (TEE)
Physical Activity Level (PAL)
Estimated Energy Requirements (EER)
Databases
References
- Olshansky, S.J.; Carnes, B.A.; Butter, R.N. If humans are built to last. Scientific American 2001, 284, 70–75. [Google Scholar]
- Olshansky, S.J.; Carnes, B.A. Quest for Immortality: Science at Frontiers of Aging; Nortons: New York, NY, 2001. [Google Scholar]
- Olshansky, S.J.; Carnes, B.A.; Desequelles, A. Prospects for Human Longevity. Science 2001, 291, 1491–1492. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, M.; Goldstein, I.F. The Refrigerator and the Universe; Harvard Press: Harvard, 1993. [Google Scholar]
- Rubner, M.Z. Biology 1883, 19, 535–562.(b)Pearl, R. The Biology of Death; J.B. Lippincott: Philadelphia, 1922. [Google Scholar]
- Annamalai, K.; Puri, I. Advanced Thermodynamics Engineering; CRC Press: Boca Raton, FL, 2002. [Google Scholar]
- Annamalai, K.; Sweeten, J.M.; Ramalingam, S. Estimation of Gross Heating Values of Biomass Fuels. Transactions of the ASAE 1987, 30, 1205–1208. [Google Scholar] [CrossRef]
- Craig, R.W.; Roger, S.S. Allometric scaling of mammalian metabolism. J. Exp. Biol. 2005, 208, 1611–1619. [Google Scholar]
- Hofman, M.A. Energy, Metabolism, Brain Size and Longevity in Mammals. Quart. Rev. Biol. 1983, 58, 495–512. [Google Scholar]Hofman, M.A. Evolution of brain size in neonatal and adult placental mammals: a theoretical approach. J. Theor. Biol. 1983, 105, 317–332. [Google Scholar] [CrossRef] [PubMed]
- Schmidt-Nielsen, K.S. Why Is Animal Size So Important? Cambridge University Press: Cambridge, 1984. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. A General Model For The Origin Of Allometric Scaling Laws In Biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Savage, V.M.; Gillooly, J.; Enquist, B.J.; Woodruff, W.H.; Brown, J.H. Response to Darveau et al.: Why Does Metabolic Rate Scale With Body Size? Nature 2003, 421, 713. [Google Scholar] [CrossRef] [PubMed]
- Payne, P.R. Assessment of the Protein Values of Diets in Relation to the Requirements of the Growing Dog. In Canine and Feline Nutritional Requirements; Graham-Jones, O., Ed.; Pergamon Press: London, 1965; pp. 19–31. [Google Scholar]
- Thonney, M.L.; Touchberry, R.W.; Goodrich, R.D.; Meiske, J.C. Intraspecies Relationship Between Fasting Heat Production and Body Weight: A Reevaluation of W75. J. Anim. Sci. 1976, 43, 690. [Google Scholar]
- Subcommittee on Dog Nutrition, Committee on Animal Nutrition, Board on Agriculture, National Research Council. Nutrient Requirements of Dogs (Revised 1985); National Academy Press: Washington, D.C., 1985. [Google Scholar]
- Demetrius, L. Caloric Restriction, Metabolic Rate, and Entropy. J. Geront. Ser. A: Biol. Sci. 2004, 59A, 902–915. [Google Scholar] [CrossRef]
- Bejan, A. The Tree of Convective Heat Streams: Its Thermal Insulation Function and the Predicted 3/4-Power Relation Between Body Heat Loss and Body Size. Int. J. Heat Mass Trans. 2001, 44, 699–704. [Google Scholar] [CrossRef]
- Bejan, A. Constructal Theory: From Thermodynamics and Geometry Optimization to Predicting Shape in Nature. Energy Conver. Mgmt. 1998, 39, 1705–1718. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. The Contructal Law and the Thermodynamic of Flow Systems with Configuration. Int. J. Heat Mass Trans. 2004, 47, 3202–3214. [Google Scholar] [CrossRef]
- Dobson, G.P. Clin. Exp. Pharmacol. Physiol. 2003, 30, 590–597. [CrossRef]
- Azbel, M.Y. Universal Biological Scaling and Mortality. Proc. Nat. Acad. Sci. USA 1994, 91D, 453–457. [Google Scholar] [CrossRef]
- Spearman, J.R. Review Body Size, Energy Metabolism and Lifespan. J. Exp. Biol. 2005, 208, 1717–1730. [Google Scholar] [CrossRef] [PubMed]
- Vaanholt, L.M. The rate of living in mice: impacts of activity and temperature on energy metabolism and longevity. Ph.D. Thesis, University of Groningen, 20 Feb. 1979. available online: http://dissertations.ub.rug.nl/faculties/science/2007/l.m.vaanholt/. [Google Scholar]
- Hershey, D. Lifespan and Factors Affecting it; Charles C. Thomas Publisher: Springfield, 1974. [Google Scholar]
- Hershey, D.; Wang, H. A New Age-Scale for Humans; Lexington Books, 1980. [Google Scholar]
- Batato, M.; Deriaz, O.; Jequier, E.; Borel, L. Second Law Analysis of The Human Body. In Proc. Florence World Energy Research Symposium, Firenze, Italy, May 1990.
- Silva Hernandez, C. Entropy Generation in the Human Body. Estimation by means of Energy Requirements. MSME Final Report; Texas A&M University, 2004. [Google Scholar]
- Anon. Dietary Reference Intakes for Energy, Carbohydrate, Fiber, Fat, Fatty Acids, Cholesterol, Protein, and Amino Acids (Macronutrients); National Academy Press, 2002. [Google Scholar]
- CIA World Fact Book. ( www.cia.gov).
- Nelson, D.; Cox, M. Lehninger Principles of Biochemistry; Worth: New York, NY, 2003. [Google Scholar]
- Romsos, D.R.; Belo, P.S.; Bennink, M.R.; Bergen, W.G.; Leveille, G.A. Effects Of Dietary Carbohydrate, Fat And Protein On Growth, Body Composition And Blood Metabolite Levels in The Dog. J. Nutr. 1976, 106, 1452. [Google Scholar] [PubMed]
- Mayhew, T.M. Allometric studies on growth and development of the human placenta: growth of tissue compartments and diffusive conductances in relation to placental volume and fetal mass. J. Anat. 2006, 208, 785–794. [Google Scholar] [CrossRef] [PubMed]
- Forbes, G. Human Body Composition, Growth, Aging, Nutrition and Activity; Springer-Verlag: New York, NY, 1987. [Google Scholar]
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Silva, C.; Annamalai, K. Entropy Generation and Human Aging: Lifespan Entropy and Effect of Physical Activity Level. Entropy 2008, 10, 100-123. https://doi.org/10.3390/entropy-e10020100
Silva C, Annamalai K. Entropy Generation and Human Aging: Lifespan Entropy and Effect of Physical Activity Level. Entropy. 2008; 10(2):100-123. https://doi.org/10.3390/entropy-e10020100
Chicago/Turabian StyleSilva, Carlos, and Kalyan Annamalai. 2008. "Entropy Generation and Human Aging: Lifespan Entropy and Effect of Physical Activity Level" Entropy 10, no. 2: 100-123. https://doi.org/10.3390/entropy-e10020100
APA StyleSilva, C., & Annamalai, K. (2008). Entropy Generation and Human Aging: Lifespan Entropy and Effect of Physical Activity Level. Entropy, 10(2), 100-123. https://doi.org/10.3390/entropy-e10020100





