Abstract
In the context of global e-commerce platform supply chains dominated by Alibaba and Amazon, power reconfiguration among tripartite stakeholders (platforms, manufacturers, and retailers) remains a critical yet underexplored issue in supply chain contract design. To analyze the strategic interactions between platforms, manufacturers, and retailers, as well as how platforms select the contract format within a tripartite supply chain, this study proposes a Stackelberg game-theoretic framework incorporating participation constraints to compare fixed-fee and revenue-sharing contracts. The results demonstrate that revenue-sharing contracts significantly enhance supply chain efficiency by aligning incentives across members, leading to improved pricing and sales outcomes. However, this coordination benefit comes with reduced platform dominance, as revenue-sharing inherently redistributes power toward upstream and downstream partners. The analysis reveals a nuanced contract selection framework: given the revenue sharing rate, as the additional value increases, the optimal contract shifts from the mode RR to the mode RF, and ultimately to the mode FF. Notably, manufacturers and retailers exhibit a consistent preference for revenue-sharing contracts due to their favorable profit alignment properties, regardless of the platform’s value proposition. These findings may contribute to platform operations theory by (1) proposing a dynamic participation framework for contract analysis, (2) exploring value-based thresholds for contract transitions, and (3) examining the power-balancing effects of alternative contract formats. This study offers actionable insights for platform operators seeking to balance control and cooperation in their supply chain relationships, while providing manufacturers and retailers with strategic guidance for contract negotiations in platform-mediated markets. These findings are especially relevant for large e-commerce platforms and their partners managing the complexities of contemporary digital supply chains.
1. Introduction
Advancements in information and platform technology have significantly transformed the way manufacturers and retailers conduct transactions [1]. The proliferation of e-commerce platforms has reshaped consumer behaviors, driving substantial growth in global transaction volumes. Between 2020 and 2023, U.S. transaction volumes increased by nearly 240 billion USD, while China saw an expansion of 3.62 trillion CYN in the same period, underscoring the vast potential of e-commerce platforms. A key determinant in capturing these market opportunities is the platform’s contract format, which influences the level of collaboration with and participation from manufacturers and retailers [2]. Platforms like Alibaba and Flipkart offer marketplace services that provide technological infrastructure, such as payment gateways and inventory management tools, while typically remaining uninvolved in direct transactions [3,4]. Through the marketplace provided by the platform, manufacturers set wholesale and direct-selling prices, while retailers focus on establishing competitive retail prices. Both manufacturers and retailers pay commissions to the platform according to various contract structures, which raises the crucial question: How should the platform select the optimal contract format to maximize its profit?
Revenue-sharing and fixed-fee contracts are the typical formats in e-commerce. In a revenue-sharing contract, manufacturers and retailers pay a percentage of their revenue to the platform as commission [5,6]. Therefore, the unit commission charged by the platform per transaction is equal to the revenue-sharing rate multiplied by the wholesale price (or retail price) set by the manufacturer (or retailer). In a fixed-fee contract, the platform charges a fixed fee per unit transaction. Thus, the commission charged by the platform is equal to the fixed fee multiplied by the transaction volume. Both contract formats are commonly utilized. For example, Alibaba charges 2.5% to 5% for strictly select products ([Online] Available: https://rulechannel.1688.com/?type=detail&ruleId=20001661&cId=3032#/rule/detail?ruleId=20001661&cId=3032, accessed on 30 June 2025), and JD.com sets rates at 1% to 8% ([Online] Available: https://rule.jd.com/rule/ruleDetail.action?ruleId=638209647311982592&type=0&btype=1, accessed on 30 June 2025). Some platforms also implement fixed-fee contracts to collect commissions. For instance, eBay charges a $0.30 fee per transaction ([Online] Available: https://www.ebay.com/sellercenter, accessed on 30 June 2025), and Poshmark imposes a $2.95 fee for items sold under $15 ([Online] Available: https://selleraider.com/poshmark-fees/, accessed on 30 June 2025).
Drawing from practical applications of contract formats, some scholars in the field of platform supply chain (PSC) analyze the choice between revenue-sharing contract and fixed-fee contract (e.g., [7,8,9]). Additionally, there are several articles in other fields that explore the differences between implementing revenue-sharing contracts and fixed-fee contracts. For instance, Avinadav and Levy (2025) [10] examine the impact of information advantage on contract design in the subscription-based application supply chain (platform + developer). He et al. (2024) [11] explore the optimal contract design issue in the live shopping scenario of the manufacturer-retailer-streamer supply chain. However, the existing research primarily focuses on two-tier PSCs and pays little attention to tripartite PSCs, despite their prevalence in the e-commerce market. For instance, Staples (manufacturer) and Mr. Pen (retailer) operate on Amazon, Alpha Group (toy manufacturer) and Shutai E-commerce Firm (retailer) are on 1688, and Three Squirrels (food manufacturer) and Fenhai Food Franchise Store (retailer) are on JD.com. These platforms facilitate both procurement and retailing by offering B2B2C technology tools [12,13]. However, these articles seldom take into account the willingness of platform supply chain members to participate. In fact, when manufacturers and retailers opt not to join the platform and instead engage in offline trade, they generate corresponding revenues, which can be considered the opportunity costs of platform participation. These practical insights, along with the existing research gap, motivate us to investigate the contract strategies for tripartite PSCs and the endogenous participation decisions of PSC members.
Notably, when collaborating with both manufacturers and retailers, the platform may charge commissions either using the same contract format or different ones. For instance, Amazon employs a revenue-sharing contract with manufacturers, where they pay a percentage of their revenue as commission. In contrast, retailers on Amazon’s Seller Central platform are charged a fixed fee per transaction ([Online] Available: https://www.sellerapp.com/blog/become-an-amazon-individual-seller/, accessed on 30 June 2025). Based on these phenomena, how should a platform optimize its contract strategy when engaging with both manufacturers and retailers? In particular, Abhishek et al. (2016) [12] assume that retailers have no channel power and that the platform does not charge them, while Wang et al. (2025) [13] acknowledge the differing channel powers of manufacturers and retailers, and consider a situation where the platform charges a commission to both parties, with the decision of whether manufacturers and retailers participate in the platform being determined exogenously. However, the situations outlined above do not always hold. Manufacturers and retailers possess varying levels of channel power. Additionally, before determining the contract formats for manufacturers and retailers, the platform must first ensure the participation of both parties. Therefore, it is essential for the platform to account for the differences between manufacturers and retailers when making operational decisions, while also considering the endogenous participation constraints.
Building on the previous discussion, the primary objective of this paper is to compare the performance differences between the two contract formats and offer recommendations for the platforms to develop an optimal contract strategy. The specific research questions are as follows: (1) What conditions are required for the manufacturers and retailers to participate in the platform? (2) What is the optimal contract format for the dominant platform when cooperating with both the manufacturers and retailers? What is the equilibrium strategy if the manufacturers and retailers can choose which contract format to accept? (3) How does the additional value provided by the platform and other system parameters affect the above results?
To address the above issues, we establish a platform supply chain (PSC) consisting of one platform, one manufacturer, and one retailer. Specifically, the platform acts as the leader and engages in a Stackelberg game. This setting is selected since manufacturers, retailers, and consumers are increasingly relying on platforms to trade products, leading to a rise in the influence and position of platforms within the PSC. For instance, Amazon’s dominance in e-commerce has transformed traditional retail models, with manufacturers and retailers now heavily dependent on the platform for transactions and visibility. Notably, the platform in this context provides marketplace services and operates under the agency model. Consequently, the platform can charge commissions through either a revenue-sharing contract or a fixed-rent format, with three alternative combinations of contract strategies available:
- Pure Fixed-Fee Contract (Mode FF): The platform charges both the manufacturer and retailer a fixed fee.
- Hybrid Contract (Mode RF): The platform charges the manufacturer a revenue-sharing fee and the retailer a fixed fee. This hybrid approach is the most common and forms the primary focus of this study.
- Pure Revenue-Sharing Contract (Mode RR): The platform charges both the manufacturer and retailer a revenue-sharing fee.
Unlike the two-tier supply chain setting explored by Gu et al. (2022) [7], it is found that the inclusion of the retailer is a dominant factor influencing the platform’s contract format strategy. Specifically, using the scenario where neither the manufacturer nor the retailer joins the platform as a baseline, the conditions under which the retailer joins the platform vary depending on the contract format. For instance, when the platform adopts either the mode RF or RR, the retailer will join the platform only if the additional value is high and the revenue-sharing rate is low. Furthermore, if the retailer has the option to choose which contract format to accept, the pure revenue-sharing contract (i.e., mode RR) is the most preferred. This partially explains why revenue-sharing contracts are so prevalent in the e-commerce market. From a managerial perspective, our results suggest that the platform should reduce the revenue-sharing rate in either the mode RF or RR to ensure the retailer joins the platform. Additionally, taking into account the retailer’s preferences, the platform should adopt the mode RR.
Indeed, several existing studies have shown the popularity of tripartite PSC, and explored the sales channel choices of manufacturers and retailers in e-commerce platforms [13,14]. This paper analyzes the platform’s contract format choices under the tripartite PSC setting and considering the participation constraints of both the manufacturers and retailers. Results show that the optimal contract mode for the platform is changing according to the variation of additional value and revenue-sharing rate. Specifically, when both the additional value and revenue-sharing rate are low, mode FF is the optimal contract. If additional value and revenue-sharing rate are moderate, mode RF is the optimal format. When the revenue-sharing is high, the platform should adopt mode RR. From the perspective of PSC, thanks to the double marginalization reduction by a revenue-sharing contract, PSC attains the highest profit under mode RR.
The paper proceeds as follows: Section 2 reviews the relevant literature and outlines the contributions of this paper. Section 3 describes the model. Section 4 analyzes the equilibrium results under different contract modes. In Section 5, we present the main insights, and Section 6 conducts the numerical analysis. In Section 7, we extend the basic model. Finally, in Section 8, we conclude the paper.
2. Literature Review
This research lies at the intersection of the literature on: (1) platform contract formats and (2) supply chain coordination. Next, this article will describe how it relates to the literature in these fields.
2.1. Platform Contract Formats
The rapid expansion of the platform economy has led to numerous studies investigating the selection of contract formats. According to the analysis perspective, the above literature can be categorized into two streams: the first stream classifies contracts into agency contracts and wholesale contracts based on platform roles [15,16,17], and the second stream distinguishes between revenue-sharing and fixed-fee contracts based on profit distribution [14,18,19]. In the first stream, Xu et al. [20] study the manufacturer’s attitude towards agency contracts and wholesale contracts under the consumer returns window (CRW). Li et al. (2024) [21] explores the platforms’ preference between agency contracts and wholesale contracts. In the second stream, Wang et al. (2022) [8] investigate the platform’s selection between revenue-sharing contracts and fixed-fee contracts, considering the information strategies about the market size. Avinadav et al. (2020) [22] study the platform’s contract design under the quality and information (market size) selections. Furthermore, Hou et al. (2023) [16] analyze the product quality, Zennyo (2020) [17] investigates product substitutability level, Rong and Wang (2023) [23] examine consumer heterogeneity, and Avinadav et al. (2022) [24] explore information sharing’s effect on the platform’s contract selections.
Existing research identifies two primary classification frameworks for platform contract forms based on selection mechanisms. The first distinguishes contracts by platform role: agency contracts, where the platform acts as an intermediary, earning a commission based on transaction volume, and wholesale contracts, where the platform purchases and resells goods at its own price. The second framework is based on profit distribution, contrasting revenue-sharing contracts (proportional income distribution) with fixed-cost contracts (prepayment of fixed costs). Other factors influencing contract choice include product substitutability, consumer heterogeneity, and supply chain information transparency. These offer promising avenues for future research.
Unlike previous literature, this research makes the following three contributions to the field. First, this paper adopts both agency and wholesale contracts, that is, the platform serves as both the marketplace and the reseller for manufacturers and retailers. Based on the platform’s dual roles, this article also compares the effects of revenue-sharing contract and fixed-fee contract on the profits of platform supply chain members. Second, many manufacturers and retailers, accustomed to the convenient and reliable transaction process provided by platforms, have joined them. This motivates the inclusion of both wholesale and retail transactions on the platform. Third, this study examines the effect of channel power on the platform’s choice between revenue-sharing and fixed-fee contracts.
2.2. Supply Chain Coordination
Scholars have devoted considerable attention to supply chain coordination [25]. Asymmetric information is a common phenomenon among supply chain members, often leading to inefficiencies [26]. To tackle these inefficiencies, Biswas et al. (2023) [27] investigate the influence of the contract sequence on profit distribution among various stakeholders in a decentralized multi-echelon supply chain. Jia et al. (2024) [28] investigate supply chain coordination and the adoption of information structures, revealing that simple contracts (such as buybacks and revenue sharing) remain effective, while more complex contracts fail and must satisfy newsboy-type transfer payment conditions. Wu et al. (2017) [29] discover that two-part tariffs can effectively coordinate the supply chain in the presence of asymmetric information, and a uniform two-part tariff can achieve coordination at equilibrium. Moreover, with technological advancements, platforms have become crucial facilitators of transactions among supply chain members.
Another area of literature focuses on coordinating platform supply chains. Based on case studies, Chi et al. [30] explore Haier and JD.com to study how digital innovation and trading platforms build supply chain ecosystems through dynamic capabilities, Tanveer et al. [31] analyze the transformative impact of digital supply chain finance (SCF) platforms on buyer–supplier relationships, particularly their role in enhancing supply chain certainty and resilience. Wang et al. [32] empirically examine how a supplier’s position in the network affects supply chain resilience and the moderating role of the supplier’s operational process speed in e-commerce supply chains. These platform case studies and empirical research highlight the existence and coordination of platform supply chains. However, further work is needed to explain the relationships among platforms and supply chain members. Contracts, a common coordination method, have led to the study of various contract formats in platform supply chains [33]. Xu et al. (2020) [34] analyze how delivery time sensitivity affects the effectiveness of wholesale pricing and cost-sharing contracts. Cai et al. (2021) [35] demonstrate how platforms use markdown sponsor (MS) contracts to mitigate the triple marginalization problem associated with wholesale pricing. Qu et al. (2024) [36] investigate the platform’s optimal revenue-sharing contract, and Wang et al. (2023) [9] study how platforms choose between revenue-sharing and fixed-fee contracts when serving as marketplaces. Many articles investigate the operations of platform supply chain through platform-lead Stackelberg games. Bian et al. (2024) [37] investigate the selling format selection and information sharing strategies of the platform under a platform-lead Stackelberg model. Hu et al. (2025) [38] assume the platform is the Stackelberg leader and explore how e-commerce platforms can help small and medium-sized enterprises (SMEs) achieve targeted advertising (TA) through membership marketing systems. Li et al. (2025) [39] analyze the interaction between blockchain technology applications and manufacturer channel invasion strategies in platform supply chains when the platform acts as the Stackelberg leader.
This stream of literature is focused primarily on addressing inefficiencies stemming from information asymmetry and incentive misalignment in traditional manufacturer–retailer relationships. As platforms emerged as dominant intermediaries, subsequent research examined various contractual mechanisms for coordinating these more complex ecosystems under platform-lead Stackelberg games, including wholesale pricing with delivery constraints, markdown sponsorship arrangements, and revenue-sharing models. While these studies have advanced our understanding of platform-mediated coordination, they largely assume automatic participation by manufacturers and retailers, neglecting the critical reality in which these actors maintain viable offline alternatives and will only join platforms when the contractual terms satisfy their participation constraints.
Our study makes several important contributions that bridge these literature gaps. First, we develop a comprehensive analytical framework that properly models the tripartite nature of platform ecosystems, capturing the strategic interactions between platforms, manufacturers, and retailers as distinct entities with competing objectives. Second, we introduce endogenous participation decisions by establishing offline scenarios as meaningful benchmarks, allowing us to examine how contract structures influence the joining decisions of manufacturers and retailers. Third, we provide the first systematic comparison of revenue-sharing and fixed-fee contracts in this three-sided context, analyzing how their relative performance varies with the value created by the platform. Finally, we quantify the conditions under which platforms should transition between different contract types as their value proposition evolves.
Table 1 presents a comprehensive summary and comparative evaluation of relevant studies, highlighting their similarities and differences with respect to the key aspects of our research. This study identifies a gap in the current literature, which predominantly concentrates on two-tier PSC, paying less attention to the tripartite platform supply chain that is essential for understanding platform contract decisions. It highlights the substantial yet diverse effects of the tripartite supply chain, including the reconfiguration of the power structure and the increased complexity and diversification of channel conflicts, all of which influence the platforms’ choices of contract formats. Furthermore, this study outlines the endogenous conditions under which manufacturers and retailers join the platforms, which are crucial for accurately representing the interactions between PSC members. Existing research, which is typically approached from an exogenous perspective, rarely addresses the proactive role of PSC members, such as manufacturers and retailers. To address these gaps, our analysis examines the contract strategies employed by platforms within a tripartite PSC, consisting of a platform, a manufacturer, and a retailer. It also investigates the conditions under which manufacturers and retailers choose to join the platform in various contract modes. This approach offers a comprehensive insight into the platform supply chain, focusing on the interactions between platforms, manufacturers, and retailers.

Table 1.
Comparison with existing articles on model structure.
3. Model Description and Assumptions
This paper considers a supply chain platform consisting of one platform (T = platform), one manufacturer (M = manufacturer), one retailer (R = retailer) and a consumer (C = consumer) that could consume multi-unit products. Specifically, T only provides the marketplace service for the transactions.
The transactions between manufacturers, retailers, and consumers are standard wholesale contracts. R purchases the product from M at the wholesale price of , and then resells the product to C at the retail price of . Through T, M can sell the product directly to C at the retail price of . The presence of varying retail prices across different channels is common in both reality and the literature [41,42]. This article explores consumers’ preferences in the market with a case study of consumer C purchasing products from retailer R and manufacturer M. The demand function of this paper can be characterized by the utility function of a representative consumer, as suggested by the studies Ingene and Parry (2007) [43], Cai (2010) [44]. Therefore, the utility function of this article can be expressed as follows: . Based on the utility function, we can derive the demand functions of M and R, that is, , .
The game sequence is as follows. First, T chooses the contract format by either declaring a revenue sharing rate or a fixed fee . Second, M decides the retail price and wholesale price . Third, R selects the retail price . The game sequence shows the relative channel power among T, M, and R, that is, . This is because T has the market access right, and based on this right, T could develop various rules, including the contract format and fee level. As for M and R, T provides a secure and reliable payment platform that simplifies the transaction process and offers customer service support to enhance their shopping experience. These services provided by T have improved the transaction efficiency for both M and R, which is represented by .
The platform supply chain model is illustrated in Figure 1.
Figure 1.
Structure of the platform supply chain model.
With the rapid development and adoption of platforms, both manufacturers and retailers have become accustomed to trading on them, leading to an increase in the channel power and status of platforms within the supply chain. Therefore, following Wang et al. (2023) [9] and Zhang and Zhang (2020) [45], we assume that the platform acts as the Stackelberg leader in the supply chain and takes the initiative in making decisions.
The platform offers marketplace services and charges the manufacturer and retailer using two alternative contract formats [9,19]. One option is the revenue-sharing contract, where the manufacturer or retailer pays a proportion λ of their revenue as a fee. The other option is the fixed-fee contract, where the manufacturer or retailer pays a fixed fee t per transaction to the platform. We exclude the membership fee (a fixed access fee for joining) from our analysis, as the platform’s revenue mainly derives from proportional or transactional fees. The fixed access fee generally represents a negligible portion of the total revenue [46]. Given the two contract formats and the supply chain structure, the platform can choose from four possible strategy combinations.
Among these basic models, we exclude Mode FR since it is uncommon in practice. For instance, Amazon Business and Alibaba.com typically charge manufacturers a revenue-sharing fee while charging retailers a unit fixed fee. However, in our extended model, we also explore the implications of Mode FR. Based on the problem description, the symbol definitions are provided in Table 2.

Table 2.
The symbol definitions.
4. Model Development and Analysis
In the following sections, we derive equilibrium results, analyzing how exogenous parameters influence pricing decisions and profits in the platform’s contract choices (RR, FF, RF). We assume zero production and retail costs, following references Tian et al. (2018) [47], Ha et al. (2022) [40], Abhishek et al. (2016) [12], Hu et al. (2022) [48], to focus on strategic considerations beyond cost.
4.1. Mode FF
In this mode, the platform T employs the fixed-fee contract to both the manufacturer M and the retailer R. The sequence: T first chooses the unit fixed-fee , M sets the wholesale price and retail price , after observing the decisions of T and M, R selects the retail price . Thus, the objective functions of supply chain members are as follows:
By backwards induction (calculation process is given in Appendix A), we obtain the above equilibrium results:
When :
When :
Now, check the feasible conditions. Under the condition of and , the above results satisfy the feasible condition.
Lemma 1.
When the platform selects the fixed-fee contract, the equilibrium results are as shown in Equations (4) and (5).
Proof.
See Appendix A. □
Lemma 1 shows that when the additional value , M and R’s equilibrium results are independent of and identical to Mode NN, making them indifferent to joining the platform. Conversely, when , i.e., the value provided by the platform, increases, the retail prices of M and R decrease while the profits of M and R increase. Higher additional value allows M and R to lower their retail prices more effectively, which in turn boosts retail volumes and increases their profits.
4.2. Mode RF
In this mode, the platform T enters into a revenue-sharing contract with the manufacturer M and a fixed-fee contract with the retailer R. The decision sequences are as follows. T announces the revenue-sharing rate and unit fixed-fee . Then, M selects the wholesale price and retail price . Finally, R sets the retail price . The objective functions of supply chain members are as follows:
By backwards induction (calculation process is presented in Appendix A), we obtain the above equilibrium results:
Now check the feasible conditions. Under the premise of and , , , , , to ensure , and , and should satisfy and .
Lemma 2.
In the mode RF, the equilibrium results are as shown in Equation (9).
Proof.
See Appendix A. □
Lemma 2 shows that increasing the revenue-sharing rate () lowers M’s and R’s retail prices (i.e., ) while raising R’s profit and reducing M’s profit (i.e., and ). The higher additional value also boosts profits for M and R, similar to mode FF. Interestingly, when is high (i.e., ), T’s profit initially rises but then follows an inverted U-shape as increases. This occurs because T captures more revenue at high , but as nears saturation, the marginal revenue for T decreases, reducing T’s profit.
4.3. Mode RR
In this mode, the platform T adopts revenue-sharing contracts to both the manufacturer M and retailer R. The game sequences are as follows. First, T announces the revenue-sharing rate . Second, M sets the wholesale price and retail price . Finally, R makes the retail price decision . Under this mode, the objective functions of the supply chain members are as follows:
By backwards induction, we obtain the above equilibrium results:
Based on the optimal decisions of M and R, we obtain the equilibrium results:
Now check the feasible conditions. Under the premise of and , , , , to ensure and , and should satisfy and .
Lemma 3.
When the platform selects the revenue-sharing contract, the equilibrium results are as shown in Equations (13) and (14).
Proof.
See Appendix A. □
Lemma 3 presents a counterintuitive finding: as the revenue-sharing rate () rises, manufacturer M and retailer R lower their retail prices (), boosting retail volumes () due to their high demand elasticities. Despite increasing and , M and R reduce retail prices to maintain profits ( and ). However, and present a U-shaped trend as increases, influenced by higher retail volumes and rising costs associated with the revenue-sharing rate.
4.4. M and R’s Participation Choices
To make our model more practical and ensure that the manufacturer and retailer are inclined to join the platform, we compare the equilibrium results under the above modes with the benchmark mode NN.
In this mode, the manufacturer M and retailer R transact offline, i.e., neither M nor R join the T. The objective functions of M and R are as follows:
Similar to the previous calculation method, we can obtain
Lemma 4.
When neither M nor R joins platform T, the equilibrium outcomes are obtained using Equation (17).
Proof.
See Appendix A. □
We compare the equilibrium profits of M and R obtained from Section 4.1, Section 4.2 and Section 4.3 with the benchmark model NN and find:
- (1)
- Under mode FF, (1) when , whether to join the platform makes no difference to M and R; (2) when , M and R are willing to join the platform.
- (2)
- Under mode RF, to ensure M and R are willing to join the platform, and need to satisfy and .
- (3)
- Under mode RR, to ensure M and R are willing to join the platform, and need to satisfy and .
5. Comparison and Analysis of Results
To ensure nonnegative profit margins and that M and R join the platform, this paper assumes and . These conditions guarantee positive margins, balanced incentives, and reduced risks. Major platforms like Alibaba, Amazon, and eBay typically set revenue-sharing rates below 25%. Given the limited value provided, some manufacturers and retailers, like ALDI and Costco, do not join platforms, making this assumption reasonable. By comparing equilibrium results from Section 4, we can derive the following conclusions.
5.1. Unit Fixed-Fees, Wholesale Prices, and Retail Prices
First, comparing the equilibrium results in the above modes, this paper obtains insights about how the platform’s contract format strategies impact the commission fees, PSC members’ wholesale prices, and retail prices, which are demonstrated in the following propositions.
Proposition 1.
(1) When , ; (2) When , .
Proof.
See Appendix B. □
Proposition 1 shows that the additional value significantly affects the unit transaction fees under pure fixed-fee (FF) and hybrid (RF) contracts. Under the hybrid contract, the optimal unit transaction fee is always equal to . For the pure fixed-fee contract, is at the boundary value of when is low, and at an interior solution when is high. Thus, is lower than . Conventional wisdom suggests that revenue-sharing contracts provide more flexible profit margins, so the unit transaction fee under mode RF is higher than that of FF when is high.
Moreover, as increases, both and increase. The higher additional value offered by the platform boosts its appeal, leading supply chain members to derive greater benefits and agree to higher transaction fees. Thus, the platform should adjust its pricing strategy as increases, gradually raising the unit fixed fee to ensure revenue growth while maintaining the engagement of transaction members.
To further explore the impact of platform contract forms on the operational strategy choices of supply chain members, we analyze the wholesale price relationships under different contract forms.
Proposition 2.
.
Proof.
See Appendix B. □
Proposition 2 demonstrates that manufacturer M’s wholesale price is the same under both the pure fixed-fee (FF) and pure revenue-sharing (RR) contracts. This is because M’s goal in both contracts is to maximize profit by setting a wholesale price that covers platform fees and maximizes net profit. Additionally, M experiences similar marginal revenue and cost dynamics in both contracts. In the RR contract, marginal revenue increases with retail volume, and platform commissions (marginal costs) rise accordingly. In the FF contract, both marginal revenue and cost are linearly related to retail volume. Thus, the optimal wholesale pricing strategy under these contracts leads to identical wholesale prices for the manufacturer.
In addition, M’s wholesale price under the hybrid-fee (RF) contract is the lowest. Under the RF contract, retailer R’s fee is directly related to her wholesale volume, making R more sensitive in procurement decisions as her cost increases with additional unit procurement. Considering R’s resistance to high wholesale price, M needs to set a lower wholesale price under the RF contract.
In summary, the RF contract establishes a pricing dynamic in which the manufacturer is required to set a lower wholesale price due to the retailer’s cost sensitivity, which is linked to procurement volume. This is a direct contrast to the FF and RR contracts, where wholesale prices can be set higher due to different cost considerations on the retailer’s side. For managers, understanding this dynamic is essential for optimizing pricing strategies, maintaining strong relationships with retailers, and ensuring smooth operations in the supply chain.
Next, we would investigate the relationship between PSC members’ retail prices.
Proposition 3.
- (1)
- Given the contract format, ,,.
- (2)
- Given the supply chain member, ,.
Proof.
See Appendix B. □
Proposition 3(1) shows that M’s retail price is always higher than R’s due to revenue composition: M’s revenue includes both retail and wholesale, while R’s revenue is purely from retail. To maintain profit, R sets a higher retail price. Proposition 3(2) reveals that the relationship between retail prices across different scenarios is unaffected by the revenue-sharing rate () and additional value (). Specifically, M’s retail price remains the same under both RR and RF modes, as the platform charges a revenue-sharing fee in both cases. For R, the pure fixed-fee (FF) contract leads to the highest retail price, while the pure revenue-sharing (RR) contract results in the lowest. Generally, retail prices are higher in the FF contract than in the RR contract. This occurs due to double marginalization in the PSC. In supply chain management, the double marginalization effect refers to the phenomenon in which multiple independent decision-making layers within the supply chain (e.g., manufacturers → retailers) mark up prices to maximize their own profits. This leads to excessively high final retail prices and, ultimately, reduces the overall profitability of the supply chain. Based on this theory, the revenue-sharing contract and fixed-fee contract can respectively mitigate and exacerbate the double marginalization effect. Under a revenue-sharing contract, the manufacturer’s cost becomes a variable cost due to the revenue-sharing rate. As the wholesale or direct-selling price increases, the manufacturer’s commission also rises accordingly. Under the fixed-fee contract, the unit fee is treated as a fixed cost. When setting the wholesale or direct-selling price, the manufacturer transfers this cost to the retailer (which is eventually passed on to the consumer) or consumer, thereby exacerbating the double marginalization effect.
A fixed fee from the platform can exacerbate this effect, raising retail prices, while revenue-sharing may lead PSC members to lower prices to stay competitive. Additionally, revenue-sharing can increase market risk, prompting members to adopt more proactive pricing strategies to mitigate uncertainty.
In summary, Proposition 3(1) shows that the manufacturer’s retail price is consistently higher than the retailer’s due to differences in revenue composition. Proposition 3(2) reveals that contract formats significantly influence retail pricing, with the FF contract leading to higher retail prices due to double marginalization and risk mitigation, while RR contracts result in lower retail prices due to the more flexible, risk-sensitive pricing strategies. Managers should carefully consider these dynamics when selecting contract formats to optimize pricing strategies, manage risks, and maintain competitiveness in the market.
The combination of Propositions 1–3 illustrates a clear contrast between the price competition mitigation offered by FF contracts and the demand expansion effect promoted by RR contracts. In FF contracts, both M and R are focused on ensuring profitability to cover fixed costs, which dampens price competition but may lead to higher retail prices. In contrast, RR contracts align the incentives of M and R, encouraging them to collaborate to maximize sales volumes by lowering prices. This alignment of interests and focus on volume expansion explains why revenue-sharing contracts are popular, particularly in dynamic and competitive markets.
For managers, these findings emphasize the importance of contract design in shaping pricing strategies and market outcomes. FF contracts are better suited for stable markets where price competition needs to be controlled, while RR contracts foster cooperation and flexibility in more volatile or competitive environments, driving growth through lower prices and increased sales volumes.
5.2. Manufacturer’s Profits
In this section, we investigate how the revenue-sharing rate () and addition valuation () affect the manufacturer M’s profits under different modes.
Proposition 4.
.
Proof.
See Appendix B. □
Proposition 4 shows that manufacturer M’s profitability is unaffected by the revenue-sharing rate () and additional valuation (). It is highest under the pure revenue-sharing contract, followed by the hybrid contract, and lowest under the pure fixed-fee contract. The pure revenue-sharing contract alleviates fixed cost pressure for both manufacturer and retailer, allowing M to maximize revenue in high-profit scenarios and stimulate higher retail quantities, which boosts wholesale revenue and results in the highest profitability for M.
The findings align with Wang et al. (2025) [9], though their study was in a competitive market while this one focuses on a monopolistic scenario. This suggests that market competition does not impact the manufacturer’s preference for the pure revenue-sharing contract. It is always beneficial for M to choose a revenue-sharing contract over a fixed-fee contract, regardless of R’s contract choice. Therefore, manufacturers should prioritize platforms offering a pure revenue-sharing contract. If that option is unavailable, the next best choice is a platform with a hybrid contract.
Proposition 4 highlights the critical role of contract design in manufacturer profitability. Pure revenue-sharing contracts (RR) consistently yield the highest profitability, regardless of market structure or retailer contract terms. This is because they align incentives between manufacturer and retailer and reduce fixed cost pressures, enabling both to focus on maximizing retail volumes. Manufacturers should prioritize platforms offering revenue-sharing contracts for the best financial outcomes. If such contracts are unavailable, hybrid fee contracts are the next best option, while pure fixed-fee contracts should be approached cautiously due to their lower profitability potential.
5.3. Retailer’s Profits
In this section, we probe how the revenue-sharing rate () and addition valuation () impact retailer R’s profits across different modes.
Proposition 5.
.
Proof.
See Appendix B. □
Proposition 5 indicates that retailer R achieves the highest profit under the pure revenue-sharing contract, followed by the hybrid contract, with the lowest profit under the pure fixed-fee contract. In the pure revenue-sharing contract, fees are proportional to revenue, allowing R to pay reasonable fees while maintaining high retail volumes and profit margins. The hybrid contract, while involving a per-unit transaction fee, still enables R to enjoy high profit margins on large volumes due to reduced product costs from the manufacturer. In contrast, the fixed-fee contract imposes a constant cost per transaction, which narrows profit margins, particularly when retail volumes are high but margins are low, leading to the lowest profit for R.
It suggests that R should prioritize the pure revenue-sharing contract to maximize profit margins, as fees rise with revenue but do not compress margins. If unavailable, the hybrid contract is a good secondary option for maintaining relatively high profits. The platform should offer diverse contract formats to meet the needs of different supply chain members, ensuring reasonable profits for all parties. This strategy will support the healthy development of the platform ecosystem.
Proposition 5 highlights the importance of contract design for retailers, demonstrating that pure revenue-sharing contracts consistently deliver the highest profitability by aligning fees with sales performance and maintaining high profit margins. Retailers should aim for RR contracts when possible, while hybrid contracts offer a strong secondary option. Fixed-fee contracts, on the other hand, compress profit margins and should be approached with caution, particularly in volume-driven industries. For platforms, offering diverse contract formats is key to accommodating the needs of both manufacturers and retailers, ensuring that all members of the platform ecosystem can remain profitable. This strategy not only supports individual businesses but also promotes the long-term health and development of the platform as a whole.
5.4. Platform’s Profits
In this section, we compare the platform’s profits across various contract formats to identify the optimal contract strategy. Our analysis yields the following results.
Proposition 6.
Compare the platform T’s equilibrium profits under different scenarios and find:
- (1)
- Given
- (a)
- FF is the optimal contract format, (i) and ; (ii) and .
- (b)
- RF is the optimal contract format, if and .
- (c)
- RR is the optimal contract format, if (i) and ; (ii) and .
- (2)
- Given and , .
Where , , , is the solution to within .
Proof.
See Appendix B. □
Proposition 6 highlights that additional value v is crucial in determining the optimal contract format for platform T. When is low, T prefers the pure fixed-fee contract as the revenue-sharing rate () increases, shifting from a pure fixed-fee to a hybrid and finally to a pure revenue-sharing contract. This shift occurs because higher allows T to extract greater profit from revenue-sharing. Integrating Propositions 4 and 5, we find that, despite potential conflicts among the platform, manufacturer, and retailer, there is scope for aligning their interests. Specifically, with a low and high , the platform and retailer can agree on a pure revenue-sharing contract to maximize profits. When is moderate and is high, the platform and manufacturer can agree on a hybrid contract.
However, the platform’s inclination towards the revenue-sharing contract format decreases as the additional value increases and the revenue-sharing rate decreases. Particularly, when falls within the middle range (as shown in Figure 2), the favored format shifts from the pure fixed-fee to the hybrid contract as rises. Additionally, it is surprising to note that when the additional value exceeds a certain threshold, the platform should prompt both the manufacturer and retailer to embrace the fixed-fee contract, regardless of the revenue-sharing rate. Detailed explanations follow.
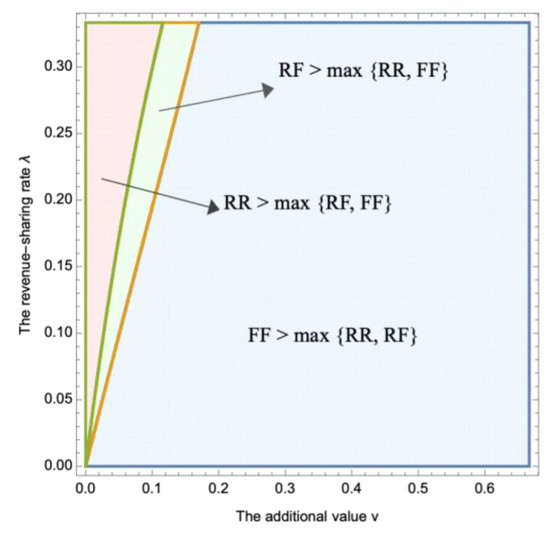
Figure 2.
Optimal contract format as a function of additional value () and revenue-sharing rate ().
First, given that the unit fixed-fee is endogenous while the revenue-sharing rate is exogenous, the platform’s fee choice directly impacts the retailer’s and manufacturer’s decisions in mode FF but not in mode RR. In the hybrid contract, the platform influences the retailer through the fixed fee but cannot affect the manufacturer, who follows the revenue-sharing contract. Consequently, the platform has more flexibility in adjusting fees under the fixed-fee contract, making mode FF the optimal contract in most cases.
Second, the fixed-fee contract’s advantage increases with higher additional value. As revenue grows, the platform charges stable fees per transaction, ensuring predictable revenue. In high-value situations, manufacturers and retailers enjoy higher profits and can better bear fixed costs, so the fixed-fee contract does not significantly impact their transaction incentives.
5.5. Supply Chain’s Profits
In this section, we perform a comparative analysis of total supply chain profits, defined as the combined profits of the platform, manufacturer, and retailer. The results are summarized in the following proposition.
Proposition 7.
, where .
The calculation process is given in Appendix B.
Proposition 7 shows that the supply chain maximizes profit under the pure revenue-sharing (RR) contract. This occurs because the platform’s revenue is directly linked to the retail performance of supply chain members, incentivizing the manufacturer and retailer to increase market promotion and retail volume. This contract format fosters enthusiasm and cooperation among supply chain members, enhancing overall performance and profitability.
The hybrid (RF) contract balances costs and incentives by charging the retailer a fixed fee and the manufacturer a revenue-sharing rate. While it does not match the pure revenue-sharing contract’s incentive strength, it still fosters cooperation through a reasonable fee structure. The platform and manufacturer share market risks, encouraging the manufacturer to focus on demand and retail strategies. However, the retailer’s fixed fee may reduce their retail enthusiasm, leading to slightly lower overall profits compared to the pure revenue-sharing model.
Under the pure fixed-fee (FF) contract, the manufacturer and retailer face fixed transaction costs regardless of market conditions, creating pressure during market fluctuations or poor sales. This rigidity dampens their enthusiasm for innovation and market expansion. The platform cannot flexibly incentivize members by adjusting costs, leading to lower overall enthusiasm and cooperation compared to the RR contract. As a result, the supply chain’s total profit is the lowest under this contract.
For platforms and supply chain managers, designing contracts that foster cooperation and align incentives is crucial for achieving the highest possible profitability. Revenue-sharing contracts should be prioritized where possible, while hybrid contracts offer a reasonable alternative when revenue-sharing is not feasible. Fixed-fee contracts, though more predictable in cost, should be approached with caution due to their potential to stifle innovation and reduce overall supply chain performance.
6. Numerical Analysis
In the previous section, we conducted a comparative analysis of the equilibrium results under three different contract formats. In this section, we explore the effects of two important parameters, additional value and revenue-sharing on equilibrium wholesale price, retail prices, and profits of different PSC members. The corresponding results are illustrated in Figure 3 and Figure 4.
6.1. The Impacts of Additional Value
First, we explore the impact of additional value on wholesale price and retail prices; specifically, we examine wholesale price in mode RF and retail prices in all the modes. For the wholesale price under mode FF and mode RR, due to the linear demand, the pricing decisions of the manufacturer and the retailer form a “symmetric split” equilibrium; thus, . For the retail price, , and it is irrelated to , so we focus on , and .
Obviously, an increase in the additional value leads to a corresponding decrease in both the wholesale and retail prices. As increases, the retail-side demand becomes more elastic (consumers become more price-sensitive). To maximize overall profit, the manufacturer must lower , enabling the retailer to set a lower retail price ().
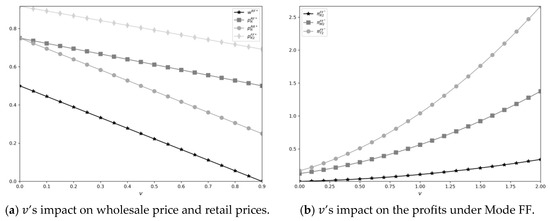
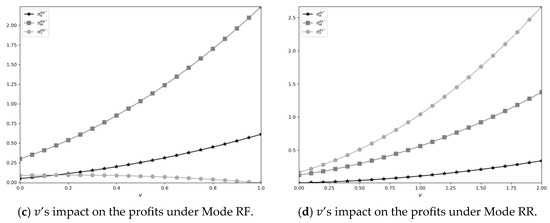
Figure 3.
’s impact on the equilibrium results.
For the profits of PSC members under different modes, increases; however, presents an inverted U-shape trend, and the other profits increase. The increase of profits is intuitive. For , as increases, its negative impact on T’s profit margin exceeds its positive on transaction volumes, causing an inverted U-shaped trend.
6.2. The Impacts of Revenue-Sharing Rate
In this subsection, we examine the effect of revenue-sharing rate on the equilibrium results under different contract formats.
As shown in Figure 4a, as increases, both the wholesale price and retail prices decrease. An increase in directly reduces the unit revenue of retailers, forcing them to lower retail prices to maintain market sales volume. In addition, such an increase exacerbates the problem of dual marginalization in the supply chain while forcing manufacturers and retailers to approach centralized decision-making, thereby reducing retail prices.
For the profits of PSC members, under mode RF, as shown in Figure 4b, with the increase of , and show an increasing trend, while presents a U-shape trend. For , as increases, due to the decrease of wholesale price, it presents an increasing trend. For , as mentioned earlier, when increases, increases, and the wholesale profit of manufacturers may increase. For , when is small, the manufacturer reduces due to the increase of , and the platform’s revenue base temporarily decreases. When is large, and increase, and the platform’s commission revenue and transaction fee revenue increase significantly.
Under Mode RR, as we can see in Figure 4c,d, when increases, and present a U-shaped trend, while presents an inverted U-shape trend. For and , when is small, the proportion of revenue extracted by the platform from manufacturers and retailers increases, directly reducing their unit profits. In addition, since is fixed at , manufacturers cannot compensate retailers for their profit losses by reducing , resulting in a decline in profits for both parties. When exceeds a certain threshold, retailers and manufacturers will adjust the retail price and direct selling price to maximize sales and compensate for the decrease in unit profit.
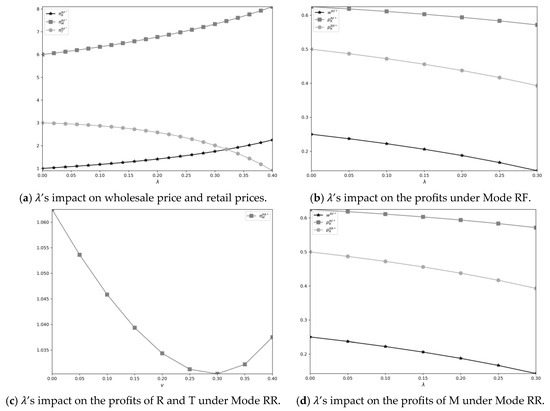
Figure 4.
’s impact on the equilibrium results.
7. Extensions
7.1. Positive Costs
The basic model assumes zero costs for all PSC members; in this section, we consider embedding producing cost and retailing cost to test the robustness of our findings. Specifically, we use to represent M’s unit producing cost and as the unit retailing cost of R, and their profit functions under the fixed-fee contract and revenue-sharing contract are, respectively, given by
When M and retailer R transact offline, the objective functions of M and R as follows:
Based on the backward induction, we can obtain
Under mode FF, we calculate and find
When :
When :
Under mode RF, we calculate and find
where , .
Under mode RR, we calculate and find
where , .
By comparing the equilibrium profits of M and R, as derived in Equations (18)–(22), with the equilibrium results of the benchmark mode NN in Equation (17), we obtain the following:
- (1)
- Under mode FF, (1) when , whether to join the platform makes no difference to M and R; (2) when , M and R are willing to join the platform.
- (2)
- Under mode RF, to ensure that M and R are willing to join the platform, and need to satisfy and .
- (3)
- Under mode RR, to ensure that M and R are willing to join the platform, and need to satisfy and .
Where , . is the real root of .
As observed, the specific levels of participation constraints in this setting differ from those in the basic model, though the structure remains the same. We will now examine the optimal contract format for the platform, considering the participation constraints of the PSC members.
- (1)
- Given
- (a)
- FF is the optimal contract format, (i) and ; (ii) and .
- (b)
- RF is the optimal contract format, if and .
- (c)
- RR is the optimal contract format, if (i) and ; (ii) and .
- (2)
- Given and , .
Where , , , is the solution to .
The above results indicate that the platform’s optimal contract varies with changes in the additional value and the revenue-sharing rate . Specifically, when is high, mode FF is the optimal contract for T. When both and are low, mode RR becomes the optimal choice. When is low and is at a moderate level, mode RF is optimal for T. These results align with those of the basic model.
7.2. Platform’s User Base
The basic model assumes that the platform solely provides a marketplace for wholesale and retail transactions. In this section, we expand this assumption by considering that the platform has an established user base. Specifically, we use to represent the potential size of the consumer base. Therefore, the demand functions of M and R, that is, , and . Through these calculations, we find the following the equilibrium results under mode FF:
When :
When :
Under mode RF, we calculate and find
where , .
Under mode RR, we calculate and find
By comparing the equilibrium profits of M and R, as derived in Equations (23)–(26), with the equilibrium results of the benchmark mode NN in Equation (17), we obtain the following:
- (1)
- Under mode FF, M and R are willing to join the platform.
- (2)
- Under mode RF, to ensure that M and R are willing to join the platform, and need to satisfy and .
- (3)
- Under mode RR, to ensure that M and R are willing to join the platform, and need to satisfy and .
Where , .
As observed, when the platform’s user base exceeds that of the offline market 1, both the manufacturer and retailer are inclined to join the platform under the FF model. This is intuitive, as the platform provides additional value per unit transaction and a larger user base. Although the manufacturer and retailer are required to pay a fixed fee for each unit transaction, this fee is still lower than the additional value generated. Therefore, under the FF model, both the manufacturer and retailer are consistently motivated to participate in the platform.
7.3. Hybrid-Fee Contract
In the basic model, we assume that the platform charges the manufacturer or retailer through either a revenue-sharing contract or a fixed-fee contract. This section examines the case in which the platform charges both the manufacturer and retailer using a combination of the revenue-sharing and fixed-fee contracts.
The profit functions of the manufacturer, retailer, and platform under the hybrid-fee contract are, respectively, given by:
Based on the backward induction, we find
where , , .
By comparing the equilibrium profits of M and R, as derived in Equation (27), with the equilibrium results of the benchmark mode NN in Equation (17), we obtain the following:
- (1)
- When , R will not join the platform; when , R would like to join the platform.
- (2)
- When , M will join the platform; when , M would like to join the platform.
To ensure both M and R join the platform, and need to satisfy and , where .
Thus, when T charges both a revenue-sharing and fixed-fee contract to M and R, the equilibrium results are given by Equation (27). To ensure the participation of M and R, the additional value and revenue-sharing rate need to satisfy and . Notice that , which implies that the participation constraints are more rigorous under a hybrid-fee contract, in which and are the participation constraints of under mode RF and mode RR, respectively.
8. Conclusions and Discussions
8.1. Conclusions
With the widespread adoption of digital technology, platforms providing marketplace services for both manufacturers and retailers have rapidly developed. Within these services, platforms can charge fees to manufacturers and retailers using two prevalent contracts: revenue-sharing and fixed-fee contracts. In this article, we examine how platforms can optimize their contract strategies when collaborating with upstream manufacturers and downstream retailers. Furthermore, we explore the participation choices of manufacturers and retailers regarding different contract formats. Through game theory modeling and analysis, we derive the following insights.
First, we find that a fixed-fee contract may reduce price competition between manufacturers and retailers, as both need to cover fixed fees. In contrast, a revenue-sharing contract aligns the interests of both parties, encouraging them to lower prices to increase retail volumes. Second, the platform’s additional value significantly influences the optimal contract format. When the additional value is high, a fixed-fee contract is preferable if the revenue-sharing rate is low, while a revenue-sharing contract is better if the rate is high. A hybrid contract is optimal for moderate revenue-sharing rates. Third, when manufacturers select the contract format, the equilibrium is typically a hybrid contract, while retailers tend to prefer a revenue-sharing contract.
8.2. Management Insights
Our review of the PSC literature indicates that while the tripartite platform supply chain has existed in the e-commerce market since the 2010s [13,14], the contract formats implemented by platforms with manufacturers and retailers may vary. For instance, Amazon uses a revenue-sharing contract to charge manufacturers, whereas retailers on Amazon’s Seller Central platform incur a fixed fee per transaction. However, to the best of our knowledge, few studies offer a theoretical explanation for this phenomenon. Based on the equilibrium of the Stackelberg game, the result in Proposition 6 provides a potential theoretical framework for the platform to select the optimal contract format, considering the participation constraints of both manufacturers and retailers. That is, as the additional value increases, the platform’s optimal contract transitions from mode RR to mode RF, and finally to mode FF. Conversely, as the revenue-sharing rate increases, the platform’s optimal contract transitions from mode FF to mode RF, and finally to mode RR.
The literature reviewed in Section 2 indicates that the contract format strategy impacts the profits of supply chain members [7,8,9]. Our contribution extends these models by exploring the platform’s contract format choices within a tripartite platform supply chain framework, while endogenously considering the participation constraints of PSC members. This extension allows us to gain new insights into how the tripartite platform supply chain framework influences the platform’s contract format strategy, which, in turn, affects the equilibrium decisions of PSC members (including participation selection, wholesale prices, and retail prices).
Our study offers valuable practical insights for platform managers involved in contract negotiations within tripartite supply chains. Building on the theoretical equilibrium outlined in Proposition 6, our findings present a data-driven framework to guide the strategic selection and negotiation of contract formats in response to prevailing market conditions. Specifically, platform managers should account for two critical market-driven factors: the additional value provided by the platform (such as logistics speed, customer reach, and data analytics) and the revenue-sharing rates, either within the broader market or for specific product categories. When the additional value is high, our analysis (Section 4.4, Proposition 6) suggests that fixed-fee contract (FF) is optimal. Given the platform’s significant unique value (e.g., superior logistics, exclusive audience, strong brand), managers could emphasize exclusive access to high-spending customers and premium fulfillment options (such as JD’s ‘211′ or Amazon’s ‘Prime’) as a rationale for adopting a per-transaction fixed-fee structure. When both the additional value and the revenue-sharing rate are in the mid-range, the hybrid contract (RF) emerges as the strategic choice. The fixed-fee component covers essential platform costs, while the revenue-sharing rate reflects the specific value-added services (e.g., premium placement, targeted marketing) provided to the partner. Given the flexibility to tailor terms based on partner contributions and category profitability (for example, Alibaba charges 2.5% to 5% for select products, while JD.com sets rates between 1% and 8%), managers could strategically promote the RF contract. When the additional value is low and the revenue-sharing is high, a pure revenue-sharing contract (RR) is optimal for the platform. This type of contract helps mitigate double marginalization, making it the preferred model for both manufacturers and retailers (Proposition 4 and Proposition 5). Consequently, managers could position the revenue share as an investment in mutual success, emphasizing how it supports the ongoing enhancement of high-value services (e.g., ultra-fast fulfillment, advanced analytics) that drive partner sales. Additionally, they could quantify the potential sales raise resulting from the reduction of double marginalization.
8.3. Future Research Directions
We now discuss some limitations of this article and suggest potential directions for future research. First, we assume deterministic demand; however, due to the multi-sided nature of platforms, demand is typically uncertain. Therefore, it is useful to introduce a random variable, , into the demand functions of M and R, such that and , to account for demand uncertainty. Second, this paper assumes no competition between the manufacturer and the retailer. In reality, the manufacturer can sell their product directly to the retailer on the platform, which may introduce competition between the two. Therefore, it is valuable to account for this competition. Specifically, we can modify the consumer’s utility as , where represents the competition intensity between the manufacturer and the retailer. From this, we can derive the demand functions of the M and R as , , respectively. Third, considering the inherent conflict between the platform’s objectives and those of the manufacturer and retailer, it is valuable to integrate the interests of both parties into the platform’s objective function, thereby promoting the platform’s long-term sustainability. Future work along these lines could yield more nuanced guidance for digital marketplace governance while advancing game-theoretic applications in platform supply chain research. These research directions would significantly enhance our understanding of how contract formats function in complex, real-world platform ecosystems.
Author Contributions
Conceptualization, Y.Q. and X.W.; methodology, Y.Q. and X.W.; validation, Y.Q., X.W., Y.M. and H.L.; formal analysis, Y.Q., X.W., Y.M. and H.L.; investigation, Y.Q. and X.W.; resources, Y.Q.; writing—original draft preparation, Y.Q. and X.W.; writing—review and editing, Y.Q., X.W., Y.M. and H.L.; visualization, Y.Q.; supervision, Y.M.; project administration, Y.Q.; funding acquisition, X.W. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Humanities and Social Sciences Research Planning Fund Project of Ministry of Education (grant numbers: 24YJA630092), National Natural Science Foundation of China (grant numbers: 71672022), and National Social Science Foundation of China (grant numbers: 21BZZ091).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the two anonymous referees for their comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
In this appendix, we present the equilibrium results deductions under different modes.
Proof of Mode FF.
According to the backwards induction, we first solve the maximization problem of R, which yields the following:
Based on R’s optimal decision, M sets and to maximize , results show
Taking into account R’s and M’s responses , and , T sets the unit fixed fee to maximize its profit:
Solving the maximization problem yields the following:
Based on the optimal decisions of all the PSC members, we obtain the equilibrium results, as follows:
When :
When :
□
Proof of Mode RF.
According to the backwards induction, we first solve the maximization problem of R, which yields the following:
Based on R’s optimal decision, M sets and to maximize , and the results are as follows:
Taking into account R’s and M’s responses , and , sets the unit fixed fee to maximize its profit:
Solving the maximization problem yields the following:
Based on the optimal decisions of all the PSC members, we obtain the equilibrium results, as follows:
□
Proof of Mode RR.
According to the backwards induction, we first solve the maximization problem of R, which yields the following:
Based on R’s optimal decision, M sets and to maximize , and the results show the following:
Based on the optimal decisions of M and R, we obtain the following equilibrium results:
□
Proof of M and R’s participation choices.
- (1)
- Compare Mode FF with Mode NN
When , the corresponding equilibrium profits of R and M under the mode FF and mode NN are equal, which means M and R are indifferent regarding whether they join the platform or not.
When , we compare M and R’s profits under scenario FF and Mode NN and obtain the following:
For Equations (A13) and (A14), given , we can find that and , and M and R are willing to join the platform.
- (2)
- Compare Mode RF with Mode NN
Under the equilibrium non-negativity constraints of and , we compare M and R’s equilibrium profits under scenario RF and bench mark and find the following:
For Equation (A15), given and , , R is inclined to join the platform.
For Equation (A16), when and , , M shows a preference for joining the platform; otherwise, M will not join it.
- (3)
- Compare Mode RR with Mode NN
Under the equilibrium nonnegativity constraint of and , when comparing the equilibrium profits of M and R under mode RR and mode NN, we find the following:
For Equation (A17), when and , R is inclined to join the platform, otherwise, R will not join the platform.
For Equation (A18), when and , M prefers to join the platform; otherwise, M will not join the platform. □
Appendix B
In this appendix, we provide the proofs of all propositions in Section 6. To guarantee that the profit margins are nonnegative and to ensure M and R join the platform in all scenarios, this paper assumes that and in the following analysis.
Proof of Proposition 1.
As shown in Equation (7), when , ; when , , ; when we compare and , we find that . Since , we can conclude that , that is, . □
Proof of Proposition 2.
As shown in Equation (6), (14), and (21), . Now, we compare and . We find that . Given and , we can derive that , which means that . □
Proof of Proposition 3.
Given and contract format, when we compare the retail prices of manufacturer and retailer, we find that , , . Thus, we can conclude that , , . In addition, given the supply chain member, when we compare the retail prices under different contract format, we find that , , , . Derived from the above results, we obtain that , .
Given , the final outcomes are identical to those observed when . □
Proof of Proposition 4.
In this proof, we show that, under the feasible conditions of all the modes and participant constraints of manufacturer and retailer, . Specifically, we need to prove that and . First, when , we compare and , , given and , , that is . Compare and , , given and , and we can find that , which means .
Second, when , and are identical to the situation when , so we only need to compare and , . Taking the derivative gives ; given and , , that is . It means that is increasing in ; plugging in , we find . Since , we can conclude that . □
Proof of Proposition 5.
In this proof, we show that, under the feasible conditions of all the modes and participant constraints of manufacturer and retailer, . Specifically, we need to prove that and . First, given , compare and , . Taking the derivative gives ; given and , , that is . It suggests that is increasing in ; plugging in , we find that . Since , we can conclude that . Next, compare and , ; given and , , that is .
Second, given , and are identical to the situation when , so we only need to compare and , . Taking the derivative gives ; given and , , that is . It demonstrates that is increasing in ; plugging in , we find that . Since , we can conclude that . □
Proof of Proposition 6.
In this proof, given , (1) we show that the platform prefers the pure fixed-fee contract if (i) and ; (ii) and ; (2) we prove that the platform favors the hybrid contract if and ; (3) we demonstrate that the pure revenue-sharing contract is the optimal contract format for the platform if (i) and ; (ii) and . Given and , we show that . Where is the solution to within .
Given , (1) We need find the sufficient conditions for and . First, compare and .
Taking the derivative of Equation (A19) gives
Under the conditions of and , . In addition, , . It can be concluded that Equation (A19) has a unique zero point for in the interval . Solving Equation (A19) we obtain and . Given , . For , when , ; when , . Thus, when , ; when , .
Second, compare and .
Taking the derivative of Equation (A21) gives
Under the conditions of and , . Moreover, , . It can be concluded that Equation (A21) has a unique zero point for in the interval . Solving Equation (A21), we obtain , . Given , , . Thus, when , ; when , .
Now we need to compare and .
Similar to the above process, we can find that, given , when , ; when , , where is the solution to within .
In summary, if (i) and ; (ii) and , pure fixed-fee contract is the optimal contract format for the platform.
(2) We need to find the sufficient conditions for and . First, as demonstrated above, given , when , . Second, we need to compare and .
Similar to the above process, we can find that, given , when , ; when , , where .
Compare and , and we have
Similar to the above process, we can find that, given , when , ; when , .
Thus, to ensure that the platform selects the hybrid contract, given , should satisfy . That is, when and , hybrid is the optimal contract format for the platform.
(3) We need to find the sufficient conditions for and . As previously deduced, given , when , ; when , .
Now we need to compare and .
Similar to the above process, we can find that, given , when , ; when , .
In summary, if (i) and ; (ii) and , pure revenue-sharing is the optimal contract format for the platform.
Given and , we first compare and .
Taking the derivative gives . Since and , we can conclude that . In addition, . Thus, , that is, .
Similarly, we can obtain .
In summary, given and , . □
Proof of Proposition 7.
In this proof, we show that, under the feasible conditions of all the modes and participant constraints of manufacturer and retailer, , where .
First, determine the supply chain profits under different modes.
Second, compare the above supply chain profits.
Taking the derivative of Equation (A30) gives
Under the conditions of and , . In addition, . Thus , that is, .
Similarly, we can find that . □
References
- Nie, T.F.; Guan, S.H.; Du, S.F.; Zhu, S.Y. Pricing strategy selection for the sharing platform with heterogeneous laborers. Com. Ind. Eng. 2022, 169, 108241. [Google Scholar] [CrossRef]
- Jovanovic, M.D.; Sjodin, D.; Parida, V. Co-evolution of platform architecture, platform services, and platform governance: Expanding the platform value of industrial digital platforms. Technovation 2022, 118, 102218. [Google Scholar] [CrossRef]
- Gu, G.Y. Technology and Disintermediation in Online Marketplaces. Manag. Sci. 2024, 70, 7868–7891. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, J.Q. Joint Pricing-Production Decisions for a Capital-Constrained Supplier in a Marketplace Platform. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 3547–3570. [Google Scholar] [CrossRef]
- Zhong, Y.G.; Liu, J.; Zhou, Y.W.; Cao, B.; Cheng, T.C.E. Robust contract design and coordination under consignment contracts with revenue sharing. Int. J. Prod. Econ. 2022, 253, 108543. [Google Scholar] [CrossRef]
- Xu, B.; Huang, J.T.; Zhang, X.D.; Alejandro, T.B. Strategic Third-Party Product Entry and Mode Choice under Self-Operating Channels and Marketplace Competition: A Game-Theoretical Analysis. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 73–94. [Google Scholar] [CrossRef]
- Gu, D.; Yao, Z.; Zhou, W. Proportional Fee vs. Unit Fee: Competition, Welfare, and Incentives. J. Ind. Econ. 2022, 70, 999–1032. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Hou, P.W. Fixed Fee or Proportional Fee? Contracts in Platform Selling Under Asymmetric Information. Int. J. Electron. Commer. 2022, 26, 245–275. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zhao, J.J.; Wang, J.C.; Lai, F.J. Strategic Choice of Commission Formats in a Supply Chain with a Platform and Competing Manufacturers. IEEE Trans. Eng. Manag. 2023, 71, 9661–9678. [Google Scholar] [CrossRef]
- Avinadav, T.; Levy, P. Contracting under information superiority in a supply chain of subscription-based apps: A comparative analysis. Ann. Oper. Res. 2025, 344, 721–757. [Google Scholar] [CrossRef]
- He, Y.; Chen, L.D.; Mu, J.J.; Ullah, A. Optimal contract design for live streaming shopping in a manufacturer-retailer-streamer supply chain. Electron. Commer. Res. 2024, 24, 1071–1093. [Google Scholar] [CrossRef]
- Abhishek, V.; Jerath, K.; Zhang, Z.J. Agency Selling or Reselling? Channel Structures in Electronic Retailing. Manag. Sci. 2016, 62, 2259–2280. [Google Scholar] [CrossRef]
- Wang, C.Y.; Sun, J.C.; Shi, S.Y.; Cheng, T.C.E. Third-party sellers’ selling formats and advertising competition on e-commerce platforms. Transp. Res. Part E Logist. Transp. Rev. 2025, 194, 103945. [Google Scholar] [CrossRef]
- Shen, Y.L.; Willems, S.P.; Dai, Y. Channel Selection and Contracting in the Presence of a Retail Platform. Prod. Oper. Manag. 2019, 28, 1173–1185. [Google Scholar] [CrossRef]
- Geng, X.J.; Tan, Y.L.; Wei, L. How Add-on Pricing Interacts with Distribution Contracts. Prod. Oper. Manag. 2018, 27, 605–623. [Google Scholar] [CrossRef]
- Hou, P.W.; Zhen, Z.Y.; Li, B. Implications of the Product Quality Differentiation on the Platform’s Distribution Contracts. IEEE Trans. Eng. Manag. 2023, 70, 3826–3835. [Google Scholar] [CrossRef]
- Zennyo, Y. Strategic contracting and hybrid use of agency and wholesale contracts in e-commerce platforms. Eur. J. Oper. Res. 2020, 281, 231–239. [Google Scholar] [CrossRef]
- Llanes, G.; Ruiz-Aliseda, F. Private contracts in two-sided platforms. Rand J. Econ. 2021, 52, 815–838. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Cao, Q.N.; He, X.L. Contract and product quality in platform selling. Eur. J. Oper. Res. 2019, 272, 928–944. [Google Scholar] [CrossRef]
- Xu, X.P.; Yan, L.L.; Choi, T.M. Platform Operations with Consumer Returns Windows: Reselling Mode Versus Marketplace Mode. IEEE Trans. Eng. Manag. 2024, 71, 3250–3265. [Google Scholar] [CrossRef]
- Li, X.F.; Ma, S.J.; Zhang, Z. Friends or Foes? The Effect of IoT Platform Entry into Smart Device Market Under Quantity Discount Pricing Contract. IEEE Trans. Eng. Manag. 2024, 71, 10984–10997. [Google Scholar] [CrossRef]
- Avinadav, T.; Chernonog, T.; Fruchter, G.E.; Prasad, A. Contract design when quality is co-created in a supply chain. Eur. J. Oper. Res. 2020, 286, 908–918. [Google Scholar] [CrossRef]
- Rong, J.X.; Wang, D.Z. Contracting in hierarchical platforms. Econ. Lett. 2023, 226, 111079. [Google Scholar] [CrossRef]
- Avinadav, T.; Chernonog, T.; Meilijson, I.; Perlman, Y. A consignment contract with revenue sharing between an app developer and a distribution platform. Int. J. Prod. Econ. 2022, 243, 108322. [Google Scholar] [CrossRef]
- Chen, S.J.; Tang, Z.B. The Impact of Enterprise Digital Capability on Supply Chain Digitalization—From the Perspective of Supply Chain Cooperation. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 3051–3066. [Google Scholar] [CrossRef]
- van Beusekom-Thoolen, P.; Holmes, P.; Jansen, W.; Vos, B.; de Boer, A. Interdisciplinary challenges associated with rapid response in the food supply chain. Supply Chain. Manag. Int. J. 2024, 29, 444–459. [Google Scholar]
- Biswas, I.; Gupta, R.; Tiwari, S.; Talluri, S. Multi-echelon supply chain coordination: Contract sequence and cut-off policies. Int. J. Prod. Econ. 2023, 259, 108823. [Google Scholar] [CrossRef]
- Jia, J.; Letizia, P.; Willems, S.P. Supply chain coordination with information design. Decis. Sci. 2024, 55, 149–158. [Google Scholar] [CrossRef]
- Wu, C.; Li, K.; Shi, T. Supply chain coordination with two-part tariffs under information asymmetry. Int. J. Prod. Res. 2017, 55, 2575–2589. [Google Scholar] [CrossRef]
- Chi, K.X.; Yan, F.; Zhang, C.X.; Wang, J.P. Research on the construction process of supply chain ecosystem led by digital platform enterprises from the perspective of dynamic capability. Supply Chain Manag. Int. J. 2024, 29, 1019–1041. [Google Scholar] [CrossRef]
- Tanveer, U.; Hoang, T.G.; Ishaq, S. Reshaping Global Trade Finance and Supply Chains Through Digital Supply Chain Finance Platforms. J. Bus. Logist. 2025, 46, e70022. [Google Scholar] [CrossRef]
- Wang, X.R.; Zhang, M.; Qi, Y.N.; Wang, Q. Developing supply chain resilience: A supply network perspective. Supply Chain Manag. Int. J. 2025, 30, 353–368. [Google Scholar] [CrossRef]
- Qin, X.H.; Su, Q.; Huang, S.H.; Wiersma, U.J.; Liu, M. Service quality coordination contracts for online shopping service supply chain with competing service providers: Integrating fairness and individual rationality. Oper. Res. 2019, 19, 269–296. [Google Scholar] [CrossRef]
- Xu, X.P.; Zhang, M.; He, P. Coordination of a supply chain with online platform considering delivery time decision. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 101990. [Google Scholar] [CrossRef]
- Cai, Y.J.; Choi, T.M.; Zhang, J.Z. Platform Supported Supply Chain Operations in the Blockchain Era: Supply Contracting and Moral Hazards. Decis. Sci. 2021, 52, 866–892. [Google Scholar] [CrossRef]
- Qu, J.; Hu, B.; Wu, Z.; Meng, C. Market Development and Revenue-Sharing Contract Design for Mobile Game Supply Chains. IEEE Trans. Eng. Manag. 2024, 71, 7207–7226. [Google Scholar] [CrossRef]
- Bian, Y.; Wang, H.; Yan, S.; Han, X. Platform channel strategy of selling format: Effect of asymmetric service information. Transp. Res. Part E Logist. Transp. Rev. 2024, 185, 103508. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, w.; Du, S.; Sun, X. How to achieve targeted advertising with the e-commerce platform’s membership system? Omega 2025, 130, 103156. [Google Scholar] [CrossRef]
- Li, L.; Yan, S.; Peng, S.; Hou, P. The interplay of blockchain and channel structure with consideration of cyber-security in a platform supply chain. Transp. Res. Part E Logist. Transp. Rev. 2025, 197, 104045. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tong, S.L.; Wang, Y.J. Channel Structures of Online Retail Platforms. Manuf. Serv. Oper. Manag. 2022, 24, 1547–1561. [Google Scholar] [CrossRef]
- Vakharia, A.J.; Wang, L. Uniform vs. Retailer-Specific Pricing: Incentive Alignment to Enhance Supply Chain Efficiency. Prod. Oper. Manag. 2014, 23, 1176–1182. [Google Scholar] [CrossRef]
- Xi, X.; Zhang, Y.L. The interplay between marketplace channel addition and pricing strategy in an e-commerce supply chain. Int. J. Prod. Econ. 2023, 258, 108807. [Google Scholar] [CrossRef]
- Ingene, C.A.; Parry, M.E. Bilateral monopoly, identical distributors, and game-theoretic analyses of distribution channels. J. Acad. Mark. Sci. 2007, 35, 586–602. [Google Scholar] [CrossRef]
- Cai, G.S. Channel Selection and Coordination in Dual-Channel Supply Chains. J. Retail. 2010, 86, 22–36. [Google Scholar] [CrossRef]
- Zhang, S.C.; Zhang, J.X. Agency selling or reselling: E-tailer information sharing with supplier offline entry. Eur. J. Oper. Res. 2020, 280, 134–151. [Google Scholar] [CrossRef]
- Hagiu, A.; Wright, J. Marketplace Leakage. Manag. Sci. 2024, 70, 1529–1553. [Google Scholar] [CrossRef]
- Tian, L.; Vakharia, A.J.; Tan, Y.; Xu, Y.F. Marketplace, reseller, or hybrid: Strategic analysis of an emerging E-Commerce model. Prod. Oper. Manag. 2018, 27, 1595–1610. [Google Scholar] [CrossRef]
- Hu, H.G.; Zheng, Q.; Pan, X.A. Agency or Wholesale? The Role of Retail Pass-Through. Manag. Sci. 2022, 68, 7538–7554. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).