Endogenous Quantity Timing Between the Online Retailer and the Third-Party Retailer

Abstract

This paper investigates the strategic interaction between an online retailer (e.g., Amazon) and a third-party retailer (3PR) under sequential and simultaneous quantity competition models. The platform and 3PR simultaneously compete and cooperate with each other. By game-theoretic analysis, we confirm that the degree of competition between the online retailer and the 3PR in the sequential quantity game is lower than that in the simultaneous quantity game. More importantly, when the two retailers’ products are sold on the platform, their profits are both much higher in the sequential quantity game than in the simultaneous quantity game, leading to a win–win situation. Meanwhile, the coexistence of the two retailers’ products on the platform is able to mitigate the double marginal effect between the online retailer and the 3PR and to increase consumer surplus and social welfare. Our results provide operational insights for platform governance and 3PR participation strategies.

1. Introduction

An increasing number of dominant platform-based online retailers, such as Amazon.com and JD.com (one of the largest B2C online retailers in China), not only sell products themselves but also allow third-party retailers (3PRs) to operate on their retail platforms. For example, there are hundreds of thousands of 3PRs selling products in the JD POP marketplace, whose transactions accounted for about 45% of JD’s total transactions in 2019–2021 [1] Opening a platform has become a popular sales model because it creates two advantages. First, the online retailer is able to increase its profit by charging 3PRs fixed participation or flexible transaction fees. Second, as more 3PRs join the online retailer’s platform, an increased product variety can attract more customers, which helps to increase the online retailer’s market share. With an open platform, JD’s market share in the B2C online retail sector grew from 22.4% in 2013 to 32.5% in 2020 [2,3].

The co-participation of the online retailer and 3PRs in the same retailing platform creates an intricate paradox. On the one hand, they are cooperating partners because the 3PRs join the online retailer’s retailing platform to create more profit for both parties. On the other hand, they are competing rivals because they may fight against each other for the same customers. Therefore, they cooperate and compete with each other simultaneously. This paradox makes it difficult for both parties to find a balance in their relationship, and conflicts can easily arise. For instance, a series of disputes occurred between JD and 3PRs including Three Squirrels, Afu Essential Oil, and Jason Wood [4,5]. This leads to some puzzling questions. What type of strategic relationship should they develop? Should they take initiatives to cooperate with, or compete against the other retailer? How do the different strategic relationships affect the consumer surplus and social welfare?

To answer these questions, we construct two game models in which the degrees of competition between the online retailer and the 3PR are different. In the first model, they simultaneously decide their product quantities, while in the second model, the online retailer decides its quantity before the 3PR. It is well established that in the duopoly market the competition in a simultaneous game is more intense than that in a sequential game under quantity decision [6]. Hamilton and Slutsky [7] and Vives [8] illustrated that in a duopoly quantity competition, the follower in a sequential game would rather play a simultaneous game to get a higher payoff. In the traditional duopoly competition game, the purpose is to defeat rivals and to capture more market share. However, in this paper, the two retailers are not only competitors, but also cooperators. Due to the dual relationship between the two parties, it is unclear which game is more beneficial for each retailer. For the 3PR, does aggressive quantity competition lead to an increased profit? Is passive quantity competition worse than aggressive quantity competition? Should the online retailer adjust its retail price? This study aims to shed light on these vaguely understood questions.

This paper investigates duopoly competition in which competition and cooperation coexist, also known as coopetition [9]. It contributes to the endogenous timing theory, given that the extant endogenous timing theoretical studies often only focus on competition between two parties, while our study focuses on coopetition. Although quantity competition is typically characterized by first-mover advantage, we demonstrate that first-mover advantage no longer exists in the coopetition context. To the best of our knowledge, this is probably the first work to take a cost perspective to study the competition and cooperation between the online retailer and 3PR. It reveals intriguing results of different operational strategies taken by the retailers in e-business, which makes a significant contribution to both operations management and information systems.

2. Literature Review

Since our research is related to issues about online retailers opening their retailing platform, we firstly review the relevant literature. Jiang et al. [10] show that Amazon can strategically learn market demand by analyzing 3PRs’ sales on its platform. Amazon may then cherry-pick the successful products to sell directly [11]. Facing this potential threat, a 3PR may intentionally hide any high demand by lowering its sales. Jiang et al. [10] use a game-theoretic model to analyze this strategic interaction between Amazon and 3PRs and find that it may not always be optimal for Amazon to separate the high-demand 3PR from the low-demand 3PR. Tang et al. [12] study a supplier’s encroachment strategy selection when transitioning from wholesale supply to a marketplace reselling model.

Generally, a 3PR may have its own website, but such an online presence only allows it to access a limited number of customers due to its low visibility and reputation. By contracting with a reputable online retailer to sell their products through the marketplace platform, 3PRs can greatly extend their access to many more customers. Sun and Liu [13] analyze the condition under which a competing 3PR has an incentive to sell its products through an online retailer marketplace platform which also sells substitutable products to the potential consumers. Mantin et al. [14] find that by opening its marketplace platform to 3PRs the online retailer could run into conflict with its upstream suppliers. Interestingly, if the online retailer’s suppliers cannot prevent 3PRs from selling their products on the marketplace platform, the online retailer will rely less on its outside option in generating profit and therefore it will increase the fees charged to 3PRs and soften the competition between the online retailer and its suppliers. As a result, the decreased competition will lead to an increase in profits of suppliers. Chen and Guo [15] indicate that the availability of low-cost advertising through social media or a search engine can be an important driving force for platform openness. Lin et al. [16] examine how the choice between reselling and agency selling models influences a marketplace’s information-sharing strategy.

Prior research is mostly focused on the competition between the online retailer and 3PRs. Yet, competition and cooperation coexist between the online retailer and 3PRs, i.e., there is a coopetition game. Brandenburgur and Nalebuff [9] introduce coopetition in a variety of business relationships between a firm and its customers, suppliers, complementors, or competitors. It is shown that over 50 percent of collaborative relations occur within the same industry or among competitors [17]. Hsu et al. [18] introduce a model in which two competitors form an alliance to purchase a common component from a supplier, yet still compete in selling their end products. Zha et al. [19] and Zhong et al. [11] study the incentive for the online retailer to share demand information with the 3PR. They find when the commission rate is high, regardless of whether product substitutability is high or low, the online retailer tends to share demand information with the 3PR. However, when the commission rate is low, the online retailer is only motivated to share demand information with the 3PR if and only if product substitutability is low. Yu et al. [20] investigate the interaction between information sharing and store brand encroachment for the online retailer. They find that information sharing induces the online retailer to adopt a store brand in reselling mode, but deters the online retailer from introducing a store brand in agency mode. In addition, a large number of case studies and empirical researches have confirmed the presence of the coopetition relationship among firms in a single supply chain or between supply chains [21,22,23].

Our work is also related to an endogenous timing game. It is well known that in duopoly, the player moving first takes first-mover advantage if the two players are identical in a quantity competition game [6]. Damme and Hurkens [24] illustrate that the low-cost firm will emerge as the endogenous Stackelberg leader. Niu et al. [25] investigate how third-party remanufacturers determine optimal capacity investment timing when their primary goal is survival probability maximization. Chen et al. [26] analyze order timing strategies in a cross-border coopetitive supply chain, revealing that both affiliated and non-affiliated retailers may face a prisoner’s dilemma. Zhang et al. [27] examine the interplay between innovation strategies and market-entry timing decisions in competitive fashion supply chains. In this paper, we pay attention to only two Cournot competition games: a simultaneous game and a sequential game with the online retailer as the Stackelberg leader. We only consider the two competition games because the situation with a 3PR retailer as the leader rarely occurs. Actually, acting as a Stackelberg follower is dominated by a Stackelberg leader in the case of the 3PRs.

3. Notation and Assumption

We consider a dominant online retailer, such as Amazon.com or JD.com, which sells products on its platform and also leases its platform to 3PRs by charging a commission for each unit sold. For the sake of concision, this study considers a special situation which involves a dominant platform-based online retailer and a 3PR who sell two vertically differentiated products, respectively.

We assume that consumers are heterogeneous in their willingness to pay for the products. We denote the consumption valuation by $v$. For analytic simplicity, following Ryan et al. [28], we assume that it is uniformly distributed between zero and one. If the 3PR sells its products on the platform, we assume the valuation of consumption to be $\delta v$, where $0<\delta \le 1$. The value of parameter $\delta$ is called the customer acceptance index for the 3PR’s products. This assumption implies that the online retailer’s products take advantage of consumer consumption valuation against the 3PR’s products. In practice, this assumption is reasonable given that the online retailer has strong reputation and high visibility [28]. For each unit sold, the online retailer will incur a cost, $c_O$, but the 3PR will incur the cost $c_{3PR}$. We assume that the 3PR has a selling cost advantage over the online retailer, i.e., $c_{3PR}<c_O$.

Without loss of generality, we normalize this potential market size to one. When the online retailer and the 3PR supply their products at price $p_O$ and $p_{3PR}$, a consumer with valuation $v$ would derive a net surplus of $v-p_O$ from buying the online retailer’s product and derive a net surplus of $\delta v-p_{3PR}$ from buying the 3PR’s product. If consumers can buy from either retailer, their decisions revolve around the comparison of the surplus derived from the online retailer and 3PR. Thus, if $v-p_O\ge \delta v-p_{3PR}$ and $v-p_O\ge 0$, a customer will choose to purchase from the online retailer. On the other hand, if $\delta v-p_{3PR}>v-p_O$ and $\delta v-p_{3PR}\ge 0$, a customer will choose to purchase from the 3PR. Finally, if $\delta v-p_{3PR}<0$ and $v-p_O<0$, a customer will purchase from neither. Based on this utility model, when the online retailer’s product and the retailer’s product coexist on the platform, the demand expressions for their products are, respectively,

$$Q_O=1-{\displaystyle \frac{p_O-p_{3PR}}{1-\delta }} \mathrm{and} Q_{3PR}={\displaystyle \frac{p_O-p_{3PR}}{1-\delta }}-{\displaystyle \frac{p_{3PR}}{\delta }}.$$

(1)

Therefore, the inverse demand functions are

$$p_O=1-Q_O-\delta Q_{3PR} \mathrm{and} p_{3PR}=\delta \left(1-Q_O-Q_{3PR}\right).$$

(2)

Hence, the online retailer’s product perfectly substitutes for the 3PR’s product. In addition, for each unit sold in the marketplace, the online retailer will charge the 3PR a transaction fee of $T>0$. Then, the profit functions of the online retailer and the 3PR are, respectively,

$${\mathit{\pi }}_O\left(T,Q_O\right)=\left(p_O-c_O\right)Q_O+T{Q}_{3PR} \mathrm{and} {\mathit{\pi }}_{3PR}\left(Q_{3PR}\right)=\left(p_{3PR}-c_{3PR}-T\right)Q_{3PR}.$$

(3)

4. Analysis

In this section, we consider two models: the simultaneous game and the sequential game. In the simultaneous game the move sequence is depicted in Figure 1. The online retailer first sets the per-unit transaction fee $T$ charged to the 3PR, and then they simultaneously choose their quantities, $Q_O$ and $Q_{3PR}$. In the sequential game the move sequence is depicted in Figure 2. Firstly, the online retailer decides the per-unit transaction fee $T$ and retailing quantity $Q_O$. Then, the 3PR decides its retailing quantity $Q_{3PR}$. Duopoly theory posits that the firm that takes actions first generally has first-mover advantage in Cournot competition [6]. This advantage is based on the condition that they solely compete with each other. If they simultaneously compete and cooperate with each other, the first-mover advantage will disappear [6].

4.1. Two Benchmarks

Before fully analyzing the sequential and simultaneous game models, we first introduce two base models: an online retailer monopoly model and a 3PR monopoly model. In the online retailer monopoly model, the online retailer does not open the marketplace to the 3PR and monopolizes the marketplace. In contrast, in the 3PR monopoly model, the online retailer does not sell its product in the marketplace and lets the 3PR monopolize the marketplace. In e-commerce, these two phenomena are common [14]. When the acceptance of the 3PR’s product is very low, the aforementioned competitive models will be reduced to the monopoly model; when the acceptance of the 3PR’s product is very high, the aforementioned competitive models will be degraded to the 3PR monopoly model.

4.1.1. Online Retailer Monopoly Model

In the monopoly model, only the online retailer’s products are provided in the marketplace. When a consumer’s valuation satisfies $v-p_O\ge 0$, they will purchase. Therefore, in this situation the demand for the online retailer’s product is $Q_O=1-p_O$, $0\le p_O\le 1$. Then, the profit of the online retailer is given as a function of $p_O$ as follows:

$${\mathit{\pi }}_O\left(Q_O\right)=Q_O\left(p_O-c_O\right).$$

(4)

Solving $Q_O$, we obtain the optimal quantity $Q_O^M={\displaystyle \frac{1-c_O}{2}}$, which results in the optimal retail price $p_O^M={\displaystyle \frac{1+c_O}{2}}$ and the maximal profit ${\mathit{\pi }}_O^M={\displaystyle \frac{{\left(1-c_O\right)}^2}{4}}$.

4.1.2. PR Monopoly Model

In the 3PR monopoly model, only the 3PR’s products are provided in the marketplace. When a consumer’s valuation satisfies $\delta v-p_{3PR}\ge 0$, they will buy. In a similar way, the demand for the 3PR’s product is $Q_{3PR}=1-{\displaystyle \frac{p_{3PR}}{\delta }}$. In this model, the online retailer first decides the per-unit marketplace transaction $T$, and then the 3PR decides its retailing quantity $Q_{3PR}$. The profits of the two retailers are given, respectively, as follows:

$${\mathit{\pi }}_O\left(T\right)=T{Q}_{3PR} \mathrm{and} {\mathit{\pi }}_{3PR}\left(Q_{3PR}\right)=\left(p_{3PR}-c_{3PR}-T\right)Q_{3PR}.$$

(5)

Using backward induction to solve this game, we can write the equilibrium transaction fee as $T^I={\displaystyle \frac{\delta -c_{3PR}}{2}}$, the equilibrium quantity as $Q_{3PR}^I={\displaystyle \frac{\delta -c_{3PR}}{4\delta }}$, and the equilibrium profits as ${\mathit{\pi }}_O^I={\displaystyle \frac{{\left(\delta -c_{3PR}\right)}^2}{8\delta }}$ and ${\mathit{\pi }}_{3PR}^I={\displaystyle \frac{{\left(\delta -c_{3PR}\right)}^2}{16\delta }}$.

4.2. Simultaneous Quantity Game

We first explore the simultaneous game in which the online retailer and the 3PR simultaneously choose their quantities. There are two stages in the game, and the timing of the events is depicted in Figure 1. In the first stage, the online retailer sets the per-unit marketplace transaction fee $T$ charged to the 3PR. In the second stage, the online retailer and the 3PR simultaneously choose their quantities, $Q_O$ and $Q_{3PR}$. We use backward induction to solve this game.

In the second stage, the online retailer and the 3PR decide the quantities of their products simultaneously to maximize their own profits for a given $T$:

$$\underset{Q_O}{\max }{\mathit{\pi }}_O\left(Q_O|T\right)=\left(1-Q_O-\delta Q_{3PR}-c_O\right)Q_O+T{Q}_{3PR},$$

(6)

$$\underset{Q_{3PR}}{\max }{\mathit{\pi }}_{3PR}\left(Q_{3PR}|T\right)=\left(\delta \left(1-Q_O-Q_{3PR}\right)-c_{3PR}-T\right)Q_{3PR}.$$

(7)

The optimal quantities are obtained for the second stage quantity game as follows:

$$Q_O\left(T\right)={\displaystyle \frac{2-\delta +c_{3PR}+T-2c_O}{4-\delta }},$$

(8)

$$Q_{3PR}\left(T\right)={\displaystyle \frac{\delta +\delta c_O-2c_{3PR}-2T}{\delta \left(4-\delta \right)}}.$$

(9)

In the first stage, the online retailer will anticipate the 3PR’s response. Therefore, substituting the above two equations into ${\mathit{\pi }}_O$, the optimal transaction fee $T$ by maximizing ${\mathit{\pi }}_O$ is

$$T^S={\displaystyle \frac{8\delta -3{\delta }^2-4\left(2-\delta \right)c_{3PR}-{\delta }^2{c}_O}{2\left(8-3\delta \right)}}.$$

(10)

Substituting the transaction fee from Equation (10) into Equations (8) and (9) yields the equilibrium retail quantities $Q_O^S$ and $Q_{3PR}^S$. Then, continuing to substitute $T^S$, $Q_O^S$, and $Q_{3PR}^S$ in Equations (6) and (7) yields the retailers’ profits ${\mathit{\pi }}_O^S$ and ${\mathit{\pi }}_{3PR}^S$.

Theorem 1. 

There exist two customer acceptance thresholds of the 3PR, $\underset{˜}{\delta }$ and $\tilde{\delta }$, labeled as 3PR entry threshold and online retailer exit threshold in the marketplace in the simultaneous game, respectively:

$$\underset{˜}{\delta }={\displaystyle \frac{c_{3PR}}{c_O} \mathit{and} }$$

$$\tilde{\delta }={\displaystyle \frac{\left(\left(1-c_O\right)\left(7+c_O\right)+3c_{3PR}\right)-2\sqrt{\left(1+c_O^2\right){\left(1-c_O\right)}^2-6c_{3PR}\left(1-5c_O\right)\left(1+3c_O\right)}}{3}.}$$

The details of the proof can be found in Appendix A.

Theorem 1 indicates that when the acceptance of the 3PR’s product exceeds $c_{3PR}/c_O$, the online retailer will allow the 3PR to sell products on its platform. Although the 3PR’s product might impede the sales of the online retailer’s product, the online retailer will be compensated for the sales loss by the transaction charges. However, when the acceptance of the 3PR’s product exceeds $\tilde{\delta }$, the online retailer’s product will be literally exiled from the marketplace. In this situation, the online retailer is better off completely withdrawing its products from the marketplace, allowing the 3PR to monopolize the marketplace. Finally, when acceptance of the 3PR’s product is low, the transaction fee will deter the 3PR from entering the marketplace.

The equilibrium prices, quantities, transaction fees, and profits are presented in

Table 1. The equilibrium decisions and profits in the simultaneous quantity game.

Equilibrium decisions and profits	$0\le \delta \le \underset{˜}{\delta }$	$\underset{˜}{\delta }<\delta <\tilde{\delta }$	$\tilde{\delta }\le \delta \le 1$
Online retailer’s price $p_O^S$	${\displaystyle \frac{1+c_O}{2}}$	${\displaystyle \frac{1+c_O}{2}}-{\displaystyle \frac{\delta c_O-c_{3PR}}{8-3\delta }}$	N/A
3PR’s price $p_{3PR}^S$	N/A	${\displaystyle \frac{\delta +c_{3PR}}{2}}+{\displaystyle \frac{\left(4-\delta \right)\left(\delta c_O-c_{3PR}\right)}{2\left(8-3\delta \right)}}$	${\displaystyle \frac{3\delta +c_{3PR}}{4}}$
Online retailer’s quantity $Q_O^S$	${\displaystyle \frac{1-c_O}{2}}$	${\displaystyle \frac{\left(8-3\delta \right)+2c_{3PR}-\left(8-\delta \right)c_O}{2\left(8-3\delta \right)}}$	N/A
3PR’s quantity $Q_{3PR}^S$	N/A	${\displaystyle \frac{2\delta c_O-2c_{3PR}}{\delta \left(8-3\delta \right)}}$	${\displaystyle \frac{\delta -c_{3PR}}{4\delta }}$
Transaction fee $T^S$	N/A	${\displaystyle \frac{\delta }{2}}-{\displaystyle \frac{4\left(2-\delta \right)c_{3PR}+{\delta }^2{c}_O}{2\left(8-3\delta \right)}}$	${\displaystyle \frac{\delta -c_{3PR}}{2}}$
Online retailer’s profit ${\mathit{\pi }}_O^S$	${\displaystyle \frac{{\left(1-c_O\right)}^2}{4}}$	${\displaystyle \frac{{\left(1-c_O\right)}^2}{4}}+{\displaystyle \frac{{\left(\delta c_O-c_{3PR}\right)}^2}{\delta \left(8-3\delta \right)}}$	${\displaystyle \frac{{\left(\delta -c_{3PR}\right)}^2}{8\delta }}$
3PR’s profit ${\mathit{\pi }}_{3PR}^S$	N/A	${\displaystyle \frac{4{\left(\delta c_O-c_{3PR}\right)}^2}{\delta {\left(8-3\delta \right)}^2}}$	${\displaystyle \frac{{\left(\delta -c_{3PR}\right)}^2}{16\delta }}$

.

4.3. Sequential Quantity Game

The only difference between the sequential quantity game and the simultaneous quantity game exhibits itself when both retailers’ products are sold on the same platform. In the sequential quantity game, the online retailer first sets the marketplace transaction fee $T$ and the retailing quantity $Q_O$, and then the 3PR decides its quantity $Q_{3PR}$. We use backward induction to solve this game.

In the second stage, the 3PR decides the quantity of its products to maximize its own profit for a given $Q_O$ and $T$ as follows:

$$\underset{Q_{3PR}}{\max }{\mathit{\pi }}_{3PR}\left(Q_{3PR}|Q_O,T\right)=\left(\delta \left(1-Q_O-Q_{3PR}\right)-c_{3PR}-T\right)Q_{3PR}.$$

(11)

From the first-order condition, the 3PR’s quantity is generated for a given $Q_O$ and $T$:

$$Q_{3PR}\left(Q_O,T\right)={\displaystyle \frac{\delta \left(1-Q_O\right)-c_{3PR}-T}{2\delta }}.$$

(12)

In the second stage, the online retailer can anticipate the 3PR’s response and try to obtain the optimal $T$ and $Q_O$ by maximizing ${\mathit{\pi }}_O$ by substituting $Q_{3PR}\left(Q_O,T\right)$ into ${\Pi }_O$:

$$Q_O^O={\displaystyle \frac{\left(2-\delta \right)+c_{3PR}-2c_O}{2\left(2-\delta \right)}},$$

(13)

$$T^O={\displaystyle \frac{\delta -c_{3PR}}{2}}.$$

(14)

Substituting $Q_O^O$ and $T^O$ into $Q_{3PR}\left(Q_O,T\right)$, we can obtain the 3PR’s equilibrium retail quantity $Q_{3PR}^O$. Then, substituting Equations (13) and (14) and $Q_{3PR}^O$ in ${\mathit{\pi }}_O$ and ${\mathit{\pi }}_{3PR}$ yields the retailers’ profits ${\mathit{\pi }}_O^O$ and ${\mathit{\pi }}_{3PR}^O$.

Theorem 2. 

There exists a customer acceptance of the 3PR, $\underset{⌣}{\delta }$, called 3PR entry threshold in the sequential game:

$$\underset{⌣}{\delta }={\displaystyle \frac{c_{3PR}}{c_O}.}$$

However, in the sequential game, the online retailer’s product will never be exiled from the marketplace.

Unlike the simultaneous game, there are only two possible situations in the sequential game. When the acceptance of the 3PR’s product is less than $c_{3PR}/c_O$, the online retailer will not allow the 3PR to join its marketplace, whereas when the acceptance of the 3PR’s product exceeds $c_{3PR}/c_O$, the online retailer will allow the 3PR to sell its products on the retail platform. In the sequential quantity game, the online retailer’s product will never be exiled from the marketplace. We will analyze the reason in the following lemma:

Lemma 1. 

$\underset{˜}{\delta }=\underset{⌣}{\delta }$, and there is an exit threshold for the online retailer in the simultaneous game but not in the sequential game.

The thresholds of 3PR entry are the same in the two games. In fact, if the online retailer has central control over both product sales in the marketplace, the threshold of the 3PR’s product is also (for details see Appendix A). This can be explained as follows: When the acceptance of the 3PR’s product is less than $c_{3PR}/c_O$, retailing of the 3PR’s product on the marketplace will cannibalize the demand of the online retailer’s product but not improve the profit of the marketplace. When the acceptance of the 3PR’s product is moderate, $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$, the entry of the 3PR’s product into the marketplace poses no threat to the online retailer. In addition, the transaction fee increases the online retailer’s revenue. However, when the acceptance of the 3PR’s product is high, $\delta \ge \tilde{\delta }$, the 3PR’s product is effectively substituted for the online retailer’s product. At this time, the 3PR has great power in the market. If a simultaneous game is played between the online retailer and the 3PR, then the competition between the two retailers is fiercer. Therefore, in order to avoid a huge loss, the online retailer is better off exiting the market. If a sequential game is played between them, the competition between them is weak. The equilibrium prices, quantities, transaction fees, and profits are shown in

Table 2. The equilibrium decisions and profits in the sequential quantity game.

Equilibrium decisions and profits	$0\le \delta \le \underset{⌣}{\delta }$	$\underset{⌣}{\delta }<\delta \le 1$
Online retailer’s price $p_O^O$	${\displaystyle \frac{1+c_O}{2}}$	${\displaystyle \frac{1+c_O}{2}}$
3PR’s price $p_{3PR}^O$	N/A	${\displaystyle \frac{\delta \left(2-\delta \right)+\left(1-\delta \right)c_{3PR}+\delta c_O}{2\left(2-\delta \right)}}$
Online retailer’s quantity $Q_O^O$	${\displaystyle \frac{1-c_O}{2}}$	${\displaystyle \frac{\left(2-\delta \right)+c_{3PR}-2c_O}{2\left(2-\delta \right)}}$
3PR’s quantity $Q_{3PR}^O$	N/A	${\displaystyle \frac{\delta c_O-c_{3PR}}{2\delta \left(2-\delta \right)}}$
Transaction fee $T^O$	N/A	${\displaystyle \frac{\delta -c_{3PR}}{2}}$
Online retailer’s profit ${\mathit{\pi }}_O^O$	${\displaystyle \frac{{\left(1-c_O\right)}^2}{4}}$	${\displaystyle \frac{{\left(1-c_O\right)}^2}{4}}+{\displaystyle \frac{{\left(\delta c_O-c_{3PR}\right)}^2}{4\delta \left(2-\delta \right)}}$
3PR’s profit ${\mathit{\pi }}_{3PR}^O$	N/A	${\displaystyle \frac{{\left(\delta c_O-c_{3PR}\right)}^2}{4\delta {\left(2-\delta \right)}^2}}$

.

5. Simultaneous Game vs. Sequential Game

Based on the results summarized in previous sections, some interesting observations can be made.

Theorem 3. 

(1) 

If $\delta \in [0,\underset{˜}{\delta }]$, the online retailer monopolizes the market, and its prices in the two games are equal to the monopoly price, $p_O^S=p_O^O=p_O^M$.

(2) 

If $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$, both retailers’ products are sold on the platform, and the prices satisfy the following relations: $p_O^S<p_O^O=p_O^C$ and $p_{3PR}^C<p_{3PR}^S<p_{3PR}^O$. ($p_O^C$ and $p_{3PR}^C$ are the prices of the online retailer and the 3PR in a centralized decision model. See

Table A1. The optimal decisions and profits in the centralized decision model.

Equilibrium decisions and profits	$0\le \delta \le \underset{\_}{\delta }$	$\underset{\_}{\delta }<\delta <\overline{\delta }$	$\overline{\delta }\le \delta \le 1$
Online retailer’s price $p_O^C$	${\displaystyle \frac{1+c_O}{2}}$	${\displaystyle \frac{1+c_O}{2}}$	N/A
3PR’s price $p_{3PR}^C$	N/A	${\displaystyle \frac{\delta +c_{3PR}}{2}}$	${\displaystyle \frac{\delta +c_{3PR}}{2}}$
Online retailer’s quantity $Q_O^C$	${\displaystyle \frac{1-c_O}{2}}$	${\displaystyle \frac{\left(1-\delta \right)+c_{3PR}-c_O}{2\left(1-\delta \right)}}$	N/A
3PR’s quantity $Q_{3PR}^C$	N/A	${\displaystyle \frac{\delta c_O-c_{3PR}}{2\delta \left(1-\delta \right)}}$	${\displaystyle \frac{\delta -c_{3PR}}{2\delta }}$
The system’s profit ${\mathit{\pi }}^C$	${\displaystyle \frac{{\left(1-c_O\right)}^2}{4}}$	${\displaystyle \frac{{\left(1-c_O\right)}^2}{4}}+{\displaystyle \frac{{\left(\delta c_O-c_{3PR}\right)}^2}{4\delta \left(1-\delta \right)}}$	${\displaystyle \frac{{\left(\delta -c_{3PR}\right)}^2}{4\delta }}$

in Appendix A for details.) Moreover, the differences between $p_O^O$ and $p_O^S$ as well as $p_{3PR}^O$ and $p_{3PR}^S$ increase when $\delta$ increases.

(3) 

If $\delta \in [\tilde{\delta },1]$, both retailers’ products are sold on the platform in the sequential game, but only the 3PR’s product is sold on the platform in the simultaneous game. The prices satisfy the following relations: $p_O^O=p_O^C$ and $p_{3PR}^C<p_{3PR}^O<p_{3PR}^S$.

Intuitively, the competition in the simultaneous game is more intense than that in the sequential game. Theorem 3 (2) confirms this conjecture. Therefore, both retail prices in the simultaneous game are lower than those in the sequential game. The classical microeconomics theory reveals that the follower’s payoff in the Stackelberg game will be lower than that in the simultaneous game; hence, the follower is motivated to simultaneously announce its strategy with the online retailer. Moreover, with the increase in the acceptance of the 3PR’s product, the 3PR has more power, and the competition between the two retailers becomes increasingly greater in the simultaneous game.

The 3PR will raise the price of its product when the online retailer withdraws products from the marketplace. After the online retailer leaves the marketplace, the 3PR becomes a monopolist in the market and can charge a higher monopoly price. The marketplace transaction fee becomes the only source of revenue for the online retailer. In this situation, the online retailer will increase the marketplace transaction fee, i.e., $T^I-T^S={\displaystyle \frac{\delta \left(\delta c_O-c_{3PR}\right)}{2\left(8-3\delta \right)}}>0$. Consequently, the operational cost for 3PR heightens, which drives up the 3PR’s product price.

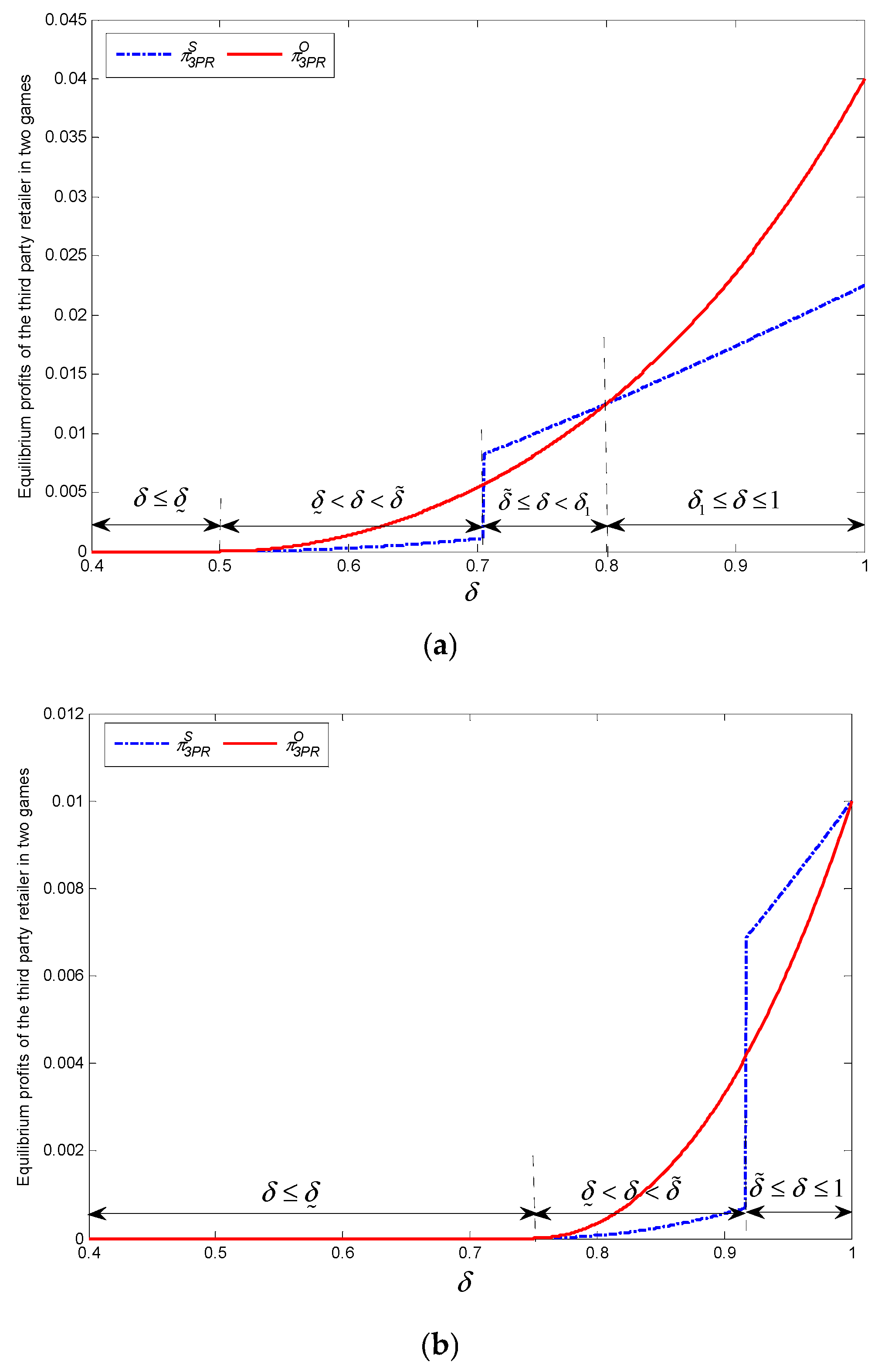
For easy characterization, we denote the 3PR’s relative cost advantage as $\kappa ={\displaystyle \frac{c_O-c_{3PR}}{1-c_O}}$. The larger the value of $\kappa$, the greater cost advantage the 3PR has. $\kappa$ is useful in characterizing the conditions that determine which quantity game is preferred by the online retailer or 3PR, or has higher consumer surplus or social welfare.

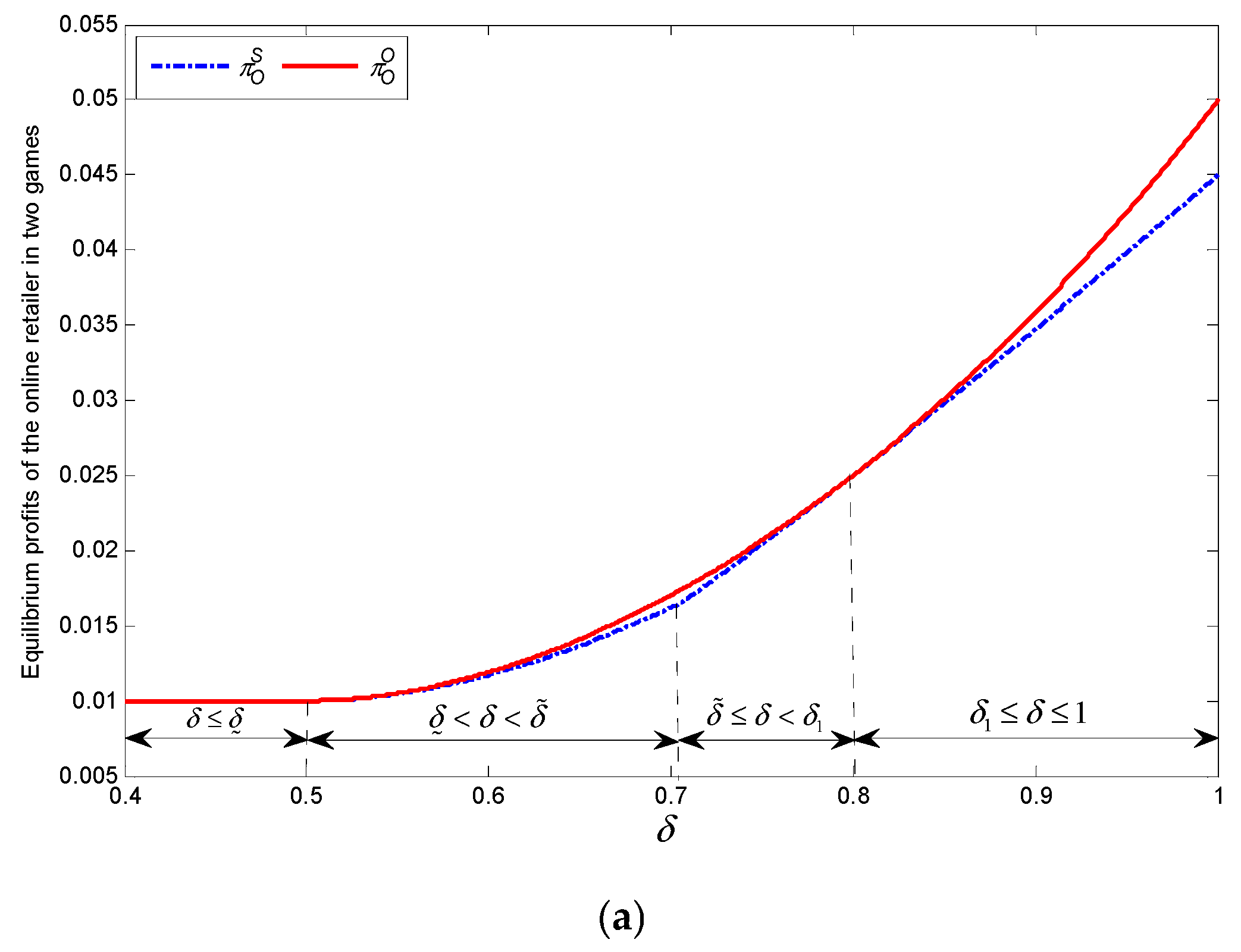
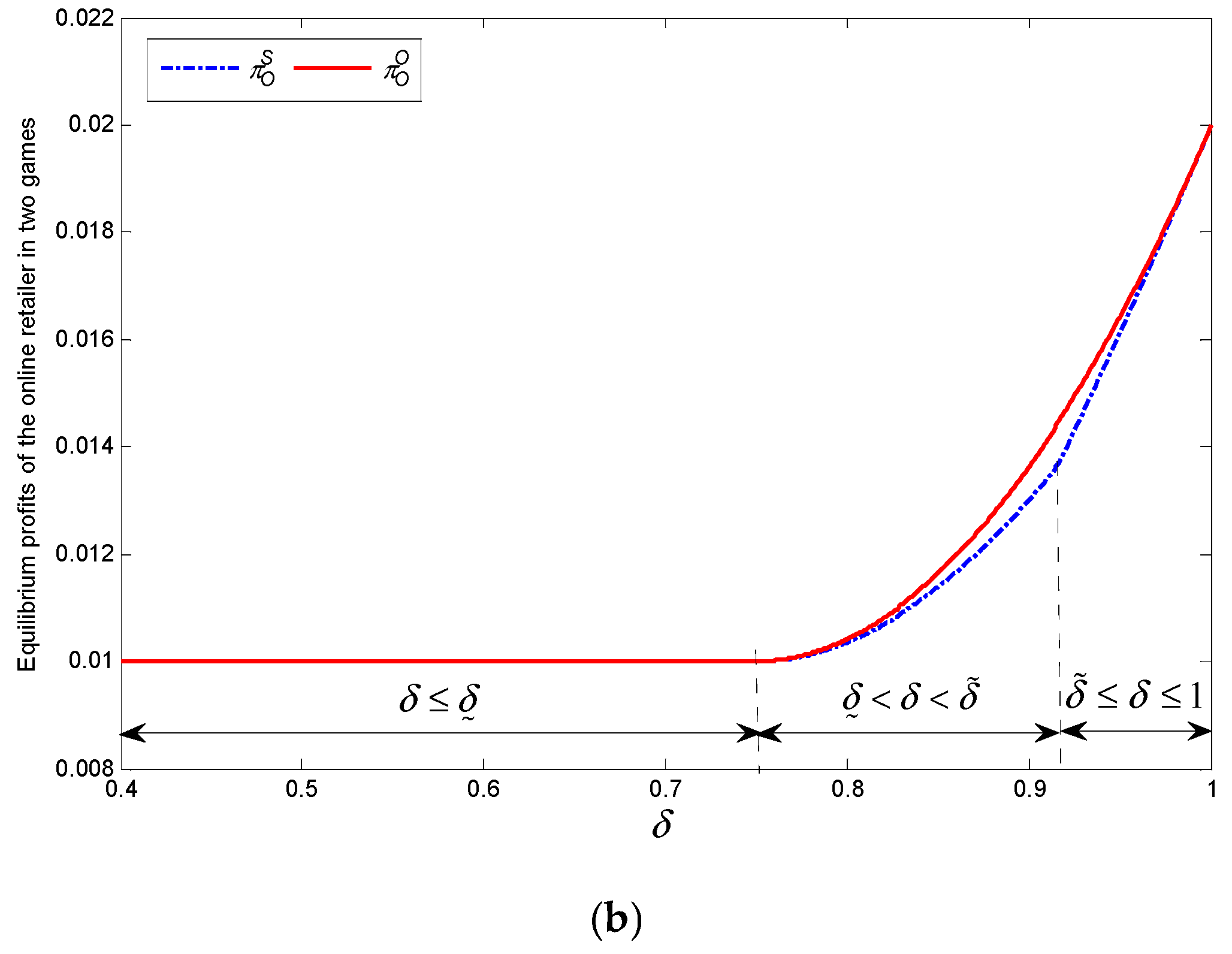
Theorem 4. 

(1) 

Regardless of the level of the acceptance of the 3PR’s product, the online retailer’s profit satisfies the following relation: ${\mathit{\pi }}_O^O\ge {\mathit{\pi }}_O^S$.

(2) 

If $\kappa \le 1$, when $\delta \in \left[0,\underset{˜}{\delta }\right]$, the 3PR’s profit satisfies the following relation: ${\mathit{\pi }}_{3PR}^O={\mathit{\pi }}_{3PR}^S=0$; when $\delta \in \left(\underset{˜}{\delta },1\right]$, the 3PR’s profit satisfies the following relation: ${\mathit{\pi }}_{3PR}^O\le {\mathit{\pi }}_{3PR}^S$. If $\kappa >1$, when $\delta \in \left[0,\underset{˜}{\delta }\right]$, the 3PR’s profit satisfies the following relation: ${\mathit{\pi }}_{3PR}^O={\mathit{\pi }}_{3PR}^S=0$; when $\delta \in \left[{\delta }_1,1\right]$ or $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$, the 3PR’s profit satisfies the following relation: ${\mathit{\pi }}_{3PR}^O\ge {\mathit{\pi }}_{3PR}^S$; when $\delta \in [\underset{˜}{\delta },{\delta }_1)$, the 3PR’s profit satisfies the following relation: ${\mathit{\pi }}_{3PR}^O<{\mathit{\pi }}_{3PR}^S$, where ${\delta }_1=2+c_{3PR}-2c_O$.

Based on classical economic theory, the follower’s profit in the sequential game will be lower than the profit it could obtain in the simultaneous game of quantity competition. Therefore, the follower is motivated to simultaneously announce its strategy with its leader to attain a higher profit. Counterintuitively, this prediction does not hold in this paper. This is largely due to the coopetition relationship between the online retailer and the 3PR. When acceptance of the 3PR’s product is sufficiently low, the online retailer completely controls the market by its product advantage and transaction fee. In this situation, the 3PR will be better off playing a submissive role; otherwise the online retailer can punish the 3PR by reducing the retail price. When the acceptance of the 3PR’s product is sufficiently high, the 3PR will achieve a large amount of profit by using cost advantage. At the same time, the online retailer’s profit is also increased by sharing the 3PR’s revenue. In this situation, the online retailer relies heavily on the 3PR. If the 3PR employs an active competition strategy, the two retailers will fall into a simultaneous quantity game, which could lead to a lose–lose situation. To avoid this pitfall, the online retailer needs to proactively withdraw its products from the marketplace.

Corollary 1. 

When the two products both sell on the platform, the two retailers achieve a win–win situation if a sequential quantity competition game is played.

We illustrate the findings in Figure 3 and Figure 4. We choose two parameter value groups as follows: $\left\{c_O=0.8,c_{3PR}=0.4\right\}$ and $\left\{c_O=0.8,c_{3PR}=0.6\right\}$. The potential market size is 1, and the acceptance of the 3PR’s product ranges from 0.4 to 1.0.

Theorem 5. 

When the 3PR’s product enters the marketplace, the online retailer will lower its retail price in the simultaneous game but not in the sequential game. Moreover, the 3PR will raise the retail price when the online retailer withdraws its product from the platform.

Proof. 

When the 3PR is not in the marketplace, the price of the online retailer’s product is ${\displaystyle \frac{1+c_O}{2}}$. If a simultaneous quantity game is played, the online retailer will set the retail price as ${\displaystyle \frac{1+c_O}{2}}-{\displaystyle \frac{\delta c_O-c_{3PR}}{8-3\delta }}$. Therefore, the online retailer lowers its retail pricing in the simultaneous quantity game when the 3PR enters the marketplace. But, if a sequential quantity game is played, the online retailer will keep the retail price as ${\displaystyle \frac{1+c_O}{2}}$. This proves the first point in Theorem 5. Next, we prove the second point. Since only in the simultaneous quantity game will the online retailer possibly withdraw its product from the platform, we will discuss the change of retail price of the 3PR’s product when the online retailer withdraws its product from the platform. When the two retailers’ products both sell on the platform in the simultaneous quantity game, the retail price of the 3PR’s product is ${\displaystyle \frac{\delta +c_{3PR}}{2}}+{\displaystyle \frac{\left(4-\delta \right)\left(\delta c_O-c_{3PR}\right)}{2\left(8-3\delta \right)}}$. But, when the online retailer withdraws its product from the platform, the 3PR monopolizes the marketplace and raises its retail price to ${\displaystyle \frac{3\delta +c_{3PR}}{4}}$. □

When the 3PR enters the online retailer’s marketplace, how should the online retailer respond to the competition from the 3PR? This theorem suggests that no matter how competitive the 3PR’s product is, the online retailer need not adjust its pricing if the online retailer is the first mover in the quantity game. However, if the two retailers engage in a simultaneous game, the online retailer will lower its retail price as a response to the competition from the 3PR. This theorem means that, in the sequential game, the online retailer effectively controls the 3PR by taking first-mover advantage. However, this balance will be broken by the intense competition between them if they play a simultaneous game. The online retailer will proactively withdraw its products from the marketplace to avoid excessive competition. In this situation, the 3PR will raise the retail price, and the dual marginal effect becomes the key factor that influences the total profit of the marketplace.

Theorem 6. 

When the two retailers both sell products on the platform, the marketplace transaction fee satisfies the following relation: $T^S<T^O$. If the online retailer exits the marketplace, the marketplace transaction fee satisfies the following relation: $T^S=T^O$.

The online retailer charges the 3PR a lower transaction fee in the simultaneous game than in the sequential game. This is counterintuitive, because the competition in the simultaneous game is more intense than in the sequential game and the intuitive choice is that the online retailer should charge a higher transaction fee in the simultaneous game. In fact, the marginal profit per-unit product for the 3PR is lower in the simultaneous game than in the sequential game. Let ${\gamma }^S=p_{3PR}^S-T^S-c_{3PR}$ and ${\gamma }^O=p_{3PR}^O-T^O-c_{3PR}$, respectively. By simple algebra, ${\gamma }^O>{\gamma }^S$ is obtained. Moreover, notice that the partial derivative satisfies $\partial \left({\gamma }^O-{\gamma }^S\right)/\partial \delta >0$, which illustrates that the difference between the two marginal profits monotonically increases with increasing $\delta$. But, if the online retailer exits from the marketplace, the transaction fee becomes the only source of the online retailer’s profit. In this situation, the online retailer will raise the transaction fee to $T^S=T^O$. Facing the increased transaction fee and having monopoly power in the marketplace, the 3PR will increase its retail price, resulting in ${\gamma }^O<{\gamma }^S$.

Corollary 1. 

In the simultaneous quantity competition game, when the online retailer exits the marketplace, the online retailer will increase the transaction fee, and the 3PR’s marginal profit per-unit product is also increased.

6. Consumer Surplus

Following Örsdemir et al. [29], we denote consumer surplus as

$$CS={\displaystyle {\int }_{1-Q_O-Q_{3PR}}^{1-Q_O}\left(\delta v-p_{3PR}\right)dv}+{\displaystyle {\int }_{1-Q_O}^1\left(v-p_O\right)dv},$$

where ${\displaystyle {\int }_{1-Q_O-Q_{3P}}^{1-Q_O}\left(\delta v-p_{3PR}\right)dv}$ represents the surplus from consumption of the 3PR’s product and ${\displaystyle {\int }_{1-Q_O}^1\left(v-p_O\right)dv}$ represents the surplus from consumption of the online retailer’s product. In addition to the situation where the two retailers’ products coexist in the marketplace, two other situations need to be considered: only the online retailer’s product or the 3PR’s product is in the marketplace. When only the online retailer’s products are in the marketplace, the consumer surplus is denoted as $CS={\displaystyle {\int }_{1-Q_O}^1\left(v-p_O\right)dv}$. When only the 3PR’s products are in the marketplace, the consumer surplus is denoted as $CS={\displaystyle {\int }_{1-Q_O-Q_{3PR}}^{1-Q_O}\left(\delta v-p_{3PR}\right)dv}$.

Theorem 7. 

(1) 

If $\kappa \le 1$, when $\delta \in \left[0,\underset{˜}{\delta }\right]$, the consumer surplus satisfies the following relation: $C{S}^S=C{S}^O=C{S}^M$ ($C{S}^M$ is the consumer surplus in the online retailer monopoly model; see the proof of Theorem 7 in Appendix A for details); when $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$, the consumer surplus satisfies the following relation: $C{S}^S\ge C{S}^O\ge C{S}^M$; when $\delta \in \left[\tilde{\delta },1\right]$, the consumer surplus satisfies the following relation: $C{S}^O\ge C{S}^M>C{S}^S$.

(2) 

If $\kappa >1$, when $\delta \in \left[0,\underset{˜}{\delta }\right]$, the consumer surplus satisfies the following relation: $C{S}^S=C{S}^O=C{S}^M$; when $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$ or $\delta \in \left[{\delta }_1,1\right]$, the consumer surplus satisfies the following relation: $C{S}^S\ge C{S}^O\ge C{S}^M$; when $[\tilde{\delta },{\delta }_1)$, the consumer surplus satisfies the following relations: $C{S}^O\ge C{S}^S$ and $C{S}^O\ge C{S}^M$.

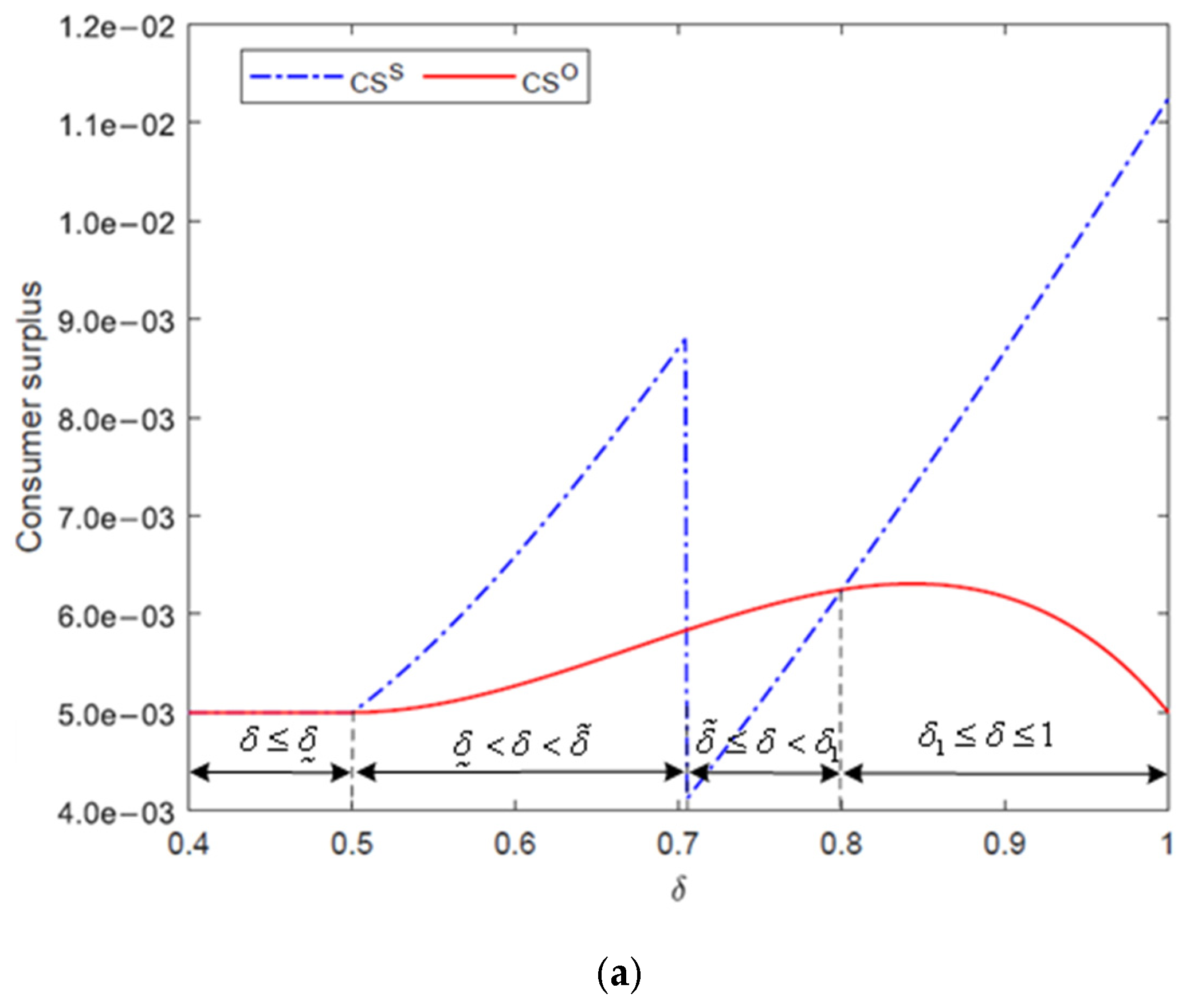
Theorem 7 indicates that competition is always beneficial to consumers. When the two retailers compete against each other in quantity, the consumers will be better off. When two similar products are sold in the same marketplace, the quantity competition in the simultaneous game is more intense than in the sequential game. Hence, the prices of both retailers’ products are lower in the simultaneous game than in the sequential game. As shown in Figure 5a,b, in the interval $\underset{˜}{\delta }<\delta <\tilde{\delta }$, the simultaneous game has a higher consumer surplus than the sequential game, and the discrepancy enlarges as the two products become more similar.

However, the drawback is that the online retailer at some point will withdraw its products from the marketplace in the simultaneous game, which will lead to a steep decline in consumer surplus. As shown in Figure 5a,b, the online retailer exits at $\delta$ = 0.70 or 0.91, and the 3PR starts monopolizing and imposes a large price increase after the online retailer’s exit, which leads to the plummeting consumer surplus. In both figures, within the interval ensuing the online retailer’s exit, consumer surplus in the simultaneous game is far below that in the sequential game. However, when $\kappa >1$, as $\delta$ increases to approach 1, which means that the 3PR’s product quality keeps increasing, the simultaneous game’s consumer surplus will gradually grow and exceed the sequential game’s at a certain point (see interval ${\delta }_1\le \delta \le 1$ in Figure 5a). In contrast, when $\kappa \le 1$, the simultaneous game will always have a lower consumer surplus than the sequential game because the 3PR’s cost advantage is too small to expel the online retailer earlier, so that the 3PR has only very limited room for improvement in product quality. As a result, the simultaneous game’s consumer surplus can at best reach the sequential game’s level with the same parameters (Figure 5b).

7. Social Welfare

In this section we investigate social welfare in the two models. We denote social welfare as

$$SW={\mathit{\pi }}_O+{\mathit{\pi }}_{3PR}+CS.$$

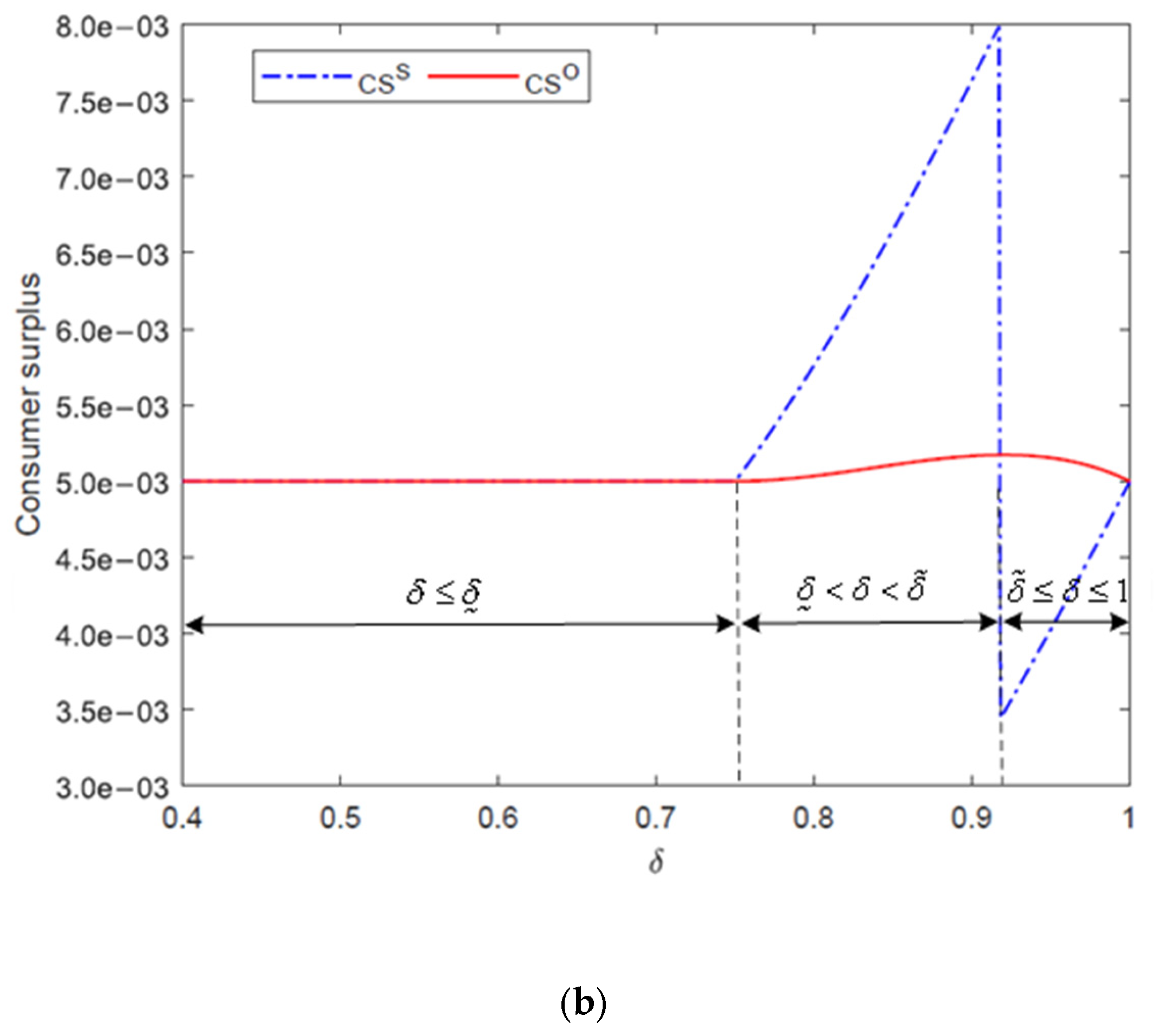
Theorem 8. 

When the two retailers’ products coexist on the platform, the social welfare is higher in the simultaneous game than in the sequential game.

(1) 

In addition, when $\kappa \le {\displaystyle \frac{5}{9}}$, the social welfare satisfies the following relations: for any $\delta$, $S{W}^S\ge S{W}^O\ge S{W}^M$ ($S{W}^M$ is the social welfare in the online retailer monopoly model. For details, see the proof of Theorem 8 in Appendix A).

(2) 

When ${\displaystyle \frac{5}{9}}<\kappa <1$, the social welfare satisfies the following relations: if $\delta \in \left[0,\underset{˜}{\delta }\right]$, $S{W}^S=S{W}^O=S{W}^M$; if $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$ or $\delta \in \left[{\delta }_2,1\right]$, $S{W}^S\ge S{W}^O\ge S{W}^M$; if $\delta \in \left(\tilde{\delta },{\delta }_2\right)$, $S{W}^O\ge S{W}^S\ge S{W}^M$.

(3) 

When $\kappa \ge 1$ the social welfare satisfies the following relations: if $\delta \in \left[0,\underset{˜}{\delta }\right]$, $S{W}^S=S{W}^O=S{W}^M$; if $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$ or $\delta \in \left[{\delta }_2,{\delta }_1\right]$, $S{W}^S\ge S{W}^O\ge S{W}^M$; if $\delta \in \left(\tilde{\delta },{\delta }_2\right)$ or $\delta \in \left({\delta }_1,1\right]$, $S{W}^O\ge S{W}^S\ge S{W}^M$, where

$${\delta }_2={\displaystyle \frac{\left(26+7c_{3PR}-10c_O\right)-\sqrt{{\left(26+7c_{3PR}-10c_O\right)}^2-224\left(3\left(1-c_O\right)+2c_{3PR}\right)}}{14}}.$$

When the two retailers’ products coexist in the marketplace, similar to consumer surplus, social welfare is slightly greater in the simultaneous quantity game than in the sequential quantity game. When the online retailer withdraws its products from the marketplace in the simultaneous game, the relationship becomes more complex. When the relative cost advantage is weak, $\kappa \le {\displaystyle \frac{5}{9}}$, the consumer surplus will rapidly decline, resulting in $S{W}^O\ge S{W}^S$ for $\delta \in \left[\tilde{\delta },1\right]$. When the relative cost advantage is moderate, ${\displaystyle \frac{5}{9}}<\kappa <1$, $S{W}^O\ge S{W}^S$ only for $\delta \in \left(\tilde{\delta },{\delta }_1\right)$; and if $\delta \in \left[{\delta }_1,1\right]$, $S{W}^S\ge S{W}^O$. When the online retailer withdraws its products, the price of the 3PR’s product is very high due to the dual marginal effect. Therefore, the consumer surplus will become very low. However, when $\delta$ becomes large, the consumer surplus gradually increases in the simultaneous game but does not increase, or even decreases, in the sequential game. For this reason, the social welfare in the simultaneous game is more than that in the sequential game. Finally, when the relative cost advantage is very significant, $\kappa \ge 1$, the social welfare is higher in the sequential game than in simultaneous game as a result of the outstanding performance of profit in the sequential game.

8. The Impact of $\kappa$ and $\delta$

We denote the cost advantage of the 3PR as $\kappa ={\displaystyle \frac{c_O-c_{3PR}}{1-c_O}}$. A larger $\kappa$ means that the 3PR has a larger cost advantage. The magnitude of $\delta$ not only reflects consumers’ acceptance of the 3PR’s product relative to the online retailer’s product, but also indicates the extent to which the 3PR’s product can substitute for the online retailer’s product. The values of $\kappa$ and $\delta$ essentially determine which game the online retailer and 3PR will prefer: the simultaneous or the sequential quantity game. They also determine which game leads to greater consumer surplus and social welfare. $\kappa =1$ is a critical threshold condition. When $\kappa \le 1$, the 3PR has no obvious cost advantage over the online retailer. Yet, when $\kappa >1$, the 3PR has a clear cost advantage. By the same token, $\delta \in \left(\underset{˜}{\delta },\tilde{\delta }\right)$, $\delta \in \left(\tilde{\delta },{\delta }_1\right)$, and $\delta \in [{\delta }_1,1]$ represent the conditions for weak, medium, and strong substitutability, respectively. If $\delta \in \left[0,\underset{˜}{\delta }\right]$, the online retailer will deny the entry of the 3PR. Since only the online retailer’s products exist on the platform, there is no preference problem in this condition.

$\kappa$ and $\delta$ have influence on the 3PR’s and the online retailer’s game strategy. As we showed earlier, regardless of consumers’ acceptance of the 3PR’s products, the online retailer always prefers the sequential quantity game; i.e., ${\Pi }_O^O\ge {\Pi }_O^S$ is always true. Although when $\kappa <1$, ${\mathit{\pi }}_O^O>{\mathit{\pi }}_O^S$, when $\kappa >1$, the online retailer has equal preference for the two games, i.e., ${\Pi }_O^O={\Pi }_O^S$, when a special criterion is met: $\delta =2+c_{3PR}-2c_O<1$. As for the 3PR, $\kappa$ and $\delta$ could heavily influence the 3PR’s game preference. When $\kappa <1$, the 3PR has weak cost advantage. If consumers’ acceptance of the 3PR’s product is low, the optimal choice for the 3PR is to be a follower (choosing the sequential quantity game). But if consumers’ acceptance of the 3PR’s product is moderate or high, the 3PR will receive higher profits by playing the simultaneous quantity game. When $\kappa >1$, the 3PR has a strong cost advantage. If consumers’ acceptance of the 3PR’s product is low or very high, the optimal choice for the 3PR is to be a follower (choosing the sequential quantity game). Only if consumers’ acceptance of the 3PR’s product is moderate, i.e., l, $\delta \in \left(\tilde{\delta },{\delta }_1\right)$, the 3PR will receive higher profits by playing the simultaneous quantity game.

In the sequential quantity game, the online retailer will never withdraw its products, and the platform will have products from both the online retailer and the 3PR. The simultaneous quantity game will produce higher consumer surplus, because the prices of both retailers’ products in this game will be lower than those in the sequential quantity game. Given that its business goal is to maximize profits, the online retailer will withdraw its products at a proper time to avoid excessive competition with the 3PR in the simultaneous quantity game. As shown in Theorem 4 and Figure 4, when the 3PR has no obvious cost advantage ($\kappa <1$), the online retailer would withdraw its products when consumers’ acceptance of the 3PR’s products is high. In contrast, when the 3PR has an obvious cost advantage ($\kappa >1$), the online retailer would withdraw its products when consumers’ acceptance of the 3PR’s products is moderate. Once the online retailer exits, the 3PR monopolizes the platform and will raise the prices of its products, as shown by Theorem 3. This monopoly would result in a great decline in consumer surplus (see Figure 5a). However, if the 3PR has an obvious cost advantage ($\kappa >1$) and consumers’ acceptance of the 3PR’s products is high (possibly due to the better quality of the 3PR’s products), the combination of lower price and better quality ($p_{3PR}^S<p_O^O$) will lead to a higher consumer surplus in the simultaneous quantity game than in the sequential quantity game.

$\kappa$ and $\delta$ also influence social welfare, which is the sum of firms’ gross profits and consumer surplus. When $\kappa \le {\displaystyle \frac{5}{9}}$, the 3PR’s cost advantage over the online retailer is low. When ${\displaystyle \frac{5}{9}}<\kappa <1$, the 3PR’s cost advantage over the online retailer is moderate. When $\kappa >1$, the 3PR’s cost advantage over the online retailer is high. As Theorem 8 and Figure 6 indicate, when the 3PR’s cost advantage is low or moderate, the simultaneous quantity game produces higher social welfare. Although, in theory, there is a range $\delta \in (\tilde{\delta },{\delta }_5)$ during which the sequential quantity game produces higher social welfare, this range is very small because $\tilde{\delta }\approx {\delta }_5$. When the 3PR’s cost advantage is high, the simultaneous quantity game will generate greater social welfare if consumers’ acceptance of the 3PR’s product is weak or moderate, and the sequential quantity game will generate greater social welfare if consumers’ acceptance of the 3PR’s product is high.

9. Concluding Remarks

While the opening of an e-commerce platform to 3PRs brings economic benefits to online retailers, it also creates conflicts between online retailers and 3PRs. Different game models can be employed to reflect different competition or cooperation states between the online retailer and the small 3PRs. In this paper, we have developed two quantity competition models: a simultaneous quantity game and a sequential quantity game with the online retailer as the leader. In the simultaneous quantity game, the online retailer and the 3PR simultaneously decide their quantities, but in the sequential quantity game the online retailer has the priority to decide its quantity first. Our analysis provides interesting insights into the research and practice of online retailing.

Firstly, we find the thresholds of 3PR entry are the same in the two games. Besides, by charging the 3PR transaction fees, the online retailer effectively controls the 3PR when acceptance of the latter’s product is very low. However, the online retailer probably has to withdraw from the platform in the simultaneous quantity game because when the acceptance of the 3PR’s product is high, the 3PR is too powerful to compete against. Therefore, in order to avoid losses due to intense competition, the online retailer will exit the market at some point in the simultaneous game. While in the sequential quantity game, the online retailer’s product and the 3PR’s product always coexist in the market harmoniously.

In the simultaneous quantity game the entry of the 3PR’s product causes reduction of the online retailer’s retail price, but in the sequential quantity game the online retailer keeps the price constant. This suggests that in the sequential quantity game, the online retailer dominates by charging transaction fees and having the privilege to decide its quantity first. Therefore, the entry of the 3PR does not create a threat to the online retailer. But when the acceptance of the 3PR’s product continuously increases, the 3PR can reduce the profit of the online retailer. The online retailer will withdraw its product from the platform if they fall into a simultaneous quantity competition game. In the sequential quantity competition game, the competition is mild and the online retailer will not withdraw its products from the market.

The most interesting result is that both the online retailer and the 3PR gain more profit in the sequential quantity game than in the simultaneous quantity game, leading to a win–win situation, because in the sequential quantity game the competition between the two retailers is mild, and the relationship between them is mainly cooperation-based. The absence of intense competition allows more benefits to be generated and shared by both retailers.

Finally, we examine consumer surplus and social welfare in the two game models. No matter in which game, the entry of the 3PR’s product increases consumer surplus and social welfare. However, the consumer surplus and social welfare are greater in the simultaneous quantity game than in the sequential quantity game when these two retailers’ products are sold on the marketplace. These results suggest that the high profits are at the expense of consumer surplus, and lead to low social welfare.

Our research suggests that online retailers, such as Amazon.com and JD.com, do not change the prices of their products after the entry of the 3PR’s products. The online retailers and 3PRs can reap more profits in the sequential quantity game than in the simultaneous quantity game when the substitutability between the 3PR’s products and the online retailer’s products is either very high or very low. When the substitutability is moderate, conflicts between the two players will likely occur, and a compensatory strategy can be applied to keep the balance. This finding has significant implications for both online retailers who open their platforms to 3PRs and 3PRs who participate in an online retailer’s platform. It suggests that in order to keep the coopetition between the two parties productive, a subtle mutual understanding needs to be developed so that a low level of competition is maintained between the two parties. A viable approach to make this possible is to let the online retailer keep its leadership role in the online marketplace while the 3PRs play a follower’s role. The online retailer needs to maintain a more powerful position than the 3PRs so that a suitable balance between cooperation and competition can be achieved. If the two parties possess similar power, the competition will be too intense to allow productive cooperation to take place. As a result, both parties will suffer from a profit decline.

We examine the impact of different timing sequences on quantity competition decisions between e-commerce platforms and third-party retailers, yielding several interesting and meaningful findings while acknowledging certain limitations that warrant future research. First, our analysis employs a deterministic demand function, whereas real-world firms typically face uncertain demand. Future studies should incorporate uncertainty characteristics into the demand function. Second, the current model considers only one third-party retailer, while actual e-commerce platforms typically serve thousands or even hundreds of thousands of retailers. Even for a single product category, dozens of retailers often compete simultaneously. Therefore, extending the model to incorporate multiple third-party retailers represents an important direction for future research. Third, our current framework adopts a single-period model, whereas in reality the competitive–cooperative interactions between e-commerce platforms and third-party retailers occur repeatedly over time. Consequently, developing a multi-period model would better reflect real-world market dynamics. These extensions would significantly enhance the model’s practical relevance and theoretical contributions.