Application of Benford’s Law on Cryptocurrencies
Abstract
:1. Introduction
- Mining transactions (mostly with mining pools) for all cryptocurrency assets that are based on the Proof of Work (PoW) [7] consensus mechanism, by which the cryptocurrency blockchain network achieves distributed consensus. Mining pools, where most of the miners are concentrated, pay out rewards to miners based on the computing power contributed. The payouts are mostly scheduled to occur once the miner is owed more than the threshold to save up on transaction fees. As many miners keep the default threshold, many transactions are possibly of the same value;
- Default transaction fees (GAS) are the same. GAS refers to the pricing value required to successfully conduct a transaction or execute a contract on the Ethereum blockchain platform.
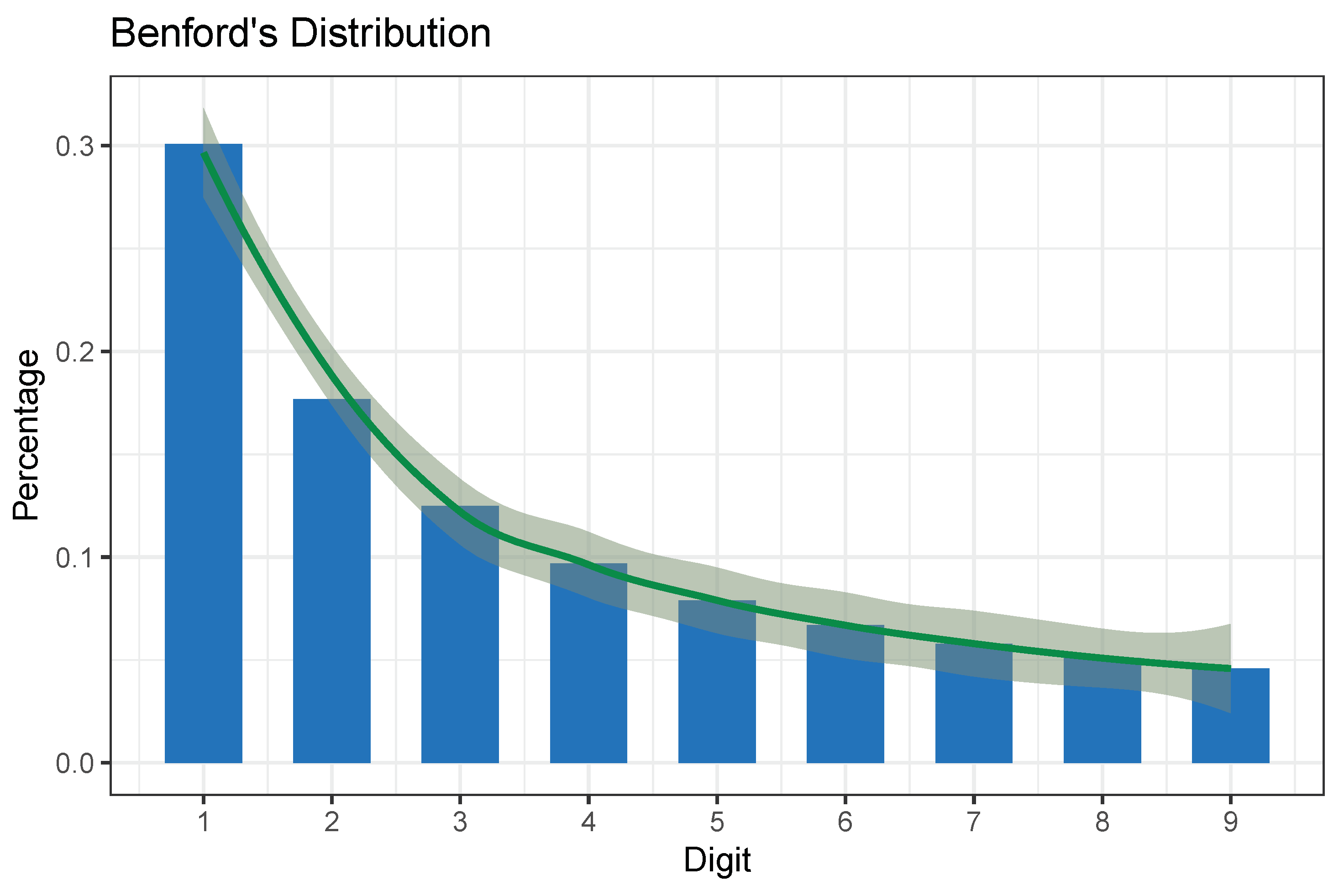
2. Benford’s Law
- Data with values from several distributions;
- Data that has a wide variety in the number of digits (e.g., data with plenty of values in the hundreds, thousands, tens of thousands, etc.);
- A data set that is fairly large, as a rule of a thumb consisting of at least 50–100 observations [10], although usually thousands of observations;
- Data is right-skewed (i.e., the mean is greater than the median), and the distribution has a long right-tail rather than being symmetric;
- Data has no predefined maximum or minimum value (with the exception of a zero minimum).
3. State of the Art
4. Methodology
4.1. Methods
- Take all major cryptocurrencies into consideration;
- Express all aggregated daily transactions in one currency—we selected USD ($) as the most used fiat currency in comparisons;
- Select a viable observation period:
- –
- Starting date for each currency was the date of the first successful transaction;
- –
- Ending date for the observation period was set long enough into the past so that the frauds or abnormal behavior were well documented (in the forms of lawsuits, scandals, vanished cryptocurrencies, well-documented special properties of specific currencies). We selected the year as the end of 2018, almost three years in the past;
- –
- A long enough observation period that makes Benford’s law conformity observation feasible (as presented in Section 2). In the body of surveyed literature, the sample size varies from 200 [33] to a few hundred thousand. We opted for doubling the minimum sample size—selecting all cryptocurrencies with 400 or more transaction days;
- –
- –
- Perform a literature review for all the currencies that do not conform to Benford’s law and establish if there are any abnormalities documented for the selected time frame.
- Conformity (0.000);
- Acceptable conformity (0.006);
- Marginally acceptable conformity (0.012);
- Nonconformity (0.015 and above).
The Criteria That the Objects under Scrutiny Must Meet
- The ledger must have support querying for transactions that contain the sending address, receiving address, amount, and timestamp;
- The assets being transferred must be denominated in any universally comparable form (any fiat currency (i.e., US Dollars) meets this criterion) at the time of transfer.
4.2. Materials
5. Results
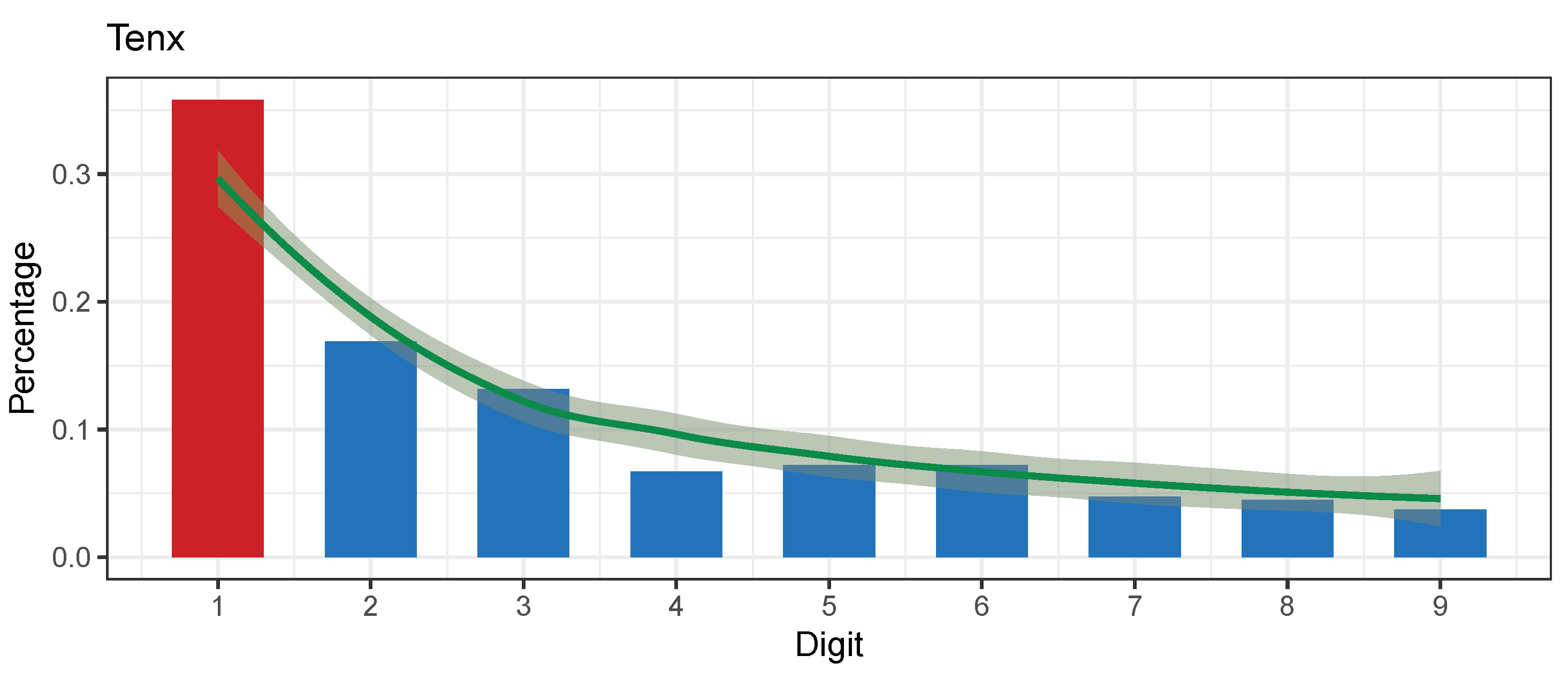
5.1. TENX Token (TENX)
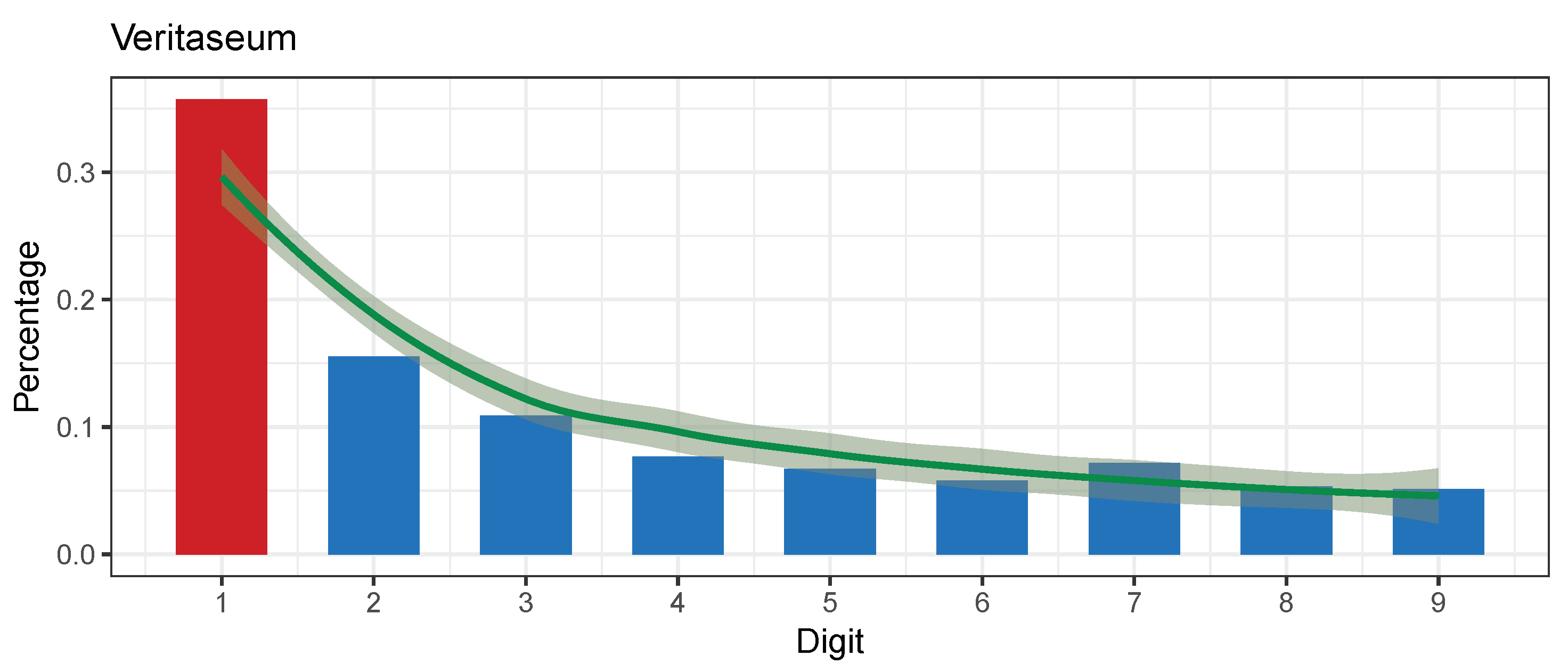
5.2. Veritaseum (VERI)
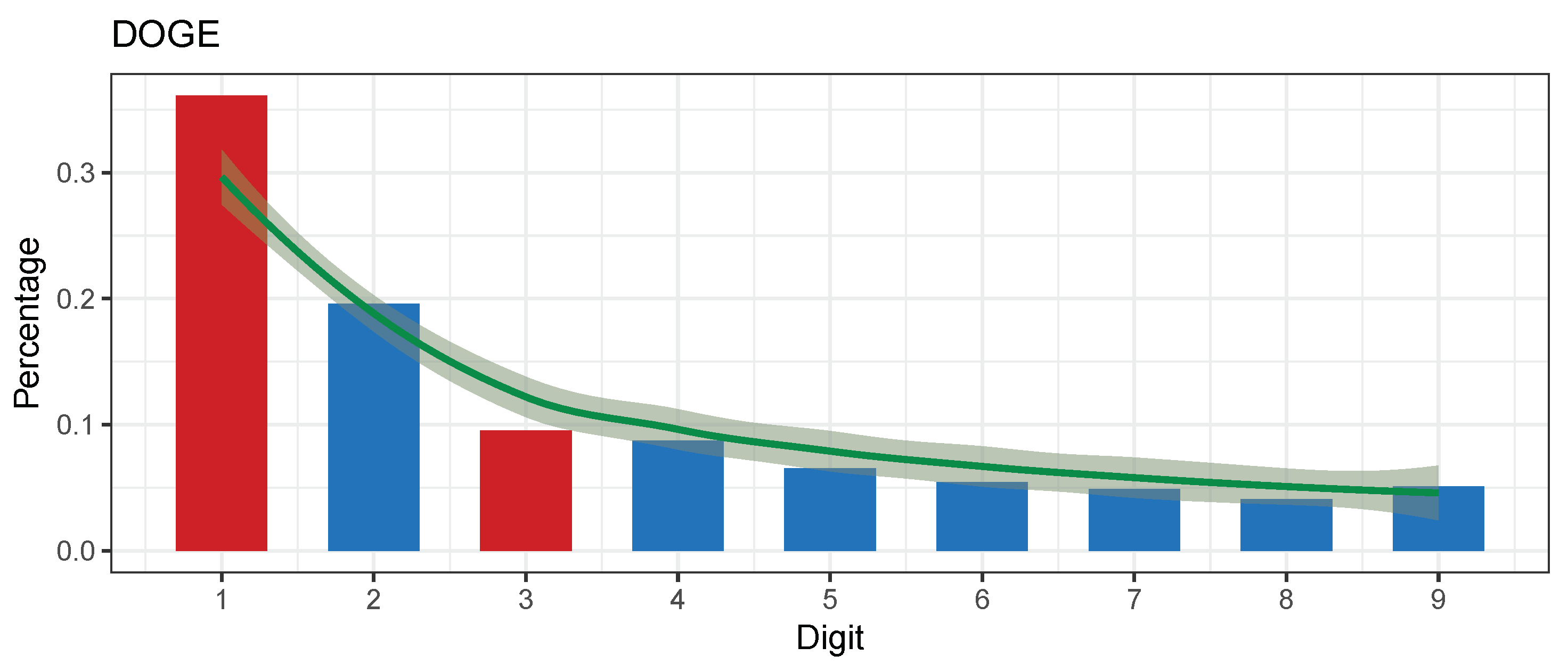
5.3. Dogecoin (DOGE)
- On the 24 September 2018 (a randomly chosen date on a working day at the end of our observation period): the last tweet from the official Tweeter account on 14 July 2018 (80 days) (Dogecoin twitter account: https://twitter.com/Dodgecoin accessed on 1 March 2021);
- Fun and friendly internet currency, the dogecoin logo is a dog from a meme;
- 24 h trading volume on all exchanges according to CoinCodex (Concodex: https://coincodex.com/crypto/XXX/exchanges/ accessed on 1 March 2021) was USD 42.51 million dollars.
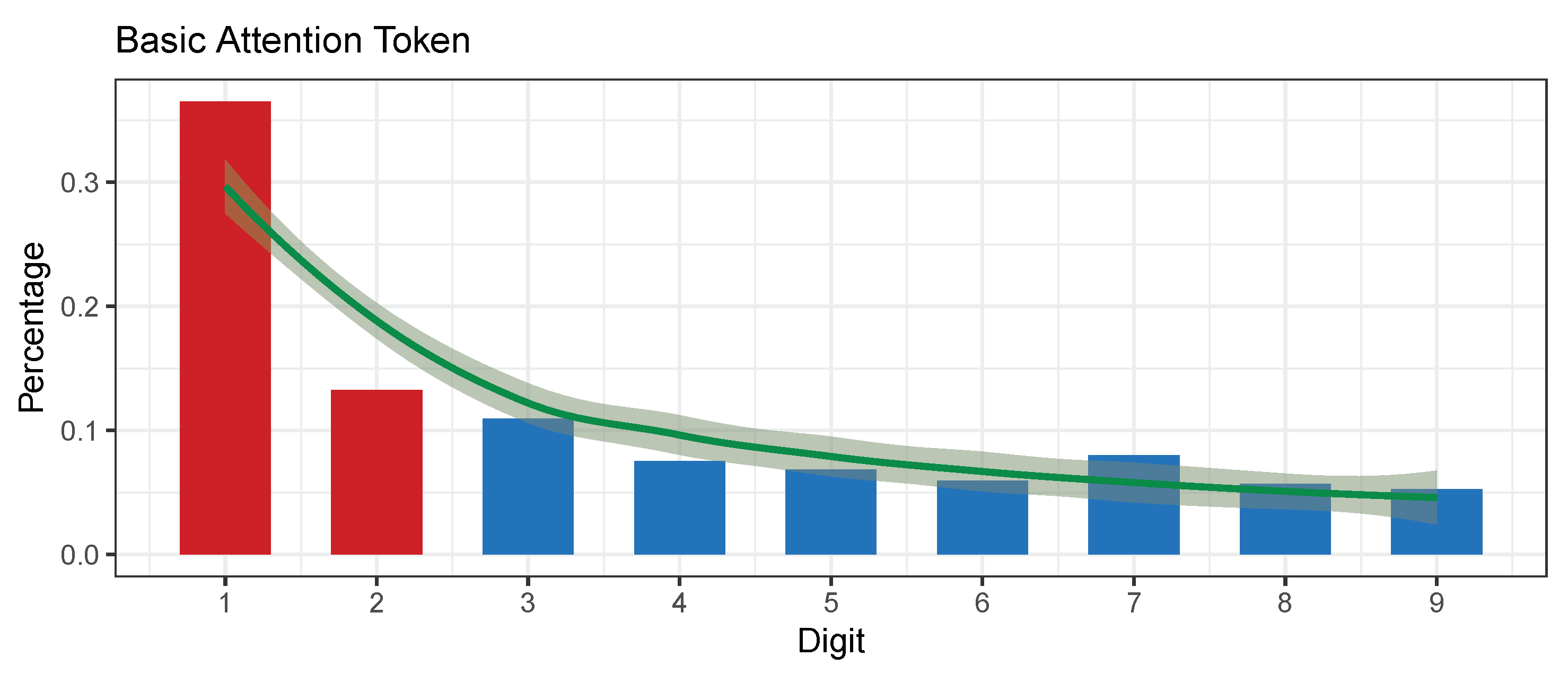
5.4. Basic Attention Token (BAT)
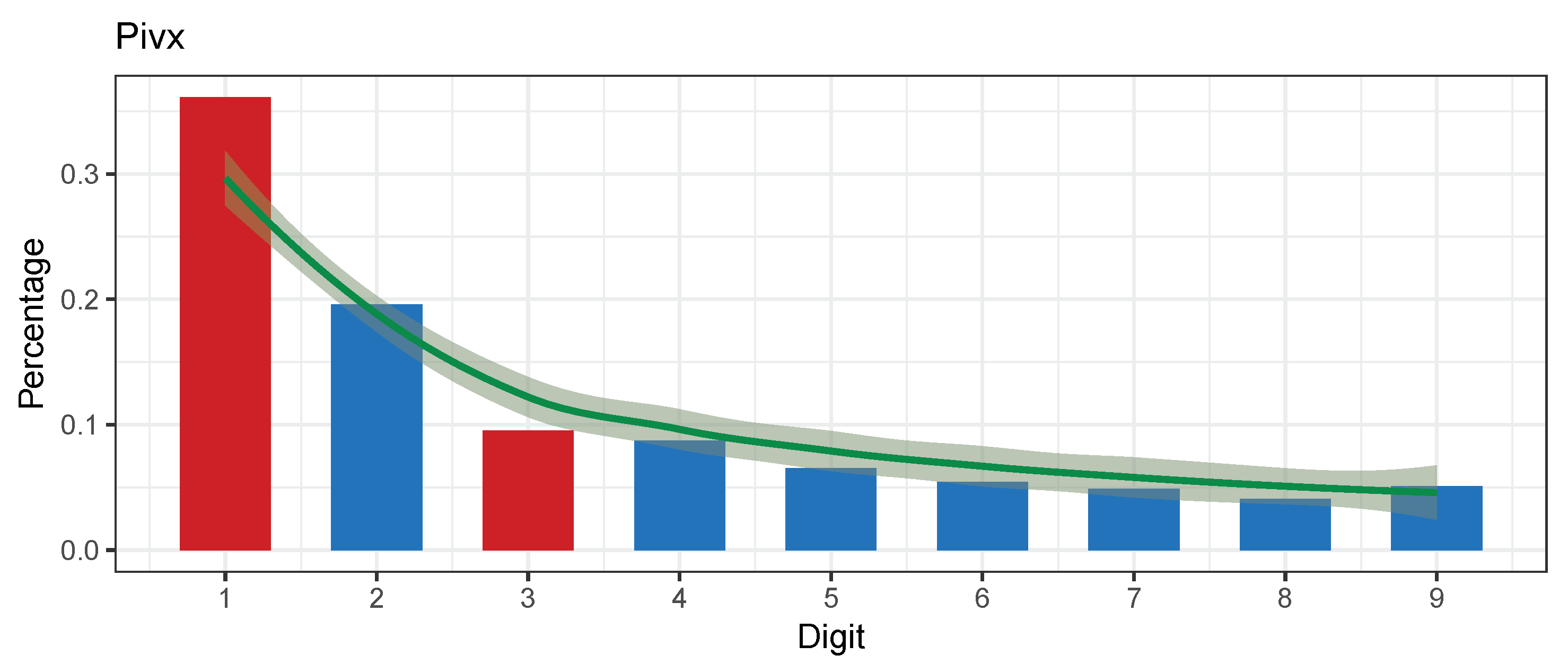
5.5. PIVX (PIVX)
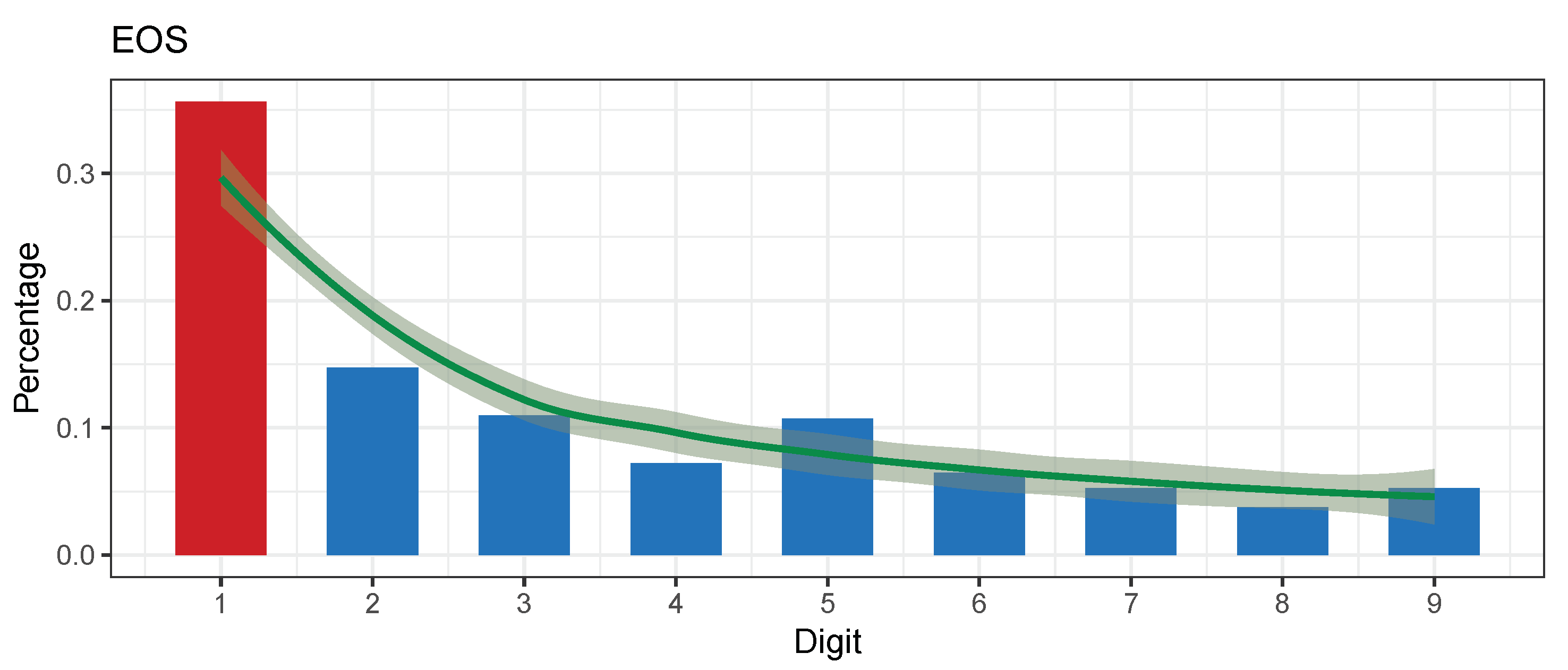
5.6. EOS (EOS)
5.7. Additional Currencies
6. Discussion and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benford, F. The law of anomalous numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Lansky, J. Possible state approaches to cryptocurrencies. J. Syst. Integr. 2018, 9, 19–31. [Google Scholar] [CrossRef]
- Noether, S. Ring SIgnature Confidential Transactions for Monero. IACR Cryptol. ePrint Arch. 2015, 2015, 1098. [Google Scholar]
- Mettler, M. Blockchain technology in healthcare: The revolution starts here. In Proceedings of the 2016 IEEE 18th International Conference on e-Health Networking, Applications and Services (Healthcom), Munich, Germany, 14–16 September 2016; pp. 1–3. [Google Scholar]
- Campbell-Verduyn, M. Bitcoin, crypto-coins, and global anti-money laundering governance. Crime Law Soc. Chang. 2018, 69, 283–305. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin Whitepaper. Technical Report. 2008. Available online: Bitcoin.org (accessed on 1 March 2021).
- Jakobsson, M.; Juels, A. Proofs of work and bread pudding protocols. In Secure Information Networks; Jakobsson, M., Juels, A., Eds.; Springer: Leuven, Belgium, 1999; pp. 258–272. [Google Scholar]
- Newcomb, S. Note on the Frequency of Use of the Different Digits in Natural Numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef] [Green Version]
- Singleton, T.W. IT Audit Basics: Understanding and Applying Benford’s Law. Isaca J. 2011, 3, 6. [Google Scholar]
- Kenny, D.A. Measuring Model Fit. 2015. Available online: http://davidakenny.net/cm/fit.htm (accessed on 1 March 2021).
- Berger, A.; Hill, T.P. A basic theory of Benford’s Law. Probab. Surv. 2011, 8, 1–126. [Google Scholar] [CrossRef]
- Fewster, R.M. A Simple Explanation of Benford’s Law. Am. Stat. 2009, 63, 26–32. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.; Bhattacharya, S. Detecting the dubious digits: Benford’s law in forensic accounting. Significance 2007, 4, 81–83. [Google Scholar] [CrossRef]
- Nigrini, M.J. Audit sampling using Benford’s law: A review of the literature with some new perspectives. J. Emerg. Technol. Account. 2017, 14, 29–46. [Google Scholar] [CrossRef]
- Drake, P.D.; Nigrini, M.J. Computer assisted analytical procedures using Benford’s Law. J. Account. Educ. 2000, 18, 127–146. [Google Scholar] [CrossRef]
- Durtschi, C.; Hillison, W.; Pacini, C. The effective use of Benford’s law to assist in detecting fraud in accounting data. J. Forensic Account. 2004, 5, 17–34. [Google Scholar]
- Cleary, R.; Thibodeau, J.C. Applying Digital Analysis Using Benford’s Law to Detect Fraud: The Dangers of Type I Errors. Audit. J. Pract. Theory 2005, 24, 77–81. [Google Scholar] [CrossRef]
- Hickman, M.J.; Rice, S.K. Digital Analysis of Crime Statistics: Does Crime Conform to Benford’s Law? J. Quant. Criminol. 2010, 26, 333–349. [Google Scholar] [CrossRef]
- Burke, J.; Kincanon, E. Benford’s law and physical constants: The distribution of initial digits. Am. J. Phys. 1991, 59, 952. [Google Scholar] [CrossRef]
- Zhang, J. Testing Case Number of Coronavirus Disease 2019 in China with Newcomb-Benford Law. arXiv 2020, arXiv:2002.05695. [Google Scholar]
- Baum, S.C. Cryptocurrency Fraud: A Look into the Frontier of Fraud. Ph.D. Thesis, Georgia Southern University, Statesboro, GA, USA, 2018. [Google Scholar]
- Zuckoff, M. Ponzi’s Scheme: The True Story of a Financial Legend; Random House Incorporated: New York, NY, USA, 2006. [Google Scholar]
- Twomey, D.; Mann, A. Fraud and manipulation within cryptocurrency markets. In Corruption and Fraud in Financial Markets: Malpractice, Misconduct and Manipulation; Alexander, C., Cumming, D., Eds.; Wiley: Hoboken, NJ, USA, 2020; pp. 205–250. [Google Scholar]
- Gao, B.; Wang, H.; Xia, P.; Wu, S.; Zhou, Y.; Luo, X.; Tyson, G. Tracking Counterfeit Cryptocurrency End-to-end. Proc. ACM Meas. Anal. Comput. Syst. 2020, 4, 1–28. [Google Scholar] [CrossRef]
- Brown, S.D. Cryptocurrency and criminality: The Bitcoin opportunity. Police J. 2016, 89, 327–339. [Google Scholar] [CrossRef]
- Brenig, C.; Müller, G. Economic Analysis of Cryptocurrency Backed Money Laundering; ECIS 2015 Completed Research Papers; Association for Information Systems: Atlanta, GA, USA, 2015; pp. 1–18. [Google Scholar]
- Farrugia, S.; Ellul, J.; Azzopardi, G. Detection of illicit accounts over the Ethereum blockchain. Expert Syst. Appl. 2020, 150, 113318. [Google Scholar] [CrossRef] [Green Version]
- Sayadi, S.; ben Rejeb, S.; Choukair, Z. Anomaly Detection Model Over Blockchain Electronic Transactions. In Proceedings of the 2019 15th International Wireless Communications Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 895–900. [Google Scholar] [CrossRef]
- Baek, H.; Oh, J.; Kim, C.Y.; Lee, K. A Model for Detecting Cryptocurrency Transactions with Discernible Purpose. In Proceedings of the 2019 Eleventh International Conference on Ubiquitous and Future Networks (ICUFN), Zagreb, Croatia, 2–5 July 2019; pp. 713–717. [Google Scholar] [CrossRef]
- Kamišalić, A.; Kramberger, R.; Fister, I. Synergy of Blockchain Technology and Data Mining Techniques for Anomaly Detection. Appl. Sci. 2021, 11, 7987. [Google Scholar] [CrossRef]
- Shi, J.; Ausloos, M.; Zhu, T. Benford’s law first significant digit and distribution distances for testing the reliability of financial reports in developing countries. Phys. A Stat. Mech. Its Appl. 2018, 492, 878–888. [Google Scholar] [CrossRef] [Green Version]
- Fischer, R.A. Statistical Methods for Research Workers; Oliver and Boyd: Edinburgh, UK, 1925. [Google Scholar]
- Carslaw, C.A. Anomalies in income numbers: Evidence of goal oriented behavior. Account. Rev. 1988, 63, 321–327. [Google Scholar]
- Gorard, S. Revisiting a 90-year-old debate: The advantages of the mean deviation. Br. J. Educ. Stud. 2005, 53, 417–430. [Google Scholar] [CrossRef]
- Nigrini, M.J.M.J. Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection; Wiley: Hoboken, NJ, USA, 2012; p. 352. [Google Scholar]
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef] [Green Version]
- Berger, V.W.; Zhou, Y. Kolmogorov–Smirnov Test: Overview; Wiley Statsref: Statistics Reference Online: Hoboken, NJ, USA, 2014. [Google Scholar]
- Freedman, L.S. Watson’s UN2 statistic for a discrete distribution. Biometrika 1981, 68, 708–711. [Google Scholar] [CrossRef]
- Nigrini, M. Digital Analysis Using Benford’s Law: Tests and Statistics for Auditors. EDPACS 2001, 28, 1–2. [Google Scholar] [CrossRef]
- Druică, E.; Oancea, B.; Vâlsan, C. Benford’s law and the limits of digit analysis. Int. J. Account. Inf. Syst. 2018, 31, 75–82. [Google Scholar] [CrossRef]
- Alexander, J.C. Remarks on the Use of Benford’s Law. 2009. Available online: http://dx.doi.org/10.2139/ssrn.1505147 (accessed on 1 March 2021).
- Livni, E. Serious money is flowing to the joke cryptocurrency Dogecoin. New York Times, 2 August 2021; pp. 1–2. [Google Scholar]
- Somin, S.; Gordon, G.; Altshuler, Y. Network analysis of erc20 tokens trading on ethereum blockchain. In International Conference on Complex Systems; Springer: Berlin/Heidelberg, Germany, 2018; pp. 439–450. [Google Scholar]
| Currency | Obs. | Pearson’s Chi-Squared Test | Mantissa Arc Test | MAD | MAD Conformity | Distortion Factor | Start Date | End Date | ||
|---|---|---|---|---|---|---|---|---|---|---|
| X-Squared | p-Value | L2 | p-Value | |||||||
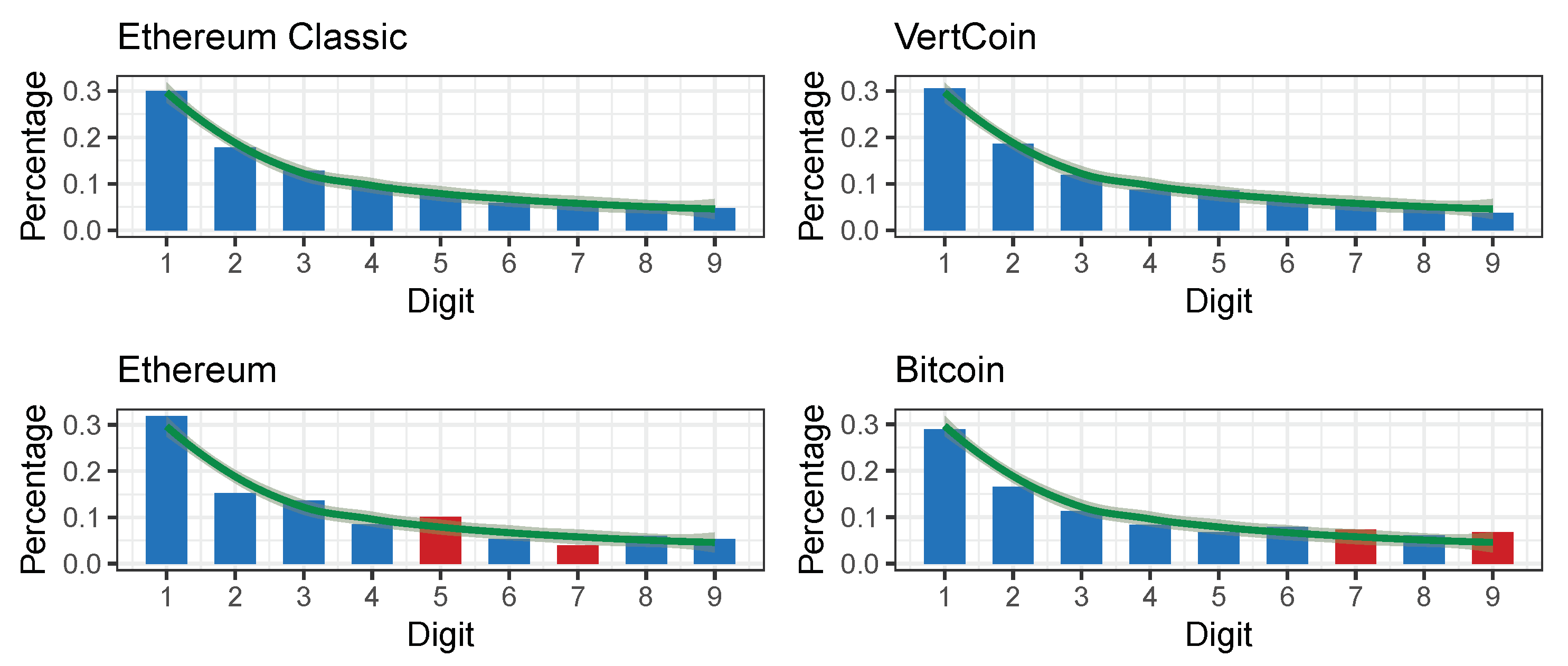
| Ethereum Classic (ETC) | 750 | 1.766027 | 0.9873638 | 0.0000861 | 0.9374726 | 0.00351481 | Close | −0.1409321 | 2015-07-30 | 2018-08-12 |
| Vertcoin (VTC) | 1666 | 7.30948 | 0.5036398 | 0.000165673 | 0.7588044 | 0.005795195 | Close | −1.621333 | 2014-01-10 | 2018-08-12 |
| Metal (MTL) | 400 | 5.15115 | 0.7413057 | 0.001522525 | 0.543889 | 0.01089584 | Acceptable | −0.1257945 | 2017-06-29 | 2018-08-12 |
| Status (SNT) | 411 | 7.692396 | 0.4640798 | 0.001050824 | 0.6492816 | 0.01005221 | Acceptable | −1.560401 | 2017-06-19 | 2018-08-12 |
| Aragon (ANT) | 452 | 5.696092 | 0.6812311 | 0.005388913 | 0.08752867 | 0.01078389 | Acceptable | 3.448495 | 2017-05-15 | 2018-08-12 |
| Waves (WAVES) | 603 | 5.14964 | 0.7414692 | 0.003501951 | 0.1210349 | 0.008216651 | Acceptable | −1.721726 | 2016-06-02 | 2018-08-12 |
| Iconomi (ICN) | 658 | 10.17673 | 0.2528404 | 0.0008252317 | 0.5810012 | 0.0104604 | Acceptable | 0.8235436 | 2016-09-30 | 2018-08-12 |
| NEO (NEO) | 665 | 3.823118 | 0.8727192 | 0.0008927334 | 0.5522979 | 0.006478303 | Acceptable | 1.316035 | 2016-09-09 | 2018-08-12 |
| Lisk (LSK) | 811 | 11.45478 | 0.1772377 | 0.001803885 | 0.231552 | 0.009606102 | Acceptable | 3.072645 | 2016-04-06 | 2018-08-12 |
| Stellar (XLM) | 1009 | 9.622045 | 0.2925614 | 0.002200075 | 0.1086226 | 0.007992198 | Acceptable | 1.221268 | 2014-08-05 | 2018-08-12 |
| Verge (XVG) | 1387 | 8.300241 | 0.4047048 | 0.002115592 | 0.05316656 | 0.007575786 | Acceptable | −2.84182 | 2014-10-09 | 2018-08-12 |
| MaidSafeCoin (MAID) | 1560 | 10.43771 | 0.2356377 | 0.003279288 | 0.006001835 | 0.007513696 | Acceptable | 3.73407 | 2014-04-22 | 2018-08-12 |
| Dash (DASH) | 1641 | 5.958045 | 0.6519316 | 0.001418531 | 0.09750916 | 0.00621291 | Acceptable | 0.8615983 | 2014-01-19 | 2018-08-12 |
| DigiByte (DGB) | 1649 | 25.9 | 0.00111 | 0.003.21 | 0.005 | 0.01088511 | Acceptable | −2.4136 | 2014-01-10 | 2018-08-12 |
| Bitcoin (BTC) | 1933 | 30.8193 | 0.0001512958 | 0.0006696828 | 0.2740357 | 0.01158613 | Acceptable | 5.881506 | 2013-04-28 | 2018-08-12 |
| Gnosis (GNO) | 468 | 8.754344 | 0.3634412 | 0.006937894 | 0.03889326 | 0.01312756 | Marginally acc. | 1.135551 | 2017-04-18 | 2018-08-12 |
| Golem (GLM) | 633 | 11.07461 | 0.1975074 | 0.003690431 | 0.0967096 | 0.0129236 | Marginally acc. | 6.131378 | 2016-11-11 | 2018-08-12 |
| Zcash (ZEC) | 653 | 20.82315 | 0.007632357 | 0.001029657 | 0.5104994 | 0.01293599 | Marginally acc. | −0.9372237 | 2016-10-28 | 2018-08-12 |
| Decred (DCR) | 915 | 17.6832 | 0.02373108 | 0.0005975181 | 0.5788401 | 0.01375337 | Marginally acc. | −1.586765 | 2016-02-08 | 2018-08-12 |
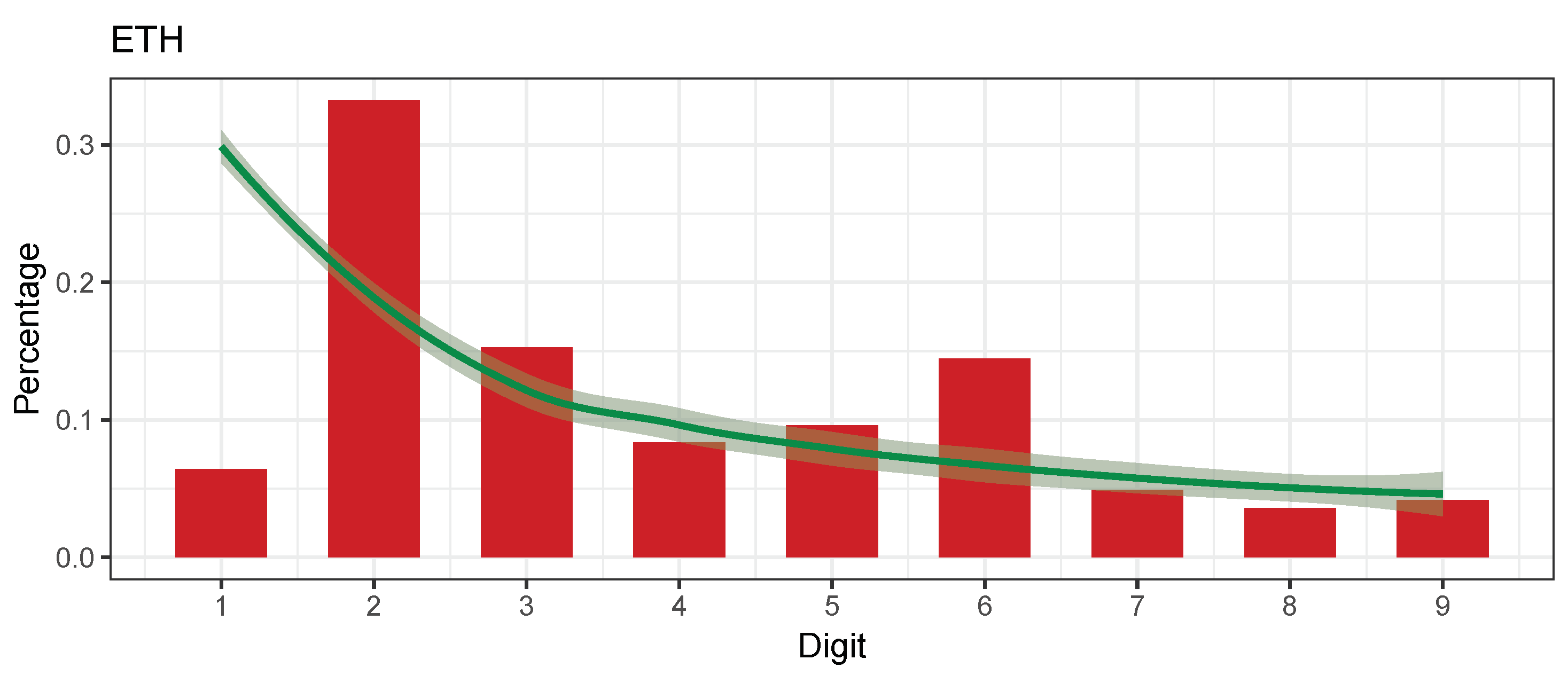
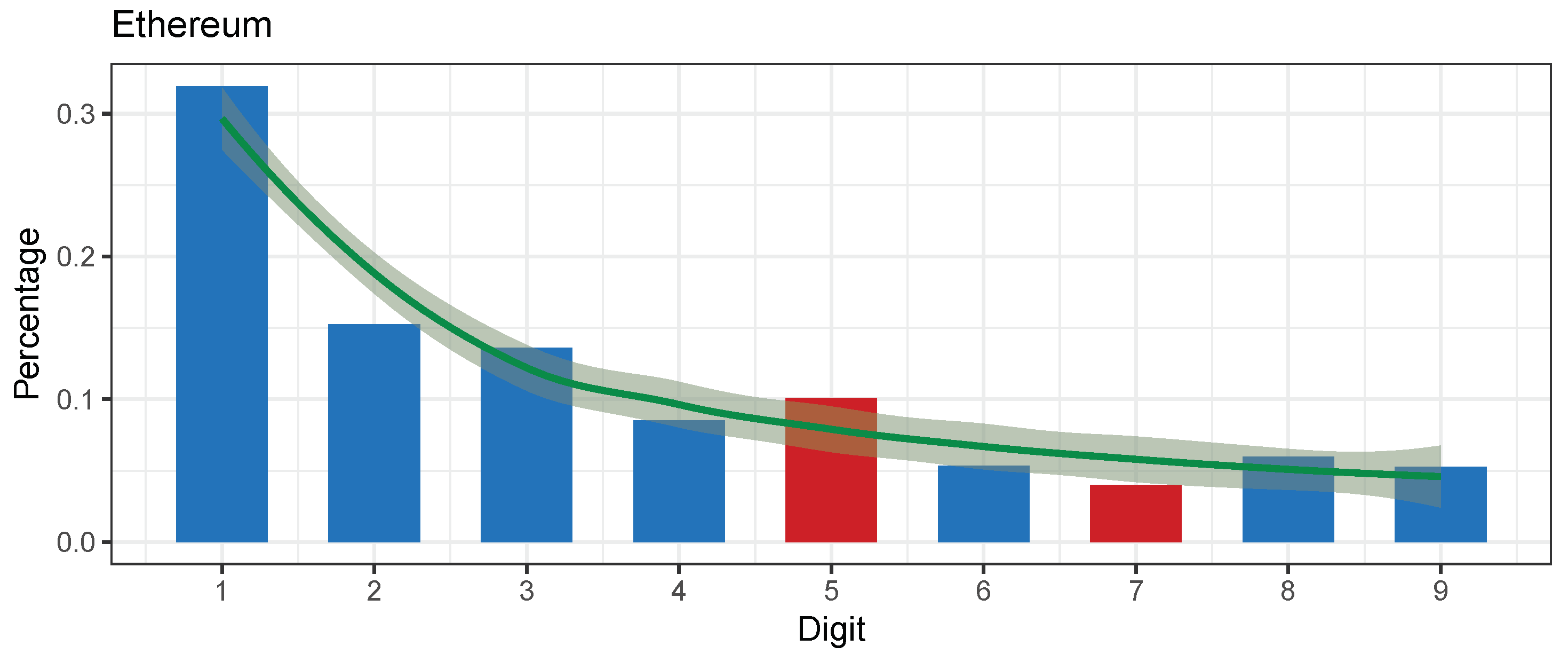
| Ethereum (ETH) | 1102 | 25.77399 | 0.00115 | 0.000378 | 0.658996 | 0.01482756 | Marginally acc. | −0.08431323 | 2015-08-07 | 2018-08-12 |
| NEM (XEM) | 1230 | 27.13364 | 0.0006703807 | 0.008295528 | 0.000037 | 0.01417723 | Marginally acc. | 3.19854 | 2015-03-29 | 2018-08-12 |
| Tether (USDT) | 1258 | 34.91683 | 0.0000277 | 0.0138 | 0.00000003 | 0.01391653 | Marginally acc. | −5.969747 | 2014-10-06 | 2018-08-12 |
| EOS (EOS) | 401 | 15.36398 | 0.05244271 | 0.003494984 | 0.2462301 | 0.0200535 | Nonconformity | −2.819878 | 2017-06-20 | 2018-08-12 |
| TENX token (TENX) | 402 | 10.5 | 0.234 | 0.00808 | 0.0389 | 0.01539412 | Nonconformity | −7.119347 | 2017-06-27 | 2018-08-12 |
| Veritaseum (VERI) | 431 | 11.32151 | 0.1841391 | 0.01211339 | 0.005402612 | 0.01726905 | Nonconformity | −1.603899 | 2017-04-25 | 2018-08-12 |
| Basic Atention T. (BAT) | 438 | 19.05523 | 0.01456707 | 0.01293943 | 0.003456598 | 0.02196946 | Nonconformity | 0.2319942 | 2017-05-29 | 2018-08-12 |
| PIVX (PIVX) | 903 | 28.08438 | 0.0004584671 | 0.01199764 | 0.0000197 | 0.01890993 | Nonconformity | −7.031687 | 2016-01-30 | 2018-08-12 |
| Dogecoin (DOGE) | 1702 | 83.1755 | 0.02422157 | 0.0214206 | Nonconformity | −9.527495 | 2013-12-08 | 2018-08-12 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vičič, J.; Tošić, A. Application of Benford’s Law on Cryptocurrencies. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 313-326. https://doi.org/10.3390/jtaer17010016
Vičič J, Tošić A. Application of Benford’s Law on Cryptocurrencies. Journal of Theoretical and Applied Electronic Commerce Research. 2022; 17(1):313-326. https://doi.org/10.3390/jtaer17010016
Chicago/Turabian StyleVičič, Jernej, and Aleksandar Tošić. 2022. "Application of Benford’s Law on Cryptocurrencies" Journal of Theoretical and Applied Electronic Commerce Research 17, no. 1: 313-326. https://doi.org/10.3390/jtaer17010016
APA StyleVičič, J., & Tošić, A. (2022). Application of Benford’s Law on Cryptocurrencies. Journal of Theoretical and Applied Electronic Commerce Research, 17(1), 313-326. https://doi.org/10.3390/jtaer17010016







