A Theoretical Analysis of the Pricing and Advertising Strategies with Lévy-Walking Consumers
Abstract
:1. Introduction
“We know every single click and what you read, what you buy, what you watch online, but the physical space has been very much unknown.” … “With more physical data, this is changing”.[3]
- (1)
- What are the effects of the consumers’ OMT on the firm’s pricing and advertising strategies, as well as social welfare (sum of firm profit and consumer surplus)?
- (2)
- How does the consumers’ AMD influence the effects of OMT?
2. Literature Review
2.1. Spatial Characteristics of Human Mobility
2.2. Research on Informative Advertising
2.2.1. Factors That Affect Consumers’ Purchasing Decisions in Advertising Context
2.2.2. Analytical Models of Informative Advertising
2.2.3. The Welfare Effects of Advertising
3. Model Setting
3.1. The Market and Consumer Mobility
- (1)
- Symmetric movement (SM), , i.e., a half of the consumers move towards the firm and the other half depart from the firm.
- (2)
- Convergent movement (CM), , i.e., the consumers have an overall tendency to converge to the firm. In other words, more than half of the consumers move towards the firm.
- (3)
- Divergent movement (DM), , i.e., the consumers have an overall tendency to diverge from the firm. In other words, more than half of the consumers depart away the firm.
3.2. Pricing and Advertising
3.3. Consumers’ Purchasing Decisions
4. Results
4.1. Pricing and Advertising Strategies
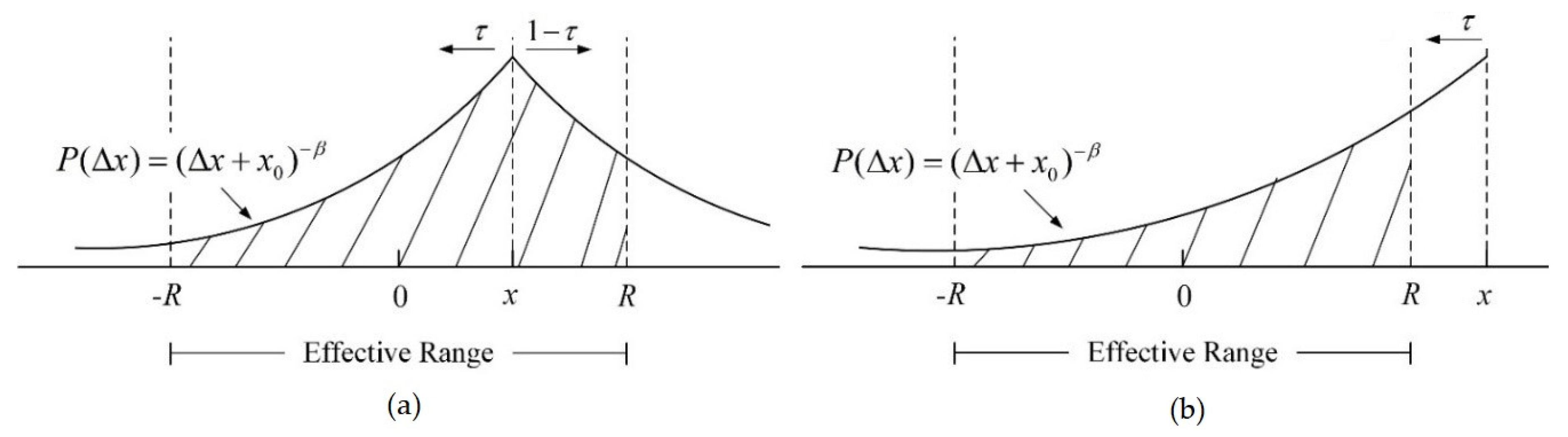
4.1.1. The Number of Effective Consumers
4.1.2. Optimal Decisions
4.2. The Effects of Consumer Mobility
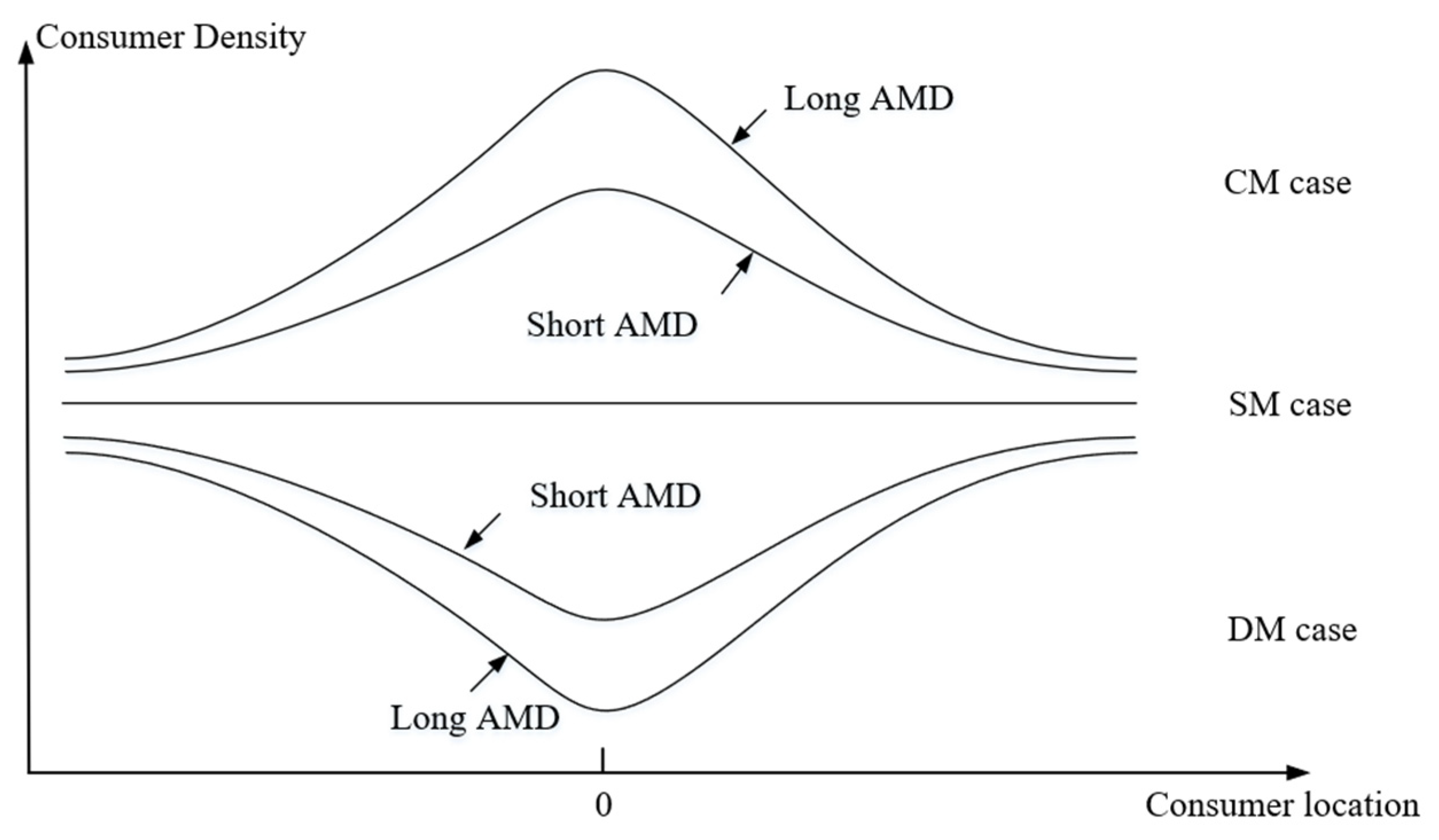
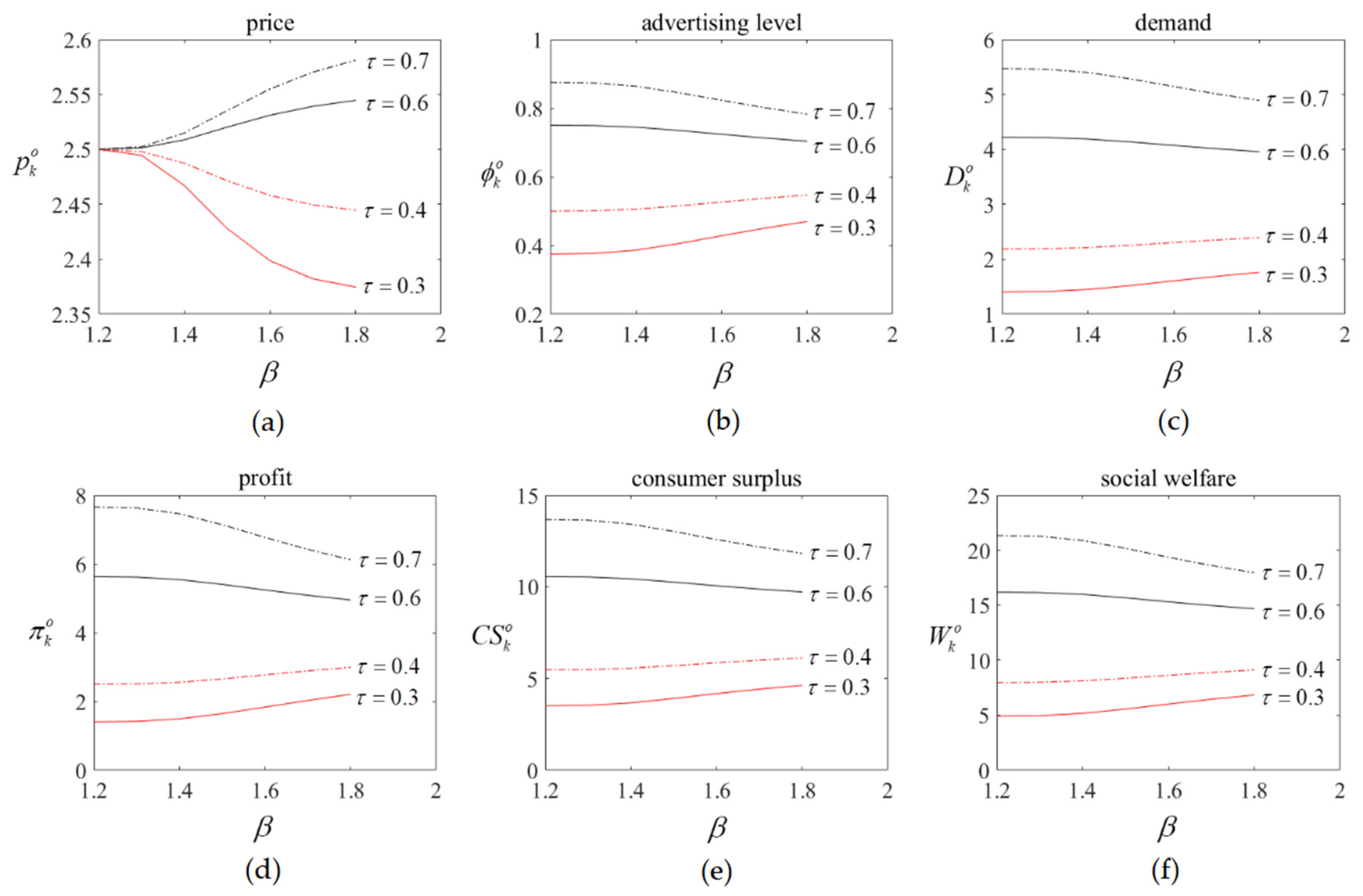
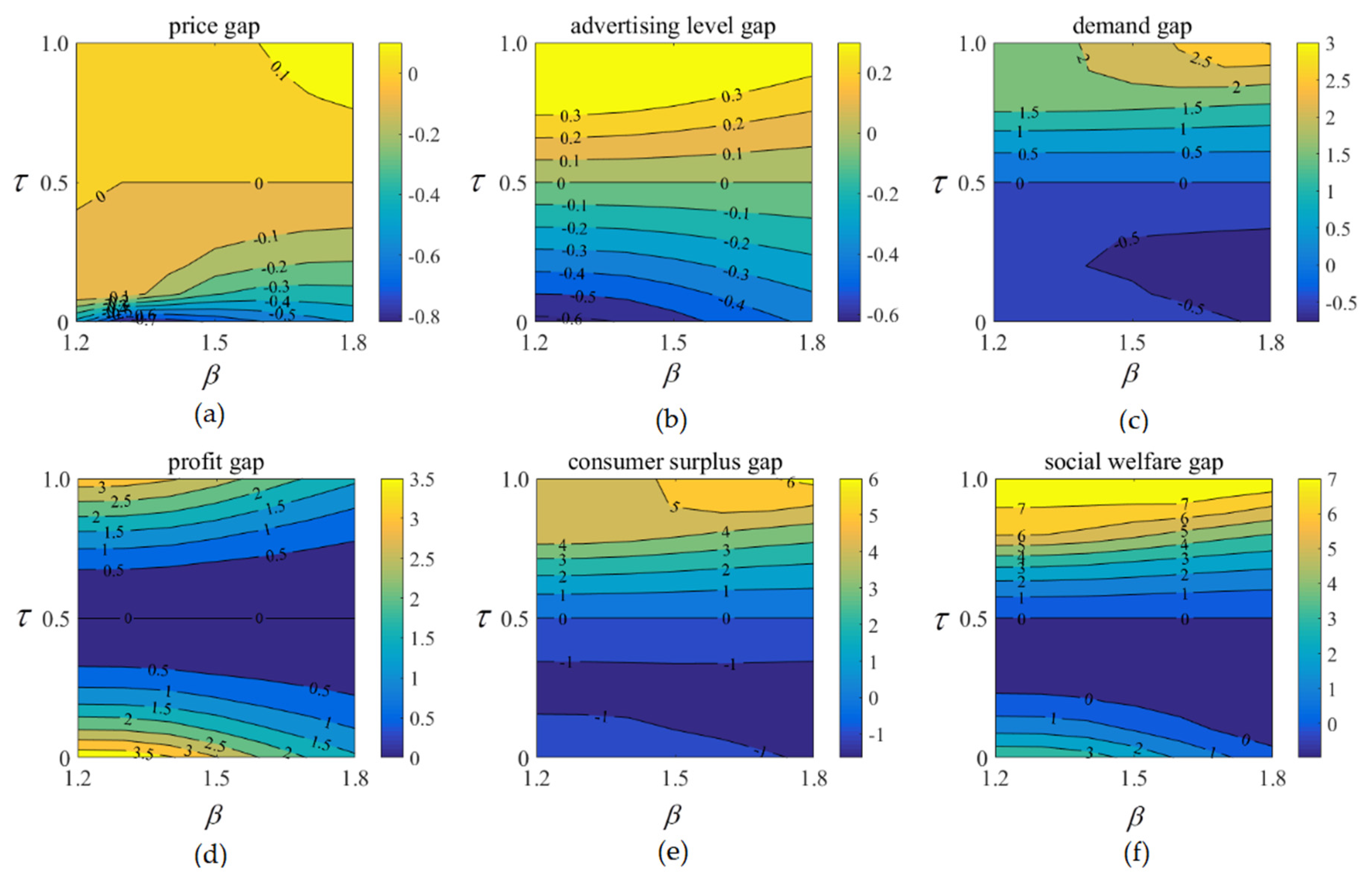
4.2.1. The Convergent Effect
4.2.2. The Scaling Effect
5. Extensions and Discussions
5.1. The DM Case
- (1)
- The firm decreases its product price and advertising level when the consumers have a stronger tendency to diverge from it, i.e.,and.
- (2)
- The firm gains a lower demand when the consumers have a stronger tendency to diverge from it, i.e.,.
- (3)
- When the consumers have a stronger tendency to diverge from the firm, social welfare decreases, i.e.,. Meanwhile, both the firm and consumers become worse-off. Mathematically,and.
- (1)
- The firm decreases its advertising level but increases its product price when the consumers have longer AMD in the DM case, i.e.,and.
- (2)
- When the consumers have longer AMD, the firm becomes worse-off in the DM case, i.e.,.
5.2. The Case without Proximity Technologies
5.3. The Firm’s Under-Advertising Behavior
6. Conclusions
6.1. Summary of the Main Findings
6.2. Limitations and Opportunities for Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- O’Dea, S. Number of Smartphone Subscriptions Worldwide from 2016 to 2026. 2021. Available online: https://www.statista.com/statistics/330695/number-of-smartphone-users-worldwide (accessed on 5 July 2020).
- eMarketer. More Marketers Use Proximity Tech, Beacons, to Get Closer to the Action. 2016. Available online: https://www.emarketer.com/Article/More-Marketers-Use-Proximity-Tech-Beacons-Closer-Action/1014428 (accessed on 7 September 2020).
- eMarketer. What Marketers Need to Know about Smart Cities. 2017. Available online: https://www.emarketer.com/Article/What-Marketers-Need-Know-About-Smart-Cities/1015956 (accessed on 7 September 2020).
- Ghose, A.; Li, B.; Liu, S. Mobile targeting using customer trajectory patterns. Manag. Sci. 2019, 65, 5027–5049. [Google Scholar] [CrossRef]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Qu, Z.; Blumm, N.; Barabasi, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Isaacman, S.; Becker, R.; Cáceres, R.; Kobourov, S.; Rowland, J.; Varshavsky, A. A tale of two cities. Workshop Mob. Comput. Syst. Appl. 2010, 19–24. [Google Scholar] [CrossRef]
- Luo, X.; Andrews, M.; Fang, Z.; Phang, C.W. Mobile targeting. Manag. Sci. 2014, 60, 1738–1756. [Google Scholar] [CrossRef] [Green Version]
- Danaher, P.J.; Smith, M.S.; Ranasinghe, K.; Danaher, T.S. Where, when, and how long: Factors that influence the redemption of mobile phone coupons. J. Mark. Res. 2015, 52, 710–725. [Google Scholar] [CrossRef]
- Fong, N.M.; Fang, Z.; Luo, X.M. Geo-conquesting: Competitive locational targeting of mobile promotions. J. Mark. Res. 2015, 52, 726–735. [Google Scholar] [CrossRef] [Green Version]
- Kats, R. BestBuy Drives Foot Traffic to Locations via Geofencing Campaign. 2012. Available online: https://www.retaildive.com/ex/mobilecommercedaily/best-buy-drives-foot-traffic-to-locations-via-geofencing-campaign (accessed on 5 July 2020).
- Tode, C. Location Targeting More Than Doubles Performance of Mobile Ads: Report. 2013. Available online: https://www.marketingdive.com/ex/mobilemarketer/cms/news/research/14731.html (accessed on 5 July 2020).
- Hotelling, H. Stability in competition. Econ. J. 1929, 39, 41–57. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Lee, K.; Hong, S.; Kim, S.; Rhee, I.; Song, C. SLAW: A new mobility model for human walks. IEEE Infocom Int. Conf. Comput. Commun. 2009, 855–863. [Google Scholar] [CrossRef]
- Song, C.M.; Koren, T.; Wang, P.; Barabasi, A.L. Modelling the scaling properties of human mobility. Nat. Phys. 2010, 6, 818–823. [Google Scholar] [CrossRef] [Green Version]
- Grossman, G.M.; Shapiro, C. Informative advertising with differentiated products. Rev. Econ. Stud. 1984, 51, 63–81. [Google Scholar] [CrossRef]
- Soberman, D.A. Research note: Additional learning and implications on the role of informative advertising. Manag. Sci. 2004, 50, 1744–1750. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, S.F. Informative advertising in differentiated oligopoly markets. Int. J. Ind. Organ. 2009, 27, 60–69. [Google Scholar] [CrossRef] [Green Version]
- Stahl, D.O. Oligopolistic pricing and advertising. J. Econ. Theor. 1994, 64, 162–177. [Google Scholar] [CrossRef]
- Stegeman, M. Advertising in competitive markets. Am. Econ. Rev. 1991, 81, 210–223. [Google Scholar]
- Esteves, R.B. Customer poaching and advertising. J. Ind. Econ. 2009, 57, 112–146. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, Q.; Yue, X. Target or not? Endogenous advertising strategy under competition. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4472–4481. [Google Scholar] [CrossRef]
- Noulas, A.; Scellato, S.; Lambiotte, R.; Pontil, M.; Mascolo, C. A tale of many cities: Universal patterns in human urban mobility. PLoS ONE 2012, 7, e37027. [Google Scholar] [CrossRef]
- Rhee, I.; Shin, M.; Hong, S.; Lee, K.; Kim, S.J.; Chong, S. On the Lévy-walk nature of human mobility. IEEE ACM Trans. Netw. 2011, 19, 630–643. [Google Scholar] [CrossRef]
- Wesolowski, A.; Eagle, N.; Noor, A.M.; Snow, R.W.; Buckee, C.O. The impact of biases in mobile phone ownership on estimates of human mobility. J. R. Soc. Interface 2013, 10, 20120986. [Google Scholar] [CrossRef] [PubMed]
- Cuttone, A.; Lehmann, S.; González, M. Understanding predictability and exploration in human mobility. EPJ Data Sci. 2018, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Damiani, M.L.; Hachem, F.; Quadri, C.; Rossini, M.; Gaito, S. On location relevance and diversity in human mobility data. ACM Trans. Spat. Algorithms Syst. 2020, 7, 1–38. [Google Scholar] [CrossRef]
- Hanson, S.; Hanson, P. The travel-activity patterns of urban residents: Dimensions and relationships to sociodemographic characteristics. Econ. Geogr. 1981, 57, 332–347. [Google Scholar] [CrossRef]
- Hanson, S.; Johnston, I. Gender differences in work-trip length. Urban Geogr. 1985, 9, 180–202. [Google Scholar] [CrossRef]
- Brahim, N.; Lahmandi-Ayed, R.; Laussel, D. Is targeted advertising always beneficial? Int. J. Ind. Organ. 2011, 29, 678–689. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.; Fung, Y.K.R.; Cheng, T.C.E. Mobile advertising and traffic conversion: The effects of front traffic and spatial competition. J. Interact. Mark. 2019, 47, 84–101. [Google Scholar] [CrossRef]
- Mogilner, C. The pursuit of happiness: Time, money, and social connection. Psychol. Sci. 2010, 21, 1348–1354. [Google Scholar] [CrossRef] [Green Version]
- Mogilner, C.; Aaker, J.; Kamvar, S.D. How happiness affects choice. J. Consum. Res. 2012, 39, 429–443. [Google Scholar] [CrossRef]
- Alba, J.W.; Williams, E.F. Pleasure principles: A review of research on hedonic consumption. J. Consum. Psychol. 2013, 23, 2–18. [Google Scholar] [CrossRef]
- Bagozzi, R.P.; Belanche, D.; Casaló, L.V.; Flavián, C. The role of anticipated emotions in purchase intentions. Psychol. Mark. 2016, 33, 629–645. [Google Scholar] [CrossRef]
- Goldberg, M.E.; Hartwick, J. The effects of advertiser reputation and extremity of advertising claim on advertising effectiveness. J. Consum. Res. 1990, 17, 172–179. [Google Scholar] [CrossRef]
- Amaldoss, W.; Jain, S. Conspicuous consumption and sophisticated thinking. Manag. Sci. 2005, 51, 1449–1466. [Google Scholar] [CrossRef] [Green Version]
- Amaldoss, W.; Jain, S. Pricing of conspicuous goods: A competitive analysis of social effects. J. Mark. Res. 2005, 42, 30–42. [Google Scholar] [CrossRef] [Green Version]
- Cheema, A.; Kaikati, A.M. The effect of need for uniqueness on word of mouth. J. Mark. Res. 2010, 47, 553–563. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Wang, Z.; Hahn, J. Scarcity strategy in crowdfunding: An empirical exploration of reward limits. Inf. Syst. Res. 2020, 31, 1107–1131. [Google Scholar] [CrossRef]
- Hu, M.; Shi, M.; Wu, J. Simultaneous vs. sequential group-buying mechanisms. Manag. Sci. 2013, 59, 2805–2822. [Google Scholar] [CrossRef]
- Wu, J.; Shi, M.; Hu, M. Threshold effects in online group buying. Manag. Sci. 2015, 61, 2025–2040. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Milner, J.; Wu, J. Liking and following and the newsvendor: Operations and marketing policies under social influence. Manag. Sci. 2016, 62, 867–879. [Google Scholar] [CrossRef] [Green Version]
- Doha, A.; Elnahla, N.; McShane, L. Social commerce as social networking. J. Retail. Consum. Serv. 2019, 47, 307–321. [Google Scholar] [CrossRef]
- Fang, Z.; Gu, B.; Luo, X.; Xu, Y. Contemporaneous and delayed sales impact of location-based mobile promotions. Inf. Syst. Res. 2015, 26, 552–564. [Google Scholar] [CrossRef]
- Li, C.; Luo, X.; Zhang, C.; Wang, X. Sunny, rainy, and cloudy with a chance of mobile promotion effectiveness. Mark. Sci. 2017, 36, 762–779. [Google Scholar] [CrossRef] [Green Version]
- Andrews, M.; Luo, X.M.; Fang, Z.; Ghose, A. Mobile Ad Effectiveness: Hyper-Contextual Targeting with Crowdedness. Mark. Sci. 2016, 35, 218–233. [Google Scholar] [CrossRef]
- Bagwell, K. The economic analysis of advertising. Handb. Ind. Organ. 2007, 3, 1701–1844. [Google Scholar]
- Butters, G.R. Equilibrium distributions of sales and advertising prices. Uncertain. Econ. 1978, 493–513. [Google Scholar] [CrossRef]
- Karray, S. Modeling brand advertising with heterogeneous consumer response: Channel implications. Ann. Oper. Res. 2015, 233, 181–199. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Zhong, W.J.; Mei, S. Competitive effects of informative advertising in distribution channels. Mark. Lett. 2012, 23, 561–584. [Google Scholar] [CrossRef]
- Ghosh, B.P.; Galbreth, M.R.; Shang, G. The competitive impact of targeted television advertisements using DVR technology. Decis. Sci. 2013, 44, 951–971. [Google Scholar] [CrossRef]
- Li, L.; Chen, J.; Raghunathan, S. Informative role of recommender systems in electronic marketplaces: A boon or a bane for competing sellers. MIS Q. 2020, 44, 1957–1985. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Sun, M. Competitive mobile geo targeting. Mark. Sci. 2017, 36, 666–682. [Google Scholar] [CrossRef] [Green Version]
- Dixit, A.; Norman, V. Advertising and welfare. Bell J. Econ. 1978, 9, 1–17. [Google Scholar] [CrossRef]
- Tremblay, C.H.; Tremblay, V.J. Advertising, price, and welfare: Evidence from the US brewing industry. South. Econ. J. 1995, 62, 367–381. [Google Scholar] [CrossRef]
- Becker, G.S.; Murphy, K.M. A simple theory of advertising as a good or bad. Q. J. Econ. 1993, 108, 941–964. [Google Scholar] [CrossRef]
- Stivers, A.; Tremblay, V.J. Advertising, search costs, and social welfare. Inf. Econ. Policy 2005, 17, 317–333. [Google Scholar] [CrossRef]
- Hernández-García, J.M. Informative advertising, imperfect targeting and welfare. Econ. Lett. 1997, 55, 131–137. [Google Scholar] [CrossRef]
- Losch, A. The economics of location. Economica. 1956, 23, 175. [Google Scholar]
- Wang, R.; Gou, Q.; Choi, T.M.; Liang, L. Advertising strategies for mobile platforms with “apps”. IEEE Trans. Syst. Man Cybern. Syst. 2016, 48, 767–778. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Wang, C. Is persuasive advertising always combative in a distribution channel? Mark. Sci. 2009, 28, 1157–1163. [Google Scholar] [CrossRef]
| Notation | Explanation |
|---|---|
| Product base value | |
| t | Unit travel cost |
| Probability of a consumer moving towards the firm | |
| c | Cost coefficient of advertising |
| p | Product price |
| Coefficient indicating AMD | |
| Firm profit | |
| R | Radius of the effective range |
| Advertising coverage rate | |
| CS | Consumer surplus |
| G | Expected number of effective consumers |
| W | Social welfare |
| Subscript | Explanation |
|---|---|
| n | The case without proximity technologies |
| c | CM case |
| s | SM case |
| d | DM case |
| k | |
| L | Long-AMD case |
| S | Short-AMD case |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Li, G. A Theoretical Analysis of the Pricing and Advertising Strategies with Lévy-Walking Consumers. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2129-2150. https://doi.org/10.3390/jtaer16060119
Wang W, Li G. A Theoretical Analysis of the Pricing and Advertising Strategies with Lévy-Walking Consumers. Journal of Theoretical and Applied Electronic Commerce Research. 2021; 16(6):2129-2150. https://doi.org/10.3390/jtaer16060119
Chicago/Turabian StyleWang, Wei, and Gang Li. 2021. "A Theoretical Analysis of the Pricing and Advertising Strategies with Lévy-Walking Consumers" Journal of Theoretical and Applied Electronic Commerce Research 16, no. 6: 2129-2150. https://doi.org/10.3390/jtaer16060119
APA StyleWang, W., & Li, G. (2021). A Theoretical Analysis of the Pricing and Advertising Strategies with Lévy-Walking Consumers. Journal of Theoretical and Applied Electronic Commerce Research, 16(6), 2129-2150. https://doi.org/10.3390/jtaer16060119







