1. Introduction
Electronic commerce and retail logistics are facing a multitude of technology-driven changes in current times [
1,
2,
3,
4,
5,
6,
7]: order picking has been identified as one of the most labor-intensive as well as costly activities within warehouse logistics and is experiencing changes due to new technologies in the form of artificial intelligence and automation. As human worker’s activities will be required for a long time to come, investigating the efficiency of the human workforce and warehouse processes is of central importance for e-commerce businesses. At the same time, quantitative insights regarding human order pickers’ performance and empirical investigations through non-parametric methods are rare. In order to address this research gap, we measure and compare the efficiency of order pickers by applying the data envelopment analysis (DEA) methodology for a dataset obtained from a large German food retailing company. The order picking data contains 6109 batches, with 865,410 picked SKU proceeded by
n = 23 pickers for one month. Each order picker is treated as an individual decision-making unit (DMU) within the analysis. This is a new method approach and could inspire more research projects on the use of non-parametric efficiency measurement techniques on specific retail and e-commerce fields.
Due to the lack of prior research on the efficiency of order pickers through non-parametric efficiency measurement, this article aspires to answer the following two research questions: (1) What are the components of an efficiency analysis aimed to evaluate picker-to-part order picking? and (2) What is the goodness-of-fit for the DEA model compared to the company’s efficiency assessment?
The relevance of these questions becomes prominent when looking at the rapid and versatile advances of digitalization, automation, and AI in warehouse logistics. Therefore, the contribution of this paper is twofold: (1) elaborating, justifying and applying Data Envelopment Analysis (DEA) as a novel method for evaluating work systems of blue-collar workers, and (2) quantifying the efficiency of order pickers through a non-parametric method with empirical real-live data.
This paper is structured as follows: the literature framework in
Section 2 highlights existing research streams on the efficiency of order picking that can be separated into (1) technology development, (2) human factors, (3) specifics in individual application areas, as well as (4) planning and optimization.
Section 3 describes the data and sample used in this research project and introduces DEA as a non-parametric performance measurement method. After selecting applicable inputs and outputs,
Section 3.4 highlights the methodological approaches that have recently been discussed to enable the use of ratio measures in DEA by applying non-convex DEA models. In the empirical results section, we present the efficiency scores of all 23 DMUs. All scores are validated through a comparison with the premium payments of the company. The formulated DEA model with a non-convex frontier through the FDH approach [
8] has a 93% goodness-of-fit. Finally, a discussion, conclusion and an outlook section on future research is presented.
2. Theoretical Framework
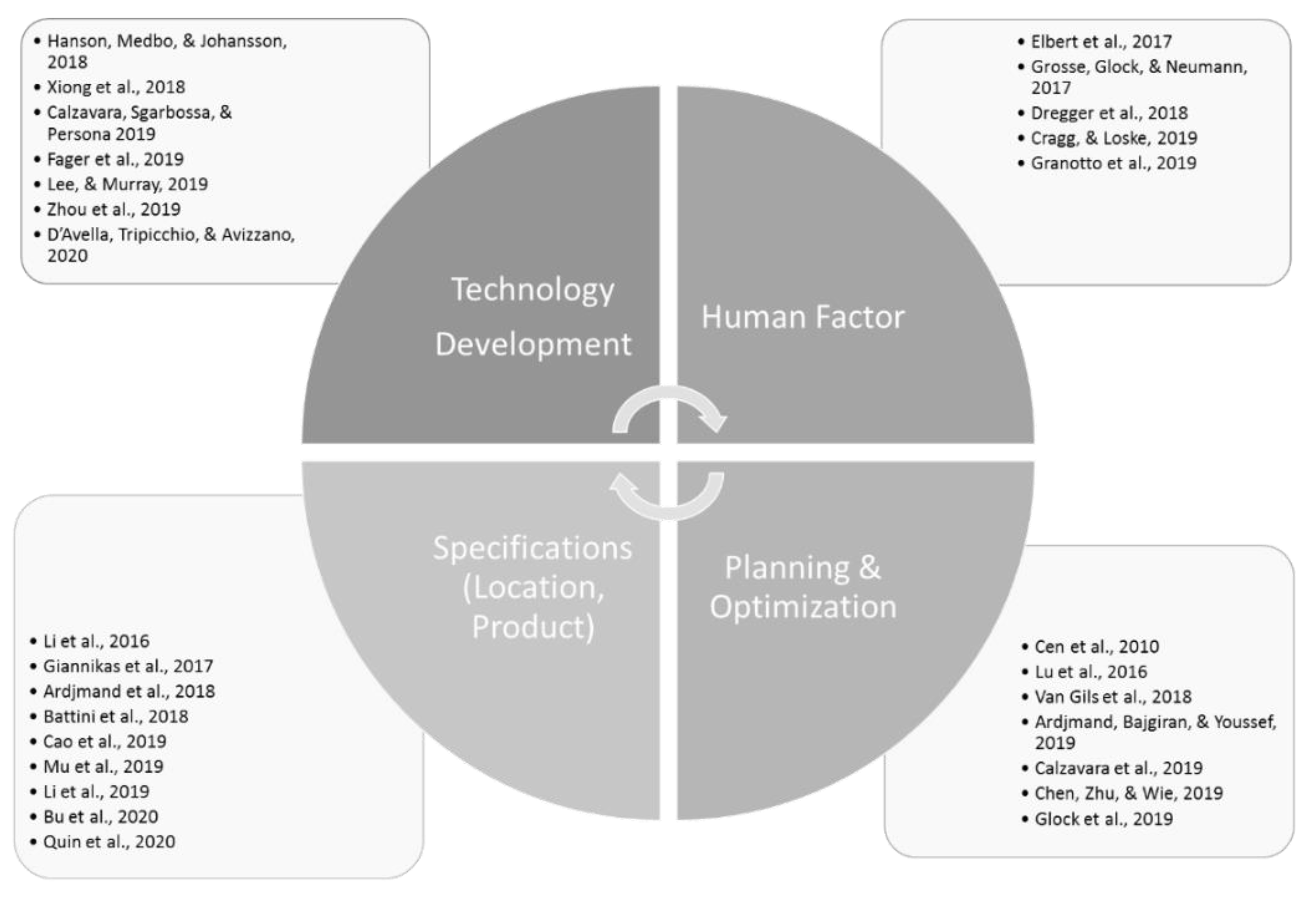
As a theoretical framework, the existing literature can be structured in four inter-connecting areas affecting each other regarding the efficiency of order picking systems (see
Figure 1): First, the technology applied as well as the continuing technology development play an essential role in order picking. As a series of authors is outlining, concurrent technical developments are affecting order picking processes and results [
9,
10,
11,
12,
13,
14,
15].
Second, the human factor is discussed in several research contributions, as picking systems require a high level of manual labor in any context. Depending on the specific application, different systems with a high or a low level of automation are implemented—but in any case, with human workers included. Topics like learning of human workers, mitigation of fatigue and tear for human workers, or general motivation and question of competences are discussed in this field of research [
16,
17,
18,
19,
20].
Third, planning and organization questions are discussion, especially in operational research contexts regarding order picking systems. New methods to plan and organize order picking processes are discussed in the literature and are evaluated compared to existing methods in order to improve the picking results, e.g., to reduce distances traveled or mistakes made while picking [
21,
22,
23,
24,
25,
26].
And a fourth area of the interconnected theoretical framework elements is the question of specifics in individual application areas. Very different application cases are discussed in research approaches, from fruit picking in agriculture to online retail order picking in e-commerce. In general, the important message herein is the fact that individual product characteristics and requirements shape many of the typical design elements of order picking systems, especially the efficient level of automation [
27,
28,
29,
30,
31,
32,
33,
34,
35].
Altogether, the research implemented regarding order picking is a small but diverse field of science within the overall e-commerce retail logistics management domain. Many factors influence the resulting picking performance, and especially efficiency analyses are in high demand as picking volumes are increasing due to, e.g., increasing online orders or general trade and retail volumes.
3. Materials and Methods
3.1. Case Study Description
The case study is implemented at a large full-range food retailing company that operates 18 logistics centers in Germany. Every logistics site has one cooled warehouse storing three major product groups according to the individual temperature zone: (1) fruits and vegetables, (2) fresh fish and meat, as well as (3) dairy products. In the course of this paper, we investigate the efficiency of order pickers employed in the warehouse area for dairy products. The warehouse areas involve a storage area, a picking area, and a material handling system that refills the picking locations with forklifts from the storage area. Order picking is performed through a picker-to-part method, whereby the pickers use industrial trucks for locomotion and a pick-by-voice system to receive information about (1) the storage location and (2) the picking quantity for an assigned batch via headsets. The maximum speed of all industrial trucks is equal.
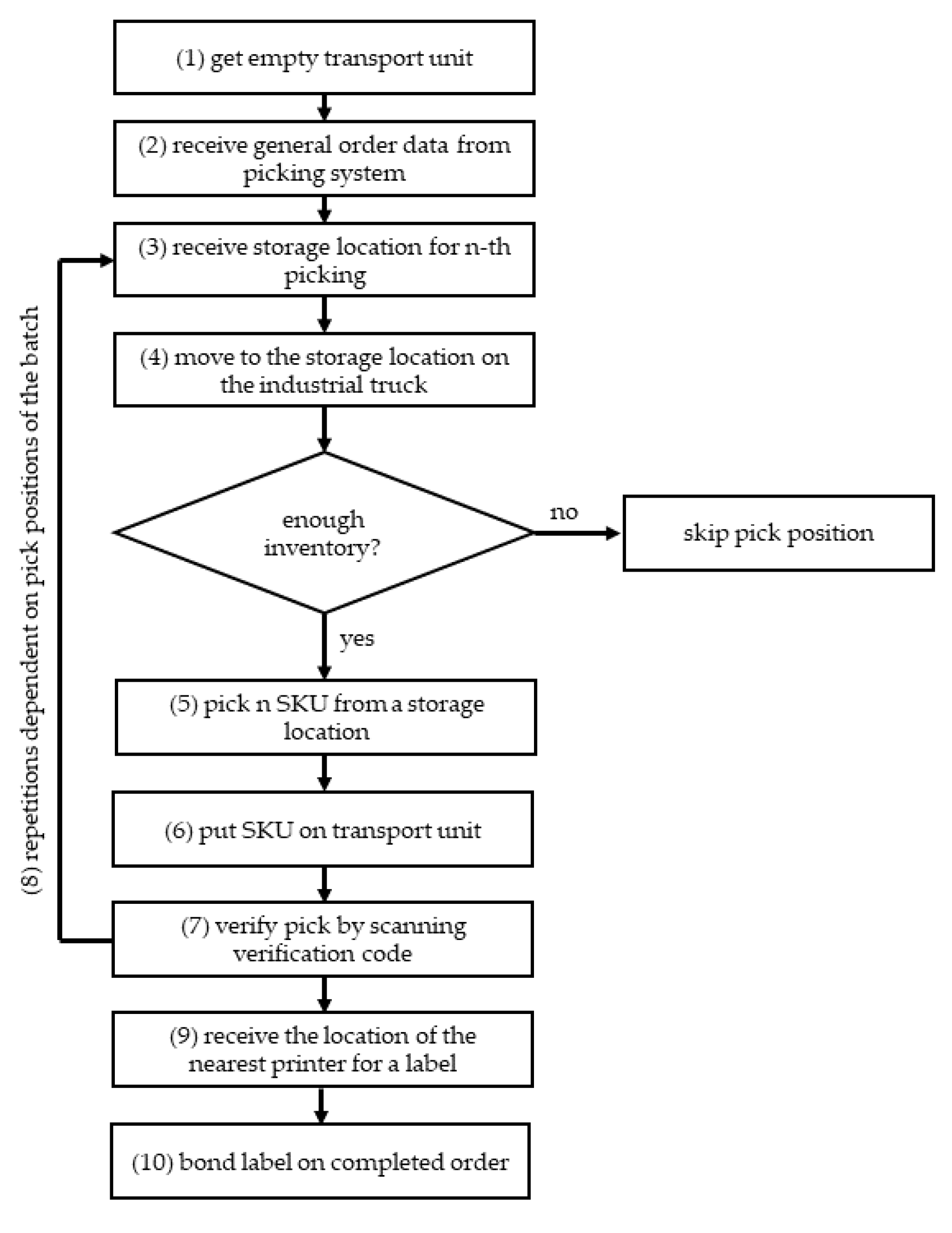
Figure 2 summarizes the picking process.
The manual order picking process is as follows: (1) get empty transportation aids; (2) receive a general order data from picking system; (3) receive a storage location for picking; (4) move to a storage location on the industrial truck; (5) pick an SKU from a storage location; (6) put SKU on a transportation aid; (7) verify pick by scanning verification code; (8) repeat (4) to (7) until the batch is finished; (9) receive the location of the nearest printer for a label; and (10) bond the label onto the completed order. Orders of the supermarket stores are decomposed into batches according to the volume of the SKU and the volume of the transportation aid, which is a rolling container for all batches examined in this case analysis. The order picking data contains 6109 batches, with 865,410 picked SKU proceeded by n = 23 pickers for one month. Each order picker is treated as an individual decision-making unit (DMUs) within the analysis.
3.2. Non-Parametric Efficiency Measurement
The DEA method is a non-parametric optimization method of linear programming for measuring the relative efficiency of decision-making units (DMUs) with multiple inputs and outputs. A basic model was introduced by Charnes, Cooper and Rhodes in 1978 and is based on Koopmans activity analysis concept [
36] together with the publications of Debreu and Farrell dealing with radial efficiency measurements [
37,
38]. The optimization method can be based on constant returns to scale (CRS) in the CCR-model [
39] or variable returns to scale (VRS) in the BCC-model [
40], and each case with an input or output orientation. The mathematical formulation of the CCR model is as follows [
39]:
where
Ur = the weight given to the output r;
yrj = amount of output r produced by DMU j;
vi = the weight given to input i;
xij = amount of input i used by DMU j;
n = the number of DMUs;
t = the number of outputs;
m = the number of inputs;
ε = a small positive number.
The basic idea is to calculate an efficiency frontier that is used as a best practice input-output combination for the underlying production scenario. A score of 1.0 indicates that a DMU is efficient and positioned on the efficiency frontier, whereas the relative inefficiency of other DMUs can be determined by measuring the distance between individual DMU performance and the efficiency frontier. Measuring the efficiency under the assumption of CRS is known as overall technical efficiency (OTE). This includes the determination of (in-) efficiency based on (1) the input-/output- transformation, meaning pure technical efficiency (PTE), as well as (2) the size of operations, meaning scale efficiency (SE). This decomposition is possible under VRS [
40,
41,
42].
The explained traditional and deterministic DEA models require the availability of exactly the known values for the specified input and output measures. Hatami-Marbini et al. (2017) argue that this kind of model is susceptible to changes or errors in data values [
43]. As the data in real-world problems tend to be imprecise or vague, researchers have been working on DEA models that aspire to deal with uncertain input and output data. Hatami-Marbini et al. (2013) differentiate between (1) stochastic approaches that manipulate uncertain data in DEA via probability distributions, which requires a priori predictable regularity or a posteriori outcome data [
44], and (2) models with membership functions of the fuzzy sets theory [
45]. A fuzzy DEA approach was first proposed by Sengupta (1992) [
46]. Lertworasirikul et al. (2003) [
47] and Hatami-Marbini, Emrouznejad, and Tavana (2011) [
48] distinguish four groups of fuzzy DEA models with (1) a fuzzy ranking approach [
49]; (2) a possibility approach [
47]; (3) a tolerance approach [
46]; and (4) an α-level-based approach [
50]. In the latter, the fuzzy DEA model is converted into a pair of parametric programs aspiring to find the lower and upper bounds of the α-level of the membership functions of the efficiency scores [
51]. In this investigation, we propose a fuzzy DEA model with an α-level-based approach to evaluate the interval efficiency of a set of DMUs with fuzzy inputs and outputs.
3.3. DEA Model Design
The selection of applicable inputs and outputs, as well as the design of a suitable DEA model, is a well-known source of pitfalls within the DEA literature [
52]. Researchers are often facing a field of tension between the (I) empirical quantitative data that is provided by companies for case studies in praxis-oriented research, (II) the restrictions of the DEA model concerning input-/output selection, and (III) the interests and preferences of managers. Therefore, we follow Jain, Triantis, and Liu, S. (2011) [
53], who propose a framework for DEA applications for manufacturing performance measurements and target setting: (step 1) select applicable inputs and outputs, (step 2) validate the inputs and outputs through company data, (step 3) select a suit-able DEA model, and (step 4,
Section 4.) execute a DEA model.
Step 1: Select applicable inputs and outputs: The selection of input and output factors is based on (1) the order picking process explained in
Section 3.1 and (2) the available data provided by the company. To ensure a high validity of our DEA model, we follow Dyson et al. (2001) [
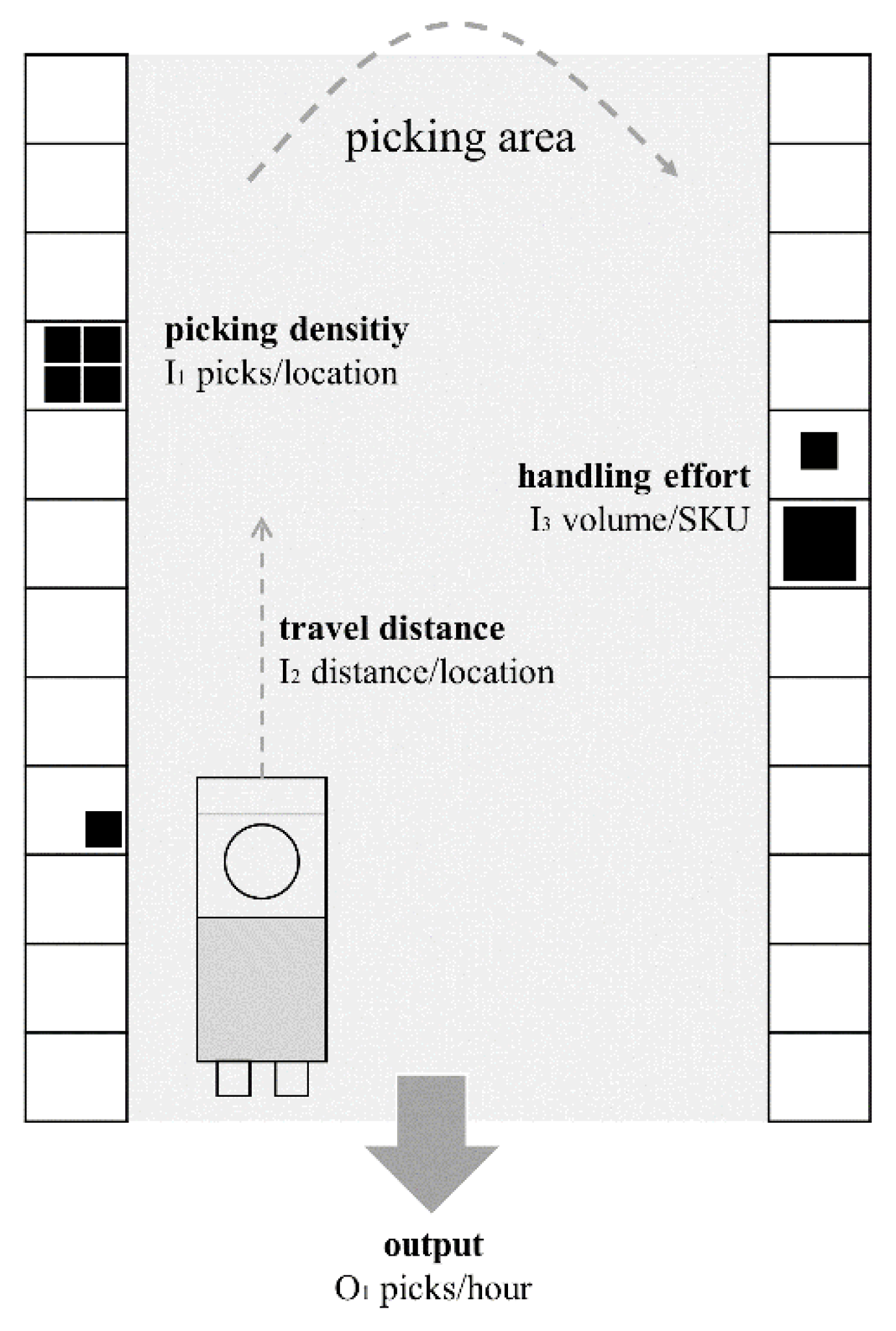
52] for the input/output selection. First, mixing indices and volume measures, as well as integrating percentages, can lead to distortions of the efficiency scores. Second, linked input/output values have to be avoided, e.g., when considering volume measures (x) such as total working hours and costs resulting from the total working hours (p × x) such as total personnel costs of order pickers. The following figure illustrates the linkage between the order picking process and input/output factors (see
Figure 3).
I1 distance/location: The distance traveled by pickers has a significant impact on the total throughput time of a batch and, consequently, the individual performance of order pickers. Pickers that process a batch with a long travel distance need to perform the picking operation faster than order pickers with a short distance when aspiring to be equally efficient. The effort of traveling a required distance to fulfill a batch is operationalized by the sum of traveled meters per location among all batches. The data are obtained per batch and per order picker.
I2 picks/location: The density of picking operations per storage place significantly influences the picking time. The efficiency of an order picker processing (1) a batch with 10 picks at 1 location, has to be treated differently compared to (2) a batch with 1 pick at 10 locations. The effort of a picking operation per storage place is operationalized by the total picks per location among all batches. The data are obtained per batch and per order picker.
I3 volume/SKU: The volume and weight of picked products is an important measure to assess the handling effort while picking SKUs. The efficiency of an order picker lifting (1) many large-scaled SKUs has to be treated differently compared to pickers that lift (2) many small-sized SKUs. As data for the weight/SKU are not available, we operationalize the volume-depending effort of pickers by volume/SKU.
O1 picks/hour: The physically compiled orders are the primary objective of every order picking process and, therefore, is a meaningful output. As all inputs are ratios, we operationalize the order pickers output with picks/hour. As a high output per hour is associated with an efficient operation, O1 is a desired output.
Step 2: Validate the inputs and outputs through company data: Dyson et al. (2001) furthermore state that a cross-correlation of the available factors has to be avoided. Therefore, the following table summarizes the key attributes of the dataset by applying descriptive statistics. Furthermore, a correlation matrix with the correlation coefficient r was calculated (see
Table 1).
The results indicate that there is no linear statistical relationship between the applied input and output measures.
Step 3: Select orientation of DEA model: DEA models can aspire to (1) maximize desirable outputs, (2) minimize undesirable outputs, (3) maximize desirable inputs, or (4) minimize normal inputs [
54]. In the course of this paper, we use an output-oriented model.
3.4. DEA Ratios
The input and output factors of the designed DEA model are ratios that quantify the relationship between two characteristics of an order picking system, e.g., picks (A) and location (B), expressing the number of times A occurs within B. Taking the basic DEA model formulation in formula (1) into consideration, the application of ratio measures with identical denominators is unproblematic. Supposing that we use a single costs input and express it per batch, the DEA model formulation remains unaltered if we also divide the outputs by the number of batches. On the other hand, the use of ratio measures with different denominators is critical for standard DEA models as the convexity axiom embedded in standard DEA models cannot be fully satisfied, which is an ongoing challenge in the DEA literature [
55]. In the debate, different streams can be identified. In the first stream, researchers argue that ratios cannot be applied in DEA models and suggest using the underlying volume measures of ratios as input/output factors, meaning the numerator and denominator in ratios [
56,
57]. This may be suitable if the data are available, which is not the case for our observation. In the second stream, authors are proposing concrete model designs for standard convex DEA models. One example is Hollingsworth and Smith (2003), who argue that the BCC model with VRS has to be used in these cases to gain reliable results [
58]. The approaches are mostly debunked by numerical examples arguing that ratio measures do not satisfy the standard production assumptions, more precisely, that the technology is a convex set. In a third stream, researchers propose new model formulations, such as the ratio-CRS and ratio-VRS by Olesen, Petersen, and Podinovski (2015) [
59].
As the main argument of the authors is the violation of the convexity assumption in standard DEA model that is not satisfied if the denominators of ratio measures are different, the question arises of how non-convex DEA models can solve this problem. Olesen, Petersen, and Podinovski (2015) state that FHD models can, in principle, be used for volume and ratio measures. They argue that inputs and outputs cannot be scaled well, leading to overestimated efficiency values and the discrimination of less efficient DMUs. However, the authors do not present numerical examples to underline their argument.
In the course of this investigation, we calculate the efficiency of the order pickers with three non-convex DEA models: (1) non-convex Free Disposal Hull (FDH) proposed by Deprins, Simar, and Tulkens in 1984 [
60], (2) non-convex Free Replicability Hull (FRH) proposed by Tulkens in 1993 and by Agrell and Tind in 2001 [
8,
61], and (3) non-convex Elementary Replicability Hull (ERH) proposed by Agrell and Tind in 2001. Hereafter, the models are calculated by applying the proposed fuzzy DEA model with an α-level-based approach to evaluate the interval efficiency of a set of DMUs with fuzzy inputs and outputs.
4. Empirical Results
In this section, we present the empirical results obtained through calculations with the above-designed DEA model and methodological variations. To validate the calculated DEA results, we oppose the efficiency scores with the performance assessment of the company. In practice, this assessment is done through premium payments paid to the order pickers, as the aim of the premium is to reward pickers for their performance. The bonus is based on a time-depending target-performance comparison per batch. The target time is calculated by the order picking system, and the real-time is obtained through the beginning (picker receives batch information) and the end of the batch (the label is printed). It is operationalized as a ratio: when the target time of a batch is 10 min, and the picker completes the batch after 8 min, the company’s indicator is 1.25. Indices <1 express that the picker needed more time than proposed (see
Table 2).
The results indicate that the FDH method meets the company’s assessment well. With a correlation coefficient of r = 0.93, it is the method of choice for the order picking case study. We interpret this as a 93% goodness-of-fit for the proposed DEA model. On the other hand, the FRH and ERH models are unsuitable, with an r = 0.37.
As the second step of the analysis, we run a fuzzy DEA model with fuzzy inputs and outputs. The fuzziness is derived from differing ratios in the whole observation time of one month. The frontier remains non-convex, as in the previous example. We present the lower and upper bond scores of the fuzzy DEA and correlate the lower-bound values with the company’s assessment to evaluate the goodness-of-fit (see
Table 3).
The minimum ratios per order picker distort the efficiency calculation, leading to underestimated efficiency values and, additionally, to significant discrimination of less efficient DMUs. Therefore, this numerical example can support the arguments of Olesen, Petersen, and Podinovski (2015) regarding the use of ratio for non-convex models, but only within the fuzzy α-level-based approach to evaluate the interval efficiency of a set of DMUs with fuzzy inputs and outputs.
5. Discussion and Limitations
5.1. Summary of Findings
The aim of this article was to develop and apply a non-parametric methodology to evaluate the efficiency of order pickers as a typical blue-collar work task in retail logistics and electronic commerce. Real-live data of n = 23 order pickers processing 6109 batches with 865,410 stock-keeping units (SKUs) was implemented and analyzed. As the convexity axiom of standard DEA models cannot be fully satisfied when using ratio measurements with different denominators, the FDH approach was applied that does not assume convexity. Validating the efficiency scores with the company’s efficiency assessment, operationalized by premium payments, shows a 93% goodness-of-fit for the proposed model. This proved that the presented methodological approach is feasible for further research in measuring the efficiency of order pickers.
5.2. Theoretical Implications
The concept suggestion and application with real-life data from retail logistics showed that non-parametric efficiency measurements for order picking processes is a feasible concept. Therefore, further theoretical applications and method extension can and will be developed based on this in individual research and method proceeding endeavors.
In addition, the specific perspective of individual order pickers is an analytical basis for efficiency evaluations in this context. This is an important change, as most research concepts (for example [
2,
30,
31]) in the past have applied the technical system perspective as a basic unit of analysis. In this sense, a new field of analysis and discussion for order picking and electronic commerce processes was opened up by this paper.
The specific efficiency measures reported from the real-life use cases have to be evaluated and replicated in other electronic commerce process settings. However, this might lead in the end to a pool of efficiency value empirical benchmarking data to be used for research as well as practical implications. For example, the feasible range of human operator order picking, depending on the products and contexts involved, might be an important theoretical outcome and a basis for further discussion, especially in the application of further digital systems in order picking.
5.3. Managerial Implications
The specific managerial implications from this research for electronic commerce logistics managements address the question of a continued analysis of human efficiency in order picking in day-to-day business practice. This paper provided a methodological approach as groundwork for this task and enables retail and e-commerce businesses to efficiently tackle the analysis question. Therefore, we reduced the transaction costs of scientific management approaches by lowering the entrance hurdles (qualification) as well as costs (time to invest) for operational retail managers interested in the efficiency of order pickers.
Additionally, the methodological approach allows logistics managers to evaluate order pickers’ efficiency though integrating multiple dimensions while simultaneously considering behavioral aspects of humans working within operations systems of electronic commerce logistics. While logistics practitioners often utilize two-dimensional measures to evaluate order pickers efficiency, e.g., picking a time per stock keeping unit, these parametric measures do not take the warehouse structure into account. Hence, practitioners tend to argue that order pickers operating under different conditions, e.g., picking in different warehouse areas, are incomparable operational processes. Our contribution is a way forward in enabling a unified view on warehouse processes in electronic commerce logistics. Last, our methodology can be applied with picking logs that are available in most warehouse management systems (WMS) without further data aggregation or analysis. While most parametric methods rely on the exact retracement of order picker movements through complex path analysis, our approach utilizes order picking data that are typically included in WMS batch data. Therefore, it is easy to adopt in practice.
A further field of practical implications is addressing the question of individual result analysis and communication for the workers measures regarding their efficiency of work. This will be a future field of research and management concepts required as human motivation may be impacted strongly by such results and their communication. Therefore, HR managers, together with logistics and electronic commerce managers, will collaborate with researchers from the fields of HRM, psychology and sociology in order to develop suitable concepts for motivating communication concepts in this domain. A fitting example might be the movement of personal fitness analysis and communication where most information is perceived as motivating and supporting instead of demotivating. To follow this line or reasoning and communication, design might be crucial for improving the measured efficiency values, avoiding too much resistance from workers on this issue.
5.4. Limitations
Limitations of the presented study include the following points which are important to understand the value of the analysis: (1) there is one case in retail logistics, with 23 persons included. This limitation is crucial for further discussions as specific situations and frameworks for this case have to be considered and complementary research approaches where the number of participants should be increased. (2) The individual performance was only measured by applying different DEA models. Further research should, therefore, survey capability-related measurements, e.g., IQ or BMI of the order pickers and oppose these results to the efficiency scores. (3) The presented case only looks into a very small area of order picking. As outlined in the theoretical framework section, high variations between different picking contexts occur, e.g., the number of articles, size of the warehouse, and product placement within the warehouse. This should be extended into further issues like quality and sustainability as well as innovation and technology development of working systems in order picking [
62,
63,
64,
65]. (4) Within this analysis, one specific timeframe is analyzed. Interesting insights in addition might be gleaned from a longer timeline and analysis approach. Therefore, methodological extensions dealing with panel data, e.g., DEA window analysis, should be tested in future research.
6. Conclusions
Altogether, the empirical efficiency of order picking systems is a major research interest from science as well as business practice perspectives in the e-commerce and retail logistics domain. First, further research could dive deeper in the non-parametric examination of order pickers efficiency trying to find the reasons for occurring inefficiencies. Therein, slack-based measurements could be a promising concept to evaluate which order picker has to minimize or maximize which input-/output factor to enhance the individual efficiency compared to best practice order pickers. Second, building a bridge between the non-parametric and the parametric schools of thought could lead to promising insights. While the beta-coefficients quantify the degree of change in the outcome variable (e.g., seconds per pick) for every 1 unit of change in the predictor variable (e.g., picks per location) within parametric methods, it can be interesting to compare these measures with the slack-based measurement in DEA expressing the reason for inefficiencies. Last, drawing on behavioral operations management, our model does not differentiate between the physical and cognitive factors of human operators. As order picking in electronic commerce logistics is a labor-intensive task, the physical state of humans may play a crucial role. Moreover, these logistics systems are highly digitalized, which requires a certain amount of mental work during the order picking process. Developing models for a joint evaluation of these factors, probably through the lens of behavioral operations management or human factors (from an engineering perspective), may result in interesting new insights.
This paper contributed in an original and specific way to the knowledge in this field by providing new empirical as well as new method knowledge on the issue of non-parametric efficiency measurements for order picking as a central process in electronic commerce environments.
Author Contributions
Conceptualization, M.K.; methodology, D.L.; software, D.L.; validation, M.K. and D.L.; formal analysis, D.L.; investigation, D.L.; resources, M.K.; writing—original draft preparation, D.L.; writing—review and editing, M.K.; supervision, M.K.; project administration, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Ethical review and approval were waived for this study, due to the fact that we used anonymous data that was not retractable to individuals at any time.
Informed Consent Statement
Patient consent was waived due to the fact that we used anonymous data that was not retractable to individuals at any time.
Data Availability Statement
No data is provided.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bach, M.P. Editorial: Electronic Commerce in the Time of Covid-19—Perspectives and Challenges. J. Theor. Appl. Electron. Commer. Res. 2021, 16. [Google Scholar] [CrossRef]
- Bozer, Y.A.; Aldarondo, F.J. A simulation-based comparison of two goods-to-person order picking systems in an online retail setting. Int. J. Prod. Res. 2018, 56, 3838–3858. [Google Scholar] [CrossRef]
- Boysen, N.; Füßler, D.; Stephan, K. See the light. Optimization of put-to-light order picking systems. Naval Res. Logist. 2020, 67, 3–20. [Google Scholar] [CrossRef]
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking. A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Bormann, R.; De Brito, B.F.; Lindermayr, J.; Omainska, M.; Patel, M. Towards Automated Order Picking Robots for Warehouses and Retail. In Proceedings of the 12th International Conference, ICVS 2019, Thessaloniki, Greece, 23–25 September 2019; Springer Nature: Cham, Switzerland, 2019; Volume 11754, pp. 185–198. [Google Scholar]
- Masae, M.; Glock, C.H.; Grosse, E.H. Order picker routing in warehouses. A systematic literature review. Int. J. Prod. Econ. 2020, 224, 107564. [Google Scholar] [CrossRef]
- Tulkens, H. On FDH efficiency analysis: Some methodological issues and applications to retail banking, courts, and urban transit. J. Prod. Anal. 1993, 4, 183–210. [Google Scholar] [CrossRef]
- Hanson, R.; Medbo, L.; Johansson, M.I. Performance Characteristics of Robotic Mobile Fulfilment Systems in Order Picking Applications. IFAC PapersOnLine 2018, 51, 1493–1498. [Google Scholar] [CrossRef]
- Xiong, J.; He, Z.; Lin, R.; Liu, Z.; Bu, R.; Yang, Z.; Peng, H.; Zou, X. Visual positioning technology of picking robots for dynamic litchi clusters with disturbance. Comput. Electron. Agric. 2018, 151, 226–237. [Google Scholar] [CrossRef]
- Calzavara, M.; Sgarbossa, F.; Persona, A. Vertical Lift Modules for small items order picking: An economic evaluation. Int. J. Prod. Econ. 2019, 210, 199–210. [Google Scholar] [CrossRef]
- Fager, P.; Hanson, R.; Medbo, L.; Johansson, M.I. Kit preparation for mixed model assembly—Efficiency impact of the picking information system. Comput. Ind. Eng. 2019, 129, 169–178. [Google Scholar] [CrossRef]
- Lee, H.-Y.; Murray, C.C. Robotics in order picking: Evaluating warehouse lay-outs for pick, place, and transport vehicle routing systems. Int. J. Prod. Res. 2019, 57, 5821–5841. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, J.; Fan, X.; Zhu, D.; Wu, P.; Cao, N. Design of V-Type Warehouse Layout and Picking Path Model Based on Internet of Things. IEEE Access 2019, 7, 58419–58428. [Google Scholar] [CrossRef]
- D’Avella, S.; Tripicchio, P.; Avizzano, C.A. A study on picking objects in cluttered environments: Exploiting depth features for a custom low-cost universal jamming gripper. Robot. Comput. Manuf. 2020, 63, 101888. [Google Scholar] [CrossRef]
- Elbert, R.; Knigge, J.-K.; Makhlouf, R.; Sarnow, T. Experimental study on user rating of virtual reality applications in manual order picking. IFAC PapersOnLine 2019, 52, 719–724. [Google Scholar] [CrossRef]
- Grosse, E.H.; Glock, C.H.; Neumann, W.P. Human factors in order picking. A content analysis of the literature. Int. J. Prod. Res. 2017, 55, 1260–1276. [Google Scholar] [CrossRef]
- Dregger, J.; Niehaus, J.; Ittermann, P.; Hirsch-Kreinsen, H.; Hompel, P.D.M.T. Challenges for the future of industrial labor in manufacturing and logistics using the example of order picking systems. Procedia CIRP 2018, 67, 140–143. [Google Scholar] [CrossRef]
- Cragg, T.; Loske, D. Perceived work autonomy in order picking systems: An empirical analysis. IFAC PapersOnLine 2019, 52, 1872–1877. [Google Scholar] [CrossRef]
- Granotto, G.F.; Sgarbossa, F.; Glock, C.H.; Grosse, E.H. The effect of worker fatigue on the performance of a bucket brigade order picking system. IFAC PapersOnLine 2019, 52, 2195–2200. [Google Scholar] [CrossRef]
- Chen, F.; Xu, G.; Wei, Y. Heuristic routing methods in multiple-block warehouses with ultra-narrow aisles and access re-striction. Int. J. Prod. Res. 2019, 57, 228–249. [Google Scholar] [CrossRef]
- Lu, W.; McFarlane, D.C.; Giannikas, E.; Zhang, Q. An algorithm for dynamic order-picking in warehouse operations. Eur. J. Oper. Res. 2016, 248, 107–122. [Google Scholar] [CrossRef]
- Van Gils, T.; Ramaekers, K.; Caris, A.; de Koster, R.B. Designing efficient order picking systems by combining planning prob-lems. State-of-the-art classification and review. Eur. J. Oper. Res. 2018, 267, 1–15. [Google Scholar] [CrossRef]
- Ardjmand, E.; Bajgiran, O.S.; Youssef, E. Using list-based simulated annealing and genetic algorithm for order batching and picker routing in put wall based picking systems. Appl. Soft Comput. 2019, 75, 106–119. [Google Scholar] [CrossRef]
- Calzavara, M.; Glock, C.H.; Grosse, E.H.; Sgarbossa, F. An integrated storage assignment method for manual order picking warehouses considering cost, workload and posture. Int. J. Prod. Res. 2018, 57, 2392–2408. [Google Scholar] [CrossRef]
- Glock, C.H.; Grosse, E.H.; Abedinnia, H.; Emde, S. An integrated model to improve ergonomic and economic performance in order picking by rotating pallets. Eur. J. Oper. Res. 2019, 273, 516–534. [Google Scholar] [CrossRef]
- Li, J.; Karkee, M.; Zhang, Q.; Xiao, K.; Feng, T. Characterizing apple picking patterns for robotic harvesting. Comput. Electron. Agric. 2016, 127, 633–640. [Google Scholar] [CrossRef]
- Giannikas, V.; Lu, W.; Robertson, B.; McFarlane, D. An interventionist strategy for warehouse order picking: Evidence from two case studies. Int. J. Prod. Econ. 2017, 189, 63–76. [Google Scholar] [CrossRef]
- Ardjmand, E.; Shakeri, H.; Singh, M.; Bajgiran, O.S. Minimizing order picking makespan with multiple pickers in a wave picking warehouse. Int. J. Prod. Econ. 2018, 206, 169–183. [Google Scholar] [CrossRef]
- Battini, D.; Calzavara, M.; Persona, A.; Sgarbossa, F. A method to choose between carton from rack picking or carton from pallet picking. Comput. Ind. Eng. 2018, 126, 88–98. [Google Scholar] [CrossRef]
- Cao, X.; Zou, X.; Jia, C.; Chen, M.; Zeng, Z. RRT-based path planning for an intelligent litchi-picking manipulator. Comput. Electron. Agric. 2019, 156, 105–118. [Google Scholar] [CrossRef]
- Li, Z.; Miao, F.; Yang, Z.; Chai, P.; Yang, S. Factors affecting human hand grasp type in tomato fruit-picking. A statistical investigation for ergonomic de-velopment of harvesting robot. Comput. Electron. Agric. 2019, 157, 90–97. [Google Scholar] [CrossRef]
- Bu, L.; Hu, G.; Chen, C.; Sugirbay, A.; Chen, J. Experimental and simulation analysis of optimum picking patterns for robotic apple harvesting. Sci. Hortic. 2020, 261, 108937. [Google Scholar] [CrossRef]
- Mu, L.; Cui, G.; Liu, Y.; Cui, Y.; Fu, L.; Gejima, Y. Design and simulation of an integrated end-effector for picking kiwifruit by robot. Inf. Process. Agric. 2020, 7, 58–71. [Google Scholar] [CrossRef]
- Qin, J.; Yin, Y.; Liu, Z.; Du, Y.; Wang, G.; Zhu, Z.; Li, Z. Optimisation of maize picking mechanism by simulation analysis and high-speed video experiments. Biosyst. Eng. 2020, 189, 84–98. [Google Scholar] [CrossRef]
- Koopmans, T.C. An analysis of production as an efficient combination of activities. In Activity Analysis of Production and Allocation. Proceeding of a Conference; Koopmans, T.C., Ed.; Wiley: London, UK, 1951; pp. 33–97. [Google Scholar]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. Ser. A 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Debreu, G. The coefficient of resource utilization. Econometrica 1951, 19, 273–292. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Banker, R.D. Estimating most productive scale size using data envelopment analysis. Eur. J. Oper. Res. 1984, 17, 35–44. [Google Scholar] [CrossRef]
- Banker, R.D.; Cooper, W.W.; Seiford, L.M.; Zhu, J. Returns to Scale in DEA. In International Series in Operations Research & Management Science; Springer Nature: Cham, Switzerland, 2011; pp. 41–70. [Google Scholar]
- Hatami-Marbini, A.; Agrell, P.J.; Fukuyama, H.; Gholami, K.; Khoshnevis, P. The role of multiplier bounds in fuzzy data envelopment analysis. Ann. Oper. Res. 2017, 250, 249–276. [Google Scholar] [CrossRef]
- Sengupta, J.K. Measuring efficiency by a fuzzy statistical approach. Fuzzy Sets Syst. 1992, 46, 73–80. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Tavana, M.; Saati, S.; Agrell, P.J. Positive and normative use of fuzzy DEA-BCC models: A critical view on NATO enlargement. Int. Trans. Oper. Res. 2012, 20, 411–433. [Google Scholar] [CrossRef]
- Sengupta, J.K. A fuzzy systems approach in data envelopment analysis. Comput. Math. Appl. 1992, 24, 259–266. [Google Scholar] [CrossRef]
- Lertworasirikul, S.; Fang, S.-C.; Joines, J.A.; Nuttle, H.L. Fuzzy data envelopment analysis (DEA): A possibility approach. Fuzzy Sets Syst. 2003, 139, 379–394. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Emrouznejad, A.; Tavana, M. A taxonomy and review of the fuzzy data envelopment analysis literature: Two decades in the making. Eur. J. Oper. Res. 2011, 214, 457–472. [Google Scholar] [CrossRef]
- Guo, P.; Tanaka, H. Fuzzy DEA. A perceptual evaluation method. Fuzzy Sets Syst. 2001, 119, 149–160. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Saati, S. Stability of RTS of efficient DMUs in DEA with fuzzy under fuzzy data. Appl. Math. Sci. 2009, 3, 2157–2166. [Google Scholar]
- Dyson, R.G.; Allen, R.; Camanho, A.S.; Podinovski, V.V.; Sarrico, C.S.; Shale, E.A. Pitfalls and protocols in DEA. Eur. J. Oper. Res. 2001, 132, 245–259. [Google Scholar] [CrossRef]
- Jain, S.; Triantis, K.P.; Liu, S. Manufacturing performance measurement and target setting: A data envelopment analysis approach. Eur. J. Oper. Res. 2011, 214, 616–626. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Agrell, P.J.; Tavana, M.; Khoshnevis, P. A flexible cross-efficiency fuzzy data envelopment analysis model for sustainable sourcing. J. Clean. Prod. 2017, 142, 2761–2779. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Toloo, M. Data envelopment analysis models with ratio data: A revisit. Comput. Ind. Eng. 2019, 133, 331–338. [Google Scholar] [CrossRef]
- Thanassoulis, E.; Boussofiane, A.; Dyson, R. Exploring output quality targets in the provision of perinatal care in England using data envelopment analysis. Eur. J. Oper. Res. 1995, 80, 588–607. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Amin, G.R. DEA models for ratio data: Convexity consideration. Appl. Math. Model. 2009, 33, 486–498. [Google Scholar] [CrossRef]
- Hollingsworth, B.; Smith, P. Use of ratios in data envelopment analysis. Appl. Econ. Lett. 2003, 10, 733–735. [Google Scholar] [CrossRef]
- Olesen, O.B.; Petersen, N.C.; Podinovski, V.V. Efficiency analysis with ratio measures. Eur. J. Oper. Res. 2015, 245, 446–462. [Google Scholar] [CrossRef]
- Deprins, D.; Simar, L.; Tulkens, H. Measuring Labor-Efficiency in Post Offices. In Public Goods, Environ-Mental Externalities and Fiscal Competition; Chander, P., Drèze, J., Lovell, C.K., Mintz, J., Eds.; Springer Science+Business Media LLC: Boston, MA, USA, 2006; pp. 285–309. [Google Scholar]
- Agrell, P.J.; Tind, J. A Dual Approach to Nonconvex Frontier Models. J. Prod. Anal. 2001, 16, 129–147. [Google Scholar] [CrossRef]
- Klumpp, M.; Zijm, H. Logistics Innovation and Social Sustainability: How to Prevent an Artificial Divide in Human–Computer Interaction. J. Bus. Logist. 2019, 40, 265–278. [Google Scholar] [CrossRef]
- Klumpp, M.; de Leeuw, S.; Regattieri, A.; de Souza, R. Humanitarian Logistics and Sustainability; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Centobelli, P.; Cerchione, R.; Esposito, E.; Oropallo, E. Surfing blockchain wave, or drowning? Shaping the future of distributed ledgers and decentralized technologies. Technol. Forecast. Soc. Chang. 2021, 165, 120463. [Google Scholar] [CrossRef]
- Di Nardo, M.; Clericuzio, M.; Murino, T.; Sepe, C. An Economic Order Quantity Stochastic Dynamic Optimization Model in a Logistic 4.0 Environment. Sustainability 2020, 12, 4075. [Google Scholar] [CrossRef]
- Di Nardo, M.; Forino, D.; Murino, T. The evolution of man–machine interaction: The role of human in Industry 4.0 paradigm. Prod. Manuf. Res. 2020, 8, 20–34. [Google Scholar] [CrossRef]
- Raut, R.D.; Mangla, S.K.; Narwane, V.S.; Dora, M.; Liu, M. Big Data Analytics as a mediator in Lean, Agile, Resilient, and Green (LARG) practices effects on sustainable supply chains. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102170. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).