4.2. Research Hypotheses
The number of submissions reflects solvers’ participation, while the level of task rewards—which relates to expected value—determines whether solvers decide to participate. According to expectation value theory, a solver’s expected value is positively correlated with the task rewards set by seekers. The higher the task rewards, the higher the expected reward of solvers, and the higher the submission number [
27]. This interpretation is consistent with most empirical tests, but it ignores whether task rewards affect the expected value in another way. As discussed, solvers are motivated by expected value rather than the total amount of task rewards [
35]. Expected value is also related to winning probability. Therefore, task rewards cannot be equated with the expected value of participation and bidding. Glazer and Hassin (1988) noted that high task rewards attract more solvers to participate, but the probability of successfully bidding then decreases because of the increased competition [
43]. Yang and Saremi (2015) contended that task rewards play a dual role in solvers’ participation decisions. On the one hand, a higher reward amount will increase solvers’ enthusiasm and make them more willing to register and compete. On the other hand, higher prices often denote significant and more complex work, which will reduce the number of solvers who are able to provide adequate solutions [
44]. Xu and Zhang (2018) found that, due to limited ability, solvers cannot be motivated infinitely in the same task. As rewards increase, solvers’ expected value will first increase and then decrease [
45].
Based on this analysis, expectation value theory and self-efficacy assessment theory can explain the effects of task rewards on submission numbers. With the increase of task rewards, the expected value of solvers, as well as the number of submissions, also increase. If the rewards are increased continually, solvers’ submissions will rise, and competition will be more intense. Until the task rewards exceed a given threshold, solvers may not participate in the contest because the increase in the degree of competition lowers winning probability and expected value. Thus, excessive task rewards reduce the number of submissions. Furthermore, in crowdsourcing contests, solvers need to assess self-efficacy and make decisions about whether to participate. The level of task rewards often reflects seekers’ task requirements. According to self-efficacy evaluation theory, if the rewards increase beyond a certain range, some solvers with low self-efficacy assessment are squeezed out. Therefore, the relationship between task rewards and submission may be an inverted U-shape, hence Hypothesis 1:
Hypothesis 1. Task rewards have an inverted U-shaped relationship with the number of submissions.
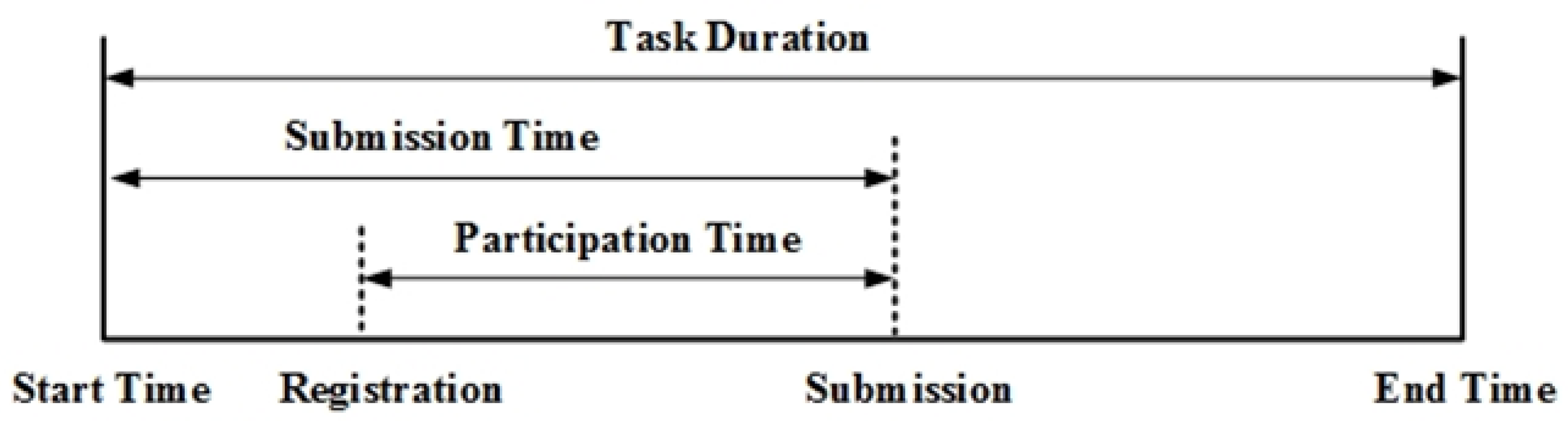
Participation time reflects the efforts of solvers who have chosen to participate in the task. Task rewards not only affect the number of submissions, but also the level of solvers’ efforts during the task process. The more efforts solvers make, the higher quality the solutions have. Levels of effort are affected by the state of participation, which is a psychological state in which a solver is willing to invest their own energy for the purpose of accomplishing a task [
46]. Solvers are usually interest-oriented [
47], meaning they have an extrinsic motivation to pursue higher economic returns. This motivation prompts solvers to continue to focus on tasks and invest more time and energy [
27]. In order to increase the probability of receiving task rewards, solvers who are in the participation stage have the motivation to contribute more time and energy to improving the quality of the solution, and therefore increase the attention given to the task. Task rewards stimulate this motivation [
16].
Thus, this study uses participation time to indicate effort level, and argues that solvers in the participation state will invest more time to increase the probability of successful bidding and obtain more revenue. However, there may only be a positive linear relationship between participation time and task rewards. Since the solver has chosen to participate in the contest by the participation stage, the extrusion effect of self-efficacy would not occur in this situation. Therefore, the second hypothesis is proposed as follows.
Hypothesis 2. Task rewards positively affect solvers’ participation time.
Solvers’ participation in crowdsourcing contests is a dynamic random process. The dynamic random process is similar to a competitive auction. The longer the auction is open, the more bidders can be included in the auction [
48]. In crowdsourcing contests, the longer the task is released, the more solvers will see the tasks posted and participate, thereby increasing the number of submissions [
5,
20]. At the same time, the longer the task duration, the more solvers will be able to participate, because most solvers use their spare time to participate in crowdsourcing contests [
49]. In terms of task quality, solvers cannot solve a task in a limited time. Many solvers are more willing to participate in crowdsourcing contests with longer task duration. As such, short task duration is not conducive to seekers who desire high-quality solutions.
However, a short duration is beneficial to solvers. According to expected value theory, solvers’ participation in crowdsourcing contests is considered as trades. Solvers’ ultimate goal is to obtain the highest expected return at the lowest cost and to recover the input cost in a short period. In short-term tasks, solvers can obtain results in a short time after the submission stage and achieve the expected value with a certain probability, which could compensate for solvers’ time and labor costs. If the duration is too long, it will increase solvers’ input costs because of its longer attention and higher time costs. In addition, there is also the opportunity cost for solvers in that investing in a task requires sacrificing the opportunity to obtain other benefits. If the expected value is lower than the opportunity cost for a certain duration of time, solvers will renounce participating in the task [
50]. Korpeoglu et al. (2017) argued that a longer task duration increases solvers’ workload and improves the quality of solutions, which increases seekers’ profitability. However, as the task duration increases, solvers’ participation reduces, and seekers’ returns are likely to decrease [
10]. Furthermore, solvers’ trust in seekers will decrease over time, motivation for participation will drop, and solutions will not be submitted; the loss of trust occurs because, in crowdsourcing contests, there have been cases of seekers using the solutions submitted by solvers but refusing to pay the rewards. Solvers therefore have less trust in a long-term contest [
27].
Accordingly, this study maintains that on the one hand, task duration can dynamically and objectively encourage more solvers to participate depending on the time allotted and obtain more task solutions. However, once the task duration reaches a certain threshold, a crowding effect causes the number of submissions to drop. Thus, Hypothesis 3 is proposed as follows:
Hypothesis 3. Task duration has an inverted U-shaped relationship with the number of submissions.
According to expectation value theory, for solvers, the longer the task duration, the more time the solvers have to solve the task; this motivates solvers to improve the quality of their solutions to obtain a higher expected value. Thus, solvers invest more attention into a long-term task [
50]. However, if the task duration is too long, solvers’ patience will decrease because of the long cost recovery period and high opportunity cost. Solvers feel that it is not necessary to invest too much time into a task with a lower expected value, thereby reducing participation time.
According to several relevant studies on self-efficacy assessment, solvers with high self-efficacy assessments have less participation time than solvers with low assessments [
40]. For an individual, an increase in self-efficacy assessment can increase the level of effort invested compared to when the self-efficacy assessment is low. When self-efficacy is assessed beyond a certain limit, it reduces a solver’s effort [
41,
51]; this may explain why, when the task duration is short, solvers show low self-efficacy assessments because of insufficient information and high requirements to solve the task in a short time. However, this dynamic stimulates solvers to exert more effort in solving a task [
27]. Nonetheless, as the task duration extends, the self-efficacy assessment to solve a task becomes higher, and the expectation of the self-efficacy assessment exceeds the actual level of self-efficacy. For example, most people think they will present a high-quality solution if given a long time, which makes it unnecessary to take too much time to solve the task [
52]. Therefore, Hypothesis 4 is proposed as follows.
Hypothesis 4. Task duration has an inverted U-shaped relationship with participation time.