1. Introduction
The concept of complementary goods belongs to the realm of microeconomics. Complementary (and substitute) goods first became the subjects of academic discourse in 1894 [
1]. Ever since that time, the problem of complementary goods has been constantly present in academic research. A comprehensive description of the development of the concept of complementarity can be found in research conducted by Lenfant [
2,
3]. According to the common understanding, complementarity is a relationship involving mutual supplementation of goods. In microeconomics, the concept of complementarity can be defined in a number of different ways. The theory of supply and demand defines complementarity by means of a cross-price elasticity of demand, which measures the responsiveness of demand for one good to a change in the price of another good (ceteris paribus). Two goods are considered to be complementary when the cross-price elasticity of demand is negative for these goods.
A very intuitive definition of complementarity is also provided by the theory of consumer choice. The definition of complementarity is based on the correlations between utility and demand. For complementary goods, the marginal utility of one good increases along with the increase in demand for another good.
The definitions of complementarity that can be found in the literature are rather difficult to apply in practice, mainly due to the insufficient amount of data describing demand fluctuations resulting from price changes, and to the necessity of making quite restrictive assumptions about the type of utility function. One of the possible ways to overcome these difficulties is to take advantage of the opportunities provided by association analysis.
Association analysis, also referred to as market basket analysis, investigates the correlations between goods based on purchases made by consumers [
4]. If two goods are considered to be complementary, then they will be more frequently purchased together. So, the more frequently a particular combination of goods appears in a basket, the greater the probability is that these goods are complementary.
The notion of complementarity (but also substitutability) lies at the heart of recommendation systems. Interesting examples of using product complementarity in creating such a system can be found in [
5,
6,
7].
The main objective of this paper is to define the concept of complementarity of goods based on association analysis. The proposed measure is called basket complementarity (or b-complementarity). It provides the possibility to consider asymmetric cases, i.e., cases when a consumer purchasing good gains greater satisfaction if he/she additionally buys good but good may also be purchased without any connection with good . Such properties can be of great importance, e.g., in building pricing strategies or in recommender systems. The ‘basket’ definition also enables identification of the relations of complementarity that exist regardless of other goods, as well as relations that are a derivative of complementarity with other goods.
The paper consists of an introduction and three sections.
Section 1 is devoted to the issue of complementarity of goods in microeconomics. It presents two main approaches to the mathematical formalization of this concept.
Section 2 describes the well-known market basket analysis concepts. In
Section 3, the definition of complementarity of goods is introduced based on individual shopping baskets. The section also provides a numerical example illustrating the possibilities of using market basket analysis in order to identify complementary goods. The paper ends with concluding remarks. The conclusions point out the advantages provided by the definition of complementarity based on the properties of shopping baskets in comparison with the classic approach, as well as the potential of using association analysis in building marketing strategies.
2. Complementarity of Goods in Microeconomics
The idea of complementarity was first introduced by Auspitz and Lieben in 1894 [
1]. Two goods are considered to be complementary if d
2u/dx
1dx
2 > 0, where u is the utility function while x
1 and x
2 represent the demand for the first and the second good, respectively. A doubtless advantage of this definition is its very intuitive interpretation. It suffices to observe that du/dx
1 is the marginal utility of the first good and du/dx
2 is the marginal utility of the second good. The complementarity condition means that the marginal utility of the first good increases as more of the second good is purchased. Another advantage of Auspitz and Lieben’s definition is the symmetry. If the first good is complementary to the second good, then the second good is also complementary to the first good.
However, the definition by Auspitz and Lieben has an essential disadvantage. From the utility function theory, it follows that monotonic transformations do not change the customer’s preferences. Bearing the above in mind, it should be expected that monotonic transformations will not change the classification of goods, i.e., complementary goods prior to the transformation will be complementary after the monotonic transformation too. Auspitz and Lieben’s definition meets this expectation but exclusively for linear transformations.
The contemporary definition of complementarity was formed as a result of many economists’ work. However, the greatest contribution was from Hicks and Allen [
8], hence it is most often ascribed to these two researchers. In contrast to the definition by Auspitz and Lieben, which is classified among the concepts of the so-called theory of cardinal utility, the definition by Hicks and Allen is a part of the ordinal utility theory which assumes that the measurement of utility in absolute scale is neither possible nor necessary. It suffices for the consumer to be able to determine the preference relation between the goods as well as the rate of exchange of one good for other ones.
Within the ordinal utility theory, complementary goods are defined based on correlations between demand and price. Two goods are complementary if dx
1/dp
2 > 0, where x
1 is the function of demand for the first good and p
2 is the price of the second good. Indifference curves for complementary goods have a characteristic hyperbolic shape. The stronger relation of complementarity, the more the shape of the indifference curve is close to the letter L. It should be mentioned that the Allen-Hicks definition occurs in two variants, which are derived from Slutsky’s theorem. The effect of the change in demand resulting from the change of a price consists of the substitution and the income effects. If the total demand is taken into account, then under Allen-Hicks’s definition it is termed gross complementarity. If demand resulting solely from a change in price relations (substitution effect) is taken into account, then it is termed net complementarity. The net complementarity relation is symmetric. The specific impact of the income effect implies that the gross complementarity relation may not be symmetric. Good
may be gross complementary to good
but good
need not be gross complementary to good
. Chris De Jaegher [
9] argues that the asymmetry of the gross complementarity relation need not be disadvantageous at all.
In contemporary research, the emphasis is placed on distinguishing different types of complementarity. Berry et al. [
10] distinguish 7 major types:
quantitative complementarity: when an increase in the quantity of one good leads to an increase in the value of another, e.g., right and left shoe;
qualitative complementarity: when an increase in the quality of one good leads to an increase in the marginal value of quality of another good, e.g., a suit paired with a tie;
within a category complementarity: when a basket of goods within the same category is selected in such manner as to best suit the customer’s current needs, e.g., a home film library;
cross-category complementarity: when goods from different categories are related with each other in order to achieve a greater value for the consumer, e.g., milk and cornflakes, or software and hardware;
provider-driven complementarity: independent goods become complementary if they are delivered by the same provider (often within a brand or series), e.g., banking services and brokerage services;
dynamic complementarity: substitute goods in static conditions become complementary in dynamic conditions, e.g., free vs. paid software version;
complementarity across individual agents: if consumers (agents) interact with each other, then their choices are complementary, e.g., a Facebook friend.
It follows from the above classification that complementarity is a complex and heterogeneous relation between goods. It can be considered from the point of view of both single and multiple consumers. Also, time can play an important role (dynamic context vs. static context), i.e., some goods may become complementary in the dynamic context even though they were not so before in the static context.
3. Basic Terminology in Association Analysis
This section reviews the basic terminology used in association analysis.
Let be the set of all available items (goods) and be the set of all transactions. Any set is termed itemset. Each transaction contains a subset of items in . An association rule is defined as an implication of the form , where and are disjoint itemsets that are respectively called the antecedent and consequent of the rule. Such a rule may be interpreted as:
If a basket contains itemset X then, with a specified probability, this basket will also contain itemset Y.
The relative number of occurrences of itemset
X in the transaction set
T is called the support of itemset and is calculated according to the following formula:
where the symbol |⋅| denotes the number of elements in a set.
The level of support signifies the percentage of transactions in which specified goods were purchased at the same time in relation to all the transactions concerned.
Let min_supp denote the minimum level of support. The itemset with support less than min_supp will be considered as insignificant. If a support for a given itemset is greater than min_supp, then the set will be referred to as a frequent itemset. Association rules are created based on frequent itemsets, and the support of an association rule equals to the support of the itemsets.
Each rule is also characterized by its level of confidence, calculated according to the following formula:
Confidence indicates the probability of occurrence of the itemset, which is the consequent of the association rule in the basket if the basket also contains the itemset being the antecedent of the rule. Let min_conf be the minimum confidence level that a rule must achieve to be considered as significant. Rules with confidence less than min_conf will be rejected.
An essential feature of confidence is its asymmetry. This implies that the value of conf() may, but need not, be equal to the value of conf(). This property will be used further on in this paper.
Another measure used to evaluate association rules is the lift [
11], which is calculated according to the following formula:
Lift measures the correlation between itemsets from antecedent and consequent of a rule. If lift = 1 itemsets X and Y are independent. When lift > 1, itemsets X and Y are positively correlated. For lift < 1, itemsets X and Y are negatively correlated.
The aforementioned measures of association rules are the most popular but not the only ones appearing in the literature. More examples of measures describing the rules can be found e.g., in [
12].
4. The Concept of Basket Complementarity
Association analysis was developed to support investigation on relations between goods in a shopping basket. Hence the alternative name Market Basket Analysis was also developed. It was developed taking advantage of the computerization of sales processes at supermarkets, which enabled collecting data on purchases made by customers. Agrawal, Imiliński and Swami [
13] made a significant contribution to the development of the discipline. The main purpose of association analysis is to discover patterns in the sets of empirical data, such as data on shopping transactions.
B-complementarity between goods may be regarded as one of such patterns.
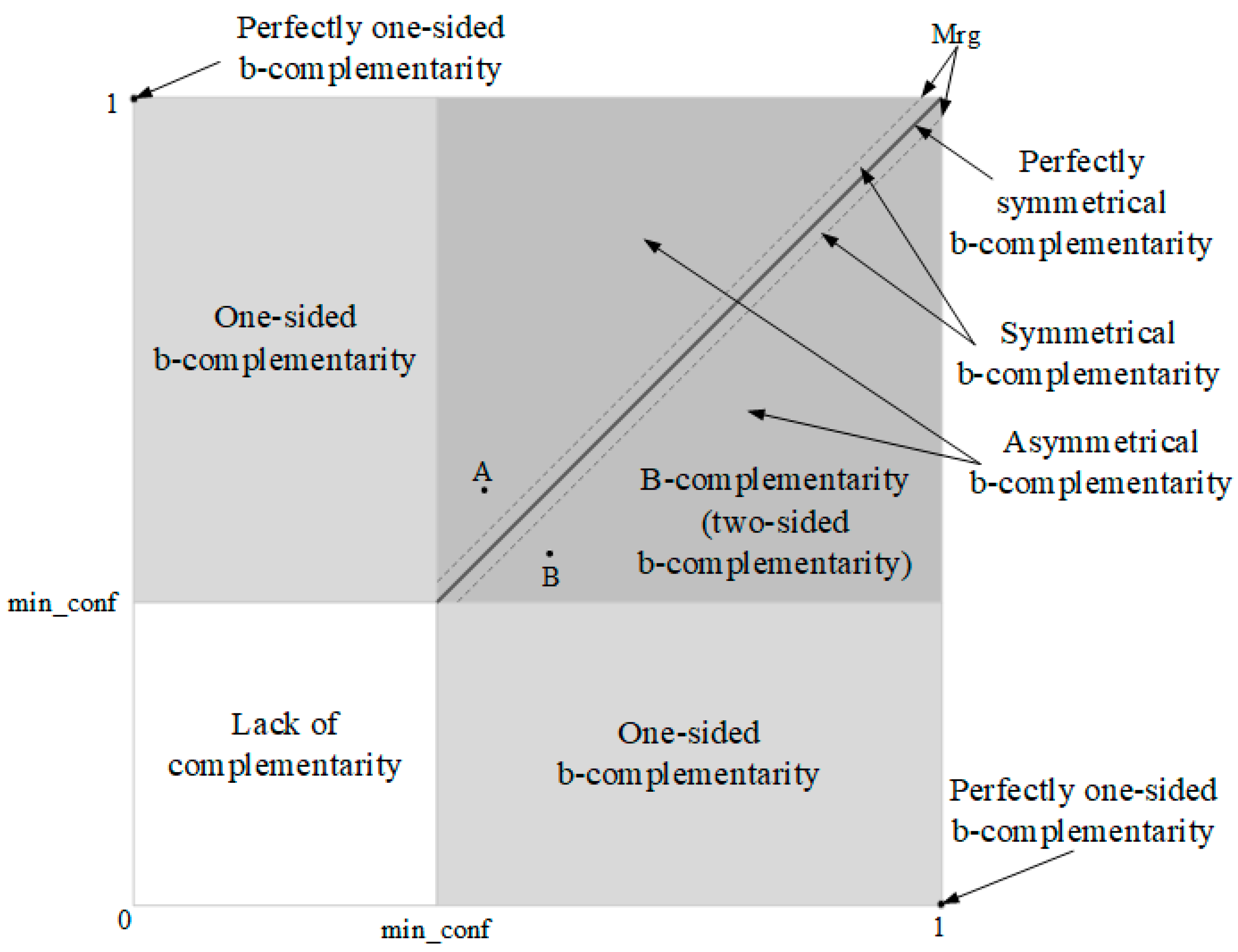
This section is organized as follows. First, the concept of b-complementarity will be formally introduced, along with all of its variants. In the next part, the most important properties of introduced concept will be presented. At the end of the section, a simple example illustrating each concept will be shown. The following types of b-complementarity may occur between any two goods:
I. One-sided b-complementarity:
Definition 1. Any two goods
are one-sided complementary if, at a given level of min_conf, the following conditions hold true: ,
and
.
One-sided b-complementarity concerns the cases when good is usually purchased together with good but good is seldom purchased together with good . This prompts the conclusion that good is purchased more frequently than good . The condition involving the level of support is intended to ensure that items and are not independent, and the relations between them are not merely a matter of coincidence.
As an example of one-sided b-complementarity, one might consider the relation between cornflakes () and milk (). It is not hard to observe that cornflakes are usually bought together with milk while milk is often bought regardless of whether cornflakes are bought or not.
A special example of one-sided b-complementarity is perfectly one-sided b-complementarity, which occurs when: and . This is when one item () serves as a complement to another item () and may be, e.g., indispensable for its functioning. At the same time, item is so universal that it can be used (purchased) with other items as well. Examples of items with possible relation of perfectly one-sided b-complementarity are: a remote control () and batteries (), a mobile phone () and a charger ().
II. B-complementarity (two-sided b-complementarity):
Definition 2. Any two goods are b-complementary (two-sided b-complementary) if, at a given level of min_conf, the following conditions hold true: , and .
B-complementarity occurs when both good is purchased with good and good is purchased with good . This is also subject to the condition that the relation between the items is not a matter of coincidence, i.e., that the items are not independent.
An example of goods with possible relation of b-complementarity might be bread and ham, where bread is usually bought with ham and, in many cases, a person buying ham also buys bread.
The relation of b-complementarity need not be a symmetric relation, i.e., the fact that good is b-complementary to need not imply that good will be to the same extent b-complementary to . If the strength of the relation between goods and is equal to the strength of the relation between and , i.e., , then this relation will be called perfectly symmetric b-complementarity. Because such an ideal match may seldom occur in real life, it is proposed to introduce the permissible margin of deviation between the values of b-complementarity, denoted as Mrg. The value of the Mrg factor should be interpreted as the maximum difference between the level of b-complementarity of two goods whose relation can be termed as symmetric. Thus, if a relation of b-complementarity between goods and satisfies the following condition: , then there occurs a relation of symmetric b-complementarity between the goods. If the difference in the strengths of relations between goods and exceeds the adopted value of Mrg, then this relation will be termed asymmetric.
Figure 1 presents the relations of
b-complementarity described above.
Both points A and B marked in the figure represent correlations between goods and and so they are positioned symmetrically with respect to the straight line denoting perfectly symmetric b-complementarity. The coordinates of the points, for example of point A, have been determined as follows:
The following part of the article presents two examples using mock data, the purpose of which is to illustrate the described definitions.
Example 1. Table 1 presents a set of 15 transactions. It is assumed that the minimum level of support min_supp = 10% and min_conf = 40%. and:
Based on the calculations presented above, it can be concluded that:
Cornflakes are complementary to Milk and this is one-sided b-complementarity;
Milk is complementary to a Bread Roll and this is symmetric b-complementarity;
Butter is complementary to a Bread Roll and this is asymmetric b-complementarity;
Butter is complementary to Milk and this is asymmetric b-complementarity.
The relations described are presented in
Figure 2. The items in the figure are marked as follows:
Bread Roll—BR,
Milk—Ml,
Cornflakes—Cf,
Butter—Bt.
For three goods, there may occur a relationship of weak b-complementarity. Weak b-complementarity should be understood as a relation of b-complementarity between goods being the result of the occurrence of a relation between other goods. Formally, a weak b-complementarity is defined as follows:
Definition 3. Three goods are provided: . Goods and are one- or two-sided b-complementary. Between goods and , there is also a relation of b-complementarity (two-sided or one-sided). If between goods and there is a relation of b-complementarity (two-sided or one-sided) and at least one of the following conditions is met: or , then the relation between goods and will be called weak b-complementarity.
Weak b-complementarity may occur when two goods, and , are strongly b-complementary to each other and one of them, e.g., , is strongly b-complementary to z. In such a case, even though there is a relation of b-complementarity between goods and , this relation may result from the relation between goods and or between and . Therefore, such a relation is termed weak b-complementarity.
Example 2. Utilizing the data from Example 1 (see Table 1), the following calculations have been carried out: Based on the obtained results, it can be concluded that the relation of b-complementarity between Milk and Butter is a weak relation. A high level of b-complementarity between these goods results from the very strong relation between Bread Roll and Butter, as well as the strong relation between Milk and Bread Roll.
5. Empirical Example
The presented concept has been verified on empirical data from “The Instacart Online Grocery Shopping Dataset 2017” [
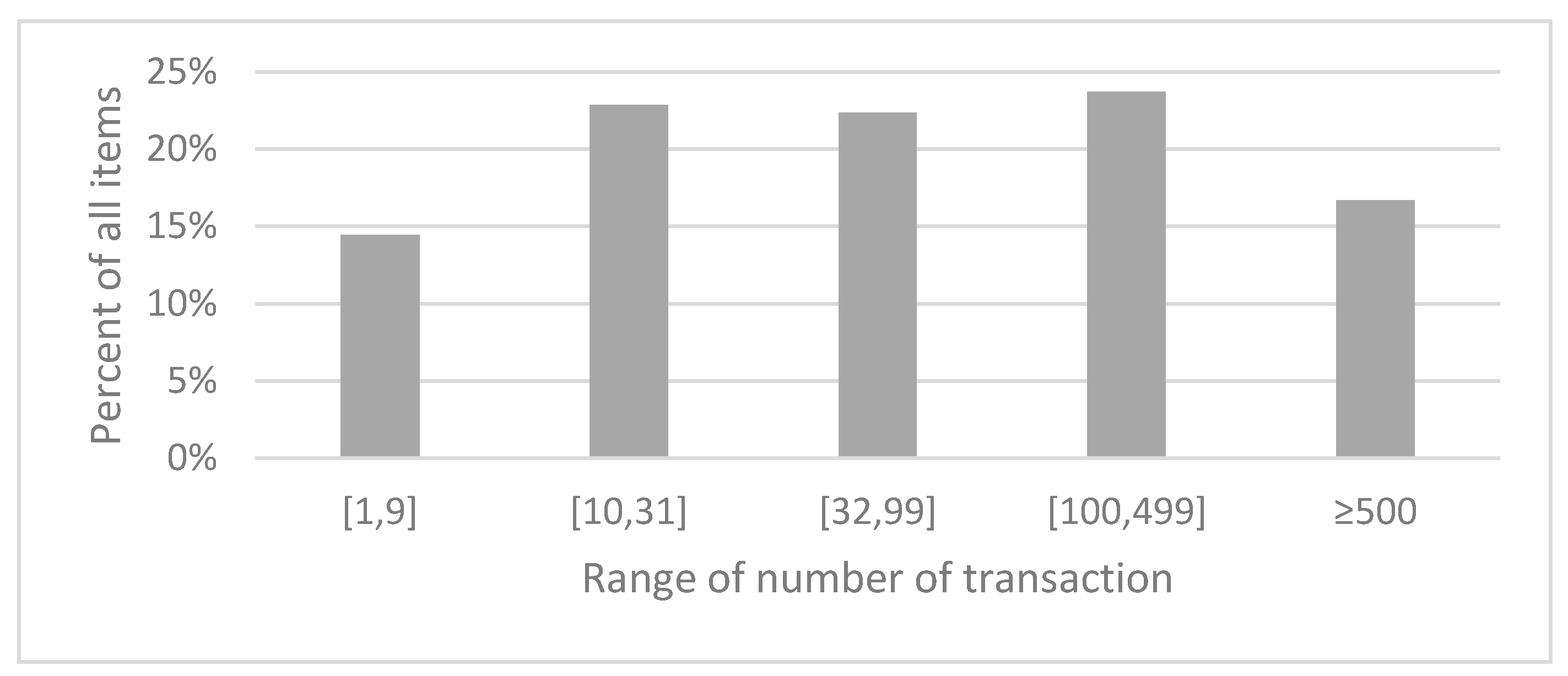
14]. The database has 49,677 items and 3,214,874 transactions. It was imported to Microsoft SQL Server 2017. The number of occurrences of each product was determined using a query that counts the number of transactions in which a given product was purchased.
Table 2 shows a summary of how many items occurred in a given number of transactions (defined by ranges). The average number of transactions for the items is 653 with a standard deviation of 4792.
As shown in
Table 2, it may be concluded that there are 7165 items that have been bought fewer than 10 times, which makes up to 14.5% of all the items. Conversely, 16.7% (8290) items were bought 500 times at the minimum. Over two thirds of all the items were bought either more than 10 times or less than 500 times. The described dependencies are presented in
Figure 3.
A minimum support level was set to 0.001%, the value of which corresponds to a minimum number of 32 transactions. The number of items meeting this condition was 31,169. On this basis, 961,000 two-element itemsets were determined that met the condition of a minimum level of support. After rejecting itemsets that did not meet the second requirement regarding item independence, 877,000 two-element itemsets remained.
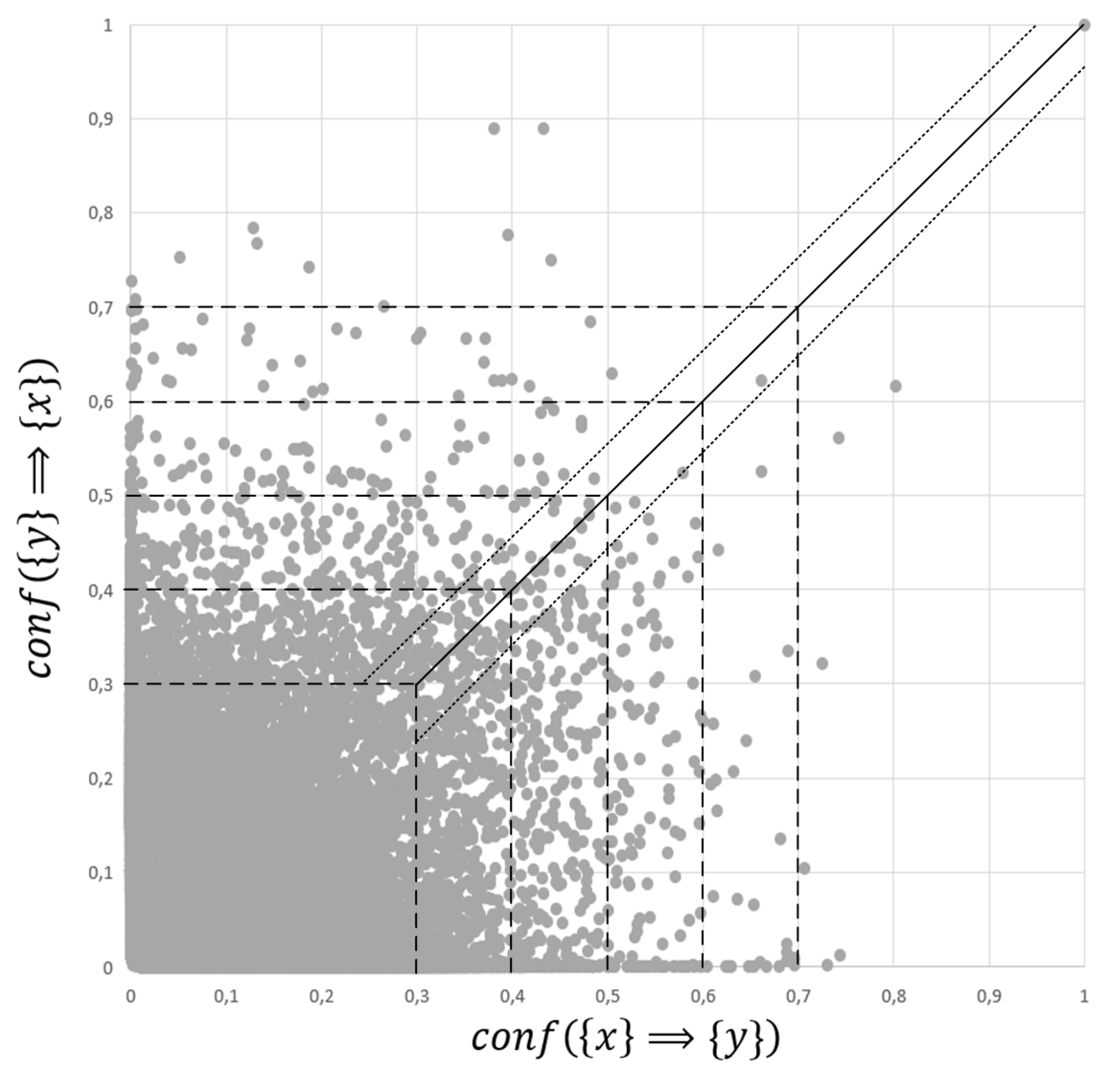
Figure 4 presents the visualization of confidence levels between the items ({x, y}) that forming a given itemset. In order to increase transparency, each pair of items was marked as exactly one point—in contrast to
Figure 2, where each pair of items corresponds to two points located symmetrically to the straight line, indicating perfectly symmetric
b-complementarity.
Vertical and horizontal dashed lines indicate support values, which correspond to the Min_conf value from
Table 3. The continuous line indicates perfect symmetry, and the diagonal dotted line—the Mrg coefficient, which is used to determine symmetric
b-complementarity—equals 5%.
Table 3 shows the number of detected one- and two-sided
b-complementarities depending on the assumed minimum confidence level. The number of cases of perfectly symmetric
b-complementarity, which depends on the assumed value of the
Mrg and
min_conf parameters, is also presented.
Based on the data from
Table 3, it can be concluded that one-sided
b-complementarity between goods occurs much more often than two-sided
b-complementarity. For symmetric
b-complementarities, depending on the value of the
Mrg parameter, the number of occurrences ranges from several (perfectly symmetric
b-complementarity for the
Mrg = 0%) to over 100 times. It is worth noting that regardless of the level of minimal support, at least 1/4 of two-sided
b-complementarities are symmetric for Mrg when it is equal to 5%.
There were no perfectly one-sided b-complementarity relationships in the data set under consideration. The strongest one-sided relations and occurred in the case of 3 itemsets.
The highest confidence levels for the detected weak b-complementarity relationships ranged from 10% to 15% (3 relationships including 1 two-sided relationship) and were therefore rejected due to the low confidence level.
The analysis of sales data leads to an interesting conclusion regarding the relationship between the number of one and two-sided complementary goods. It turns out that the number of cases of one-sided b-complementarity (for all analyzed levels of minimal support) is an order of magnitude greater than the number of cases of two-sided b-complementarity. Such an observation may be the basis for reconsidering the assumptions underlying the classic definition of complementarity between goods.
6. Conclusions
Within the theory of supply and demand, complementarity is defined on the basis of relations between price and demand. Goods are deemed to be complementary if the cross-price elasticity of demand is negative. Estimation of cross-price elasticity of demand requires data on demand at different prices, ceteris paribus. Data of this kind are typically difficult to access, their quantity is largely insufficient and the ceteris paribus assumption is in clear contradiction to the size of the sample. The definition of b-complementarity introduced in the paper makes use of data on transactions made by customers and does not require information on the prices, although such information can be taken into account as well in future research. The accessibility of this kind of data (e.g., in the e-commerce industry) is incomparably greater than price and demand data, which means that opportunities for automatic identification of complementary goods are greater too.
The definition is based on the assumption that if goods
b-complement each other, then they will be more frequently purchased together. Thus, goods deemed to be
b-complementary are goods for which the frequency of occurrence in one basket is at an appropriately high level. There is no doubt that this is compliant with the intuitive understanding of complementarity in microeconomics. At the present stage of the investigation, it is still unknown whether there is a closer relation between the
b-complementarity as introduced by the authors and complementarity in the sense of the definitions provided by Auspitz and Lieben [
1] or by Hicks and Allen [
8]. Both the classic definitions and the one introduced in the paper describe the same kind of relation between goods. It can be suspected that for the majority of goods, the same results will be obtained, i.e., complementary goods in the sense of the classic definitions will also be
b-complementary.
When analyzing the relation of b-complementarity, it is easy to notice that there are goods for which this relation occurs in both directions, but there are some where the relation is one-sided. The definition introduced in the paper distinguishes between these types of b-complementarity relations by introducing the concepts of one- and two-sided b-complementarity. Examples provided in the paper indicate that one-sided relations of b-complementarity are not a rare phenomenon. Neglecting them or classifying them in the same category as two-sided relations is a major simplification; in some situations, it can even be an error. Furthermore, the introduced definition of b-complementarity makes it possible to distinguish if a relation of b-complementarity between goods being observed exists regardless of other goods or is a consequence of other relations. The proposed method is based on a basket analysis, which requires the digitization of a company’s transaction data. Too short a period of analyzed data (not taking into account seasonality) may distort the obtained results. Another problem may be the use of alternative sources of supply by customers and the sharing of orders between different suppliers. The measures of complementarity proposed in the article require that the goods under analysis should be purchased within one transaction.
The main objective of this paper was an attempt at defining the concept of
b-complementarity. The paper focused on the formal aspects of all definition of
b-complementarity. Nevertheless, it turned out to be possible to prepare a representative example explaining the introduced concepts. An important part of this paper was empirical studies on a large sample of sales data. These empirical studies showed the presence of all types of
b-complementarity between goods. It also turned out that the number of cases of one-sided
b-complementarity is by an order of magnitude greater than the number of two-sided
b-complementarity cases. The results of empirical research are so promising that it is worth considering developing a ‘basket’ definition of substitution goods. An interesting direction of development also appears in the field of recommendation systems. The concept of complementarity and substitutability of products could be the basis for the construction of many recommendation systems [
5,
6,
7,
15,
16,
17,
18]. There is no obstacle preventing the application of
b-complementarity for making recommendations in such a system.
The concept of
b-complementarity can be used to measure all of the types of complementarity introduced by Berry, et al. [
10]. Contrary to the known measures of complementarity created for recommendation systems [
5,
6,
7,
15,
16,
17,
18], it distinguishes between many different aspects of complementarity. It is also better focused on measuring complementarity than measures of complementarity from recommendation systems.