Dark Matter and Static, Spherically-Symmetric Solutions of the Extended Einstein Equations

Abstract

In this paper we present a brief review of extended general relativity in four dimensions and solve versions of the extended equations for the case of static spherical symmetry in various contexts, for a previously studied Lagrangian. The exterior vacuum yields a Schwarzschild solution with an additional scalar field potential that falls off logarithmically, the latter essentially an inverse square force. That is probably not adequate as a dark matter force, but might contribute. When a constant density field of ions holds sway in the exterior, a solution identical to the cosmological constant extension of Schwarzschild occurs, together with a scalar field potential declining as $r^{-3/2}$, however it is not asymptotically flat. An inverse square declining distribution of ionic material, according to perturbation theory, results in an additional linear gravity potential that would provide further attraction in the gravity term. A limited exact solution in the same case yields a cubic equation with a Schwarzschild solution, corresponding to $A=0$, and two MOND-like possible potentials, one vanishing at infinity, but a better solution must be found. The approximate solution is complex (one of many) and the system requires further study. Ionic matter is ubiquitous in the universe and provides a source for the scalar field, which suggests that the extended Einstein equations could be of utility in the dark matter problem, provided such an electromagnetic scalar force could be found and differentiated from the usual, far stronger electromagnetic forces. Further, it’s possible that the strong photon flux outside stars might have an influence, and is under current investigation. These calculations show that extending the concept of curvature and working in four dimensions with larger operators may bring new tools to the study of physics and unified field theories.

1. Introduction

This section is a brief review of extended general relativity as developed in [1], which can be taken as a less stringent generalization of general relativity than the original work by Kaluza [2] and Klein [3], in that it generalizes functions on a four-dimensional manifold rather than positing an additional spacetime dimension. This current paper follows the original work in Vuille [4,5], and is better adapted to the requirements of physics. A similar extensive work, for plane symmetric cosmologies, has been published [6]. Without recourse to additional dimensions, that latter paper showed that for the given Lagrangian, the inflaton and dark energy solutions were possible in these theories. Further, the source of the forces is a new scalar field that acts on charge squared. The extended Ricci tensor in this theory, as will be shown below, exhibits the usual equations of general relativity, electromagnetism, and in addition, a relativistic scalar field. In this paper, we explore the possibility that this version of the theory could predict the effects of dark matter.

Mordehai Milgrom invented the idea of MOND in 1983 [7]. Modified Newtonian Dynamics (MOND) posits that the gravity force changes form when very weak, strengthening, sufficient to maintain too-rapidly-moving stars in their galactic orbits. This problem was first recognized by Fritz Zwicky [8,9] and proven later by Vera Rubin and Kent Ford [10]. Whereas undetected matter, the dark matter, is often cited as the extra gravitational pull, Milgrom supposed that Newtonian dynamics changed when gravitational accelerations were very small. An example is

$$ma\left({\displaystyle \frac{1}{1+(a_0/a)}}\right)=F$$

(1)

where $a_0$ is the acceleration where the transformation holds. This is one of many parameterizations. For circular orbits in the galaxy, where $a=v^2/r$, this implies that asymptotically, rather than continuing to decline with radius, the speed of matter declines to value of $v={\left(a_{0}MG\right)}^{1/4}$. If no physical dark matter exists in sufficient quantities, the extra force at large distances could explain the retention of stars in galactic orbits despite their speed. There are a number or relativistic generalizations of this theory [11]. Some transformation of Newtonian dynamics may be possible, but clearly, there could also be gravitational contributions from unseen matter. In this paper, the formalism suggests that an additional scalar force, connected with electromagnetism, may be operative, as well. If so, this would avoid some of the difficulties faced in the relativistic versions.

The standard Kaluza-Klein models invoke a fifth physical dimension, which is not actually necessary to extend the size of the mathematical entities in question. The mathematical approach taken in this much newer theory is that direct sums of tensors of different type, called tensor multinomials, have a geometric interpretation as elements of the universal covering algebra for tensors, as originally pointed out by Christodoulu [12]. Tensor multinomials are dense in the space of all smooth, nonlinear differential operators on four-manifolds. The different fields of mathematical physics—general relativity, electromagnetism, and possible scalar fields—can be viewed as parts of a single tensor multinomial.

The fact that general tensor multinomials are dense in the space of all smooth functions on a manifold means any smooth function of the coordinates and four-velocities—like distributions in statistical mechanics—can be expanded in Taylor series and converted by truncation to a finite tensor multinomial. Existing theories suggest keeping the first three orders, corresponding to scalar fields, covector fields, and type two covariant tensor fields. After implicitly finding the Christoffel symbols of such a theory using a method advocated by Adler, Bazin, and Schiffer [13], curvature can be defined and calculated. In this way general relativity can be extended, and vector and scalar components of a tensor multinomial contribute to a generalized concept of curvature in only four dimensions.

These new geometric objects can be defined to act on charge-momentum extended-vectors, or x-vectors, a generalization of the usual four-vector of general relativity. The theory naturally predicts an additional scalar component of the electromagnetic interaction that would be weak under most circumstances, coupling to the particle-charge squared. If this interpretation is correct, such a field would have implications under special circumstances, such as the gravity field of stars, of collapsed matter, the beginning of the universe, and possibly the large scale evolution of the universe. Here the focus is on the spherically symmetric gravity field appropriate for stars.

1.1. The Ricci X-Tensor

Particles are turned by fields due to their momentum and charge, giving rise to x-vectors, the charge-momentum vectors of extended general relativity. The equivalent Ricci tensor, found by calculating a commutator of x-covariant derivatives on an x-vector, is given by the expression

$${\tilde{R}}_{AB}={\displaystyle \frac{\partial {\tilde{\mathsf{\Gamma }}}_{AB}^C}{\partial {\tilde{x}}^C}}-{\displaystyle \frac{\partial {\tilde{\mathsf{\Gamma }}}_{AC}^C}{\partial {\tilde{x}}^B}}+{\tilde{\mathsf{\Gamma }}}_{AB}^E{\tilde{\mathsf{\Gamma }}}_{CE}^C-{\tilde{\mathsf{\Gamma }}}_{AC}^E{\tilde{\mathsf{\Gamma }}}_{BE}^C$$

(2)

Using the extended C-symbols (see [1]), this equation results in three component equations of different tensorial order. The rank two tensor equation is given by:

$${\tilde{R}}_{ab}={\displaystyle \frac{\partial {\mathsf{\Gamma }}_{ab}^c}{\partial x^c}}-{\displaystyle \frac{\partial {\mathsf{\Gamma }}_{ac}^c}{\partial x^b}}+{\mathsf{\Gamma }}_{ab}^e{\mathsf{\Gamma }}_{ce}^c-{\mathsf{\Gamma }}_{ac}^e{\mathsf{\Gamma }}_{be}^c$$

(3)

the usual Ricci tensor of general relativity. The vector component yields

$${\tilde{R}}_{a0}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial {F^c}_a}{\partial x^c}}+{\mathsf{\Gamma }}_{cd}^c{F^d}_a-{\mathsf{\Gamma }}_{ca}^d{F^c}_d\right)$$

(4)

with

$$F_{ba}={\displaystyle \frac{\partial A_b}{\partial x^a}}-{\displaystyle \frac{\partial A_a}{\partial x^b}}$$

(5)

which is half the covariant form of Maxwell’s equation in curved space-time. Finally, the scalar component is

$${\tilde{R}}_{00}=-{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\partial }{\partial x^c}}\left(g^{dc}{\displaystyle \frac{\partial \psi }{\partial x^d}}\right)+{\mathsf{\Gamma }}_{ce}^c\left(g^{de}{\displaystyle \frac{\partial \psi }{\partial x^d}}\right)\right]-{\displaystyle \frac{1}{4}}{g}^{de}{g}^{fc}{F}_{dc}{F}_{fe}$$

(6)

which is a second-order wave equation for $\psi$ with the difference in the squares of the electric and magnetic energy densities acting as a source.

So in vacuum, the x-Ricci appears to give the equations of general relativity and electromagnetism, however they are coupled to a scalar field. The scalar field could lead to predictions that are not supported by experiment. If, however, the coupling constant associated with the scalar field is extremely small, deviations might not be observable in most contexts while creating physical observables near singularities, such as cosmic inflation at the beginning of the universe. Determining whether predictions are physical requires completing the theory by introducing the sources and writing the equation connecting the Ricci x-tensor to the analogous stress-energy, as in the next section.

1.2. The Lagrangian

There are many possible Lagrangians that could describe extended general relativity. The choice made here yields equations that are similar to those in general relativity and electromagnetism. In this paper, a field equation will take the form

$${\tilde{R}}_{AB}-{\displaystyle \frac{1}{2}}\tilde{R}{\tilde{k}}_{AB}={\tilde{T}}_{AB}$$

(7)

where $\tilde{R}$ is the x-Ricci scalar of four-dimensional extended general relativity, ${\tilde{k}}_{AB}$ is the ordinary metric tensor $g_{ab}$ with electromagnetic and scalar fields zero, and ${\tilde{T}}_{AB}$ is the extended stress-energy tensor, which includes sources for the electromagnetic and scalar fields. This equation could come from a Lagrangian for Equation (7) using a Lagrange multiplier field, ${\mathsf{\Omega }}^{AB}$. Here, the constraint equation is given by Equation (7), itself, and constitutes the full Lagrangian density:

$$\mathcal{L}=\int {\mathsf{\Omega }}^{AB}\left({\tilde{R}}_{AB}-{\displaystyle \frac{1}{2}}\tilde{R}{\tilde{k}}_{AB}-{\tilde{T}}_{AB}\right)\sqrt{-g}{d}^{4}x$$

(8)

The variation with respect to ${\mathsf{\Omega }}^{AB}$ immediately yields Equation (7). Variations with respect to the metric, the electromagnetic, and scalar fields result in equations for the various components of ${\mathsf{\Omega }}^{AB}$. That said, ${\mathsf{\Omega }}^{AB}$ is not easy to find explicitly from the derived equations. The study of special cases may lead the way to discovering an explicit, exact Lagrangian using this method.

2. Spherically Symmetric Static Solutions

In this subsection, we present several related spherically symmetric static solutions for Equation (7). The simplest non-trivial case involves an exterior static field. In this solution a central, spherically-symmetric plasma is electrically neutral but creates a scalar field because a charge-squared distribution is additive. Here, the focus is on a vacuum field exterior to that plasma. The assumption is that of a spherically-symmetric extended metric:

$$d\tilde{s}=-e^{\nu }d{t}^2\oplus e^{\lambda }d{r}^2\oplus r^2\left(d{\theta }^2\oplus {sin}^2\theta d{\varphi }^2\right)\oplus \psi$$

(9)

We have emphasized the true character of the “plus” signs by writing them all as direct sums, which is what they are. For an elementary introduction to direct sums, see Herstein [14]. The functions $\nu$, $\lambda$, and $\psi$ are all functions of r. Here, it will be assumed that the x-metric Lagrangian holds and that there is a scalar field source, $\mu \psi$, of the scalar field equation, where $\mu$ may be constant or variable. The non-zero field equations are therefore:

$${\tilde{G}}_{00}=-{\displaystyle \frac{1}{2}}\left(e^{-\lambda }{\psi }^{″}+e^{-\lambda }\left({\displaystyle \frac{{\nu }^{\prime }}{2}}-{\displaystyle \frac{{\lambda }^{\prime }}{2}}+{\displaystyle \frac{2}{r}}\right){\psi }^{\prime }\right)=\mu \psi$$

(10)

$${\tilde{G}}_{44}=e^{\nu -\lambda }\left({\displaystyle \frac{{\lambda }^{\prime }}{r}}-{\displaystyle \frac{1}{r^2}}\right)+{\displaystyle \frac{e^{\nu }}{r^2}}+{\displaystyle \frac{1}{2}}{e}^{\nu }{\psi }^{-1}{\tilde{R}}_{00}=e^{\nu }\kappa \rho c^2$$

(11)

$${\tilde{G}}_{11}={\displaystyle \frac{{\nu }^{\prime }}{r}}+{\displaystyle \frac{1}{r^2}}-{\displaystyle \frac{e^{\lambda }}{r^2}}-{\displaystyle \frac{1}{2}}{e}^{\lambda }{\psi }^{-1}{\tilde{R}}_{00}=\kappa P{e}^{\lambda }$$

(12)

$${\tilde{G}}_{22}=r^2{e}^{-\lambda }\left({\displaystyle \frac{{\nu }^{″}}{2}}+{\displaystyle \frac{{\nu }^{\prime 2}}{4}}-{\displaystyle \frac{{\nu }^{\prime }{\lambda }^{\prime }}{4}}-{\displaystyle \frac{{\lambda }^{\prime }}{2r}}+{\displaystyle \frac{{\nu }^{\prime }}{2r}}\right)-{\displaystyle \frac{1}{2}}{r}^2{\psi }^{-1}{\tilde{R}}_{00}=\kappa P{r}^2$$

(13)

where ${\tilde{G}}_{00}$ is the scalar field equation, ${\tilde{G}}_{44}$ the time-time component, ${\tilde{G}}_{11}$ the $r-r$ component, and the spherical terms are ${\tilde{G}}_{22}$ and finally ${\tilde{G}}_{33}$, which is redundant. Certain special solutions follow.

2.1. Exterior Metric with $P=\rho =\mu =0$

For the exterior neglecting any substance, we take $P=\rho =\mu =0$. It can be easily verified that $e^{-\nu +\lambda }{G}_{44}+G_{11}=0$ implies that $\lambda =-\nu$. Dropping the now-redundant Equation (12), the field equations can therefore be written:

$$G_{00}=-{\displaystyle \frac{e^{\nu }}{2}}\left({\psi }^{″}+\left({\nu }^{\prime }+{\displaystyle \frac{2}{r}}\right){\psi }^{\prime }\right)=0$$

(14)

$$e^{-\nu }{G}_{44}=e^{\nu }\left(-{\displaystyle \frac{{\nu }^{\prime }}{r}}-{\displaystyle \frac{1}{r^2}}\right)+{\displaystyle \frac{1}{r^2}}+{\displaystyle \frac{1}{2}}{\psi }^{-1}{\tilde{R}}_{00}=0$$

(15)

$$G_{22}/r^2=e^{\nu }\left({\displaystyle \frac{{\nu }^{″}}{2}}+{\displaystyle \frac{{\nu }^{\prime 2}}{2}}+{\displaystyle \frac{{\nu }^{\prime }}{r}}\right)-{\displaystyle \frac{1}{2}}{\psi }^{-1}{\tilde{R}}_{00}=0$$

(16)

In this case, $\mu =0$, assumed constant. From Equation (16), with ${\tilde{R}}_{00}=0$ and after $e^{\nu }=f$, we find that

$$e^{\nu }=f=1+{\displaystyle \frac{a}{r}}$$

(17)

which is the usual Schwarzschild solution when $a=-2MG/c^2$. Returning to Equation (14), obtain:

$${\psi }^{″}+\left({\nu }^{\prime }+{\displaystyle \frac{2}{r}}\right){\psi }^{\prime }=0$$

(18)

Integrating once yields

$$ln\left({\psi }^{\prime }\right)=-\nu +ln\left(r^{-2}\right)+C$$

(19)

or

$${\psi }^{\prime }={\displaystyle \frac{k}{e^{\nu }{r}^2}}={\displaystyle \frac{k}{(1+a/r)r^2}}={\displaystyle \frac{k}{(r+a)r}}$$

(20)

and

$$\psi ={\displaystyle \frac{k}{a}}ln\left({\displaystyle \frac{r}{r+a}}\right)+D$$

(21)

where D is an arbitrary constant. The scalar force exerted on charges therefore, for $r>>a$, yields a standard inverse square potential that is either attractive or repulsive, depending on the selected sign of k. It doesn’t change the gravity force. With a suitable choice of the constants, it could affect charged particles via a scalar force.

2.2. Exterior Solution with Constant $\mu \ne 0$

For $P=\rho =0$ and $\mu \ne 0$, we again obtain that ${\lambda }^{\prime }=-{\nu }^{\prime }$, so

$$G_{00}=-{\displaystyle \frac{e^{\nu }}{2}}\left({\psi }^{″}+\left({\nu }^{\prime }+{\displaystyle \frac{2}{r}}\right){\psi }^{\prime }\right)=\mu \psi$$

(22)

$$e^{-\nu }{G}_{44}=e^{\nu }\left(-{\displaystyle \frac{{\nu }^{\prime }}{r}}-{\displaystyle \frac{1}{r^2}}\right)+{\displaystyle \frac{1}{r^2}}+{\displaystyle \frac{1}{2}}{\psi }^{-1}{\tilde{R}}_{00}=0$$

(23)

$$G_{22}/r^2=e^{\nu }\left({\displaystyle \frac{{\nu }^{″}}{2}}+{\displaystyle \frac{{\nu }^{\prime 2}}{2}}+{\displaystyle \frac{{\nu }^{\prime }}{r}}\right)-{\displaystyle \frac{1}{2}}{\psi }^{-1}{\tilde{R}}_{00}=0$$

(24)

It follows that Equations (23) and (24) results in

$$e^{\nu }\left({\nu }^{″}+{\nu }^{\prime 2}-{\displaystyle \frac{2}{r^2}}\right)+{\displaystyle \frac{2}{r^2}}=0$$

Setting $f=e^{\nu }$ yields

$$f^{″}-{\displaystyle \frac{2}{r^2}}f-{\displaystyle \frac{2}{r^2}}=0$$

(25)

which has solution

$$e^{\nu }=f=1+{\displaystyle \frac{a}{r}}+b{r}^2$$

(26)

The other Einstein equations imply that $\mu =6b$, so for a static x-metric, constant $\mu$ is a requirement. The metric part is the usual static, spherically symmetric solution to Einstein’s equations with a cosmological constant, if $a=-2MG/c^2$. The difference is the scalar field that results along with it. Using the metric functions as found, the scalar field equation is

$${\psi }^{″}+\left({\displaystyle \frac{\frac{-a}{r^2}+\frac{1}{3}\mu r}{1+\frac{a}{r}+\frac{1}{6}\mu r^2}}+{\displaystyle \frac{2}{r}}\right){\psi }^{\prime }+{\displaystyle \frac{2\mu }{1+\frac{a}{r}+\frac{1}{6}\mu r^2}}\psi =0$$

(27)

This equation is linear but difficult to solve exactly due to the variable coefficients. Asymptotically, for large r, the $\mu$ terms dominate, and the equation becomes

$${\psi }_{\infty }^{″}+{\displaystyle \frac{4}{r}}{\psi }_{\infty }^{\prime }+{\displaystyle \frac{12}{r^2}}{\psi }_{\infty }=0$$

(28)

This can be solved with Euler’s method, putting $r=r_0{e}^u$. The solution becomes:

$${\psi }_{\infty }={\left({\displaystyle \frac{r}{r_0}}\right)}^{-3/2}\left[Acos(ln{(r/r_0)}^{\gamma })+Bsin(ln{(r/r_0)}^{\gamma })\right]$$

(29)

where A, B, and $r_0$ are arbitrary constants and $\gamma =\sqrt{39}/2$. Half the derivative is roughly the magnitude of a force, showing that the force caused by $\psi$ at a great distance is proportional to $r^{-5/2}$, falling off faster than the gravity force. However, the scalar field stimulates the development of the time-time metric coefficient $g_{44}=-\left(1-2MG/r+{\displaystyle \frac{1}{6}}\mu r^2\right)$, so if $\mu$ is positive, it will result in an attractive force that at some distance will be superior in magnitude to the usual gravity force. This force must be very small in a typical solar system, but large far outside it. Evidence exists for this kind of force in the high speeds of stars circling galaxies, but may not be so because of the Newtonian dynamics of widely separated binary stars [15]. Other calculations, however, may support MOND-like deviations at large separations [16]. Further, a recent publication by Mistele et al. [17] indicates circular velocities remain flat far outside distant galaxies. We note, however, that the metric portion is not asymptotically flat, which suggests $\mu =constant$ would not result in a proper MOND potential.

Note that the solar wind fills the space external to the Sun with charged particles, and that the density of the particles falls off with increasing area, hence is not constant. Finding the effect requires a non-constant value for $\mu$ proportional to the inverse of the area of spheres around the sun. This idea is taken up in the next subsection.

2.3. Charged, Static, Falling Density Ionic Dust

Here the ions are flowing outward from the Sun, about 1.5 million tons of material per second, nonuniformly distributed, at various (usually high) speeds. For simplicity, in this approximation we assume that $\mu$ varies with radial position but is otherwise static, and the field equations are therefore:

$${\tilde{G}}_{00}=-{\displaystyle \frac{1}{2}}\left(e^{-\lambda }{\psi }^{″}+e^{-\lambda }\left({\displaystyle \frac{{\nu }^{\prime }}{2}}-{\displaystyle \frac{{\lambda }^{\prime }}{2}}+{\displaystyle \frac{2}{r}}\right){\psi }^{\prime }\right)=\mu \psi$$

(30)

$${\tilde{G}}_{44}=e^{\nu -\lambda }\left({\displaystyle \frac{{\lambda }^{\prime }}{r}}-{\displaystyle \frac{1}{r^2}}\right)+{\displaystyle \frac{e^{\nu }}{r^2}}+{\displaystyle \frac{1}{2}}{e}^{\nu }{\psi }^{-1}{\tilde{R}}_{00}=e^{\nu }\kappa \rho c^2$$

(31)

$${\tilde{G}}_{11}={\displaystyle \frac{{\nu }^{\prime }}{r}}+{\displaystyle \frac{1}{r^2}}-{\displaystyle \frac{e^{\lambda }}{r^2}}-{\displaystyle \frac{1}{2}}{e}^{\lambda }{\psi }^{-1}{\tilde{R}}_{00}=0$$

(32)

$${\tilde{G}}_{22}=r^2{e}^{-\lambda }\left({\displaystyle \frac{{\nu }^{″}}{2}}+{\displaystyle \frac{{\nu }^{\prime 2}}{4}}-{\displaystyle \frac{{\nu }^{\prime }{\lambda }^{\prime }}{4}}-{\displaystyle \frac{{\lambda }^{\prime }}{2r}}+{\displaystyle \frac{{\nu }^{\prime }}{2r}}\right)-{\displaystyle \frac{1}{2}}{r}^2{\psi }^{-1}{\tilde{R}}_{00}=0$$

(33)

Note that ${\psi }^{-1}{\tilde{R}}_{00}=\mu$. Obtain from the sum of $e^{-\nu +\lambda }$ Equations (31) and (32) that

$$\kappa \rho c^2=e^{-\lambda }\left({\displaystyle \frac{{\lambda }^{\prime }+{\nu }^{\prime }}{r}}\right)$$

(34)

We also have, from Equation (32):

$${\nu }^{\prime }=-{\displaystyle \frac{1}{r}}+{\displaystyle \frac{e^{\lambda }}{r}}+{\displaystyle \frac{1}{2}}r{e}^{\lambda }\mu$$

(35)

and

$$e^{\lambda }={\displaystyle \frac{r{\nu }^{\prime }+1}{1+\frac{1}{2}\mu r^2}}$$

(36)

Use Equation (36) to eliminate $\lambda$ from Equation (33). With $f=e^{\nu }$, arrive at:

$${\displaystyle \frac{f^{\prime }}{f}}{\displaystyle \frac{f^{″}}{f}}\left(1+\frac{1}{2}\mu r^2\right)+{\left({\displaystyle \frac{f^{\prime }}{f}}\right)}^2\left({\displaystyle \frac{2}{r}}+\frac{1}{2}{\mu }^{\prime }{r}^2\right)+{\displaystyle \frac{f^{\prime }}{f}}\left(-\mu +{\displaystyle \frac{3}{2}}{\mu }^{\prime }r\right)+{\mu }^{\prime }=0$$

(37)

If $\mu$ is constant, then we can regain the solution of the previous subsection. Instead, assume

$$\mu ={\displaystyle \frac{A}{r^2}}$$

(38)

The equation then becomes:

$${\displaystyle \frac{f^{\prime }}{f}}{\displaystyle \frac{f^{″}}{f}}\left(1+{\displaystyle \frac{A}{2}}\right)+{\left({\displaystyle \frac{f^{\prime }}{f}}\right)}^2\left({\displaystyle \frac{2-A}{r}}\right)+{\displaystyle \frac{f^{\prime }}{f}}\left(-{\displaystyle \frac{4A}{r^2}}\right)-{\displaystyle \frac{2A}{r^3}}=0$$

(39)

This equation can be solved in perturbation with $f=f_0+A{f}_1+\dots$. Zeroth order gives

$$f_0^{\prime }{f}_0^{″}+{\displaystyle \frac{2}{r}}{f}_0^{\prime 2}=0$$

(40)

which has the solution $f_0=\mathrm{constant}$, corresponding to circular orbits, and a Schwarzschild solution,

$$f_0=1+{\displaystyle \frac{a}{r}}$$

(41)

whereas we have

$$f_1^{″}+{\displaystyle \frac{2}{r}}{f}_1^{\prime }+{\displaystyle \frac{2}{ar}}=0$$

(42)

for a first order solution. That solution is

$$f_1=-{\displaystyle \frac{r}{a}}+{\displaystyle \frac{b}{r}}+c_0$$

(43)

Here we can take $c_0=0$. It is possible that $b=0$, or that it causes a very slight change in the $1/r$ potential term. So with $a=-2MG/c^2$:

$$f\approx f_0+A{f}_1=1-{\displaystyle \frac{2MG}{c^{2}r}}+{\displaystyle \frac{c^{2}A}{2MG}}r$$

(44)

The last term will give an additional attractive gravity force, the size depending on the constants in the expression, likely very small close to a star, as A is small and $2MG/c^2$, for all stars, will be relatively large, e.g., about 3000 m for the Sun. Note, however, that a negative value of A will create a repulsive force.

Again, using $r=r_0{e}^u$, it is also possible to seek an exact solution. This transformation results in the equation

$$f^{\prime }{f}^{″}\left(1+{\displaystyle \frac{A}{2}}\right)+f^{\prime 2}\left(1-\frac{3}{2}A\right)-4A{f}^{\prime }f-2A{f}^2=0$$

(45)

where the primes now refer to the new variable, u. This system has the advantage of eliminating the dependent coefficients, but is evidently quadratic in f. The Schwarzschild solution, $f=1-2MG/c^{2}r=1-(2MG/c^2{r}_0)e^{-u}$, yields $A=0$ and otherwise solves the equation. A simple exponential solution, $f=a{e}^{\alpha u}$, quickly leads to a solution that is cubic in $\alpha$ that depends on the value of A. It is easy to solve, as by inspection $\alpha =-1$ is a solution, corresponding to a $1/r$ potential in the metric. In general,

$$\alpha =-1,{\displaystyle \frac{A\pm \sqrt{2}{\left(A^2+A\right)}^{1/2}}{1+\frac{1}{2}A}}$$

(46)

Each of these numbers is a possible solution to $f\left(u\right)=a{e}^{\alpha u}$, and corresponds to a power of $r/r_0$:

$$f_1\left(r\right)=a{\displaystyle \frac{r_0}{r}}$$

(47)

$$f_2\left(r\right)=a{\left({\displaystyle \frac{r}{r_0}}\right)}^{{\displaystyle \frac{A+\sqrt{2}{\left(A^2+A\right)}^{1/2}}{1+\frac{1}{2}A}}}$$

(48)

$$f_3\left(r\right)=a{\left({\displaystyle \frac{r}{r_0}}\right)}^{{\displaystyle \frac{A-\sqrt{2}{\left(A^2+A\right)}^{1/2}}{1+\frac{1}{2}A}}}$$

(49)

If A is small, as it must be, then $f_{2,3}\approx a{(r/r_0)}^{\pm \sqrt{2A}}$. Either of these would dominate the $r^{-1}$ potential eventually, in deep space, although the negative power might be preferable, as that would vanish at infinity. Of interest would be a more complete either exact, or approximate, solution showing the behavior in the space nearer a star and its change on reaching deep interstellar space. That is the subject of the next section.

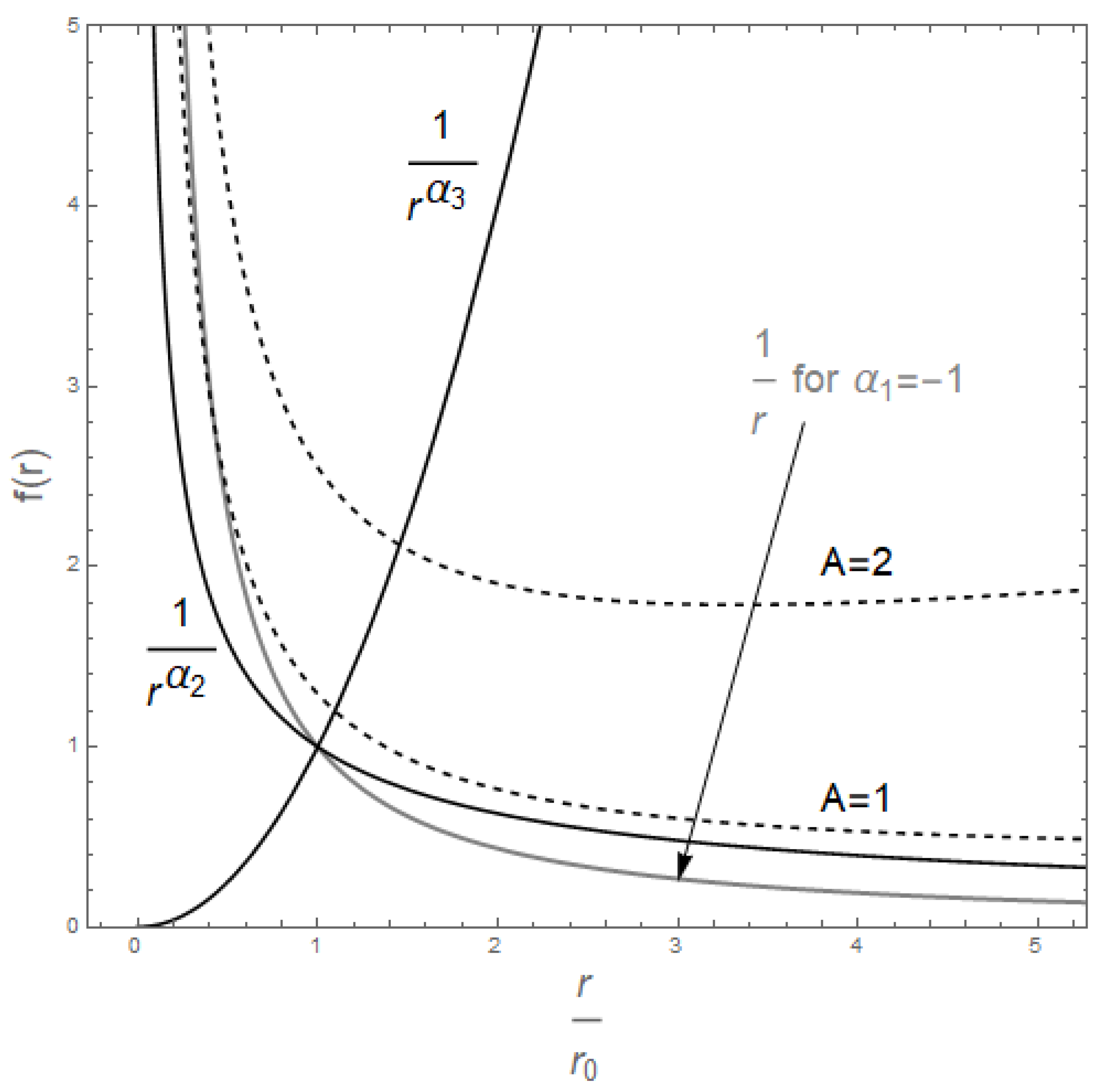
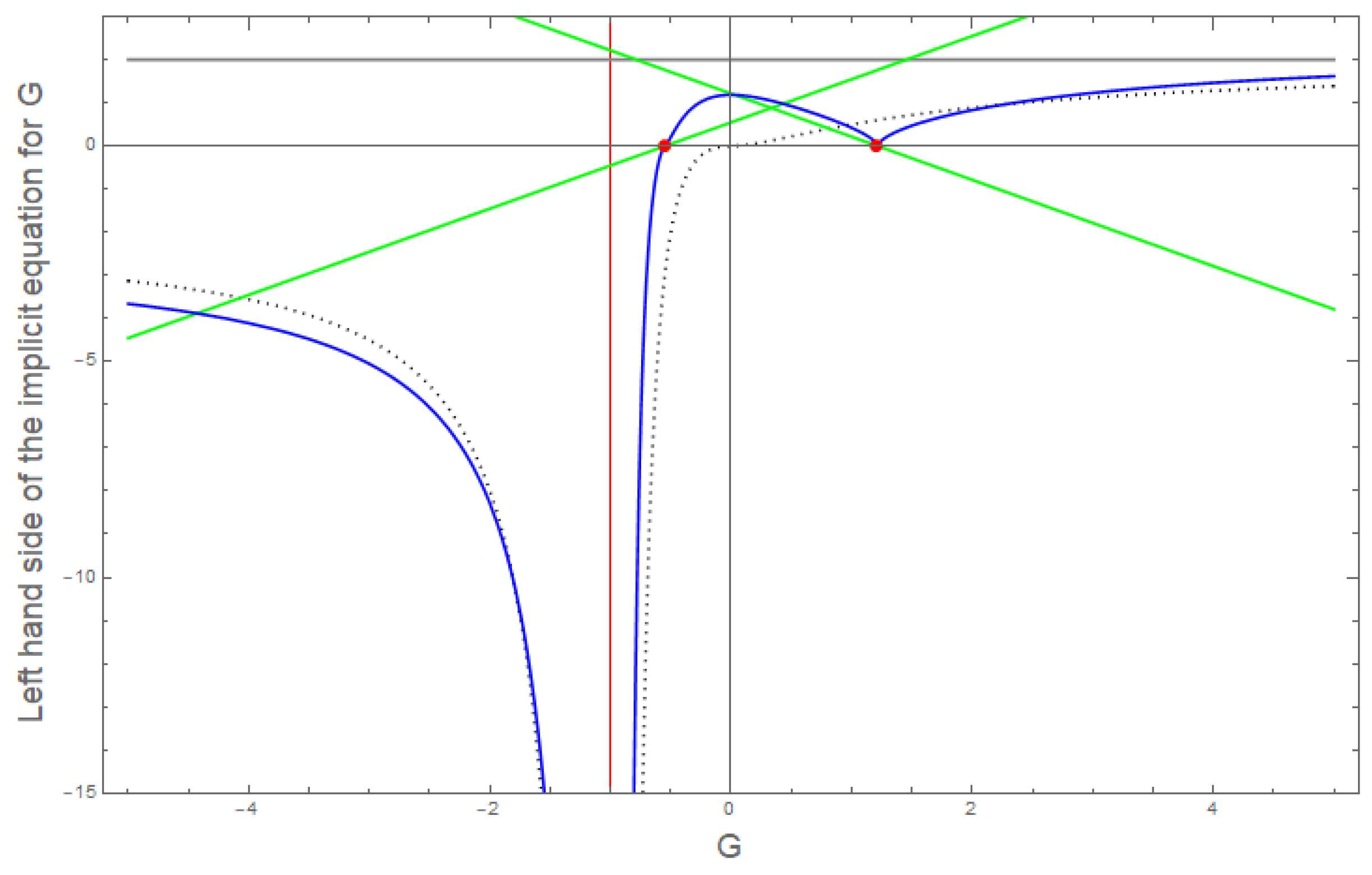
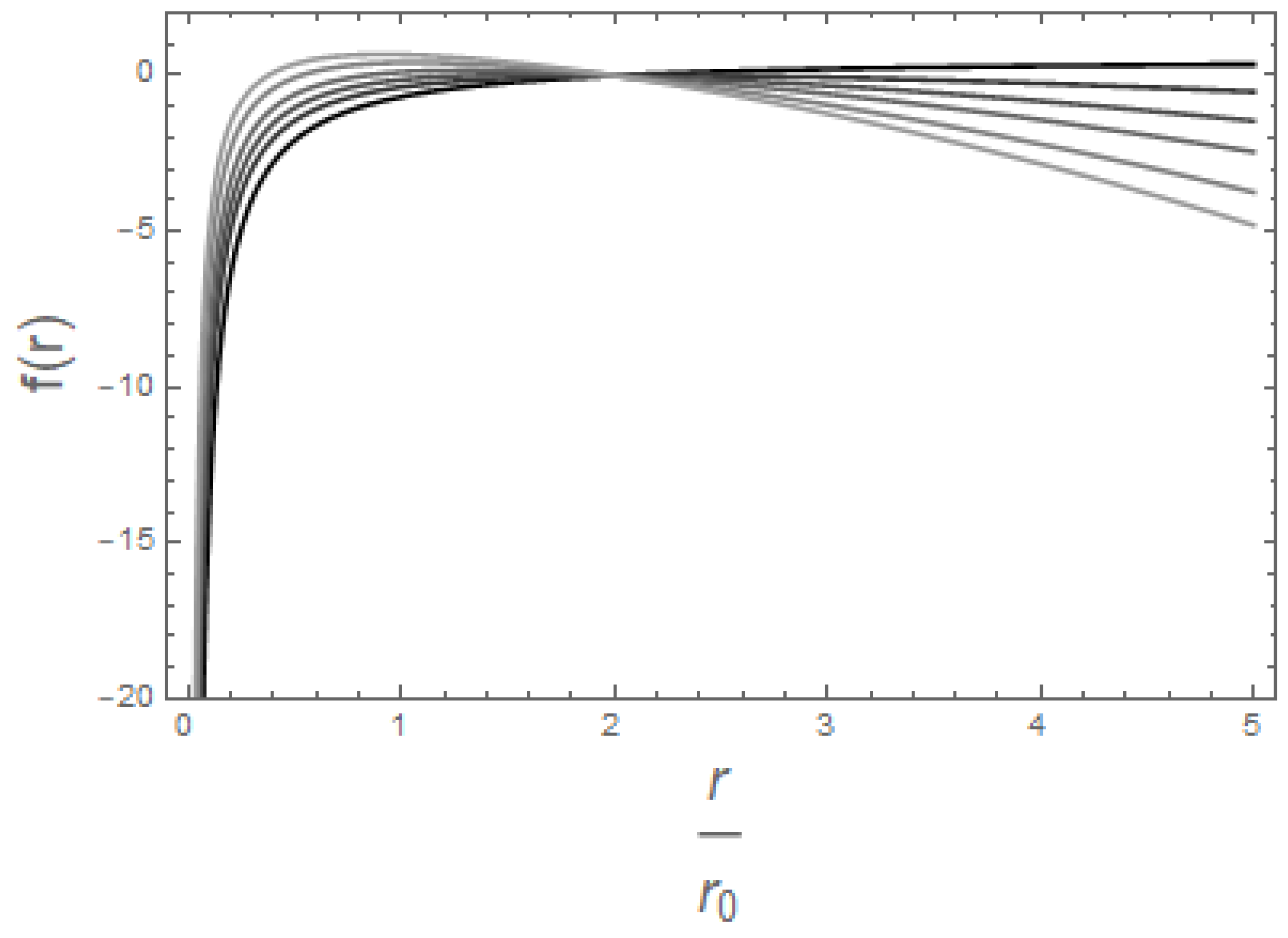
3. Approximate Solutions for a General Form of the Field Equation

In this section we put the equation derived in the previous subsection to further analysis. It results in an interesting approximate solution. In this development, we have benefited from discussions in references [18,19].

3.1. General Form of the Equation

Given the nonlinear autonomous ordinary differential equation

$$a{f}^{\prime }{f}^{″}+b{f}^{\prime 2}+cf{f}^{\prime }+d{f}^2=0,$$

(50)

with $a,b,c,d$ constants, we build the general solution $f\left(x\right)$ using the substitution $y\left(x\right)=f^{\prime }\left(x\right)$, in order to transform Equation (50) into a generalized Abel equation of the second kind in the form:

$$ay{y}^{\prime }+b{y}^2+cyf+d{f}^2=0,$$

or in explicit form

$$y^{\prime }=-{\displaystyle \frac{1}{a}}\left(by+cf+d{\displaystyle \frac{f^2}{y}}\right),$$

(51)

similar to the Emden-Fowler equation [18]. On intervals where $y^{\prime }$ is invertible we can implement a functional transformation of Majorana type [19] in the form $x=F^{-1}\left(f\right)$. It results in $y\left(x\right)=y\left(F^{-1}\left(f\right)\right)=Y\left(f\right)$, and from the implicit functions theorem we have

$$Y^{\prime }={\displaystyle \frac{dY}{df}}={\displaystyle \frac{y^{\prime }}{f^{\prime }}}.$$

Implementing this in Equation (51) we get a differential equation for $Y\left(f\right)$:

$${\left(Y^2\right)}^{\prime }=-{\displaystyle \frac{2}{a}}\left(bY+cf+d{\displaystyle \frac{f^2}{Y}}\right)$$

(52)

This is a nonlinear but homogeneous type of equation and it always has a logarithmic type of solution. To obtain this solution we solve the algebraic equation

$$2a{\chi }^3+b{\chi }^2+c\chi +d=0,$$

(53)

and denote its roots by ${\chi }_k$, $k=1,\dots ,3$. Then, the solution of Equation (52) is given by the implicit equation

$$\sum _{k=1}^3{\displaystyle \frac{{\chi }_k^{2}ln\left(-{\chi }_k+\frac{Y}{f}\right)}{6{\chi }_k^2+2b{\chi }_k+c}}=C-{\displaystyle \frac{lnf}{2a}},$$

(54)

with C arbitrary constant of integration.

Equation (54) can be written in a different form:

$$\prod _{k=1}^3{\left({\displaystyle \frac{Y}{f}}-{\chi }_k\right)}^{{\pi }_k}=Cf,$$

(55)

with

$${\pi }_k=-{\displaystyle \frac{{\chi }_k^2}{2a(6{\chi }_k^2+2b{\chi }_k+c)}}$$

To study the solution of Equation (50) from this expression we would need to first solve either Equation (54) or Equation (55) for $Y\left(f\right)$, and then implement this solution into the differential equation

$$\int {\displaystyle \frac{df}{Y\left(f\right)}}=x+C,$$

(56)

and from here we can obtain $f\left(x\right)$ by integration and inversion.

For any point $(x_0,f_0)$ the solution Equations (54)–(56), or equivalently Equations (55) and (56), of Equation (50) is unique under the initial conditions $f\left(x_0\right)=f_0$ on an open interval around $x_0$ if the expression $f^2/f^{\prime }$ is Lipschitz-continuous on that interval. The proof follows from the Picard–Lindelöf theorem [20].

3.2. Particular Case for the Equation

For a particular model we can choose the coefficients of Equation (50)

$$a{f}^{\prime }{f}^{″}+b{f}^{\prime 2}+cf{f}^{\prime }+d{f}^2=0,$$

in the form

$$a=1+{\displaystyle \frac{A}{2}},b=1-{\displaystyle \frac{3A}{2}},c=-4A,d=-2A,$$

where $A\ge 0$ is a free parameter. Equation (50) becomes

$$f^{\prime }{f}^{″}\left(1+{\displaystyle \frac{A}{2}}\right)+f^{\prime 2}\left(1-{\displaystyle \frac{3A}{2}}\right)-4A{f}^{\prime }f-2A{f}^2=0,$$

(57)

which is exactly Equation (44). Even being nonlinear, this ODE has a homogeneous form of order 2 in f so it accepts exponential solutions. It is easy to check that we have three simple solutions in the form

$$f_i\left(u\right)=C_1+C_2{e}^{{\alpha }_{i}u},{\alpha }_1=-1,{\alpha }_{2,3}={\displaystyle \frac{2\left(A\pm \sqrt{2(A+A^2)}\right)}{2+A}}$$

(58)

Here, $C_1$ is a constant for case 1 but zero for cases 2,3. We note that ${\alpha }_2\in [0,2(1+\sqrt{2}))$, ${\alpha }_3\in (2(1-\sqrt{2}),0]$ and ${\alpha }_3\le 0\le {\alpha }_2$ and ${\alpha }_2={\alpha }_3=0$ only when $A=0$. We look for the general solution of Equation (57) in the form

$$f\left(u\right)=C{e}^{{\int }_{-\infty }^{u}G\left(u^{\prime }\right)d{u}^{\prime }},$$

(59)

without any loss of generality because G can have complex values. Equation (57) becomes

$$(2+A)G{G}^{\prime }+(2+A)G^3+(2-3A)G^2-8AG-4A=0$$

(60)

If $G^{\prime }=0$ Equation (60) becomes an algebraic equation and the solutions reproduce the exponential solutions Equation (58) $G={\alpha }_i$. A validation of the solution can be made by setting $A=0$ in Equation (61). In this case we obtain 2 isolated solutions $G=-1$ and $G=-1+e^u/(e^u+C)$, yet both are absorbed in the trivial solution $f\sim 1/r$ when we apply the exponential.

The general solution $G\left(u\right)$ of Equation (60) can be obtained by one quadrature. Taking into account the signs of ${\alpha }_{2,3}$ the only well defined real solution is given by the implicit form

$${\displaystyle \frac{{({\alpha }_2-G)}^{\frac{{\alpha }_2}{(1+{\alpha }_2)({\alpha }_2-{\alpha }_3)}}{({\alpha }_3-G)}^{\frac{{\alpha }_3}{(1+{\alpha }_3)({\alpha }_3-{\alpha }_2)}}}{(1+G)}}=C_3{e}^{-u},$$

(61)

with arbitrary $C_3$ and $G\left(u\right)\in (-1,{\alpha }_3)$. To obtain the general form for $f\left(u\right)$ we solve the transcendental Equation (61) numerically and integrate it with respect to u to obtain the exponential realization from Equation (59). Examples of solutions $f\left(r\right)$ for $A=0,1,2$ are presented in Figure 1.

In order to understand the relative contribution of the terms of Equation (50), or more specifically in the form of Equation (57), we write the general solution of Equation (50) following the same substitution as in Equation (59)

$$f\left(u\right)=C{e}^{{\int }_{-\infty }^{u}G\left(u^{\prime }\right)d{u}^{\prime }}.$$

In this case the general solution of Equation (50) (equivalent to the solution provided by Equation (61) for the particular case depending only on A) as a function of the parameters $a,b,c,d$ has the form

$$\prod _{i=1}^3{(G\left(u\right)-r_i)}^{{\displaystyle \frac{r_i}{c+2r_i+3a{r}_i^2}}}=C_1+C_2{e}^{-{\displaystyle \frac{u}{a}}}$$

(62)

where $r_i$ are the roots of the algebraic equation

$$d+cr+b{r}^2+a{r}^3=0.$$

(63)

In the particular case of Equation (57) these roots are simply ${\alpha }_i$ from Equation (58).

The first observation is that the term $f^{\prime }{f}^{″}$, of coefficient a (i.e., $1+A/2$ later on) is the most important. On one hand it tunes the space scale of the interaction, because it occurs as the denominator of the exponent in the RHS of Equation (62) and controls the range of u (which is importance for $r_0$). On the other hand, this term secures a third order algebraic equation Equation (63) and consequently three roots. With only two roots ($a=0$) the solutions $f\left(u\right)$ become multivalued or singular. The other three terms $f^{\prime 2},f{f}^{\prime },f^2$ are equally important because they build the roots of the third order algebraic equation. So, basically the structure of the solution $f\left(u\right)$ strongly depends on the position of the roots ${\alpha }_{2,3}$ depending on A.

It is also important for the good behavior of the solutions to have one root independent of the invariant A, in order to guarantee a singularity for $G\left(u\right)$ at a fixed point, i.e., the one at ${\alpha }_1=-1$. It is difficult to find out the relative importance of the three terms with respect to this request, in general. Nevertheless, a numerical perturbative analysis shows the following: The term $f^2$ is not so crucial. Its role is shifting the graph of the algebraic equation Equation (63) along the vertical axis, so it preserves the structure of the roots, except shifting them to some extent. The terms $f{f}^{\prime }$ and $f^{\prime 2}$ have the most impact on the solution. For example, if the absolute value of the original coefficient $\left|c\right|$ is below a certain value, the roots become complex, which again dramatically changes the structure of $f\left(u\right)$. In Figure 2 we present this analysis. We plot the left hand side of Equation (61) as a function of G. The dotted curve represents the behavior of G for the case $A=0$ with $f\sim 1/r$, and the blue curve represents the same expression for $A=1$. The three algebraic roots ${\alpha }_i$ are represented by the red vertical asymptote at $G={\alpha }_1-1$, and the two red dots. The factors $G-{\alpha }_3$ and ${\alpha }_2-G$ have changes of signs at these points, and if depending on the value of A, the powers of these factors can be odd or even or no parity, consequently some solution segments can be discontinuous or even removed.

3.3. Approximations

The implicit Equation (61) can be explicitly solved in the approximation of small A values. If we expand Equation (61) in a power series with respect to A, we obtain in order $\mathcal{O}\left(A^2\right)$:

$${\displaystyle \frac{G}{1+G}}-{\displaystyle \frac{A}{G(1+G)}}+{\displaystyle \frac{A^2(3G^2-8G-3)}{6G^3(1+G)}}+\mathcal{O}\left(A^3\right)=C_3{e}^{-u}$$

Within this approximation Equation (59) can be exactly integrated, and we obtain

$$f\left(r\right)=C_4{\sqrt{A}}^{\sqrt{A}}\left(C_3{\displaystyle \frac{r_0}{r}}-1\right)\left[C_3-A\left({\displaystyle \frac{C_3}{2}}-{\displaystyle \frac{r}{r_0}}\right)-{\displaystyle \frac{A^2}{8C_3}}{\left(C_3-2{\displaystyle \frac{r}{r_0}}\right)}^2\right]+\mathcal{O}\left(A^3\right),$$

(64)

where $C_{3,4}$ are constants of integration resulting from the second order original Equation (57). Their values can be adjusted from physical interpretation in the limit $a\to 0$. In this case Equation (64) approaches

$${f\left(r\right)|}_{A=0}=C_4{C}_3\left(C_3{\displaystyle \frac{r_0}{r}}-1\right)\to 1-{\displaystyle \frac{2MG}{c^{2}r}}$$

so

$$C_3=-{\displaystyle \frac{2MG}{r_0{c}^2}},C_4=-{\displaystyle \frac{1}{C_3}}.$$

Equation (64) becomes

$$f\left(r\right)={\sqrt{A}}^{\sqrt{A}}\left({\displaystyle \frac{r_0{c}^2}{2MG}}-{\displaystyle \frac{r_0}{r}}\right)\left[{\displaystyle \frac{2MG}{r_0{c}^2}}-A\left({\displaystyle \frac{MG}{r_0{c}^2}}+{\displaystyle \frac{r}{r_0}}\right)-{\displaystyle \frac{A^2{r}_0{c}^2}{4r_0{c}^2-MG}}{\left({\displaystyle \frac{MG}{r_0{c}^2}}+{\displaystyle \frac{r}{r_0}}\right)}^2\right]+\mathcal{O}\left(A^3\right)$$

(65)

Some examples of this solutions are presented in Figure 3. Given that $r_0=2MG/c^2$ for cases of interest, we can obtain a simplified form:

$$f\left(r\right)={\sqrt{A}}^{\sqrt{A}}\left(1-{\displaystyle \frac{r_0}{r}}\right)\left[1-A\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{r}{r_0}}\right)-{\displaystyle \frac{2}{7}}{A}^2{\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{r}{r_0}}\right)}^2\right]+\mathcal{O}\left(A^3\right)$$

(66)

This particular approximate solution, to this order and for positive A, actually reduces the effect of the $r_0/r$ term, while producing other positive and negative factors. Further study will be required to determine whether it’s a suitable dark matter effect.

4. Concluding Remarks

In this particular formulation of extended general relativity using the given implicit Lagrangian and the universal covering group of tensors, solutions can be found indicating ionic material exhibits an additional scalar force, and in addition, creates changes in the usual metric tensor. These changes have the potential of creating additional attraction and leading to MOND-like forces that could prevent galaxies from flying apart, despite the high speed of stars within them. As yet, it is not clear that the theory will produce metric-components that are asymptotically flat, or forces that will be invisible on a solar scale but otherwise act appropriately on a galactic scale. In addition to dynamic changes suggested by MOND, some form of dark matter may exis that contributes, as well. The complexity of these interactions demand further study, which we are carrying out. This study will include the effect on the scalar field and metric of the photons streaming from stars. The latter study will likely not involve the Vaidya metric, as that is not truly a Maxwell electromagnetic field [21].

Researchers have studied systems with additional dimensions for over a century. One of the great benefits of enlarging the function space, instead, and maintaining four dimensions, is that there is no need for compactification. It can be found that in higher dimensional spacetimes, the gravitational potential can change, unless compactification is carried out [22]. All the same, regardless, tensor multinomials can be defined on any number of dimensions, meaning that the concept expands the number of ways we can study nature.

Of further interest is the realization that the concept of curvature can be extended and used to represent other fields, such as electromagnetism. In some sense, then, a single equation involving entities consisting of scalar, covector, and tensor type two components can represent gravity, electromagnetism, and a new scalar force. This may lead to a deeper understanding of the long-range potentials describing these theories. The addition of a scalar force as part of this union, with an equivalent equation, could conceivably supplant the oft-necessity of putting those fields in by hand.

Given the interesting dark energy and inflaton solutions found in [6], further study of this extension of general relativity, and similar systems with alternate Lagrangians, has merit and will be undertaken. Plasmas are the most abundant form of matter in the universe, and it is conceivable we have overlooked a much weaker, scalar potential force that over distances can add to the known gravitational attraction of matter. Experiments must be designed and conducted to determine the force’s existence and separate this additional ionic potential, if possible, from the usual known electromagnetic field.