Drapeability and Λ-Frames
Abstract
1. Introduction
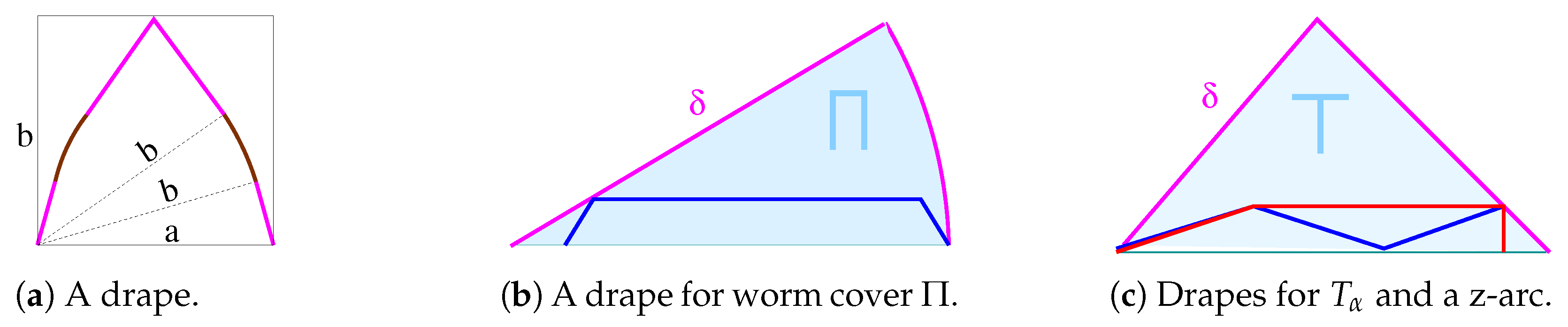
2. Draping Arcs with Frames
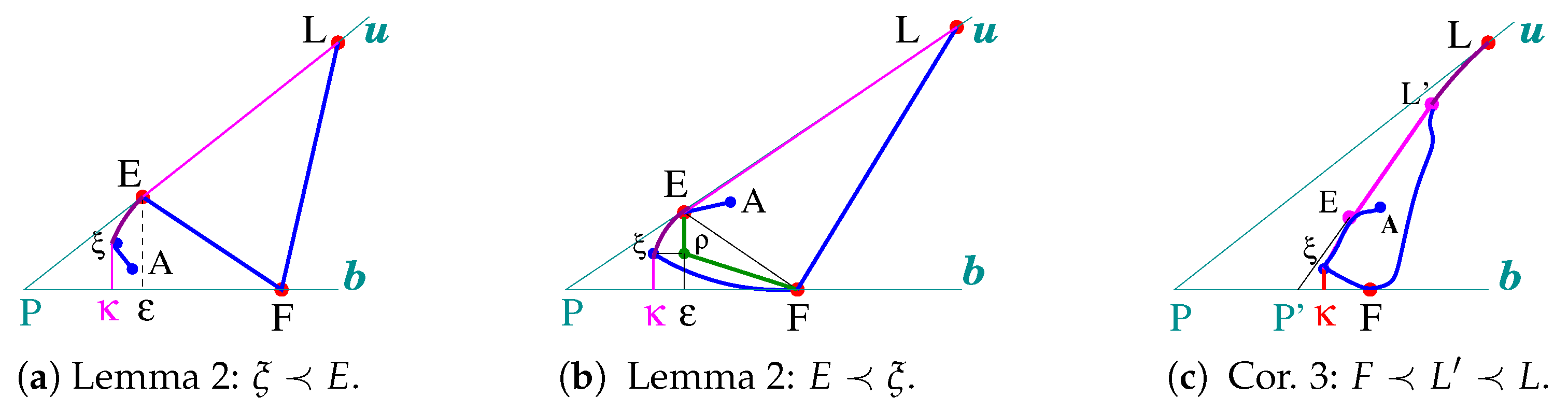
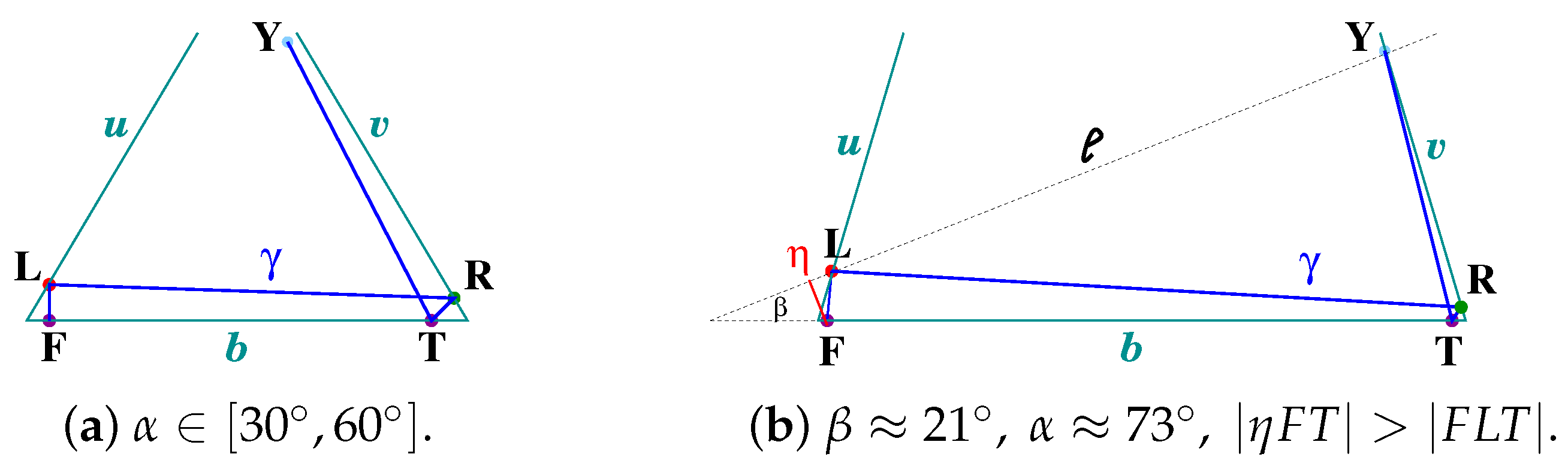
2.1. Lemma 1 and Non-Drapeable Arcs with
2.2. Drapeable Arrangements of -Triples, Draping Simple Arcs
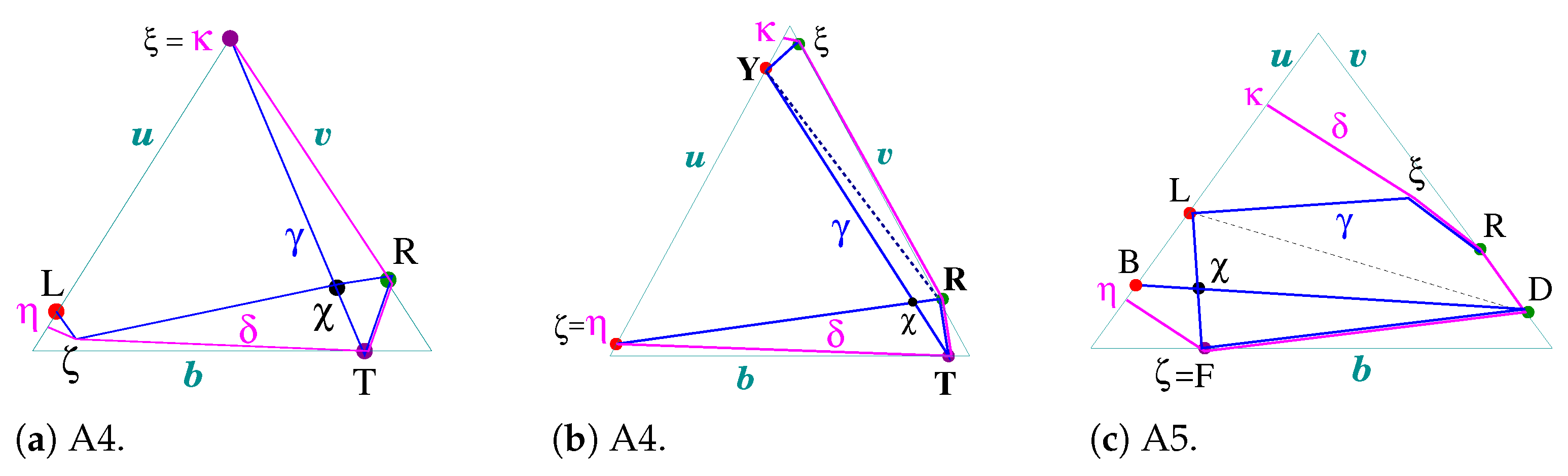
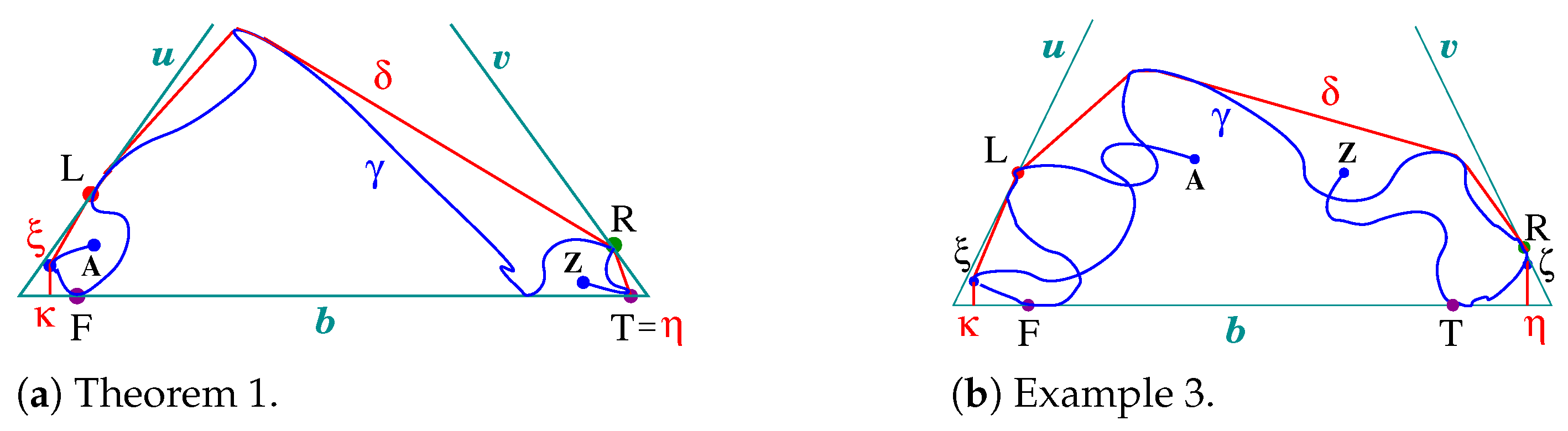
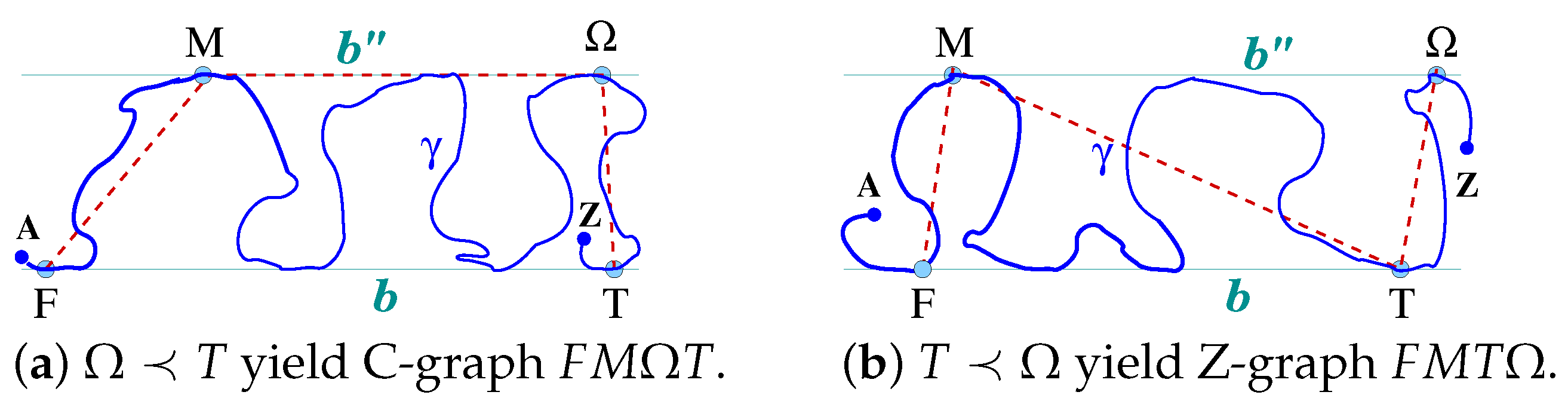
2.3. Draping Non-Simple Arc with A-Graphs A1
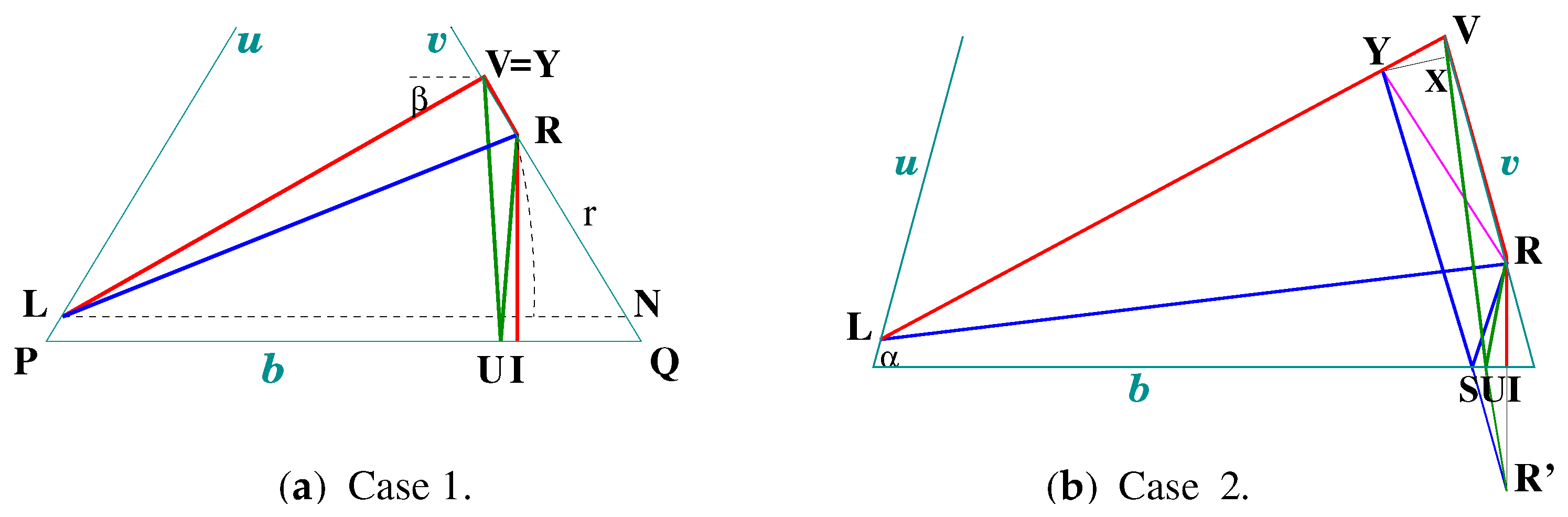
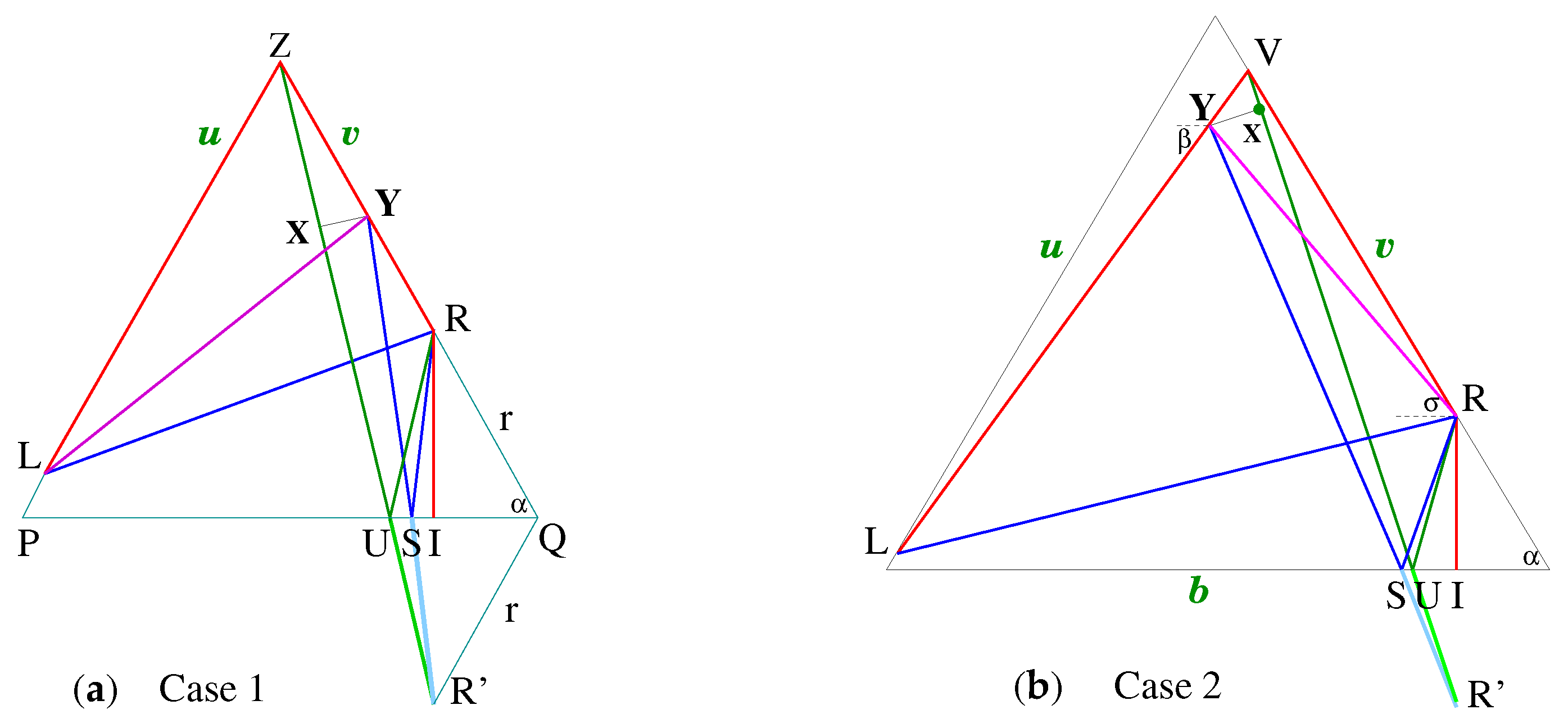
2.4. Arcs LRSY, LYRI, FLRTY, and BFLRTY
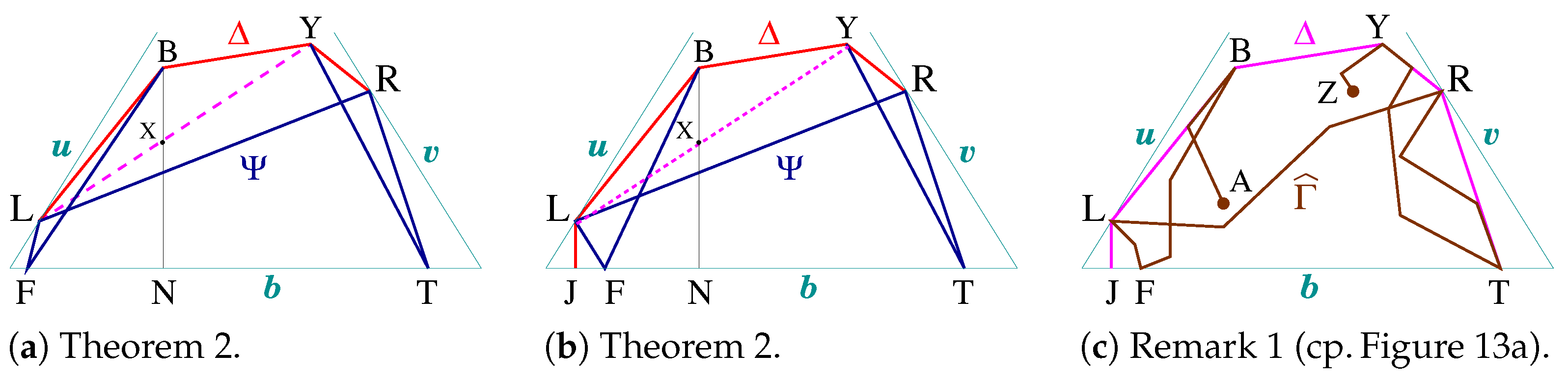
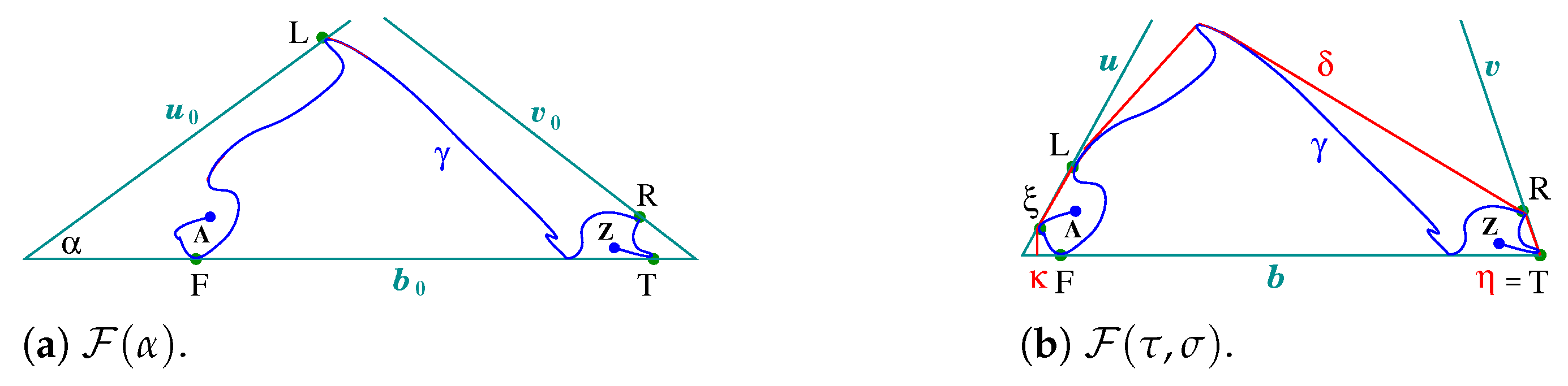
2.5. Base Drape for Arcs in Definition 4 Satisfying Theorem 2
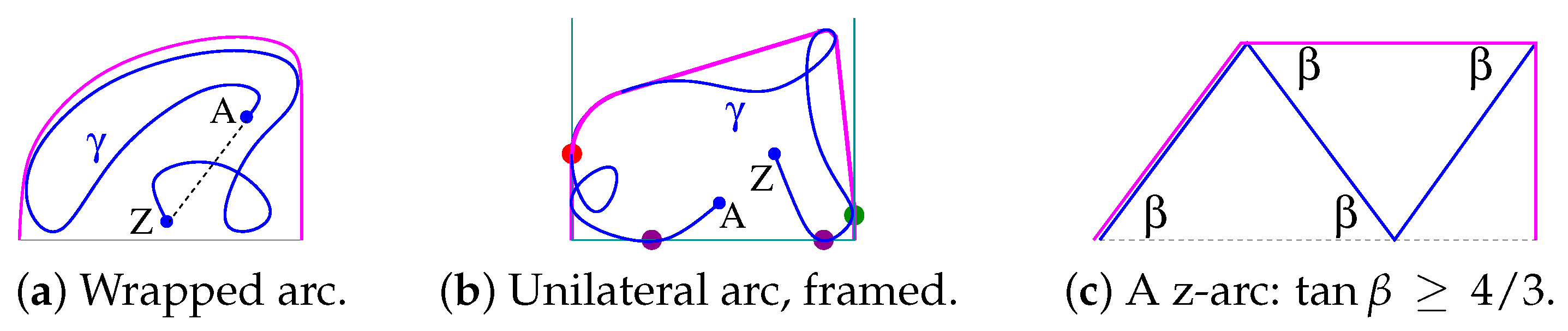
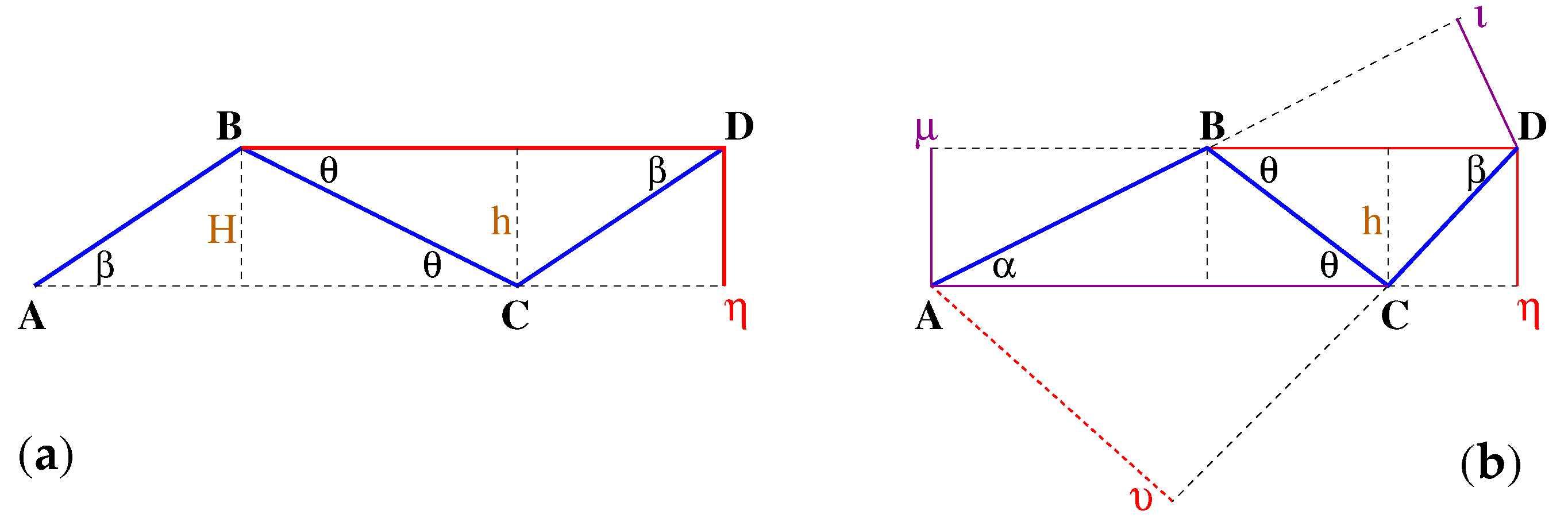
3. Drapeability of z-Arcs
3.1. Symmetric z-Arc
3.2. Z-Arc ABCD with AC and BD Parallel
3.3. General z-Arc
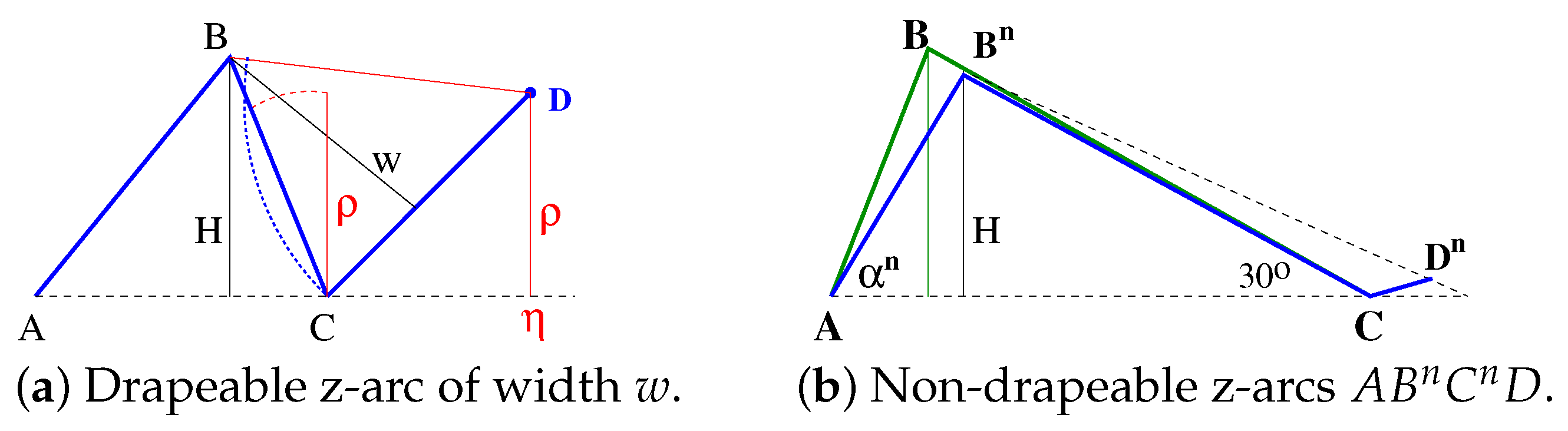
3.4. The Width of Non-Drapeable z-Worms
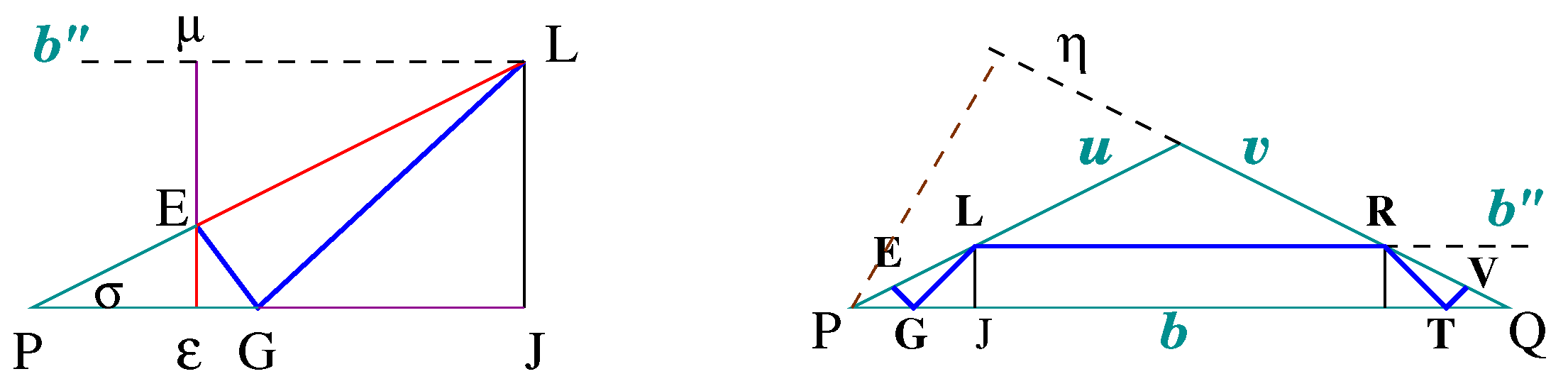
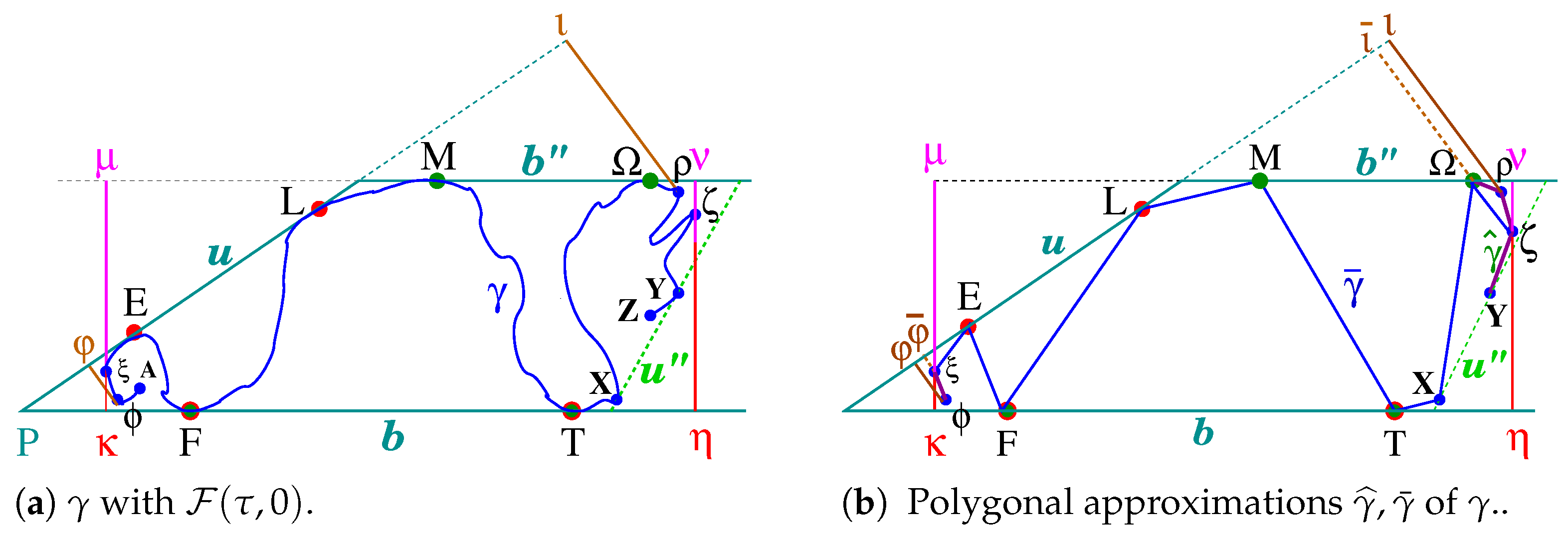
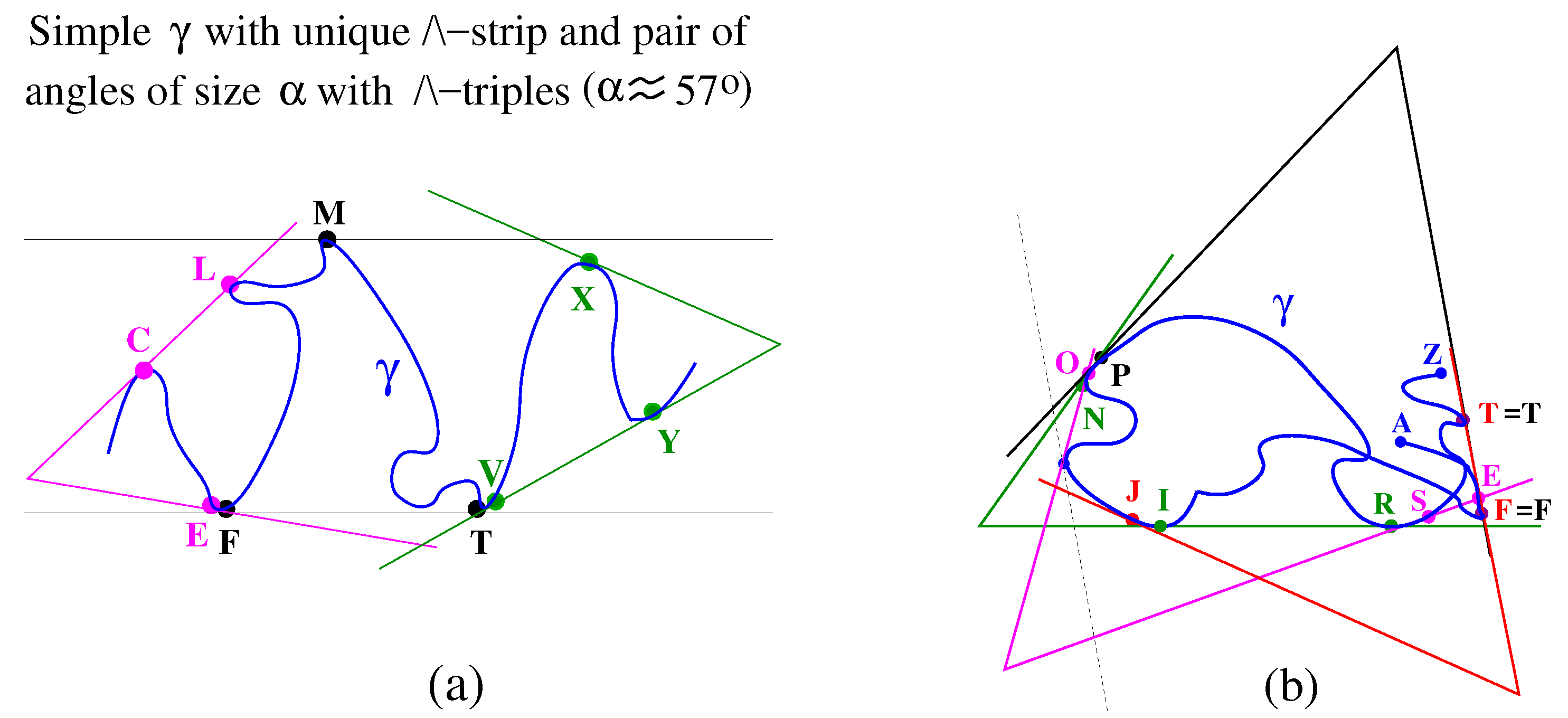
4. The -Frame of a Simple Open Arc
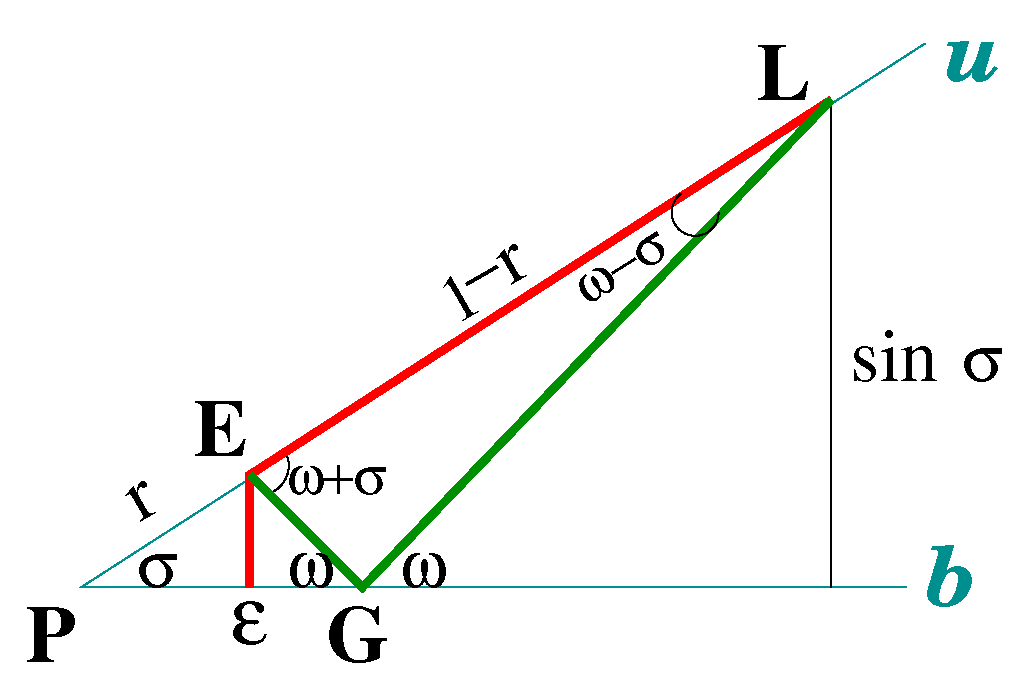
4.1. Definition of the Frame and Proof of its Existence
4.2. Draping Simple Open Arcs Using -Frames
5. Review of Known Results: Proof of Fact 1: Summary
5.1. “Drapeability” [1]
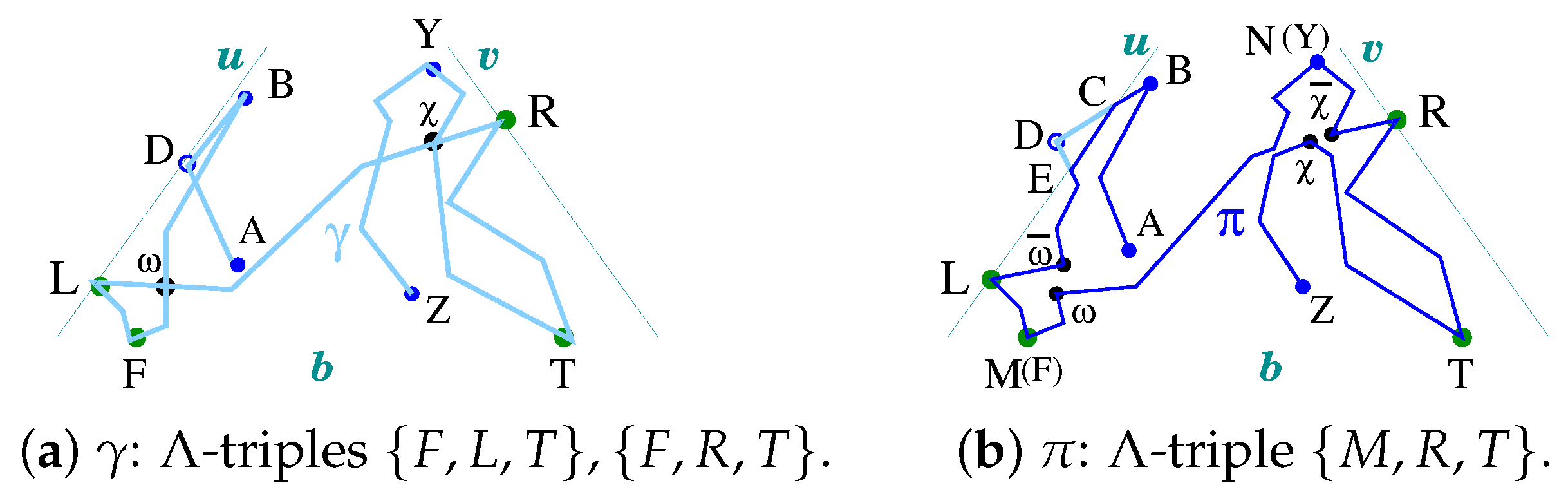
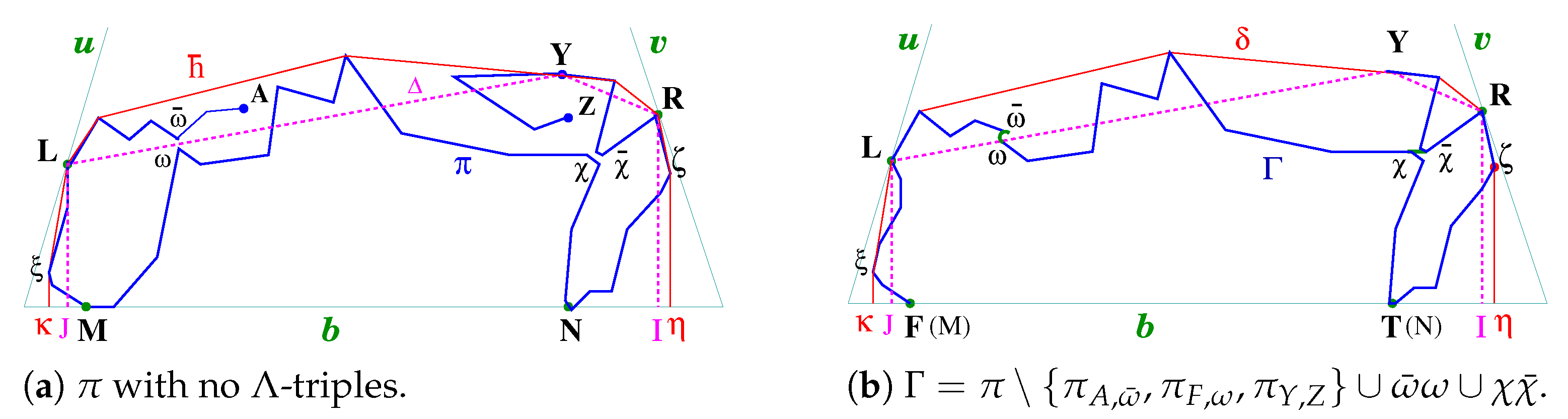
5.2. Λ-Configurations
5.3. Proof of Fact 1
5.4. Summary of Properties of a Non-Drapeable Arc
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maki, J.M.; Wetzel, J.E.; Wichirimala, W. Drapeability. Discret. Comput. Geom. 2005, 34, 637–657. [Google Scholar] [CrossRef]
- Finch, S.R.; Wetzel, J.E. Lost in a forest. Am. Math. Mon. 2004, 111, 645–654. [Google Scholar] [CrossRef]
- Movshovich, Y. Recent Advances in the Worm Problem. Eur. J. Math. 2025, 11, 71. [Google Scholar] [CrossRef]
- Benson, R.V. Euclidean Geometry and Convexity; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Brass, P.; Moser, W.; Pach, J. Research Problems in Discrete Geometry; Springer: New York, NY, USA, 2005. [Google Scholar]
- Croft, H.T.; Falconer, K.J.; Guy, R.K. Unsolved Problems in Geometry; Springer: New York, NY, USA, 1991. [Google Scholar]
- Eggleston, H.G. Convexity; Cambridge University Press: Cambridge, UK, 1958. [Google Scholar]
- Kelly, P.J.; Weiss, M.L. Geometry and Convexity; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Santaló, L.A. Integral Geometry and Geometric Probability (Encyclopedia of Mathematics and Its Applications); Addison-Wesley, Reading: Boston, MA, USA, 1976; Volume 1. [Google Scholar]
- Schaer, J. The Broadest Curve of Length 1; Research Paper No. 52; Department of Mathematics & Computer Science, University of Calgary: Calgary, AB, Canada, 1968. [Google Scholar]
- Zalgaller, V.A. How to get out of the woods? On a problem of Bellman. Mat.-Prosveshchenie 1961, 6, 191–195. [Google Scholar]
- Movshovich, Y. z-Arcs in the thirty degrees sector. J. Appl. Anal. 2021, 27, 299–320. [Google Scholar] [CrossRef]
- Panraksa, C.; Wichiramala, W. Wetzel’s sector covers unit arcs. Period. Math. Hungar. 2020, 82, 213–222. [Google Scholar] [CrossRef]
- Coulton, P.; Movshovich, Y. Besicovitch triangles cover unit arcs. Geom. Dedicata 2006, 123, 79–88. [Google Scholar] [CrossRef]
- Besicovitch, S. On arcs that cannot be covered by an open equilateral triangle of side 1. Math. Gaz. 1965, 49, 286–288. [Google Scholar] [CrossRef]
- Ghomi, M. The length, width, and inradius of space curves. Geom. Dedicata 2018, 196, 123–143. [Google Scholar] [CrossRef]
- Moser, L. Poorly Formulated Unsolved Problems in Combinatorial Geometry. Mimeogr. List 1966. [Google Scholar]
- Moser, W.O.J. Problems, problems, problems. Discrete Appl. Math. 1991, 31, 201–225. [Google Scholar] [CrossRef]
- Movshovich, Y.; Wetzel, J.E. Drapeable unit arcs fit in the unit 30° sector. Adv. Geom. 2017, 17, 497–506. [Google Scholar] [CrossRef]
- Movshovich, Y. Λ-Configuration and embedding. J. Geom. 2020, 111, 37. [Google Scholar] [CrossRef]
- Panraksa, C.; Wetzel, J.E.; Wichiramala, W. The broadest three-segment unit arc. Period. Math. Hungar. 2007, 55, 157–168. [Google Scholar] [CrossRef]
- Pál, J. Über ein elementares Variationesproblem. Math. Fys. Medd. Danske Vid. Selsk. 1920, 3, 35. [Google Scholar]


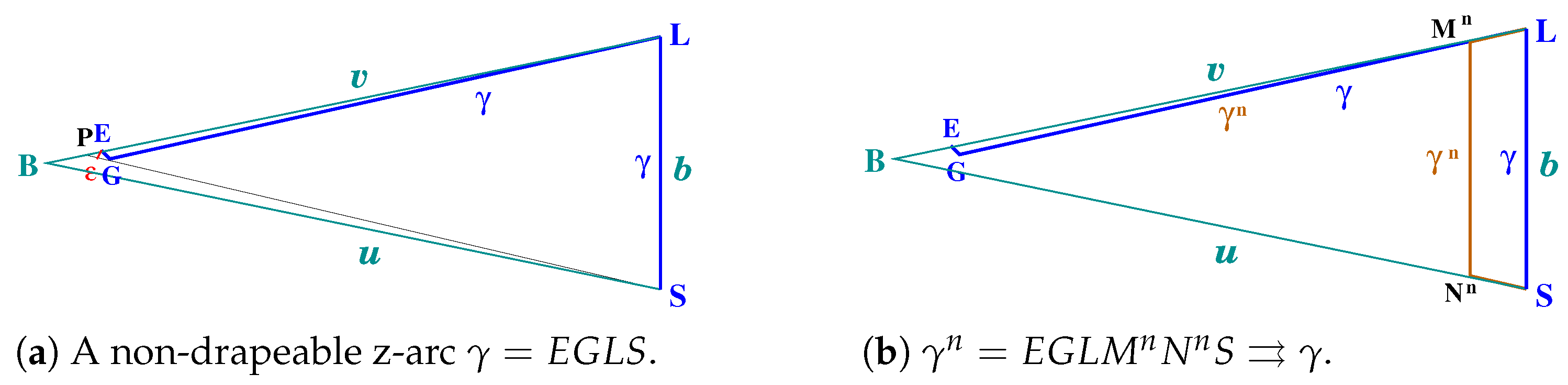



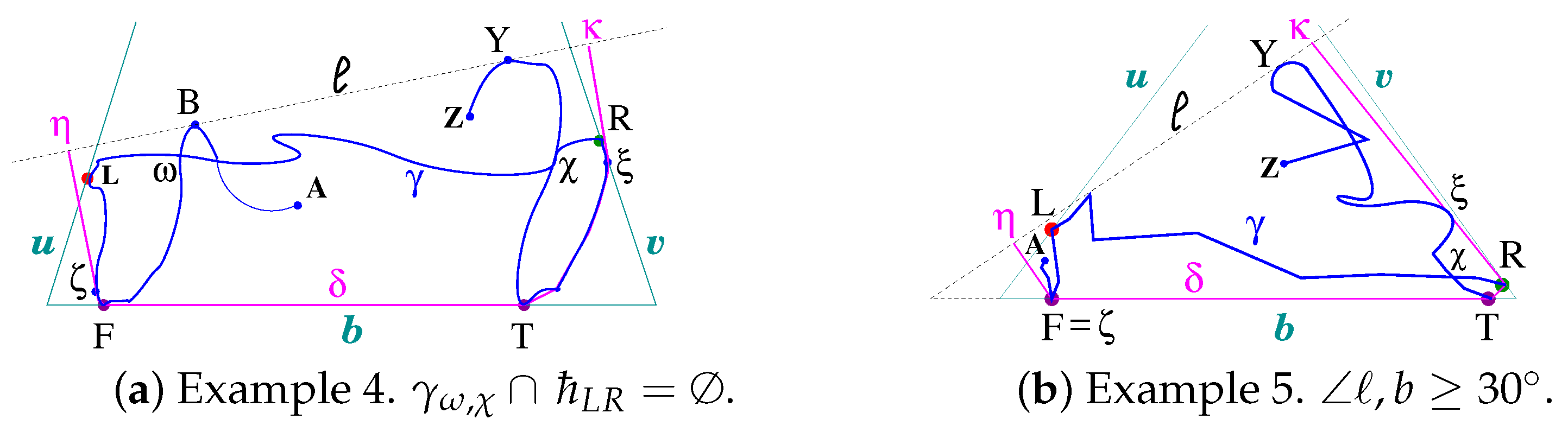
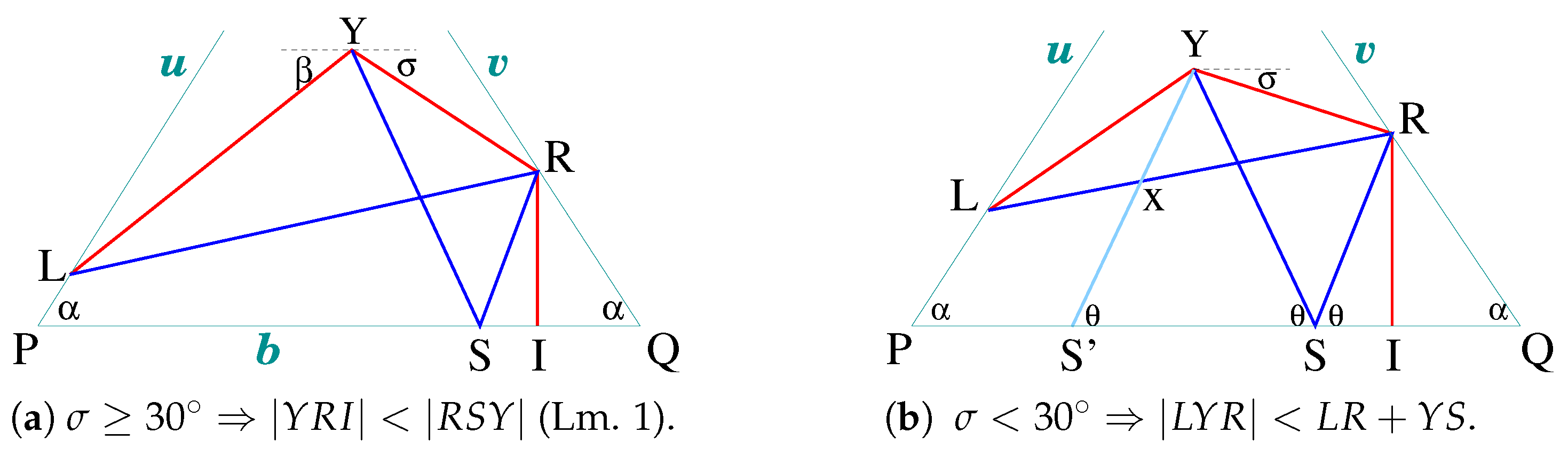

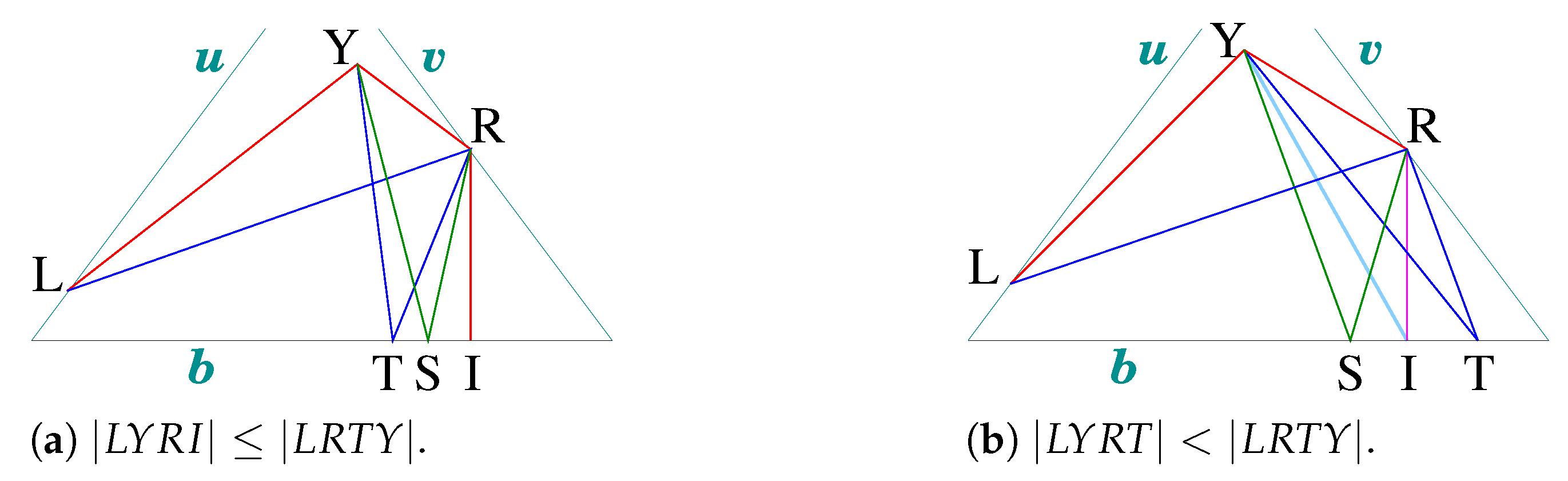







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Movshovich, Y.; Wetzel, J. Drapeability and Λ-Frames. Geometry 2025, 2, 18. https://doi.org/10.3390/geometry2040018
Movshovich Y, Wetzel J. Drapeability and Λ-Frames. Geometry. 2025; 2(4):18. https://doi.org/10.3390/geometry2040018
Chicago/Turabian StyleMovshovich, Yevgenya, and John Wetzel. 2025. "Drapeability and Λ-Frames" Geometry 2, no. 4: 18. https://doi.org/10.3390/geometry2040018
APA StyleMovshovich, Y., & Wetzel, J. (2025). Drapeability and Λ-Frames. Geometry, 2(4), 18. https://doi.org/10.3390/geometry2040018




