1. Introduction
Digital assessments are on the rise, with many countries around the world making the transition from paper-based to computer-based assessments for at least some of their school- or national-level examinations. International large-scale assessments in education, such as the Program for International Student Assessment (PISA) and the Trends in International Mathematics and Science Study (TIMSS), made the transition to a digital format in 2015 and 2019, respectively [
1,
2]. To fully take advantage of the digital platform, test developers usually incorporate new innovative item types (e.g., technology-rich items) in these assessments to enhance test-taking engagement and potentially improve the measurement quality of intended constructs. In addition, various types of process data are often captured in the background (e.g., item response times and event log data) to help uncover greater insights into students’ test-taking process [
3].
In eTIMSS 2019—the digital version of TIMSS 2019—in addition to the usual 14 student booklets that are included in the paper-based version of TIMSS, two additional booklets (Booklets 15 and 16) were developed comprising innovative problem-solving and inquiry (PSI) tasks. These tasks were designed around real-life scenarios and incorporated various interactive elements to engage the students and capture their responses [
3]. In each of the two booklets, the tasks were identical but placed in different orders to counterbalance potential position effects on item statistics and achievement [
4]. Upon analysis of data from the PSI tasks, Mullis et al. [
3] noted that there were differences between students’ completion rates for each block of tasks in the two booklets. For example, the completion rate was generally higher when a task was presented earlier in a test session. Further analysis revealed that among those students who did not complete all the items, a higher proportion of students stopped responding rather than running out of time on the test [
3]. This finding suggests that items’ positions on a test might have impacted students’ use of time during the test, their test-taking motivation (or effort), and their performance.
Previous studies on position effects in large-scale assessments have mainly focused on its impact on item parameters, such as item difficulty, to address the concern of fairness (e.g., [
5,
6,
7,
8,
9]). Several more recent studies have also examined how position effects could vary in different subject domains (e.g., [
10,
11]), for different item types (e.g., [
11,
12]), or given different student characteristics such as ability levels (e.g., [
11,
13]) or gender (e.g., [
14]). Other studies have explored the relationship between position effect and test-taking effort (e.g., [
15,
16]) or the relationship between ability and speed, including potential applications of response time in measuring or predicting achievement [
17,
18,
19,
20]. However, only a few studies have examined the effects of item position on test-taking speed. Given the increasing adoption of digital assessments involving innovative item types, it is also essential to study position effects within this context. In this study, we make use of response data from the eTIMSS 2019 Grade 4 Mathematics and Science PSI tasks and examine the associations between block positions, students’ test-taking speed, and their ability. Findings from this study could offer insight into the interplay of these variables in a computer-based test with technology-enhanced items and potentially help to inform future test development practices.
2. Theoretical Framework
In large-scale educational assessments such as PISA and TIMSS, booklet designs are typically used for test assembly and administration [
21]. As such, each student is administered a particular booklet that contains a subset of all items that are used in the assessment, organized into item blocks. The same block of items usually appears in more than one booklet, so that items can be linked and calibrated on a common scale [
8]. Item blocks are intentionally distributed so that the same item block will appear at different positions in different booklets. This approach helps enhance the test security [
13] and counterbalance position effects on item statistics [
21,
22]. The eTIMSS 2019 PSI booklets used a similar counterbalancing booklet design, but in this case, there were only two booklets, each containing all five PSI items (see
Table 1).
Researchers have shown significant interest in item position effects, driven by the prevalent use of test designs where students encounter the same items at different points during the assessment. This phenomenon applies to booklet designs and computerized adaptive tests or multistage adaptive tests, where item and testlet positions cannot be fully controlled [
6,
23]. Numerous studies have explored how items’ position influences item parameters, particularly item difficulty, employing various modeling approaches. Researchers have often advocated for the review and potential removal of items displaying substantial position effects to enhance test fairness [
6,
23].
Generally, two types of position effects have been reported in the literature [
24]: a positive position effect (i.e., when an item becomes easier when administered at later positions, see for example [
10]) and, more frequently, a negative position effect (i.e., when an item becomes more difficult when administered at later positions, see for example [
11]). Kingston and Dorans [
23] and Ong et al. [
12] found that the susceptibility to position effects appears to be item-type-specific. In particular, they found that longer items with higher reading demands were more susceptible to item position effects. Demirkol and Kelecioğlu [
11] found stronger negative position effects in reading items compared to mathematics items using PISA 2015 data from Turkey. On the other hand, Hohensinn et al. [
8] did not find any significant position effects for mathematical or quantitative items given unspeeded conditions (i.e., when sufficient time was given to complete all items). This supported Kingston and Dorans’ [
23] earlier findings and led the researchers to suggest that “position effects should be examined for every newly constructed assessment which deals with booklet designs” (p. 508). Debeer and Janssen [
13] conducted an empirical study using PISA 2006 data and found that position effects could differ for individuals with different latent abilities (students with a higher ability tend to be less susceptible to position effects). Weirich et al.’s [
16] study partly supported this finding and further demonstrated that changes in test-taking effort may also moderate position effects throughout a test.
In the context of eTIMSS 2019, Fishbein et al. [
22] acknowledged the presence of position effects occurring in the PSI booklets, especially for mathematics. PSI item blocks appearing in the second half of a test session were more difficult and had more not-reached responses than item blocks appearing in the first half [
22]. The actual completion rates for each task also varied based on block position [
3]. These findings suggest that there could have been a booklet effect on students’ overall achievement and their performance on individual items. In this case, the availability of response time data also presents a unique opportunity to examine the booklet effect on students’ use of time during the test as an indicator of their test-taking speed.
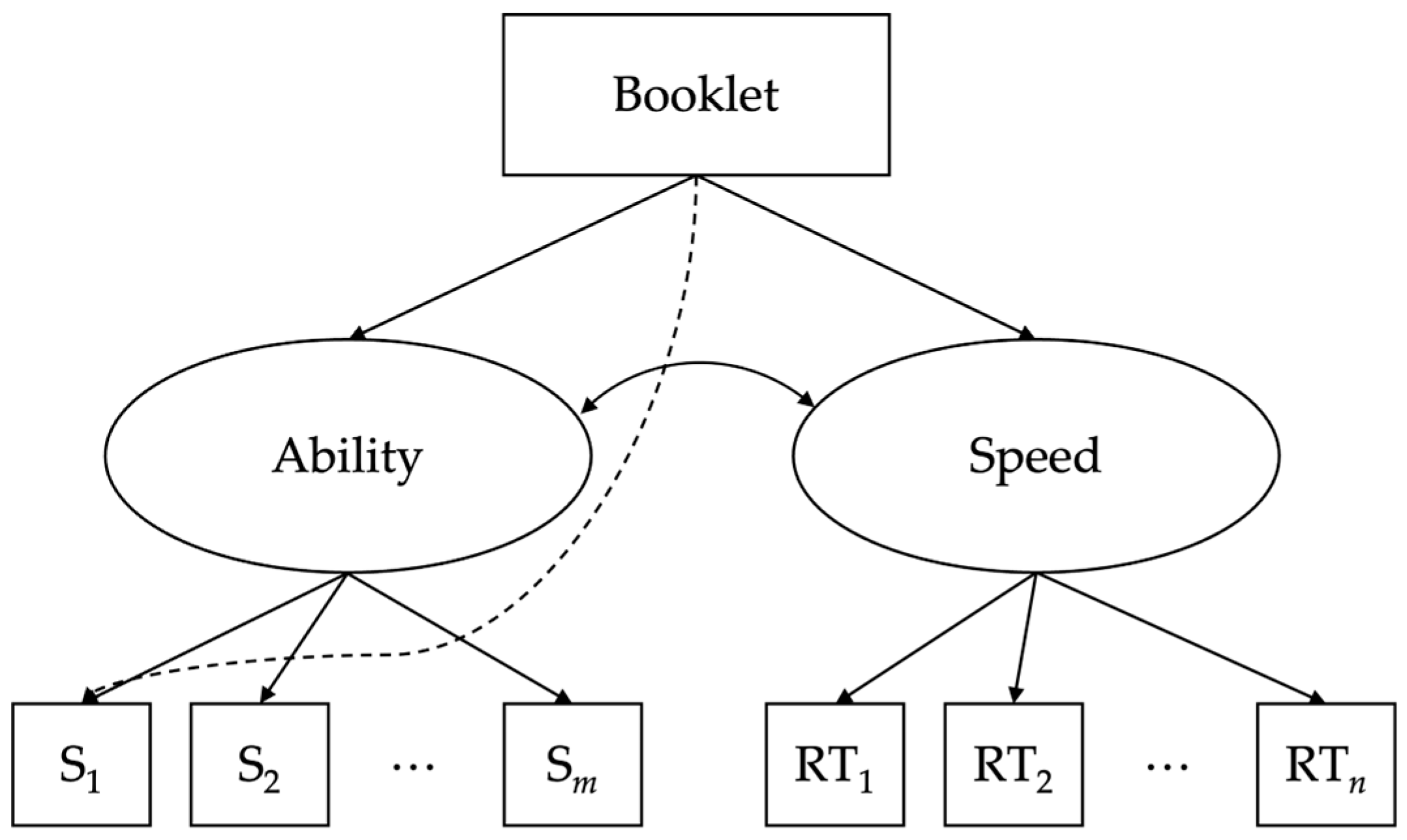
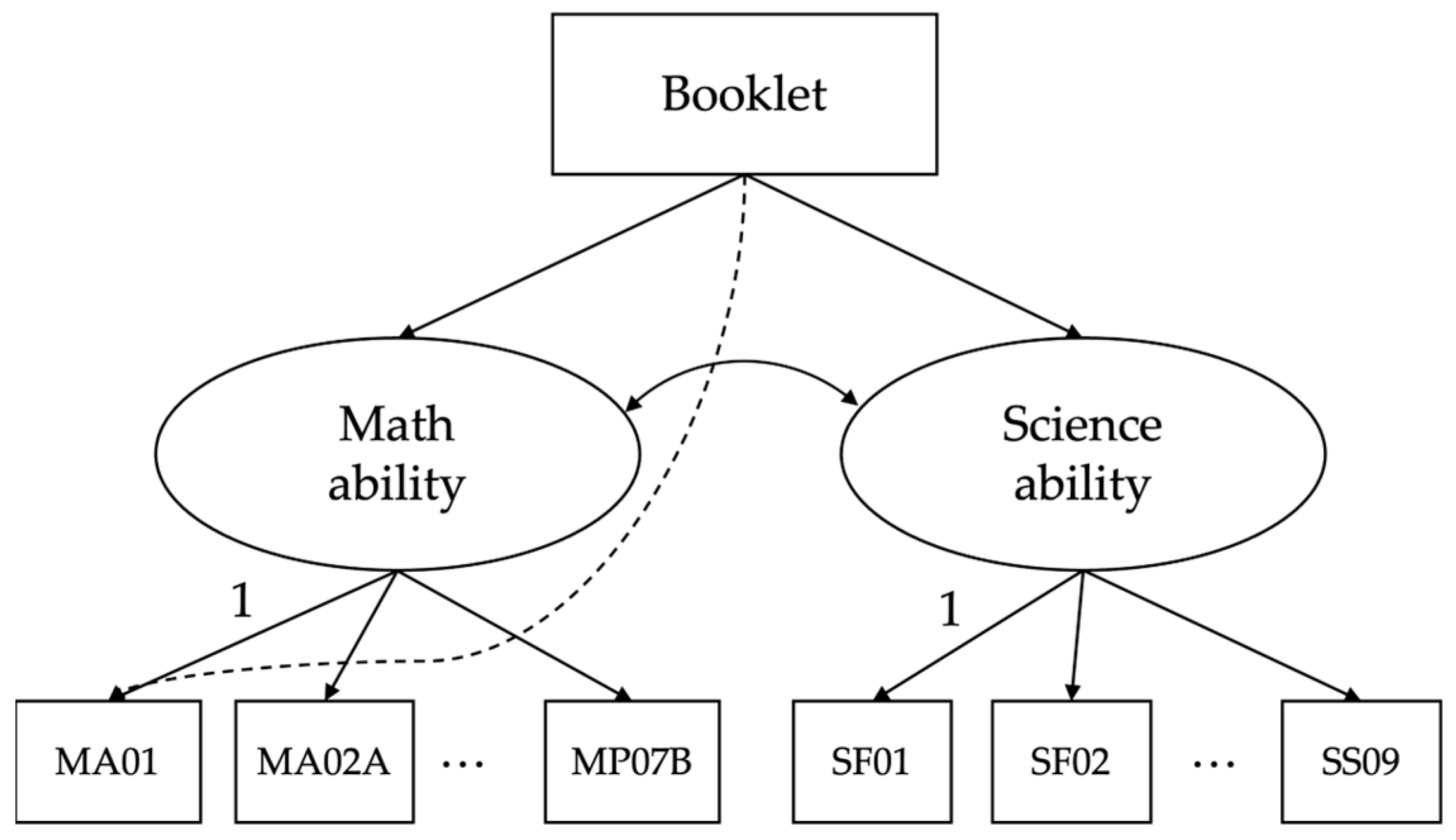
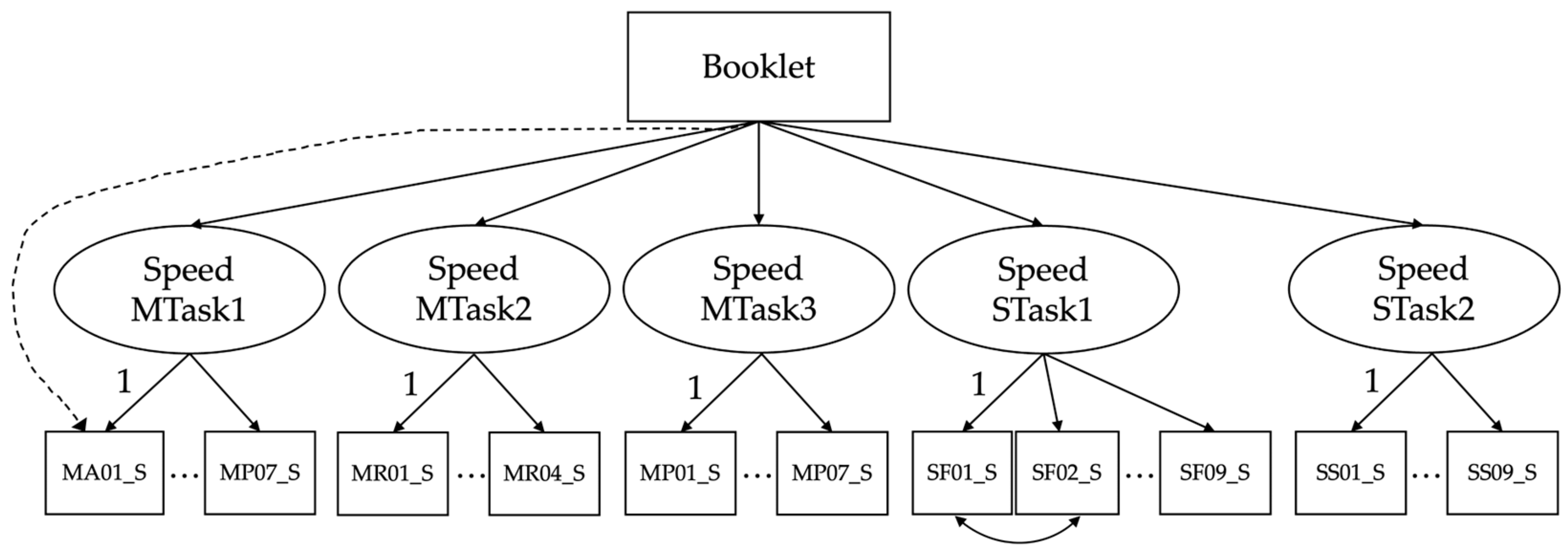
Figure 1 shows a theoretical model demonstrating the relationship between items, booklets, and response times. The model defines two latent variables: ability, with item-level scores as its indicators, and speed, with screen-level response times as its indicators (item-level response times were not available for the PSI tasks in TIMSS 2019). Booklet is a binary variable in this context, and its effect on ability and speed will be examined. In the model, it is also possible to examine the booklet effect on ability and speed across individual items and screens throughout the test. This addition could offer greater insight, especially when viewed in conjunction with individual item characteristics.
Ability and speed are commonly associated with each other (e.g., [
18,
19,
25,
26]). There are generally two perspectives on the relationship between speed and ability. One perspective is that spending more time on an item (i.e., working more slowly) increases the probability of answering the item correctly, whereas speeding up reduces the expected response accuracy. This phenomenon is commonly referred to as the within-person “speed–ability trade-off” [
19,
27]. On the other hand, a person with stronger ability in a domain could exhibit faster speed due to greater skill and fluency [
28]. Goldhammer [
19] pointed out that most assessments are a mixture of speed and ability tests, as they typically have a time limit and include items of varying difficulty, so it can be very difficult to separate these measures. Goldhammer et al. [
28] closely examined the relationship between the time spent on a task and task success using large-scale assessment data from the computer-based Programme for the International Assessment of Adult Competencies (PIAAC) and found that the time spent on task effect is moderated by the task difficulty and skill. Notably, the researchers found that task success is positively related to time spent on task for more difficult tasks, such as problem-solving, and negatively related to more routine or easier tasks. These findings suggest that the relationship between speed and ability is complex and could vary in different contexts. In
Figure 1, the relationship between speed and ability is left as a correlation, as there is no theoretical basis to say that either one causes the other.
Position, ability, and speed have all been modeled in different ways through various studies that examined different combinations of these ideas. For speed, a well-known approach to model response times is the lognormal model introduced by van der Linden [
29]. This model is based on item response theory (IRT) and has been extended in various ways to incorporate other variables, such as with a multivariate multilevel regression structure [
30] and with structural equation modeling (SEM) [
31]. For a detailed overview of modeling techniques involving response times, see De Boeck and Jeon’s [
32] recent review. For position effects, researchers often employed IRT-based methodologies such as Rasch or 2PL models, incorporating random or fixed position effects (e.g., [
9,
33]), or explanatory IRT approaches based on generalized linear mixed models (e.g., [
8,
11,
12,
16]). Bulut et al. [
6] introduced a factor analytic approach using the SEM framework, which allows for the examination of linear position effects and interaction effects in the same model and provides added flexibility for assessments with more complex designs. In this study, an SEM approach was employed to allow us to model position, ability, and test-taking speed within the same model. Due to the way in which response times were captured (at the screen level rather than at the item level), it was not appropriate to use an IRT-based approach.
The following hypotheses, derived from a thorough literature review, can offer insights into the PSI tasks in TIMSS 2019. First, a negative correlation is anticipated between speed and ability, owing to the problem-solving nature of PSI tasks—implying that heightened speed may correspond to diminished ability. Second, a shift in booklet order from 15 to 16 is predicted to be associated with an elevation in science ability but a reduction in mathematics ability. This expectation arises from the alteration in the subject sequencing. Third, the impact of booklet changes is expected to manifest across all four item blocks, with a potentially heightened influence on items in blocks M1 and S2 due to the more substantial positional change between Block Position 1 and Block Position 4.
The current study aims to contribute to the existing literature in several ways. First, previous research examining position effects typically used item data from more traditional forms of assessment (e.g., multiple-choice items). In this study, position effects are studied in the context of a computer-based assessment with technology-rich items, which could offer valuable insights, especially as more PSI-type items are planned to be incorporated in future cycles of eTIMSS [
34]. Second, few studies have incorporated response times into research on position effects (e.g., [
35]). Since response times are routinely captured in digital assessments, tapping into this data source would add value to current discussions.
5. Discussion
This study examined booklet effects on students’ ability and test-taking speed in a digital problem-solving and inquiry assessment in eTIMSS 2019. The two booklets contained the same tasks and items but differed in the position of the various item blocks. The results from the analysis on overall ability suggested a small but statistically significant booklet effect on overall mathematics and science ability, both being slightly lower for Booklet 16. In the booklet design, the order of the subjects and the order of appearance of the item blocks in each test session were switched in Booklet 16. Referring to the IRT item parameters published by TIMSS [
4], the average difficulty (b) parameters for the four item blocks were 0.317 (M1), 0.861 (M2), 0.227 (S1), and 0.463 (S2), respectively, meaning that the items in M2 and S2 were generally more difficult than the ones in M1 and S1. In Booklet 16, students were first presented with the more difficult blocks in both test sessions. This could be a possible explanation for the observed booklet effect, which is consistent with previous research (e.g., [
45,
46,
47]), which found that hard-to-easy item arrangements on a test tended to predict a lower test performance compared to easy-to-hard or random arrangements, particularly when there is an imposed time limit. These studies were typically conducted using traditional pen-and-paper multiple-choice tests.
The results from the analysis at the item level suggested a booklet effect on both ability and speed for the items appearing in the same block. When item blocks were placed in the first half of a test session, students’ speed on those items was slower and performance was better. This points to a negative position effect, which is consistent with numerous other studies (e.g., [
9,
11,
13,
24]). An intuitive explanation would be that students tended to go through items more carefully and slowly at the start of each test session, but they may feel more tired, less motivated, or rushed for time toward the end of the test. Previous research surrounding item position effects often discussed fatigue effects and practice effects (e.g., [
8,
10,
23,
48]), suggesting that performance could decrease as a test progresses due to fatigue or increase due to practice if students become more familiar with the test material [
49]. Due to the problem-solving nature of the PSI tasks, the presence of a fatigue effect seems more likely than a practice effect, as each item was crafted to be unique. However, as each test session was only 36 minutes long, another plausible explanation is that students might have felt more rushed for time when they attempted the second item block, affecting their performance. This finding echoes Albano’s [
5] argument that items with more complex content or wording may be more susceptible to position effects (i.e., perceived as more difficult) when testing time is limited. In a more recent study, Demirkol and Kelecioğlu [
11] found negative position effects in the reading and mathematics domains in PISA 2015, with stronger position effects for reading and for open-ended items in mathematics, which are more complex than multiple-choice items in the same domain. Weirich et al. [
16] further found that position effects were more pronounced for students whose test-taking effort decreased more throughout a test, but also pointed out that position effects remained, even in students with persistently high test-taking effort. These findings suggest that there could be multiple causes of position effects, and further research could help uncover when and why they occur.
Interestingly, all the key findings in this study pointed towards booklet effects that were unique to each item block. The swapped order of mathematics and science between the two booklets did not seem to have impacted students’ performance or speed as much as the ordering of blocks within each test session. This finding suggests that the short 15-minute break between the two test sessions acted almost like a “reset button”, which mitigated the position effect and gave students equal time and opportunity to perform in both portions of the assessment. In a study by Rose et al. [
50], item position and domain order effects were examined concurrently in a computer-based assessment with mathematics, science, and reading items and were found to interact substantially. However, in this case, the assessment did not incorporate any breaks between the domains. When discussing the speed–ability trade-off, Goldhammer [
19] recommended that item-level speed limits be set on assessments to estimate ability levels more accurately. The confounding effect of speed would be removed by ensuring that students have the same amount of time to work on each item. This controlled speed idea was later tested in a more recent study [
51]. In practice, it may be challenging to implement this condition due to various technical and logistical issues. However, the results of this study suggest that administering a long assessment in separately timed sessions could be a feasible alternative to improve measurement, especially if each portion is aimed at a different construct.
Limitations and Future Research
It is necessary to acknowledge the limitations of this study. First, even though the results hinted at a possible relationship between students’ ability and speed in this context (e.g., a slower speed may be related to a better performance), it was not possible to test this directly in the SEM model due to poor model fit in the combined model. In eTIMSS 2019, the total response time on each screen was captured throughout the assessment. This measured the total time that students spent on each screen, but this may not be the best measure of the actual response time (i.e., the amount of time that students spent engaging with items on each screen). For example, some students may have finished the test early or decided to take a break halfway through and lingered on some screens for longer. It was also unclear whether the screen times included overhead times (e.g., screen loading times), which could vary on different devices and contribute to increased screen times if students visited the same screen multiple times. In this study, response time outliers were removed as best as possible from the two ends of the distribution, but it was still a challenge to model speed with the existing data. More fine-grained response time data, such as those available in PISA 2018 [
52], may be helpful for researchers looking to use response time data to model test-taking speed.
Second, the dataset used in this study consisted of students from all the countries who took the eTIMSS 2019 PSI booklets. While this approach provided further insights into booklet effects occurring for all students, there may be country-specific differences that could be analyzed within each country’s context. Student motivation, engagement, and exposure to PSI-like items could vary widely in different countries, in addition to the level of ability. As eTIMSS is a low-stakes assessment, the results from this study may not apply to high-stakes assessments, where speed and ability may be more tightly related. As pointed out by Ong et al. [
12], results from position effect studies that incorporate examinee variables (e.g., gender, effort, anxiety) tended to vary depending on the features of the testing context (e.g., content, format, and stakes associated with the test). More research is thus needed to reveal how different groups of students may be impacted by position effects in different testing contexts.
Digital assessments incorporating elements of authentic assessment (e.g., scenario-based assessment) and interactive item types are increasingly used to evaluate students’ learning. As such, contextual item blocks resembling those seen in the PSI assessment may increasingly replace the typical discrete items that are used in mathematics and science assessments. This study showed that students tended to spend more time and perform better on item blocks when they were placed earlier in a test session. Test developers should be mindful of the potential effects of different orderings of item blocks on students’ test-taking process. In practice, the relative difficulty of item blocks and position effects due to blocks appearing earlier or later in a test session should be considered when assembling multiple test forms.
In the PSI section of eTIMSS 2019, each task consists of a set of items that follow a narrative or theme surrounding a real-life context. Even though the items themselves are independent of each other [
3], students’ response and response time patterns could still be related to the specific tasks. Our findings suggested that in this context, response time patterns could be task specific. More research could be carried out to examine these patterns within a task and between tasks, alongside item-specific features such as the inclusion of interactive elements, to provide insights into students’ use of time and performance in such innovative digital assessments. Future research could also examine position effects alongside item-specific and examinee-specific features to better inform test development. In this study, we analyzed data from all the countries that participated in the PSI assessment. A future study could explore country-level variations in the observed position effects and their underlying causes. Lastly, it is also worthwhile to explore how speed could be better modeled using response time data, and how the response time could be better captured in digital assessments, which may allow researchers to draw a link between ability and speed in this context.