Baryonic Matter, Ising Anyons and Strong Quantum Gravity

Abstract

We find that the whole set of known baryons of spin parity $J^P={{\displaystyle \frac{1}{2}}}^{+}$ (the ground state) and $J^P={{\displaystyle \frac{3}{2}}}^{+}$ (the first excited state) is organized in multiplets which may efficiently be encoded by the multiplets of conjugacy classes in the small finite group $G=(192, 187)$. A subset of the theory is the small group $(48, 29)\cong GL(2, 3)$ whose conjugacy classes are in correspondence with the baryon families of Gell-Mann’s octet and decuplet. G has many of its irreducible characters that are minimal and informationally complete quantum measurements that we assign to the baryon families. Since G is isomorphic to the group of braiding matrices of $SU{\left(2\right)}_2$ Ising anyons, we explore the view that baryonic matter has a topological origin. We are interested in the holographic gravity dual $Ad{S}_3/QF{T}_2$ of the Ising model. This dual corresponds to a strongly coupled pure Einstein gravity with central charge $c=1/2$ and AdS radius of the order of the Planck scale. Some physical issues related to our approach are discussed.

1. Introduction

It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience [1].

I consider it quite possible that physics cannot be based on the field concept, i.e., continuous structure. In that case, nothing remains of my entire castle in the air, gravitation theory included, (and of) the rest of modern physics [2].

Baryons are a family of subatomic particles made up of three quarks bound together by the strong nuclear force. They are one of the two main categories of hadrons, the other being mesons (which are made of one quark and one antiquark).

The name ‘baryon’ comes from a Greek word meaning ‘heavy’, as baryons were originally thought to be heavier than other particles like electrons or neutrinos. A baryon is composed of three quarks. These quarks come in six ‘flavors’—up, down, charm, strange, top and bottom—and the type of quarks determines the baryon properties, such as the charge, mass and stability. The quarks inside a baryon are held together by the strong nuclear force, mediated by particles called gluons.

The most familiar baryons are the proton $\left(p\right)$ and neutron $\left(n\right)$, which make up the nucleus of atoms as identified in the early 20th century. Over time, more baryons were discovered, including those containing heavier quarks like charm, strange and bottom quarks. In 1964, physicists Murray Gell-Mann and George Zweig proposed the quark model, suggesting that baryons are composed of three quarks [3]. Currently, baryons are described by quantum chromodynamics, the theory of the strong interaction. QCD explains how quarks interact via gluons and why baryons are bound states of three quarks. Baryons are the primary constituents of visible matter in the universe, forming stars, planets and all living beings.

The groups $SU\left(2\right)$ and $SU\left(3\right)$ are crucial in the theoretical description of baryons because they provide the mathematical framework to describe the symmetries and dynamics of quarks within baryons.

In the context of baryons, $SU\left(2\right)$ corresponds to isospin symmetry, a concept introduced by Werner Heisenberg in 1932. Isospin is an approximate symmetry of the strong nuclear force, treating the proton and neutron as two states of the same particle (nucleons). The quarks up $\left(u\right)$ and down $\left(d\right)$ are the building blocks of protons and neutrons, and they form a doublet $\left(\begin{array}{c}u\\ d\end{array}\right)$. Protons and neutrons are also organized into an isospin doublet under $SU\left(2\right)$, with isospin projections $I_3={\displaystyle \frac{1}{2}}$ (proton) and $I_3=-{\displaystyle \frac{1}{2}}$ (neutron). The concept of isospin helps classify baryons like nucleons $(p, n)$. Isospin symmetry is approximate because it neglects differences in the masses of the up and down quarks and the effects of the electromagnetic force.

In particle physics, $SU\left(3\right)$ represents the flavor symmetry of the up $\left(u\right)$, down $\left(d\right)$ and strange $\left(s\right)$ quarks. The u, d and s quarks form the basis of the fundamental representation $\left(\begin{array}{c}u\\ d\\ s\end{array}\right)$ of $SU\left(3\right)$. The baryons are built by combining three quarks, and the $SU\left(3\right)$ flavor symmetry organizes them into multiplets based on their quark content.

Isospin symmetry with $SU\left(2\right)$ and flavor symmetry with $SU\left(3\right)$ are essential ingredients of the classification of baryons made of u, d and s into octets (8 baryons) and decuplets (10 baryons) in an approach called the ‘Eightfold way’ [3,4], see Figure 1. But heavier baryons containing c and b quarks need higher groups like $SU\left(4\right)$ and $SU\left(5\right)$, providing an imperfect description, firstly because their symmetries are strongly broken and because they predict nonobserved baryons.

In the present paper, we offer an alternative description of the symmetries of baryon multiplets based on a finite group. See [5] for another attempt to approach quantum mechanics with finite mathematics. There already exists an efficient approach of the mixing patterns for the three generations of quarks and leptons through the irreducible characters of an appropriate finite group. The efforts in this direction could be summarized in a paper by the author and coauthors [6]. According to the approach, the character table of an appropriate finite group should contain both two- and three-dimensional representations being minimal and informationally complete in the sense of POVMs (positive operator valued measures). A similar approach of using the irreducible characters of an appropriate finite group was taken in the context of the genetic code [7]. The goal of the present paper is to discover an optimal discrete group whose irreducible characters fit the multiplets of baryons while preserving, as much as possible, the minimal and complete quantum informational aspect of the characters.

We are successful in this quest by discovering a series of small groups fitting in a good way with the baryon families. The first member of the series, the group $GL(2, 3)$, has a character table with eight characters that can be assigned to the eight multiplets of the octet + decuplet of Gell-Mann’s model of flavor symmetry. Then, it is shown that the group ${\mathbb{Z}}_3\times GL(2, 3)$, with 24 characters, contains the baryon families with u, d, s or c quarks. Finally, the small group $G=(192, 87)\cong P_1⋊{\mathbb{Z}}_{12}$, with $P_1\cong (16, 13)$, the single qubit Pauli group, adds known baryons containing the bottom quark b.

Most remarkably, we show that the group G is isomorphic to the group of braids underlying Ising anyons [8]. The proposal fits well with earlier work seeing baryons in dense matter as quantum Hall droplets [9]. It means that the Ising anyons can be used to encode baryonic matter. There exists a gravity dual to the Ising anyons through the minimal model with central charge $c={\displaystyle \frac{1}{2}}$, as described through the $Ad{S}_3/QF{T}_2$ correspondence. The correspondence means that ‘Ising baryons’ have a three-dimensional gravitational dual in a strongly coupled quantum regime at the Planck scale.

The structure of this paper is as follows. Section 2 recalls how the irreducible characters of a finite group with d conjugacy classes may be seen as a collection of minimal, possibly quantum informationally complete, positive operator valued measures (POVMs). This approach is described in papers [10,11]. Section 3 briefly describes the classification of baryon families according to their quark content.

Diagrams of the baryon octet and decuplet describing flavor symmetry are given in Figure 1. $SU\left(4\right)$-plets for c- and b- baryons are shown in Figure A1 and Figure A2 of Appendix A to serve as a reference to our own finite-group-based description.

Such a new description is developed step by step in Section 4. The character table for the group $GL(2, 3)$ is shown to fit the baryon octet and decuplet by assigning the eight conjugacy classes to the eight multiplets of flavor symmetry. The small group $G=(192, 187)$ is shown to appropriately fit all the known baryon multiplets with spin parity $J^P={{\displaystyle \frac{1}{2}}}^{+}$ or ${{\displaystyle \frac{3}{2}}}^{+}$ in its character table, leaving no room for unobserved baryons. In Section 5, we use the fact that G is isomorphic in the group of braid matrices for Ising anyons. We explore the $Ad{S}_3/CF{T}_2$ correspondence at central charge $c={\displaystyle \frac{1}{2}}$ corresponding to the minimal Ising model. Finally, Section 6 discusses the strengths and limits of this new approach of coupling baryonic matter to quantum gravity, opening new challenges for future work.

2. Representation Theory of Finite Groups and Minimal Informationally Complete POVMs

Let ${\mathcal{H}}_d$ be a d-dimensional complex Hilbert space and $\{E_1,\dots ,E_m\}$ be a collection of positive semi-definite operators (POVMs) that sum to the identity. Taking the unknown quantum state as a rank 1 projector $\rho =\left|\psi \right.〉\left.〈\psi \right|$ (with ${\rho }^2=\rho$ and $\mathrm{t}\mathrm{r}\left(\rho \right)=1$), the i-th outcome is obtained with a probability given by the Born rule $p\left(i\right)=\mathrm{t}\mathrm{r}\left(\rho E_i\right)$. A minimal and informationally complete POVM (or MIC) requires $d^2$ one-dimensional projectors ${\Pi }_i=\left|{\psi }_i\right.〉\left.〈{\psi }_i\right|$, with ${\Pi }_i=d{E}_i$, such that the rank of the Gram matrix with elements $\mathrm{t}\mathrm{r}\left({\Pi }_i{\Pi }_j\right)$ is precisely $d^2$.

With an MIC, the complete recovery of a state $\rho$ is possible at a minimal cost from the probabilities $p\left(i\right)$. In the best case, the MIC is symmetric and called an SIC with a further relation ${\left|〈{\psi }_i|{\psi }_j〉\right|}^2=\mathrm{t}\mathrm{r}\left({\Pi }_i{\Pi }_j\right)={\displaystyle \frac{d{\delta }_{ij}+1}{d+1}}$ so that the density matrix $\rho$ can be made explicit [10].

In our earlier references [11], a large collection of MICs is derived. They correspond to Hermitian angles ${\left|〈{\psi }_i|{\psi }_j〉\right|}_{i\ne j}\in A=\{a_1,\dots ,a_l\}$ belonging to a discrete set of values of small cardinality l. They arise from the action of a Pauli group ${\mathcal{P}}_d$ [12] on an appropriate magic state pertaining to the coset structure of subgroups of index d of a free group with relations.

An entirely new class of MICs in the Hilbert space ${\mathcal{H}}_d$, relevant for the lepton and quark mixing patterns, is obtained by taking fiducial/magic states as characters of a finite group G possessing d conjugacy classes and using the action of a Pauli group ${\mathcal{P}}_d$ on them [6]. The same approach was followed for recovering the genetic code [7]. Here, we go back to the context of particle physics by searching finite groups whose characters may be associated with the multiplets of baryons: singlets, doublets and quadruplets.

As already mentioned, in the standard model approach, such multiplets are shown in the octet spin-${\displaystyle \frac{1}{2}}$ and decuplet spin-${\displaystyle \frac{3}{2}}$ representation of baryons under the (continuous) $SU\left(2\right)$ isospin group and $SU\left(3\right)$ flavor group [3]. And, $SU\left(4\right)$-plets complete the standard description, adding baryons containing charm and bottom quarks.

3. A Primer on Baryon Families

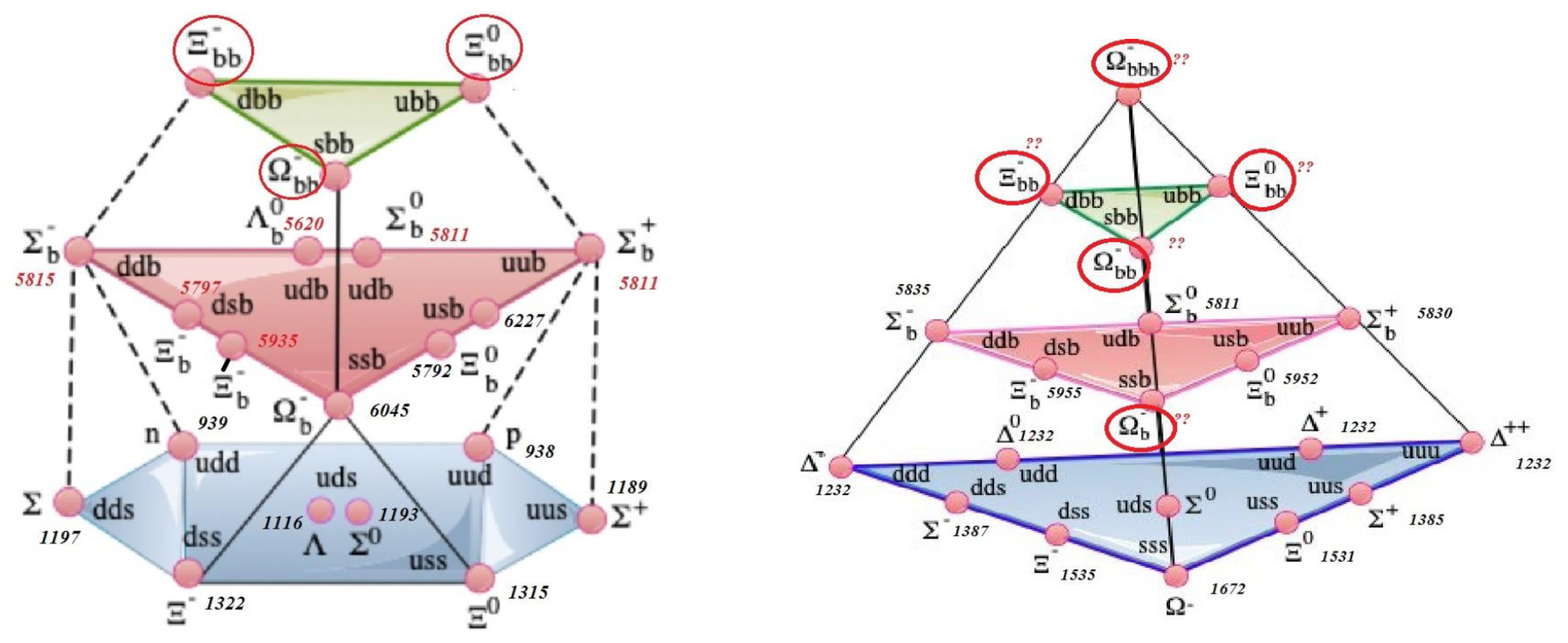
In this section, we provide a brief account of the known baryon families as updated in [13] (pp. 92–111). The baryon octet and decuplet of flavor symmetry are shown in Figure 1. For observed and expected symmetries of baryon multiplets containing the charm $\left(c\right)$ and bottom $\left(b\right)$ quarks, figures found in papers by Imran Khan are appropriate [Figure A1 based on $SU\left(4\right)$ symmetry for c quarks [14,15] and Figure A2 based on $SU\left(4\right)$ symmetry for b quarks [16]].

3.1. N-Baryons

N-baryons (also called nucleons) include the proton (p) and neutron (n). Protons were identified as the building blocks of nuclei, and neutrons were discovered by James Chadwick in 1932. Together, protons and neutrons form the nucleus of atoms, known as nucleons. The development of the quark model by Gell-Mann and Zweig in 1964 explained nucleons as composite particles made of three quarks. The proton ($uud$) and neutron ($udd$) were recognized as the lightest baryons, forming part of the baryon octet in $SU\left(3\right)$ flavor symmetry [3]. In the late 20th century, nucleon resonances (excited states of protons and neutrons) were experimentally observed in scattering experiments, leading to the identification of N-baryon resonances. The N-baryons are held together by gluons via the strong nuclear force. Quantum chromodynamics (QCD) is the theory of the strong interaction.

The proton has charge $Q=+1$, spin parity $J^P={{\displaystyle \frac{1}{2}}}^{+}$, mass $938.272\mathrm{MeV}/{\mathrm{c}}^2$ and is considered to be stable (infinite life time). The neutron is electrically neutral of charge $Q=0$, $J^P={{\displaystyle \frac{1}{2}}}^{+}$, mass $939.565\mathrm{MeV}/{\mathrm{c}}^2$ and life time about 880 s (decaying via weak interactions). Excited states of protons and neutrons are typically observed in pion–nucleon scattering experiments. They are short-lived (about ${10}^{-23}$ s) and their masses are in the range from $1\mathrm{GeV}/{\mathrm{c}}^2$ to several $\mathrm{GeV}/{\mathrm{c}}^2$.

3.2. Delta Baryons

The Delta baryons ($\Delta$) are the first known excited states of nucleons (protons and neutrons) [17]. Their discovery and study were pivotal in understanding baryon resonances and the quark model. The discovery of the $\Delta$-baryon family in experiments confirmed the existence of isospin quartets, aligned with Gell-Mann’s and Zweig’s quark model predictions. Delta baryons have been extensively studied as part of the baryon decuplet in $SU\left(3\right)$ flavor symmetry. $\Delta$ baryons are combinations of u and d quarks in a quadruplet $\{uuu, uud, udd, ddd\}$. Their spin is $J={\displaystyle \frac{3}{2}}$ (unlike the one $J={\displaystyle \frac{1}{2}}$ of nucleons). They have positive parity $J^P={{\displaystyle \frac{3}{2}}}^{+}$. The isospin quartet is $I={\displaystyle \frac{3}{2}}$ and $I_3=(+{\displaystyle \frac{3}{2}},+{\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{2}},-{\displaystyle \frac{3}{2}})$.

Delta baryons were first observed in pion–nucleon scattering experiments. Their mass is about $1232\mathrm{MeV}/{\mathrm{c}}^2$. Delta baryons decay predominantly via the strong interaction.

3.3. Lambda Baryons

The Lambda baryons ($\Lambda$) were among the first strange particles discovered and played a key role in the development of the quark model and the understanding of the strong and weak interactions. In 1947, the ${\Lambda }^0$ baryon was discovered in cosmic ray experiments by Rochester and Butler [18], marking the first identification of a particle containing a strange quark. The quark model by Gell-Mann and Zweig classified ${\Lambda }^0$ as a baryon with one strange quark (s) and two light quarks ($u, d$) forming an isoscalar ($I=0$) state. The quark content of ${\Lambda }^0$ is $uds$, with spin parity $J^P={{\displaystyle \frac{1}{2}}}^{+}$ in the ground state, mass 1115.683 MeV/c² and a life time about $2.6\times {10}^{-10}$ s, long for a baryon, as it decays via the weak interaction, predominantly to a proton or a neutron with a pion. Numerous excited states ${\Delta }^{\ast }$ have been observed with masses ranging from 1405 MeV/c² to over 2500 MeV/c². Excited ${\Lambda }^{\ast }$ decays via a strong interaction.

3.4. Sigma Baryons

The Sigma baryons ($\Sigma$) were among the first strange baryons discovered, playing a central role in understanding the strong and weak interactions [19]. The discovery of $\Sigma$ particles, along with $\Lambda$, marked the first experimental evidence of strange quarks in cosmic ray experiments. The quark model classified $\Sigma$ baryons as baryons containing one strange quark (s) and two light quarks ($u, d$), fitting within the baryon octet of $SU\left(3\right)$ flavor symmetry. In the ground state, there is a triplet $({\Sigma }^{+}, {\Sigma }^0, {\Sigma }^{-})$ with masses (1189.37, 1192.64, 1197.45) MeV/c² and life times of about $(0.8\times {10}^{-10},{10}^{-20},1.5\times {10}^{-10}$) s. Baryons ${\Sigma }^{+}$ and ${\Sigma }^{-}$ decay via strong interactions with a neutron and a pion and ${\Sigma }^0$ decays via strong interactions with ${\Lambda }_0$ and a $\gamma$ photon. Many excited states ${\Sigma }^{\ast }$ with various decay modes are also observed.

3.5. Xi Baryons

The Xi baryons ($\Xi$), also known as cascade baryons, were discovered in the mid-20th century [20] and provided critical insight into the nature of strange quarks and the quark model. Xi baryons contain two strange quarks (s) and one light quark (u or d). They form doublets ($uss, dss)$, where $J^P={{\displaystyle \frac{1}{2}}}^{+}$ for the ground state and $J^P={{\displaystyle \frac{3}{2}}}^{+}$ for the first excited state ${\Xi }^{\ast }$. The masses for the ground state are 1314.86 MeV/c² for ${\Xi }^0$ and 1321.71 MeV/c² for ${\Xi }^{-}$, with life times $2.90\times {10}^{-10}$ s and $1.64\times {10}^{-10}$ s, respectively. They decay via weak interactions with a ${\Lambda }^0$ and a pion. The excited states ${\Xi }^{\ast }$ decay via strong interactions.

3.6. Omega Baryons

The Omega baryons $\Omega$ are unique among baryons due to their quark content involving strange quarks (s). They played a pivotal role in confirming the quark model. The ${\Omega }^{-}$ baryon ($sss$) was discovered at Brookhaven National Laboratory in 1964 [21], marking a major success for Gell-Mann’s SU(3) flavor symmetry predictions. Its observation solidified the quark model. In the modern era, experiments have identified excited ${\Omega }^{-}$ baryon states and extended studies to charm and bottom counterparts. Omega baryons are baryons with two or three strange quarks (s), or their charm or bottom analogs, ${\Omega }_c^0$ with quark content $ssc$ and ${\Omega }_b^{-}$ with quark content $ssb$. For the ground state, the spin parity is $J^P={{\displaystyle \frac{3}{2}}}^{+}$. The fully strange baryon ${\Omega }^{-}$ has mass 1672.45 MeV/c², life time $0.82\times {10}^{-10}$ s, and decays weakly into ${\Lambda }^0$ and a kaon or ${\Xi }^0$ and a pion.

3.7. Charmed Baryons

Charmed baryons contain at least one charm quark (c) along with light quarks ($u, d, s$) and are crucial for studying quantum chromodynamics (QCD) in systems with heavy quarks. Following its prediction in the 1970s, the ${\Lambda }_c^{+}$ baryon was observed in 1975 in electron–positron collisions [22], marking the first discovery of a charmed baryon. Charmed baryons are baryons containing at least one charm quark (c), alongside light ($u, d, s$) quarks.

Ground states of singly charmed baryons form isoscalar singlets with $I=0$: ${\Lambda }_c^{+}\left(udc\right)$ with mass 2286.46 MeV/c² and ${\Omega }_c^0\left(ssc\right)$ with mass 2695.2 MeV/c², the isodoublet ${\Xi }_c(usc, dsc)$ with $I={\displaystyle \frac{1}{2}}$ and masses (2467.71, 2470.44) MeV/c² and the isotriplet ${\Sigma }_c(uuc, udc, ddc)$ with $I=1$ and masses (2453.97, 2452.55, 2453.75) MeV/c². Higher-spin or radially excited states have been observed for all ground-state families. Charmed baryons decay primarily via the weak interaction but can also undergo strong and electromagnetic decays, especially for excited states.

Doubly charmed baryons consist of two charm quarks (c) and a light quark ($u, d, s$). They theoretically consist of an isoscalar ${\Omega }_{cc}^{+}=scc$ with $I=0$ (not yet observed) and a doublet $({\Xi }_{cc}^{++}, {\Xi }_{cc}^{+})=(ucc, dcc)$, with $I={\displaystyle \frac{1}{2}}$, spin parity $J={{\displaystyle \frac{1}{2}}}^{+}$ and masses of the order 3621 MeV/c² as predicted by QCD. No excited doubly charmed baryons have been conclusively observed yet.

3.8. Bottom Baryons

Bottom baryons contain at least one bottom quark (b) along with light quarks ($u, d, s$), and their discovery has been a key milestone in exploring heavy quark systems. The bottom quark (b) was discovered in 1977 [23], leading to predictions of bottom baryons. In the years 1980s to 1990s, ground states of bottom baryons, such as ${\Lambda }_b^0$ and ${\Xi }_b^{-}$, were observed. In 2007, an international collaboration announced the discovery of ${\Omega }_b^{-}$. Since then, many excited states have been observed.

In the ground state, the spin parity is $J^P={{\displaystyle \frac{1}{2}}}^{+}$ with ${\Lambda }_b^0\left(udb\right)$, a singlet, the lightest bottom baryon of mass 5619.60 MeV/c². Another singlet is ${\Omega }_b^{-}\left(ssb\right)$ of mass 6045.0 MeV/c². The doublet $({\Xi }_b^0, {\Xi }_b^{-})=(usb, dsb)$ has masses (5791.40, 5797.00) MeV/c². The triplet $({\Sigma }_b^{+},{\Sigma }_b^0,{\Sigma }_b^{-})=(uub, udb, ddb)$ has masses (5810.56, 5813.43, 5815.64) MeV/c².

The following expected excited states with spin parity $J^P={{\displaystyle \frac{3}{2}}}^{+}$ are the singlet ${\Omega }_b^{\ast }\left(ssb\right)$ with predicted mass 6080 MeV/c² (not yet observed), the doublets $({\Xi }_b^{\ast 0}, {\Xi }_b^{\ast -})=(usb, dsb)$ of masses (5935, 5935) MeV/c² (not yet observed) and the triplet $({\Sigma }_b^{\ast +},{\Sigma }_b^{\ast 0},{\Sigma }_b^{\ast -})=(uub, udb, ddb)$ of masses about 5830 MeV/c².

4. Finite Group Classification of Baryon Multiplets

In this section, we show that irreducible characters, some of them informationally complete (IC), of appropriate finite groups may be made in correspondence with baryon families.

Let us start with the $18=8+10$ baryon families forming the baryon octet and decuplet shown in Figure 1 and listed in

Table 1. Upper box: The list of eight baryon families (the 18 baryons forming the standard baryon octet and decuplet shown in Figure 1). Column 1 is for the baryon type; column 2 provides the quark triplets; in column 3, I is the isospin quantum number and $J^P$ is spin parity; and column 4 provides the measured baryon masses. The star * means an excited state with $J^P={{\displaystyle \frac{3}{2}}}^{+}$. Data are available in [13] (pp. 92–97). The character table of the group $GL(2, 3)$ described in Table 2 can be considered as a discrete alternative to the ground state baryon octet and decuplet with flavor symmetry, as shown in Figure 1. Lower box: Higher $\Delta$ resonances. These resonances cannot be accounted for by the octet + decuplet diagram, nor by the corresponding character table of the finite group $GL(2, 3)$, but by higher-order finite groups, as described below in this section.

Baryon Type	Quarks	$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	Mass (MeV/c2)
N	$uud, udd$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	p(938), n(939)
$\Delta$	$uuu, uud, udd, ddd$	${\displaystyle \frac{3}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Delta }^{++}\left(1232\right),{\Delta }^{+}\left(1232\right),{\Delta }^0\left(1232\right),{\Delta }^{-}\left(1232\right)$
$\Sigma$	$uus, uds, dds$	$1\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Sigma }^{+}\left(1189\right),{\Sigma }^0\left(1192\right),{\Sigma }^{-}\left(1197\right)$
.	.	$1\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Sigma }^{\ast +}\left(1385\right),{\Sigma }^{\ast 0}\left(1384\right),{\Sigma }^{\ast -}\left(1387\right)$
$\Xi$	$uss, dss$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Xi }^0\left(1315\right),{\Xi }^{-}\left(1322\right)$
.	.	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Xi }^{\ast 0}\left(1530\right),{\Xi }^{\ast -}\left(1532\right)$
$\Lambda$	$uds$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Lambda }^0\left(1115\right)$
$\Omega$	$sss$	$0\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Omega }^{-}\left(1672\right)$
$\Delta$	$uuu, uud, udd, ddd$	${\displaystyle \frac{3}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	$\Delta \left(1232\right)$
.	.	.	$\Delta \left(1600\right)$
.	.	${\displaystyle \frac{3}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	$\Delta \left(1910\right)$

. The finite groups of smaller size able to support the baryon multiplets are groups $(48, 28)\cong 2O$, where $2O$ is the binary octahedral group, and $(48, 29)\cong GL(2, 3)$. Both groups were already used in [7] for assigning their character table to codons. Looking at [7] (Table 6), it is clear that the latter group is more appropriate in the context of N-baryons since its characters are MIC or almost MIC. The assignment of N-baryons to the character table of $GL(2, 3)$ is shown in

Table 2. The character table for group $G=GL(2, 3)=(48, 29)$. There are eight conjugacy classes of elements of multiplicities $1(\times 2)$, $2(\times 3)$, $3(\times 2)$ and 4. The size and the order of an element in the class are as shown. The last eight rows of the table are the irreducible characters ${\kappa }_i$, $i=1\dots 8$, of G. To each of them is associated the rank of the Gram matrix defined in Section 2, the identification of characters to multiplets of baryons. Characters associated with doublets and containing the pure imaginary number I, $I^2=-1$, are informationally complete with rank of the Gram matrix $d^2=8^2=64$.

Char	Dim								Gram	Quarks	Baryons
${\kappa }_1$	1	1	1	1	1	1	1	1	56	$uds$	${\Lambda }^0$
${\kappa }_2$	1	1	−1	1	1	1	−1	−1	58	$sss$	${\Omega }^{-}$
${\kappa }_3$	2	2	0	−1	2	−1	0	0	59	$uud, udd$	$p, n$
${\kappa }_4$	2	−2	0	−1	0	1	$-I\sqrt{2}$	$I\sqrt{2}$	$d^2$	$uss, dss$	${\Xi }^0,{\Xi }^{-}$
${\kappa }_5$	2	−2	0	−1	0	1	$I\sqrt{2}$	$-I\sqrt{2}$	$d^2$	.	${\Xi }^{\ast 0},{\Xi }^{\ast -}$
${\kappa }_6$	3	3	1	0	−1	0	−1	−1	63	$uus, uds, dds$	${\Sigma }^{+},{\Sigma }^0,{\Sigma }^{-}$
${\kappa }_7$	3	3	−1	0	−1	0	1	1	63	.	${\Sigma }^{\ast +},{\Sigma }^{\ast 0},{\Sigma }^{\ast -}$
${\kappa }_8$	4	−4	0	1	0	−1	0	0	61	$uuu, uud, udd, dsd$	${\Delta }^{++},{\Delta }^{+},{\Delta }^0,{\Delta }^{-}$

. Thus, we already have a discrete option based on $GL(2, 3)$ against the continuous groups $SU\left(2\right)$ and $SU\left(3\right)$ to capture the symmetries of some baryon families.

Let us go ahead. Our discussion below is summarized in Table 3.

The smallest finite groups able to assign their characters to N-baryons and most non strange singly charmed baryons are groups $(96, 66)\cong {\mathbb{Z}}_2⋊2O$ and $(96, 67)\cong P_1⋊{\mathbb{Z}}_6$, where $P_1\cong (16, 13)$ rules the commutation relations of a single qubit. The latter group is more appropriate than the first one because its characters are MICs or almost MICS, as shown in

Table 4. The character table for the group $G=(96, 67)\cong P_1⋊{\mathbb{Z}}_6$, where $P_1\cong (16, 13)$ is isomorphic to the single qubit Pauli group. There are sixteen conjugacy classes of elements of multiplicities $1(\times 4)$, $2(\times 6)$, $3(\times 4)$ and $4(\times 2)$. Compared to Table 1, the present table adds some charmed baryons when they exist or should exist and the first higher-order resonance $\Delta \left(1620\right)$ (we use the bold notation for them). Characters associated with doublets and triplets and containing the pure imaginary number I, $I^2=-1$, are informationally complete with rank of the Gram matrix $d^2={16}^2=256$.

Char	Dim									Gram	Quarks	Baryons
${\kappa }_1$	1⋯	1	1	1	1	1	1	1	1	16	$uds$	${\Lambda }^0$
${\kappa }_2$	1⋯	−1	−1	−1	1	−1	−1	1	1	208	$sss$	${\Omega }^{-}$
${\kappa }_3$	1⋯	−I	I	1	1	I	−I	−1	−1	238	$\mathit{udc}$	${\Lambda }_c^{+}$
${\kappa }_4$	1⋯	I	−I	1	1	−I	I	−1	−1	238	$scc$	${\Omega }_{cc}^{+}$
${\kappa }_5$	2⋯	0	0	2	−1	0	0	−1	−1	244	$uud, udd$	$p,n$
${\kappa }_6$	2⋯	0	0	2	−1	0	0	1	1	240	$\mathit{dcc},\mathit{ucc}$	${\Xi }_{cc}^{+},{\Xi }_{cc}^{++}$
${\kappa }_7$	2⋯	1 − I	1 − I	0	1	0	0	I	−I	$d^2$	$uss, dss$	${\Xi }^0,{\Xi }^{-}$
${\kappa }_8$	2⋯	1 − I	1 − I	0	1	0	0	−I	I	$d^2$	.	${\Xi }^{\ast 0},{\Xi }^{\ast -}$
${\kappa }_9$	2⋯	1 + I	1 + I	0	1	0	0	I	−I	$d^2$	$\mathit{usc},\mathit{dsc}$	${\Sigma }_c^{+},{\Sigma }_c^0$
${\kappa }_{10}$	2⋯	1 + I	1 + I	0	0	0	0	−I	I	$d^2$	.	${\Sigma }_c^{\ast +},{\Sigma }_c^{\ast 0}$
${\kappa }_{11}$	3⋯	1	1	−1	0	−1	−1	0	0	248	$uus, uds, dds$	${\Sigma }^{+},{\Sigma }^0,{\Sigma }^{-}$
${\kappa }_{12}$	3⋯	−1	−1	−1	0	1	1	0	0	244	.	${\Sigma }^{\ast +},{\Sigma }^{\ast 0},{\Sigma }^{\ast -}$
${\kappa }_{13}$	3⋯	−I	I	−1	0	−I	I	0	0	$d^2$	$\mathit{uuc},\mathit{udc},\mathit{ddc}$	${\Sigma }_c^{++},{\Sigma }_c^{+},{\Sigma }_c^0$
${\kappa }_{14}$	3⋯	I	−I	−1	0	I	−I	0	0	$d^2$	.	${\Sigma }_c^{\ast ++},{\Sigma }_c^{\ast +},{\Sigma }_c^{\ast }0$
${\kappa }_{15}$	4⋯	0	0	0	−1	0	0	I	−I	244	$uuu, uud, udd, ddd$	${\Delta }^{++},{\Delta }^{+},{\Delta }^0,{\Delta }^{-}$
${\kappa }_{16}$	4⋯	0	0	0	−1	0	0	−I	I	244	.	$\Delta \left(1232\right)$

. The table adds to the $GL(2, 3)$ table nonstrange singly charmed baryons when they exist or should exist (we use the bold notation for them). The row for character ${\kappa }_{16}$ is not compatible with baryon families allowed by the standard model (SM) of particles. The quadruplet $(uuu, uuc, ucc, ccc)$ is not an SM multiplet under any known flavor or isospin symmetry.

Table 3. Upper box: the list of six charmed baryon families having room in Table 4 representing the irreducible characters of the group $G=(96, 67)\cong P_1⋊{\mathbb{Z}}_6$. Middle box: the list of extra three charmed baryon families having room in Table 4 representing the irreducible characters of the group $G=(144, 122)\cong {\mathbb{Z}}_3\times GL(2, 3)$. Lower box: the list of six bottom baryon families having room in

Table 5. The character table for the group $G=(192, 187)={\mathbb{Z}}_{12}⋊P_1$, where $P_1\cong (16, 13)$ is the single qubit Pauli group. There are 32 conjugacy classes of elements of multiplicities $1(\times 8)$, $2(\times 12)$, $3(\times 8)$ and $4(\times 4)$. Compared to Table 6, the present table adds the baryons containing bottom quarks when they exist or should exist as well as $\Delta \left(1910\right)$ and $\Delta \left(1920\right)$ resonances (we use the bold notation for them). In some of their entries, many characters contain the pure imaginary I, $I^2=-1$, $J=exp(2i\pi /3)$, $u={\displaystyle \frac{\sqrt{2}}{2}}(1+I)$, $v=\sqrt{1-{\displaystyle \frac{\sqrt{2}}{2}}}+I\sqrt{1+{\displaystyle \frac{\sqrt{2}}{2}}}$ and $w={\displaystyle \frac{\sqrt{2}}{2}}(1+I)$. Characters associated with doublets and containing the complex numbers v are informationally complete (MICs) with rank of the Gram matrix $d^2={32}^2=1024$. The four triplets containing the complex numbers w are also MICs. The not-assigned characters only have relative integers 0, $\pm 1$, $\pm 2$ or $\pm 3$ in their entries.

Char	Dim							Gram	Quarks	Baryons
${\kappa }_1$	1⋯	1	1	1	1	1	1	32	$uds$	${\Lambda }^0$
${\kappa }_2$	1⋯	−1	−1	1	1	1	1	834	$sss$	${\Omega }^{-}$
${\kappa }_3$	1⋯	I	−I	−1	−1	−1	−1	985	$udc$	${\Lambda }_c^{+}$
${\kappa }_4$	1⋯	−I	I	−1	−1	−1	−1	985	$ssc$	${\Omega }_c^0$
${\kappa }_5$	1⋯	$-Iu$	u	−I	I	−I	I	993	$scc$	${\Omega }_{cc}^{+}$
${\kappa }_6$	1⋯	u	$-Iu$	I	−I	I	−I	993	.	${\Omega }_{cc}^{\ast +}$
${\kappa }_7$	1⋯	$Iu$	$-u$	−I	I	−I	I	993	$\mathit{udb}$	${\Lambda }_b^0$
${\kappa }_8$	1⋯	$-u$	$Iu$	I	−I	I	−I	993	$\mathit{ssb}$	${\Omega }_b^{-}$
${\kappa }_9$	2⋯	0	0	1	−1	−1	−1	1003	?	unknown
${\kappa }_{10}$	2⋯	0	0	1	1	1	1	1003	?	unknown
${\kappa }_{11}$	2⋯	0	0	−I	I	−I	I	1023	$uud, udd$	$p,n$
${\kappa }_{12}$	2⋯	0	0	I	−I	I	−I	1023	$dcc, ucc$	${\Xi }_{cc}^{+},{\Xi }_{cc}^{++}$
${\kappa }_{13}$	2⋯	$Iv$	$-Iv$	$Iv$	$-Iv$	$-v$	$-\overline{v}$⋯	$d^2$	$uss, dss$	${\Xi }^0,{\Xi }^{-}$
${\kappa }_{14}$	2⋯	$-\overline{v}$	$\overline{v}$	$-v$	v	$-Iv$	$-Iv$⋯	$d^2$	.	${\Xi }^{\ast 0},{\Xi }^{\ast -}$
${\kappa }_{15}$	2⋯	$Iv$	$-Iv$	$Iv$	$-Iv$	$-\overline{v}$	$-v$⋯	$d^2$	$ucc, dcc$	${\Sigma }_{cc}^{++},{\Sigma }_{cc}^{+}$
${\kappa }_{16}$	2⋯	v	$-v$	$\overline{v}$	$-\overline{v}$	$Iv$	$Iv$⋯	$d^2$	.	${\Sigma }_{cc}^{\ast ++},{\Sigma }_{cc}^{\ast +}$
${\kappa }_{17}$	2⋯	$-Iv$	$Iv$	$-Iv$	v	$\overline{v}$	$\overline{v}$⋯	$d^2$	$usc, dsc$	${\Xi }_c^{+},{\Xi }_c^0$
${\kappa }_{18}$	2⋯	$\overline{v}$	$-\overline{v}$	v	$-v$	$Iv$	$Iv$⋯	$d^2$	.	${\Xi }_c^{\ast +},{\Xi }_c^{\ast 0}$
${\kappa }_{19}$	2⋯	$-Iv$	$Iv$	$-Iv$	$Iv$	$\overline{v}$	v⋯	$d^2$	$\mathit{usb},\mathit{dsb}$	${\Xi }_b^0,{\Xi }_b^{-}$
${\kappa }_{20}$	2⋯	-v	v	$-\overline{v}$	$\overline{v}$	$-Iv$	$-Iv$⋯	$d^2$	.	${\Xi }_b^{\ast 0},{\Xi }_b^{\ast -}$
${\kappa }_{21}$	3⋯	-1	-1	0	0	0	0	1008	?	unknown
${\kappa }_{22}$	3⋯	1	1	0	0	0	0	1006	?	unknown
${\kappa }_{23}$	3⋯	-I	I	0	0	0	0	1004	$\mathit{uub},\mathit{udb},\mathit{ddb}$	${\Sigma }_b^{+},{\Sigma }_b^0,{\Sigma }_b^{-}$
${\kappa }_{24}$	3⋯	I	-I	0	0	0	0	1004	.	${\Sigma }_b^{\ast +},{\Sigma }_b^{\ast 0},{\Sigma }_b^{\ast -}$
${\kappa }_{25}$	3⋯	$-\overline{w}$	w	0	0	0	0	$d^2$	$uus, uds, dds$	${\Sigma }^{+},{\Sigma }^0,{\Sigma }^{-}$
${\kappa }_{26}$	3⋯	w	$-\overline{w}$	0	0	0	0	$d^2$	.	${\Sigma }^{\ast +},{\Sigma }^{\ast 0},{\Sigma }^{\ast -}$
${\kappa }_{27}$	3⋯	$\overline{w}$	$-w$	0	0	0	0	$d^2$	$uuc, udc, ddc$	${\Sigma }_c^{++},{\Sigma }_c^{+},{\Sigma }_c^0$
${\kappa }_{28}$	3⋯	$-w$	$\overline{w}$	0	0	0	0	$d^2$	.	${\Sigma }_c^{\ast ++},{\Sigma }_c^{\ast +},{\Sigma }_c^{\ast }0$
${\kappa }_{29}$	4⋯	0	0	$-\overline{w}$	$-w$	$\overline{w}$	w	1023	$uuu, uud, udd, ddd$	${\Delta }^{++},{\Delta }^{+},{\Delta }^0,{\Delta }^{-}$
${\kappa }_{30}$	4⋯	0	0	$\overline{w}$	w	$\overline{w}$	$-w$	1023	.	$\Delta \left(1232\right)$
${\kappa }_{31}$	4⋯	0	0	w	$\overline{w}$	$-w$	$-\overline{w}$	1023	.	$\Delta \left(1600\right)$
${\kappa }_{32}$	4⋯	0	0	$-w$	$-\overline{w}$	w	$\overline{w}$	1023	.	$\Delta \left(1910\right)$

representing the irreducible characters of the group $G=(192, 187)\cong P_1⋊{\mathbb{Z}}_{12}$. As in Table 1, column 1 is for the baryon type; column 2 provides the quark triplets; in column 3, I is the isospin and $J^P$ is spin parity; and column 4 provides the measured baryon masses. As before, the star * means an excited state with $J^P={{\displaystyle \frac{3}{2}}}^{+}$. The question mark ? indicates a lack of experimental evidence. Data are available in [13] (pp. 92–111).

Baryon Type	Quarks	$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	Mass (MeV/c2)
$\Sigma$	$uuc, udc, ddc$	$1\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Sigma }_c^{++}\left(2454\right),{\Sigma }_c^{+}\left(2454\right),{\Sigma }_c^0\left(2454\right)$
.	.	$1\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Sigma }_c^{\ast ++}\left(2520\right),{\Sigma }_c^{\ast +}\left(2520\right),{\Sigma }_c^{\ast 0}\left(2520\right)$
$\Xi$	$usc, dsc$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Xi }_c^{+}\left(2468\right),{\Xi }_c^0\left(2470\right)$
.	.	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Xi }_c{\left(2645\right)}^{+},{\Xi }_c{\left(2645\right)}^0$
$\Lambda$	$udc$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Lambda }_c^{+}\left(2286\right)$
$\Omega$	$scc$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Omega }_{cc}^{+}(3916?)$
$\Omega$	$ssc$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Omega }_c^0\left(2695\right)$
$\Xi$	$ucc, dcc$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Xi }_{cc}^{++}\left(3621\right),{\Xi }_{cc}^{+}(3610?)$
.	.	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Xi }_{cc}^{\ast ++}(?),{\Xi }_{cc}^{\ast +}(?)$
$\Lambda$	$udb$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Lambda }_b^0\left(5619\right)$
$\Omega$	$ssb$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Omega }_b^{-}\left(6045\right)$
$\Xi$	$usb,dsb$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Xi }_b^0\left(5791\right),{\Xi }_b^{-}\left(5797\right)$
.	.	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Xi }_b^{\ast }{\left(5945\right)}^0,{\Xi }_b^{\ast }{\left(5955\right)}^{-}$
$\Sigma$	$uub, udb, ddb$	$1\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Sigma }_b^{+}\left(5811\right),{\Sigma }_b^0\left(5813\right),{\Sigma }_b^{-}\left(5815\right)$
.	.	$1\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Sigma }_b^{\ast }{\left(5830\right)}^{+},{\Sigma }_b^{\ast }{\left(5833\right)}^0,{\Sigma }_b^{\ast }{\left(5835\right)}^{-}$

Table 3. Upper box: the list of six charmed baryon families having room in Table 4 representing the irreducible characters of the group $G=(96, 67)\cong P_1⋊{\mathbb{Z}}_6$. Middle box: the list of extra three charmed baryon families having room in Table 4 representing the irreducible characters of the group $G=(144, 122)\cong {\mathbb{Z}}_3\times GL(2, 3)$. Lower box: the list of six bottom baryon families having room in Table 5 representing the irreducible characters of the group $G=(192, 187)\cong P_1⋊{\mathbb{Z}}_{12}$. As in Table 1, column 1 is for the baryon type; column 2 provides the quark triplets; in column 3, I is the isospin and $J^P$ is spin parity; and column 4 provides the measured baryon masses. As before, the star * means an excited state with $J^P={{\displaystyle \frac{3}{2}}}^{+}$. The question mark ? indicates a lack of experimental evidence. Data are available in [13] (pp. 92–111).

Baryon Type	Quarks	$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	Mass (MeV/c2)
$\Sigma$	$uuc, udc, ddc$	$1\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Sigma }_c^{++}\left(2454\right),{\Sigma }_c^{+}\left(2454\right),{\Sigma }_c^0\left(2454\right)$
.	.	$1\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Sigma }_c^{\ast ++}\left(2520\right),{\Sigma }_c^{\ast +}\left(2520\right),{\Sigma }_c^{\ast 0}\left(2520\right)$
$\Xi$	$usc, dsc$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Xi }_c^{+}\left(2468\right),{\Xi }_c^0\left(2470\right)$
.	.	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Xi }_c{\left(2645\right)}^{+},{\Xi }_c{\left(2645\right)}^0$
$\Lambda$	$udc$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Lambda }_c^{+}\left(2286\right)$
$\Omega$	$scc$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Omega }_{cc}^{+}(3916?)$
$\Omega$	$ssc$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Omega }_c^0\left(2695\right)$
$\Xi$	$ucc, dcc$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Xi }_{cc}^{++}\left(3621\right),{\Xi }_{cc}^{+}(3610?)$
.	.	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Xi }_{cc}^{\ast ++}(?),{\Xi }_{cc}^{\ast +}(?)$
$\Lambda$	$udb$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Lambda }_b^0\left(5619\right)$
$\Omega$	$ssb$	$0\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Omega }_b^{-}\left(6045\right)$
$\Xi$	$usb,dsb$	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Xi }_b^0\left(5791\right),{\Xi }_b^{-}\left(5797\right)$
.	.	${\displaystyle \frac{1}{2}}\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Xi }_b^{\ast }{\left(5945\right)}^0,{\Xi }_b^{\ast }{\left(5955\right)}^{-}$
$\Sigma$	$uub, udb, ddb$	$1\left({{\displaystyle \frac{1}{2}}}^{+}\right)$	${\Sigma }_b^{+}\left(5811\right),{\Sigma }_b^0\left(5813\right),{\Sigma }_b^{-}\left(5815\right)$
.	.	$1\left({{\displaystyle \frac{3}{2}}}^{+}\right)$	${\Sigma }_b^{\ast }{\left(5830\right)}^{+},{\Sigma }_b^{\ast }{\left(5833\right)}^0,{\Sigma }_b^{\ast }{\left(5835\right)}^{-}$

Note that the first-order resonance $\Delta (1620$ of $\Delta$ quadruplet) has room in the character table of the small group $(96, 67)$.

In a further step,

Table 6. The character table for the group $G=(144,122)\cong {\mathbb{Z}}_3\times GL(2,3)$. There are 24 conjugacy classes of elements of multiplicities $1(\times 6)$, $2(\times 9)$, $3(\times 6)$ and $4(\times 3)$. Compared to Table 4, the present table adds further charmed baryons when they exist or should exist (we use the bold notation for them). In some of their entries, many characters contain the complex number $J=exp(2i\pi /3)$. For four of the extra multiplets, no such imaginary number is present in the corresponding character (bold notation: undetermined is used). In the table, $z_1=-I\sqrt{2}$ and $z_2=(\sqrt{3}+I\sqrt{2})/2$. Characters associated with doublets and containing the complex numbers $z_1$ or $z_2$ are informationally complete with rank of the Gram matrix $d^2={24}^2=576$. The not-assigned characters only have relative integers in their entries.

Char	Dim							Gram	Quarks	Baryons
${\kappa }_1$	1⋯	1	1	1	1	1	1	24	$uds$	${\Lambda }^0$
${\kappa }_2$	1⋯	1	1	−1	−1	−1	−1	515	$sss$	${\Omega }^{-}$
${\kappa }_3$	1⋯	J	−1 − J	1 + J	1 + J	−J	−J	553	$udc$	${\Lambda }_c^{+}$
${\kappa }_4$	1⋯	J	−1 − J	−1 − J	−1 − J	J	J	547	$\mathit{ssc}$	${\Omega }_c^0$
${\kappa }_5$	1⋯	−1 − J	J	−J	−J	1 + J	1 + J	553	$scc$	${\Omega }_{cc}^{+}$
${\kappa }_6$	1⋯	−1 − J	J	J	J	−1 − J	−1 − J	547	.	${\Omega }_{cc}^{\ast +}$
${\kappa }_7$	2⋯	2	2	0	0	0	0	553	?	unknown
${\kappa }_8$	2⋯	2J	−2 − 2J	0	0	0	0	$d^2$	$uud,udd$	$p,n$
${\kappa }_9$	2⋯	−2 − 2J	2J	0	0	0	0	$d^2$	$dcc,ucc$	${\Xi }_{cc}^{+},{\Xi }_{cc}^{++}$
${\kappa }_{10}$	2⋯	0	0	$z_1$	$-z_1$	$-z_1$	$z_1$	573	$uss,dss$	${\Xi }^0,{\Xi }^{-}$
${\kappa }_{11}$	2⋯	0	0	$-z_1$	$z_1$	$z_1$	$-z_1$	573	.	${\Xi }^{\ast 0},{\Xi }^{\ast -}$
${\kappa }_{12}$	2⋯	0	0	$z_2$	$-z_2$	$\overline{z_2}$	$-\overline{z_2}$	$d^2$	$\mathit{ucc},\mathit{dcc}$	${\Sigma }_{cc}^{++},{\Sigma }_{cc}^{+}$
${\kappa }_{13}$	2⋯	0	0	$-z_2$	$z_2$	$-\overline{z_2}$	$\overline{z_2}$	$d^2$	.	${\Sigma }_{cc}^{\ast ++},{\Sigma }_{cc}^{\ast +}$
${\kappa }_{14}$	2⋯	0	0	$-\overline{z_2}$	$\overline{z_2}$	$-z_2$	$z_2$	$d^2$	$usc,dsc$	${\Xi }_c^{+},{\Xi }_c^0$
${\kappa }_{15}$	2⋯	0	0	$\overline{z_2}$	$-\overline{z_2}$	$z_2$	$-z_2$	$d^2$	.	${\Xi }_c^{\ast +},{\Xi }_c^{\ast 0}$
${\kappa }_{16}$	3⋯	−1	−1	−1	−1	−1	−1	562	?	unknown
${\kappa }_{17}$	3⋯	−1	−1	1	1	1	1	564	?	unknown
${\kappa }_{18}$	3⋯	1 + J	−J	−J	−J	1 + J	1 + J	574	$uus,uds,dds$	${\Sigma }^{+},{\Sigma }^0,{\Sigma }^{-}$
${\kappa }_{19}$	3⋯	1 + J	−J	J	J	−1 − J	−1 − J	574	.	${\Sigma }^{\ast +},{\Sigma }^{\ast 0},{\Sigma }^{\ast -}$
${\kappa }_{20}$	3⋯	−J	1 + J	1 + J	1 + J	−J	−J	574	$uuc,udc,ddc$	${\Sigma }_c^{++},{\Sigma }_c^{+},{\Sigma }_c^0$
${\kappa }_{21}$	3⋯	−J	1 + J	−1 − J	−1 − J	J	J	574	.	${\Sigma }_c^{\ast ++},{\Sigma }_c^{\ast +},{\Sigma }_c^{\ast }0$
${\kappa }_{22}$	4⋯	0	−4	−4	−1	−1	−1 ⋯	563	?	unkwown
${\kappa }_{23}$	4⋯	0	−4J	4 + 4J	−J	−1	1 + J ⋯	$d^2$	$uuu,uud,udd,ddd$	${\Delta }^{++},{\Delta }^{+},{\Delta }^0,{\Delta }^{-}$
${\kappa }_{24}$	4⋯	0	4 + 4J	−4J	1 + J	−1	−J ⋯	$d^2$	.	$\Delta \left(1232\right)$

adds the excited baryon ${\Omega }_{cc}^{+}$ of quark content $scc$ and baryons containing charmed and strange quarks when they exist or should exist (we use the bold notation for them). The table corresponds to the group $G=(144, 122)\cong {\mathbb{Z}}_3\times GL(2, 3)$, which together with the group $G=(144, 121)$ is the smallest group able to produce the necessary assignments to the aforementioned baryon families. The latter group is less appropriate than the former one because it is less efficient in terms of MICs. There are undermined multiplets (one doublet and two triplets) whose corresponding characters have entries that are relative integers (not complex numbers). These not-assigned characters could potentially correspond to neutral non-baryonic matter under a beyond standard model (BSM model).

Our final discrete group is in Table 5. Compared to Table 6, the present table adds the baryons containing bottom quarks when they exist or should exist, as well as higher $\Delta$ resonances listed in the lower box of Table 1 (we use the bold notation for them). Table 5 is the character table for the group $G=(192, 187)\cong P_1⋊{\mathbb{Z}}_{12}$, where $P_1\cong (16, 13)$ is the single qubit Pauli group. Group $(192, 183)\cong {\mathbb{Z}}_4⋊20$ would be an alternative but it does not have characters that are MICs. Thus, group $G=(192,187)$ is optimal for assigning its characters to the known ground states and excited states of baryon families with $J^P={{\displaystyle \frac{1}{2}}}^{+}$ or $J^P={{\displaystyle \frac{3}{2}}}^{+}$ that include higher resonances of the $\Delta$ quadruplet. Compared to the standard view of using representations of continuous groups $SU\left(2\right)$ and $SU\left(3\right)$ for baryonic matter, the series of discrete groups we considered that are $GL(2, 3)$, $(96, 67)$, $(144, 122)$ and $(192, 187)$ and that carry (almost) complete quantum information in their irreducible representations offer a new perspective to the understanding of baryonic matter. The assignment problem remains unsolved for four irreducible characters, the doublets ${\kappa }_9$ and ${\kappa }_{10}$ as well as the triplets ${\kappa }_{21}$ and ${\kappa }_{22}$, whose entries are relative integers.

In the next section, we comment about the new perspective of the encoding group $(192, 187)$ by Ising anyons. This ‘neutral’ character could perhaps correspond to non-baryonic matter yet to be defined.

5. Baryonic Matter and Ising Anyons

A possible relationship between baryonic families and Ising anyons exists in the literature [9]. In this section, we explore this correspondence based on the fact that the discrete group $G=(192, 187)$ that we described above in the context of baryon symmetries also describes the braiding matrices of the Ising anyons [8] (Section 3.3). It is challenging to discover the physical meaning of the character table of G in the context of Ising anyons.

The $SU{\left(2\right)}_2$ Ising anyons are quasiparticles in a (2+1)-dimensional topological quantum field theory (TQFT). They are associated with the conformal Ising model, which is linked to a central charge $c={\displaystyle \frac{1}{2}}$ conformal field theory. It is also compelling to explore the ‘holographic’ correspondence of the type $Ad{S}_3/QF{T}_2$ between Ising anyons—encoding baryon families—and three-dimensional quantum gravity. The key idea is that the $Ad{S}_3$ ‘bulk’ world has gravity while the boundary two-dimensional world $QF{T}_2$ has (baryonic) matter with no gravity.

Let us introduce this set of ideas step by step.

5.1. Ising CFT and Ising Anyons

The Ising conformal field theory (CFT) is a ‘minimal model CFT’ of central charge $c={\displaystyle \frac{1}{2}}$ [24,25]. The primary fields in the Ising CFT are the identity (1), which represents the vacuum state; the spin ($\sigma$), which corresponds to the anyon type with non-Abelian statistics; and the fermion ($\psi$), which effectively represents a Majorana fermion.

The fusion rules for Ising anyons are

$$\sigma \otimes \sigma =1+\psi ,\sigma \otimes \psi =\sigma ,\psi \otimes \psi =1.$$

The boundary fermion $\psi$ can be identified with the boundary limit of a bulk Majorana fermion or, in terms of Chern–Simons (CS) theory, a specific holonomy condition in the gauge field.

As for any anyon class, the associativity of anyon fusion is captured by an F-matrix, and the exchange of anyons, with the phase factor added, is captured by an R-matrix. Contrary to the phase factor $\pm 1$ for bosons and fermions, the phase factor for anyons is an arbitrary complex number. The F-matrix is the anyonic version of the Wigner’s $6j$-symbols, and it is associated with a pentagon diagram. The combined action of F- and R-matrices satisfies the hexagon equations [26]. Explicit constructions for F- and R-matrices can be found in [27,28,29], (Appendix B).

The entries of the R-matrix have the simple form [30]

$$R_c^{ab}\left(q\right)={(-1)}^{(a+b+c)/2}{q}^{-\left[a\right(a+2)+b(b+2)-c(c+2\left)\right]/2},$$

(1)

where q is the Kauffman variable for the Ising model below $q=iexp\left({\displaystyle \frac{-2i\pi }{16}}\right)$.

The S-matrix takes the form

$$S_{Isi}={\displaystyle \frac{1}{2}}\left(\begin{array}{ccc}1& \sqrt{2}& 1\\ \sqrt{2}& 0& -\sqrt{2}\\ 1& -\sqrt{2}& 1\end{array}\right)$$

The F- and R-matrices are

$$R_{Isi}=\left(\begin{array}{cc}{R}_0^{11}\left(q\right)& 0\\ 0& R_2^{11}\left(q\right)\end{array}\right)=exp(-i\pi /8)\left(\begin{array}{cc}1& 0\\ 0& i\end{array}\right),F_{Isi}={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right).$$

Braiding matrices for the Ising anyons are obtained as

$${\sigma }_1=R_{Isi},{\sigma }_2={\left(FR{F}^{-1}\right)}_{Isi}={\displaystyle \frac{exp(-4i\pi /8)}{\sqrt{2}}}\left(\begin{array}{cc}1& i\\ i& 1\end{array}\right).$$

(2)

Both matrices ${\sigma }_1$ and ${\sigma }_2$ together generate the finite group $(192, 187)$ isomorphic to the group $P_1⋊{\mathbb{Z}}_{12}$ [8].

5.2. The $Ad{S}_3/QF{T}_2$ Correspondence with (Ising) Baryons

In reference [24,25], it is shown that the gravity dual of the Ising model is such that the partition function for this dual is the same as the partition function for the Ising model itself, corresponding to pure Einstein gravity and providing evidence that the two theories are dual. This supports the idea that most baryonic matter, encoded by Ising anyons, maps directly onto the gravity dual as a strongly quantum bulk system.

The critical observation of Brown and Henneaux [31] is that the symmetry group relevant for gravity in $Ad{S}_3$ is the two-dimensional conformal group with central charge:

$$c={\displaystyle \frac{3l}{2G}},$$

where l is the AdS radius and G is the dimensionless Newton’s constant.

The critical Ising model is but the first of an infinite family of exactly solvable CFTs, the Virasoro minimal models with $c<1$ [32]. Virasoro minimal models are labeled by two coprime integers $p<p^{\prime }$ with central charge:

$$c(p,p^{\prime })=1-{\displaystyle \frac{6{(p-p^{\prime })}^2}{p{p}^{\prime }}}.$$

The simplest case $(p,p^{\prime })=(3,4)$ is the Ising mode.

There are strengths in our approach. The equivalence between the Ising model and pure $Ad{S}_3$ gravity implies that the bulk theory is minimal, with no need for additional fields or symmetries. With l at the Planck scale, space–time becomes strongly quantum, and the bulk theory is dominated by topological or non-local effects, consistent with the anyonic nature of baryons. Both the algebraic structure of Ising anyons and the modular properties of the Ising CFT partition function are naturally encoded in Einstein gravity. This provides a unified framework for describing baryonic matter and its quantum gravity dual.

6. Discussion

We developed a fully new approach to the symmetries underlying baryonic matter.

The representations of the continuous groups $SU\left(2\right)$ and $SU\left(3\right)$ in the standard model of particle physics play crucial roles in organizing and describing the properties of baryons within the framework of gauge symmetries and flavor symmetries. By combining weak isospin $SU\left(2\right)$ and flavor $SU\left(3\right)$, the standard model provides a complete description of the symmetries relevant to strange baryon families, showing how they emerge from fundamental quark interactions and their organizing principles. For charmed baryons, the addition of the c quark to the light quarks extends the flavor symmetry to the group $SU\left(4\right)$, see the expected families in Figure A1 and Figure A2. Since the c quark has a large mass, this symmetry is expected to be more strongly broken than the $SU\left(3\right)$ symmetry of the three light quarks u, d and s [13] (Section 15). The same $SU\left(4\right)$ multiplets may be constructed for the bottom baryons by replacing the c quark with the b (bottom) quark, see Figure A2.

In contrast with continuous theory, we used the characters of appropriate discrete groups to account for the organization of baryon families. Our approach does not leave room for some of the baryon families expected but the $SU\left(4\right)$ model (but not observed), which is shown in Figure A1 and Figure A2, giving credit to the thesis that such baryon families may not exist. But the character tables of small groups $(96, 67)$ (Table 4), $(144, 122)$ (Table 6) and $(192, 187)$ (Table 5) reveal irreducible characters that cannot be assigned to such putative baryon families. The meaning of such gaps in the assignments is not known. Either it means that the claimed Ising symmetry is broken or that a type of non-baryonic matter is expected. This resonates with the topic of dark matter.

Some challenges for baryonic physics are well known:

1.

The standard quark model predicts more baryon resonances than are observed, raising questions about ‘missing’ states.

2.

Hyperons (strange baryons) may exist in neutron star cores and probe CP violation through subtle decay modes.

3.

Quantum chromodynamics (QCD) is the theory of strong force, through which quarks and gluons interact. Heavy quark baryons (charm/bottom) are testbeds for heavy quark effective theory (HQET) and clarify hadronization in high-energy collisions.

4.

The proton spin is not fully explained by quark/gluon angular momentum; baryon resonances may clarify spin–flavor interactions.

5.

Baryon decay anomalies can hint at new physics, making a thorough baryon classification vital for beyond standard model (BSM) research.

Other challenges are about baryonic matter versus dark matter:

1.

Cosmic composition: Baryons are only about 5% of the universe; dark matter is about 25%. Why these amounts?

2.

Structure formation: dark matter forms gravitational wells; baryons fall in, creating galaxies.

3.

Dark baryons?: MACHOs and other baryonic dark matter are ruled out as major contributors.

4.

Exotic baryons: primordial black holes or remnants might be a small dark matter fraction.

5.

Galaxy observables: baryonic feedback affects dark matter profiles (the core–cusp problem).

6.

Potential interactions: any new baryon–dark matter coupling could show up in cosmic or direct-detection data.

Further challenges are related to our approach:

1.

There are mainly two broad families of hadrons that are baryons made of three quarks and mesons made of one quark and one antiquark. Baryons are the stable building blocks of matter whereas mesons primarily act as force carriers that mediate the strong interaction between baryons. How to relate the proposed finite symmetry of baryons to that of mesons?

2.

Beyond hadrons, the gluons, that are massless, mediate the strong interaction between quarks, acting as the exchange particle for the interaction. There are eight colors of gluons which are equivalent to Gell-Mann matrices. But the possible existence of pomerons, odderons and glueballs challenges the current gluon model. A three-gluon state such as the odderon seems to have been detected [33]. Is our topological viewpoint relevant to these questions?

3.

Generalizing to higher dimensions: The argument is specific to $Ad{S}_3/CF{T}_2$. Extending it to $3+1$-dimensional space–time (where baryons exist in the real universe) is non-trivial. The dynamics of pure Einstein gravity in $Ad{S}_3$ may not generalize straightforwardly to higher dimensions.

4.

Explicit baryon/Ising Equivalence [9]: More details about the correspondence are needed. For example, what are the braids associated with the baryon octet and decuplet of N-baryons corresponding to the $GL(2, 3)$ group?

5.

Exploring the connection between other anyon classes and quantum gravity as in [34].

The works of other authors explored the possibility of using finite groups in the context of particle physics. In addition to the many papers written to account for the symmetries of mixing matrices of quarks and leptons that are quoted in [6], we mention the work of Robert Wilson [35]. For recent work relating the $AdS/CFT$ correspondence and quantum information, we recommend [36]. The dark matter problem at the Planck scale is related to string theory in [37]. A holographic version of QCD related to baryons is described in [38].