Counting Polynomials in Chemistry II

Abstract

Some polynomials find their way into chemical graph theory less often than others. They could provide new ways of understanding the origins of regularities in the chemistry of specific classes of compounds. This study’s objective is to depict the place of polynomials in chemical graph theory. Different approaches and notations are explained and levelled. The mathematical aspects of a series of such polynomials are put into the context of recent research. The directions in which this project was intended to proceed and where it stands right now are presented.

1. Introduction

Polynomials have a long history in chemistry [1]. Through counting polynomials, practically any matrix-based characterization of a graph may have at least one polynomial associated to it [2]. This fact means that quite a large amount of polynomials can be formulated and used. Additionally, new topological index formulations continue to be proposed [3]. However, some polynomials are more important than others, despite the fact that they have important uses. In a previous review, a good amount of polynomials were included [4]. This project was intended to fill some of the gap left by previous work [4], in order to conduct a similarity search in areas such as energy storage. The following are some topics already covered by the project leader: extending the context of the counting and characteristic polynomials with an entropy-based approach in [5]; analytical formulas derived in [6] (paths, stars, trees) and [7] (cyclic patterns); dealing with nano-cages in [8]; efficient algorithms in [9]; review of characteristics in [1]; extension in [10]; eigenproblem in [11]; conformer’s case in [12]; correlation studies in general [13]; and modelling properties in [14].

A polynomial is a more general treatment than an index. The advantage of a polynomial is the reduction in degeneration since it is an invariant relative to the numbering of atoms. Until August Kekulé’s time, it was common to refer only to the chemical positions of atoms in molecules and not to topology. Chemical graph theory is the topology branch of mathematical chemistry that applies graph theory to the mathematical modelling of chemical phenomena. Figure 1 depicts how one can start from a molecule, draw its graph theoretical representation, write down the matrices needed for a polynomial—identity [Id] and adjacency [Ad], for example—and use them to arrive at ChP [15,16]. There are also other more simple or more complicated situations.

Another way of introducing polynomials in chemistry was discussed in a previous review [4], which can be considered the first part. This second review can be considered the second part. It will describe the directions in which the project was intended to proceed and where it stands right now.

One very important property of the characteristic polynomial has already been described [11], and the roots of the characteristic polynomial of a molecular graph are always real when topology adjacency is used; by replacing the adjacencies with the Cartesian coordinates, the polynomial is always degenerated with null roots, except for two imaginary ones. This has been used to assess biochemical similarity [17].

The extension of the characteristic polynomial to account for changes in the atom type and bond order [10] is of great help for analyzing heteroatom-based [18] and -containing nanostructures, while a recent review on nano-porous carbon [19] is helpful in devising the synthetic routes [20].

On the other hand, polynomials formulated from undirected and unlabeled graphs are the most general case of a polynomial reflecting the topology of the graph and, because of this fact, are the ones that have the greatest likelihood of matching different molecules based on similarity.

It should be kept in mind that, for the discussion that presents polynomials, the same notations as in [4] will be used.

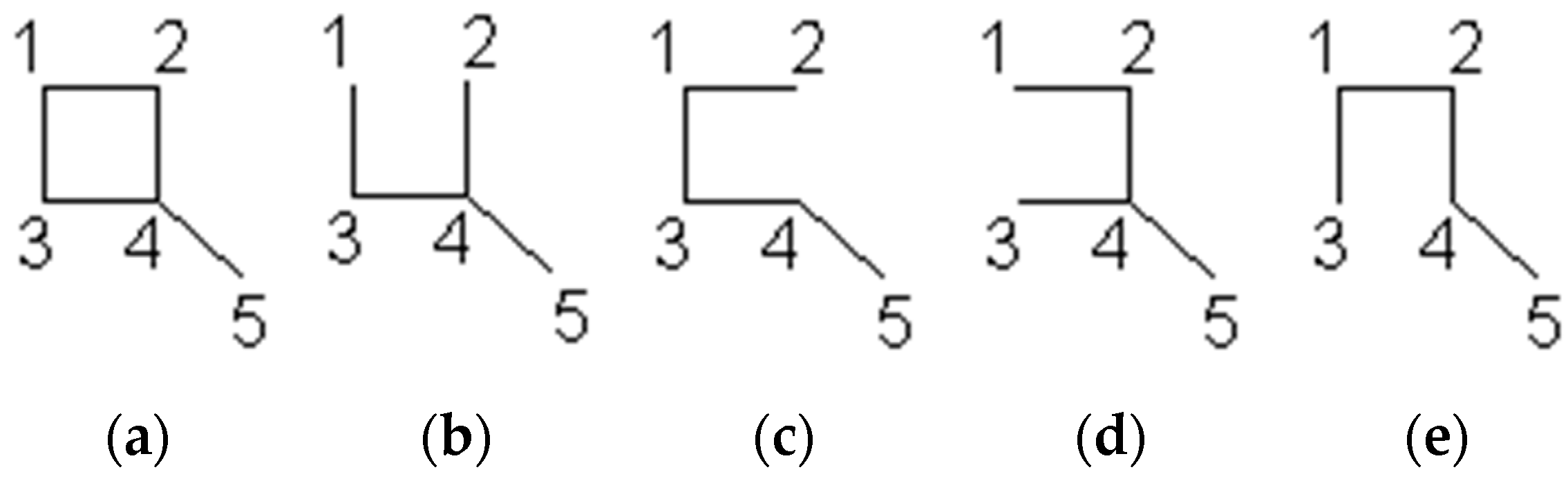
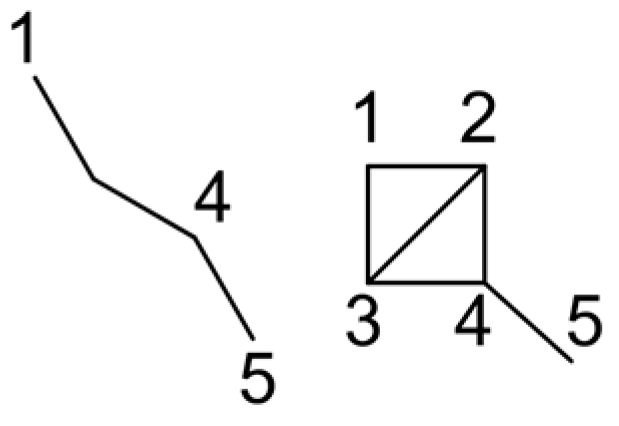
2. μ-Polynomial

Since the characteristic and matching polynomials are considerably studied, an effort towards their unification has led to another polynomial (proposed as the Mülheim polynomial, but it ended up as μ). It is relevant for the topological theory of conjugated molecules [21]. A reasonably chosen function was designed, μ(G, t) (where t is the r-tuple variable), which continuously transforms ChP_G into MP_G when the parameter t changes from unity to zero [22,23]:

$$\mu \left(G,\overrightarrow{t}\right)=\mu \left(G,\overrightarrow{t},x\right)\equiv ChP\left(G,x\right)\equiv MP(G,\lambda )$$

$$\mu (G,\overrightarrow{1},x)=ChP(G,x)$$

(1)

$$\mu (G,\overrightarrow{0},\lambda )=MP(G,\lambda )$$

(2)

$$\mu =\sum _{s\in S_k}{\left(-1\right)}^{c\left(s\right)}·2^{r\left(s\right)}·x^{a-k\left(s\right)}T(s)$$

(3)

Let S_k be the set of all Sachs subgraphs (s), with “k” vertices of any graph G and “a” the total number of vertices of G. The number of components of the Sachs subgraph is c(s) and the number of rings r(s).

The components of vector t can be interpreted as weights of the cycles. If t = 0, then all cyclic Sachs graphs have a zero contribution to Summation (3) and, thus, it is reduced to Equation (2). In the case of t = 1, all T(s)s are equal to one and (3) is reduced to (1). The components of vector t can be thought of as weights of corresponding cycles, by which they contribute to Sachs-type summation (Formula (3)) [21].

If t ≠ 0, 1, the zeros of μ are not necessarily real, opposed to those of ChP and MP.

μ seems to be a special case of the general class of graphic polynomials, the F-polynomials [22]. Later, Farrell and Wahid expressed some general results that can be used to construct larger classes from any given class [24].

Radenkovic et al. used the r-tuple variable (t) of μ to offer a mathematical explanation for the effect of phenyl–cyclopentadienyl fragments, amplifying the intensity of cyclic conjugation in the five-membered ring [25].

Gutman and Polansky developed a method to analyze the total π-electron energy, π-electron charge, and π-electron bond order and formulated a number of topological rules of the modulo 4 type [26].

μ includes other graph polynomials in addition to ChP and MP as special cases: the circuit polynomials, if the cycle weights are chosen so that all cycles of the same size have equal weights, or the β-polynomial [27].

Gutman shows further directions of research for a similar auxiliary polynomial [28].

3. F-Polynomial

In another effort towards unification, Farrell [22] introduced the FP (forgotten, family, F polynomial) in 1979. It is useful for surveying the structure of nanotubes and nanotorus [29]. It should not be confused with this F polynomial for oriented link diagrams, which is good at distinguishing knots and links from their mirror images [30].

Let F be a family of connected graphs. With each element α ∈ F, a weight w_α, or just x, can be associated. Let G be a graph. An F-cover of G is a spanning subgraph of G in which every component belongs to F. For simplicity, an F-cover will just be a cover (C).

$$FP=\sum x\left(C\right)$$

(4)

It is useful to know how many covers can be drawn. Consider G = G₁ (Figure 1b), and the adjacency [${Ad}_{G_1}$] and degree [$D_{G_1}$] matrices for G₁ are written.

Let $[A]={[D}_{G_1}]-{[Ad}_{G_1}]$:

$$[A]=\left(\begin{array}{ccccc}2& 0& 0& 0& 0\\ 0& 2& 0& 0& 0\\ 0& 0& 2& 0& 0\\ 0& 0& 0& 3& 0\\ 0& 0& 0& 0& 1\end{array}\right)-\left(\begin{array}{ccccc}0& 1& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0\\ 0& 1& 1& 0& 1\\ 0& 0& 0& 1& 0\end{array}\right)$$

Next, the cofactors (C_i,j) need to be calculated, which implies determining the minors (M_i,j). All the cofactors are 4, so only one shall be exemplified, for the element on row 5, column 4:

$$M_{\mathrm{5,4}}=\det \left(\begin{array}{cccc}2& -1& -1& 0\\ -1& 2& 0& 0\\ -1& 0& 2& 0\\ 0& -1& -1& -1\end{array}\right)=\left(-1\right)·4=-4$$

C_i,j = (−1)^i+j · M_i,j, as such C_5,4 = (−1)⁵⁺⁴ · M_5,4 = 4.

In Figure 2, there is G₁—(a) and the 4 covers of G₁—(b–e):

With every cover of G, a monomial π(C) = ∏_αw_α can be associated, where the product is taken over all components of the cover.${FP}_{G_1}$= ∑π(C), where the sum is taken over all covers in G.

Alsharafi and Alameri computed the F-polynomial for V-Phenylenic nanotubes and nanotorus [29]. Salman et al. investigated the F-polynomial for the hexagonal network HX_n, the honeycomb network HC_n, the silicate sheet network SL_n and the oxide network OX_n [31]. Jeyanthi and Selvarajan described an application of the forgotten polynomial for pharmaceutical design [32].

The µ-polynomial appears to be a special case of an F-polynomial [21].

The Clar covering polynomial is also a kind of F-polynomial [33].

If every non-node member of FP consists of exactly one block, then the corresponding class of F-polynomials is called block polynomials. Matching, characteristic, and permanental polynomials are B-polynomials; stars and paths are not blocks and so do not give rise to B-polynomials [34]. The B-polynomial generalizes the strict chromatic polynomial [35]. These are not to be confused with the β-polynomial.

4. β-Polynomial

The β-polynomial (circuit characteristic polynomial) is useful in the calculation of the effect of an individual circuit on various π-electron properties of a polycyclic conjugated molecule, especially on its total π-electron energy [27]. Aihara [36] conceptualized it, and Li et al. [37] gave a complete solution to support it.

It is defined using the MP. Let there be a graph G with at least one ring Ci:

$$\beta (G,Ci)=MP\left(G\right)\pm 2·MP(G-Ci)$$

(5)

For a Hückel-type circuit, “−” is used, and “+”—for a Möbius-type circuit.

Take, for example, G₁ (Figure 2a), where the single ring in the molecule to obtain G₁ − Ci is removed as such:

$${MP}_{G_1}=1·1·x^5+(-1)·5·x^3+1·4·x$$

$${MP}_{(G_1-Ci)}=1$$

$${\beta }_{(G_1,Ci)}=x^5-5·x^3+4·x-2$$

Hückel assumed that the π electrons can be treated separately to those involved in sigma bonds for unsaturated organic compounds. In fact, a π orbital is antisymmetric for reflection through the plane of the molecule, whilst a sigma one is symmetric. A monocyclic conjugated system with a (4n + 2)-membered circuit is stable (aromatic), and one with a 4n-membered circuit is unstable (antiaromatic). A generalized Hiickel rule exists for polycyclic conjugated systems. The stability of Mobius annulenes also depends on the modes of cyclic conjugation of the π electrons but shows the opposite tendency to the stability of Hiickel annulenes [38,39].

Recently, Gutman generalized Aihara’s resonance energy concept. The cycle energy depends on the size of the corresponding cycle [40]. Some difficulties with topological resonance energy are discussed in [23,41,42].

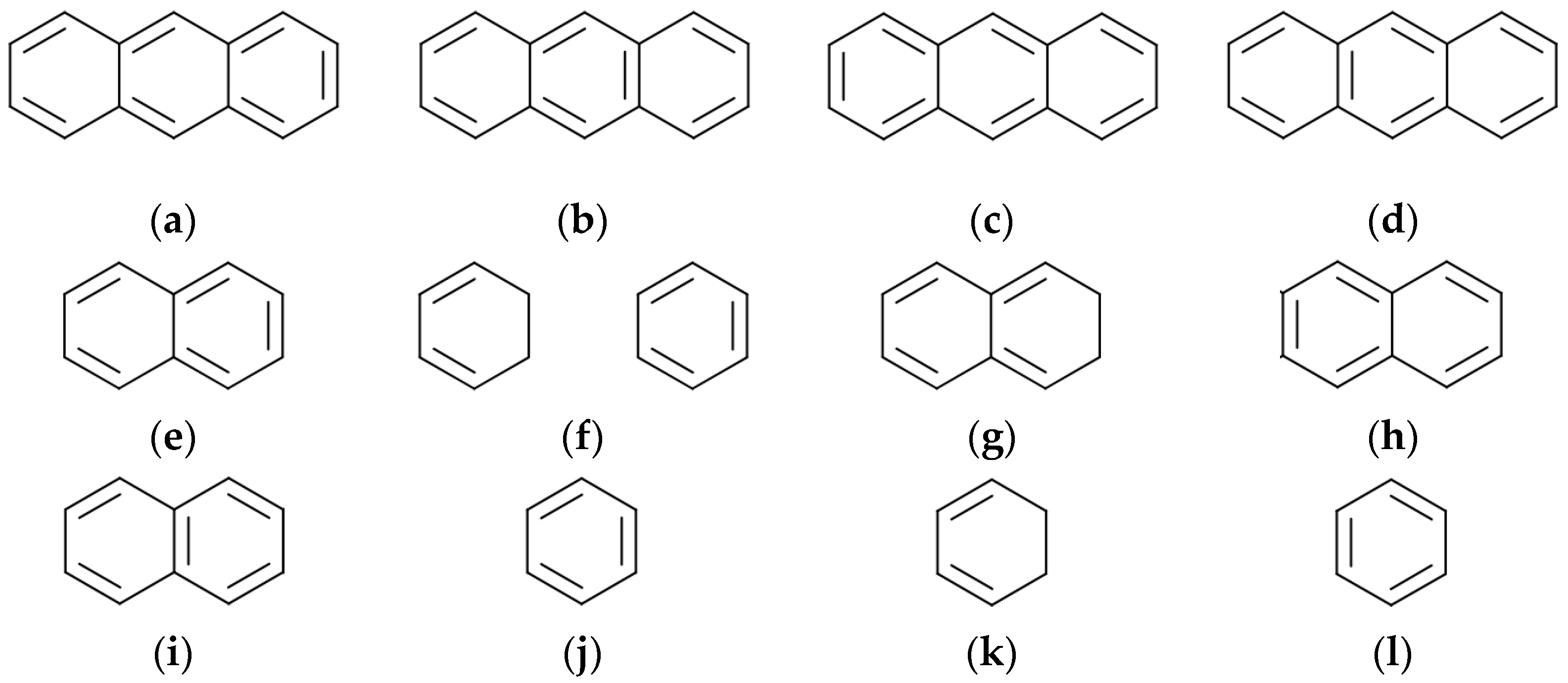
5. Cyclic Polynomial (Knop and Trinajstić)

The cyclic polynomial (denoted in the review of CyP, which can also be found as P^C) is more general than the sextet polynomial, because it enumerates 6-, 10-, 14-membered rings in benzenoid hydrocarbons and is useful for expressing resonance energy, as described by Knop and Trinajstić [26].

A cycle consists of a sequence of adjacent and distinct nodes in a graph. The only exception is that the first and last nodes of the cycle sequence must be the same node. It can be concluded that every cycle is a circuit, and the contrary is not true, but every Hamiltonian circuit is a cycle. A graph with cycles is called a cyclic graph; one without cycles is an acyclic graph, and if this last one is also a connected graph, it is called a tree. The notations of Ci and Cy are there only to differentiate the two polynomials. The same ring can be both Hückel and Hamiltonian, or the other variants. For a chemist, it is firstly a ring. It can be better differentiated by writing with context, such as Hückel circuit versus Möbius circuit, and Hamiltonian circuit versus Eulerian circuit. Unfortunately, it is not possible to know about all attempts to define a polynomial with a similar name.

Counting the circuit number of a graph G, n(G − Cy_m;k), by the general CoP (Equation (1) in [4]), one can define the number of Kekulé structures in the subgraph G − Cy_m obtained after eliminating k-disconnected conjugated circuits [26,43]:

$${CyP}_G=\sum _{m>0}\sum _{k=0}^{L}n(G-{Cy}_m;k){·x}_m^k$$

(6)

where m counts the size of circuits (1 for 6-atom circuits, 2: 10, 3: 14), k the number of eliminated disconnected conjugated circuits, n the remaining Kekulé structures, and Cy_m refers to the size of eliminated circuits.

Consider another former example, anthracene, as G₂ (in Figure 3a):

• for any m ≥ 0, and k = 0, one does not eliminate rings and remain with n(G − Cy_m; k = 0) = 4 Kekulé structures (Figure 3a–d) = SP_x=1 (the sextet polynomial for x = 1 [4,26]);
• for m ≥ 0, and k > 1, it is not possible to find more than one disconnected conjugated ring in graph G₂. Therefore, what is left is k = 1 and to describe the cases of m = 1, 2, and 3;
• for m = 1, and k = 1, n(G − Cy₁; 1) = 3 Kekulé structures; from Figure 3a, one ring is eliminated, the result being Figure 3e,g. What is left is naphthalene Figure 3e, whose Kekulé structures are Figure 3e,h,i [43]; in Figure 3f, there are two separated structures remaining, so n = 0;
• for m = 2 and k = 1, n(G − Cy₂; 1) = 2 Kekulé structures; from Figure 3j,k, the remaining result is benzene Figure 3j, whose Kekulé structures are Figure 3j,l;
• for m = 3 and k = 1, n(G − Cy₃; 1) = 1, as the result is the empty graph after eliminating the 14-atom ring.
• As such, ${CyP}_{G_2}=4+3{·x}_1+2·x_2+x_3$.

It would be useful to find a polynomial that also enumerates other rings, except 6-, 10-, and 14-atom rings. There is an older circuit polynomial, related by name [22,34,44,45].

6. Chromatic Polynomial

George David Birkhoff defined chromatic polynomials (denoted in the present review as ChrP) in 1912 [46]. Its coefficients count strict colorings [44]. A chromatic polynomial calculator is available at [47].

The coloring of a graph is closely related to the independent set. A proper coloring means that no two adjacent vertices have the same color. “Proper” can usually not be mentioned. Colors can actually be other labels, such as integers or chemical elements.

Some properties are important for these polynomials: the chromatic number = the minimum number of colors required is usually denoted by χ; the independence number = the maximum size of an independent set is usually denoted by α. A graph with n atoms and no edges has χ = 1 and α = n, while a complete graph has χ = n and α = 1.

A necessary and sufficient condition for a proper coloring of graph G is k ≥ χ(G), where k is the number of used colors. Colors can symbolize ligands that can be substituted in order to avoid the adjacency of two identical/similar ligands. The roots of the chromatic polynomial can possess constructional information, for example, the existence of Hamiltonian paths [44].

By the general CoP (Equation (1) in [4]), one can define $n_k$, the number of possible ways k colors can be used in a molecule (chemical graph G₁, Figure 2a) such that no bonded (adjacent) atoms (vertices) have the same color.

$${ChrP}_G=\sum _{k\ge 0}{n}_k\left(x\right)$$

(7)

Taking methyl-cyclo-butane (Figure 2a), for example, one can start by choosing x colors for atom 5 (x ⋯…). For every one of these cases, the result is x − 1 colors to choose from for atom 4 (x⋯(x − 1)…).

Now, there are two kinds of cases (x⋯(x − 1)⋯[i + ii]) (as can be seen in Figure 4): case i—atoms 2 and 3 have the same color and (x − 1) colors can be assigned to them; or case ii—they have different colors and (x − 1)⋯(x − 2) possibilities can be found.

$$\left\{\begin{array}{c}i=(x-1)...\\ ii=(x-1)·(x-2)...\end{array}\right.$$

(8)

It is useful to visualize these cases from another point of view, a contracting/bonding algorithm: case i—atoms 2 and 3 become one, they are contracted—this can be written as G_i = G₁/(2;3), since atoms 2 and 3 are no more; case ii—G_ii = G₁ + (2,3), atoms 2 and 3 are bonded and (2,3) is a new bond (edge).

Continuing case i, atom 1 can have (x − 1) colors, substituting the dots in the first equality in Equation (8), i = (x − 1) · (x − 1); in case ii, only (x − 2) colors, substituting the dots in the second equality in Equation (8), ii = (x − 1) · (x − 2) · (x − 2).

As such,${ChrP}_{G_1}=x·(x-1)·\left[\right(x-1)·((x-1)+(x-1)·(x-2)·\left(x-2\right)]=x^5-5·x^4+10·x^3-9·x^2+3·x$.

The chromatic polynomial for certain classes of graphs can be obtained from the matching polynomial with some substitutions [48].

A generalization of the chromatic polynomial is the Tutte polynomial [49].

7. Tutte Polynomial

Initially the dichromatic polynomial [50], the Tutte polynomial is an isomorphism invariant of graphs that generalizes the chromatic and the flow polynomials [51]. It is related to a B (block) polynomial and described in [49,52,53,54]. The polynomial is well put into context in the recent literature. A history of the scientist Tutte can also be found [55].

This polynomial can be defined by the following relations [56]:

$${TP}_G\left(x,y\right)=\left\{\begin{array}{cc}\hfill x{T}_{G/e}\left(x;y\right)& \mathrm{if}e\mathrm{is}\mathrm{a}\mathrm{bridge}\hfill \\ \hfill y{T}_{G-e}\left(x;y\right)& \mathrm{if}e\mathrm{is}\mathrm{a}\mathrm{loop}\hfill \\ \hfill T_{G-e}\left(x;y\right)+T_{G/e}\left(x;y\right)& \mathrm{if}e\mathrm{is}\mathrm{an}\mathrm{ordinary}\mathrm{edge}\hfill \end{array}\right.$$

An example of computing the Tutte can be defined by linear recursion: deleting and contracting ordinary bonds (edges). The results are trees and loops, as seen in Figure 5.

TP (G₁; x, y) = TP (G₁\b; x, y) + TP (G₁/b; x, y).

The first deleted bond yields a four-segment graph, which is written as x⁴, and by contracting, the result is a non-elementary graph (atoms 2 and 4 become one). This last one suffers again a deletion/contraction scheme and x³ is obtained, and also another non-elementary graph (atoms 1, 2 and 4 become one, and it looks like a double bond between this group and atom 3). Lastly, there is x² and a graph consisting of a simple bond (x), and a simple loop (y), which is denoted by x·y.

Björklund et al. developed a faster algorithm that computes the Tutte polynomial and other invariants of an arbitrary graph in time within a polynomial factor of the number of connected vertex sets. The algorithm evaluates a multivariate generalization of the Tutte polynomial by making use of an identity due to Fortuin and Kasteleyn [57].

Fath-Tabar et al. presented a simple formula for computing the Tutte polynomial of a benzenoid chain [58]. Szu and Dai computed Tutte polynomials and obtained some numeric characteristics for some benzodiazepines [59]. Gong et al. obtained an explicit expression for the Tutte polynomial of benzenoid systems with one branched hexagon and the number of spanning trees [60]. Ren et al. introduced a graph vector at a given edge related to the Tutte polynomial and used three class transfer matrices, obtaining the reduction formula for the Tutte polynomial and the number of spanning trees of any catacondensed benzenoid system [61]. Ma et al. obtained the Tutte polynomials of fan-like graphs via generating functions [62].

Chen and Guo considered some special cases of alternating polycyclic chains and used the Tutte polynomial to obtain the explicit closed formula of the number of spanning trees, the number of spanning forests, and the number of spanning connected subgraphs of phenylenes/dicyclobutadieno derivatives [63].

Chbili et al. proved that the coefficients of the Tutte polynomial of a graph satisfy certain conditions if the automorphism group of the graph contains an element of prime order p [51].

Chen and Li give a simpler and more efficient method to obtain the Tutte polynomials of alternating polycyclic chains. They also obtained the explicit expressions for these polynomials and the number of spanning trees of phenylene systems with a given number of branching hexagons. Additionally, they determined the extremal values of the number of spanning trees among the phenylene systems and characterized these phenylene systems [64].

Chen derived the Tutte polynomials for silicate molecular networks and benzenoid systems, exact formulas, the explicit closed-form analytic expressions for the number of spanning trees, connected spanning subgraphs, spanning forests, and acyclic orientations, via a combinatorial decomposition technique. They stated that spanning tree entropy is an important measure parameter for some topological property of a graph [65].

Awan and Bernardi generalized the Tutte polynomial for directed graphs to the B-polynomial [35].

8. Other Polynomials

8.1. Information Polynomial

A novel graph polynomial called the information polynomial of a graph has been proposed [66]. In short, for the calculation of this polynomial, one must replace the adjacency matrix with a new one:

$$A_{PD}=\left(\begin{array}{ccccc}1& \cdots & a_{1,j}& \cdots & a_{1,n}\\ ⋮& \ddots & ⋮& ⋮& ⋮\\ a_{i,1}& \cdots & a_{i,j}& \cdots & a_{i,n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ a_{n,1}& \cdots & a_{n,j}& \cdots & 1\end{array}\right)$$

(9)

with a_i,i = 1 and

$$a_{i,j}=1-{\displaystyle \frac{\left|f\left(i\right)-f\left(j\right)\right|}{2^{d(i,j)}·\sum _{i=1}^{n}f\left(i\right)}},$$

(10)

where d is the classical topological distance operating on vertex labels and $f\left(i\right)=\sum _{k=1}^{\rho }{c}_k·\left|S_k\left(i\right)\right|$, with ρ being the diameter of the graph, S the set containing the vertices at distance k from i, |S_k(i)| the size of that set, and c an array with arbitrary weights (set to c₁ = 0.4, c₂ = 0.3, c₃ = 0.2, c₄ = 0.1, and c_k = 0.0 for k > 4 in [66], or c₁ = 4, c₂ = 3, c₃ = 2, c₄ = 1, and c_k = 0 for k > 4 below Equation (10); it is the same in terms of Equation (9), rewritten as “a_i,j = “ above).

Additionally, its definition is IP(G, A_PD, x) = det(A_PD − x·E), where E is the entropy of the underlying graph topology. The structural information content is defined and interpreted as the entropy of the underlying graph topology.

8.2. Orbit Polynomial

Dehmer and coauthors came up with a term, the orbit polynomial [67], to define a series of the form $\sum _{k=1}^{\Xi }{c}_k{x}^k$, where c_k is the number of the automorphism group of G of size k and Ξ the size of the highest sized orbit(s). For P_n (Figure 6), a branched path with n vertices, the orbit polynomial is:

$$O_{DM}(P_n;x)=\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}·x^2,\hfill & \mathrm{for}n\mathrm{even}\hfill \\ \left(⌈{\displaystyle \frac{n}{2}}⌉-1\right)·x^2+x,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

It is stated that molecular symmetry and topologically equivalent atoms or bonds are important in NMR spectra interpretation, automated synthesis planning, and for isomer generation.

8.3. B-Polynomial

The block polynomial (B, or BP) was introduced by Farrell and Rosenfeld while studying the spectral properties of graphs with articulation points [48].

In the context of covers (of FP), if every non-node member consists of exactly one block, the corresponding class of F-polynomials is called B-polynomials. If F is a family of cycles, then every non-node member of F is a block (also applies to cliques). All special circuit polynomials (MP, ChP, and π) are B-polynomials. Stars and paths are not blocks and do not give rise to B-polynomials [34].

Further study was proposed for all possible types of graph polynomials of dendrimers (spectra and eigenvalues) to try and predict thermodynamic properties [68].

8.4. Clar Covering Polynomial

The Clar covering polynomial was introduced in [33]. They show how to obtain the number of aromatic sextets, the number of Kekulé structures, and the first Herndon number from the polynomial.

Zhang obtained the difference of the Clar covering polynomials for S,T isomers [69]. Later on, he established a relation between the Clar covering polynomial and chromatic polynomials of hexagonal systems [70].

Zhang et al. showed how to obtain better accuracy using this polynomial for calculating the resonance energy of condensed aromatic hydrocarbons [71].

Witek and Kang presented these polynomials for isomers of (5,6)-fullerenes C_20–50. For benzo[e]pyrene, it decodes the most important topological invariants [72].

Li et al. proposed a Matlab algorithm for this polynomial for any double-hexagonal chain. Topological resonance energy is linearly related to its natural logarithm [73].

8.5. Forcing and Anti-Forcing Polynomials

Klein and Rosenfeld bring to life a series of discussions about forcing, freedom, and uniqueness in chemical graph theory. This general idea of forcing has many points in common with the general notion of “filters” from topology [74].

Zhao and Zhang proposed the polynomials in a series of manuscripts. The first one counts perfect matchings with the same forcing number for a benzenoid parallelogram and its related benzenoids [75]. They prove that the anti-forcing spectrum of any cata-condensed hexagonal system is continuous [76]. Later on, they obtain a recurrence relation of the anti-forcing polynomial of benzenoid systems with forcing edges [77]. Next, they focus on 2 × n and 3 × 2n grids and obtain the explicit expressions of their forcing and anti-forcing polynomials and spectra [78]. Zhao deduced recurrence formulas of forcing polynomials for monotonic constructible hexagonal systems and constructible hexagonal systems with one turning [79]. He derived a recurrence relation of forcing polynomial for double-hexagonal chains [80]. Most recently, he derived a recurrence relation of the anti-forcing polynomial for catacondensed hexagonal systems [81].

Deng et al. obtained the explicit expressions of forcing and anti-forcing polynomials of a pyrene system [82]. Deng et al. computed the forcing and anti-forcing polynomials of a type of polyomino graph [83].

8.6. Some More Polynomials

Randić searched for structural invariants, and some of these polynomials are as follows: Altenburg, distance, terminal, bipartite and vicial polynomials [84].

9. Discussion

The current research proposal was inspired by a recent (2021) Nature review [85], which reveals its growing interest from the scientific community and potential for new findings in clusters and conformers research.

Template-based methods have the promise to exact precise control over cluster nuclearity and composition. Choosing the right molecule and right conformer is the key of fitting into the holes [85].

Conformer design may be conducted via molecular alignment on the one hand [86], and molecular alignment facilitates later engaging of virtual screening in search for their potent biological applications [87] As an example, it is a well-known fact that fructose, glucose, and galactose share the same molecular formula—e.g., they are conformers [88]—but have different sweetness [20] and different solubility [88]. There are differences with a major impact in their processing in the human body, even if, again, all have about the same calorific value of 4 kcal per gram. Some may say the conformation is all that matters.

Finding sets of related vertices in graphs is a way of clustering, and for more details, the reader should go to [89]. An alternate route for generating conformers is by partition of the vertices of the graphs into chemically relevant groups. Partition of the graph vertices leads to the recognition of 2-subcolorable [90], bipartite [91], cluster [92], dominable [93], monopolar [94], r-partite [95], split [96], unipolar [97], trapezoid graphs [98], etc.; algorithms to work efficiently with special classes of graphs have been devised (for monopolar and 2-subcolorable in [99]; for unipolar and generalized split in [100]; for partition a big graph into k sub-graphs in [101,102]; for graphs that do not contain as induced subgraph a claw [103]). Each of all these partitioning outcomes gives the opportunity to redirect the research of the project in case of a jam. This will provide (if necessary) alternate routes and approaches [99]. Basic principles will be evaluated for conformer analysis using polynomials and strategies proposed in [104,105]. Also, vertex coloring in graphs may solve a series of real problems in many scientific fields. Different coloring schemes have been proposed based on distances [106], templates [107], adjacencies [108], heuristics [109], and pseudo-random (with constrains, Grundy and color-dominating) in [110], while the properties of the colorings were studied in [111], and the counting of distinguishing (symmetry breaking) colorings with k colors in [112]. Polynomials may serve very well for providing different coloring schemes, and this fact reveals an interesting theoretical alternate route to the proposed use of them.

Applicative directions always have an impact. Just some examples are given here, such as radio-labelled boron clusters, which have applications in the diagnosis and treatment of cancer. Biologically active conformations are always on the top wanted list of drug designers. It is proposed to give a new use for polynomials in conjunction with conformer and cluster analysis.

Other extent directions of the proposal, moving away from chemical applications, include the following: cutting a graph into smaller pieces is one of the fundamental algorithmic operations; partitioning large graphs is often an important sub-problem for complexity reduction or parallelization [113]; the balanced connected k-partition problem is addressed, with (or without [114]) nonnegative weights on vertices [115,116]; in the same context, the minimum gap graph partitioning problem is addressed [117]; partition strategies on resource description framework graphs have been studied [118,119]; graph contraction (creating of a graph minor [120]) serves in some specific graph-related problems [121]; when parallel motif discovery is employed in complex networks [122], graph partitioning divides the network for an efficient parallelization (divide into an approximately equal number of vertices to parts); strategies based on spectral [123] (eigenproblem in [11]), combinatorial [124], geometric [125], or multi-level [126] heuristics are available.

Applying a similarity search to compounds used in energy storage systems has proved a difficult task (an article is under development). Currently, the ChP is applicable to amino acids and is being applied to the abovementioned compounds (used in energy storage). Attempts to implement other polynomials will be made if the present search fails.