Embeddings of Graphs: Tessellate and Decussate Structures

Abstract

We address the problem of finding a unique graph embedding that best describes a graph’s “topology” i.e., a canonical embedding (spatial graph). This question is of particular interest in the chemistry of materials. Graphs that admit a tiling in 3-dimensional Euclidean space are termed tessellate, those that do not decussate. We give examples of decussate and tessellate graphs that are finite and 3-periodic. We conjecture that a graph has at most one tessellate embedding. We give reasons for considering this the default “topology” of periodic graphs.

1. Introduction

1.1. General

When referring to structures based on a periodic graph, such as the diamond graph, it is common to state that the structure has the “diamond topology”. However, a recent article [1] showed that a graph may have many embeddings of distinct topology. The question arises: “What is the best (default) graph embedding?”. This is the question we address here.

We remind the reader of the generally accepted meanings of topology and graph. From the Oxford Dictionary of Mathematics [2]:

Topology: The area of mathematics concerned with the general properties of shapes and space, and in particular with the study of properties that are not changed by continuous distortions.

Graph: A number of vertices, some of which are joined by edges.

It is a common practice to analyze the structures of chemical compounds in terms of underlying graphs that describe the linking of components. Such analysis usually involves the determination of graph invariants such as coordination sequences and vertex symbols [3,4]. Although not rigorously unique identifiers, in practice, these are reliable when used by programs like ToposPro [5]. For most 2- and 3-periodic graphs, the program Systre [6] definitively identifies the graph given crystallographic definitions of edges. Graphs can be identified by a 3-letter lower-case-bold symbol such as dia for the graph of the diamond structure. So far, so good; but the trouble comes when, as almost invariably, the result is reported as “a structure” having “the dia topology”.

As a graph may have many embeddings with different topologies, what do we mean when we refer to “the dia topology”? The 3-letter lower-case-bold symbols originate in the Reticular Chemistry Structure Resource (RCSR) [7]. The RCSR is a collection of embedded graphs and includes interwoven (interlinked) nets, knots, links, and alternative embeddings of a given graph—all with different topologies.

The problem is that the “diamond graph”, for example, can have embeddings with different topologies (belonging to different ambient isotopies). One such alternative embedding in actual materials is known to the RCSR as dia-z. If ToposPro or Systre analyzes a structure based on that topology, the graph is again reported correctly as the dia graph. Still, its structure and that of the diamond are not ambient isotopes—they have different topologies. Other examples of alternative embeddings of 3-periodic graphs were given in the earlier paper [1]. Here, we attempt to clarify the ambiguity in terminology.

1.2. Terminology and Definitions

We are concerned with tilings that fill space with generalized polyhedral cages, which may have 2-coordinated vertices but never 1-coordinated (leaves) or 0-coordinated vertices (isolated vertices). A face symbol $M^m{.N}^n\dots$. indicates that the tile has $m$ $M$-sided faces, $n$ $N$-sided faces, etc. Tiles with 2-coordinated vertices are called cages. They are often extended polyhedra in which 2-coordinated vertices are inserted in some or all edges of the polyhedron. Figure 1 shows examples of cages that are relevant to what follows. An $n$-theta graph is a graph of just two vertices joined by $n$ edges. The extended 4-theta graph is an important space-filling solid, as is the tile of the net, bcu, of the body-centered cubic lattice.

If a tiling has $p$ kinds of symmetry-related vertices, $q$ kinds of edges, $r$ kinds of faces, and $s$ kinds of tiles, the transitivity [8], four integers, is expressed as $\left[pqrs\right]$. For a graph, we similarly express the number of types of vertices and edges by $\left[pq\right]$. Vertex-transitive structures ($p=1$) are termed isogonal. Tilings with the full symmetry of the graph they carry are termed proper tilings [9].

All our structures are 3-dimensional and exist in Euclidean space. They may be 0-, 1-, 2-, or 3-periodic. Their symmetries are the point, rod, plane, layer, or space groups—best expressed in the Hermann–Mauguin (International) symbolism [1]. Structures whose graph admits a tiling are called tessellate, and those that do not are termed decussate, a word that comes from the Latin word for 10 (symbol X) and means having crossings (as in weaving). The vertices of graphs can be assigned barycentric coordinates in which the coordinates of a vertex are the mean of the coordinates of its connected neighbors. The graph is said to have collisions if two or more vertices have the same barycentric coordinates. A significant result [6] is that for a periodic graph without collisions, the full symmetry of the graph is a crystallographic space group, and Systre can always identify that “maximum symmetry” group. Graphs with collisions are of minor importance in the chemistry of materials; for examples, see our earlier paper [1].

An adjacency matrix readily specifies a finite graph. However, showing that two graphs are the same requires identifying a vertex numbering that is the same in both matrices. Since there are $N!$ ways to number a graph with $N$ vertices, this becomes practically impossible for large $N$. This issue is at the heart of the so-called “graph isomorphism problem”. The quotient graph can be given [6] for periodic graphs. In this case, a unique vertex numbering can be found for graphs where all vertices have non-identical barycentric coordinates. Such graphs are termed “crystallographic” as their symmetries are crystallographic space groups. The program Systre [6] unambiguously determines the identity and symmetry of such graphs.

For a given straight-edge (piecewise-linear) graph embedding, we define girth as the ratio of the shortest distance between edges to the length of the longest edge. Girth is, in effect, a measure of the maximum stoutness of the sticks with which the edges of the structure can be built without any stick overlap. For many embeddings, sticks are slender (low girth). The larger-girth embeddings are particularly interesting to us as they represent structures that are easier to build as molecules. In finding possible embeddings of graphs for a given symmetry, we first identify edges between vertices $i$ and $j$, $x_i,y_i,z_i$ to $x_j,y_j,z_j$. We then search coordinate space for the local maximum girth by a gradient-descent method. Generally, to go from one maximum girth to another, some edges must cross, forcing the girth to pass through zero, transforming the structure to a topologically different embedding—to a different ambient isotopy. Occasionally, two or more local (ambient isotopic) maxima arise corresponding to the same topology but separated by “logjams”; that is, the girth must decrease momentarily to unjam the structure, thereby allowing the ambient isotopic maximum girth to be reached without any stick intersections. In crucial cases, we can visually inspect different embeddings to verify they are different topologies. We give examples below.

2. Embeddings of Finite Graphs

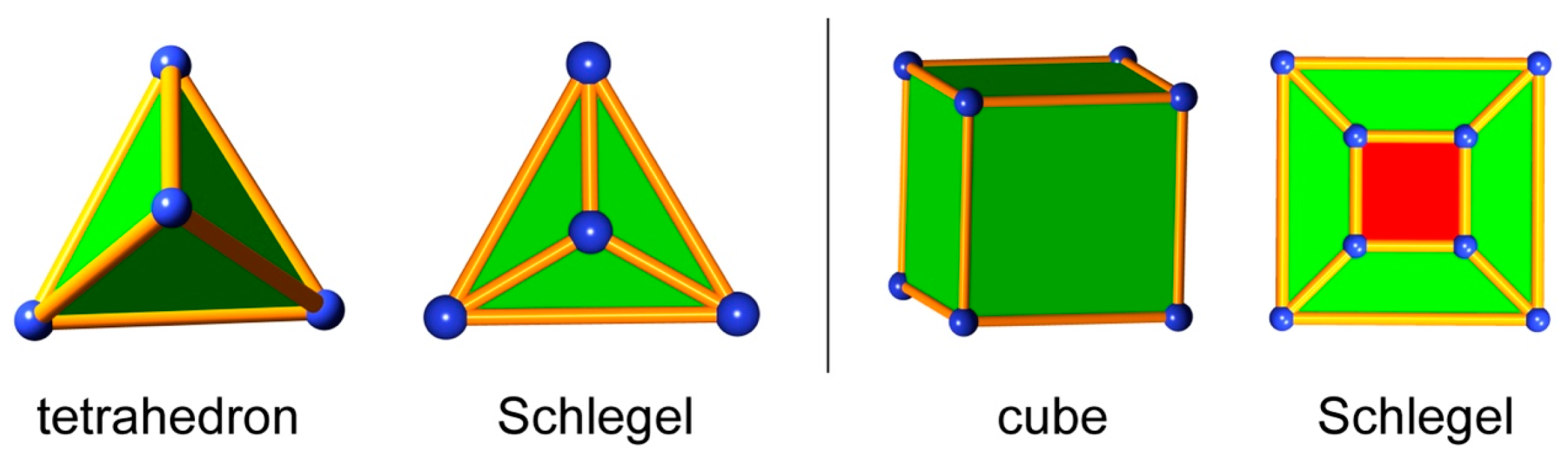
Finite graphs have long been classified as planar or nonplanar. A planar graph has a 2-dimensional embedding without intersecting edges. If a planar graph is 3-connected—meaning that at least three vertices and their incident edges must be deleted to separate the graph into disjoint components—the graph is then the graph of a polyhedron. A 2-dimensional embedding of the graph of a polyhedron is known as a Schlegel diagram. Note that the perimeter of the Schlegel diagram is a face of the polyhedron. Figure 2 shows two simple examples of Schlegel diagrams. These are clearly tessellate embeddings. In our earlier paper [1], we showed alternative embeddings of the cube graph. These all contained links or knots as subgraphs, and those alternative embeddings are therefore decussate. This leads to the, perhaps obvious, conclusion that the unique tessellate embedding of a polyhedron graph can be interpreted as the canonical embedding.

A well-established result is that every nonplanar graph contains, as a subgraph, either the complete graph on five vertices, $K_5$, or the complete bipartite graph on two sets of three vertices, $K_{33}$. It is instructive to examine complete and bipartite graphs further. It was shown [10] for complete graphs that every embedding of $K_6$ in 3-dimensional Euclidean space contains two linked triangles, and every embedding of $K_7$ contains a knot. As noted earlier [1], $K_n$ has an automorphism group, the permutation group $S_n$ of order $n!$. $S_4$ is isomorphic with the tetrahedral group, but no symmetry group in 3-D Euclidean space contains $S_n$ for $n>4$.

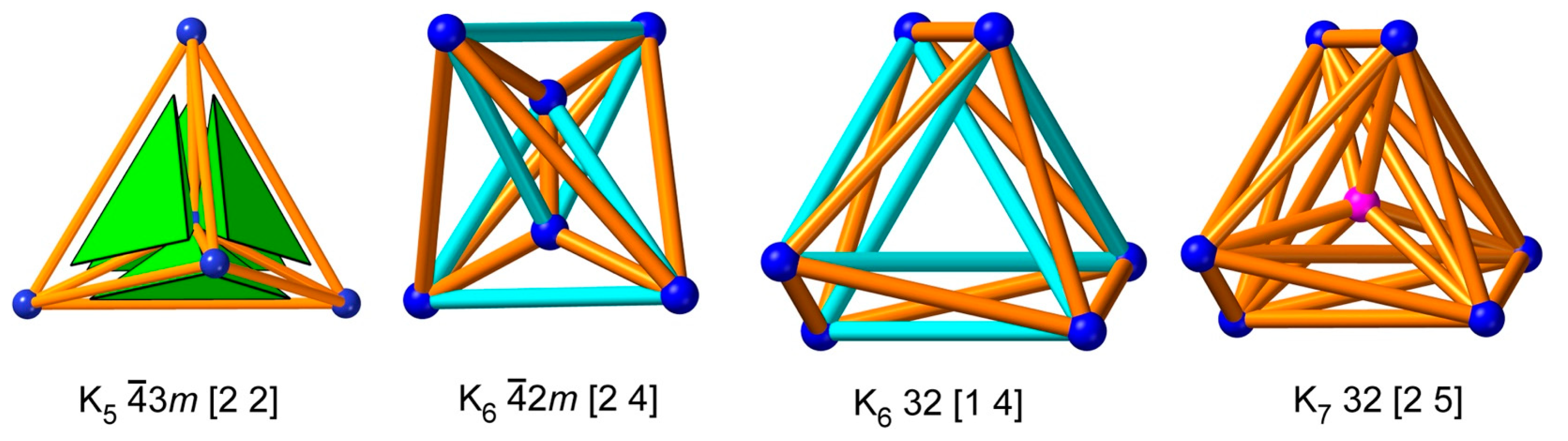
Figure 3 shows embeddings of $K_5$, $K_6$, and $K_7$. For $K_5$, there is a tessellate embedding of four tetrahedra inside an envelope of a fifth tetrahedron. This is the Schlegel diagram of the 4-dimensional simplex and seems clearly to be the canonical embedding in 3-D; the symmetry is $\overline{4}3m$. For $K_6$ the situation is less clear. In one embedding shown, with symmetry $\overline{4}2m$, the transitivity is $\left[24\right]$ and contains the predicted link of two triangles (light blue edges). However, we also show an embedding in symmetry $32$, with transitivity $\left[14\right]$, which is now “more tangled” as it also contains a trefoil knot (light blue edges). These two embeddings of the same graph are not ambient isotopic, and this leaves the question of a canonical embedding of “the topology” of the graph moot since neither is tessellate. An embedding is found for $K_7$ by adding an extra vertex to the 32 embedding of $K_6$, which includes the predicted knot. The transitivity of the embedding is now $\left[25\right]$. We remark that a graph of transitivity $\left[11\right]$, and an automorphism group of order $7!=8040$, has a “best” embedding in 3-D with symmetry of order $6$ and transitivity $\left[25\right]$, albeit still decussate.

Turning to the bipartite graphs $K_{nn}$: One, $K_{33}$, is known as a “Möbius ladder graph” [11] and has been recognized in a chemical structure [12]. This embedding, with symmetry $32$, and transitivity $\left[13\right]$, is shown in Figure 4; this is decussate as it contains a trefoil knot as a subgraph. We also show a second embedding with symmetry $\overline{6}m2$, and transitivity $\left[32\right]$. This is now tessellate, the tiling consisting of two extended 3-theta cages inside an envelope that is also an extended 3-theta cage. The situation is similar for $K_{44}$. There is an isogonal decussate embedding with symmetry $422$, and transitivity $\left[14\right]$ that contains the 8-crossing torus knot $8_{19}$. There is also an embedding with symmetry $4/mmm$, and transitivity $\left[32\right]$, that is tessellate with tiles that are extended 4-theta cages. Generalizing for $K_{nn}$, there are isogonal decussate embeddings with symmetry $n2$ ($n$ odd) or $n22$ ($n$ even) and a second tessellate embedding with symmetry $\overline{\left(2n\right)}m2$ ($n$ odd) or $n/mmm$ ($n$ even). The tessellate embedding has $n$ extended $n$-theta cages as tiles. The best or “canonical” embedding is a choice between an isogonal decussate embedding or a non-isogonal tessellate embedding.

3. Embeddings of Periodic Graphs

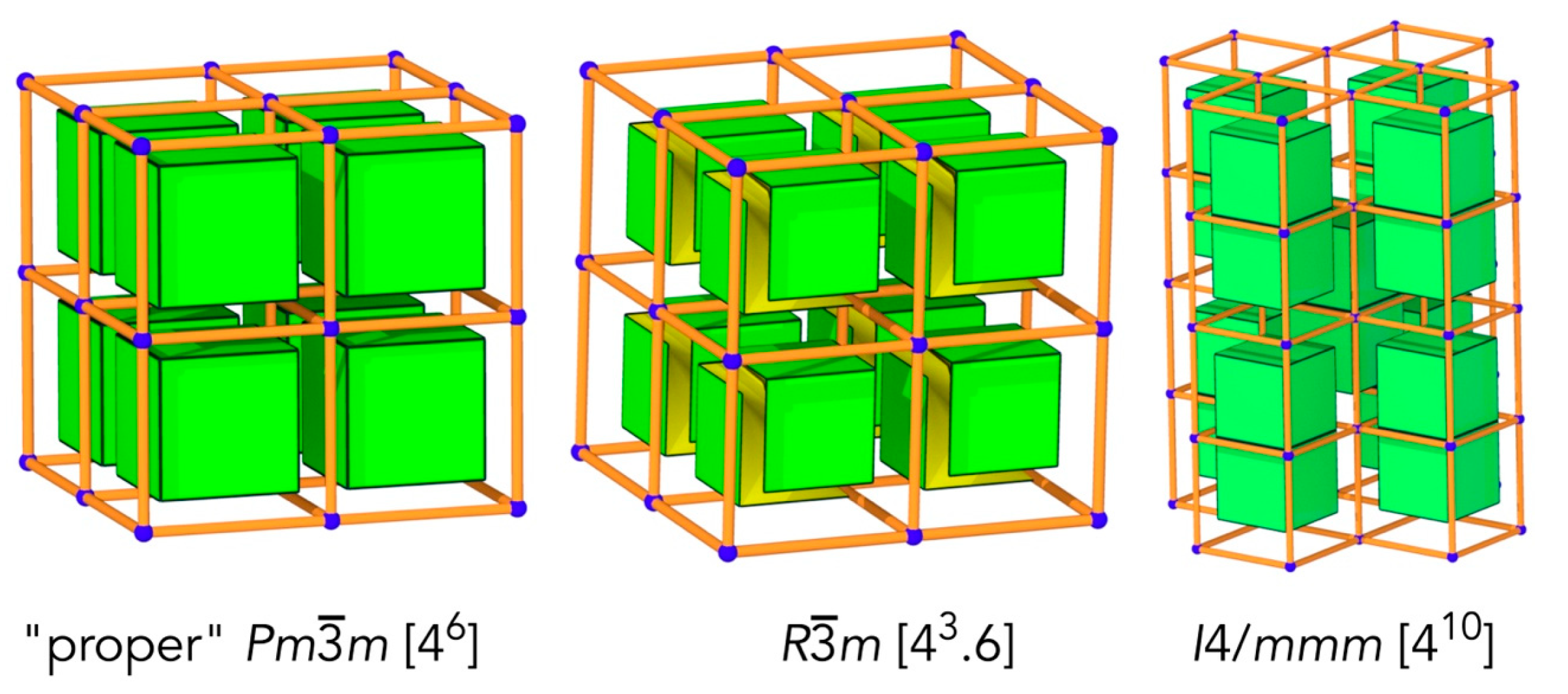
We note first that 3-periodic graphs may be tessellate, decussate, or both and that the tiles of a tiling may be polyhedra or cages, or both. We deal with simple periodic structures for which the intrinsic symmetry is a crystallographic space group: the so-called crystallographic graphs [1]. For such a structure, a maximum-symmetry tiling is a proper tiling [9]. There may be more than one proper tiling, but they all carry the same embedding of the net. There also may be possibilities for lower symmetry tilings of a net. In Figure 5, we show examples of lower-symmetry embeddings of pcu. These carry the same embedding of the pcu graph. This leads to the following claim: if a graph admits tilings, each tiling carries an ambient isotopic embedding of that graph.

We turn now to embeddings in general. Changing the unit cell parameters of an embedding of a periodic graph affects the scale (uniform compression or expansion) or shear but not the topology. To get different topologies, the free coordinates must be varied. The RCSR presently contains data for 1250 3-periodic structures with cubic symmetry. Of these, 141 have fixed coordinates and thus have a unique full symmetry embedding. These include basic nets like srs, the unique 3-coordinated net with transitivity [1 1], the dia net of the diamond structure, and pcu, the net of the primitive cubic lattice. These, therefore, have a unique full symmetry embedding. However, we showed earlier [1] that these all have topologically distinct lower symmetry embeddings.

3.1. ana and rhr

Further examination of the RCSR shows that, of the cubic graphs, 210 have just one free coordinate, and of these, just two, ana and rhr, have transitivity $\left[11\right]$. For rhr, the edge is specified as having symmetry $Im\overline{3}m$, with edges given by connecting vertices $x,x,0$ to $1/2-x,1/\mathrm{2,1}/2-x$, where $x$ is the free parameter. Examination of the girths for a wide range of $x$ $(-3\le x\le 3)$ shows that there is just one embedding (i.e., one ambient isotopy). This embedding is tessellate, as illustrated in the RCSR.

For ana, the edge is specified by space group $Ia\overline{3}d$, with edges between vertices $1/8,y,1/4-y$ to $y,3/4-y,-1/8$. Now, 32 embeddings are found for the free parameter $y$ in the range $(-3\le y\le 3)$. There is one large girth (1.0) embedding which admits a tiling. Two tiles are shown in Figure 6: an expanded trigonal prism $[6^2.8^3]$; the “two-headed fish”, $[4^2.8^2]$, is an expanded version of the 4-vertex trivalent graph shown. All the other embeddings are intricately tangled, have much lower girth (all with slender edges), and are decussate. In Figure 6, we show a fragment of the largest-girth decussate structure (girth = 0.034); this has linked 4-rings inhibiting the formation of a tiling.

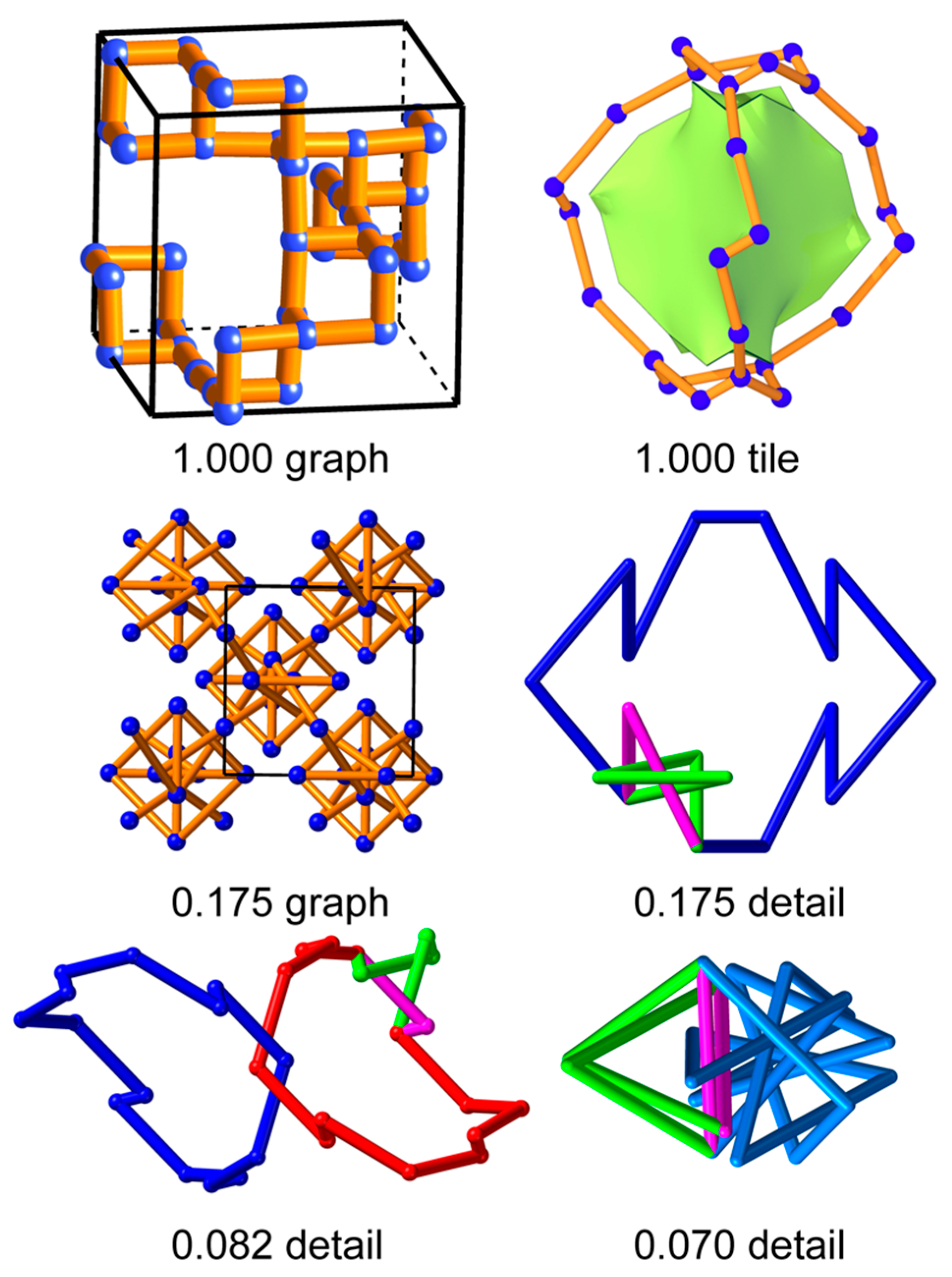
3.2. bmn

Turning to cubic graphs with one coordinate degree of freedom and transitivity $\left[12\right]$, the RCSR contains 42 entries. We examined just one in detail: bmn. This graph has symmetry $I{4}_{1}32$, and edges are from $x,\mathrm{0,1}/4$ to $1/4-x,\mathrm{0,1}/4$, and to $\mathrm{0,1}/\mathrm{4,1}/4-x$. The largest-girth structure (girth = 1) is tessellate with a single space-filling cage $[6^2.{14}^3]$, an extended trigonal prism. There are just three other embeddings with $x$ in the range $-3\le x<3$. All three are topologically distinct and decussate, as demonstrated in Figure 7. The largest-girth (0.175) decussate structure has a knotted 6-ring (trefoil) and an unknotted 14-ring. In the second decussate structure, with girth 0.082, neither ring is knotted, but the 14-rings are linked. In the third structure, with girth 0.070, the 6-ring and 14-ring are knotted and interlinked.

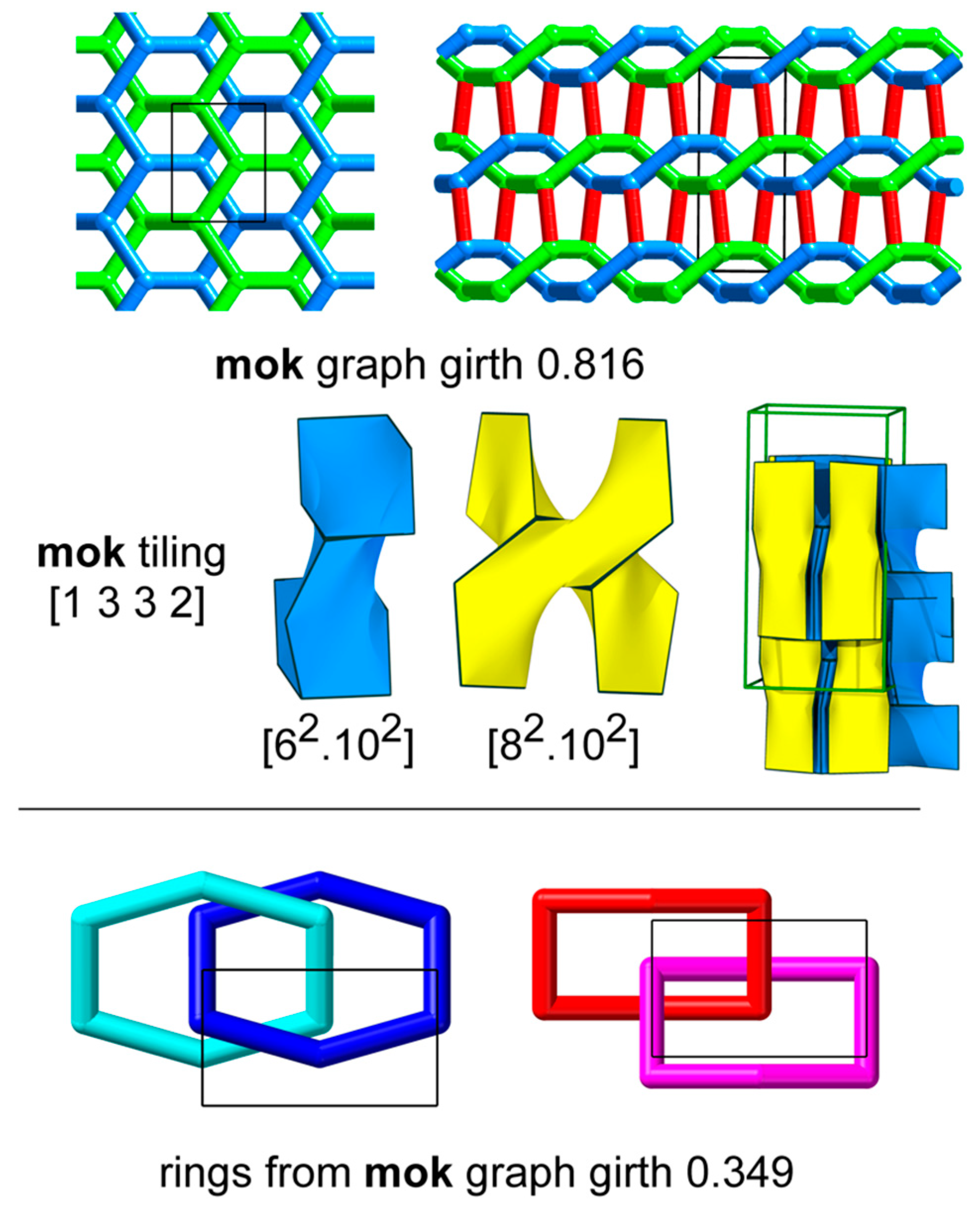
3.3. mok

The mok graph was introduced initially [13] as a simple example of a self-entangled periodic graph. Figure 8 shows that mok comprises interlinked layers of interpenetrating honeycomb (hcb) graphs. It contains four cycles (strong rings) that are not the sum of smaller cycles, two 6-ring, an 8-ring, and a 10-ring. The 6-rings of the hcb layers are linked, but a tiling can be constructed from the other three unlinked strong rings, as shown in Figure 8. The transitivity is [1 3 3 2]. Thus, perhaps surprisingly, the interlinking of the hcb-type layers does not proscribe a tessellate structure.

Vertex coordinates for the mok graph are of the form $x,y,0$. The three symmetry-inequivalent edges are formed by connecting that vertex to its images at: $-x,-y,0$; $1/2-x,1/2-y,0$; and $1-x,y,-1/2$. We find ten topologically distinct embeddings for the free-parameter ranges $-1\le x,y<1$. The one tessellate embedding has the largest girth (0.816). The next-largest embedding, with girth 0.349, is clearly decussate as both types of 6-rings are linked with other rings of the same kind, as shown in the figure.

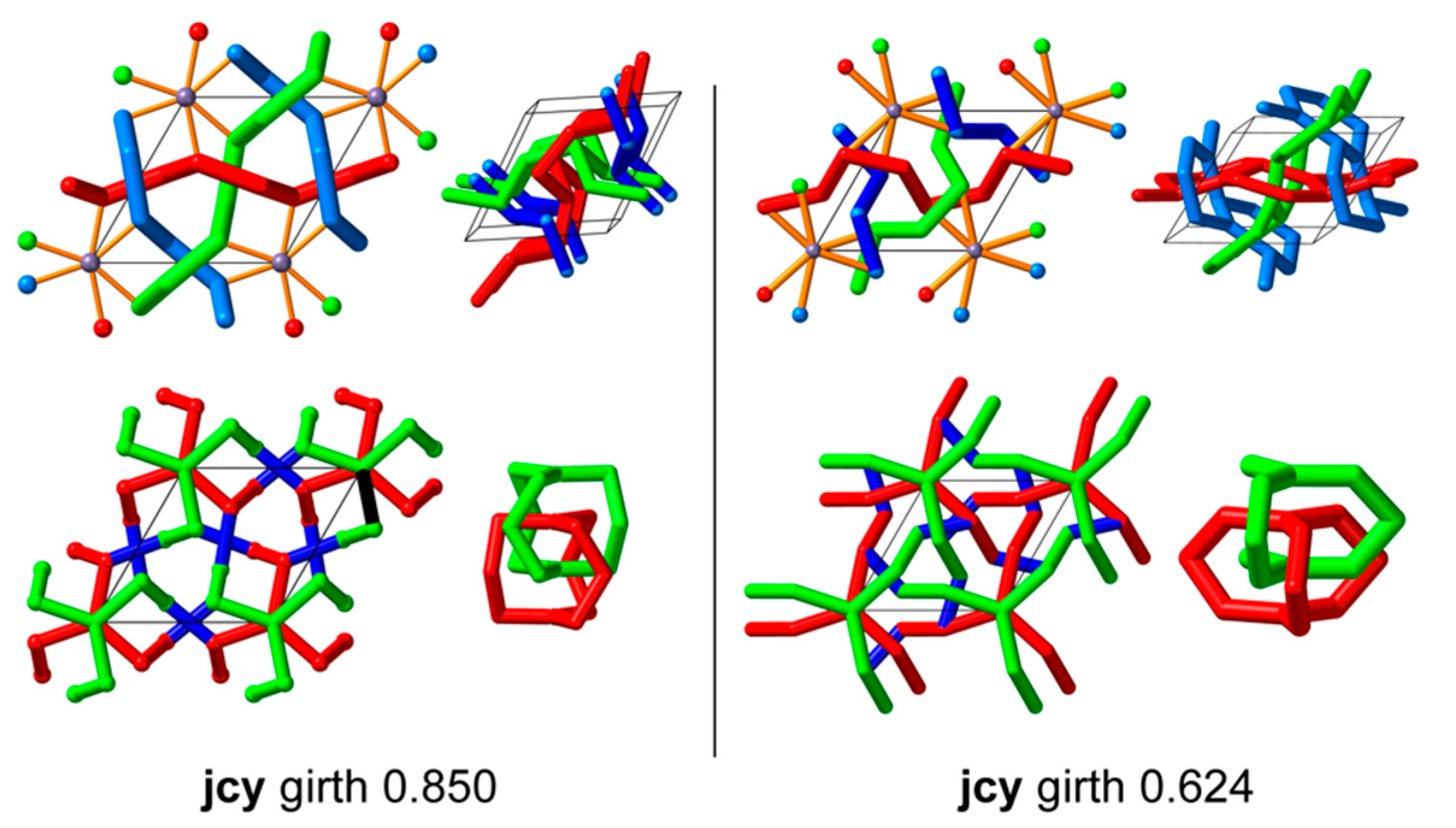
3.4. jcy

A second graph was adduced [14] as being self-entangled, jcy. This graph, observed as the underlying graph of a crystal structure, has transitivity $\left[33\right]$ and four coordinate degrees of freedom. The structure contains, as substructures, three sets of hcb nets interwoven, with an additional vertex linking triplets of hcb graphs. For a full symmetry $\left(P\overline{6}2c\right)$ and vertex range $\pm 1$, we find 34 embeddings of the underlying graph, each with a different girth. We examined the two largest-girth examples, shown in Figure 9. Both are decussate, with linked 6-rings and linked 8-rings (these are the shortest cycles in the graph). As shown in the figure, the topological difference between the two embeddings is subtle, highlighting the need for a general method of distinguishing topologies. No tessellate embedding was found.

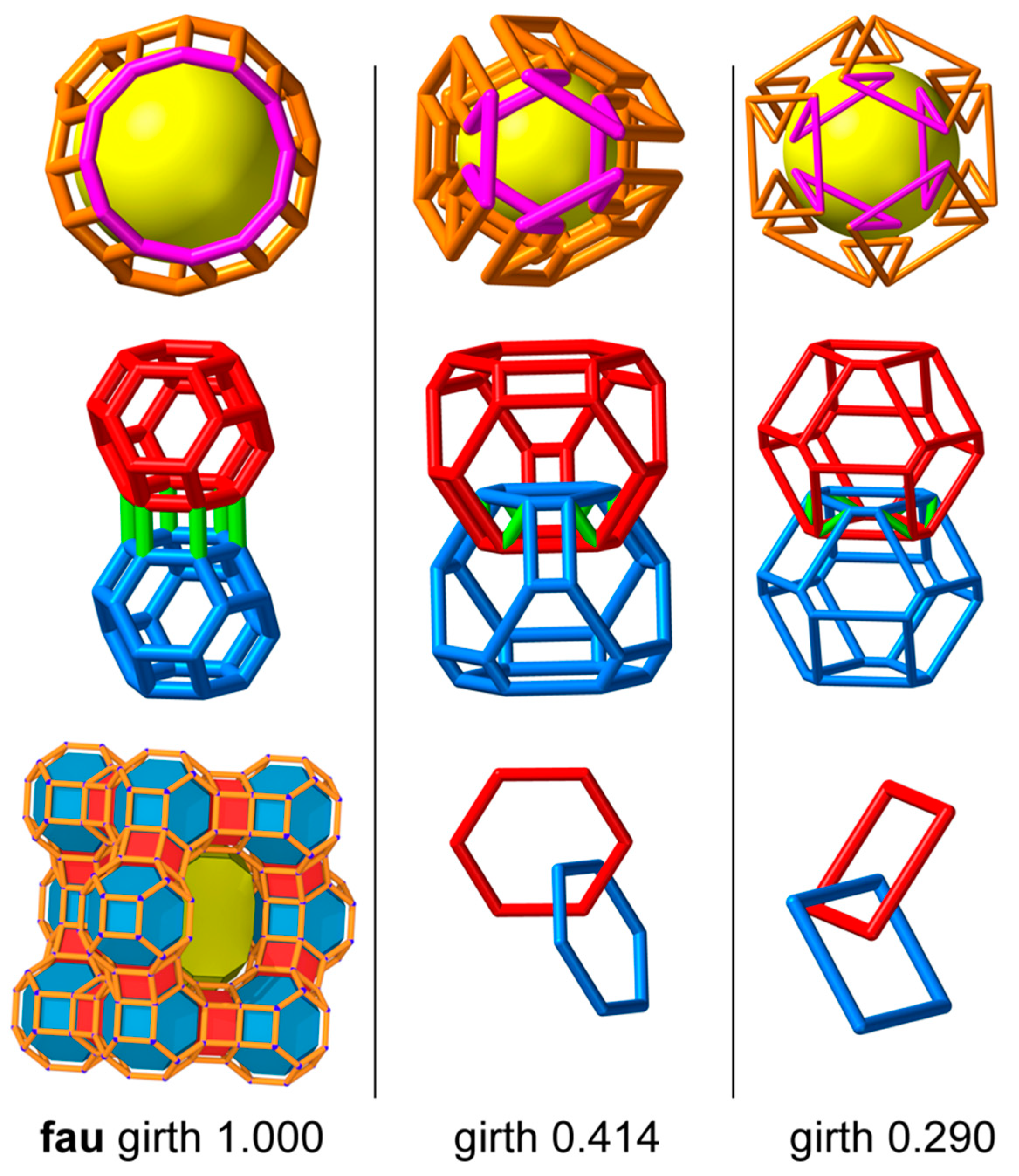
3.5. fau

Zeolite structures are distinguished by a bold upper-case three-letter symbol, such as FAU, for the faujasite structure. These are recognized by the International Union of Pure and Applied Chemistry (IUPAC) to indicate “framework type” [15]. The simpler of these are in the RCSR with lower-case symbols, such as fau. FAU materials are of exceptional economic importance, so we have examined the full symmetry ($Fd\overline{3}m)$ embeddings of the fau graph, which has transitivity $\left[14\right]$ and three variable coordinates. We find just three embeddings for a coordinate range of $-1\le x,y,z<1$. As depicted in Figure 10, the girth = 1 structure is tessellate, the well-known structural form adopted by the alumino-silicate zeolite. The other two are distinct decussate embeddings. We cannot resist adding that their girths are exactly $1/\left(\sqrt{2}+1\right)$ and $1/\left(\sqrt{6}+1\right)$.

4. Conclusions

We present some observations that we feel are relevant to the following unanswered questions: (a) is there a preferred embedding of a graph that can unambiguously be called the “topology”? and (b) how do we identify and distinguish between different graph embeddings (topologies)?

For planar finite graphs, general usage is clear, and we take the unique tessellate embedding, particularly for polyhedra. All other embeddings are decussate as they contain knots and/or links and are referred to as tangles [16]. What is needed is a system for identifying each embedding in the same way as has been developed for knots and links. In this context, we remark that knots are just different embeddings of the graph of the unknot (a simple loop). There is an infinite number of knots, which by definition are decussate, but only one planar embedding—the unknot loop.

Tessellate embeddings may exist for nonplanar finite graphs, but as we have remarked for the case of K₃₃, an embedding with lower transitivity may be preferred as the default “topology”.

Turning to periodic graphs: for a small number (some 3000) of particular interest in chemistry and materials science, an RCSR symbol leads to a specific embedding of that graph. But many more graphs have been identified. The Topos Topological Database has 200,000 “hypothetical and real nets that have been observed” [17]. This suggests a pressing need for methods of distinguishing between various embeddings of these structures. As shown here, a periodic graph may have many embeddings, even at full symmetry.

The embeddings of graphs in the RCSR, as reported by Systre, are obtained by finding the minimum density subject to the constraint of fixed equal-edge lengths. This approach was inspired by the observation [18] that such constrained maximum-volume configurations are often close approximations of the actual structure of simple ionic crystals. In our experience, this is also the maximum-girth embedding and, when it exists, the tessellate embedding.

We have made the claim:

Conjecture 1: if a graph admits tilings, each tiling carries an ambient isotopic embedding of that graph.

This raises an open question, leading to an additional claim:

Conjecture 2: there is, at most, only one tessellate ambient isotopy of a periodic graph.

We know of no counterexamples of graphs with two or more tessellate ambient isotopies (embeddings). Further, our observations indicate that the tessellate embedding is always the maximum-girth embedding—the structure built with the stoutest sticks.

To the authors’ knowledge, no software tool is available that reliably explores the isotopic spaces of a graph to identify whether a tessellate embedding is accessible. In general, too many degrees of freedom are involved, except for the simplest graphs. It would be useful to identify an intrinsic property that makes a graph tessellate, apart from maximum volume and maximum girth, which do not definitively define the tessellate embedding.

The term decussate was inspired by Samuel Johnson’s definition of “network” [19]: “Anything reticulated or decussated, at equal distances, with interstices between the intersections.” This led, in turn, to the description of the science of linking together symmetric modules into (generally tessellate) periodic framework structures as reticular chemistry [20]. Recently, there has been a rapid increase in interest in synthesizing structures based on knots, periodic and finite links, tangles, weaving, knitting, and other decussate structures. The systematics of this might well be considered as decussate chemistry.