Machine Learning-Driven Prediction of Heat Transfer Coefficients for Pure Refrigerants in Diverse Heat Exchangers Types
Abstract
1. Introduction
2. Machine Learning-Based Prediction Models
2.1. Linear Regression
Assumptions
- Linearity: The relationship between predictors and the response is linear.
- Independence: Observations are independent of each other.
- Homoscedasticity: Constant variance of errors across observations.
- Normality: Errors are normally distributed.
2.2. Wide Neural Networks
2.3. Support Vector Machines
2.3.1. Mathematical Model
2.3.2. The Kernel Method
3. Date Base Description
Input Data Selection
4. Results
4.1. Evaluation of the Prediction Performance
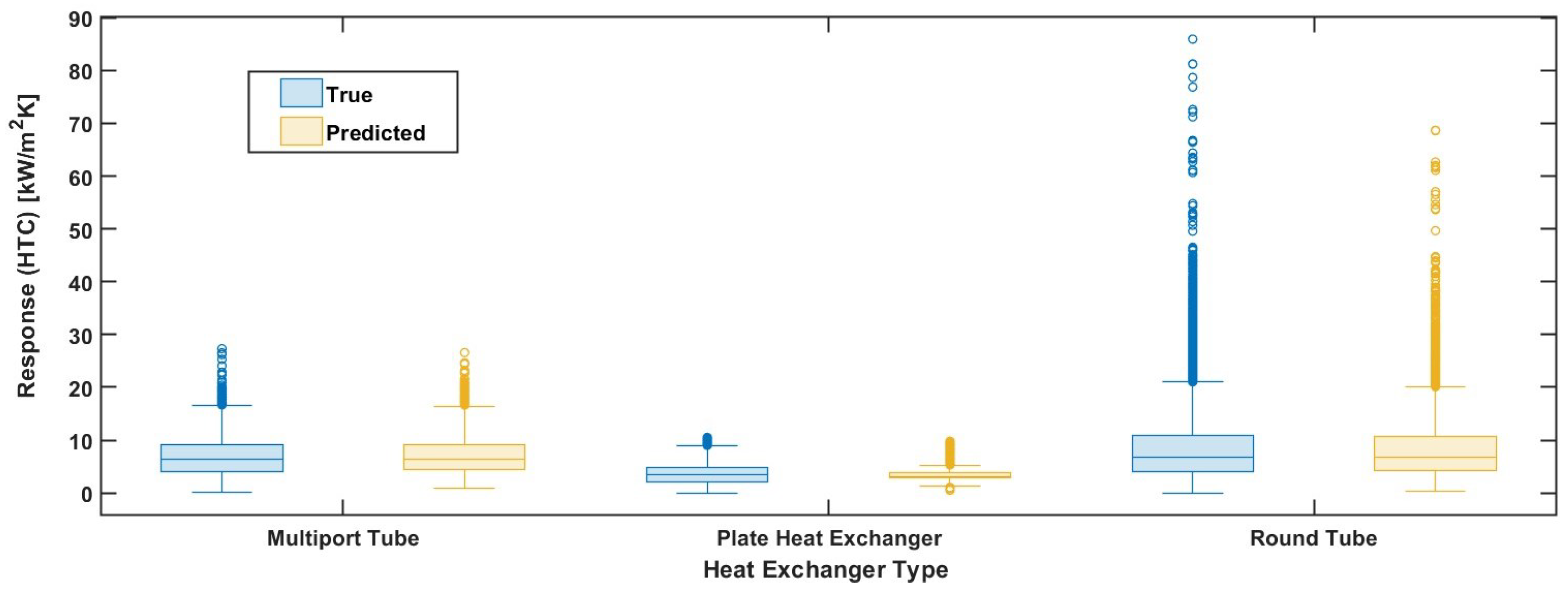
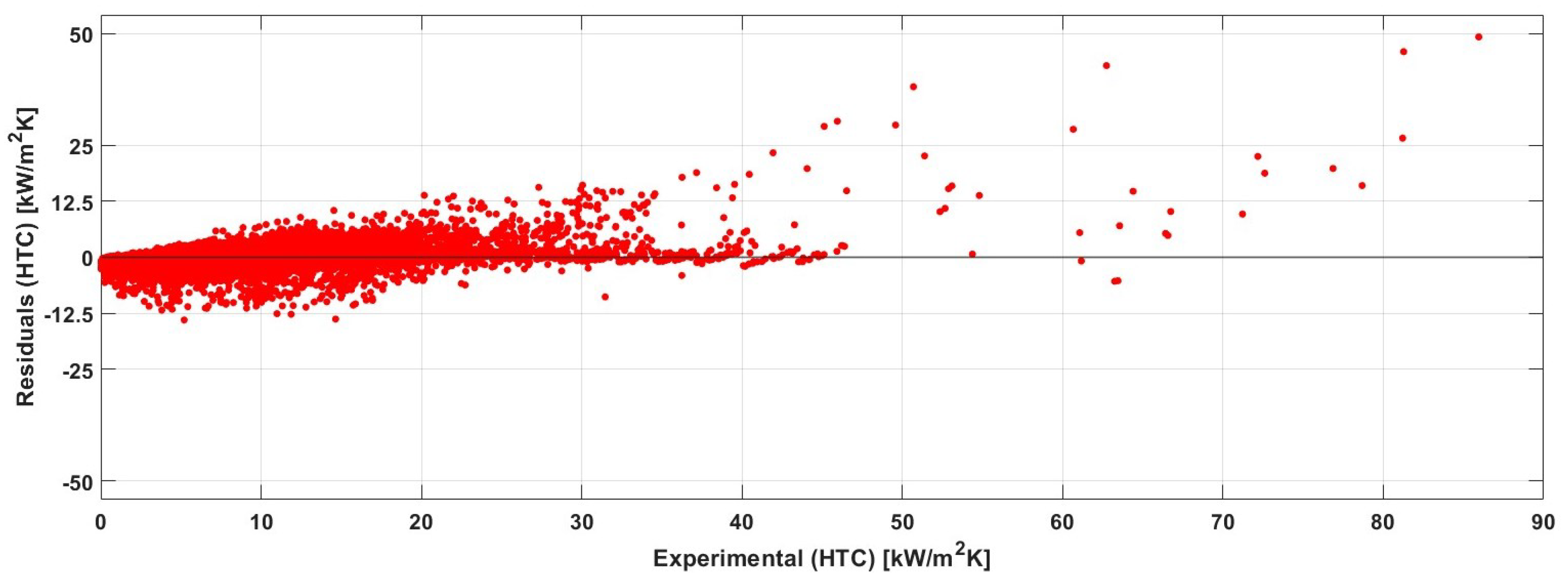
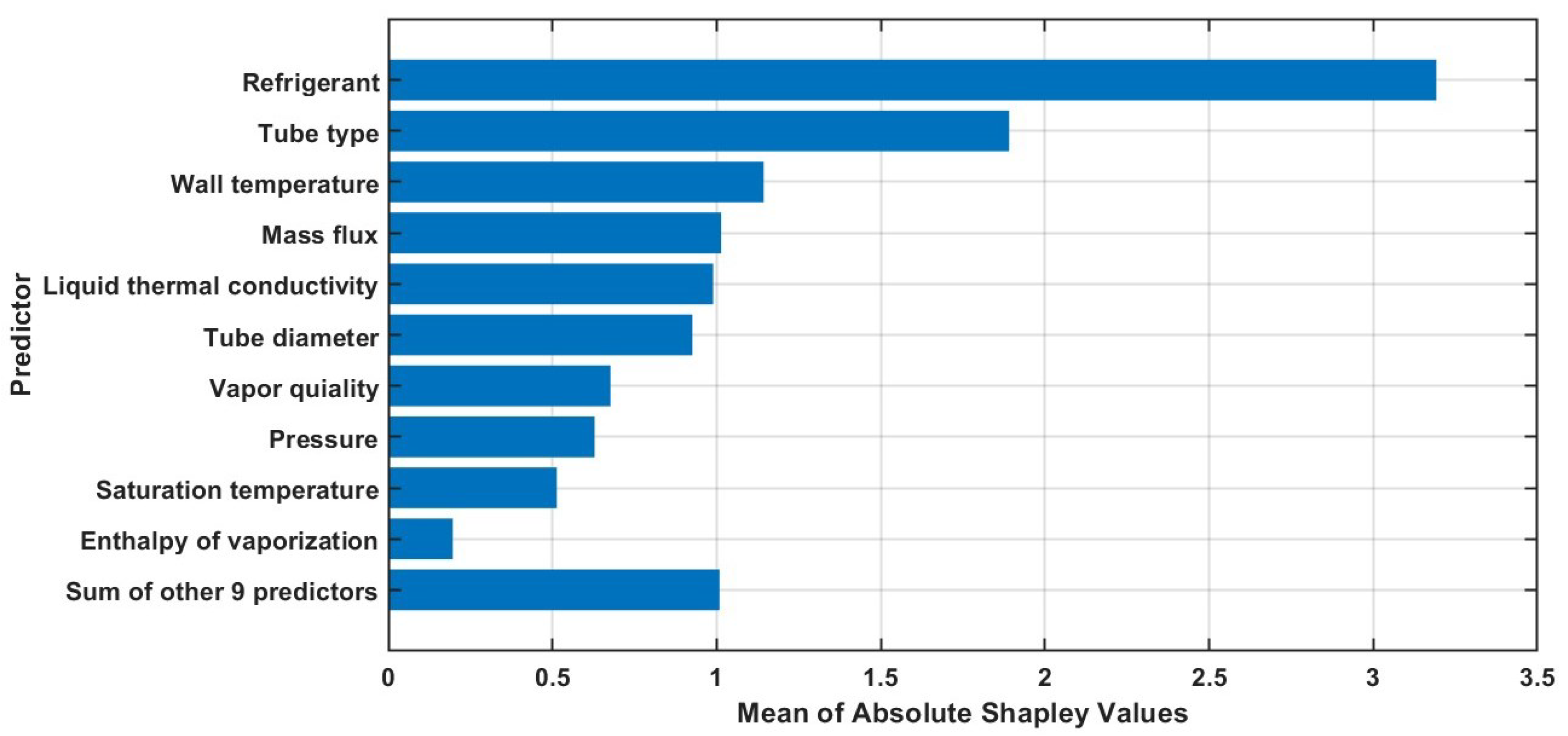
4.2. Bagged Trees Model Result Analysis
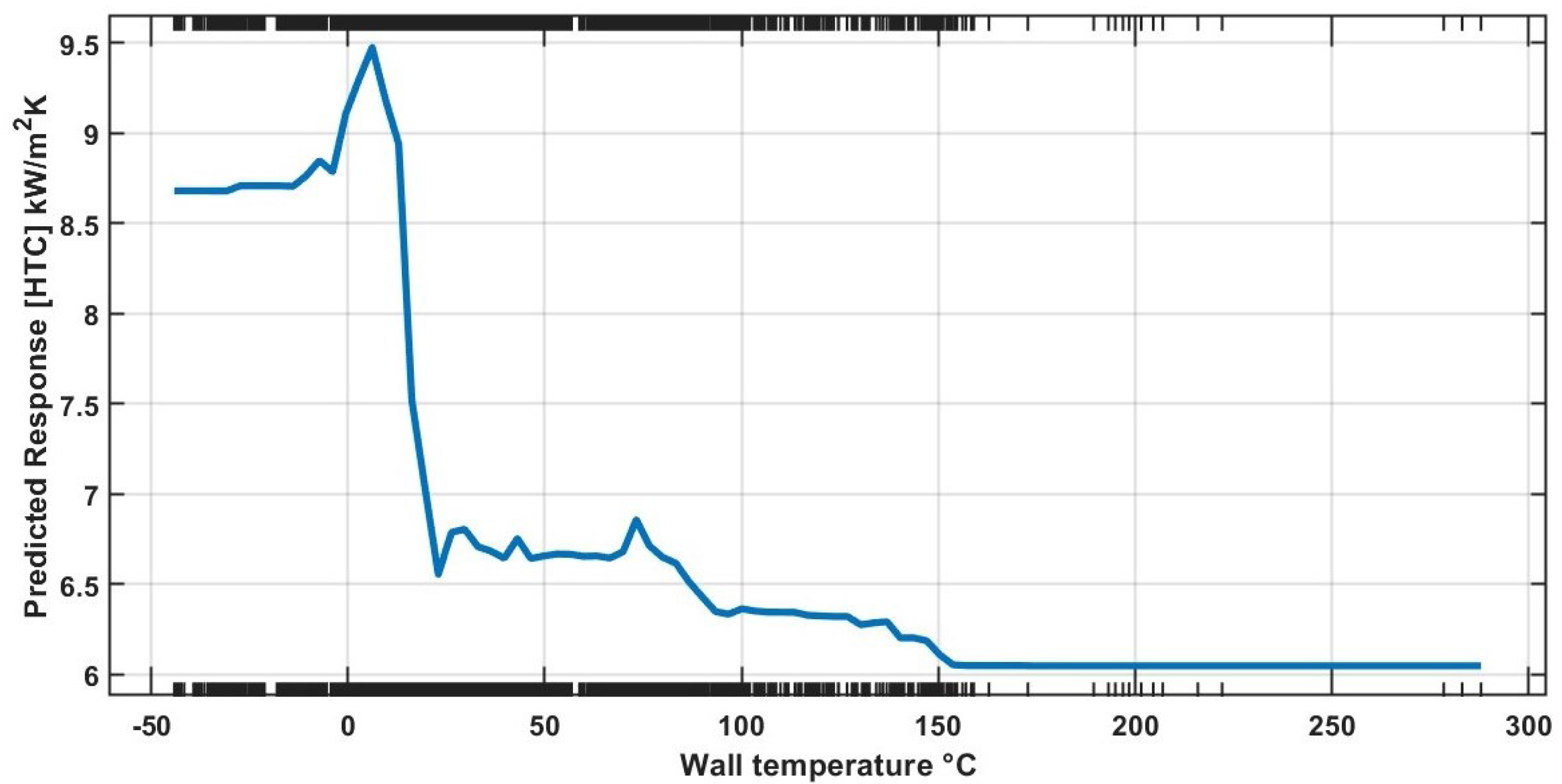
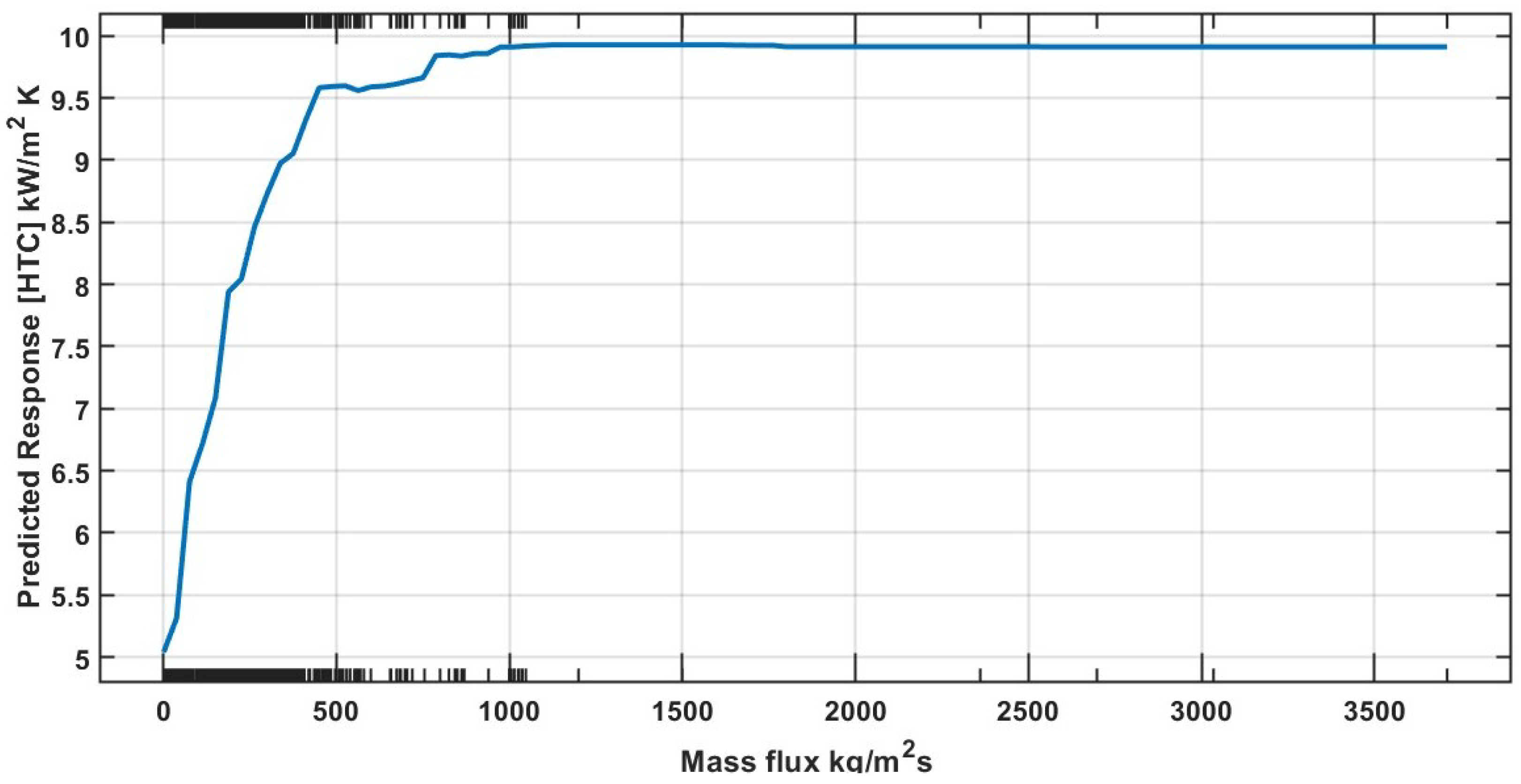
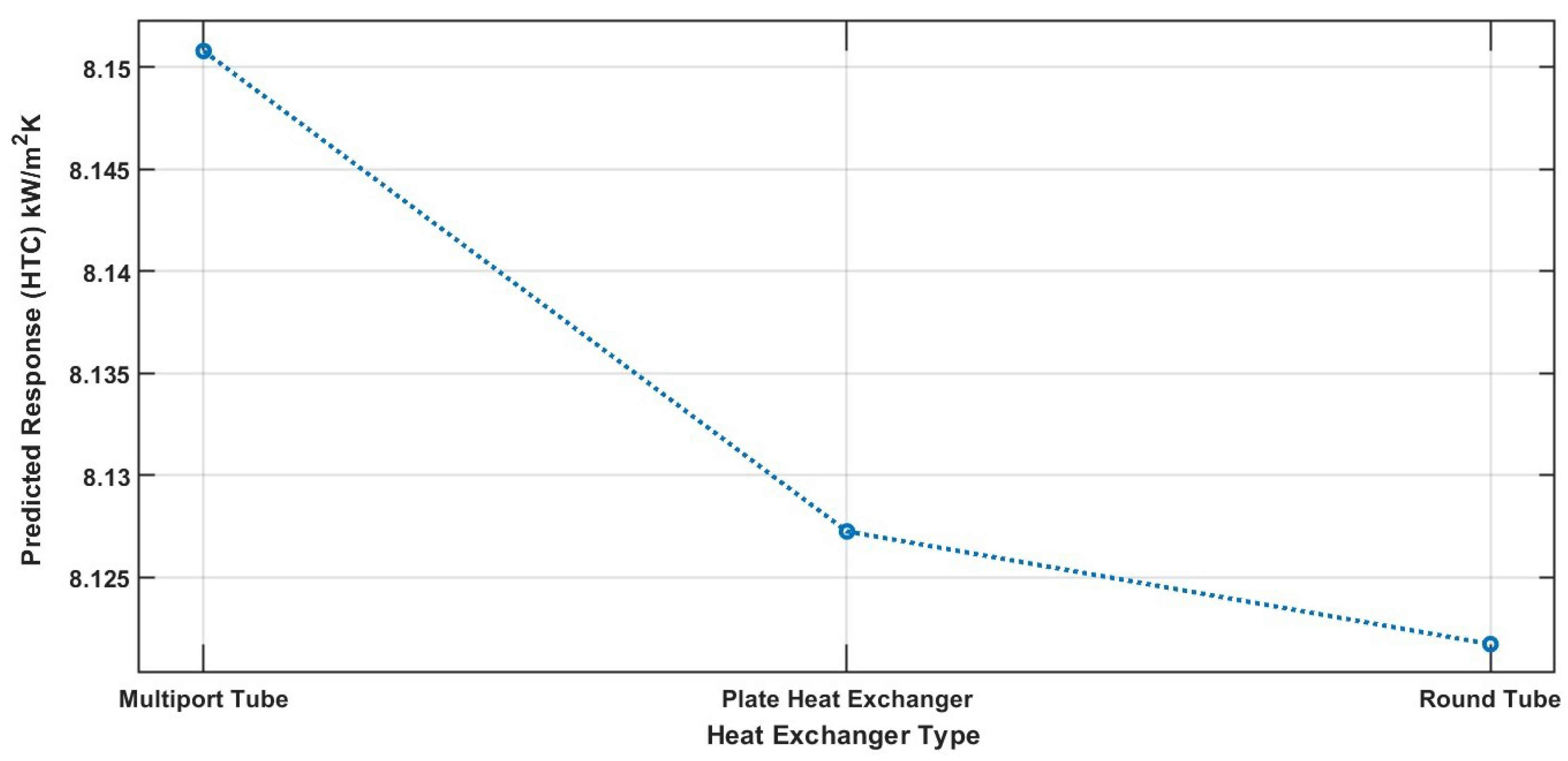
4.3. Partial Dependence Plot for the Bagged Trees Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNEP. Amendment to the Montreal Protocol on Substances That Deplete the Ozone Layer, Kigali, 15 October 2016. Available online: https://treaties.un.org/doc/Publication/CN/2016/CN.872.2016-Eng.pdf (accessed on 9 April 2025).
- Calm, J.M. The next generation of refrigerants-historical review, considerations, and outlook. Int. J. Refrig. 2008, 7, 1123–1133. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). ANSI/ASHRAE Standard 34, Designation and Safety Classification of Refrigerants. 2016. Available online: https://www.ashrae.org/file%20library/technical%20resources/standards%20and%20guidelines/standards%20addenda/34_2016_g_20180628.pdf (accessed on 20 January 2024).
- Ganesan, V.; Patel, R.; Hartwig, J.; Mudawar, I. Review of databases and correlations for saturated flow boiling heat transfer coefficient for cryogens in uniformly heated tubes, and development of new consolidated database and universal correlations. Int. J. Heat Mass Transf. 2021, 179, 121656. [Google Scholar] [CrossRef]
- Wan, J. The heat transfer coefficient predictions in engineering applications. J. Phys. Conf. Ser. 2021, 2108, 012022. [Google Scholar] [CrossRef]
- Bertsch, S.-S.; Groll, E.-A.; Garimella, S.-V. A composite heat transfer correlation for saturated flow boiling in small channels. Int. J. Heat Mass Transf. 2009, 52, 2110–2118. [Google Scholar] [CrossRef]
- Kim, S.-M.; Mudawar, I. Universal approach to predicting saturated flow boiling heat transfer in mini/micro-channels—Part II. Two-phase heat transfer coefficient. Int. J. Heat Mass Transf. 2013, 64, 1239–1256. [Google Scholar] [CrossRef]
- Fang, X.D.; Wu, Q.; Yuan, Y. A general correlation for saturated flow boiling heat transfer in channels of various sizes and flow directions. Int. J. Heat Mass Transf. 2016, 107, 972–981. [Google Scholar] [CrossRef]
- Zhu, G.; Wen, T.; Zhang, T.-D. Machine learning based approach for the prediction of flow boiling/condensation heat transfer performance in mini channels with serrated fins. Int. J. Heat Mass Transf. 2021, 166, 120783. [Google Scholar] [CrossRef]
- Reynoso-Jardón, E.; Tlatelpa-Becerro, A.; Rico-Martínez, R.; Calderón-Ramírez, M.; Urquiza, G. Artificial neural networks (ANN) to predict overall heat transfer coefficient and pressure drop on a simulated heat exchanger. Int. J. Appl. Eng. Res. 2019, 14, 3097–3103. [Google Scholar]
- Hughes, M.T.; Chen, S.M.; Garimella, S. Machine-learning-based heat transfer and pressure drop model for internal flow condensation of binary mixtures. Int. J. Heat Mass Transf. 2022, 194, 123109. [Google Scholar] [CrossRef]
- Rossos, S.; Agrafioti, P.; Sotiroudas, V.; Athanassiou, C.G.; Kaloudis, E. Predicting Heat Treatment Duration for Pest Control Using Machine Learning on a Large-Scale Dataset. Agronomy 2025, 15, 1254. [Google Scholar] [CrossRef]
- Qiu, Y.; Garg, D.; Zhou, L.; Kharangate, C.-R.; Kim, S.-M.; Mudawar, I. An artificial neural network model to predict mini/micro-channels saturated flow boiling heat transfer coefficient based on universal consolidated data. Int. J. Heat Mass Transf. 2020, 149, 119211. [Google Scholar] [CrossRef]
- Son, S.; Heo, J.Y.; Lee, J.I. Prediction of inner pinch for supercritical CO2 heat exchanger using artificial neural network and evaluation of its impact on cycle design. Energy Convers. Manag. 2018, 163, 66–73. [Google Scholar] [CrossRef]
- Sami, M.; Sierra, F. Using Machine Learning (ML) for Heat Transfer Coefficient (HTC) measurement in buildings: A systematic review. Build. Environ. 2025, 281, 113220. [Google Scholar] [CrossRef]
- Enoki, K.; Sei, Y.; Okawa, T.; Saito, K. Prediction for flow boiling heat transfer in small diameter tube using deep learning. Jpn. J. Multiph. Flow 2017, 31, 412–421. [Google Scholar] [CrossRef]
- Zhou, L.; Garg, D.; Qiu, Y.; Kim, S.M.; Mudawar, I.; Kharangate, C.R. Machine learning algorithms to predict flow condensation heat transfer coefficient in mini/micro-channel utilizing universal data. Int. J. Heat Mass Transf. 2020, 162, 120351. [Google Scholar] [CrossRef]
- Santiago-Galicia, E.; Hernandez-Matamoros, A.; Miyara, A. Prediction of heat transfer coefficient and pressure drop of flow boiling and condensation using machine learning. J. Phys. Conf. Ser. 2024, 2766, 012152. [Google Scholar] [CrossRef]
- Santiago-Galicia, E.; Hernandez-Matamoros, A.; Miyara, A. Machine Learning-Based Approach to Correct Saturated Flow Boiling Heat Transfer Correlations. Front. Artif. Intell. Appl. 2024, 389, 235–248. [Google Scholar]
- Kinjo, T.; Sei, Y.; Giannetti, N.; Saito, K.; Enoki, K. Prediction of Boiling Heat Transfer Coefficient for Micro-Fin Using Mini-Channel. Appl. Sci. 2024, 14, 6777. [Google Scholar]
- Scalabrin, G.; Condosta, M.; Marchi, P. Modeling flow boiling heat transfer of pure fluids through artificial neural networks. Int. J. Therm. Sci. 2006, 45, 643–663. [Google Scholar] [CrossRef]
- Bard, A.; Qiu, Y.; Kharangate, C.R.; French, R. Consolidated modeling and prediction of heat transfer coefficients for saturated flow boiling in mini/micro-channels using machine learning methods. Appl. Therm. Eng. 2022, 210, 118305. [Google Scholar] [CrossRef]
- Lin, L.; Gao, L.; Kedzierski, M.A.; Hwang, Y. A general model for flow boiling heat transfer in microfin tubes based on a new neural network architecture. Energy AI 2022, 8, 100151. [Google Scholar] [CrossRef]
- Christopher, M. Bishop: Pattern Recognition and Machine Learning, Chapter 4.3.4. Available online: https://www.microsoft.com/en-us/research/wp-content/uploads/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf (accessed on 16 January 2025).
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- McCullagh, P.; Nelder, J. Generalized Linear Models, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1989; ISBN 0-412-31760-5. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Duan, K.B.; Sathiya, S.K. Which Is the Best Multiclass SVM Method? An Empirical Study. Mult. Classif. Syst. LNCS 2005, 3451, 278–285. [Google Scholar]
- Cortes, C.; Vapkin, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Refrigerant Evaporator and Condenser Database. Available online: https://www.recdb.org/ (accessed on 11 August 2025).
- Lemmon, E.W.; Bell Ian, H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-Refprop, Version 10.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- The MathWorks Inc. MATLAB, Version: 24.1.0.2578822 (R2024a); The MathWorks Inc.: Natick, MA, USA, 2024. [Google Scholar]
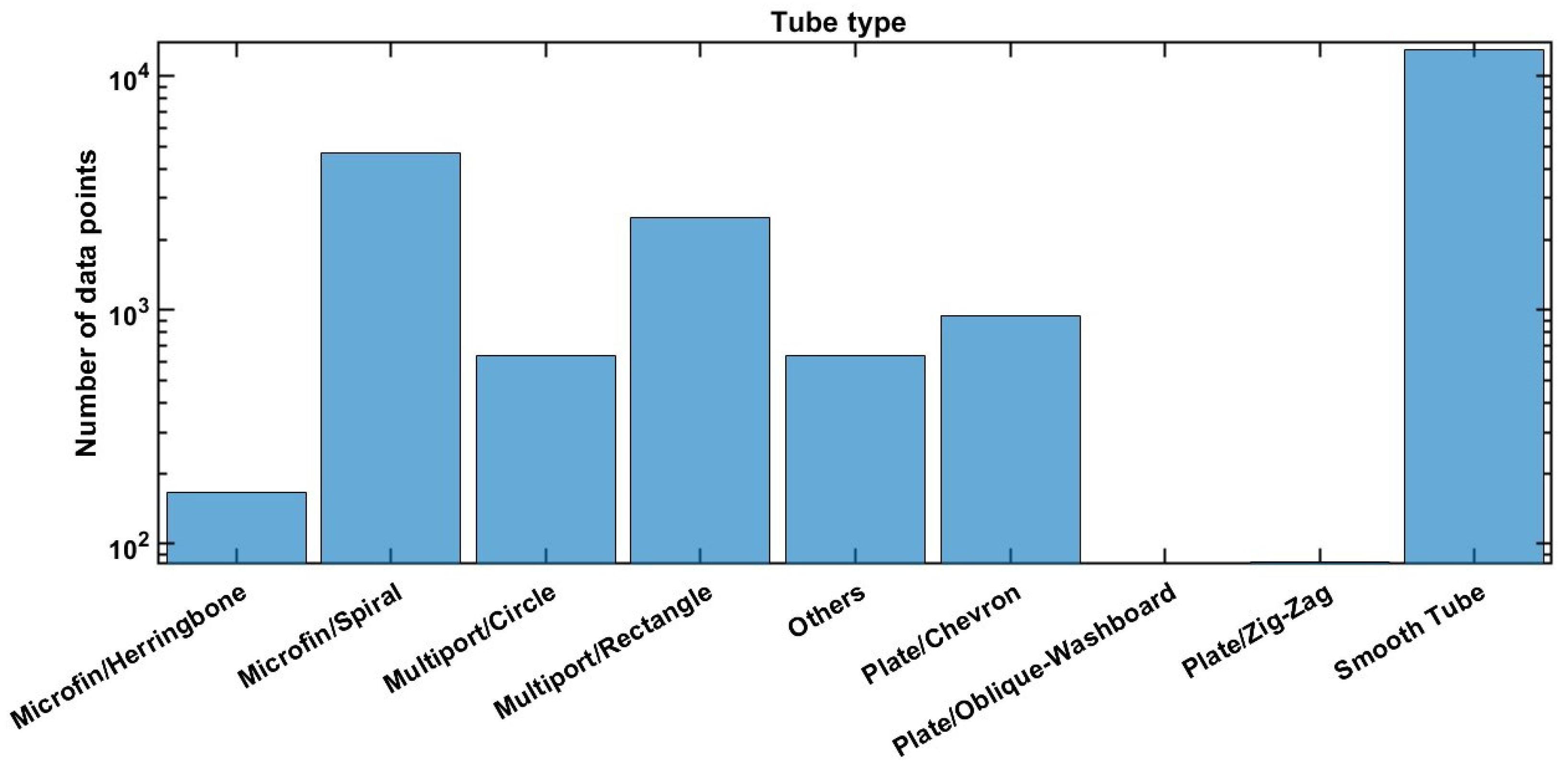
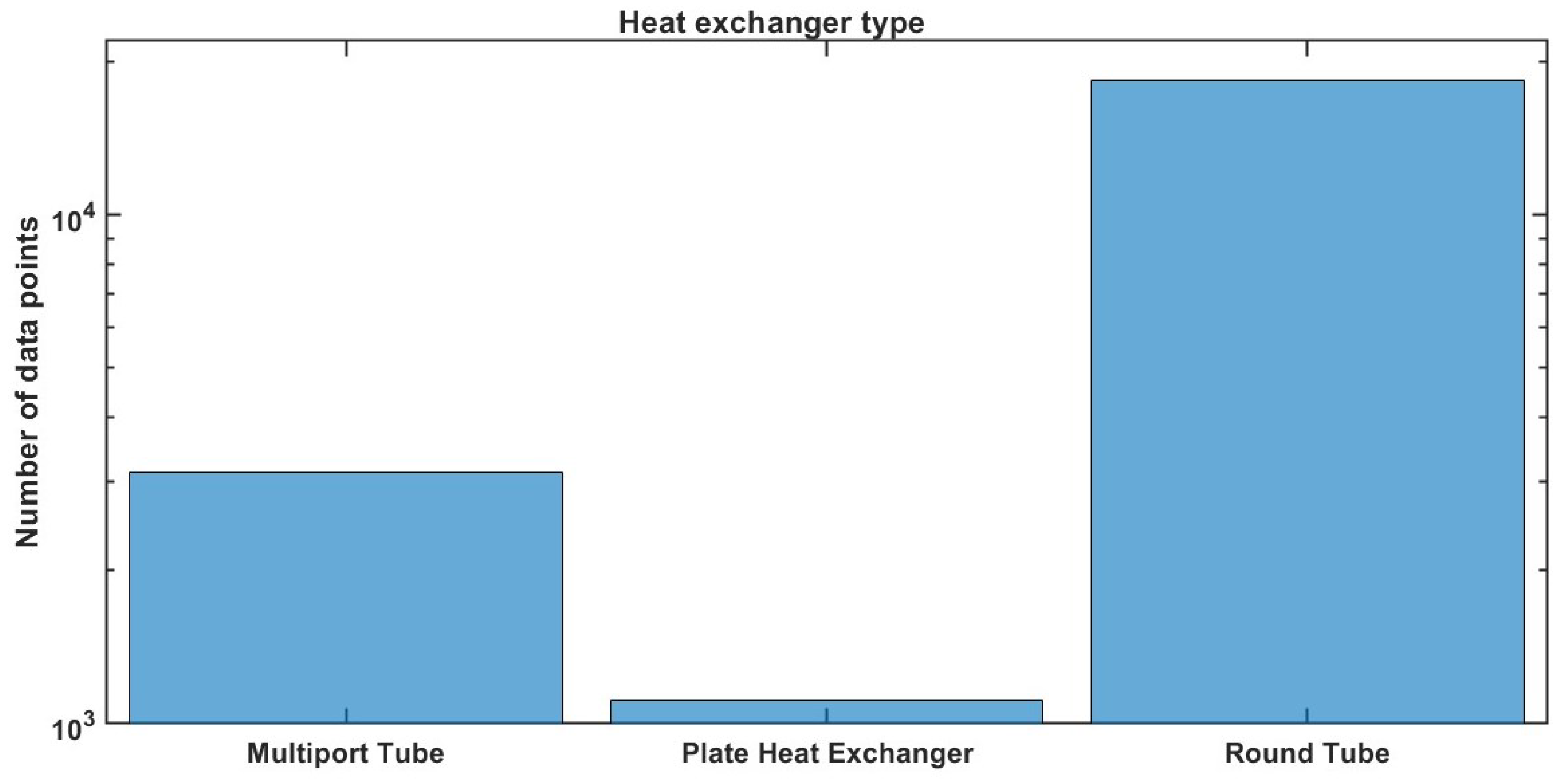
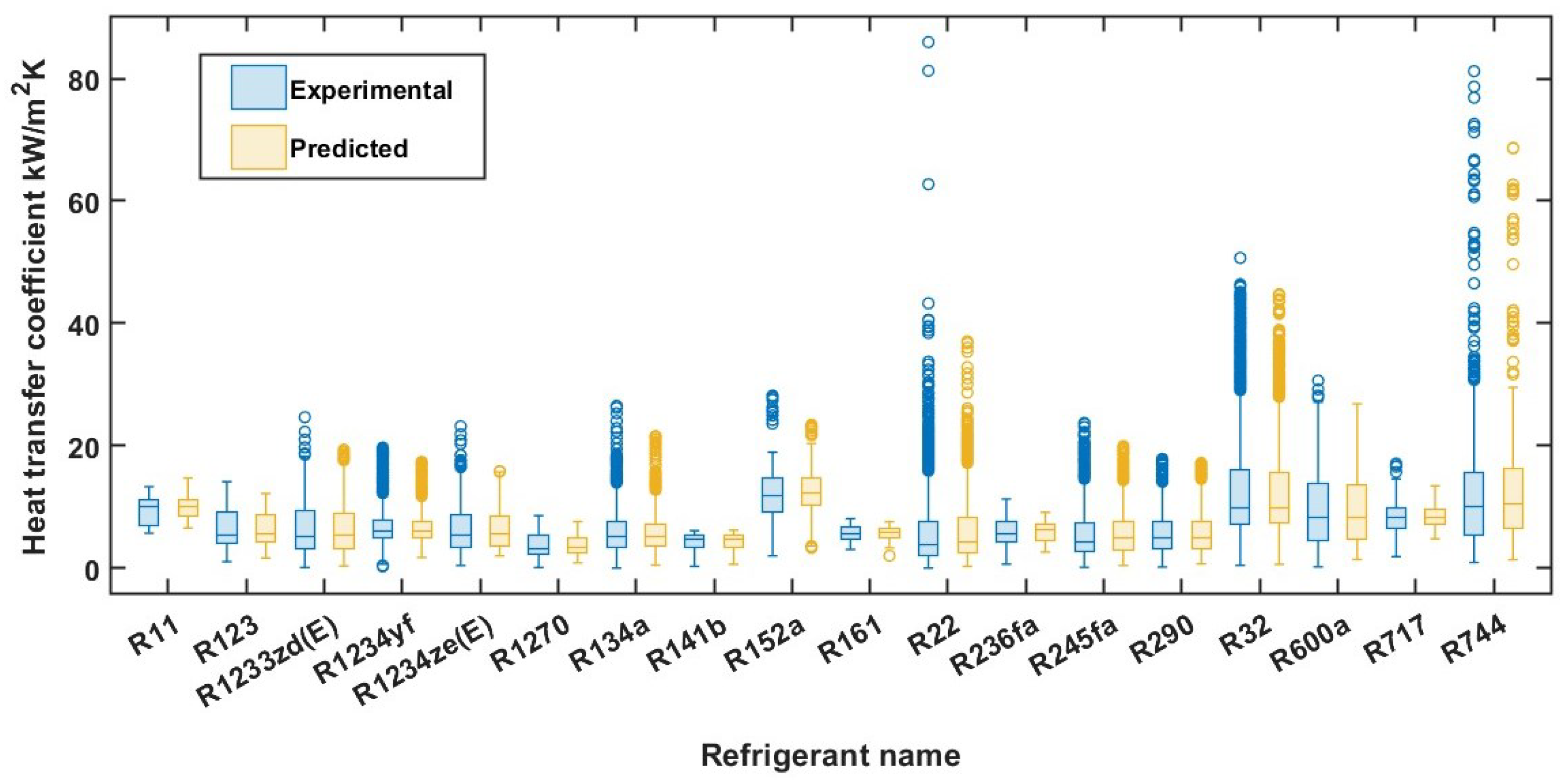
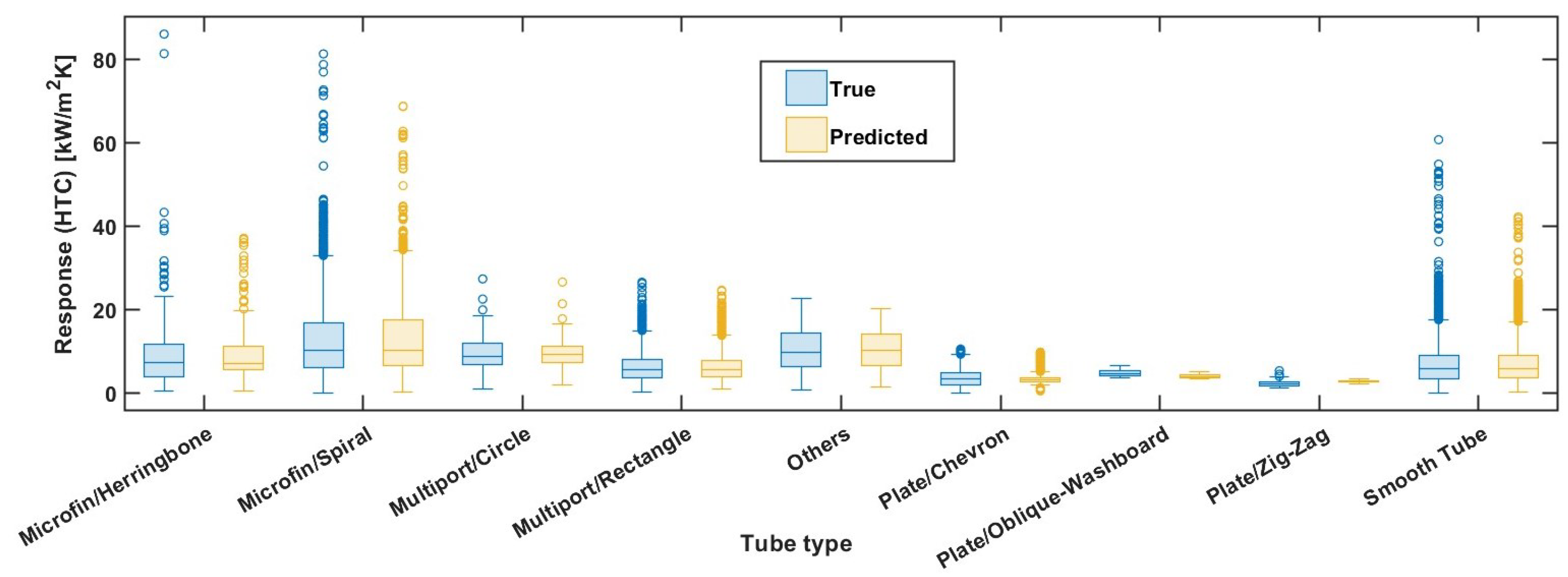

| Refrigerant | Pressure | Vapor Quality | Mass Flux | Hidraulic Diameter | Liquid Thermal Conductivity | Liquid Density | Boiling Data Points | ||
|---|---|---|---|---|---|---|---|---|---|
| [°C] | [°C] | [MPa] | [x] | [kg/m2s] | [mm] | [mW/m· K] | [kg/m3] | ||
| R11 | 57–75 | 69–85 | 0.29–0.47 | 0−0.99 | 150–560 | 1.95 | 72.8–77.6 | 1348–1395 | 100 |
| R123 | 49–81 | 51–132 | 0.208–0.50 | −0.3–0.85 | 167–470 | 0.19–1.95 | 62.4–70 | 1306–1399 | 213 |
| R1233zd(E) | 25–145 | 0–173 | 0.129–2.49 | 0–0.9 | 30–1000 | 0.650–6 | 51.3–82.7 | 842–1263 | 1371 |
| R1234yf | 6–41 | 6–60 | 0.385–1.04 | 0–0.99 | 50–940 | 0.564–4 | 58.7–69.4 | 1029–1157 | 1828 |
| R1234ze(E) | 0–72 | 0–77.32 | 0.215–1.7 | 0–0.99 | 20–940 | 0.65–1.75 | 59–83.1 | 974–1240 | 2124 |
| R1270 | 5–20 | 7–107 | 0.676–1.01 | 0–0.95 | 50–300 | 4–9.43 | 107–113 | 514–538 | 158 |
| R134a | −7–70 | −1.4–103 | 0.22–2.11 | −0.1–1.07 | 1–3710 | 1.9–12.7 | 61.6–95.4 | 996–1319 | 3100 |
| R141b | 34–60 | 39–63 | 0.108–0.25 | 0–0.93 | 50–306 | 8.6–10.92 | 81–88.1 | 1162–1216 | 122 |
| R152a | 10–32 | 12–67 | 0.372–0.73 | 0.0–0.96 | 100–580 | 1.1284–2 | 95–104 | 881–936 | 251 |
| R161 | −5–8 | −1–17 | 0.368–0.56 | 0–0.99 | 100–250 | 6.34 | 121.7–129 | 733–757 | 160 |
| R22 | −15.5–35 | −14–287 | 0.29–1.354 | −0.06–1 | 50–700 | 1.5–13.84 | 78.9–101.7 | 1150–1332 | 2104 |
| R236fa | 31 | 34–53 | 0.330780 | −0.02–0.8 | 200–1200 | 1.03 | 71 | 1338 | 151 |
| R245fa | 18–130 | 0–204 | 0.116–2.34 | −0.03–1 | 15–1500 | 0.636–1.75 | 55.4–90.2 | 938–1355 | 2392 |
| R290 | 0–35 | 2–94 | 0.47–1.21 | 0–0.99 | 50–499 | 1.54–9.43 | 89.1–105.9 | 476–528. | 731 |
| R32 | 8–40 | 9–92 | 0.364–2.48 | 0–1 | 45–499 | 0.643–6 | 77.6–138.8 | 892–1195 | 3609 |
| R600a | −20–41 | −18–142 | 0.072–0.54 | 0–0.99 | 20–500 | 1–9.43 | 83.7–106.6 | 529–602 | 1460 |
| R717 | −25–10 | −14–8 | 0.151–0.61 | 0–0.96 | 8–100 | 4 | 502–566 | 625–671 | 347 |
| R744 | −50–25 | −44–28 | 0.687–6.43 | 0–1 | 76–720 | 0.81–11.46 | 80.7–168.7 | 710–1153 | 2387 |
| Total | 22,608 |
| Trainig Model Preset | RMSE | MSE | RSquared | MAE | MAPE % |
|---|---|---|---|---|---|
| Bagged Trees | 1.97 | 3.88 | 0.91 | 1.02 | 28.85 |
| Fine Tree | 2.20 | 4.86 | 0.88 | 1.07 | 28.35 |
| Medium Tree | 2.58 | 6.64 | 0.84 | 1.37 | 34.22 |
| Exponential GPR | 2.77 | 7.65 | 0.82 | 1.65 | 63.39 |
| Rational Quadratic GPR | 2.79 | 7.79 | 0.81 | 1.69 | 64.33 |
| Matern 5/2 GPR | 2.84 | 8.07 | 0.81 | 1.74 | 66.12 |
| Wide Neural Network | 2.87 | 8.21 | 0.80 | 1.86 | 75.15 |
| Squared Exponential GPR | 2.87 | 8.22 | 0.80 | 1.77 | 67.35 |
| Trilayered Neural Network | 3.10 | 9.62 | 0.77 | 2.14 | 77.29 |
| Bilayered Neural Network | 3.16 | 9.98 | 0.76 | 2.21 | 80.91 |
| Coarse Tree | 3.18 | 10.10 | 0.76 | 1.85 | 44.85 |
| Fine Gaussian SVM | 3.21 | 10.31 | 0.75 | 1.78 | 66.32 |
| Least Squares Regression Kernel | 3.23 | 10.44 | 0.75 | 2.11 | 76.95 |
| Medium Neural Network | 3.30 | 10.92 | 0.74 | 2.26 | 82.53 |
| Narrow Neural Network | 3.64 | 13.23 | 0.69 | 2.51 | 86.69 |
| Boosted Trees | 3.77 | 14.18 | 0.66 | 2.52 | 63.36 |
| Cubic SVM | 3.86 | 14.89 | 0.65 | 2.46 | 84.43 |
| SVM Kernel | 3.94 | 15.51 | 0.63 | 2.25 | 76.22 |
| Medium Gaussian SVM | 4.15 | 17.23 | 0.59 | 2.43 | 76.78 |
| Quadratic SVM | 4.28 | 18.33 | 0.56 | 2.58 | 85.87 |
| Stepwise Linear | 4.64 | 21.56 | 0.52 | 2.45 | 56.20 |
| Coarse Gaussian SVM | 5.05 | 25.53 | 0.39 | 3.09 | 98.68 |
| Linear | 5.12 | 26.21 | 0.41 | 3.40 | 86.95 |
| Linear SVM | 5.26 | 27.67 | 0.34 | 3.32 | 111.09 |
| Robust Linear | 5.56 | 30.94 | 0.31 | 3.29 | 69.42 |
| Efficient Linear Least Squares | 6.41 | 41.06 | 0.02 | 4.36 | 145.44 |
| Efficient Linear SVM | 6.62 | 43.77 | −0.04 | 4.16 | 119.09 |
| Interactions Linear | 6.96 | 48.47 | −0.08 | 2.37 | 53.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santiago Galicia, E.; Hernandez-Matamoros, A.; Miyara, A. Machine Learning-Driven Prediction of Heat Transfer Coefficients for Pure Refrigerants in Diverse Heat Exchangers Types. J. Exp. Theor. Anal. 2025, 3, 32. https://doi.org/10.3390/jeta3040032
Santiago Galicia E, Hernandez-Matamoros A, Miyara A. Machine Learning-Driven Prediction of Heat Transfer Coefficients for Pure Refrigerants in Diverse Heat Exchangers Types. Journal of Experimental and Theoretical Analyses. 2025; 3(4):32. https://doi.org/10.3390/jeta3040032
Chicago/Turabian StyleSantiago Galicia, Edgar, Andres Hernandez-Matamoros, and Akio Miyara. 2025. "Machine Learning-Driven Prediction of Heat Transfer Coefficients for Pure Refrigerants in Diverse Heat Exchangers Types" Journal of Experimental and Theoretical Analyses 3, no. 4: 32. https://doi.org/10.3390/jeta3040032
APA StyleSantiago Galicia, E., Hernandez-Matamoros, A., & Miyara, A. (2025). Machine Learning-Driven Prediction of Heat Transfer Coefficients for Pure Refrigerants in Diverse Heat Exchangers Types. Journal of Experimental and Theoretical Analyses, 3(4), 32. https://doi.org/10.3390/jeta3040032








