Abstract
To demonstrate the difference between non-ideal experiments and idealized analytical models, bending vibrations of a frame structure have been analyzed in the context of hands-on teaching in structural dynamics. Both experimental modal analysis and model-based evaluation of system dynamics have been performed. The investigations have been limited to mechanical vibrations in the low-frequency range. It has been found that even simple mechanical models are very useful to explain, understand, and validate experimental results. The latter have been derived from one key principle of analytical dynamics—the Lagrange formalism. The article is written for students in mechanical engineering and related fields as well as for the academic community. The latter could use the results as a benchmark problem in academic teaching as well as in applied research.
1. Introduction
Structural dynamics is an important topic in the theory of mechanical vibrations [1,2]. It is a traditional but still relevant field in many engineering studies. It is especially important for mechanical and civil engineering as well as for automotive, aeronautical, and aerospace engineering [3,4]. Beside these classical disciplines, structural dynamics is closely connected to engineering acoustics [5], analytical and numerical methods of applied mathematics [6], as well as to the theory of signals and systems [7] including experimental methods [8,9,10,11]. Thus, structural dynamics is a cross-disciplinary approach (as also shown in the present paper) and it is therefore impossible to honor the important contributions of all scientists working in this field. For this reason, the list of text book references presented in the present paper is limited to a very small number that nonetheless allows for finding a starting point based on well-established text books.
Furthermore, structural dynamics is an academic field with ongoing actual development. This is true for theoretical research as well as for the development and application of experimental methods (such as experimental modal analysis) in several disciplines of engineering. A general overview on advances in vibration engineering and structural dynamics covering a broad range of topics such as rotor dynamics, structural vibrations of beam and shell structures, and structural vibrations in civil engineering is given in [12]. A particular problem in structural dynamics is given by the presence of non-linear effects. The latter have to be taken into account in numerical simulations [13,14] as well as in experimental investigations [15,16].
Another novel trend in structural dynamics is the application of wavelet transform methods [17] in modal analysis and damage detection approaches. Identification of modal parameters using wavelet transform has been discussed in [18]. A case study in which continuous wavelet transform (CWT) has been applied to perform structural dynamic analysis of a beam structure has been presented in [19]. Experimental modal analysis based on CWT applied to the transient response of a beam structure is discussed in [20], whereas the damage detection based on a wavelet method has been presented in [21].
Recent studies in which experimental modal analyses have been applied to aircraft structures have been published in [22,23,24,25,26]. A ground vibration test of an aircraft wing structure has been described in [22]. It has been shown that the results of experimental modal analysis can be very sensitive to small changes in the experimental setup, such as the position of the suspension, decreasing the frequency range of the input signal, or using different nodes for excitation. Operational modal analysis of an aircraft composite panel which considers multiple impacts and was originally intended for studying the effect of hail, birds, or other unidentified projectiles test approach is discussed in [23]. This approach takes advantages of a complex setup and expensive facilities. The authors concluded that this novel approach was capable of identifying the natural frequencies, damping ratios, and full-field mode shapes of different modes of the panel up to 600 Hz. An approach to modal analysis based on numerical models is presented in [24]. Different wing modes have been analyzed. It has been shown that the structural stability of a wing design can be analyzed successfully using commercial software programs. The automatization of experimental and operational modal analysis has been discussed in [25]. These methods are not yet chosen for safety-critical applications. For this reason, the authors present a new method that not only enables fully automated modal analysis, but also learns an optimal way to analyze the data in a supervised manner. The problem of uncertainty quantification in the modal analysis is discussed in [26], considering aircraft stiffeners as a representative example. A perturbation technique, based on Taylor series expansions, has been used to model uncertainties in aircraft stiffeners based on a stochastic formulation of the finite element (FE) method.
Model analyses applied to vehicle structures have been discuses in [27,28,29,30]. Naturally, modal analysis plays an important role in the analysis of classical structures in civil engineering, such as buildings and bridges [30,31]. However, timber structures have also been analyzed and characterized by the application of modal analysis [32,33]. Furthermore, experimental modal analysis is nowadays also an established approach in polymer science [34].
Considering all these references it can be concluded that structural dynamics, including some highly specialized analysis methods such as experimental modal analyses or wavelet transform methods, is still an evolving research area that is relevant for many disciplines of engineering. Thus, it is still also a relevant topic in the development of academic curricula [35].
If so many references can be found, one question arises. This question can be formulated in the following way: Is it necessary to publish a paper on a particular problem? To answer this question it can be useful to remember a typical challenge in teaching structural dynamics. The latter is connected with the establishment of proper non-trivial models. On the one hand, these models must be capable of describing the vibrational behavior of the analyzed system. On the other hand, these models must not be sophisticated so that solutions can be found without high-end simulation techniques. However, the mechanical models that can be found in many text books on structural dynamics are highly idealized. Therefore, it is possible to derive analytical solutions for many sample problems.
But it is not easy to design simple experiments that are useful to demonstrate the results derived from some of these basic models. This is especially true in the context of hands-on teaching in structural dynamics, including classroom experiments based on structures with non-ideal properties such as incomplete realization of symmetry conditions or imperfections in the realization of boundary conditions. Furthermore, the application of sensors (such as easy-to-handle ordinary piezoelectric acceleration sensors) as well as the connection of actuators can cause effects that are not included in basic mechanical models of structures. Unfortunately, the effects caused by these imperfections will be found in the experimental data. The task for the engineer is, however, to interpret the measurement data based on simple but at the same time also adequate and reliable models.
The present paper is an attempt to contribute to this teaching challenge. It is written for the academic community as well as for Master’s students in engineering science. Even if it is not a classical research article, the problem described in great detail in the present paper can contribute to applied research if it is used as a benchmark model. The latter is designed to demonstrate the difference between non-ideal experiments and idealized analytical models used to describe bending vibrations of a frame structure.
The paper is structured as follows. Experimental investigations in the time-domain and frequency-domain, including experimental modal analysis, are described in Section 2. Analytical models (applied to understand the experimental findings) are discussed in Section 3. The paper closes with Section 4, which presents a short summary of the main findings.
2. Experimental Investigations
2.1. Description of Frame Structure
The frame structure analyzed in a particular classroom setting is shown in Figure 1. It consists of two vertical parts of length and one horizontal part of length . It is clamped at both ends. The structure has a rectangular cross section with width and height . It is made of aluminum. As also shown in Figure 1, three concentrated weights are connected at the positions . The specific data are given in Table 1.

Figure 1.
Setup for experimental investigations.

Table 1.
Physical parameter of frame structure.
As also shown in Figure 1, three ordinary acceleration sensors (labeled with “Left”, “Middle”, and “Right”, each having a weight of approximately 0.01 kg) are connected to the horizontal part of the frame structure. The structure is driven by an electro-dynamical exciter. The connection between the structure and actuator is established by a soft rubber band. The excitation signal is generated by the soundcard of an ordinary personal computer using a sampling rate of 44.1 kHz. All cables have been arranged in such a way that any friction between structure and cable has been avoided. Some more details about the measurement equipment are given in Appendix A.
2.2. Time-Domain and Frequency-Domain Analysis
At first the system response to a step-input signal (manually applied by hand) has been analyzed. Only the system outputs have been determined. The results are shown in Figure 2. The time-domain response is shown on the left, considering the acceleration signals normalized to the peak value for each channel. The associated magnitudes of the Fourier spectra are shown on the right. The latter are also normalized to the maximum value.
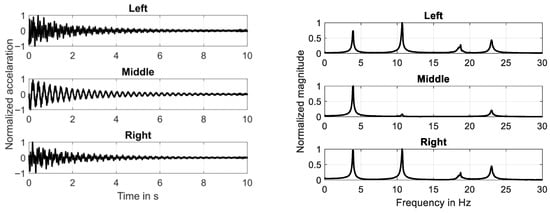
Figure 2.
Time response and frequency response of system to step-signal input.
It can be seen that the frame structure is slightly damped and the system response is based on four natural modes. It can clearly be seen that the first natural mode dominates the response measured at the center position (“Middle”) of the frame structure. Furthermore, it can be seen that the acceleration sensor at the center position is located close to nodal points of the second and third mode.
To analyze transfer behavior of the structure, the experiment has been repeated using a sine-sweep as the input signal. Thus, the response (acceleration) is measured at three positions due the single system input (voltage) applied to the electro-dynamical exciter. The time-domain behavior and frequency-domain behavior of the input signal are shown in Figure 3. The time-series is typical for a sine-sweep signal. The instantaneous frequency increases with time. Thus, the instantaneous for one period is reduced. This effect can clearly be seen in Figure 3.
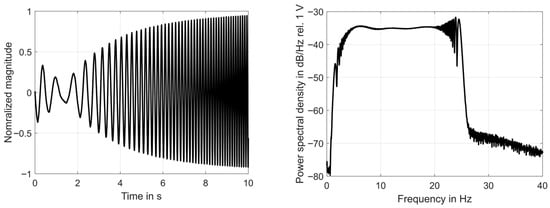
Figure 3.
Time-series and power spectrum of sweep-signal input.
Because the highest natural frequency is below 25 Hz, the frequency range for the excitation signal is between 0 Hz and 25 Hz. It can be seen that the magnitude of the excitation signal is constant over the main part of the analyzed frequency range.
The time-domain representation and frequency-domain representation of the three output signals are shown in Figure 4. The presented time-series proves that resonances are present in the system response. This is obvious because the magnitude of the normalized output signals varies with time. Maximum values can be found in all three graphs at the same point in time. The same holds for the minima. Thus, resonances as well as anti-resonances are to be found in all measurement signals. The system output peaks at the resonance frequencies. Because the system is only slightly damped it can be expected that natural frequencies and resonance frequencies are nearly identical.
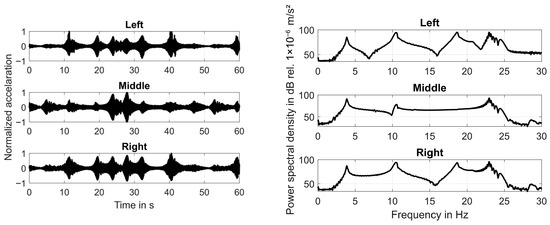
Figure 4.
Time response and frequency response of system to sweep-signal input.
In order to identify both natural frequencies and the associated mode shapes, the frequency response functions (FRFs) have been determined. Magnitude response and phase response curves are shown in Figure 5. The associated real parts of the FRFs as well as the imaginary parts of the FRFs are shown in Figure 6. The resonance frequencies and the associated modes (identified on the basis of these FRFs) are listed in Table 2 and Table 3. All modes are normalized to the response measured at the “Left” sensor position. Please note that the spectral analysis presented in this paper is based on Welch’s method.
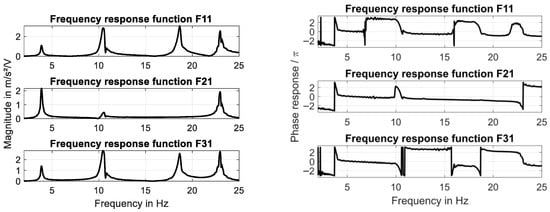
Figure 5.
Frequency response curves (F11 -> Left, F21 -> Middle, and F31 -> Right).
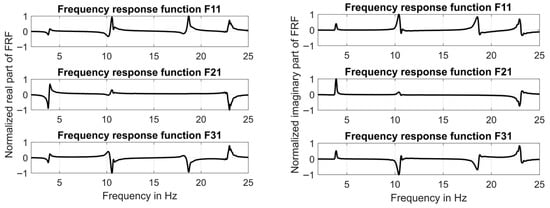
Figure 6.
Real part and imaginary part of FRFs (F11 -> Left, F21 -> Middle, F31 -> Right).

Table 2.
Normalized magnitudes at resonance frequencies.

Table 3.
Phase relations at resonance frequencies.
It can be seen that the second and third mode are not identical in frequency but identical in shape. This is an interesting result. In both modes the signals measured at the “Left” and the “Right” sensor positions are opposite in phase and more or less identical in magnitude. The “Middle” sensor position is a nodal point for both mode shapes.
To confirm this result the modal assurance criteria proposed in [36] has been applied. This criteria is valid for both real valued and complex eigenvectors. It is calculated according to Equation (1), which is as follows:
where is the i-th eigenvector and is the j-th eigenvector. The value is in the range . The minimum value indicates that the modes i and j are completely independent of each other. The maximum value indicates that the mode shape of the i-th mode is completely identical to the mode shape of the and j-th mode. The upper index T in Equation (1) is used to indicate the transposition of a vector, whereas the upper index H is represents the Hermitian of a vector that is equal to its own conjugate transpose form.
All calculated modal assurance values are listed in Table 4. The results presented in this table are proof that the eigenvectors and represent identical mode shapes. However, these mode shapes are orthogonal to the eigenvectors represented by and . Furthermore, the eigenvector is orthogonal to the eigenvector .

Table 4.
Modal assurance criteria values for measured mode shapes.
2.3. Synthesis of Mode Shapes
To complete the experimental investigations, models for the FRFs have been analyzed by experimental model analysis. Because the resonance frequencies are clearly separated, the simple method of peak pinking (PP) [10] has been applied. This method is based on the i FRFs of each modal degree of freedom (DOF)—also known as generalized coordinates. These FRFs can be represented by rational functions such as:
where is the i-th generalized mass, is the modal damping in the i-th mode, is the angular frequency associated with the i-th natural frequency , and is the angular frequency associated with the frequency of excitation . The modal damping parameter have been determined by the half-bandwidth method [10] for each resonance frequency, such as:
where is the frequency at the −3 dB point left to the i-th resonance frequency, and is the frequency at the −3 dB point right to the i-th resonance frequency. All modal damping parameters are listed in Table 5. The data indicate that the system is indeed slightly damped. The maximum modal damping is below 3%.

Table 5.
Modal damping in resonance.
To perform experimental modal analysis using PP it is also necessary to determine the peak value of the magnitude response, which is compared to Figure 5, for each resonance frequency.
These data are summarized in Table 6. They are required to calculate the modal contribution of the i-th mode to the system response at position r according to the excitation acting at position s, such as:

Table 6.
Peak magnitudes at resonance frequencies in m/s2/V.
The connection between the real world FRFs and the FRFs of the modal coordinates is established by the modal transformation such as:
where the modal matrix
contains the eigenvector of each mode, such as:
It is a straightforward calculation to prove that the three real world FRFs of the analyzed system can be represented by the following transfer function models (TFMs):
A comparison between the measured FRFs and the identified TFMs is shown in Figure 7. The match in magnitude is nearly perfect and the similarity in phase is sufficient considering the application of the simple PP method.
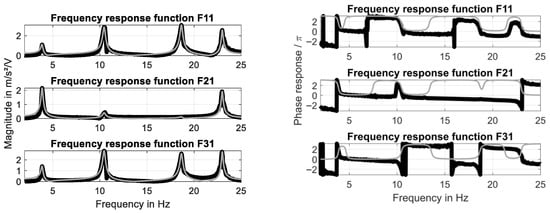
Figure 7.
Identified transfer function models (in gray) compared to measured FRFs.
However, even if adequate response models can be identified by a very simple approach, it is still necessary to explain the similarities between the mode shape of the second resonance on the one hand and the mode shape of the third resonance on the other hand. To explain this result analytical analysis of simple models can be helpful.
3. Theoretical Analysis—Understanding the Experimental Data
The interpretation of experimental data is much more intuitive if the results can be mapped to the behavior of models of vibrating structures. These models should be as exact as necessary and as simple as possible at the same time. It is obvious that the frame structure shown in Figure 1 executes bending vibrations in the vertical direction. As shown in [2], the associated vibration modes can be described by a combination of global shape functions and generalized coordinates , such as:
In our investigation we will consider only the first three bending modes, assuming simply supported boundary conditions. For this reason the set of shape functions reads as follows:
Because the kinetic energy and the potential energy of the physical structure vibrating in the i-th mode is equivalent to the kinetic energy and potential energy of the i-th generalized structure, compared to [2], we can calculate the elements of the mass matrix as follows:
where is the DIRAC distribution and is the n-th concentrated mass at the position . The elements of the stiffness matrix depend on the curvature, as known from Bernoulli’s beam theory. These elements are given by the following integral:
Considering a constant density as well as a constant cross section , the mass matrix is given by the superposition of the contributions of the continuous beam structure, which can be calculated using the first summand in Equation (13):
and the contributions of the concentrated point mases. The latter are given by symmetric matrices that, in general, contain non-zero off-diagonal elements. These contributions are defined by Equation (14) as follows:
where
is a dimensionless length, indicating the position of the n-th concentrated mass on the horizontal part of the frame structure, which can be found in Figure 1 and Table 1. Considering a constant bending stiffness , the solution of Equation (12) reads as follows:
In order to derive the equation of motion we have to formulate the expressions for both the kinetic energy T and the potential energy U based on the generalized coordinates , such as:
Applying Lagrange’s principle, which is as follows:
the equations of motion are given by:
To determine the natural frequencies for the bending modes , it is necessary to find the zeros of the associated characteristic polynomial. This problem reads:
However, the solution of Equation (2) only yields three natural frequencies associated with three bending modes. A simple model that can be used to explain the fourth resonance frequency determined in the experimental investigation is still needed. Such a model can be derived if the bending vibration of the vertical parts of the frame structure is taken into account. If the horizontal part of the frame structure (including the three concentrated mass points) is seen as a concentrated rigid mass connected to two springs acting in parallel (horizontal parts of the frame structure) then we can establish a fourth DOF. The mass associated with this horizontal DOF is given by the following:
whereas the associated effective stiffness reads:
The multiplier “2” represents the fact that the two vertical parts of the frame structure are acting in parallel. The second term in Equation (22) represents the bending stiffness of a beam that is fixed at one end and free at the other end [2]. The formula for the associated natural frequency is given in Equation (23):
Numerical data for the four natural frequencies and based on the parameter given in Table 1 are listed in Table 7. It can be seen that the three natural frequencies calculated for bending vibrations in the vertical direction are in fair agreement with the resonance frequencies determined for the first, second, and fourth mode shape in the experimental investigations.

Table 7.
Natural frequencies for first three bending modes and first horizontal mode.
The natural frequency calculated from the simple model describing the horizontal vibration is in fair agreement with the third resonance frequency determined in the experimental investigations. It can be concluded that due to imperfections in the experimental setup this horizontal mode couples with the second vertical bending mode that is in its shape similar to the third mode shape determined for a resonance frequency of 18.7 Hz. Please note that the natural frequencies for the bending modes are verified by the results obtained from the simple FE model presented in Appendix B.
4. Conclusions
The intension of this paper was to present an intuitive but not trivial problem related to structural dynamics. This problem has been demonstrated to students of aeronautical engineering, automotive engineering, and mechatronics in many courses over the last decade. The demonstration by itself is simple. However, because of imperfections—going hand-in-hand with hands-on teaching—it is not easy to interpret the results. In order to overcome this problem it is helpful to apply adequate dynamic models that can be derived from the principles used in structural dynamics. The main conclusions can be summarized as follows:
- The established methods of experimental modal analysis are useful to demonstrate the determination of modal parameters such as resonance frequencies, mode shapes, and modal damping for non-trivial test structures.
- The interpretation of experimental results is easier if models capable of describing the dynamic behavior of the structure are taken into account. These models should not be sophisticated in order to derive robust analytical solutions in a short period of time.
As written in the introduction, this paper has been written for both the scientific community and students of engineering science. The analyzed problem has been described in great detail. It is very easy to reproduce. Thus, it could serve as a benchmark model to validate new experimental techniques. However, it is also possible to use the results for the validation of new numerical approaches.
The paper contains all relevant data and equations. All findings can be reproduced without knowledge of the few but very excellent references. This can be advantageous for students of advanced courses in structural dynamics and related field, because a non-trivial problem is described by experimental and analytical methods in a compact and consistent way. Furthermore, everyone teaching structural dynamics can easily derive a simple demonstration experiment based on the published data. Perhaps for this reason it is a small contribution to stimulating a deeper interest in structural dynamics.
Finally, it is necessary to comment on the following question: How the presented setup and analysis may be used for benchmarking experimental techniques or validating numerical approaches? One answer to this question can be given considering non-standard analysis methods such as wavelet transform methods [17,18,19,20,21]. These methods are not necessary to analyze the problem presented in the present paper. However, if new methods in structural health monitoring [11] and damage detection [21] based on experimental structural analysis have to be validated, the presented experiment could be used as a starting point for the undamaged structure. Because it is simple to manufacture copies of the presented structure it is also easy to produce twins including defined artificial damage (represented by slots and gaps of different size and shape). Thus, the original structure in combination with artificially damaged twins can serve as benchmark models to validate damage detection approaches.
Another reason why this may be used as a benchmark is given by the fact that the point masses shown in Figure 1 are connected by screws. An imperfect connection (this could also be interpreted as a particular aspect of damage) would result in additional damping caused by dry friction. Thus, the experiment presented in this paper could also be used to validate non-linear models in structural dynamics that include damping models based on dry friction between a base structure (beam) and attached substructures (concentrated point masses).
A last benchmark-related idea can be initiated when considering the fact that a detailed modal analysis of a large structure results in a large data set that has to be analyzed. At this point artificial intelligence and machine learning methods become relevant. Machine learning in the context of non-linear structural dynamics has been discussed in [37]. However, a simplified analytical model has been used to generate the data. The presented experiments could be a simple alternative to generate a sufficient set of real world data. This is especially true if random excitation signals are used. A machine learning-based approach to structural health monitoring and its application to a realistic bridge structure has been presented in [38]. The structure analyzed in this reference is more sophisticated than the structure presented in this paper. However, the methodology applied in [38] could be verified using the well-defined simple structure presented in this article. The same holds for the approach presented in [39].
The state-of-the-art in automated operational modal identification has been summarized in [40], considering various AI-driven approaches. The authors conclude that: “Challenges such as identifying double and multiple modes, modes with low observability, damped modes and systems with high damping, and systems subjected to combined excitations (random and harmonic) can be considered key challenges faced by intelligent system identification algorithms.” The system presented in this article generates a double mode (as shown for the second and third mode shape) if the excitation is not harmonic. Furthermore, it is easy to choose nodal points at which a mode shape is difficult to observe (this is especially true for the center position of the beam at the second and third natural frequencies). Finally, the presented problem is well suited to combine harmonic and random excitation signals. Thus, it is possible for the reader to define research questions inspired by [40] that could be investigated on the basis of the presented well-defined benchmark model.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We acknowledge support for the article processing charge by the Open Access Publication Fund of Hamburg University of Applied Sciences.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
This appendix has been added in order to provide some more details about the equipment used for the experimental investigations discussed in Section 2. However, the information is presented in a way that makes it possible to find adequate equipment without pointing to a specific manufacturer.
Appendix A.1. Actuator
A small shaker with integrated power amplifier has been used in the experiments. In order not to alter the stiffness of the system, the actuator has been connected to the frame via an ordinary rubber band. This actuator can be characterized in the following way:
- Power supply: 60 W, 19 V DC output, 100–240 V AC input;
- Peak sine force: 31 N with up to 13 mm stroke;
- Maximum payload: 0.901 kg;
- Distortion: <0.02%;
- Frequency Range: DC to 9.0 kHz;
- Dimensions (H × W × D): 135 × 171 × 89 mm;
- Weight: 3.1 kg.
Appendix A.2. Sensors
Common piezoelectric sensors (driven by 2 mA current supply) have been used. These sensors can be characterized in the following way:
- Sensitivity: (±10%) 10.2 mV/(m/s2);
- Measurement Range: ±490 m/s2 pk;
- Broadband Resolution: 0.0015 m/s2 rms;
- Frequency Range: (±5%) 0.5 to 10.0 kHz;
- Weight: 5.8 g.
Appendix A.3. Computer Interfacing
The excitation signal has been generated by the soundcard of an ordinary personal computer using a sampling rate of 44.1 kHz. The output of the soundcard has been the headphone jack. The signal generated by the computer has been fed to the BNC input of the actuator using a chinch-to-BNC adapter. The output signals of the acceleration sensors have been fed to the BNC input channel of a sound card-based measurement device. This device has been able to provide the power supply for the sensors. It has been working at a sampling rate of 44.1 kHz.
Appendix B
In addition to the model derived in Section 3, a simple model based on the FE method is presented. This model is based on the Euler–Bernoulli theory for elastic beams. A detailed description for the derivation of the element mass matrix and the element stiffness matrix is presented in [4]. These matrices are given by Equation (A1) as follows:
where is the density in the element, is the elements cross section, is the length of the element, and with is the contribution of a discrete mass at the right end of the element, as well as by the following Equation (A2):
where is the bending stiffness of the element. For our problem all these data are to be found in Table 1.
In order to illustrate how a simple FE model can be derived, different stages of model development are shown in Figure A1. The topological model represents the beam structure shown in Figure 1. Furthermore, the global coordinate system is attached to this model. The simplified mechanical model has been used to perform the theoretical investigations presented in Section 3. It clarifies how the boundary conditions have been modeled considering simply supported conditions at both ends of the beam. The FE representation of the beam structure is useful to understand the arrangement of elements and nodes as well as the global degrees of freedom that have been taken into account.
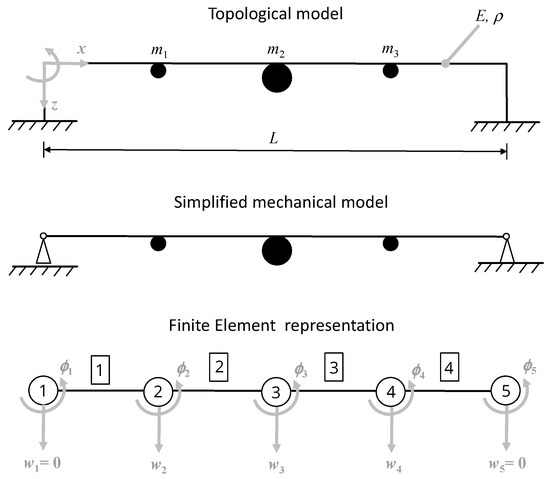
Figure A1.
Topological, mechanical, and finite element representation of beam structure.
Considering the boundary conditions of a simply supported beam and the remaining eight non-zero global degrees of freedom, the following can be obtained:
where is the rotation at the k-th node and is the vertical displacement at the m-th node. It is straightforward to calculate the reduced global stiffness matrix with as well as the reduced global mass matrix with . The non-zero elements of these symmetric matrices are given by Equation (A4):
and by Equation (A5):
The associated equations of motion are given by the following:
To determine the natural frequencies it is necessary to find the zeros of the associated characteristic polynomial. This problem reads as follows:
The first three natural frequencies are listed in Table A1. The results calculated with this simple FE model are in very good agreement compared to the results presented in Table 2.

Table A1.
Natural frequencies for first three bending modes calculated with the FE model.
Table A1.
Natural frequencies for first three bending modes calculated with the FE model.
| Mode | Bending, 1 | Bending, 2 | Bending, 3 |
|---|---|---|---|
| f/Hz | 2.28 | 10.5 | 20.3 |
References
- Seto, W.W. Mechanical Vibrations, 1st ed.; McGRAW-HILL: New York, NY, USA, 1964. [Google Scholar]
- Brommundt, E.; Sachau, D. Schwingungslehre mit Maschinendynamik, 1st ed.; Springer: Berlin/Heildelberg, Germany, 2008. [Google Scholar]
- Gasch, R.; Knothe, K. Strukturdynamik—Band1: DiskreteSysteme, 1st ed.; Springer: Berlin, Germany, 1987. [Google Scholar]
- Gasch, R.; Knothe, K. Strukturdynamik—Band2: Kontinua und ihre Diskretisierung, 1st ed.; Springer: Berlin, Germany, 1989. [Google Scholar]
- Fahy, F.; Gardonio, P. Sound and Structural Vibration, 1st ed.; Academic Press: London, UK, 2007. [Google Scholar]
- Börm, S.; Mehl, C. Numerical Methods for Eigenvalue Problems, 1st ed.; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H. Signals and Systems, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Randall, R.R. Application of B&K Equipment to Frequency Analysis, 2nd ed.; Brüel & Kjær: Nærum, Denmark, 1977. [Google Scholar]
- Broch, J.T. Mechanical Vibration and Shock Measurements, 2nd ed.; Larsen and Søn: Søborg, Denmark, 1980. [Google Scholar]
- Ewins, D.J. Modal Testing. Theory, Practice and Application, 2nd ed.; WILEY: Hoboken, NJ, USA, 2000. [Google Scholar]
- Randall, R.R. Vibration Based Condition Monitoring, 1st ed.; WILEY: Hoboken, NJ, USA, 2021. [Google Scholar]
- Beltrán-Carbajal, F. Advances in Vibration Engineering and Structural Dynamics, 1st ed.; INTECH: Rijeka, Croatia, 2019. [Google Scholar]
- Lee, Y.-y. Free Vibration Analysis of Nonlinear Structural-Acoustic System with Non-Rigid Boundaries Using the Elliptic Integral Approach. Mathematics 2020, 8, 2150. [Google Scholar] [CrossRef]
- Maio, D.D. A novel analysis method for calculating nonlinear frequency response functions. J. Struct. Dyn. 2025, 3, 30–57. [Google Scholar] [CrossRef]
- Zhuo, X.; Xu, P.-Y.; Li, H.; Chu, C.; Sun, P.-Y.; Gu, D.-W.; Shi, D.-S.; Li, H.; Han, Q.-K.; Wen, B.-C. The analysis of nonlinear vibration characteristics of fiber-reinforced composite thin wall truncated conical shell: Theoretical and experimental investigation. Eur. J. Mech.-A/Solids 2024, 105, 105268. [Google Scholar] [CrossRef]
- Dolbachian, L.; Harizi, W.; Aboura, Z. Experimental linear and nonlinear vibration methods for the structural health monitoring (SHM) of polymer-matrix composites (PMCs): A literature review. Vibration 2024, 7, 281–325. [Google Scholar] [CrossRef]
- Chui, C. An Introduction to Wavelets, 1st ed.; Academic Press: New York, NY, USA, 1992. [Google Scholar]
- Lardies, J.; Gouttebroze, S. Identification of modal parameters using the wavelet transform. Int. J. Mech. Sci. 2002, 44, 2263–2283. [Google Scholar] [CrossRef]
- Oviedo, T.C.A.; Mendez, Q.J.E. Structural dynamic analysis using wavelets. J. Phys. Conf. Ser. 2019, 1160, 012016. [Google Scholar] [CrossRef]
- Régal, X.; Cumunel, G.; Bornert, M.; Quiertant, M. Assessment of 2D digital image correlation for experimental modal analysis of transient response of beams using a continuous wavelet transform method. Appl. Sci. 2023, 13, 4792. [Google Scholar] [CrossRef]
- Dziedziech, K.; Staszewski, W.J.; Mendrok, K.; Basu, B. Wavelet-based transmissibility for structural damage detection. Materials 2022, 15, 2722. [Google Scholar] [CrossRef]
- Gasparetto, V.E.L.; Machado, M.R.; Carneiro, S.H.S. Experimental modal analysis of an aircraft wing prototype for SAE Aerodesign Competition. Dyna 2020, 87, 100–110. Available online: https://www.redalyc.org/journal/496/49666177012/html/ (accessed on 10 October 2025). [CrossRef]
- Molina-Viedma, Á.; López-Alba, E.; Felipe-Sesé, L.; Díaz, F. Full-field operational modal analysis of an aircraft composite panel from the dynamic response in multi-impact test. Sensors 2021, 21, 1602. [Google Scholar] [CrossRef] [PubMed]
- Radha Krishna, K.R.; Jadhav, S.D.; Mishra, A.K. Comparative modal analysis on different aircraft wing models. Int. J. Enhanc. Res. Sci. Technol. Eng. 2023, 12, 42–49. [Google Scholar]
- Volkmar, R.; Soal, K.; Govers, Y.; Böswald, M. Experimental and operational modal analysis: Automated system identification for safety-critical applications. Mech. Syst. Signal Process. 2023, 183, 109658. [Google Scholar] [CrossRef]
- Scinocca, F.; Nabarrete, A.; Santos, F.L. Uncertainty quantification in the modal analysis of aircraft stiffeners: A perturbation technique approach in SFEM. Eng. Struct. 2025, 323, 119187. [Google Scholar] [CrossRef]
- Chen, H.; Lu, C.; Liu, Z.; Shen, C.; Sun, Y.; Sun, M. Structural Modal Analysis and Optimization of SUV Door Based on Response Surface Method. Shock Vib. 2020, 2020, 9362434. [Google Scholar] [CrossRef]
- Longoni, F.; Hägglund, A.; Ripamonti, F.; Pennacchi, P.L.M. Powertrain modal analysis for defining the requirements for a vehicle drivability study. Machines 2022, 10, 1120. [Google Scholar] [CrossRef]
- Peng, F.; Chen, L.; Ye, J.; Yan, F. A method for identifying common and unique issues in body in white dynamic stiffness based on modal contribution analysis. Sci. Rep. 2025, 15, 11911. [Google Scholar] [CrossRef]
- Li, J.; Bao, T.; Ventura, C.E. A robust methodology for output-only modal identification of civil engineering structures. Eng. Struct. 2022, 270, 114764. [Google Scholar] [CrossRef]
- Golnary, F.; Kalhori, H.; Liu, W.; Li, B. Vehicle-based autonomous modal analysis for enhanced bridge health monitoring. Int. J. Mech. Sci. 2025, 287, 109910. [Google Scholar] [CrossRef]
- Bondsman, B.; Peplow, A. Experimental modal analysis and variability assessment in cross-laminated timber. Mech. Syst. Signal Process. 2025, 228, 112466. [Google Scholar] [CrossRef]
- Marciniak, P.; Pawlak, Z.M.; Wyczałek, I. The use of experimental modal analysis in modeling the complex timber structure of a historical building. Appl. Sci. 2024, 14, 8517. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Crittenden, K.; Weiss, L.; Bardaweel, H. Experimental modal analysis and characterization of additively manufactured polymers. Polymers 2022, 14, 2071. [Google Scholar] [CrossRef]
- Yang, H.; Sun, J. Reform and practice of teaching “Structural Dynamics and Its Engineering Applications” Based on the OBE concept. Glob. J. Eng. Sci. 2024, 11, 1–4. [Google Scholar] [CrossRef]
- Vacher, P.; Jacquier, B.; Bucharles, A. Extensions of the MAC criterion to complex modes. In Proceedings of the ISMA2010-USD2010 Conference, Leuven, Belgium, 20–22 September 2010; pp. 2713–2726. Available online: https://past.isma-isaac.be/isma2010/ (accessed on 10 October 2025).
- Worden, K.; Green, P.L. A machine learning approach to nonlinear modal analysis. Mech. Syst. Signal Process. 2015, 84, 34–53. [Google Scholar] [CrossRef]
- Civera, M.; Mugnaini, V.; Fragonara, L.Z. Machine learning-based automatic operational modal analysis: A structural health monitoring application to masonry arch bridges. Struct. Control Health Monit. 2022, 29, e3028. [Google Scholar] [CrossRef]
- Mugnaini, V.; Fragonara, L.Z.; Civera, M. A machine learning approach for automatic operational modal analysis. Mech. Syst. Signal Process. 2022, 170, 108813. [Google Scholar] [CrossRef]
- Mostafaei, H.; Ghamami, M. State of the art in automated operational modal identification: Algorithms, Applications, and Future Perspectives. Machines 2025, 13, 39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).