Advancing Pressure-Based Flow Rate Soft Sensors: Signal Filtering Effects and Non-Laminar Flow Rate Determination
Abstract
1. Introduction
2. Materials and Methods
2.1. Flow Rate Measurement Methods & Models
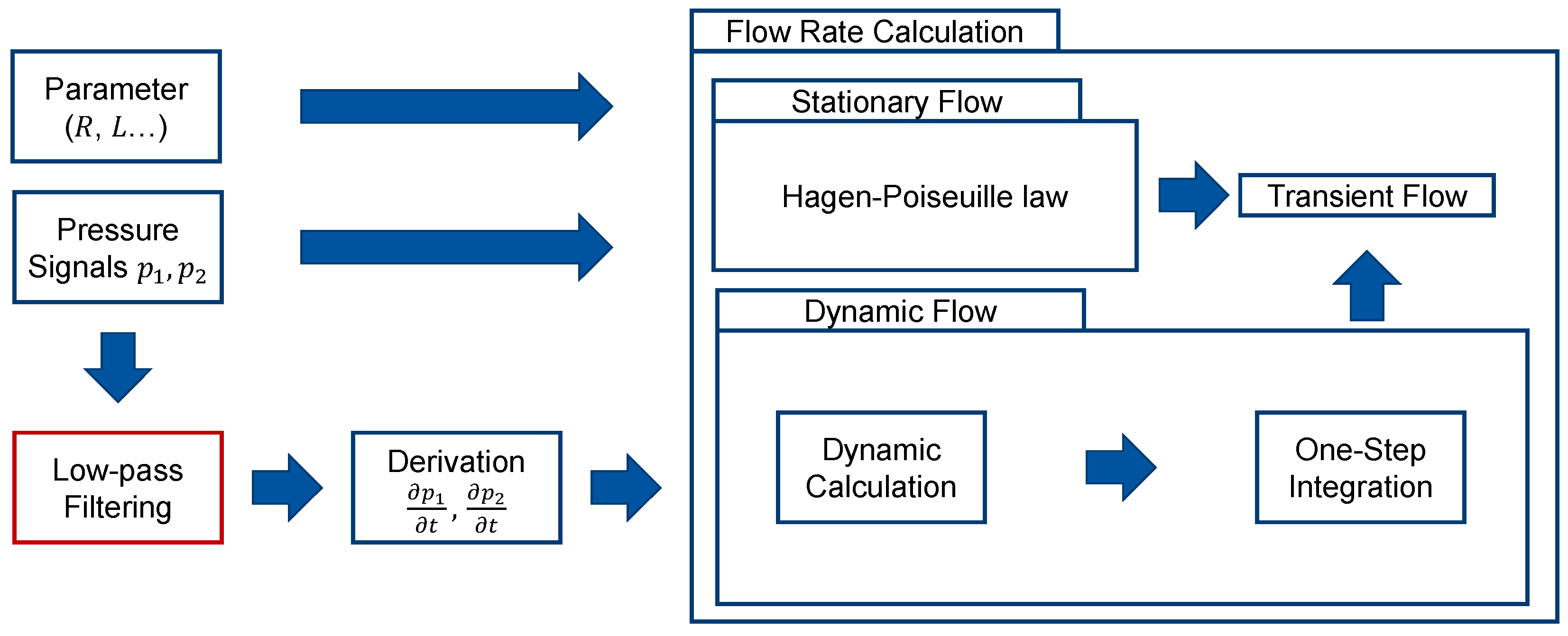
2.2. Pressure-Based Flow Rate Soft Sensor
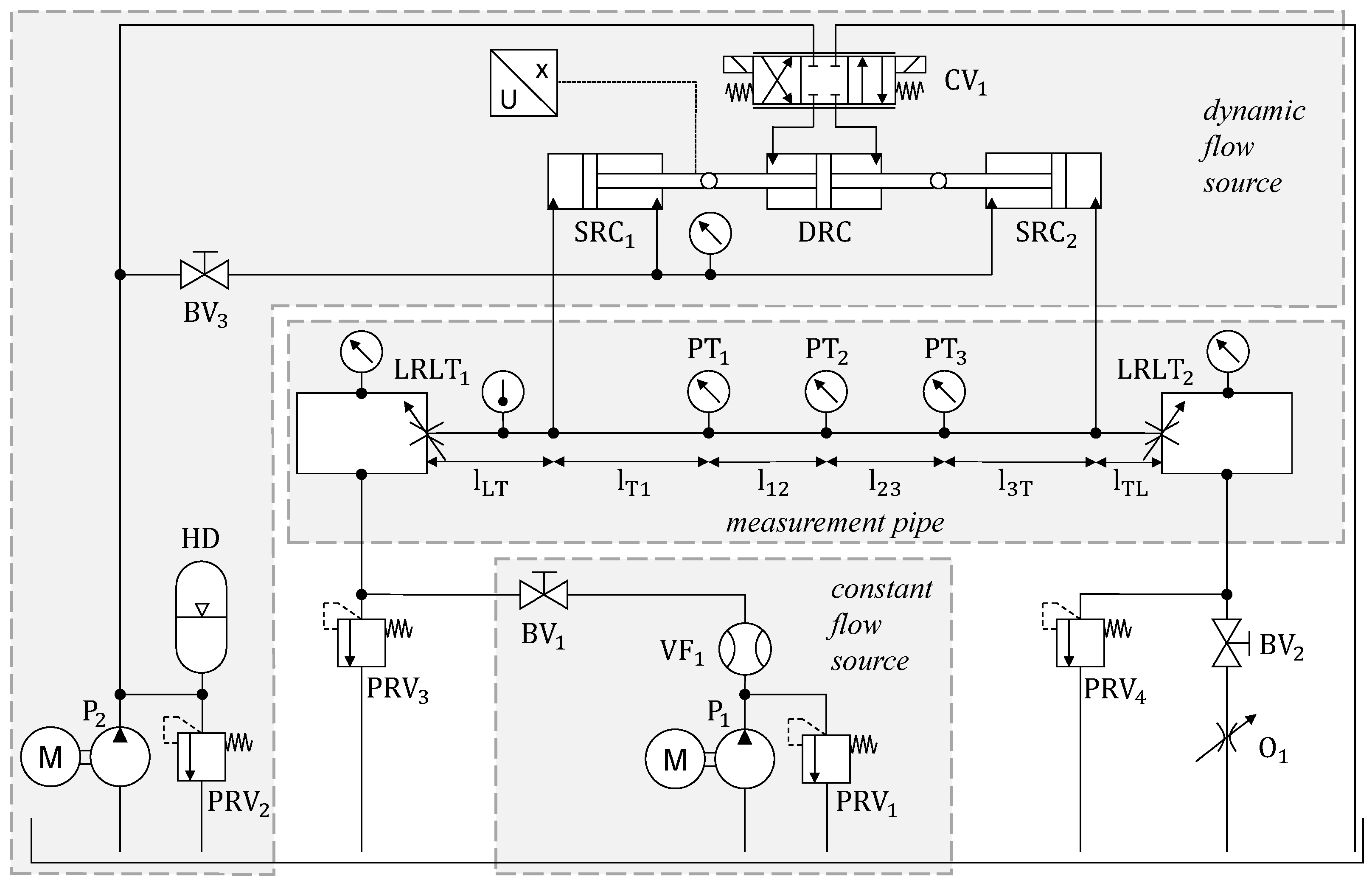
2.3. Test Rig
2.4. Test Cases
3. Results
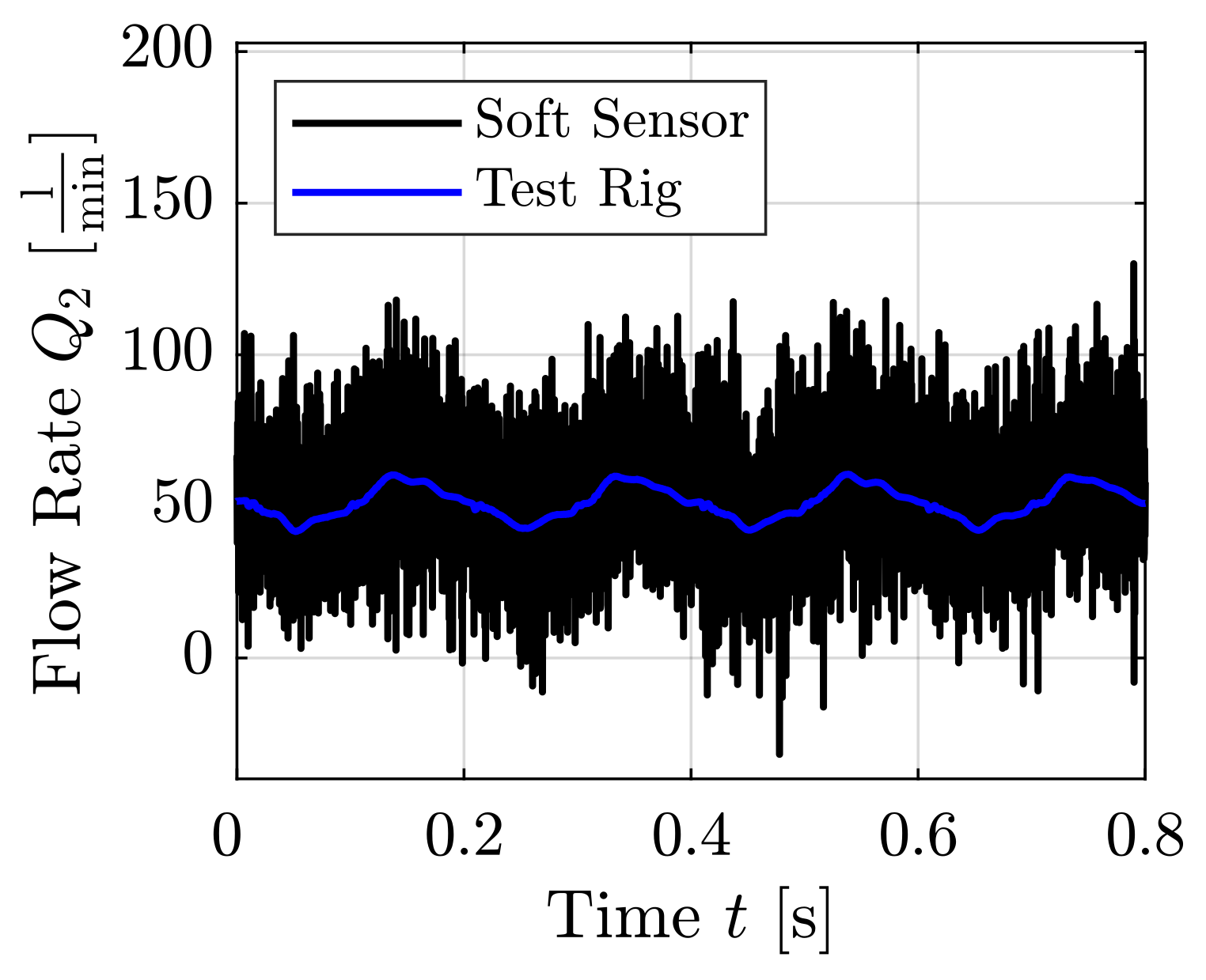
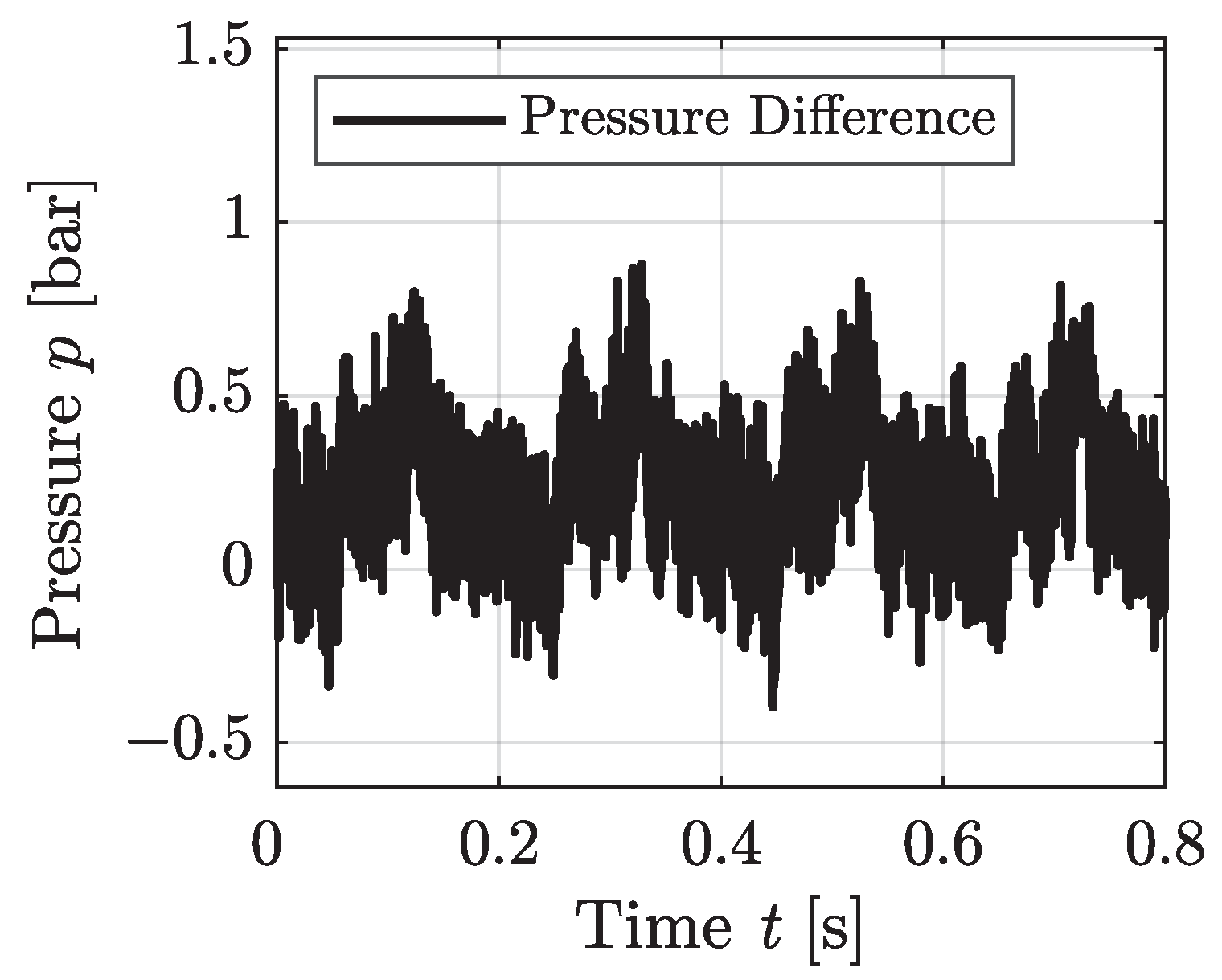
3.1. Laminar Test Cases
3.2. Non-Laminar Test Cases
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BV | Ball Valve |
| CV | Control Valve |
| DRC | Double-rod Cylinder |
| FFT | Fast Fourier Transform |
| HD | Hydraulic Damper |
| HP | Hagen–Poiseuille |
| LRLT | Low-reflection line terminator |
| O | Adjustable Orifice |
| P | Hydraulic Pump |
| PIV | Particle Image Velocimetry |
| PT | Pressure Transducer |
| Re | Reynolds number |
| SRC | Single-rod Cylinder |
| SV | Switching Valve |
| VF | Volumetric Flow Rate Sensor |
Nomenclature
| Symbol | Definition | Unit |
| * | Denotation of a Variable in the Laplace Domain | [/s] |
| A | Cross-section of the Cylinder | [] |
| First Parameter of Temperature-dependent Viscosity Model | [/s] | |
| First Parameter of the Temperature-dependent Density Model | [kg/°] | |
| Geometric Parameter | [] | |
| Cross-section of the Pipe | [] | |
| Second Parameter of the Temperature-dependent Viscosity Model | [−] | |
| Second Parameter of the Temperature-dependent Density Model | [] | |
| C | Third Parameter of Temperature-dependent Viscosity Model | [1/°C] |
| Dissipation Number | [-] | |
| f | Frequency | [Hz] |
| K | Bulk Modulus | [Pa] |
| l | Pipe section length | [m] |
| L | Length of the Pipe | [m] |
| Pressure Difference | [-] | |
| Pressure at Inlet | [bar] | |
| Pressure at Outlet | [bar] | |
| Q | Volumetric Flow Rate | [/s] |
| Volumetric Flow Rate from the Cylinder | [/s] | |
| Mean Volumetric Flow Rate | [/s] | |
| Stationary Volumetric Flow Rate | [/s] | |
| Dynamic Volumetric Flow Rate | [/s] | |
| Volumetric flow rate at Inlet: and Outlet: | [/s] | |
| R | Radius of the Pipe | [m] |
| Reynolds Number | [-] | |
| Hydraulic Resistance | [Pa/(/s)] | |
| t | Time | [s] |
| Normalized Time | [-] | |
| v | Axial Fluid Velocity | [m/s] |
| v | Velocity of the Cylinder | [m/s] |
| Weighting function at End of the Pipe | [-] | |
| Weighting function at port | [-] | |
| Negative of | [-] | |
| Compressible Weighting Function at port 1 | [-] | |
| Incompressible Weighting Function | [-] | |
| Discharge Coefficient | [-] | |
| Dynamic Viscosity | [Pas] | |
| Kinematic Viscosity | [/s] | |
| Fluid Density | [] | |
| Time | [s] | |
| Normalized Time | [s] |
Appendix A. Fluid Model
| Parameter | C | ||||||
|---|---|---|---|---|---|---|---|
| − | − | ||||||
| − | − | − | 1 | 1 |
References
- Richardson, E.G.; Tyler, E. The transverse velocity gradient near the mouths of pipes in which an alternating or continuous flow of air is established. Proc. Phys. Soc. 1929, 42, 1–15. [Google Scholar] [CrossRef]
- Brumand-Poor, F.; Kotte, T.; Pasquini, E.; Kratschun, F.; Enking, J.; Schmitz, K. Unsteady flow rate in transient, incompressible pipe flow. Z. Angew Math Mech. 2024, 105, e202300125. [Google Scholar] [CrossRef]
- Brumand-Poor, F.; Kotte, T.; Pasquini, E.; Schmitz, K. Signal Processing for High-Frequency Flow Rate Determination: An Analytical Soft Sensor Using Two Pressure Signals. Preprints 2024. [Google Scholar] [CrossRef]
- Brumand-Poor, F.; Schüpfer, M.; Merkel, A.; Schmitz, K. Development of a Hydraulic Test Rig for a Virtual Flow Sensor. In Proceedings of the Eighteenth Scandinavian International Conference on Fluid Power (SICFP’23), Tampere, Finland, 30 May–1 June 2023. [Google Scholar]
- Brumand-Poor, F.; Kotte, T.; Schüpfer, M.; Figge, F.; Schmitz, K. High-Frequency Flow Rate Determination—A Pressure-Based Measurement Approach. Preprints 2024. [Google Scholar] [CrossRef]
- Manhartsgruber, B. Instantaneous Liquid Flow Rate Measurement Utilizing the Dynamics of Laminar Pipe Flow. J. Fluids Eng. 2008, 130, 121402. [Google Scholar] [CrossRef]
- Kashima, A.; Lee, P.; Ghidaoui, M. A selective literature review of methods for measuring the flow rate in pipe transient flows. In Proceedings of the BHR Group—11th International Conferences on Pressure Surges, Lisbon, Portugal, 24–26 October 2012; pp. 733–742. [Google Scholar]
- Wiklund, D.; Peluso, M. Quantifying and Specifying the Dynamic Response of Flowmeters. Conf. ISA 2002, 422, 463–476. [Google Scholar]
- Brunone, B.; Berni, A. Wall Shear Stress in Transient Turbulent Pipe Flow by Local Velocity Measurement. J. Hydraul. Eng. 2010, 136, 10. [Google Scholar] [CrossRef]
- Grant, I. Particle image velocimetry: A review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1997, 211, 55–76. [Google Scholar] [CrossRef]
- Brereton, G.J.; Schock, H.J.; Rahi, M.A.A. An indirect pressure-gradient technique for measuring instantaneous flow rates in unsteady duct flows. Exp. Fluids 2006, 40, 238–244. [Google Scholar] [CrossRef]
- Brereton, G.J.; Schock, H.J.; Bedford, J.C. An indirect technique for determining instantaneous flow rate from centerline velocity in unsteady duct flows. Flow Meas. Instrum. 2008, 19, 9–15. [Google Scholar] [CrossRef]
- Sundstrom, L.R.J.; Saemi, S.; Raisee, M.; Cervantes, M.J. Improved frictional modeling for the pressure-time method. Flow Meas. Instrum. 2019, 69, 101604. [Google Scholar] [CrossRef]
- Foucault, E.; Szeger, P. Unsteady flowmeter. Flow Meas. Instrum. 2019, 69, 101607. [Google Scholar] [CrossRef]
- García García, F.J.; Fariñas Alvariño, P. On the analytic explanation of experiments where turbulence vanishes in pipe flow. J. Fluid Mech. 2022, 951, A4. [Google Scholar] [CrossRef]
- García García, F.J.; Fariñas Alvariño, P. On an analytic solution for general unsteady/transient turbulent pipe flow and starting turbulent flow. Eur. J. Mech.-B/Fluids 2019, 74, 200–210. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Stosiak, M.; Deptuła, A.; Karpenko, M. Navier–Stokes Solutions for Accelerating Pipe Flow—A Review of Analytical Models. Energies 2023, 16, 1407. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Stosiak, M.; Karpenko, M.; Bogdevičius, M. Developments in analytical wall shear stress modelling for water hammer phenomena. J. Sound Vib. 2023, 562, 117848. [Google Scholar] [CrossRef]
- Bayle, A.; Rein, F.; Plouraboué, F. Frequency varying rheology-based fluid–structure-interactions waves in liquid-filled visco-elastic pipes. J. Sound Vib. 2023, 562, 117824. [Google Scholar] [CrossRef]
- Bayle, A.; Plouraboue, F. Laplace-Domain Fluid–Structure Interaction Solutions for Water Hammer Waves in a Pipe. J. Hydraul. Eng. 2024, 150, 2. [Google Scholar] [CrossRef]
- Hucko, S.; Krampe, H.; Schmitz, K. Evaluation of a Soft Sensor Concept for Indirect Flow Rate Estimation in Solenoid-Operated Spool Valves. Actuators 2023, 12, 148. [Google Scholar] [CrossRef]
- Butterworth, S. On the Theory of Filter Amplifiers. Exp. Wirel. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Schmitz, K.; Murrenhoff, H. Hydraulik, vollständig neu bearbeitete auflage ed.; Reihe Fluidtechnik; Shaker Verlag: Aachen, Germany, 2018; Volume 2. [Google Scholar]
- Vardy, A.E.; Brown, J.M. Transient Turbulent Friction In Smooth Pipe Flows. J. Sound Vib. 2003, 259, 1011–1036. [Google Scholar] [CrossRef]
- Bartel, D. Simulation von Tribosystemen; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]

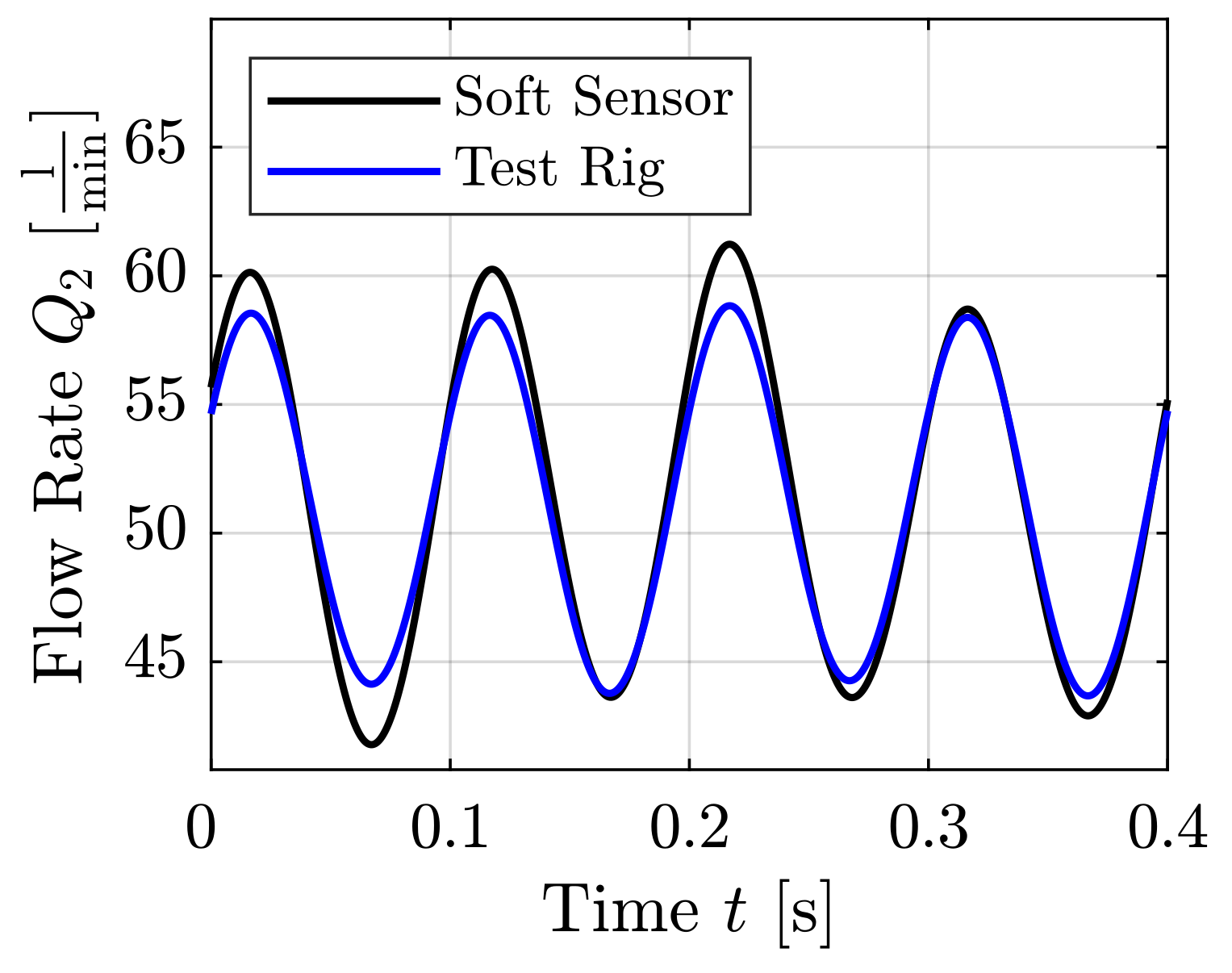
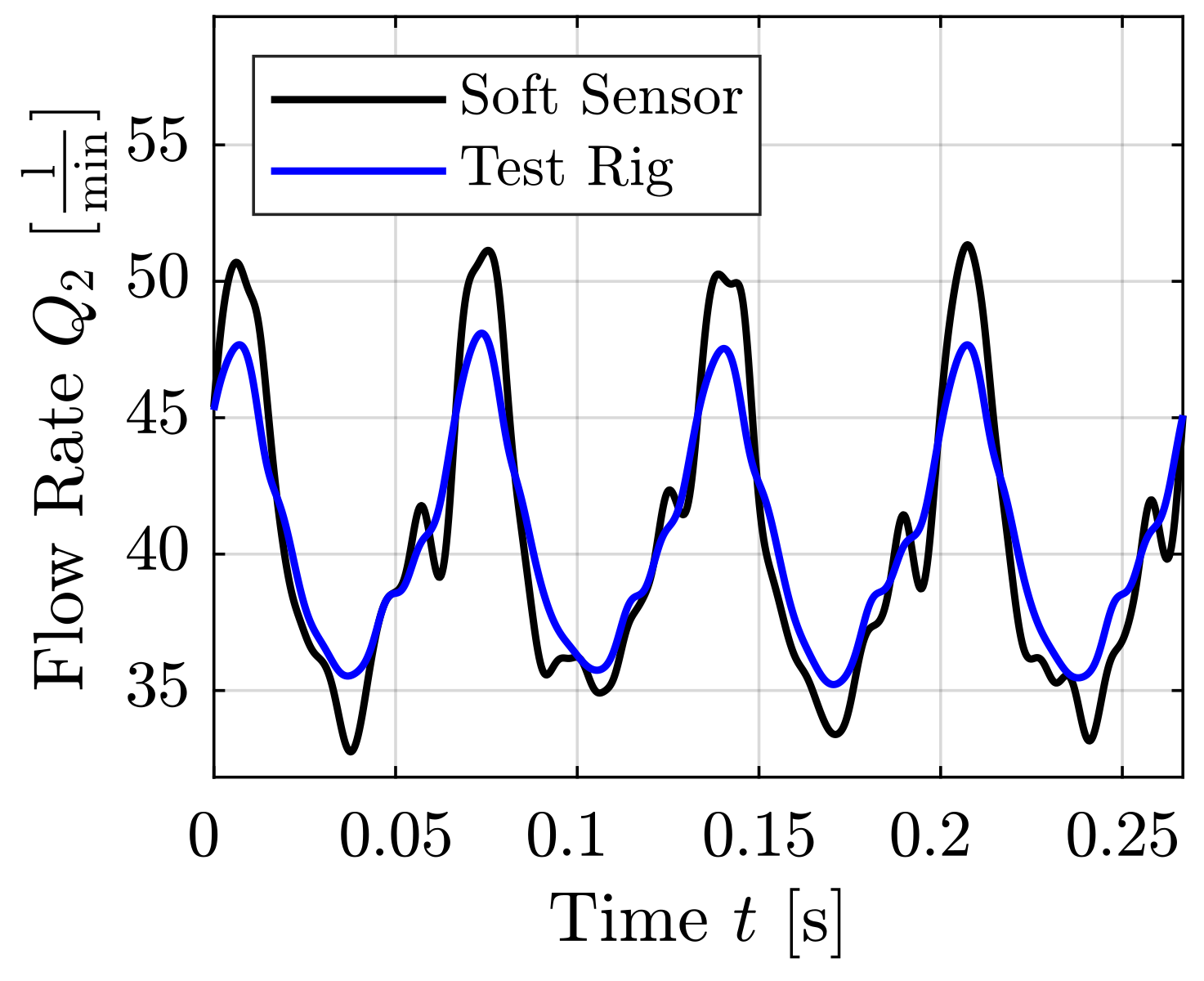
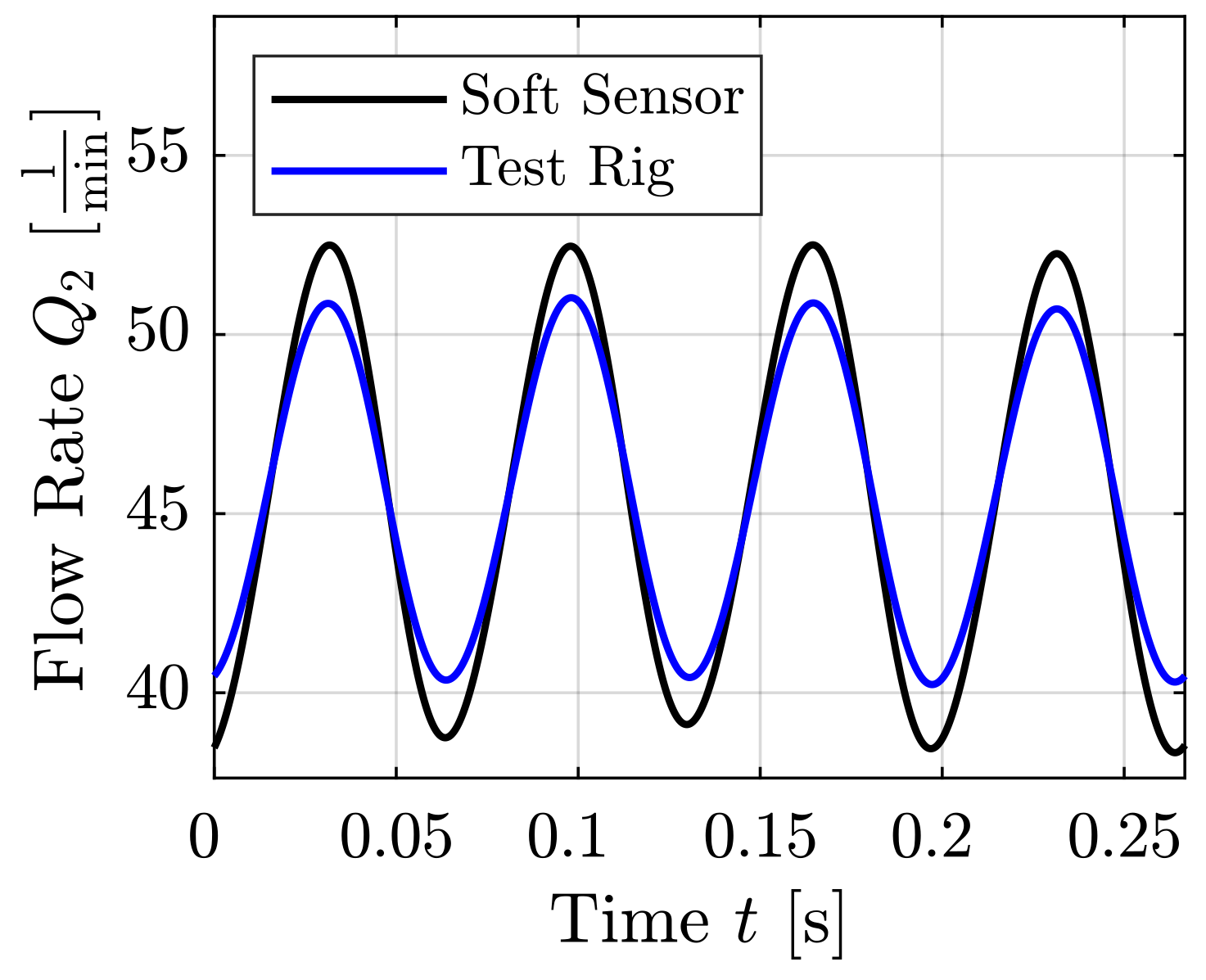
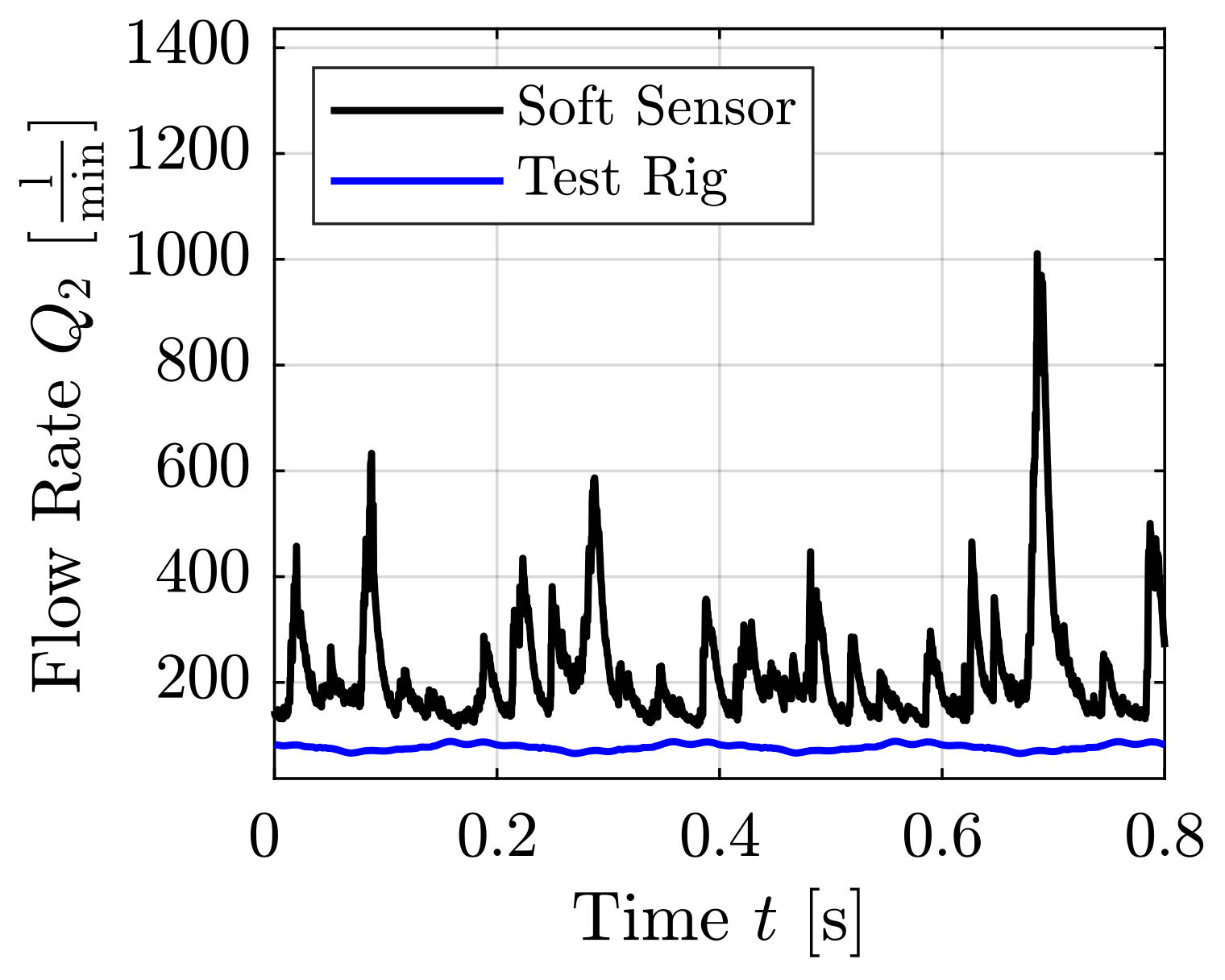

| Test Case | Mean Volumetric Flow Rate [L/min] | Reynolds Number [-] | Frequency f [Hz] | Temperature T [°C] | Kinematic Viscosity [/s] | Density [] |
|---|---|---|---|---|---|---|
| Sine (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8) | 50 | 1339 | 5 | |||
| Sine (Figure 9 and Figure 10) | 50 | 1355 | 10 | 57 | 863 | |
| Sine (Figure 11 and Figure 12) | 50 | 1355 | 15 | 57 | 863 | |
| Sine (Figure 13 and Figure 14) | 77 | 3279 | 5 | 47 | ||
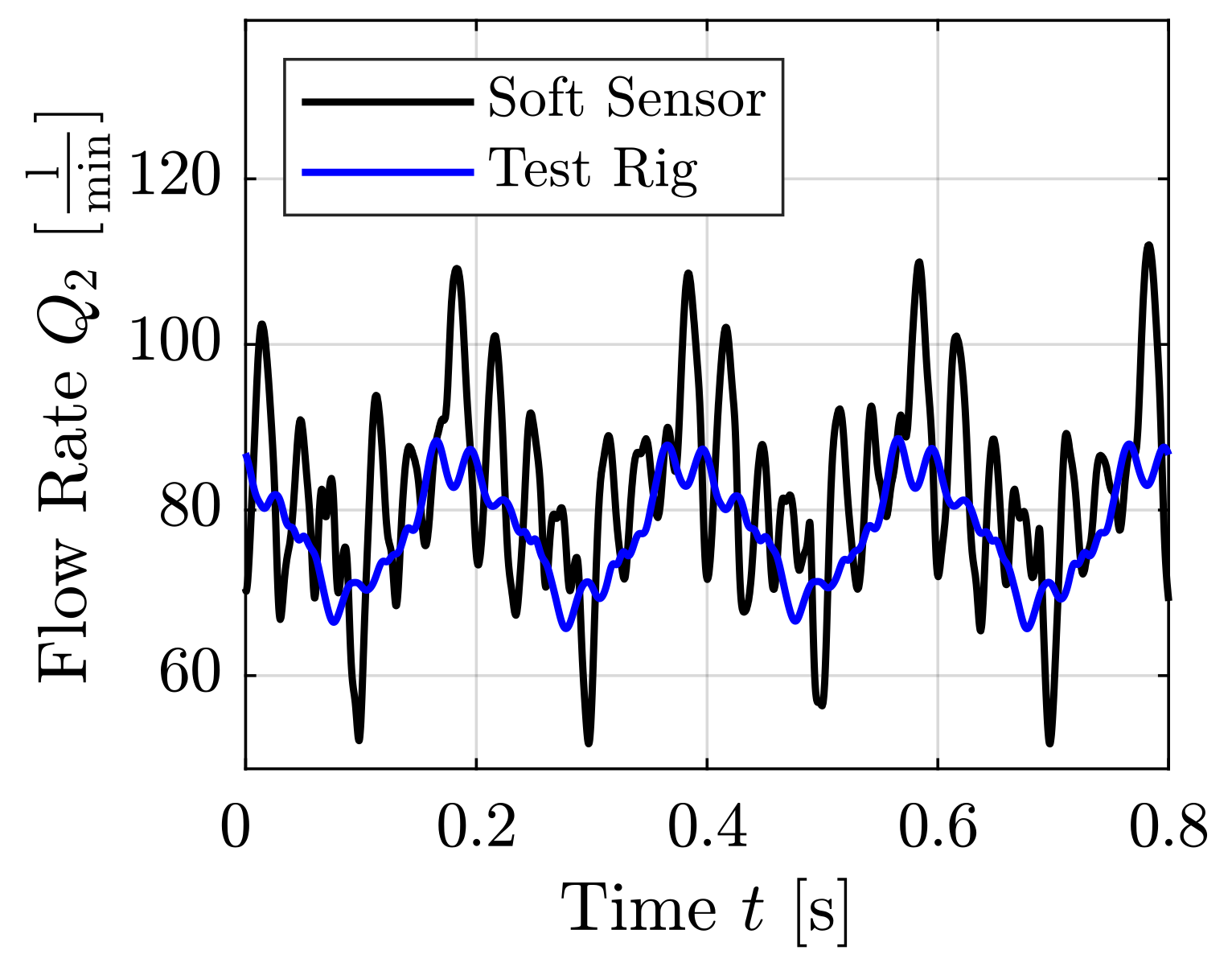
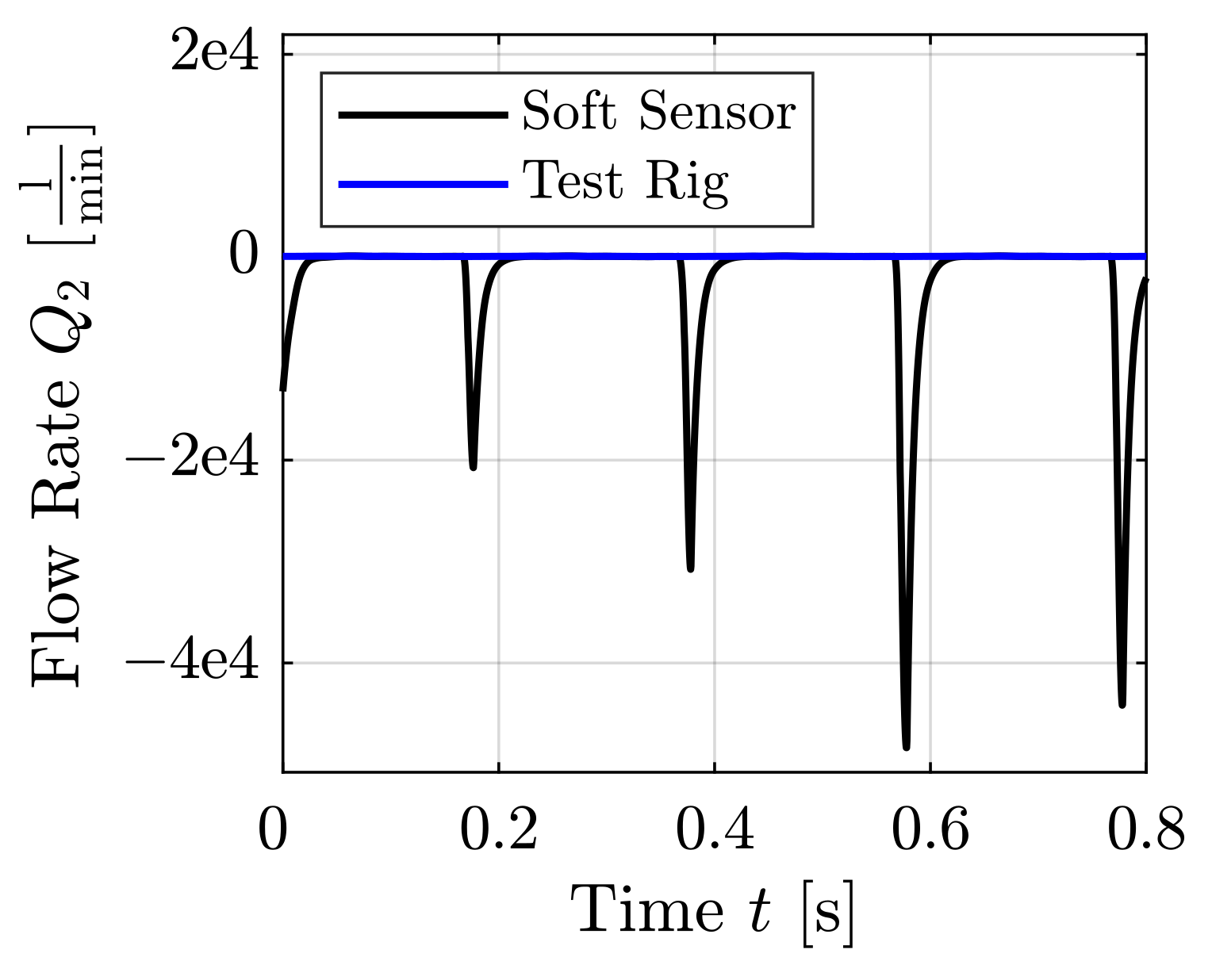
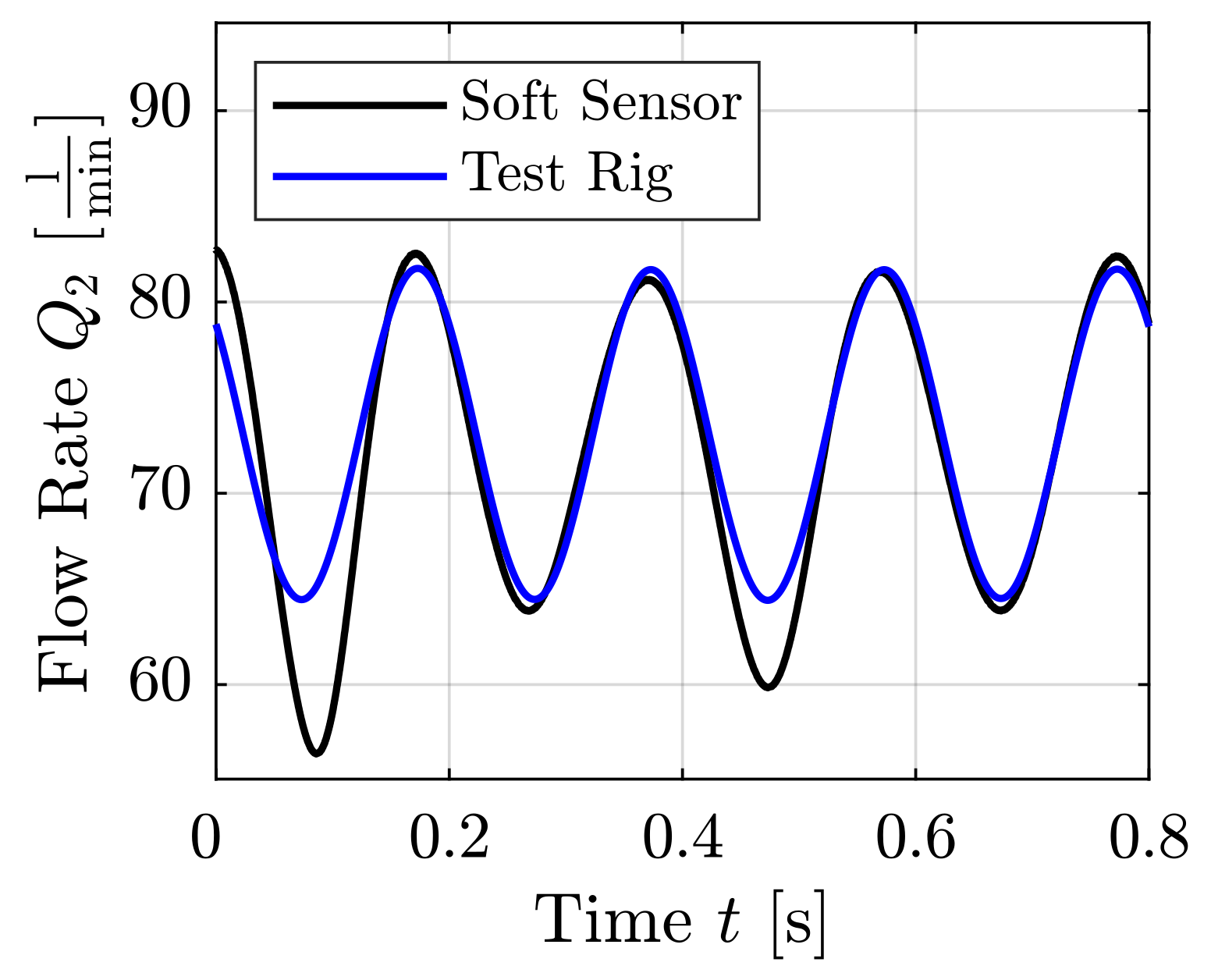
| Sine (Figures 16 and 17) | 86 | 2703 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brumand-Poor, F.; Kotte, T.; Hanifa, A.; Reese, C.; Hofmeister, M.; Schmitz, K. Advancing Pressure-Based Flow Rate Soft Sensors: Signal Filtering Effects and Non-Laminar Flow Rate Determination. J. Exp. Theor. Anal. 2025, 3, 8. https://doi.org/10.3390/jeta3010008
Brumand-Poor F, Kotte T, Hanifa A, Reese C, Hofmeister M, Schmitz K. Advancing Pressure-Based Flow Rate Soft Sensors: Signal Filtering Effects and Non-Laminar Flow Rate Determination. Journal of Experimental and Theoretical Analyses. 2025; 3(1):8. https://doi.org/10.3390/jeta3010008
Chicago/Turabian StyleBrumand-Poor, Faras, Tim Kotte, Abdulaziz Hanifa, Christian Reese, Marius Hofmeister, and Katharina Schmitz. 2025. "Advancing Pressure-Based Flow Rate Soft Sensors: Signal Filtering Effects and Non-Laminar Flow Rate Determination" Journal of Experimental and Theoretical Analyses 3, no. 1: 8. https://doi.org/10.3390/jeta3010008
APA StyleBrumand-Poor, F., Kotte, T., Hanifa, A., Reese, C., Hofmeister, M., & Schmitz, K. (2025). Advancing Pressure-Based Flow Rate Soft Sensors: Signal Filtering Effects and Non-Laminar Flow Rate Determination. Journal of Experimental and Theoretical Analyses, 3(1), 8. https://doi.org/10.3390/jeta3010008






