How Explainable Really Is AI? Benchmarking Explainable AI
Abstract
1. Introduction
2. Related Works
2.1. Verified AI
2.2. Explainable AI
2.2.1. Data Representation Hierarchy
2.2.2. Provenance
2.3. General AI
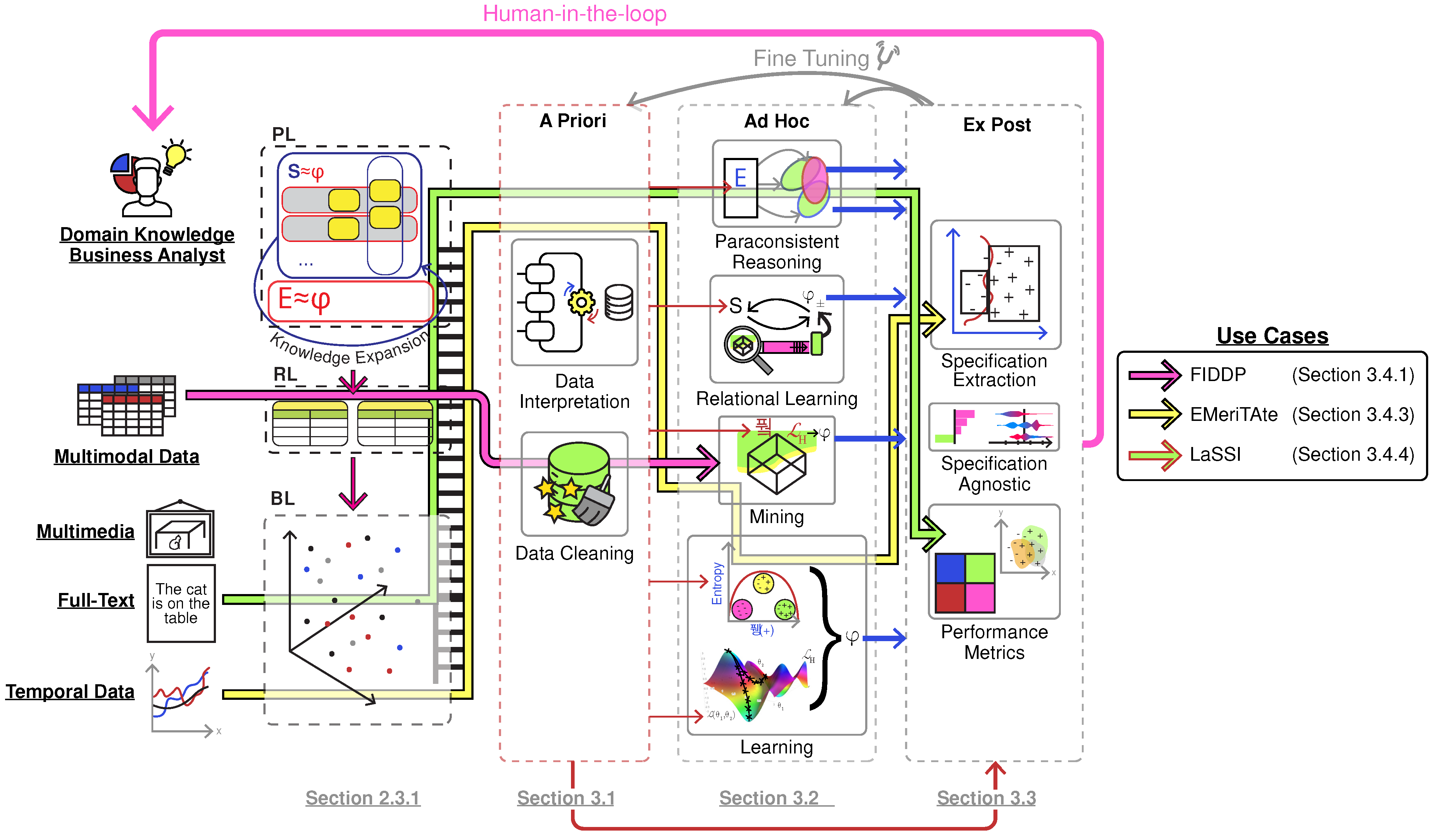
3. A Framework for General, Explainable, and Verified Artificial Intelligence (GEVAI)
3.1. A Priori
3.2. Ad Hoc
3.2.1. Classical Learning
3.2.2. Mining
3.2.3. Relational Learning
3.2.4. Paraconsistent Reasoning
3.3. Ex Post
3.3.1. Performance Metrics
3.3.2. Specification Agnostic
3.3.3. Extractors
3.4. Hybrid Explainability
3.4.1. Financial Institution DeDuplication Pipeline (FIDDP)
3.4.2. Automating AI Benchmarking with AV-GEVAI
3.4.3. (DataFul)Explainable Multivariate Correlational Temporal Artificial Intelligence (EMeriTAte+DF)
3.4.4. Logical, Structural, and Semantic Text Interpretation (LaSSI)
4. Evaluation
4.1. AV-GEVAI
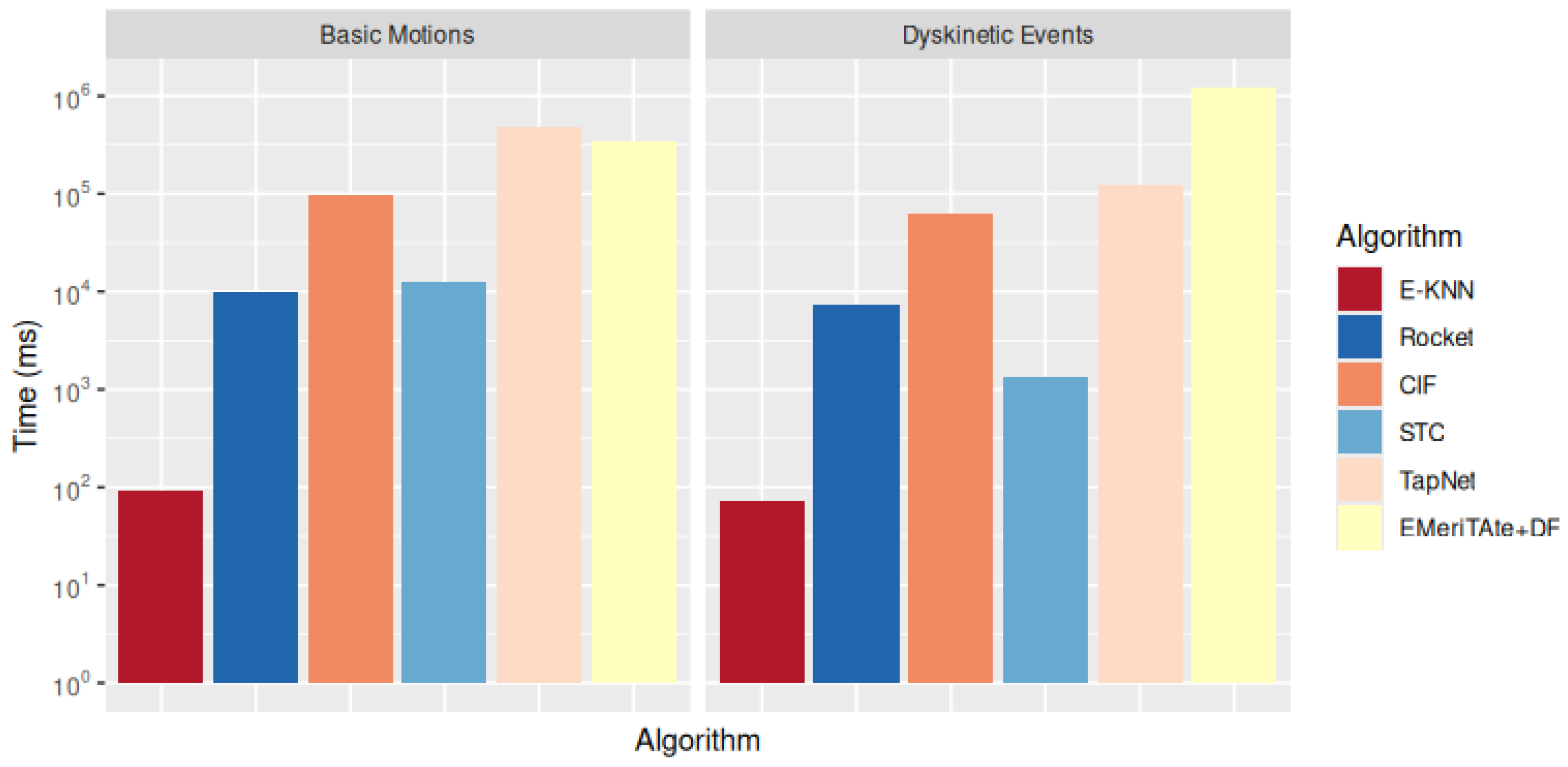
4.1.1. Efficiency
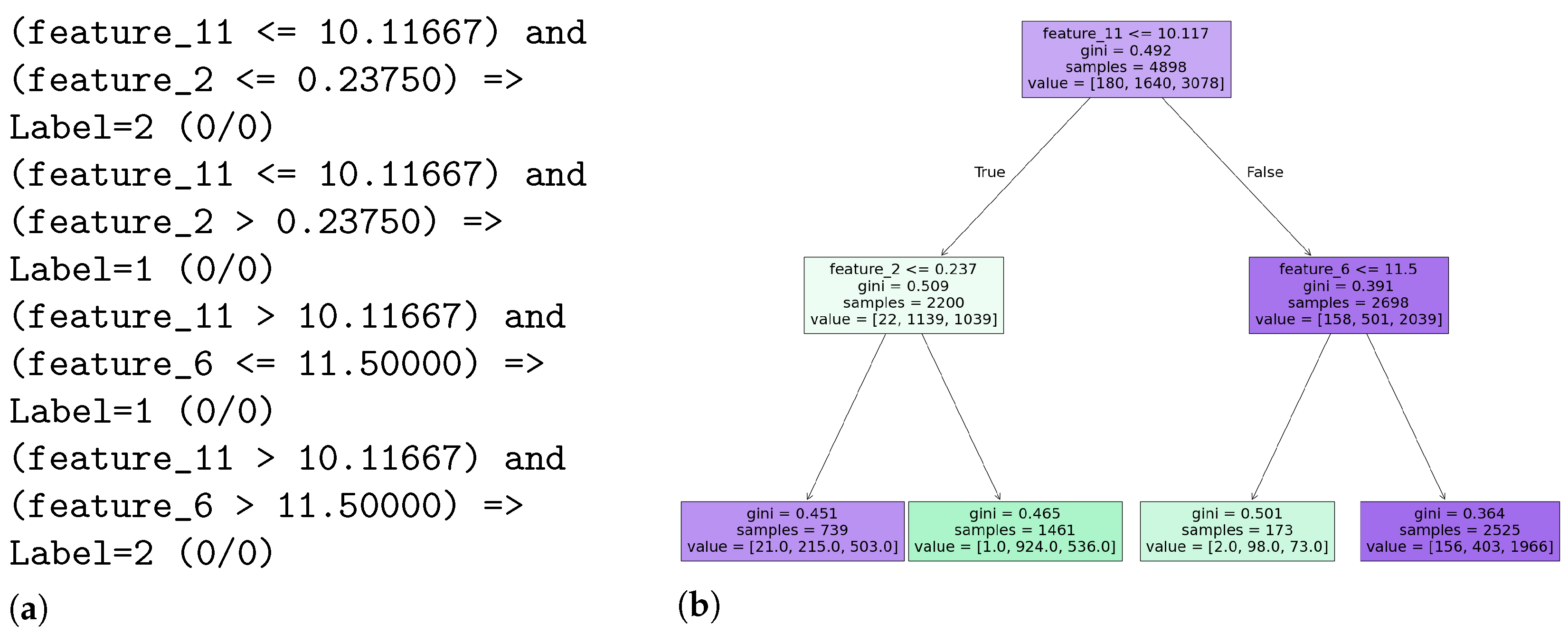
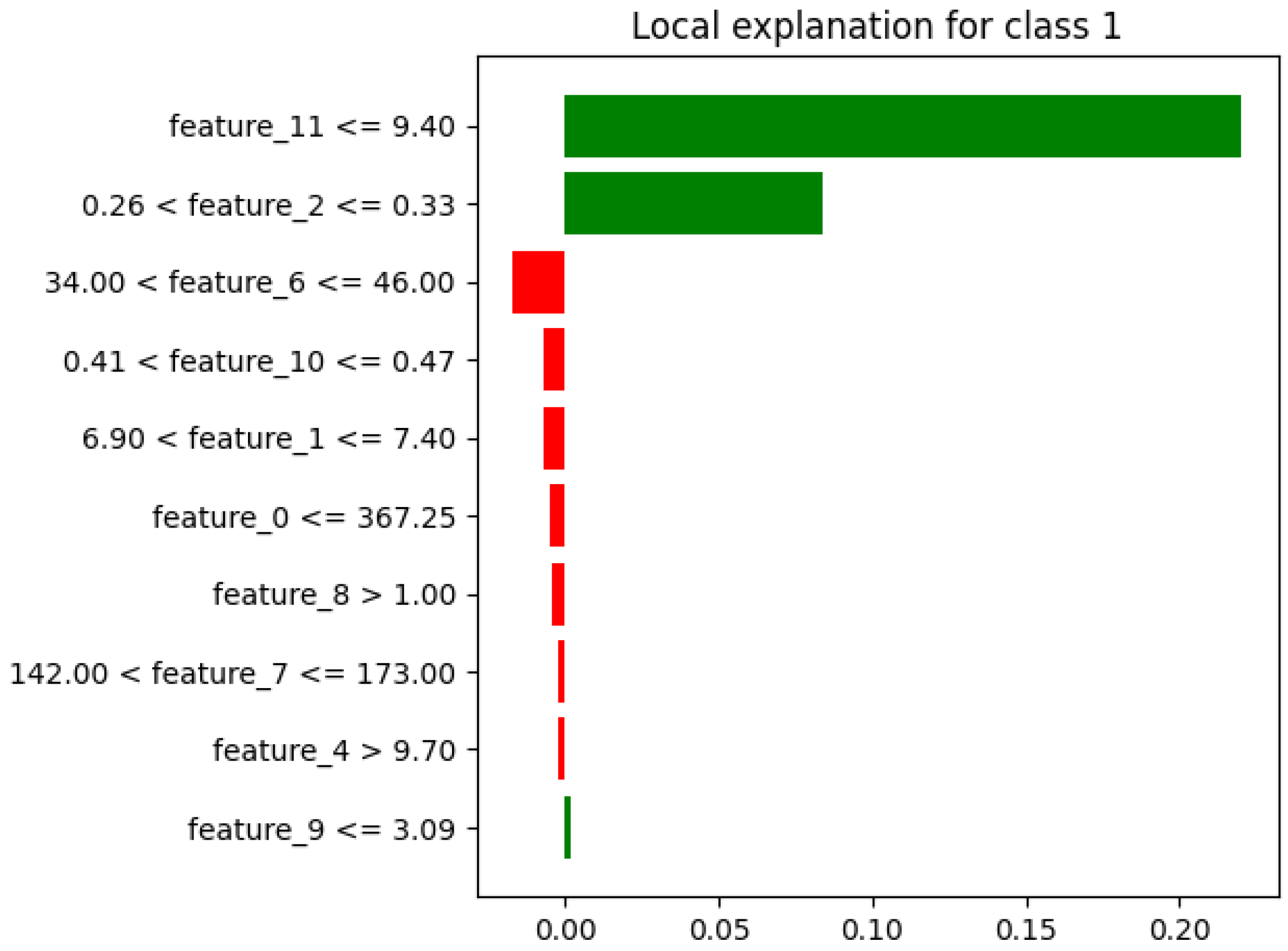
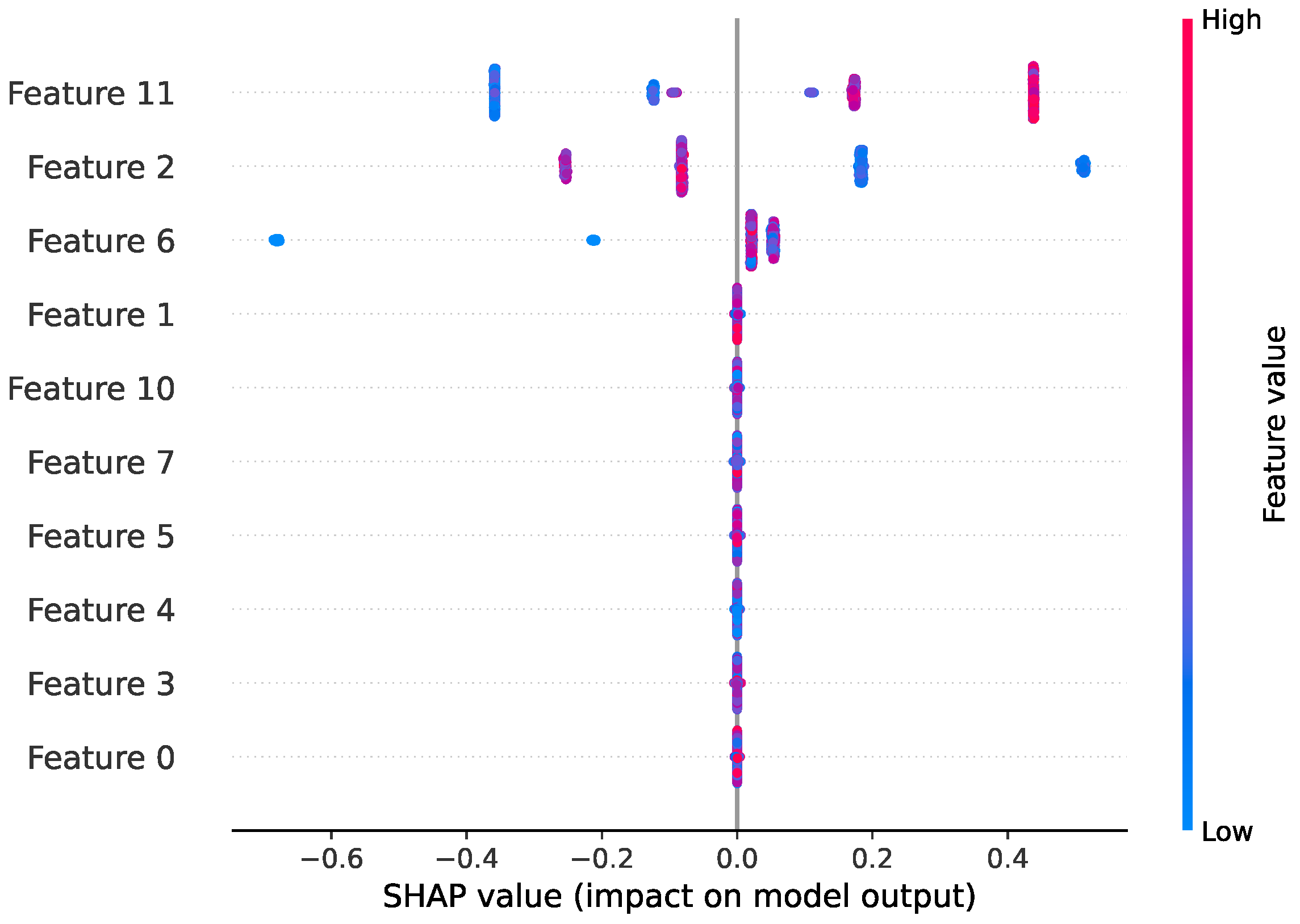
4.1.2. Explainability
Performance Metrics
Extractors
Specification Agnostic
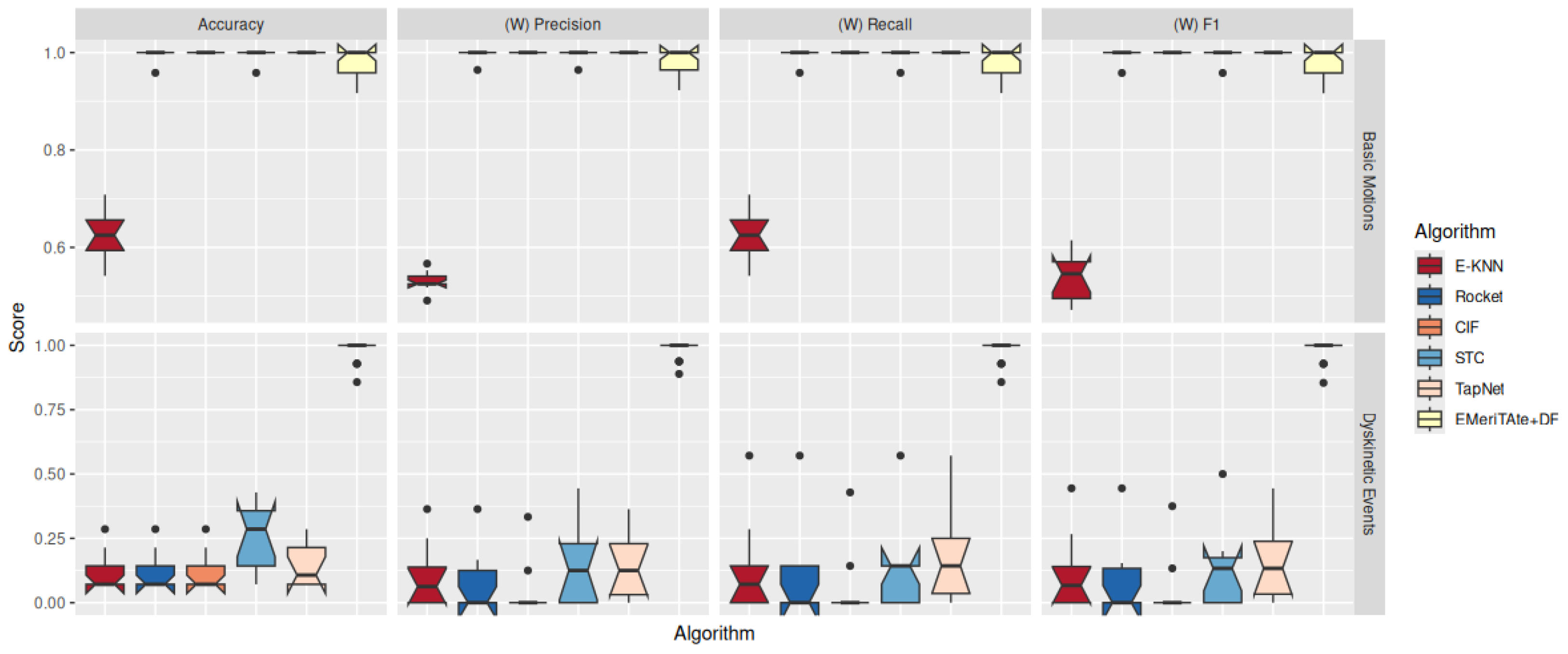
4.2. (DataFul) Explainable Multivariate Correlational Temporal Artificial Intelligence (EMeriTAte)
4.3. Logical, Structural, and Semantic Text Interpretation (LaSSI)
5. Discussion and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bergami, G.; Fox, O.R.; Morgan, G. Extracting Specifications Through Verified and Explainable AI: Interpretability, Interoperability, and Trade-Offs. In Explainable Artificial Intelligence for Trustworthy Decisions in Smart Applications; Springer: Cham, Switzerland, 2025; Chapter 2; in press. [Google Scholar]
- Seshia, S.A.; Sadigh, D.; Sastry, S.S. Toward verified artificial intelligence. Commun. AC2 2022, 65, 46–55. [Google Scholar] [CrossRef]
- van der Aalst, W.M.P. Process Mining-Data Science in Action, Second Edition; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Bergami, G.; Maggi, F.M.; Montali, M.; Peñaloza, R. A Tool for Computing Probabilistic Trace Alignments. In Proceedings of the Intelligent Information Systems-CAiSE Forum 2021, Melbourne, VIC, Australia, 28 June–2 July 2021; Nurcan, S., Korthaus, A., Eds.; Lecture Notes in Business Information Processing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 424, pp. 118–126. [Google Scholar]
- Bergami, G.; Maggi, F.M.; Marrella, A.; Montali, M. Aligning Data-Aware Declarative Process Models and Event Logs. In Business Process Management; Polyvyanyy, A., Wynn, M.T., Van Looy, A., Reichert, M., Eds.; Springer: Cham, Switzerland, 2021; pp. 235–251. [Google Scholar]
- Megill, J.L. Are we paraconsistent? On the Luca-Penrose argument and the computational theory of mind. Auslegung J. Philos. 2019, 27, 23–30. [Google Scholar] [CrossRef]
- LaForte, G.; Hayes, P.J.; Ford, K.M. Why Gödel’s theorem cannot refute computationalism. Artif. Intell. 1998, 104, 265–286. [Google Scholar] [CrossRef]
- Bergami, G.; Packer, E.; Scott, K.; Del Din, S. Predicting Dyskinetic Events Through Verified Multivariate Time Series Classification. In Database Engineered Applications; Chbeir, R., Ilarri, S., Manolopoulos, Y., Revesz, P.Z., Bernardino, J., Leung, C.K., Eds.; Springer: Cham, Switzerland, 2025; pp. 49–62. [Google Scholar]
- Bergami, G.; Packer, E.; Scott, K.; Del Din, S. Towards Explainable Sequential Learning. arXiv 2025, arXiv:2505.23624. [Google Scholar]
- Camacho, A.; Toro Icarte, R.; Klassen, T.Q.; Valenzano, R.; McIlraith, S.A. LTL and Beyond: Formal Languages for Reward Function Specification in Reinforcement Learning. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, Macao, China, 10–16 August 2019; Volume 7, pp. 6065–6073. [Google Scholar]
- Maltoni, D.; Lomonaco, V. Continuous learning in single-incremental-task scenarios. Neural Netw. 2019, 116, 56–73. [Google Scholar] [CrossRef] [PubMed]
- Tammet, T.; Järv, P.; Verrev, M.; Draheim, D. An Experimental Pipeline for Automated Reasoning in Natural Language (Short Paper). In Automated Deduction–CADE 29; Pientka, B., Tinelli, C., Eds.; Springer: Cham, Switzerland, 2023; pp. 509–521. [Google Scholar]
- Zini, J.E.; Awad, M. On the Explainability of Natural Language Processing Deep Models. ACM Comput. Surv. 2023, 55, 103:1–103:31. [Google Scholar] [CrossRef]
- Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G.; et al. Explainable AI (XAI): Core Ideas, Techniques, and Solutions. ACM Comput. Surv. 2023, 55, 1–33. [Google Scholar] [CrossRef]
- de Raedt, L. Logical and Relational Learning: From ILP to MRDM (Cognitive Technologies); Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Bergami, G.; Fox, O.R.; Morgan, G. Matching and Rewriting Rules in Object-Oriented Databases. Mathematics 2024, 12, 2677. [Google Scholar] [CrossRef]
- Elmasri, R.A.; Navathe, S.B. Fundamentals of Database Systems, 7th ed.; Pearson: London, UK, 2016. [Google Scholar]
- Johnson, J. Hypernetworks in the Science of Complex Systems; Imperial College Press: London, UK, 2011. [Google Scholar]
- Fuhr, N.; Rölleke, T. A Probabilistic Relational Algebra for the Integration of Information Retrieval and Database Systems. ACM Trans. Inf. Syst. 1997, 15, 32–66. [Google Scholar] [CrossRef]
- Andrzejewski, W.; Bębel, B.; Boiński, P.; Wrembel, R. On tuning parameters guiding similarity computations in a data deduplication pipeline for customers records: Experience from a R&D project. Inf. Syst. 2024, 121, 102323. [Google Scholar]
- Rekatsinas, T.; Chu, X.; Ilyas, I.F.; Ré, C. HoloClean: Holistic Data Repairs with Probabilistic Inference. Proc. VLDB Endow. 2017, 10, 1190–1201. [Google Scholar] [CrossRef]
- D’Agostino, G.; Reed, C.A.; Puccinelli, D. Segmentation of Complex Question Turns for Argument Mining: A Corpus-based Study in the Financial Domain. In Proceedings of the 2024 Joint International Conference on Computational Linguistics, Language Resources and Evaluation, LREC/COLING 2024, Torino, Italy, 20–25 May 2024; pp. 14524–14530. [Google Scholar]
- Green, T.J.; Karvounarakis, G.; Tannen, V. Provenance semirings. In Proceedings of the Twenty-Sixth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, New York, NY, USA, 11–13 June 2007; pp. 31–40. [Google Scholar]
- Harrison, J. Handbook of Practical Logic and Automated Reasoning; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Clocksin, W.F.; Mellish, C.S. Programming in Prolog, 4th ed.; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Chapman, A.; Lauro, L.; Missier, P.; Torlone, R. Supporting Better Insights of Data Science Pipelines with Fine-grained Provenance. ACM Trans. Database Syst. 2024, 49, 6:1–6:42. [Google Scholar] [CrossRef]
- Ferrucci, D.A. Introduction to “This is Watson”. Ibm J. Res. Dev. 2012, 56, 1:1–1:15. [Google Scholar] [CrossRef]
- Goertzel, B. Artificial General Intelligence: Concept, State of the Art, and Future Prospects. J. Artif. Gen. Intell. 2014, 5, 1–48. [Google Scholar] [CrossRef]
- Searle, J.R. Minds, brains, and programs. In Mind Design; MIT Press: Cambridge, MA, USA, 1985; pp. 282–307. [Google Scholar]
- Bubeck, S.; Chandrasekaran, V.; Eldan, R.; Gehrke, J.; Horvitz, E.; Kamar, E.; Lee, P.; Lee, Y.T.; Li, Y.; Lundberg, S.M.; et al. Sparks of Artificial General Intelligence: Early experiments with GPT-4. arXiv 2023, arXiv:2303.12712. [Google Scholar]
- Dhar, V. The Paradigm Shifts in Artificial Intelligence. Commun. ACM 2024, 67, 50–59. [Google Scholar] [CrossRef]
- Hicks, M.T.; Humphries, J.; Slater, J. ChatGPT is bullshit. Ethics Inf. Technol. 2024, 26, 38. [Google Scholar] [CrossRef]
- Bender, E.M.; Gebru, T.; McMillan-Major, A.; Shmitchell, S. On the Dangers of Stochastic Parrots: Can Language Models Be Too Big? In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, New York, NY, USA, 3–10 March 2021; pp. 610–623. [Google Scholar]
- Chen, Y.; Wang, D.Z. Knowledge expansion over probabilistic knowledge bases. In Proceedings of the International Conference on Management of Data, SIGMOD 2014, Snowbird, UT, USA, 22–27 June 2014; Dyreson, C.E., Li, F., Özsu, M.T., Eds.; ACM: New York, NY, USA, 2014; pp. 649–660. [Google Scholar]
- Bergami, G. A framework supporting imprecise queries and data. arXiv 2019, arXiv:1912.12531. [Google Scholar]
- Kyburg, H.E. Probability and the Logic of Rational Belief; Wesleyan University Press: Middletown, CT, USA, 1961. [Google Scholar]
- Brown, B. Inconsistency measures and paraconsistent consequence. In Measuring Inconsistency in Information; Grant, J., Martinez, M.V., Eds.; College Press: Harare, Zimbabwe, 2018; Chapter 8; pp. 219–234. [Google Scholar]
- Graydon, M.S.; Lehman, S.M. Examining Proposed Uses of LLMs to Produce or Assess Assurance Arguments. NTRS-NASA Technical Reports Server: Washington, DC, USA, 2025. [Google Scholar]
- Bergami, G. Towards automating microservices orchestration through data-driven evolutionary architectures. Serv. Oriented Comput. Appl. 2024, 18, 1–12. [Google Scholar] [CrossRef]
- Niles, I.; Pease, A. Towards a standard upper ontology. In Proceedings of the 2nd International Conference on Formal Ontology in Information Systems, FOIS, Ogunquit, ME, USA, 17–19 October 2001; ACM: New York, NY, USA, 2001; pp. 2–9. [Google Scholar] [CrossRef]
- Yu, Z.; Chu, X. PIClean: A Probabilistic and Interactive Data Cleaning System. In Proceedings of the 2019 International Conference on Management of Data, SIGMOD Conference 2019, Amsterdam, The Netherlands, 30 June–5 July 2019; Boncz, P.A., Manegold, S., Ailamaki, A., Deshpande, A., Kraska, T., Eds.; ACM: New York, NY, USA, 2019; pp. 2021–2024. [Google Scholar]
- Picado, J.; Davis, J.; Termehchy, A.; Lee, G.Y. Learning Over Dirty Data Without Cleaning. In Proceedings of the 2020 International Conference on Management of Data, SIGMOD Conference 2020, online conference, Portland, OR, USA, 14–19 June 2020; Maier, D., Pottinger, R., Doan, A., Tan, W., Alawini, A., Ngo, H.Q., Eds.; ACM: New York, NY, USA, 2020; pp. 1301–1316. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models—Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Jäger, S.; Allhorn, A.; Bießmann, F. A Benchmark for Data Imputation Methods. Front. Big Data 2021, 4, 693674. [Google Scholar] [CrossRef]
- Dallachiesa, M.; Ebaid, A.; Eldawy, A.; Elmagarmid, A.; Ilyas, I.F.; Ouzzani, M.; Tang, N. NADEEF: A commodity data cleaning system. In Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 541–552. [Google Scholar]
- Euzenat, J.; Shvaiko, P. Ontology Matching, Second Edition; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Groß, A.; Hartung, M.; Kirsten, T.; Rahm, E. Mapping Composition for Matching Large Life Science Ontologies. In Proceedings of the 2nd International Conference on Biomedical Ontology, Buffalo, NY, USA, 26–30 July 2011. [Google Scholar]
- Melnik, S. Generic Model Management: Concepts and Algorithms; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2967. [Google Scholar]
- Buchanan, B.G.; Shortliffe, E.H. Rule-Based Expert Systems: The MYCIN Experiments of the Stanford Heuristic Programming Project; Addison-Wesley: Boston, MA, USA, 1984. [Google Scholar]
- Xie, X.; Chang, J.; Kassem, M.; Parlikad, A. Resolving inconsistency in building information using uncertain knowledge graphs: A case of building space management. In Proceedings of the 2023 European Conference on Computing in Construction and the 40th International CIB W78 Conference, Heraklion, Greece, 10–12 July 2023; Computing in Construction. Volume 4. [Google Scholar]
- Finkel, J.R.; Manning, C.D. Nested Named Entity Recognition. In Proceedings of the 2009 Conference on Empirical Methods in Natural Language Processing, EMNLP 2009, Singapore, 6–7 August 2009; A Meeting of SIGDAT, a Special Interest Group of the ACL. ACL: Cambridge, MA, USA, 2009; pp. 141–150. [Google Scholar]
- Detroja, K.; Bhensdadia, C.; Bhatt, B.S. A survey on Relation Extraction. Intell. Syst. Appl. 2023, 19, 200244. [Google Scholar] [CrossRef]
- Fox, O.R.; Bergami, G.; Morgan, G. LaSSI: Logical, Structural, and Semantic Text Interpretation. In Database Engineered Applications; Chbeir, R., Ilarri, S., Manolopoulos, Y., Revesz, P.Z., Bernardino, J., Leung, C.K., Eds.; Springer: Cham, Switzerland, 2025; pp. 106–121. [Google Scholar]
- Fox, O.R.; Bergami, G.; Morgan, G. Verified Language Processing with Hybrid Explainability. arXiv 2025, arXiv:2507.05017. [Google Scholar]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object Detection With Deep Learning: A Review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef]
- Wang, L.; Lin, P.; Cheng, J.; Liu, F.; Ma, X.; Yin, J. Visual relationship detection with recurrent attention and negative sampling. Neurocomputing 2021, 434, 55–66. [Google Scholar] [CrossRef]
- Hastie, T.; Friedman, J.H.; Tibshirani, R. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Eliason, S.R. Maximum Likelihood Estimation: Logic and Practice; SAGE: Thousand Oaks, CA, USA, 1993. [Google Scholar]
- von Winterfeldt, D.; Edwards, W. Decision Analysis and Behavioral Research; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Zaki, M.J.; Meira, W., Jr. Data Mining and Machine Learning: Fundamental Concepts and Algorithms, 2nd ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Feurer, M.; Hutter, F. Hyperparameter optimization. In AutoML: Methods, Systems, Challenges; Hutter, F., Kotthoff, L., Vanschoren, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Chapter 6; pp. 113–134. [Google Scholar]
- Romero, E. Benchmarking the selection of the hidden-layer weights in extreme learning machines. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1607–1614. [Google Scholar] [CrossRef]
- Prates, M.; Avelar, P.H.C.; Lemos, H.; Lamb, L.C.; Vardi, M.Y. Learning to solve NP-complete problems: A graph neural network for decision TSP. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; AAAI’19/IAAI’19/EAAI’19. AAAI Press: Washington, DC, USA, 2019. [Google Scholar]
- de Raedt, L.; Bruynooghe, M. A unifying framework for concept-learning algorithms. Knowl. Eng. Rev. 1992, 7, 251–269. [Google Scholar] [CrossRef]
- Bergami, G.; Appleby, S.; Morgan, G. Specification Mining over Temporal Data. Computers 2023, 12, 185. [Google Scholar] [CrossRef]
- Petermann, A.; Micale, G.; Bergami, G.; Pulvirenti, A.; Rahm, E. Mining and ranking of generalized multi-dimensional frequent subgraphs. In Proceedings of the Twelfth International Conference on Digital Information Management, ICDIM 2017, Fukuoka, Japan, 12–14 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 236–245. [Google Scholar]
- Vosoughi, S.; Roy, D.; Aral, S. The spread of true and false news online. Science 2018, 359, 1146–1151. Available online: https://www.science.org/doi/pdf/10.1126/science.aap9559 (accessed on 28 July 2025). [CrossRef] [PubMed]
- Picado, J.; Termehchy, A.; Fern, A.; Ataei, P. Logical scalability and efficiency of relational learning algorithms. VLDB J. 2019, 28, 147–171. [Google Scholar] [CrossRef]
- Zhang, T.; Subburathinam, A.; Shi, G.; Huang, L.; Lu, D.; Pan, X.; Li, M.; Zhang, B.; Wang, Q.; Whitehead, S.; et al. GAIA - A Multi-media Multi-lingual Knowledge Extraction and Hypothesis Generation System. In Proceedings of the2018 Text Analysis Conference, TAC 2018, Gaithersburg, MD, USA, 13–14 November 2018; NIST: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Eiter, T.; Gottlob, G. On the Computational Cost of Disjunctive Logic Programming: Propositional Case. Ann. Math. Artif. Intell. 1995, 15, 289–323. [Google Scholar] [CrossRef]
- Malouf, R. Maximal Consistent Subsets. Comput. Linguist. 2007, 33, 153–160. Available online: https://direct.mit.edu/coli/article-pdf/33/2/153/1798390/coli.2007.33.2.153.pdf (accessed on 28 July 2025). [CrossRef]
- Hunter, A.; Konieczny, S. Measuring Inconsistency through Minimal Inconsistent Sets. In Proceedings of the Principles of Knowledge Representation and Reasoning: Proceedings of the Eleventh International Conference, KR 2008, Sydney, Australia, 16–19 September 2008; Brewka, G., Lang, J., Eds.; AAAI Press: Washington, DC, USA, 2008; pp. 358–366. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Krishnapuram, B., Shah, M., Smola, A.J., Aggarwal, C.C., Shen, D., Rastogi, R., Eds.; ACM: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-Precision Model-Agnostic Explanations. Proc. AAAI Conf. Artif. Intell. 2018, 32, 1527–1535. [Google Scholar] [CrossRef]
- Watson, D.S.; O’Hara, J.; Tax, N.; Mudd, R.; Guy, I. Explaining Predictive Uncertainty with Information Theoretic Shapley Values. In Proceedings of the Advances in Neural Information Processing Systems 36: Annual Conference on Neural Information Processing Systems 2023, NeurIPS 2023, New Orleans, LA, USA, 10–16 December 2023; Oh, A., Naumann, T., Globerson, A., Saenko, K., Hardt, M., Levine, S., Eds.; Curran Associates Inc.: Red Hook, New York, NY, USA, 2023. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Manning Publications: Greenwich, CT, USA, 2017. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. In Proceedings of the ECML PKDD Workshop: Languages for Data Mining and Machine Learning; 2013; pp. 108–122. Available online: https://dtai.cs.kuleuven.be/events/lml2013/informal_proceedings_lml_2013.pdf (accessed on 28 July 2025).
- Tsamardinos, I.; Charonyktakis, P.; Papoutsoglou, G.; Borboudakis, G.; Lakiotaki, K.; Zenklusen, J.C.; Juhl, H.; Chatzaki, E.; Lagani, V. Just Add Data: Automated predictive modeling for knowledge discovery and feature selection. Npj Precis. Oncol. 2022, 6, 38. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. Available online: https://wires.onlinelibrary.wiley.com/doi/pdf/10.1002/widm.8 (accessed on 28 July 2025). [CrossRef]
- Cohen, W.W. Fast Effective Rule Induction. In Machine Learning Proceedings 1995; Prieditis, A., Russell, S., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 115–123. [Google Scholar] [CrossRef]
- Pham, H.; Guan, M.; Zoph, B.; Le, Q.; Dean, J. Efficient Neural Architecture Search via Parameters Sharing. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 4095–4104. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning, 5th ed.; Information science and statistics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Huo, X.; Hao, K.; Chen, L.; Song Tang, X.; Wang, T.; Cai, X. A dynamic soft sensor of industrial fuzzy time series with propositional linear temporal logic. Expert Syst. Appl. 2022, 201, 117176. [Google Scholar] [CrossRef]
- Lubba, C.H.; Sethi, S.S.; Knaute, P.; Schultz, S.R.; Fulcher, B.D.; Jones, N.S. catch22: CAnonical Time-series CHaracteristics - Selected through highly comparative time-series analysis. Data Min. Knowl. Discov. 2019, 33, 1821–1852. [Google Scholar] [CrossRef]
- Chen, D.; Manning, C.D. A Fast and Accurate Dependency Parser using Neural Networks. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, EMNLP 2014, Doha, Qatar, 25–29 October 2014; A Meeting of SIGDAT, a Special Interest Group of the ACL; Moschitti, A., Pang, B., Daelemans, W., Eds.; ACL: Cambridge, MA, USA, 2014; pp. 740–750. [Google Scholar]
- Chang, A.X.; Manning, C.D. SUTime: A library for recognizing and normalizing time expressions. In Proceedings of the Eighth International Conference on Language Resources and Evaluation, LREC 2012, Istanbul, Turkey, 23–25 May 2012; Calzolari, N., Choukri, K., Declerck, T., Dogan, M.U., Maegaard, B., Mariani, J., Odijk, J., Piperidis, S., Eds.; European Language Resources Association (ELRA): Paris, France, 2012; pp. 3735–3740. [Google Scholar]
- Bond, F.; Bond, A. GeoNames Wordnet (geown): Extracting wordnets from GeoNames. In Proceedings of the 10th Global Wordnet Conference, GWC 2019, Wroclaw, Poland, 23–27 July 2019; Vossen, P., Fellbaum, C., Eds.; Global Wordnet Association: Wroclaw, Poland, 2019; pp. 387–393. [Google Scholar]
- Cortez, P.; Cerdeira, A.; Almeida, F.; Matos, T.; Reis, J. Modeling wine preferences by data mining from physicochemical properties. Decis. Support Syst. 2009, 47, 547–553. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Wang, W.; Bao, H.; Huang, S.; Dong, L.; Wei, F. MiniLMv2: Multi-Head Self-Attention Relation Distillation for Compressing Pretrained Transformers. In Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021; Zong, C., Xia, F., Li, W., Navigli, R., Eds.; ACL Anthology: Stroudsburg, PA, USA, 2021; pp. 2140–2151. [Google Scholar] [CrossRef]
- Song, K.; Tan, X.; Qin, T.; Lu, J.; Liu, T. MPNet: Masked and Permuted Pre-training for Language Understanding. arXiv 2020, arXiv:2004.09297. [Google Scholar]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. RoBERTa: A Robustly Optimized BERT Pretraining Approach. arXiv 2019, arXiv:1907.11692. [Google Scholar] [CrossRef]
- Bao, Q.; Peng, A.Y.; Deng, Z.; Zhong, W.; Gendron, G.; Pistotti, T.; Tan, N.; Young, N.; Chen, Y.; Zhu, Y.; et al. Abstract Meaning Representation-Based Logic-Driven Data Augmentation for Logical Reasoning. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2024, Bangkok, Thailand, 16–21 June 2024; Ku, L.W., Martins, A., Srikumar, V., Eds.; ACL Anthology: Stroudsburg, PA, USA, 2024; pp. 5914–5934. [Google Scholar] [CrossRef]
- Santhanam, K.; Khattab, O.; Saad-Falcon, J.; Potts, C.; Zaharia, M. ColBERTv2: Effective and Efficient Retrieval via Lightweight Late Interaction. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Seattle, WA, USA, 10–15 July 2022; pp. 3715–3734. [Google Scholar] [CrossRef]
- Verbeek, E.; Buijs, J.C.A.M.; van Dongen, B.F.; van der Aalst, W.M.P. ProM 6: The Process Mining Toolkit. In Proceedings of the Proceedings of the Business Process Management 2010 Demonstration Track, Hoboken, NJ, USA, 14–16 September 2010; Rosa, M.L., Ed.; CEUR-WS.org, 2010, CEURWorkshop Proceedings; Volume 615.
- Grafberger, S.; Groth, P.; Schelter, S. Automating and Optimizing Data-Centric What-If Analyses on Native Machine Learning Pipelines. Proc. ACM Manag. Data 2023, 1, 1–26. [Google Scholar] [CrossRef]
- Chen, S.; Tang, N.; Fan, J.; Yan, X.; Chai, C.; Li, G.; Du, X. HAIPipe: Combining Human-generated and Machine-generated Pipelines for Data Preparation. Proc. ACM Manag. Data 2023, 1, 1–26. [Google Scholar] [CrossRef]
- Ghallab, M.; Nau, D.S.; Traverso, P. Automated Planning-Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Chondamrongkul, N.; Sun, J. Software evolutionary architecture: Automated planning for functional changes. Sci. Comput. Program. 2023, 230, 102978. [Google Scholar] [CrossRef]



| Explainability | Name | System, S | Spec./Env., /E | Function Type | |
|---|---|---|---|---|---|
| A Priori | • Data Cleaning | Any | Any | ||
| • Climbing the Repre- sentation Ladder | Any | ||||
| Ad Hoc | • Learning [15] | Any | |||
| • Mining [15] | Any | ||||
| • Relational Learning | |||||
| • Paraconsistent Reasoning | disj.-free | disj.-free | |||
| Ex Post | • Performance Metrics | Any | Any | ||
| • Specification Agnostic | Any | Any | |||
| • Extraction | Any | ||||
| Metric Type | Average | DecisionTree | MLPNAS | RipperK |
|---|---|---|---|---|
| Accuracy | - | 0.6990 | 0.3282 | 0.7439 |
| F1 Score | Macro | 0.4541 | 0.1522 | 0.4499 |
| Weighted | 0.6847 | 0.2278 | 0.6987 | |
| Precision | Macro | 0.4481 | 0.1702 | 0.5420 |
| Weighted | 0.6714 | 0.2846 | 0.7550 | |
| Recall | Macro | 0.4607 | 0.3256 | 0.4484 |
| Weighted | 0.6990 | 0.3282 | 0.7439 |
| Metric | Average | Clustering | SGs | LGs | Logical | T1 | T2 | T3 | T4 | T5 | T6 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | - | HAC | 0.21 | 0.23 | 1.00 | 0.28 | 0.29 | 0.27 | 0.29 | 0.21 | 0.29 |
| k-Medoids | 0.21 | 0.23 | 1.00 | 0.28 | 0.29 | 0.27 | 0.29 | 0.21 | 0.29 | ||
| F1 | Macro | HAC | 0.24 | 0.28 | 1.00 | 0.37 | 0.38 | 0.34 | 0.38 | 0.21 | 0.37 |
| k-Medoids | 0.24 | 0.28 | 1.00 | 0.37 | 0.38 | 0.34 | 0.38 | 0.21 | 0.37 | ||
| Weighted | HAC | 0.13 | 0.15 | 1.00 | 0.21 | 0.22 | 0.18 | 0.22 | 0.11 | 0.20 | |
| k-Medoids | 0.13 | 0.15 | 1.00 | 0.21 | 0.22 | 0.18 | 0.22 | 0.11 | 0.20 | ||
| Precision | Macro | HAC | 0.35 | 0.37 | 1.00 | 0.46 | 0.49 | 0.35 | 0.54 | 0.20 | 0.37 |
| k-Medoids | 0.35 | 0.37 | 1.00 | 0.46 | 0.49 | 0.35 | 0.54 | 0.20 | 0.37 | ||
| Weighted | HAC | 0.20 | 0.20 | 1.00 | 0.37 | 0.43 | 0.19 | 0.53 | 0.11 | 0.20 | |
| k-Medoids | 0.20 | 0.20 | 1.00 | 0.37 | 0.43 | 0.19 | 0.53 | 0.11 | 0.20 | ||
| Recall | Macro | HAC | 0.41 | 0.46 | 1.00 | 0.54 | 0.54 | 0.52 | 0.54 | 0.41 | 0.56 |
| k-Medoids | 0.41 | 0.46 | 1.00 | 0.54 | 0.54 | 0.52 | 0.54 | 0.41 | 0.56 | ||
| Weighted | HAC | 0.21 | 0.23 | 1.00 | 0.28 | 0.29 | 0.27 | 0.29 | 0.21 | 0.29 | |
| k-Medoids | 0.21 | 0.23 | 1.00 | 0.28 | 0.29 | 0.27 | 0.29 | 0.21 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergami, G.; Fox, O.R. How Explainable Really Is AI? Benchmarking Explainable AI. Logics 2025, 3, 9. https://doi.org/10.3390/logics3030009
Bergami G, Fox OR. How Explainable Really Is AI? Benchmarking Explainable AI. Logics. 2025; 3(3):9. https://doi.org/10.3390/logics3030009
Chicago/Turabian StyleBergami, Giacomo, and Oliver Robert Fox. 2025. "How Explainable Really Is AI? Benchmarking Explainable AI" Logics 3, no. 3: 9. https://doi.org/10.3390/logics3030009
APA StyleBergami, G., & Fox, O. R. (2025). How Explainable Really Is AI? Benchmarking Explainable AI. Logics, 3(3), 9. https://doi.org/10.3390/logics3030009







