Abstract
We present Stratified Metric Temporal Logic (SMTL), a novel formalism for specifying and verifying the properties of complex cyber–physical systems that exhibit behaviors across multiple temporal and abstraction scales. SMTL extends existing temporal logics by incorporating a stratification operator, enabling the association of temporal properties with specific abstraction levels. This allows for the natural expression of multi-scale requirements while maintaining formal reasoning about inter-level relationships. We formalize the syntax and semantics of SMTL, proving that it strictly subsumes metric temporal logic (MTL) and offers enhanced expressiveness by capturing properties unattainable in existing logics. Numerical simulations comparing agents operating under MTL and SMTL specifications show that SMTL enhances agent coordination and safety, reducing collision rates without substantial computational overhead or compromising path efficiency. These findings highlight SMTL’s potential as a valuable tool for designing and verifying complex multi-agent systems operating across diverse temporal and abstraction scales.
1. Introduction
Cyber–physical systems (CPS) exhibit behaviors across multiple temporal and abstraction scales, from millisecond-level control loops to hour-long mission objectives. While temporal logics have proven invaluable for specifying and verifying system properties [1], existing formalisms such as metric temporal logic (MTL) and signal temporal logic (STL) struggle to efficiently capture and reason about such multi-scale behaviors. This limitation becomes particularly acute in systems such as autonomous vehicles, where safety properties must be simultaneously maintained at the level of individual actuators, trajectory planning, and mission execution.
Existing temporal logics enforce a uniform treatment of time, requiring specifications to operate at the finest required temporal granularity [2]. Consider an autonomous drone delivery system: at the lowest level, motor control requires millisecond-precision timing; at the intermediate level, trajectory following operates on a timescale of seconds; and at the highest level, delivery scheduling involves minutes or hours. Expressing all of these requirements in MTL or STL requires reasoning on a millisecond scale throughout, leading to unnecessary complexity and computational overhead. The key challenge lies in the lack of formal mechanisms for stratifying temporal properties across different abstraction levels while maintaining sound logical relationships between these levels. Existing approaches typically handle multi-scale properties through informal decomposition or through separate specifications at different levels, losing the ability to reason formally about inter-level dependencies.
1.1. Paper Contributions
This paper introduces SMTL, an extension of traditional temporal logics incorporating a stratification operator to enable multi-scale temporal specification. The key contributions are as follows:
- We formalize the syntax and semantics of SMTL, proving that it strictly subsumes MTL and offers enhanced expressiveness by capturing properties unattainable in existing logics.
- We analyze the decidability and computational complexity of SMTL model checking, identifying decidable fragments with complexities comparable to MTL for bounded-time properties
- Through case studies and numerical simulations, we demonstrate SMTL’s practical utility in specifying multi-scale requirements and improving verification efficiency, enhancing agent coordination and safety.
The practical utility of SMTL is demonstrated through case studies, where we show how SMTL specifications naturally capture requirements that span multiple time scales while allowing more efficient verification compared to traditional approaches.
1.2. Related Work
Various temporal logics have been developed to specify and reason about temporal properties in CPS and control systems. STL and MTL are prominent examples that extend LTL to handle real-valued signals and timing constraints [3]. Probabilistic STL (PrSTL) extends STL with probabilistic operators to reason about stochastic CPS [4]. Truncated linear temporal logic (LTL) is a variant of LTL interpreted over finite traces and has been used to specify complex rules for RL agents. Robustness TL (RobTL) is a logic for specifying distances between CPS behaviors over a finite time horizon [5]. The use of temporal logics such as computation tree logic (CTL) and LTL provided a foundation for expressing desired behaviors in multi-agent systems [6,7,8,9,10,11].
SMTL builds upon the foundations of MTL to address the complexities of agent coordination and collision avoidance. MTL extends LTL by incorporating quantitative temporal constraints, enabling the specification of properties over real-time systems. While MTL has been used for specifying timing constraints and verifying system behaviors, it lacks mechanisms to prioritize different types of constraints, which is important in multi-agent coordination where safety and goal achievement may conflict. SMTL is a response to this limitation that introduces a stratification of temporal constraints, allowing agents to prioritize safety and coordination over individual objectives. The stratification concept aligns with the hierarchical organization of specifications, where higher-priority constraints must be satisfied before considering lower-priority ones. This approach is particularly relevant in multi-agent systems, where agents operate concurrently and interactions can lead to emergent behaviors.
Previous efforts have explored the use of hierarchical and prioritized logics in multi-agent planning and verification. For instance, ref. [12] developed TLA as a framework for reasoning about concurrent systems, with a focus on simplifying temporal logic reasoning. Separately, ref. [13] developed real-time logics to enable quantitative reasoning about timing delays in real-time applications. Research in multi-agent coordination employs various formal methods, including temporal logics, to specify and verify interaction protocols and ensure safe coordination between agents. These methods focus on specifying conventions of social interaction and rules that govern agent behavior in multi-agent systems [14]. Furthermore, research on robot control synthesis has focused on using LTL to specify both safety requirements (describing how the robot should always behave) and liveness specifications (describing goals that must eventually be achieved) [15].
Stratification has been well established in database theory through Stratified Datalog, where it provides a way to handle negation and recursion by organizing rules into strata. This concept has been extended to temporal reasoning through formalisms like DatalogMTL, which incorporates metric temporal operators [16]. In recent years, the application of formal methods in multi-agent pathfinding has gained traction, with work using satisfiability modulo theories (SMTs) and other verification techniques to ensure safe navigation [17]. Sharon et al. developed conflict-based search (CBS) algorithms that decompose multi-agent pathfinding problems into individual agent plans while resolving conflicts iteratively [18]. These methods do not inherently incorporate stratified priorities in their formulations. The introduction of SMTL contributes to this landscape by providing a logical framework that inherently supports priority stratification. By structuring temporal constraints into layers, SMTL facilitates the design of agents that can dynamically adjust their actions based on the priority of constraints, leading to improved coordination and safety in complex environments. Moreover, the integration of SMTL into multi-agent systems aligns with the broader trend of incorporating formal verification into agent-based modeling. The works of Belta et al. on formal methods for control synthesis have emphasized the importance of temporal logic in specifying desired behaviors, although the stratification aspect has remained less explored [19]. An additional dimension relevant to stratified logic is the use of multi-fidelity modeling and verification techniques [20,21,22,23,24]. Multi-fidelity approaches involve employing models of varying levels of detail and accuracy to balance the trade-off between computational efficiency and the precision of system analysis.
The closest work to our approach is multi-type LTL (MLTLM), which focuses on heterogeneous data types (e.g., Boolean, integer, real signals) within a single-level temporal logic framework, enabling us to write and verify properties involving different kinds of signals at once [25]. By contrast, SMTL emphasizes hierarchical or multi-scale abstractions. While MLTLM is about handling various data domains in one logic, SMTL is about cleanly separating and coordinating multiple levels of temporal or system detail in a single formalism.
1.3. Paper Organization
The remainder of this paper is organized as follows. Section 2 provides the necessary background on temporal logics and introduces the mathematical framework for stratified systems. Section 3 presents the formal syntax and semantics of SMTL, including examples that demonstrate its expressiveness. Section 4 develops the theoretical results, proving SMTL’s properties and complexity bounds. Section 5 presents experimental results comparing SMTL and MTL in multi-agent coordination scenarios. Finally, Section 6 concludes with a discussion of our findings and future research directions.
2. Preliminaries
Before introducing SMTL, we review the essential concepts of metric temporal logic and establish the mathematical framework for reasoning about stratified systems. Throughout this paper, we use the notation presented in Table 1.

Table 1.
Symbols and complexity measures used in the formalism.
2.1. Metric Temporal Logic
MTL extends propositional temporal logic with timing constraints on temporal operators. Let be a set of atomic propositions and be the set of non-empty intervals in with endpoints in .
Definition 1
(MTL Syntax). An MTL formula φ is built according to the grammar
where and .
Additional temporal operators are defined as the following abbreviations:
Definition 2
(Timed State Sequence). A timed state sequence is a pair where
- is an infinite sequence of states ;
- is an infinite sequence of time stamps , with and for all .
Definition 3
(MTL Semantics). For a timed state sequence and position , the satisfaction relation ⊧ is defined inductively:
2.2. Stratified Systems and Abstraction Hierarchies
We now introduce the mathematical framework for reasoning about systems at multiple abstraction levels.
Definition 4
(Abstraction Function). An abstraction function maps concrete states to abstract states, where S and are state spaces. An abstraction hierarchy is a sequence of state spaces and abstraction functions where
- is the state space at level k;
- maps states from level to level k.
Definition 5
(Abstraction Properties). An abstraction hierarchy satisfies the following:
- Monotonicity: For , .
- Preservation: For any property φ preserved by , if , then .
- Refinement: For states , if , then and are equivalent at level k.
Definition 6
(Temporal Resolution). Each abstraction level k has an associated temporal resolution , representing the minimum granularity of time distinguishable at that level. The temporal resolution hierarchy satisfies the following:
3. Syntax and Semantics of SMTL
3.1. Syntax
Definition 7
(SMTL Syntax). Let be a set of atomic propositions and be the set of non-empty intervals in with endpoints in . An SMTL formula φ is built according to the grammar
where is an atomic proposition, is a time interval, is an abstraction level, and is the stratification operator for level k.
As in MTL, we define additional temporal operators using the following abbreviations:
The stratification operator can be nested, allowing for relationships between abstraction levels:
Definition 8
(Well-Formed SMTL Formula). An SMTL formula φ is well formed if for any nested stratification operators ( and ) appearing in φ, where is within the scope of , we have .
3.2. Semantics
The semantics of SMTL is defined over timed state sequences with multiple abstraction levels.
Definition 9
(Stratified Timed State Sequence). A stratified timed state sequence is a tuple where
- is an infinite sequence of states at level k, with ;
- is an infinite sequence of time stamps with and ;
- For each k, consecutive states in are separated by at least time units.
Definition 10
(Abstraction Consistency). A stratified timed state sequence ρ is abstraction consistent if for all levels and all positions n,
where is the abstraction function from level i to level j.
Definition 11
(SMTL Semantics). For a stratified timed state sequence , position , and abstraction level m, the satisfaction relation is defined inductively:
The semantics of the stratification operator ensures the following:
- Properties at level k are evaluated using the state sequence ;
- The temporal resolution at level k is respected ();
- Abstraction consistency is maintained between levels.
3.3. Practical Implications of SMTL Expressiveness
Here, we provide two examples that demonstrate the enhanced expressiveness of SMTL over MTL.
Example 1
(Multi-Scale System Specification). Consider an autonomous vehicle navigation system operating on multiple time scales. Existing MTL specifications struggle to capture requirements that span different temporal granularities. SMTL naturally expresses such multi-scale requirements through a single coherent formula:
This formula simultaneously captures millisecond-level actuator control (), second-level trajectory tracking (), and minute-level mission objectives (). The stratification operator cleanly separates these concerns while maintaining their logical relationships.
Example 2
(Abstraction in Software Architecture). The expressiveness of SMTL aligns with layered software architectures. Consider a robotic system with a three-tier architecture:
where each layer’s specification might involve temporal properties. The crucial advantage of SMTL lies in its ability to express inter-layer dependencies:
This hierarchical specification captures both the independence of different architectural layers and their temporal coupling, a feat impossible in standard MTL.
4. Theoretical Analysis
Theorem 1
(Stratification Soundness). For any SMTL formula φ and abstraction levels ,
Proof.
This follows directly from the semantics of and abstraction consistency. When , the formula is evaluated at level j using , which, due to abstraction consistency, is a valid abstraction of states at level i. □
Theorem 2
(Temporal Resolution Hierarchy). For any SMTL formula φ and levels ,
Proof.
According to the definition of stratified timed state sequences, the states at level i must be separated by at least time units. Therefore, any temporal property at level i must span at least this duration. □
4.1. Expressiveness of SMTL
We begin by establishing the foundational properties of abstraction functions that underpin the stratified nature of our logic. An abstraction function maps a concrete signal to an abstract signal at abstraction level k, where represents the signal space at level k. These functions form a hierarchy satisfying crucial properties: monotonicity ensures that for , ; consistency guarantees that if holds for , then there exists some higher level where holds for ; and the refinement property ensures that distinct signals remain distinguishable at some abstraction level.
Theorem 3
(Strict Expressiveness). SMTL is strictly more expressive than MTL. This relationship manifests both in SMTL’s ability to express all MTL properties and in its capacity to express properties that are inexpressible in MTL.
Proof.
The proof proceeds in two parts, first establishing that SMTL subsumes MTL, then demonstrating that SMTL can express properties beyond MTL’s capabilities. To show that SMTL subsumes MTL, we construct a translation function defined inductively on the structure of MTL formulas:
Through structural induction, we prove that for any signal and time point t, the satisfaction relation preserves equivalence: . The base case for atomic propositions follows directly from the definition. For the inductive step, we consider each operator, with particular attention to the metric unit operator:
To establish SMTL’s strictly greater expressiveness, we construct an SMTL formula that cannot be expressed in MTL. Consider the formula
We prove its MTL-inexpressibility through a contradiction argument. Let be the set of Boolean signals. Define two signals, and , that differ only at a single point:
Define abstraction functions where smooths out isolated points while maintains the original signal:
In this context, means () is the identity function. The identity function is being used at abstraction level 2 to represent “no abstraction” or “keep all details”. This contrasts with which does perform abstraction. Under these definitions, , while . However, any MTL formula must be evaluated equivalently on both signals: , as MTL cannot distinguish signals that differ at isolated points. This contradiction establishes that no MTL formula can express the property captured by . □
Corollary 1
(Stratification Power). Let be the language of SMTL, and be the language of MTL. From Theorem 3, we know that , which means the following:
- Every MTL formula φ has an equivalent SMTL formula .
- There exists at least one formula such that .
Because leverages the stratification operator in a way that cannot be emulated by standard MTL syntax or semantics, the stratification mechanism is strictly more powerful. Hence, the operator effectively extends the expressive frontier of the logic, allowing one to specify behaviors or constraints at multiple abstraction levels that cannot be collapsed into a single, uniform time scale.
Corollary 2
(Multi-Scale Properties). Consider a CPS model with a hierarchy of time resolutions and corresponding state abstractions . From Definition 5 (abstraction consistency) and the semantics of , if a property is designated at level k, then it is evaluated (i) using time steps separated by at least , and (ii) in a state space consistent with . Thus, a single SMTL specification
can encode requirements at multiple time granularities. No purely single-scale temporal logic (MTL/STL) can replicate this multifaceted time-resolution property in a single unified formula without artificially inflating the timescale or losing key abstraction details. As a result, SMTL natively captures multiscale temporal requirements under one logical framework.
Definition 12
(Bounded-Time SMTL Formula). An SMTL formula is called bounded-time if, for every temporal operator in φ (e.g., ), the corresponding time interval I is a subset of for some finite . Equivalently, no time interval may be of the form or .
This definition confines verification to finite time horizons for each temporal operator. By contrast, a lemph{unbounded-time} formula is one that includes at least one interval or .
Theorem 4
(SMTL Model-Checking Complexity). Let ϕ be an SMTL formula and be a finite-state transition system. Denote as K the maximum abstraction level in ϕ, and as the largest integer constant appearing in its temporal intervals. The complexity of checking satisfies the following:
- (Bounded-Time Case) For formulas with only bounded intervals, the model-checking problem is EXPTIME-complete.
- (Unbounded-Time Case) If ϕ includes at least one unbounded interval, the model-checking problem is 2EXPTIME-complete.
Moreover, the complexity grows polynomially in K.
4.2. Proof Sketch
The bounded-time result (EXPTIME-complete) follows from constructing a region automaton where each clock is bounded by the largest integer constant in . Because the transitions and clock valuations remain finite under bounded intervals, the automaton state space can be explored in exponential time with respect to and . For each abstraction level k, we build an automaton of comparable size, yielding an overall EXPTIME procedure multiplied by a factor polynomial in K. For the unbounded-time case, we note that SMTL strictly generalizes MTL. It is known that model checking unbounded MTL is complete in 2EXPTIME, due to the necessity of handling infinite paths and the resulting exponential blow-ups when automating temporal logic over infinite horizons. We can reduce the unbounded MTL problem to SMTL by embedding an MTL formula into SMTL (see Theorem 3). Therefore, no asymptotically lower complexity can be applied to an unbounded SMTL, establishing a 2EXPTIME-hard lower bound. Since our upper bound construction also leads to a 2EXPTIME procedure, this completes the 2EXPTIME-completeness result for unbounded-time SMTL formulas.
Corollary 3.
The 2EXPTIME-hardness for unbounded-time SMTL directly follows from the fact that there exists a linear-time many-to-one reduction from unbounded MTL model checking (itself 2EXPTIME-complete) to SMTL model checking.
In summary, if all intervals are finite, the complexity is contained in EXPTIME, whereas unbounded intervals invoke the 2EXPTIME-complete complexity class. This aligns with classical results on MTL, thus confirming both the bounded- and unbounded-time complexity claims for SMTL.
Corollary 4
(Incremental Verification). Let be an SMTL formula with maximum abstraction level K, and let be a finite-state transition system. Suppose has already been verified. Now, consider a new SMTL formula obtained from by adding or modifying constraints solely at a new level . Formally,
where each is a fresh subformula (or a refinement of existing constraints) that did not previously appear in , and no constraints at levels are altered. Then, to check whether , it suffices to carry out the following: 1. Verify the newly introduced subformulas at level within the abstract transition system . 2. Check the consistency between levels and K, ensuring that correctly abstracts to for each state index n, in accordance with Definition 5 (abstraction consistency). Because the properties at the existing levels remain unchanged—and have already been verified—no further verification is required for those levels. As a result, the incremental-verification cost is polynomial in the size of and (as opposed to repeating a full model check from scratch). Hence, adding each new level only imposes overhead for the newly introduced constraints and their immediate interactions with the immediately lower level, confirming an efficient incremental-verification process.
5. Numerical Results
To evaluate the effectiveness of SMTL in enhancing multi-agent coordination and safety, we conducted a series of simulations comparing the performance of agents operating under SMTL and MTL specifications. The experiments were designed to assess how the introduction of stratification in temporal logic influences agent behavior in terms of collision avoidance and path efficiency. In our experimental setup, agents navigated grid worlds of dimensions ranging from to . Each grid represented a discrete environment in which agents moved from randomly assigned starting positions to specified target locations. Obstacles were randomly placed within the grids. Agents were programmed to move one unit per time step in any of the four cardinal directions, provided the destination cell was within the grid boundaries and not occupied by an obstacle or another agent. The primary objective for each agent was to reach its goal while avoiding collisions with other agents and obstacles.
Under the MTL framework, agents were governed by temporal logic specifications that dictated their movement towards goals without consideration of other agents. The MTL specification used can be mathematically expressed as
This formula specifies that globally, from time 0 to T, if an agent intends to reach its goal (reachGoal), then eventually, within time T, it must be at the goal position (atGoal). In contrast, agents operating under SMTL incorporated stratified reasoning to anticipate and avoid potential conflicts with other agents. The SMTL specification extended the MTL formula to include collision avoidance at a higher level of reasoning:
Here, represents the stratification level where agents consider not only their goal-reaching objectives but also the positions of other agents to prevent collisions. The term ensures that at all times, agents avoid occupying the same position as any other agent. In this case study, the stratified nature of SMTL matches its temporal stratification through the separation of agent behaviors and constraints according to their temporal characteristics:
- Short-Term Temporal Constraints (Fine-Grained Temporal Level): Agents using SMTL enforce collision avoidance at every time step. This is a temporal property that requires agents to ensure that they do not occupy the same position as any other agent. In SMTL, this corresponds to a higher-priority constraint specified at a lower stratification level (e.g., ), which operates at a finer temporal granularity. The logic enforces that safety properties hold at all times or within very short time intervals.
- Long-Term Temporal Objectives (Coarse-Grained Temporal Level): Agents aim to reach their designated goals, which is a temporal property considered over a longer time horizon. In SMTL, this is captured at a higher stratification level (e.g., or ), where the temporal properties involve longer intervals or eventualities.
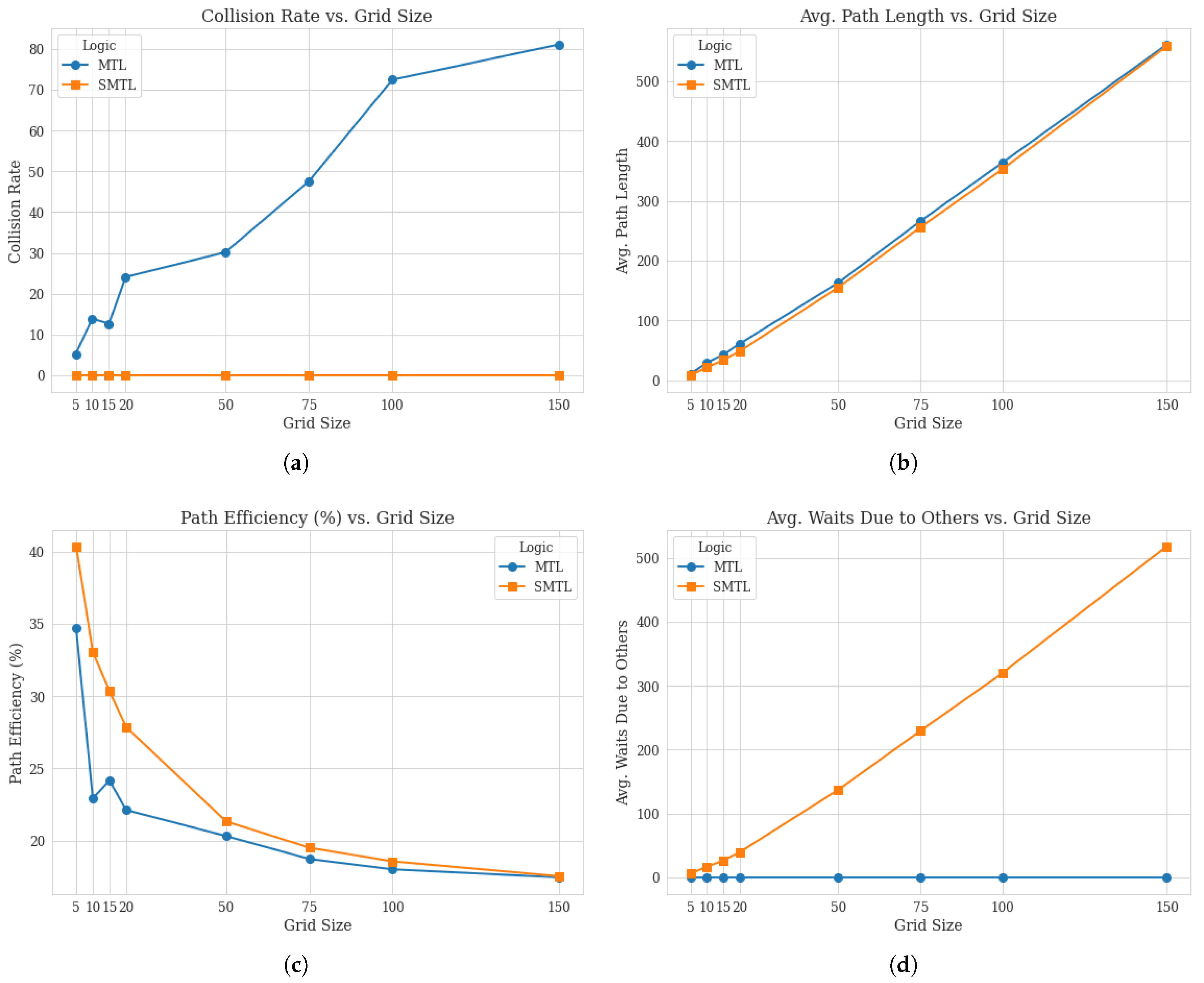
The experimental results presented in Figure 1 provide a comparison of agent performance under MTL and SMTL. For each grid size, the number of agents corresponds to the grid dimension, ensuring a consistent agent density across different environment scales. The key performance metrics evaluated include (i) collision rate, (ii) average path length, (iii) path efficiency, (iv) and average waits due to others. A key observation from the data is the contrast in collision rates between the MTL and SMTL agents. MTL agents show a non-zero collision rate across all grid sizes, with the collision rate generally increasing as the grid size and the number of agents grow. Specifically, MTL agents experience an average collision rate of 5.20 collisions per agent on the grid, which escalates to over 81 collisions per agent in the grid.
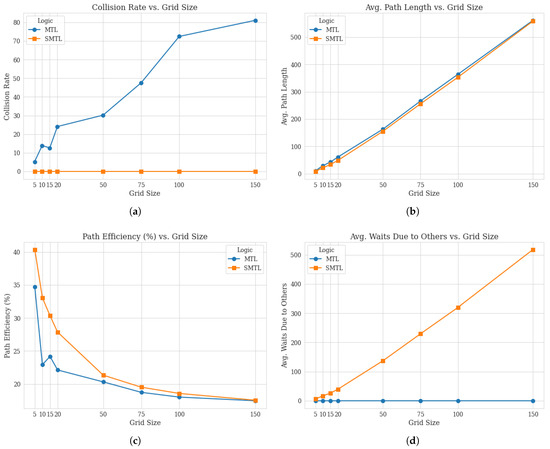
Figure 1.
Comparison of agent performance metrics under MTL and SMTL across different grid sizes: (a) collision rate, (b) average path length, (c) path efficiency, and (d) average waits due to others.
In contrast, SMTL agents maintain a collision rate of zero across all grid sizes, demonstrating their effectiveness in collision avoidance regardless of the environment’s scale. This result highlights the efficacy of the stratification approach in SMTL, which allows agents to prioritize safety and coordination over individual objectives. The ability of SMTL agents to completely avoid collisions, even in densely populated and extensive grids, signifies a substantial improvement over traditional MTL agents and validates the practical utility of SMTL in multi-agent systems. Analyzing the average path length reveals that SMTL agents often have shorter or comparable path lengths compared to MTL agents, especially in smaller grids. For example, on the grid, SMTL agents achieve an average path length of 8.40 units, whereas MTL agents average 10.47 units. This suggests that SMTL agents are capable of reaching their goals more efficiently in less congested environments. However, as the grid size increases, the difference in average path length between SMTL and MTL agents diminishes. In the grid, SMTL agents have an average path length of approximately 558.57 units, compared to 561.24 units for MTL agents. This convergence indicates that in larger environments, both agent types require similar path lengths to reach their goals, likely due to the proportional increase in distances that need to be traversed. The path efficiency metric, calculated as the ratio of the shortest possible path length to the actual path length, provides insight into the agents’ navigational effectiveness relative to the optimal path. SMTL agents consistently show higher path efficiency percentages than MTL agents across all grid sizes. In the grid, SMTL agents attain a path efficiency of approximately 40.37%, surpassing the 34.68% efficiency of MTL agents. Although both agent types experience a decline in path efficiency as the grid size increases—reflecting the greater complexity and potential detours in larger environments—SMTL agents maintain a slight advantage. This efficiency suggests that SMTL agents effectively balance the need for collision avoidance with the pursuit of efficient paths. A notable distinction between the two agent types is observed in the average waits due to others. SMTL agents exhibit a substantial number of waits, which increases with grid size—from an average of 5.93 waits in the grid to over 517 waits in the grid. This behavior reflects the SMTL agents’ strategy of waiting to avoid potential collisions, emphasizing their prioritization of safety and adherence to collision avoidance constraints. In contrast, MTL agents have zero waits across all grid sizes, indicating that they proceed toward their goals without regard for other agents, even if it results in collisions. The willingness of SMTL agents to wait highlights their commitment to coordination and safe operation within shared environments.
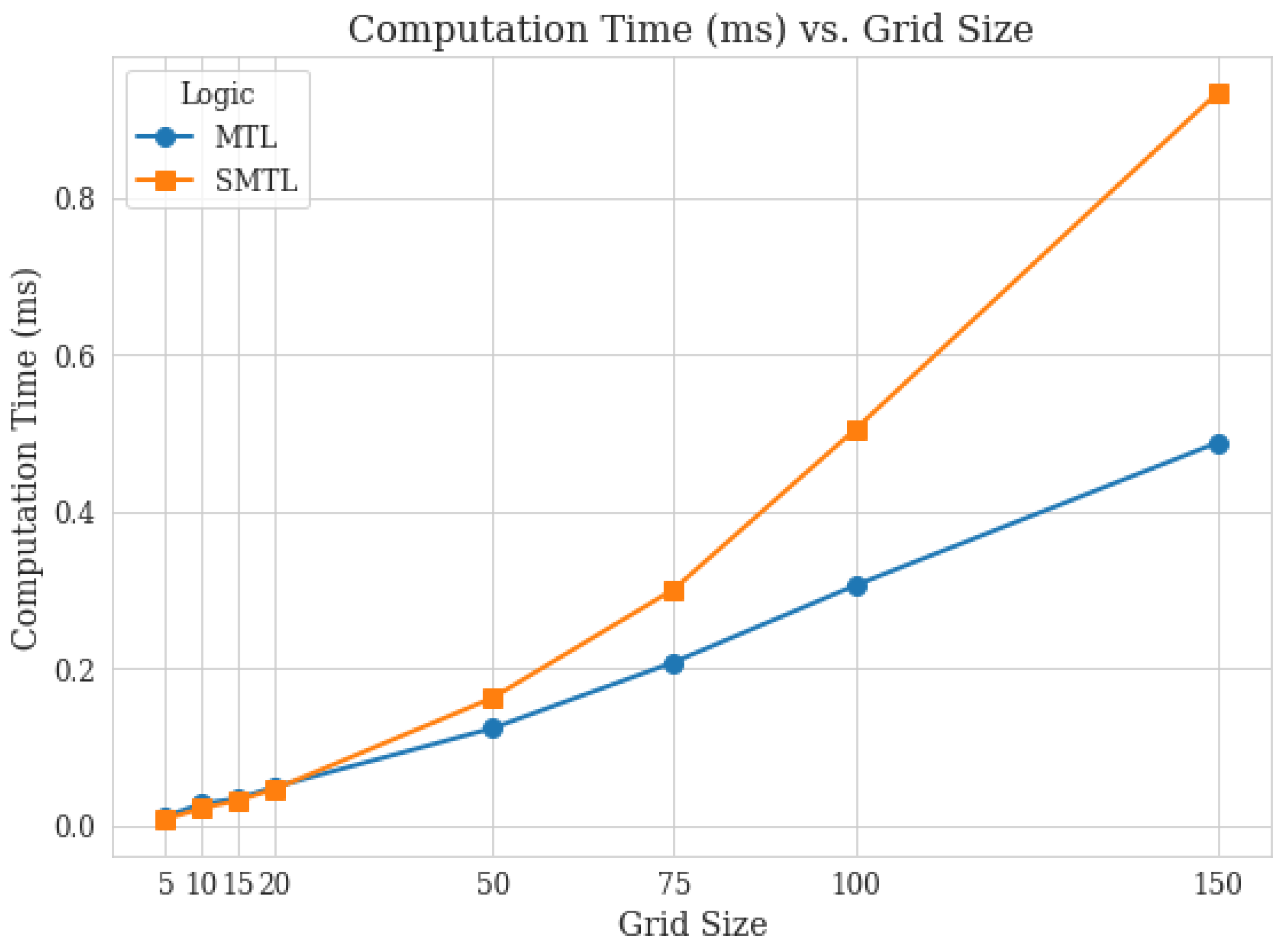
Computation time per step per agent is another metric where SMTL agents demonstrate competitive performance. Figure 2 shows this comparison. While SMTL agents incur slightly higher computation times compared to MTL agents, the difference is marginal. For example, in the grid, SMTL agents have an average computation time of approximately 0.935 milliseconds per step, compared to 0.489 milliseconds for MTL agents. This increase can be attributed to the additional processing required for collision avoidance and coordination with other agents. These results indicate that the coordination achieved by SMTL agents does not come at the expense of prohibitive computational costs.
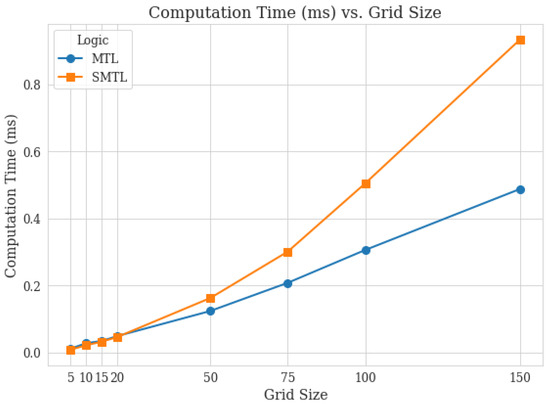
Figure 2.
Comparison of computation time per step between two agents.
6. Conclusions
In this paper, we proposed SMTL as a formalism for specifying and verifying properties of complex cyber–physical systems exhibiting behaviors across multiple temporal and abstraction scales. By incorporating a stratification operator into traditional temporal logics, SMTL enables the association of temporal properties with specific abstraction levels, facilitating the natural expression of multi-scale requirements while preserving formal reasoning about inter-level relationships. We formalized the syntax and semantics of SMTL, proving that it strictly subsumes MTL and offers enhanced expressiveness by capturing properties unattainable in existing logics. Through numerical simulations, we demonstrated the utility of SMTL in improving agent coordination and safety. The simulations comparing agents operating under MTL and SMTL specifications revealed that SMTL significantly reduces collision rates without incurring substantial computational overhead or compromising path efficiency. Specifically, SMTL agents maintained a zero collision rate at various grid sizes, highlighting the effectiveness of stratified reasoning in avoiding conflicts and improving overall system reliability. Our findings emphasize the potential of SMTL as a valuable tool for designing and verifying complex multi-agent systems operating across diverse temporal and abstraction scales.
Future Work
In future work, we plan to explore integrations and comparisons between SMTL and other hierarchical methods (e.g., MLTLM and CBS), aiming to assess how these approaches complement or further enhance SMTL’s multi-scale coordination capabilities. Furthermore, we plan to explore the integration of SMTL with automated synthesis tools to generate controllers that guarantee compliance with multi-scale specifications. Furthermore, investigating the application of SMTL in other domains, such as distributed sensor networks or human–robot interaction, could further validate its effectiveness. Extending SMTL to incorporate probabilistic reasoning or learning-based components may also enhance its applicability to systems with inherent uncertainties. Finally, the development of optimized algorithms for the checking of the SMTL model can facilitate its adoption in large-scale industrial applications.
Author Contributions
Conceptualization, A.B. and P.W.; methodology, A.B.; software, A.B.; validation, A.B.; formal analysis, A.B.; investigation, A.B.; resources, A.B.; data curation, A.B.; writing—original draft preparation, A.B.; writing—review and editing, A.B. and P.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bartocci, E.; Deshmukh, J.; Donzé, A.; Fainekos, G.; Maler, O.; Ničković, D.; Sankaranarayanan, S. Specification-based monitoring of cyber-physical systems: A survey on theory, tools and applications. In Lectures on Runtime Verification: Introductory and Advanced Topics; Springer: Cham, Switzerland, 2018; pp. 135–175. [Google Scholar]
- Eappen, J.; Xiong, Z.; Patel, D.; Bera, A.; Jagannathan, S. Scaling Safe Multi-Agent Control for Signal Temporal Logic Specifications. In Proceedings of the CoRL Workshop on Safe and Robust Robot Learning for Operation in the Real World, Munich, Germany, 6–9 November 2024. [Google Scholar]
- Momtaz, A.; Abbas, H.; Bonakdarpour, B. Monitoring signal temporal logic in distributed cyber-physical systems. In Proceedings of the ACM/IEEE 14th International Conference on Cyber-Physical Systems (With CPS-IoT Week 2023), San Antonio, TX, USA, 9–12 May 2023; pp. 154–165. [Google Scholar]
- Yoo, C.; Belta, C. Control with probabilistic signal temporal logic. arXiv 2015, arXiv:1510.08474. [Google Scholar]
- Fainekos, G.E.; Pappas, G.J. Robustness of temporal logic specifications. In Formal Approaches to Software Testing and Runtime Verification, Proceedings of the First Combined International Workshops FATES 2006 and RV 2006, Seattle, WA, USA, 15–16 August 2006; Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2006; pp. 178–192. [Google Scholar]
- Fisher, M. Temporal development methods for agent-based. Auton. Agents Multi-Agent Syst. 2005, 10, 41–66. [Google Scholar] [CrossRef]
- Nilsson, P.; Ozay, N. Control synthesis for large collections of systems with mode-counting constraints. In Proceedings of the 19th International Conference on Hybrid Systems: Computation and Control, Vienna, Austria, 12–14 April 2016; pp. 205–214. [Google Scholar]
- Sahin, Y.E.; Nilsson, P.; Ozay, N. Provably-correct coordination of large collections of agents with counting temporal logic constraints. In Proceedings of the 2017 ACM/IEEE 8th International Conference on Cyber-Physical Systems (ICCPS), Pittsburgh PA, USA, 18–20 April 2017. [Google Scholar]
- Xu, Z.; Julius, A.A. Census signal temporal logic inference for multiagent group behavior analysis. IEEE Trans. Autom. Sci. Eng. 2016, 15, 264–277. [Google Scholar] [CrossRef]
- Leahy, K.; Jones, A.; Vasile, C.I. Fast decomposition of temporal logic specifications for heterogeneous teams. IEEE Robot. Autom. Lett. 2022, 7, 2297–2304. [Google Scholar] [CrossRef]
- Kantaros, Y.; Zavlanos, M.M. Stylus*: A temporal logic optimal control synthesis algorithm for large-scale multi-robot systems. Int. J. Robot. Res. 2020, 39, 812–836. [Google Scholar] [CrossRef]
- Lamport, L. The temporal logic of actions. ACM Trans. Program. Lang. Syst. (TOPLAS) 1994, 16, 872–923. [Google Scholar] [CrossRef]
- Alur, R.; Henzinger, T.A. Real-time logics: Complexity and expressiveness. Inf. Comput. 1993, 104, 35–77. [Google Scholar] [CrossRef]
- Endriss, U. Temporal logics for representing agent communication protocols. In Proceedings of the International Workshops on Agent Communication, Utrecht, The Netherlands, 25 July 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 15–29. [Google Scholar]
- Kress-Gazit, H.; Lahijanian, M.; Raman, V. Synthesis for robots: Guarantees and feedback for robot behavior. Annu. Rev. Control. Robot. Auton. Syst. 2018, 1, 211–236. [Google Scholar] [CrossRef]
- Cucala, D.J.T.; Wałęga, P.A.; Grau, B.C.; Kostylev, E. Stratified negation in Datalog with metric temporal operators. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 6488–6495. [Google Scholar]
- Felli, P.; Gianola, A.; Montali, M. SMT-based safety checking of parameterized multi-agent systems. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 6321–6330. [Google Scholar]
- Sharon, G.; Stern, R.; Felner, A.; Sturtevant, N.R. Conflict-based search for optimal multi-agent pathfinding. Artif. Intell. 2015, 219, 40–66. [Google Scholar] [CrossRef]
- Belta, C.; Sadraddini, S. Formal methods for control synthesis: An optimization perspective. Annu. Rev. Control. Robot. Auton. Syst. 2019, 2, 115–140. [Google Scholar] [CrossRef]
- Shahrooei, Z.; Kochenderfer, M.J.; Baheri, A. Optimizing Falsification for Learning-Based Control Systems: A Multi-Fidelity Bayesian Approach. arXiv 2024, arXiv:2409.08097. [Google Scholar]
- Baheri, A. Safety Validation of Learning-Based Autonomous Systems: A Multi-Fidelity Approach. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, p. 15432. [Google Scholar]
- Baheri, A. Exploring the role of simulator fidelity in the safety validation of learning-enabled autonomous systems. AI Mag. 2023, 44, 453–459. [Google Scholar] [CrossRef]
- Shahrooei, Z.; Kochenderfer, M.J.; Baheri, A. Falsification of Learning-Based Controllers through Multi-Fidelity Bayesian Optimization. In Proceedings of the European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023. [Google Scholar]
- Beard, J.J.; Baheri, A. Safety verification of autonomous systems: A multi-fidelity reinforcement learning approach. arXiv 2022, arXiv:2203.03451. [Google Scholar]
- Hariharan, G.; Kempa, B.; Wongpiromsarn, T.; Jones, P.H.; Rozier, K.Y. MLTL multi-type (MLTLM): A logic for reasoning about signals of different types. In Proceedings of the International Workshop on Numerical Software Verification, Haifa, Israel, 11 August 2022; Springer: Cham, Switzerland, 2022; pp. 187–204. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).