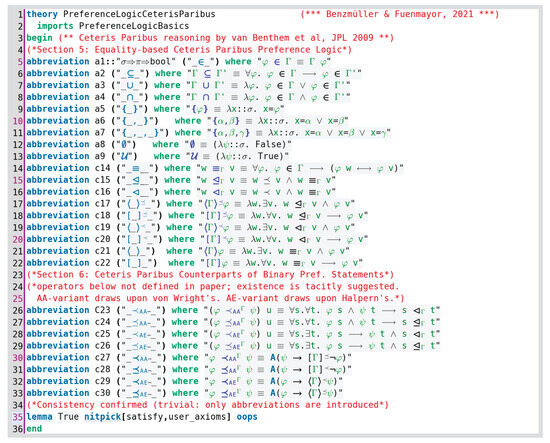
Abstract
The logico-pluralist LogiKEy knowledge engineering methodology and framework is applied to the modelling of a theory of legal balancing, in which legal knowledge (cases and laws) is encoded by utilising context-dependent value preferences. The theory obtained is then used to formalise, automatically evaluate, and reconstruct illustrative property law cases (involving the appropriation of wild animals) within the Isabelle/HOL proof assistant system, illustrating how LogiKEy can harness interactive and automated theorem-proving technology to provide a testbed for the development and formal verification of legal domain-specific languages and theories. Modelling value-oriented legal reasoning in that framework, we establish novel bridges between the latest research in knowledge representation and reasoning in non-classical logics, automated theorem proving, and applications in legal reasoning.
1. Introduction
Law today has to reflect highly pluralistic environments in which a plurality of values, world views and logics coexist. One function of modern, reflexive law is to enable the social interaction within and between such worlds (Teubner [1], Lomfeld [2]). Any sound model of legal reasoning needs to be pluralistic, supporting different value systems, value preferences, and maybe even different logical notions, while at the same time reflecting the uniting force of law.
Adopting such a perspective, in this paper, we apply the logico-pluralistic LogiKEy knowledge engineering methodology and framework (Benzmüller et al. [3]) to the modelling of a theory of value-based legal balancing, a discoursive grammar of justification (Lomfeld [4]), which we then employ to formally reconstruct and automatically assess, using the Isabelle/HOL proof assistant system, some illustrative property law cases involving the appropriation of wild animals (termed “wild animal cases”; cf. Bench-Capon and Sartor [5], Berman and Hafner [6], and Merrill and Smith [7] (Ch. II. A.1) for background). Lomfeld’s discoursive grammar is encoded, for our purposes, as a logic-based domain-specific language (DSL), in which the legal knowledge embodied in statutes and case corpora becomes represented as context-dependent preferences among (combinations of) values constituting a pluralistic value system or ontology. This knowledge can thus be complemented by further legal and world knowledge, e.g., from legal ontologies (Casanovas et al. [8], Hoekstra et al. [9]).
The LogiKEy framework supports plurality at different layers; cf. Figure 1. Classical higher-order logic (HOL) is fixed as a universal meta-logic (Benzmüller [10]) at the base layer (L0), on top of which a plurality of (combinations of) object logics can become encoded (layer L1). Employing these logical notions, we can now articulate a variety of logic-based domain-specific languages (DSLs), theories and ontologies at the next layer (L2), thus enabling the modelling and automated assessment of different application scenarios (layer L3). These linked layers, as featured in the LogiKEy approach, facilitate fruitful interdisciplinary collaboration between specialists in different AI-related domains and domain experts in the design and development of knowledge-based systems.
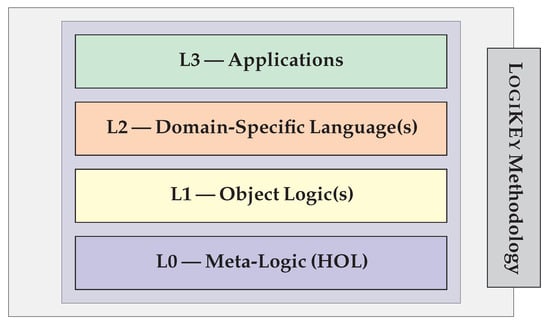
Figure 1.
LogiKEy development methodology.
LogiKEy, in this sense, fosters a division of labour among different specialist roles. For example, ‘logic theorists’ can concentrate on investigating the semantics and proof calculi for different object logics, while ‘logic engineers’ (e.g., with a computer science background) can focus on the encoding of suitable combinations of those formalisms in the meta-logic HOL and on the development and/or integration of relevant automated reasoning technology. Knowledge engineers can then employ these object logics for knowledge representation (by developing ontologies, taxonomies, controlled languages, etc.), while domain experts (ethicists, lawyers, etc.) collaborate with requirements elicitation and analysis, as well as providing domain-specific counselling and feedback. These tasks can be supported in an integrated fashion by harnessing (and extending) modern mathematical proof assistant systems (i.e., interactive theorem provers), which thus become a testbed for the development of logics and ethico-legal theories.
The work reported below is a LogiKEy-supported collaborative research effort involving two computer scientists (Benzmüller and Fuenmayor) together with a lawyer and legal philosopher (Lomfeld), who have joined forces with the goal of studying the computer-encoding and automation of a theory of value-based legal balancing: Lomfeld’s discoursive grammar (Lomfeld [4]). A formally verifiable legal domain-specific language (DSL) has been developed for the encoding of this theory (at LogiKEy’s layer L2). This DSL has been built on top of a suitably chosen object-logical language: a modal logic of preferences (at layer L1), by drawing upon the representation and reasoning infrastructure integrated within the proof assistant Isabelle/HOL (layer L0). The resulting system is then employed for the assessment of legal cases in property law (at layer L3), which includes the formal modelling of background legal and world knowledge as required to enable the verification of predicted legal case outcomes and the automatic generation of value-oriented logical justifications (backings) for them.
From a wider perspective, LogiKEy aims at supporting the practical development of computational tools for legal and normative reasoning based on formal methods. One of the main drives for its development has been the introduction of automated reasoning techniques for the design, verification (offline and online), and control of intelligent autonomous systems, as a step towards explicit ethical agents (Moor [11], Scheutz [12]). The argument here is that ethico-legal control mechanisms (such as ethical governors; cf. Arkin et al. [13]) of intelligent autonomous systems should be understood and designed as knowledge-based systems, where the required ethical and legal knowledge becomes explicitly represented as a logical theory, i.e., as a set of formulas (axioms, definitions, and theorems) encoded in a logic. We have set a special focus on the (re-)use of modern proof assistants based on HOL (Isabelle/HOL, HOL-Light, HOL4, etc.) and integrated automated reasoning tools (theorem provers and model generators) for the interactive development and verification of ethico-legal theories. To carry out the technical work reported in this paper, we have chosen to work with Isabelle/HOL, but the essence of our contributions can easily be applied to other proof assistants and automated reasoning systems for HOL.
Technical results concerning, in particular, our Isabelle/HOL encoding have been presented at the International Conference on Interactive Theorem Proving (ITP 2021) (Benzmüller and Fuenmayor [14]), and earlier ideas have been discussed at the Workshop on Models of Legal Reasoning (MLR 2020). In the present paper, we elaborate on these results and provide a more self-contained exposition by giving further background information on Lomfeld’s discoursive grammar, on the meta-logic HOL, and on the modal logic of preferences by van Benthem et al. [15].
More fundamentally, this paper presents the full picture as framed by the underlying LogiKEy framework and highlights methodological insights, applications, and perspectives relevant to the AI and Law community. One of our main motivations is to help build bridges between recent research in knowledge representation and reasoning in non-classical logics, automated theorem proving, and applications in normative and legal reasoning.
Paper Structure
After summarising the domain legal theory of value-based legal balancing (Lomfeld’s discoursive grammar) in Section 2, we briefly depict the LogiKEy development and knowledge engineering methodology in Section 3, and our meta-logic HOL in Section 4. We then outline our object logic of choice—a (quantified) modal logic of preferences—in Section 5, where we also present its encoding in the meta-logic HOL and formally verify the preservation of meta-theoretical properties using the Isabelle/HOL proof assistant. Subsequently, we model discoursive grammar in Section 6 and provide a custom-built DSL, which is again formally assessed using Isabelle/HOL. As an illustrative application of our framework, we present in Section 7 the formal reconstruction and assessment of well-known example legal cases in property law (“wild animal cases”), together with some considerations regarding the encoding of required legal and world knowledge. Related and further work is addressed in Section 8, and Section 9 concludes the article.
The Isabelle/HOL sources of our formalisation work are available at http://logikey.org (accessed on 12 December 2023) under https://github.com/cbenzmueller/LogiKEy/tree/master/Preference-Logics/EncodingLegalBalancing (accessed on 12 December 2023) (Preference-Logics/EncodingLegalBalancing). They are also explained in some detail in Appendix A.
2. A Theory of Legal Values: Discoursive Grammar of Justification
The case study with which we illustrate the LogiKEy methodology in the present paper consists in the formal encoding and assessment on the computer of a theory of value-based legal balancing as put forward by Lomfeld [4]. This theory proposes a general set of dialectical (socio-legal) values referred to as a discoursive grammar of justification discourses. Lomfeld himself has played the role of the domain expert in our joint research, which from a methodological perspective, can be characterised as being both in part theoretical and in part empirical. Lomfeld’s primary role has been to provide background legal domain knowledge and to assess the adequacy of our formalisation results, while informing us of relevant conceptual and legal distinctions that needed to be made. In a sense, this created a the legal theory (discoursive grammar) and LogiKEy’s methodology have been put to the test. This section presents discoursive grammar and discusses some of its merits in comparison to related approaches.
Logical reconstructions quite often separate deductive rule application and inductive case-contextual interpretation as completely distinct ways of legal reasoning (cf. the overview in Prakken and Sartor [16]). Understanding the whole process of legal reasoning as an exchange of opposing action-guiding arguments, i.e., practical argumentation (Alexy [17], Feteris [18]), a strict separation between logically distinct ways of legal reasoning breaks down. Yet, a variety of modes of rule-based (Hage [19], Prakken [20], Modgil and Prakken [21]), case-based (Ashley [22], Aleven [23], Horty [24]) and value-based (Berman and Hafner [6], Bench-Capon et al. [25], Grabmair [26]) reasoning coexist in legal theory and (court) practice.
In line with current computational models combining these different modes of reasoning (e.g., Bench-Capon and Sartor [5], Maranhao and Sartor [27]), we argue that a discourse theory of law can consistently integrate them in the form of a multi-level system of legal reasoning. Legal rules or case precedents can thus be translated into (or analysed as) the balancing of plural and opposing (socio-legal) values on a deeper level of reasoning (Lomfeld [28]).
There exist indeed some models for quantifying legal balancing, i.e., for weighing competing reasons in a case (e.g., Alexy [29], Sartor [30]). We share the opinion that these approaches need to get “integrated with logic and argumentation to provide a comprehensive account of value-oriented reasoning” (Sartor [31]). Hence, a suitable model of legal balancing would need to reconstruct rule subsumption and case distinction as argumentation processes involving conflicting values.
Here, the functional differentiation of legal norms into rules and principles reveals its potential (Dworkin [32], Alexy [33]). Whereas legal rules have a binary all-or-nothing validity driving out conflicting rules, legal principles allow for a scalable dimension of weight. Thus, principles could outweigh each other without rebutting the normative validity of colliding principles. Legal principles can be understood as a set of plural and conflicting values on a deep level of socio-legal balancing, which is structured by legal rules on an explicit and more concrete level of legal reasoning (Lomfeld [28]). The two-faceted argumentative relation is partly mirrored in the functional differentiation between goal-norms and action-norms (Sartor [30]) but should not be mixed up with a general understanding of principles as abstract rules (Raz [34], Verheij et al. [35]) or as specific constitutional law elements (Neves [36], Barak [37]).
In any event, if preferences between defeasible rules are reconstructed and justified in terms of preferences between underlying values, some questions about values necessarily pop up. In the words of Bench-Capon and Sartor [5]: “Are values scalar? […] Can values be ordered at all? […] How can sets of values be compared? […] Can values conflict so the promotion of their combination is worse than promoting either separately? Can several less important values together overcome a more important value?”.
Hence, an encompassing approach for legal reasoning as practical argumentation needs not only a formal reconstruction of the relation between legal values (or principles) and legal rules but also a substantial framework of values (a basic value system) that allows to systematise value comparison and conflicts as a discoursive grammar (Lomfeld [4,28]) of argumentation. In this article, we define a value system not as a “preference order on sets of values” (van der Weide et al. [38]) but as a pluralistic set of values which allow for different preference orders. The computational conceptualisation (as a formal logical theory) of such a set of representational primitives for a pluralist basic value system can then be considered a value “ontology” (Gruber [39,40], Smith [41]), which of course needs to be complemented by further ontologies for relevant background legal and world knowledge (see Casanovas et al. [8], Hoekstra et al. [9]).
Combining the discourse-theoretical idea that legal reasoning is practical argumentation with a two-faceted model of legal norms, legal rules could be logically reconstructed as conditional preference relations between conflicting underlying value principles (Lomfeld [28], Alexy [33]). The legal consequence of a rule R thus implies the preference of value principle A over value principle B, noted (e.g., health security outweighs freedom to move)1. This value preference applies under the condition that the rule’s prerequisites and hold. Thus, if the propositions and are true in a given situation (e.g., a virus pandemic occurs and voluntary shutdown fails), then the value preference is obtained. This value preference can be said to weight or balance the two values A and B against each other. We can thus translate this concrete legal rule as a conditional preference relation between colliding value principles:
More generally, A and B could also be structured as aggregates of value principles, whereas the condition of the rule can consist in a conjunction of arbitrary propositions. Moreover, it may well happen that, given some conditions, several rules become relevant in a concrete legal case. In such cases, the rules determine a structure of legal balancing between conflicting plural value principles. Moreover, making explicit the underlying balancing of values against each other (as value preferences) helps to justify a legal consequence (e.g., sanctioned lockdown) or ruling in favour of a party (e.g., defendant) in a legal case.
But which value principles are to be balanced? How can we find a suitable justification framework? Based on comparative discourse analyses in different legal systems, one can reconstruct a general dialectical (antagonistic) taxonomy of legal value principles used in (at least Western) legislation, legislative materials, cases, textbooks and scholar writings (Lomfeld [28]). The idea is to provide a plural and yet consistent system of basic legal values and principles (a discoursive grammar), independent of concrete cases or legal fields, to justify legal decisions.
The proposed legal value system (Lomfeld [4]), see Figure 2, is consistent with many existing taxonomies of antagonistic psychological (Rokeach [42], Schwartz [43]), political (Eysenck [44], Mitchell [45]), and economic values (Clark [46])2. In all social orders, one can observe a general antinomy between individual and collective values. Ideal types of this fundamental normative dialectic are the basic value of FREEDOM for the individual, and the basic value of SECURITY for the collective perspective. Another classic social value antinomy is between a functional–economic (utilitarian) and a more idealistic (egalitarian) viewpoint, represented in the ethical debate by the essential dialectic concerning the basic values of UTILITY versus EQUALITY. These four normative poles stretch two axes of value coordinates for the general value system construction. We thus speak of a normative dialectics since each of the antagonistic basic values and related principles can (and in most situations will) collide with each other.
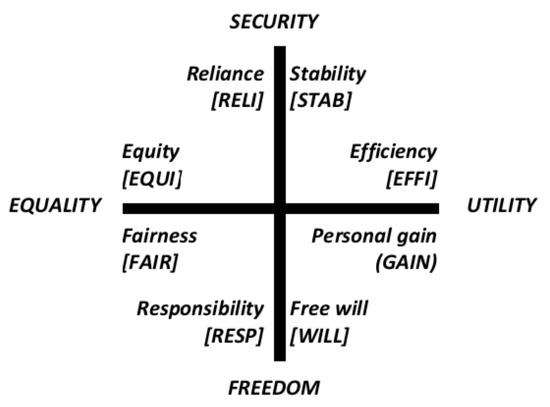
Figure 2.
Basic legal value system (ontology) by Lomfeld [4].
Within this dialectical matrix, eight more concrete legal value principles are identified. FREEDOM represents the normative basic value of individual autonomy and comprises the legal (value) principles of (more functional) individual choice or ‘free will’ (WILL) and (more idealistic) (self-)‘responsibility’ (RESP). The basic value of SECURITY addresses the collective dimension of public order and comprises the legal principles of the (more functional) collective ‘stability’ (STAB) of a social system and (more idealistic) social trust or ‘reliance’ (RELI). The value of UTILITY means economic welfare on the personal and collective levels and comprises the legal principles of collective overall welfare maximisation, i.e., ‘efficiency’ (EFFI), and individual welfare maximisation, i.e., economic benefit or ‘gain’ (GAIN). Finally, EQUALITY represents the normative ideal of equal treatment and equal allocation of resources and comprises the legal principles of (more individual) equal opportunity or procedural ‘fairness’ (FAIR) and (more collective) distributional equality or ‘equity’ (EQUI).
The general value system (or ontology) of the proposed discoursive grammar can consistently embed existing AI and Law value sets. Earlier accounts of value-oriented reasoning are all tailoring distinct domain value sets for specific case areas. The most prominent and widespread examples are common law property cases concerning the appropriation of (wild) animals (e.g., Berman and Hafner [6], Bench-Capon et al. [25], Sartor [50], Prakken [51]) and its modern variant of a straying baseball (e.g., Bench-Capon [52], Gordon and Walton [53]). In both settings, the defendant’s claim to link property to actual possession is justified with the stability value of (legal) certainty and contrasted with the liberal idea to protect individual activities from (legal) interference favouring the plaintiff (Berman and Hafner [6], Bench-Capon [52]). The discoursive grammar reconstructs this normative tension as collision between the general values of SECURITY and FREEDOM. The underlying dialectic reappears in many typical constitutional right cases, where individual liberty collides with collective security issues (Sartor [30]), e.g., also in the form of privacy versus law enforcement in the analysed Fourth Amendment cases (Bench-Capon and Prakken [54]).
The other dialectic dimension of UTILITY v EQUALITY is also represented in the AI and Law value reconstructions. ’UTILITY’ (Bench-Capon [52]) could be understood to embrace the values of ’competition’ (Berman and Hafner [6]), ’economic activity’ (Bench-Capon et al. [25]), ’economic benefit’ (Prakken [51]), and economic ’productivity’ (Sartor [50]). On the other hand, ’EQUALITY’ is addressed with values of ’fairness’, ’equity’, and ’public order’ (Berman and Hafner [6], Bench-Capon [52], Gordon and Walton [53]).
The discoursive grammar taxonomy works as well within another classic field of AI and Law reconstruction, i.e., trade secret law (Chorley and Bench-Capon [55]), following the long-standing HYPO modelling tradition (Ashley [22], Bench-Capon [56]). The two-dimensional, four-pole matrix also covers the basic trade secret domain values (Grabmair [26]): ’property’ (SECURITY, UTILITY) and ’confidentiality’ (SECURITY) interests versus free and equal public access to information (FREEDOM, EQUALITY) and open competition (UTILITY, FREEDOM).
A key feature of the dialectical discoursive grammar approach to value argumentation consists in its purely qualitative modelling of legal balancing in terms of context-dependent logic-based preferences among values, without any need for (but the possibility of) determining quantitative weights. The modelling is thus more flexible than more hierarchical approaches to value representation (Verheij [57]).
3. The LogiKEy Methodology
LogiKEy, as a methodology (Benzmüller et al. [3]), refers to the principles underlying the organisation and the conduct of complex knowledge design and engineering processes, with a particular focus on the legal and ethical domain. Knowledge engineering refers to all the technical and scientific aspects involved in building, maintaining and using knowledge-based systems, employing logical formalisms as a representation language. In particular, we speak of logic engineering to highlight those tasks directly related to the syntactic and semantic definition, as well as to the meta-logical encoding and automation, of different combinations of object logics. It is also LogiKEy’s objective to fruitfully integrate contributions from different research communities (such as interactive and automated theorem proving, non-classical logics, knowledge representation, and domain specialists) and to make them accessible at a suitable level of abstraction and technicality to practitioners in diverse fields.
A fundamental characteristic of the LogiKEy methodology consists in the utilisation of classical higher-order logic (HOL, cf. Benzmüller and Andrews [58]) as a general-purpose logical formalism in which to encode different (combinations of) object logics. This enabling technique is known as shallow3 semantical embeddings (SSEs). HOL thus acts as the substrate in which a plurality of logical languages, organised hierarchically at different abstraction layers, become ultimately encoded and reasoned with. This in turn enables the provision of powerful tool support: we can harness mathematical proof assistants (e.g., Isabelle/HOL) as a testbed for the development of logics, and ethico-legal DSLs and theories. More concretely, off-the-shelf theorem provers and (counter-)model generators for HOL as provided, for example, in the interactive proof assistant Isabelle/HOL (Blanchette et al. [61]), are assisting the LogiKEy knowledge and logic engineers (as well as domain experts) to flexibly experiment with underlying (object) logics and their combinations, with general and domain knowledge, and with concrete use cases—all at the same time. Thus, continuous improvements of these off-the-shelf provers, without further ado, leverage the reasoning performance in LogiKEy.
The LogiKEy methodology, cf. Figure 1, has been instantiated in this article to support and guide the simultaneous development of the different modelling layers as depicted in Figure 3, which will be the subject of discussion in the following sections. According to the logico-pluralistic nature of LogiKEy, only the lowest layer (L0), meta-logic HOL (cf. Section 4), remains fixed, while all other layers are subject to dynamic adjustments until a satisfying overall solution in the overall modelling process is reached. At the next layer (L1), we are faced with the choice of an object logic, in our case, a modal logic of preference (cf. Section 5). A legal DSL (cf. Section 6), created after discoursive grammar (cf. Section 2), further extends this object logic at a higher level of abstraction (layer L2). At the upper layer (layer L3), we use this legal DSL to encode and automatically assess some example legal cases (“wild animal cases”) in property law (cf. Section 7) by relying upon previously encoded background legal and world knowledge.4 The higher layers thus make use of the concepts introduced at the lower layers. Moreover, at each layer, the encoding efforts are guided by selected tests and ‘sanity checks’ in order to formally verify relevant properties of the encodings at and up to that level.

Figure 3.
LogiKEy development methodology as instantiated in the given context.
It is worth noting that the application of our approach to deciding concrete legal cases reflects ideas in the AI and Law literature about understanding the solution of legal cases as theory construction, i.e., “building, evaluating and using theories” (Bench-Capon and Sartor [5], Maranhao and Sartor [27])5. This multi-layered, iterative knowledge engineering process is supported in our LogiKEy framework by adapting interactive and automated reasoning technology for HOL (as a meta-logic).
An important aspect thereby is that the LogiKEy methodology foresees and enables the knowledge engineer to flexibly switch between the modelling layers and to suitably adapt the encodings also at lower layers if needed. The engineering process thus has backtracking points, and several work cycles may be required; thereby, the higher layers may also pose modification requests to the lower layers. Such demands, unlike in most other approaches, may also involve far-reaching modifications of the chosen logical foundations, e.g., in the particularly chosen modal preference logic.
The work we present in this article is, in fact, the result of an iterative, give-and-take process encompassing several cycles of modelling, assessment, and testing activities, whereby a (modular) logical theory gradually evolves until eventually reaching a state of highest coherence and acceptability. In line with previous work on computational hermeneutics (Fuenmayor and Benzmüller [63]), we may then speak of arriving at a state of reflective equilibrium (Daniels [64]) as the end-point of an iterative process of mutual adjustment among (general) principles and (particular) judgements, where the latter are intended to become logically entailed by the former. A similar idea of reflective equilibrium has been introduced by the philosopher John Rawls in moral and political philosophy as a method for the development of a consistent theory of justice (Rawls [65]). An even earlier formulation of this approach is often credited to the philosopher Nelson Goodman, who proposed the idea of reflective equilibrium as a method for the development of (inference rules for) deductive and inductive logical systems (Goodman [66]). Again, the spirit of LogiKEypoints very much in the same direction.
4. Meta-Logic (L0)—Classical Higher-Order Logic
To keep this article sufficiently self-contained, we briefly introduce a classical higher-order logic, termed HOL; more detailed information on HOL and its automation can be found in the literature (Benzmüller and Andrews [58], Andrews [67], Andrews [68], Benzmüller et al. [69], Benzmüller and Miller [70]).
The notion of HOL used in this article refers to a simply typed logic of functions that has been put forward by Church [71]. Hence, all terms of HOL are assigned a fixed and unique type, commonly written as a subscript (i.e., the term has as its type). HOL provides notation as an elegant and useful means to denote unnamed functions, predicates, and sets; notation also supports compositionality, a feature we heavily exploit to obtain elegant, non-recursive encoding definitions for our logic embeddings in the remainder. Types in HOL eliminate paradoxes and inconsistencies.
HOL comes with a set T of simple types, which is freely generated from a set of basic types using the function type constructor → (written as a right-associative infix operator). For instance, o, and are types. The type o denotes a two-element set of truth values, and denotes a non-empty set of individuals6. Further base types may be added as the need arises.
The terms of HOL are inductively defined starting from typed constant symbols () and typed variable symbols () using λ-abstraction () and function application (), thereby obeying type constraints as indicated. Type subscripts and parentheses are usually omitted to improve readability, if obvious from the context or irrelevant. Observe that abstractions introduce unnamed functions. For example, the function that adds two to a given argument x can be encoded as , and the function that adds two numbers can be encoded as 7. HOL terms of type o are also called formulas8.
Moreover, to obtain a proper logic, we add and (for each type ) as predefined typed constant symbols to our language and call them primitive logical connectives. Binder notation for quantifiers is used as an abbreviation for .
The primitive logical connectives are given a fixed interpretation as usual, and from them, other logical connectives can be introduced as abbreviations. Material implication and existential quantification , for example, may be introduced as shortcuts for and , respectively. Additionally, description or choice operators or primitive equality (for each type ), abbreviated as , may be added. Equality can also be defined by exploiting Leibniz’ principle, expressing that two objects are equal if they share the same properties.
It is well known that, as a consequence of Gödel’s Incompleteness Theorems, HOL with standard semantics is necessarily incomplete. In contrast, theorem-proving in HOL is usually considered with respect to so-called general semantics (or Henkin semantics), in which a meaningful notion of completeness can be achieved (Andrews [68], Henkin [73]). Note that standard models are subsumed by Henkin general models such that valid HOL formulas with respect to general semantics are also valid in the standard sense.
For the purposes of the present article, we shall omit the formal presentation of HOL semantics and of its proof system(s). We fix instead some useful notation for use in the remainder. We write if formula of HOL is true in a Henkin general model ; denotes that is (Henkin) valid, i.e., that for all Henkin models .
5. Object Logic (L1)—A Modal Logic of Preferences
Adopting the LogiKEy methodology of Section 3 to support the given formalisation challenge, the first question to be addressed is how to (initially) select the object logic at layer L1. The chosen logic not only must be expressive enough to allow the encoding of knowledge about the law (and the world) as required for the application domain (cf. our case study in Section 7) but must also provide the means to represent the kind of conditional value preferences featured in discoursive grammar (as described in Section 2). Importantly, it must also enable the adequate modelling of the notions of value aggregation and conflict as featured in our legal DSL (discussed in Section 6).
Our initial choice has been the family of modal logics of preference presented by van Benthem et al. [15], which we abbreviate by in the remainder. has been put forward as a modal logic framework for the formalisation of preferences which also allows for the modelling of ceteris paribus clauses in the sense of “all other things being equal”. This reading goes back to the seminal work of von Wright in the early 1960s (von Wright [74])9.
appears well suited for effective automation using the SSEs approach, which has been an important selection criterion. This judgment is based on good prior experience with SSEs of related (monadic) modal logic frameworks (Benzmüller and Paulson [75,76]), whose semantics employs accessibility relations between possible worlds/states, just as does. We note, however, that this choice of (a family of) object logics () is just one out of a variety of logical systems which can be encoded as fragments of HOL employing the shallow semantical embedding approach; cf. Benzmüller [10]. This approach also allows us ‘upgrade’ our object logic whenever necessary. In fact, we add quantifiers and conditionals to in Section 5.4. Moreover, we may consider combining with other logics, e.g., with normal modal logics by the mechanisms of fusion and product (Carnielli and Coniglio [77]), or, more generally, by algebraic fibring (Carnielli et al. [78] (Ch. 2–3)). This illustrates a central objective of the LogiKEy approach, namely that the precise choice of a formalisation logic (i.e., the object logic at L1) is to be seen as a parameter.
In the subsections below, we start by informally outlining the family of modal logics of preferences (their formal definition can be found in Appendix A.1). We then discuss its embedding as a fragment of HOL using the SSE approach. As for Section 4, the technically and formally less interested reader may actually skip the content of these subsections and return later.
5.1. The Modal Logic of Preferences
We sketch the syntax and semantics of adapting the description from van Benthem et al. [15] (see Appendix A.1 for more details).
The formulas of are inductively defined as follows (where ranges over a set of propositional constant symbols):
As usual in modal logic, van Benthem et al. [15] give a Kripke-style semantics, which models propositions as sets of states or ‘worlds’. semantics employs a reflexive and transitive accessibility relation ⪯ (respectively, its strict counterpart ≺) to define the modal operators in the usual way. This relation is called a betterness ordering (between states or ‘worlds’).
For the sake of self-containedness, we summarize below the semantics of .
A preference model is a triple where (i) is a set of worlds/states; (ii) ⪯ is a betterness relation (reflexive and transitive) on , where its strict subrelation ≺ is defined as := for all (totality of ⪯, i.e., , is generally not assumed); and (iii) is a standard modal valuation. Below, we show the truth conditions for ’s modal connectives (the rest being standard):
A formula is true at world in model if . is globally true in , denoted , if is true at every . Moreover, is valid (in a class of models ) if globally true in every (), denoted ().
Thus, (respectively, ) can informally be read as “ is true in a state that is considered to be at least as good as (respectively, strictly better than) the current state”, and can be read as “there is a state where is true”.
Further, standard connectives such as ∨, →, and ↔ can also be defined in the usual way. The dual operators (respectively, ) and can also be defined as (respectively, ) and .
Readers acquainted with Kripke semantics for modal logic will notice that features normal S4 and K4 diamonds operators and , together with a global existential modality E. We can thus give the usual reading to □ and ⋄ as necessity and possibility, respectively.
Moreover, note that since the strict betterness relation ≺ is not reflexive, it does not hold in general that (modal axiom T). Hence, we can also give a ‘deontic reading’ to and ; the former could then read as “ is admissible/permissible” and the latter as “ is recommended/obligatory”. This deontic interpretation can be further strengthened so that the latter entails the former by extending with the postulate (modal axiom D), or alternatively, by postulating the corresponding (meta-logical) semantic condition, namely, that for each state, there exists a strictly better one (seriality for ≺).
Observe that we use boldface fonts to distinguish standard logical connectives of from their counterparts in HOL.
Similarly, eight different binary connectives for modelling preference statements between propositions can be defined in :
These connectives arise from four different ways of ‘lifting’ the betterness ordering ⪯ (respectively, ≺) on states to a preference ordering on sets of states or propositions:
Thus, different choices for a logic of preference are possible if we restrict ourselves to employing only a selected preference connective, where each choice provides the logic with particular characteristics so that we can interpret preference statements between propositions (i.e., sets of states) in a variety of ways. As an illustration, according to the semantic interpretation provided by van Benthem et al. [15], we can read as “every -state being better than every -state”, and read as “every -state having a better -state” (and analogously for others).
In fact, the family of preference logics can be seen as encompassing, in substance, the proposals by von Wright [74] (variant ) and Halpern [79] (variants )10. As we will see later in Section 6, there are only four choices ( and ) of modal preference relations that satisfy the minimal conditions we impose for a logic of value aggregation. Moreover, they are the only ones which satisfy transitivity, a quite controversial property in the literature on preferences.
Last but not least, van Benthem et al. [15] have provided ‘syntactic’ counterparts for these binary preference connectives as derived operators in the language of (i.e., defined by employing the modal operators (respectively, ). We note these ‘syntactic variants’ in boldface font:
The relationship between both, i.e., the semantically and syntactically defined families of binary preference connectives is discussed in van Benthem et al. [15]. In a nutshell, as regards the EE and the AE variants, both definitions (syntactic and semantic) are equivalent; concerning the EA and the AA variants, the equivalence only holds for a total ⪯ relation. In fact, drawing upon our encoding of as presented in the next subsection Section 5.2, we have employed Isabelle/HOL for automatically verifying this sort of meta-theoretic correspondence; cf. Lines 4–12 in Figure A4 in Appendix A.1.
5.2. Embedding in HOL
For the implementation of we utilise the shallow semantical embeddings (SSE) technique, which encodes the language constituents of an object logic, in our case, as expressions (-terms) in HOL. A core idea is to model (relevant parts of) the semantical structures of the object logic explicitly in HOL. This essentially shows that the object logic can be unravelled as a fragment of HOL and hence automated as such. For (multi-)modal normal logics, like , the relevant semantical structures are relational frames constituted by sets of possible worlds/states and their accessibility relations. formulas can thus be encoded as predicates in HOL taking possible worlds/states as arguments11. The detailed SSE of the basic operators of in HOL is presented and formally tested in Appendix A.1. Further extensions to support reasoning with ceteris paribus clauses in are studied there as well.
As a result, we obtain a combined interactive and automated theorem prover and model finder for (and its extensions; cf. Section 5.4) realised within Isabelle/HOL. This is a new contribution since we are not aware of any other existing implementation and automation of such a logic. Moreover, as we will demonstrate below, the SSE technique supports the automated assessment of the meta-logical properties of the embedded logic in Isabelle/HOL, which in turn provides practical evidence for the correctness of our encoding.
The embedding starts out with declaring the HOL base type , which is denoting the set of possible states (or worlds) in our formalisation. propositions are modelled as predicates on objects of type (i.e., as truth sets of states/worlds) and, hence, they are given the type , which is abbreviated as in the remainder. The betterness relation⪯ of is introduced as an uninterpreted constant symbol in HOL, and its strict variant ≺ is introduced as an abbreviation standing for the HOL term . In accordance with van Benthem et al. [15], we postulate that ⪯ is a preorder, i.e., reflexive and transitive.
In a next step, the -type lifted logical connectives of are introduced as abbreviations for -terms in the meta-logic HOL. The conjunction operator ∧ of , for example, is introduced as an abbreviation , which stands for the HOL term , so that reduces to , denoting the set12 of all possible states w in which both and hold. Analogously, for the negation, we introduce an abbreviation which stands for .
The operators and use ⪯ and ≺ as guards in their definitions. These operators are introduced as shorthand and abbreviating the HOL terms and , respectively. thus reduces to , denoting the set of all worlds w so that holds in some world v that is at least as good as w; analogously, for . Additionally, the global existential modality is introduced as a shorthand for the HOL term . The duals , and can easily be added so that they are equivalent to , and , respectively.
Moreover, a special predicate (read is valid) for -type lifted formulas in HOL is defined as an abbreviation for the HOL term .
The encoding of object logic in meta-logic HOL is presented in full detail in Appendix A.1.
Remember again that in the LogiKEy methodology, the modeller is not enforced to make an irreversible selection of an object logic (L1) before proceeding with the formalisation work at higher LogiKEy layers. Instead, the framework enables preliminary choices at all layers, which can easily be revised by the modeller later on if this is indicated by, for example, practical experiments.
5.3. Formally Verifying Encoding’s Adequacy
A pen-and-paper proof of the faithfulness (soundness and completeness) of the SSE easily follows from previous results regarding the SSE of propositional multi-modal logics (Benzmüller and Paulson [75]) and their quantified extensions (Benzmüller and Paulson [76]); cf. also Benzmüller [10] and the references therein. We sketch such an argument below, as it provides an insight into the underpinnings of SSE for the interested reader.
By drawing upon the approach in Benzmüller and Paulson [75], it is possible to define a mapping between semantic structures of the object logic (preference models ) and the corresponding structures in HOL (general Henkin models ) in such a way that
where denotes derivability in the (complete) calculus axiomatised by van Benthem et al. [15]. Observe that HOL() corresponds to HOL extended with the relevant types and constants plus a set of axioms encoding semantic conditions, e.g., the reflexivity and transitivity of .
The soundness of the SSE (i.e., implies that ) is particularly important since it ensures that our modelling does not give any ‘false positives’, i.e., proofs of non-theorems. The completeness of the SSE (i.e., implies ) means that our modelling does not give any ‘false negatives’, i.e., spurious counterexamples. Besides the pen-and-paper proof, completeness can also be mechanically verified by deriving the -type lifted axioms and inference rules in HOL(); cf. Figure A4 and Figure A5 in Appendix A.1.
To gain practical evidence of the faithfulness of our SSE of in Isabelle/HOL and also to assess the proof automation performance, we have conducted numerous experiments in which we automatically verify the meta-theoretical results on as presented by van Benthem et al. [15]13. Note that these statements thus play a role analogous to that of a requirements specification document (cf. Figure A4 and Figure A5 in Appendix A.1).
5.4. Beyond : Extending the Encoding with Quantifiers and Conditionals
We can further extend our encoded logic by adding quantifiers. This is performed by identifying with the HOL term and with ; cf. binder notation in Section 4. This way, quantified expressions can be seamlessly employed in our modelling at the upper layers (as performed exemplarily in Section 7). We refer the reader to Benzmüller and Paulson [76] for a more detailed discussion (including faithfulness proofs) of SSEs for quantified (multi-)modal logics.
Moreover, observe that having a semantics based on preferential structures allows us to extend our logic with a (defeasible) conditional connective ⇒. This can be performed in several closely related ways. As an illustration, drawing upon an approach by Boutilier [88], we can further extend the SSE of by defining the connective:
An intuitive reading of this conditional statement would be “every -state has a reachable -state such that holds there in also in every reachable -state” (where we can interpret “reachable” as “at least as good”). This is equivalent, for finite models, to demanding that all ‘best’ states are states; cf. Lewis [89]. This can indeed be shown equivalent to the approach of Halpern [79], who axiomatises a strict binary preference relation , interpreted as “relative likelihood”14. For further discussion regarding the properties and applications of this—and other similar—preference-based conditionals, we refer the interested reader to the discussions in van Benthem [90] and Liu [91] (Ch. 3).
6. Domain Specific Language (L2)—Value-Oriented Legal Theory
In this section, we incrementally define a domain-specific language (DSL) for reasoning with values in a legal context. We start by defining a “logic of value preferences” on top of the object logic (layer L1). This logic is subsequently encoded in Isabelle/HOL, and in the process, it becomes suitably extended with custom means to encode the discoursive grammar in Section 2. We thus obtain a HOL-based DSL formally modelling discoursive grammar. This formally verifiable DSL is then put to the test using theorem provers and model generators.
Recall from the discussion of the discoursive grammar in Section 2 that value-oriented legal rules can become expressed as context-dependent preference statements between value principles (e.g., RELIance, STABility, and WILL). Moreover, these value principles were informally associated with basic values (i.e., FREEDOM, UTILITY, SECURITY and EQUALITY), in such a way as to arrange the first over (the quadrants of) a plane generated by two axes labelled by the latter. More specifically, each axis’ pole is labelled by a basic value, with values lying at contrary poles playing somehow antagonistic roles (e.g., FREEDOM vs. SECURITY). We recall the corresponding diagram (Figure 2) below for the sake of illustration.
Inspired by this theory, we model the notion of a (value) principle as consisting of a collection (in this case, a set15) of basic values. Thus, by considering principles as structured entities, we can more easily define adequate notions of aggregation and conflict among them; cf. Section 6.
From a logical point of view, it is additionally required to conceive value principles as truth bearers, i.e., propositions16. We thus seem to face a dichotomy between, at the same time, modelling value principles as sets of basic values and modelling them as sets of worlds. In order to adequately tackle this modelling challenge, we make use of the mathematical notion of a Galois connection17.
For the sake of exposition, Galois connections are to be exemplified by the notion of derivation operators in the theory of Formal Concept Analysis (FCA), from which we took inspiration; cf. Ganter and Wille [93]. FCA is a mathematical theory of concepts and concept hierarchies as formal ontologies, which finds practical application in many computer science fields, such as data mining, machine learning, knowledge engineering, semantic web, etc.18.
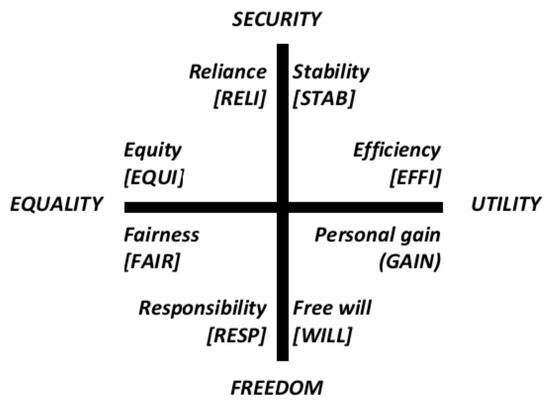
Figure 4.
Basic legal value system (ontology) by Lomfeld [4].
6.1. Some Basic FCA Notions
A formal context is a triple , where G is a set of objects, M is a set of attributes, and I is a relation between G and M (usually called incidence relation), i.e., . We read as “the object g has the attribute m”. Additionally, we define two so-called derivation operators ↑ and ↓ as follows:
is the set of all attributes shared by all objects from A, which we call the intent of A. Dually, is the set of all objects sharing all attributes from B, which we call the extent of B. This pair of derivation operators thus forms an antitone Galois connection between (the powersets of) G and M, and we always have that iff ; cf. Figure 5.
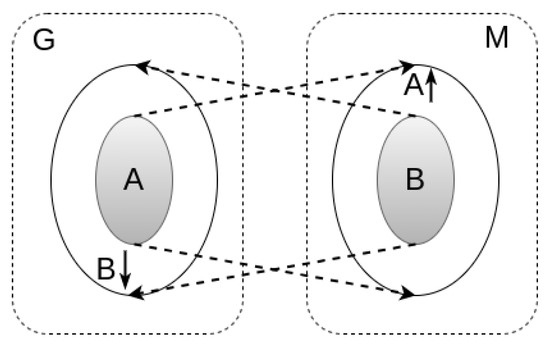
Figure 5.
A suggestive representation of a Galois connection between a set of objects G (e.g., worlds) and set of their attributes M (e.g., values).
A formal concept (in a context K) is defined as a pair such that , , , and . We call A and B the extent and the intent of the concept , respectively19. Indeed, and are always concepts.
The set of concepts in a formal context is partially ordered by set inclusion of their extents, or, dually, by the (reversing) inclusion of their intents. In fact, for a given formal context, this ordering forms a complete lattice: its concept lattice. Conversely, it can be shown that every complete lattice is isomorphic to the concept lattice of some formal context. We can thus define lattice-theoretical meet and join operations on FCA concepts in order to obtain an algebra of concepts20:
6.2. A Logic of Value Preferences
In order to enable the modelling of the legal theory (discoursive grammar) as discussed in Section 2, we will enhance our object logic with additional expressive means by drawing upon the FCA notions expounded above and by assuming an arbitrary domain set of basic values.
A first step towards our legal DSL is to define a pair of operators ↑ and ↓ such that they form a Galois connection between the semantic domain of worlds/states of (as ‘objects’ G) and the set of basic values (as ‘attributes’ M). By employing the operators ↑ and ↓ in an appropriate way, we can obtain additional well-formed terms, thus converting our object logic in a logic of value preferences21. Details follow.
6.2.1. Principles, Values and Propositions
We introduce a formal context composed by the set of worlds , the set of basic values , and the (implicit) relation , which we might interpret, intuitively, in a teleological sense: means that value v provides reasons for the situation (world/state) w to obtain.
Now, recall that we aim at modelling value principles as sets of basic values (i.e., elements of ), while, at the same time, conceiving of them as propositions (elements of ). Indeed, drawing upon the above FCA notions allows us to overcome this dichotomy. Given the formal context , we can define the pair of derivation operators ↑ and ↓ employing the corresponding definitions ((1)–(2)) above.
We can now employ these derivation operators to switch between the ‘(value) principles as sets of (basic) values’ and the ‘principles as propositions (sets of worlds)’ perspectives. Hence, we can now—recalling the informal discussion of the semantics of the object logic in Section 5—give an intuitive reading for truth at a world in a preference model to terms of the form ; namely, we can read as “principle P provides a reason for (state of affairs) w to obtain”. In the same vein, we can read as “principle P provides a reason for proposition A being the case”22.
6.2.2. Value Aggregation
Recalling discoursive grammar, as discussed in Section 2, our logic of value preferences must provide means for expressing conditional preferences between value principles, according to the schema:
As regards the preference relation (connective ≺), we might think that, in principle, any choice among the eight preference relation variants in (cf. Section 5) will work. Let us recall, however, that discoursive grammar also presupposed some (no further specified) mechanism for aggregating value principles (operator ⊕); thus, the joint selection of both a preference relation and a aggregation operator cannot be arbitrary: they need to interact in an appropriate way. We explore first a suitable mechanism for value aggregation before we get back to this issue.
Suppose that, for example, we are interested in modelling a legal case in which, say, the principle of “respect for property” together with the principle “economic benefit for society” outweighs the principle of “legal certainty”23. A binary connective ⊕ for modelling this notion of together with, i.e., for aggregating legal principles (as reasons) must, expectedly, satisfy particular logical constraints in interaction with a (suitably selected) value preference relation ≺:
For our purposes, the aggregation connectives are most conveniently defined using set union (FCA join), which gives us commutativity. As it happens, only the and variants from Section 5 satisfy the first two conditions. They are also the only variants satisfying transitivity. Moreover, if we choose to enforce the optional third aggregation principle (called “union property”; cf. Halpern [79]), then we would be left with only one variant to consider, namely 24.
In the end, after extensive computer-supported experiments in Isabelle/HOL we identified the following candidate definitions for the value aggregation and preference connectives, which satisfy our modelling desiderata25:
- For the binary value aggregation connective ⊕, we identified the following two candidates (both taking two value principles and returning a proposition):Observe that is based upon the join operation on the corresponding FCA formal concepts (see Equation (4)). is a strengthening of the first since .
- For a binary preference connective ≺ between propositions, we have as candidates:
In line with the LogiKEy methodology, we consider the concrete choices of definitions for ≺, ⊕, and even ⇒ (classical or defeasible) as parameters in our overall modelling process. No particular determination is enforced in the LogiKEy approach, and we may alter any preliminary choices as soon as this appears appropriate. In this spirit, we experimented with the listed different definition candidates for our connectives and explored their behaviour. We will present our final selection in Section 6.3.
6.2.3. Promoting Values
Given that we aim at providing a logic of value preferences for use in legal reasoning, we still need to consider the mechanism by which we can link legal decisions, together with other legally relevant facts, to values. We conceive of such a mechanism as a sentence schema, which reads intuitively as “Taking decision D in the presence of facts Fpromotes (value) principle P”. The formalisation of this schema can indeed be seen as a new predicate in the domain-specific language (DSL) that we have been gradually defining in this section. In the expression Promotes(F,D,P), we have that F is a conjunction of facts relevant to the case (a proposition), D is the legal decision, and P is the value principle thereby promoted26:
It is important to remark that, in the spirit of the LogiKEy methodology, the definition above has arisen from the many iterations of encoding, testing and ‘debugging’ of the modelling of the ‘wild animal cases’ in Section 7 (until reaching a reflective equilibrium). We can still try to give this definition a somewhat intuitive interpretation, which might read along the lines of “given the facts F, taking decision D is (necessarily) tantamount to (possibly) observing principle P”, with the caveat that the (bracketed) modal expressions would need to be read in a non-alethic mood (e.g., deontically as discussed in Section 5.1).
6.2.4. Value Conflict
Another important idea inspired from discoursive grammar in Section 2 is the notion of value conflict. As discussed there (see Figure 2), values are disposed around two axes of value coordinates, with values lying at contrary poles playing antagonistic roles. For our modelling purposes, it makes thus sense to consider a predicate Conflict on worlds (i.e., a proposition) signalling situations where value conflicts appear. Taking inspiration from the traditional logical principle of ex contradictio sequitur quodlibet, which we may intuitively paraphrase for the present purposes as ex conflictio sequitur quodlibet27, we define Conflict as the set of those worlds in which all basic values become applicable:
Of course, and in the spirit of the LogiKEy methodology, the specification of such a predicate can be further improved upon by the modeller as the need arises.
6.3. Instantiation as a HOL-Based Legal DSL
In this subsection, we encode our logic of value preferences in HOL (recall discussion in Section 4), building incrementally on top of the corresponding HOL encoding for our (extended) object logic in Section 5.2. In the process, our encoding will be gradually extended with custom means to encode the domain legal theory (cf. discoursive grammar in Section 2). For the sake of illustrating a concrete, formally verifiable modelling, we also present in most cases the corresponding encoding in Isabelle/HOL (see also Appendix A.2).
In a preliminary step, we introduce a new base HOL-type c (for “contender”) as an (extensible) two-valued type introducing the legal parties “plaintiff” (p) and “defendant” (d). For this, we employ in Isabelle/HOL the keyword datatype, which has the advantage of automatically generating (under the hood) the adequate axiomatic constraints (i.e., the elements p and d are distinct and exhaustive).
We also introduce a function, suggestively termed , with notation . This function is used to return for a given party the other one, i.e., and . Moreover, we add a (-lifted) predicate to model the ruling for a given party and postulate that it always has to be ruled for either one party or the other: .

As a next step, in order to enable the encoding of basic values, we introduce a four-valued datatype (corresponding to our domain of all values). Observe that this datatype is parameterised with a type variable . In the remainder, we will always instantiate with the type c (see discussion below):
We also introduce some convenient type aliases.
is introduced as the type for (characteristic functions of) sets of basic values. The reader will recall that this corresponds to the characterisation of value principles as given in the previous subsection (i.e., elements of ).
It is important to note, however, that to enable the modelling of legal cases (plaintiff v. defendant), we need to further specify legal value principles with respect to a legal party, either plaintiff or defendant. For this, we define intended as the type for specific legal (value) principles (with respect to a legal party) so that they are functions taking objects of type c (either p or d) to sets of basic values.

We introduce useful set-constructor operators for basic values () and a superscript notation for specification with respect to a legal party. As an illustration, recalling the discussion in Section 2, we have that, for example, the legal principle of STABility with respect to the plaintiff (notation ) can be encoded as a two-element set of basic values (with respect to the plaintiff), i.e., , .
The corresponding Isabelle/HOL encoding is as follows.

After defining legal (value) principles as combinations (in this case, sets28) of basic values (with respect to a legal party), we need to relate them to propositions (sets of worlds/states) in our logic . For this, we employ the derivation operators introduced in Section 6, whereby each value principle (set of basic values) becomes associated with a proposition (set of worlds) by means of the operator ↓ (conversely for ↑). We encode this by defining the corresponding incidence relation, or, equivalently, a function mapping worlds/states (type ) to sets of basic values (type ). We define so that, given some set of basic values , denotes the set of all worlds that are related to every value in V (analogously for ). The modelling in the Isabelle/HOL proof assistant is as follows.

Thus, we can intuitively read the proposition (set of worlds) denoted by as (those worlds in which) “the legal principle of STABility is observed with respect to the plaintiff”. For convenience, we introduce square brackets () as an alternative notation to ↓ postfixing in our DSL, so we have .
Now, our concrete choice of an aggregation operator for values (out of the two options presented in Section 6.2) is , which thus becomes encoded in HOL as:
Analogously, the chosen preference relation (≺) is the variant (i.e., from the candidate modelling options discussed in Section 6), which, recalling Section 5.1, becomes equivalently encoded as any of the following:
In a similar fashion, we encode in HOL the value-logical predicate Promotes as introduced in the previous subsection Section 6.2. The corresponding Isabelle/HOL encoding is shown below.

We have similarly encoded the proposition Conflict in HOL.

6.4. Formally Verifying the Adequacy of DSL
In this subsection, we put our HOL-based legal DSL to the test by employing the automated tools integrated into Isabelle/HOL. In this process, the discoursive grammar, as well as the continuous feedback by our legal domain expert (Lomfeld), served the role of a requirements specification for the formal verification of the adequacy of our modelling. We briefly discuss some of the conducted tests as shown in Figure 6; further tests are presented in Figure A9 in Appendix A.2 and in Benzmüller and Fuenmayor [14].

Figure 6.
Verifying the DSL.
In accordance with the dialectical interpretation of the discoursive grammar (recall Figure 2 in Section 2), our modelling foresees that observing values (with respect to the same party) from two opposing value quadrants, say RESP and STAB, or RELI and WILL, entails a value conflict; theorem provers quickly confirm this as shown in Figure 6 (Lines 4–5). Moreover, observing values from two non-opposed quadrants, such as WILL and STAB (Line 7), should not imply any conflict: the model finder Nitpick29 computes and reports a countermodel (not shown here) to the stated conjecture. A value conflict is also not implied if values from opposing quadrants are observed with respect to different parties (Lines 9–10).
Note that the notion of value conflict has deliberately not been aligned with logical inconsistency, neither in the object logic nor in the meta-logic HOL. Instead, an explicit, legal party-dependent notion of conflict is introduced as an additional predicate. This way, we can represent conflict situations in which, for instance, RELI and WILL (being conflicting values, see Line 5 in Figure 6) are observed with respect to the plaintiff (p), without leading to a logical inconsistency in Isabelle/HOL (thus avoiding ‘explosion’). This also has the technical advantage that value conflicts can be explicitly analysed and reported by the model finder Nitpick, which would otherwise just report that there are no satisfying models. In Line 11 of Figure 6, for example, Nitpick is called simultaneously in both modes in order to confirm the contingency of the statement; as expected, both a model (cf. Figure 7) and countermodel (not displayed here) for the statement are returned. This value conflict can also be spotted by inspecting the satisfying models generated by Nitpick. One such model is depicted in Figure 7, where it is shown that (in the given possible world ) all of the basic values (EQUALITY, SECURITY, UTILITY, and FREEDOM) are simultaneously observed with respect to p, which implies a value conflict according to our definition. For further illustrations of such models (with and without value conflict), we refer to the tests reported in Figure A9 in Appendix A.2.

Figure 7.
Satisfying model for the statement in Line 11 of Figure 6.
Such model structures as computed by Nitpick are ideally communicated to (and inspected with) domain experts (Lomfeld in our case) early on and checked for plausibility, which, in the case of issues, might trigger adaptions to the axioms and definitions. Such a process may require several cycles until arriving at a state of reflective equilibrium (recall the discussion from Section 3) and, as a useful side effect, it conveniently fosters cross-disciplinary mutual understanding.
Further tests in Figure 6 (Lines 13–20) assess the behaviour of the aggregation operator ⊕ by itself, and also in combination with value preferences. For example, we test for a correct behaviour when ‘strengthening’ the right-hand side: if STAB is preferred over WILL, then STAB combined with, say, RELI is also preferred over WILL alone (Line 15). Similar tests are conducted for the ‘weakening’ of the left-hand side30.
7. Applications (L3)—Assessment of Legal Cases
In this section, we provide a concrete illustration of our reasoning framework by formally encoding and assessing two classic common law property cases concerning the appropriation of wild animals (“wild animal cases”): Pierson v. Post, and Conti v. ASPCA31.
Before starting with the analysis, a word is in order about the support of our work by the tools Sledgehammer (Blanchette et al. [61,98]) and Nitpick (Blanchette and Nipkow [95]) in Isabelle/HOL. The ATP systems integrated via Sledgehammer in Isabelle/HOL include higher-order ATP systems, first-order ATP systems, and SMT (satisfiability modulo theories) solvers, and many of these systems in turn use efficient SAT solver technology internally. Indeed, proof automation with Sledgehammer and (counter) model finding with Nitpick were invaluable in supporting our exploratory modelling approach at various levels. These tools were very responsive in automatically proving (Sledgehammer), disproving (Nitpick), or showing consistency by providing a model (Nitpick). In the first case, references to the required axioms and lemmas were returned (which can be seen as a kind of abduction), and in the case of models and counter-models, they often proved to be very readable and intuitive. In this section, we highlight some explicit use cases of Sledgehammer and Nitpick. They have been similarly applied at all levels as mentioned before.
We have split our analysis in layer L3 into two ‘sub-layers’ in order to highlight the separation between general legal and world knowledge (legal concepts and norms), from its ‘application’ to relevant facts in the process of deciding a case (factual/contextual knowledge). We shall first address the modelling of some background legal and world knowledge in Section 7.1 as minimally required in order to formulate each of our legal cases in the form of a logical Isabelle/HOL theory (cf. Section 7.2).
7.1. General Legal and World Knowledge
The realistic modelling of concrete legal cases requires further legal and world knowledge (LWK) to be taken into account. LWK is typically modelled in so-called “upper” and “domain” ontologies. The question about which particular notion belongs to which category is difficult, and apparently there is no generally agreed answer in the literature. Anyhow, we introduce only a small and monolithic exemplary logical Isabelle/HOL theory32, called “GeneralKnowledge”, with a minimal amount of axioms and definitions as required to encode our legal cases. This LWK example includes a small excerpt of a much simplified “animal appropriation taxonomy”, where we associate “animal appropriation” (kinds of) situations with the value preferences they imply (i.e., conditional preference relations as discussed in Section 2 and Section 6).
In a more realistic setting, this knowledge base would be further split and structured similarly to other legal or general ontologies, e.g., in the Semantic Web (Casanovas et al. [8], Hoekstra et al. [9]). Note, however, that the expressiveness in our approach, unlike in many other legal ontologies or taxonomies, is by no means limited to definite underlying (but fixed) logical language foundations. We could thus easily decide for a more realistic modelling, e.g., avoiding simplifying propositional abstractions. For instance, the proposition “appWildAnimal”, representing the appropriation of one or more wild animals, can anytime be replaced by a more complex formula (featuring, for example, quantifiers, modalities, and conditionals; see Section 5.4).
Next steps include interrelating notions introduced in our Isabelle/HOL theory “GeneralKnowledge” with values and value preferences as introduced in the previous sections. It is here where the preference relations and modal operators of as well as the notions introduced in our legal DSL are most useful. Remember that, at a later point and in line with the LogiKEy methodology, we may in fact exchange by an alternative choice of an object logic; or, on top of it, we may further modify our legal DSL, e.g., we might choose and assess alternative candidates for our connectives ≺ and ⊕. Moreover, we may want to replace material implication → by a conditional implication to better support defeasible legal reasoning33.
We now briefly outline the Isabelle/HOL encoding of our example LWK; see Figure A10 in Appendix A.3 for the full details.
First, some non-logical constants that stand for kinds of legally relevant situations (here, of appropriation) are introduced, and their meaning is constrained by some postulates:

Then, the ‘default’34 legal rules for several situations (here, the appropriation of animals) are formulated as conditional preference relations.

For example, rule R2 could be read as “In a wild-animals-appropriation kind of situation, observing STABility with respect to a party (say, the plaintiff) is preferred over observing WILL with respect to the other party (defendant)”. If there is no more specific legal rule from a precedent or a codified statute, then these ‘default’ preference relations determine the result. Of course, this default is not arbitrary but is itself an implicit normative setting of the existing legal statutes or cases. Moreover, we can have rules conditioned on more concrete legal factors35. As a didactic example, the legal rule R4 states that the ownership (say, the plaintiff’s) of the land on which the appropriation took place, together with the fact that the opposing party (defendant) acted out of malice implies a value preference of reliance (in ownership) and responsibility (for malevolence) over stability (induced by possession as an obvious external sign of appropriation). This rule has been chosen to reflect the famous common law precedent of Keeble v. Hickeringill (1704, 103 ER 1127; cf. also Berman and Hafner [6], Bench-Capon [96]).

As already discussed, for ease of illustration, terms like “appWildAnimal” are modelled here as simple propositional constants. In practice, however, they may later be replaced, or logically implied, by a more realistic modelling of the relevant situational facts, utilising suitably complex (even quantified; cf. Section 5.4) formulas depicting states of affairs to some desired level of granularity.
For the sake of modelling the appropriation of objects, we have introduced an additional base type in our meta-logic HOL (recall Section 4). The type e (for ‘entities’) can be employed for terms denoting individuals (things, animals, etc.) when modelling legally relevant situations. Some simple vocabulary and taxonomic relationships (here, for wild and domestic animals) are specified to illustrate this.

As mentioned before, we have introduced some convenient legal factors into our example LWK to allow for the encoding of legal knowledge originating from precedents or statutes at a more abstract level. In our approach, these factors are to be logically implied (as deductive arguments) from the concrete facts of the case (as exemplified in Appendix A.4 below). Observe that our framework also allows us to introduce definitions for those factors for which clear legal specifications exist, such as property or possession. At the present stage, we will provide some simple postulates constraining the factors’ interpretation.

Recalling Section 6, we relate the introduced legal factors (and relevant situational facts) to value principles and outcomes by means of the Promotes predicate36:

Finally, the consistency of all axioms and rules provided is confirmed by Nitpick.
7.2. Pierson v. Post
This famous legal case can be succinctly described as follows (Bench-Capon et al. [25], Gordon and Walton [97]):
Pierson killed and carried off a fox which Post already was hunting with hounds on public land. The Court found for Pierson (1805, 3 Cai R 175).
For the sake of illustration, we will consider in this subsection two modelling scenarios: in the first one, a case is built to favour the defendant (Pierson), and in the second one, a case favouring the plaintiff (Post).
7.2.1. Ruling for Pierson
The formal modelling of an argument in favour of Pierson is outlined next37.
First, we introduce some minimal vocabulary: a constant of type e (denoting the appropriated animal), and the relations pursue and capture between the animal and one of the parties (of type c). A background (generic) theory as well as the (contingent) case facts as suitably interpreted by Pierson’s party are then stipulated.

The aforementioned decision of the court for Pierson was justified by the majority opinion. The essential preference relation in the case is implied in the idea that the appropriation of (free-roaming) wild animals requires actual corporal possession. The manifest corporal link to the possessor creates legal certainty, which is represented by the value STABility and outweighs the mere WILL to possess by the plaintiff; cf. the arguments of classic lawyers cited by the majority opinion: “pursuit alone vests no property” (Justinian), and “corporal possession creates legal certainty” (Pufendorf). According to the discoursive grammar in Section 2 (cf. Figure 2), this corresponds to a basic value preference of SECURITY over FREEDOM. We can see that this legal rule R2 as introduced in the previous section (Section 7.1)38 is indeed employed by Isabelle/HOL’s automated tools to prove that, given a suitable defendant’s theory, the (contingent) facts imply a decision in favour of Pierson in all ‘better’ worlds (which we could even give a ‘deontic’ reading as some sort of recommendation).

The previous ‘one-liner’ proof has indeed been automatically suggested by Sledgehammer (Blanchette et al. [61,98]) which we credit, together with the model finder Nitpick (Blanchette and Nipkow [95]), for doing the proof heavy-lifting in our work.
A proof argument in favour of Pierson that uses the same dependencies can also be constructed interactively using Isabelle’s human-readable proof language Isar (Isabelle/Isar; cf. Wenzel [101]). The individual steps of the proof are, this time, formulated with respect to an explicit world/situation parameter w. The argument goes roughly as follows:
- From Pierson’s facts and theory, we infer that in the disputed situation w, a wild animal has been appropriated: .
- In this context, by applying the value preference rule R2, we obtain that observing STAB with respect to Pierson (d) is preferred over observing WILL with respect to Post (p): .
- The possibility of observing WILL with respect to Post thus entails the possibility of observing STAB with respect to Pierson: .
- Moreover, after instantiating the value promotion schema F1 (Section 7.1) for Post (p), and acknowledging that his pursuing the animal (Pursue p ) entails his intention to possess (Intent p), we obtain (for the given situation w) a recommendation to ‘align’ any ruling for Post with the possibility of observing WILL with respect to Post: . Following the interpretation of the Promotes predicate given in Section 6, we can read this ‘alignment’ as involving both a logical entailment (left to right) and a justification (right to left); thus the possibility of observing WILL (with respect to Post) both entails and justifies (as a reason) a legal decision for Post.
- Analogously, in view of Pierson’s (d) capture of the animal (Capture d), thus having taken possession of it (Poss d), we infer from the instantiation of value promotion schema F3 (for Pierson) a recommendation to align a ruling for Pierson with the possibility of observing the value principle STAB with respect to Pierson):
- From (4) and (5) in combination with the court’s duty to find a ruling for one of both parties (axiom ForAx) we infer, for the given situation w, that either the possibility of observing WILL with respect to Post or the possibility of observing STAB with respect to Pierson (or both) hold in every ‘better’ world/situation (thus becoming a recommended condition): .
- From this and (3), we thus obtain that the possibility of observing STAB with respect to Pierson is recommended in the given situation w: .
- And this together with (5) finally implies the recommendation to rule in favour of Pierson in the given situation w: .
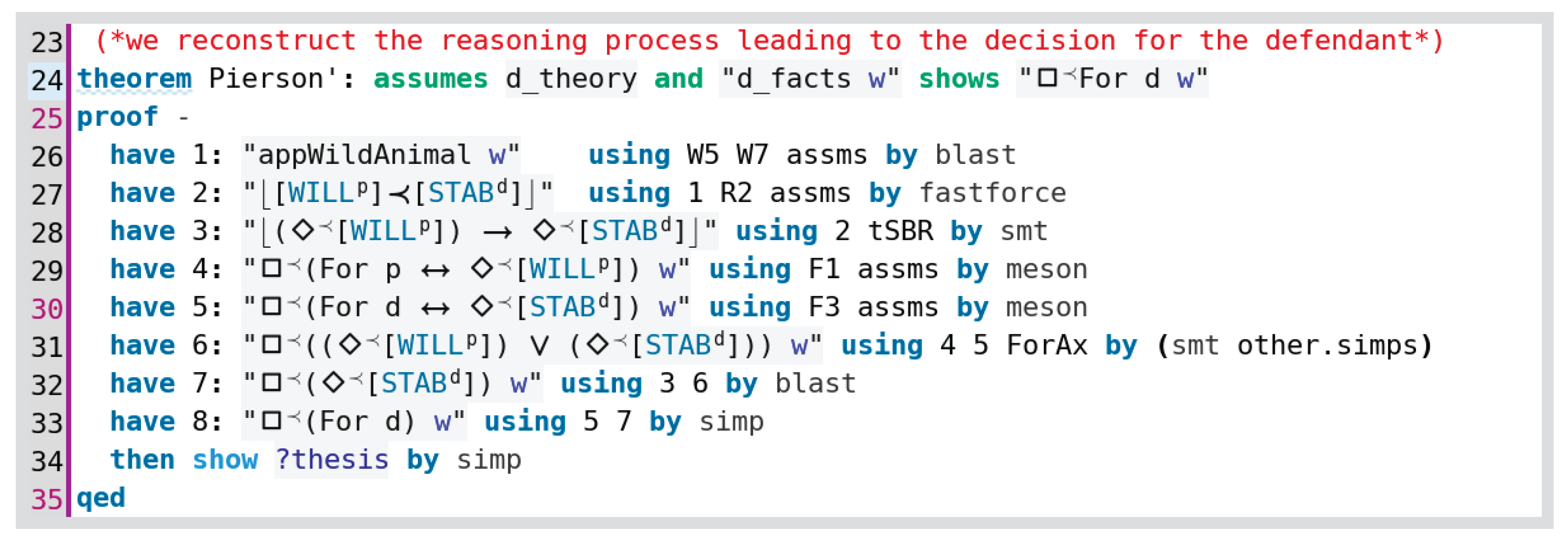
The consistency of the assumed theory and facts (favouring Pierson) together with the other postulates from the previously introduced logical theories “GeneralKnowledge” and “ValueOntology” is verified by generating a (non-trivial) model using Nitpick (Line 38). Further tests confirm that the decision for Pierson (and analogously for Post) is compatible with the premises and, moreover, that for neither party, value conflicts are implied.

We show next how it is indeed possible to construct a case (theory) suiting Post using our approach.
7.2.2. Ruling for Post
We model a possible counterargument in favour of Post claiming an interpretation (i.e., a distinction in case law methodology) in that the animal, being vigorously pursued (with large dogs and hounds) by a professional hunter, is not “free-roaming” anymore but already in (quasi) possession of the hunter. In this interpretation, the value preference (for appropriation of wild animals), as in the previous Pierson’s argument, is not obtained. Furthermore, Post’s party postulates an alternative (suitable) value preference for hunting situations.

An alternative legal rule (i.e., a possible argument for overruling in case law methodology) is presented (in Line 16 above), entailing a value preference of the value principle combination EFFIciency together with WILL over STABility: . Following the argument put forward by the dissenting opinion in the original case (3 Cai R 175), we might justify this new rule (inverting the initial value preference in the presence of EFFI) by pointing to the alleged public benefit of hunters getting rid of foxes since the latter cause depredations in farms. The hunting of foxes, thus, promotes collective economic utility.
Accepting these modified assumptions, the deductive validity of a decision for Post can in fact be proved and confirmed automatically, again, thanks to Sledgehammer:

Similar to the above, a detailed, interactive proof for the argument in favour of Post is encoded and verified in Isabelle/Isar. We have also conducted further tests confirming the consistency of the assumptions and the absence of value conflicts39.
7.3. Conti v. ASPCA
An additional illustrative case study we have modelled in our framework is Conti v. ASPCA (353 NYS 2d 288). In a nutshell is the following (Bench-Capon et al. [25]):
Chester, a parrot owned by the ASPCA, escaped and was recaptured by Conti. The ASPCA found this out and reclaimed Chester from Conti. The court found for ASPCA.
In this case, the court made clear that for domestic animals, the opposite preference relation as the standard in Pierson’s case applies. More specifically, it was ruled that for a domestic animal, it is in fact sufficient that the owner did not neglect or stop caring for the animal, i.e., actively give up the responsibility for its maintenance (RESP). This, together with the reliance of ASPCA (RELI) in the parrot’s property, outweighs Conti’s corporal possession of the animal as a ’stable’ external indication (STAB) of property: . Observe that a corresponding rule had previously been integrated as R3 into our legal and world knowledge (Section 7.1).
The plaintiff’s theory and facts are encoded analogously to the previous case:

Accepting these assumptions, the deductive validity of a decision for the plaintiff (ASPCA) can again be proved and confirmed automatically (thanks to Sledgehammer):

In an analogous manner to Pierson’s case, an interactive proof in Isabelle/Isar has been encoded and verified, and the consistency of the assumptions and the absence of value conflicts has been confirmed40.
8. Related and Further Work
Custom software systems for legal case-based reasoning have been developed in the AI and Law community, beginning with the influential HYPO system in the 1980s (Rissland and Ashley [102]); cf. also the survey paper by Bench-Capon [56]. In later years, there has been a gradual shift of interest from rule-based non-monotonic reasoning (e.g., logic programming) towards argumentation-based approaches (see Prakken and Sartor [16] for an overview); however, we are not aware of any other work that uses higher-order theorem proving and proof assistants (the argumentation logic of Krause et al. [103] is an early related effort that is worth mentioning). Another important aspect of our work concerns value-oriented legal reasoning and deliberation, where a considerable amount of work has been presented in AI and Law in response to the challenge posed by Berman and Hafner [6]. Our approach, based mainly on discoursive grammar (Lomfeld [4,28]), has also been influenced by some of this work, in particular, by Bench-Capon and Sartor [5], Prakken [51], Bench-Capon [96].
We are currently working towards further refining the modelling of our domain legal theory (discoursive grammar) with the aim of providing more expressive (combinations of) object logics at LogiKEy layer L1. In this regard, it is somehow remarkable that the use of material implication to encode rules has proven sufficient for the illustrative purposes of this paper. However, it is important to note that a more realistic modelling of legal cases must also provide mechanisms to deal with the inevitable emergence of conflicts and contradictions in normative reasoning (overruling, conflict resolution, etc.). In line with the LogiKEy approach, we are working at introducing conditional connectives in our object logics with the aim of enabling defeasible (or default) reasoning. Such connectives can be introduced by reusing the modal operators of (recalling the discussion in Section 5.4) or, alternatively, through the shallow semantical embedding (Benzmüller [10]) of a suitable conditional logic in HOL (Benzmüller [81]). Moreover, special kinds of paraconsistent (modal-like) Logics of Formal Inconsistency (Carnielli et al. [104]) can also be integrated into our modelling to enable the non-explosive representation of (and recovery from) contradictions by purely object-logical means (cf. Fuenmayor [105] for a related encoding in Isabelle/HOL). In a similar vein, we think that some of the recent work that employs expressive deontic logics for value-based legal balancing (e.g., Maranhao and Sartor [27] and the references therein) can be fruitfully integrated in our approach. It is the pluralistic nature of LogiKEy, realised within a dynamic modelling framework (e.g., Isabelle/HOL), that enables and supports such improvements without requiring expensive technical adjustments to the underlying base reasoning technology.
As a broader application scenario, we are currently proposing that ethico-legal value-oriented theories and ontologies should constitute a core ingredient to enable the computation, assessment, and communication of rational justifications and explanations in the future ethico-legal governance of AI (Benzmüller and Lomfeld [106]). Thus, a sound and trustworthy implementation of any legally accountable ‘moral machine’ requires the development of formal theories and ontologies for the legal domain to guide and interconnect the encoding of concrete regulatory codes and legal cases. Understanding legal reasoning as dialectical practical argumentation, the pluralist interpretation of concrete legal rules arguably requires a complementary ethico-legal value-oriented theory, such as the discoursive grammar of justification by Lomfeld [4], which we formally encoded in this paper. In this sense, some first positive evidence has been provided regarding challenges that we have previously identified with respect to the ethical–legal governance of future AI systems (Fuenmayor and Benzmüller [107]). Indeed, it was this broader vision that primarily motivated our work on value-oriented legal reasoning in the first place.
9. Conclusions
We illustrate the application of the LogiKEy knowledge engineering methodology and framework to enable the interdisciplinary collaboration among different specialist roles. In the present case, they are a lawyer and legal philosopher and two computer scientists who joined forces with the aim of formally modelling a value-oriented legal theory (discoursive grammar by Lomfeld [4]) for the sake of providing means for computer-automated prediction and assessment of legal case decisions.
From a technical perspective, the core objective of this article has been to demonstrate that the LogiKEy methodology appears indeed suitable for the task of value-oriented legal reasoning. As instantiated in the present work, the LogiKEy methodology builds upon a HOL-encoding of a modal logic of preferences to model a domain-specific theory of value-based legal balancing. In combination with further legal and world knowledge, this theory has been successfully employed for the formal encoding and computer-supported assessment, using the Isabelle/HOL system, of illustrative legal cases in property law (“wild animal cases”).
It is the flexibility of the multi-layer modelling which is novel in our approach, in combination with a very rich support for automated reasoning in expressive, quantified classical and non-classical logics, thereby rejecting the idea that knowledge representation means should be limited prima facie to decidable logic frameworks, due to complexity or performance considerations41. In the LogiKEy approach, the choice of a particular object logic is deliberately left to the knowledge engineer. The range of options varies from well-manageable decidable logics to sophisticated quantified non-classical logics and combinations thereof, depending on what is best suited to handle a particular knowledge representation (and reasoning) task at hand.
From a legal perspective, the reconstruction of legal balancing is, already with classical argumentative tools, a non-trivial task, which is methodologically not yet settled. Here, our work proposed the structuring of legal balancing by means of a dialectical ethico-legal value system (discoursive grammar). Legal rules and their various interpretations can thus be represented within a unified yet pluralistic logic of value preferences. The integration of this logic and the value system within the dynamic HOL-based modelling environment allows us to experiment with different forms of interpretation. This enables us not only to find more accurate reconstructions of legal argumentation but also supports the modelling of value-based legal balancing, taking into account notions of value preference, aggregation, promotion and conflict, and also in a manner amenable to computer automation. The modelling of discoursive grammar in LogiKEy enabled us to successfully predict (and, to some extent, justify) case outcomes by ‘just using logic’, employing qualitative value preferences without the necessity to bring in numbers and weights into the model. At the same time, our account could easily be extended to a quantitative model of legal balancing.
From a general perspective, supporting interactive and automated value-oriented legal argumentation on the computer is a non-trivial challenge which we address, for reasons as defended by Bench-Capon [111], with symbolic AI techniques and formal methods. Motivated by recent pleas for explainable and trustworthy AI, our primary goal is to work towards the development of ethico-legal governors for future generations of intelligent systems, or more generally, towards some form of legally and ethically reasonable machines (Benzmüller and Lomfeld [106]) capable of exchanging rational justifications for the actions they take. While building up a capacity to engage in value-oriented legal argumentation is just one of a multitude of challenges this vision is faced with, it clearly constitutes an important stepping stone towards this ambitious long-term goal.
Author Contributions
Conceptualization, all authors; methodology, C.B. and D.F.; formal modeling, D.F. and C.B.; validation, D.F. and C.B.; writing—original draft preparation, D.F., C.B. and B.L.; writing—review and editing, C.B., D.F. and B.L.; visualization, D.F.; supervision, C.B.; project administration, C.B.; funding acquisition, C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. However, it was intellectually supported by the Fonds National de la Recherche Luxembourg through the projects “Automated Reasoning with Legal Entities (AuReLeE)” (CORE C20/IS/14616644) and “Deontic Logic for Epistemic Rights (DELIGHT)” (OPEN O20/14776480).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data is available at https://github.com/cbenzmueller/LogiKEy/tree/master/Preference-Logics/EncodingLegalBalancing (accessed on 12 December 2023).
Acknowledgments
We would like to thank the reviewers for their valuable comments. Our thanks also go to the entire LogiKEy team, especially our collaboration partners at the University of Luxembourg.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Appendix —Isabelle/HOL Encoding
Appendix A.1. SSE of PL in HOL
We comment on the implementation of the SSE of in Isabelle/HOL as displayed in Figure A1 and Figure A2; see van van Benthem et al. [15] for further details on . The defined theory is named “PreferenceLogicBasics”, and it relies on base logic HOL, imported here as theory “Main”.

Figure A1.
SSE of (van Benthem et al. [15]) in HOL (continued in Figure A2).
First, a new base type is declared (Line 6), denoting the set of possible worlds or states. Subsequently (Lines 7–11), useful type abbreviations are introduced, including the type for propositions, which are modelled as predicates on objects of type (i.e., as truth-sets of worlds/states). A betterness relation⪯ and its strict variant ≺ are introduced (Lines 13–14), with ⪯-accessible worlds interpreted as those that are at least as good as the present one. Definitions for relation properties are provided, and it is postulated that ⪯ is a preorder, i.e., reflexive and transitive (Lines 15–18).
Subsequently, the -type lifted logical connectives of are introduced as abbreviations of -terms in the meta-logic HOL (Lines 21–33). The operators and use ⪯ and ≺ as guards in their definitions (Lines 28 and 30); analogous for and . An universal modality and its dual are also introduced (Lines 32–33). Moreover, a notion of (global) truth for formulas is defined (Line 35): proposition is globally true, we also say ‘valid’, if and only if it is true in all worlds.
Figure A2.
SSE of (van Benthem et al. [15]) in HOL (continued from Figure A1).
As a first test, some expected dualities of the modal operators are automatically proved (Line 36).
Subsequently, the betterness ordering ⪯ (respectively, ≺) is lifted to a preference relation between propositions (sets of worlds). Eight possible semantic definitions for such preferences are encoded in HOL (Lines 40–47 in Figure A2). The semantic definitions are complemented by eight syntactic definitions of the same binary preferences stated within the object language (Lines 48–55). (ATP systems prove the meta-theoretic correspondences between these semantic and syntactic definitions; cf. Lines 4–12 in Figure A4).
is extended by adding quantifiers (Lines 57–60); cf. (Benzmüller and Paulson [76]) for explanations on the SSE of quantified modal logics. Moreover, useful polymorphic operators for subset, union, and intersection are defined (Lines 62–64).
The model finder Nitpick (Blanchette and Nipkow [95]) confirms the consistency of the introduced theory (Line 66) by generating and presenting a model (not shown here), in which the relation satisfies the constraints imposed on it. Thus, the axioms of object logic are simultaneously satisfiable.
To gain practical evidence for the faithfulness of our SSE of in Isabelle/HOL, and also to assess the proof automation performance, we have conducted numerous experiments, in which we automatically reconstruct the meta-theoretical results on ; see Figure A4 and Figure A5.
Extending our SSE of in HOL, some further preference relations for are defined in Figure A3. These additional relations support ceteris paribus reasoning in .
We give some explanations:
- Lines 5–13
- Useful set theoretic notions are introduced as abbreviations for corresponding -terms in HOL.
- Lines 14–22
- is further extended with (equality-based) ceteris paribus preference relations and modalities; here, represents a set of formulas that are assumed constant between two possible worlds to compare. Hence, our variant can be understood as “these (given) things being equal” preferences. This variant can be used for modelling von Wright’s notion of ceteris paribus (“all other things being equal”) preferences, eliciting an appropriate by extra-logical means.
- Lines 26–33:
- Except for , the remaining operators we define here were not explicitly defined by van Benthem et al. [15]; however, their existence is tacitly suggested.
Meta-theoretical results on as presented by van Benthem et al. [15] are automatically verified by the reasoning tools in Isabelle/HOL; see Figure A3–Figure A7. In fact, we prove all relevant results from (van Benthem et al. [15]). The experiments shown in Figure A4 are briefly commented.

Figure A4.
Experiments: testing the meta-theory of .
- Lines 5–13
- Correspondences between the semantically and syntactically defined preference relations are proved.
- Lines 15–22
- It is proved that (e.g., inclusion and interaction) axioms for follow as theorems in our SSE. This tests the faithfulness of the embedding in one direction.
- Lines 25–47
- We continue the mechanical verification of theorems, and generate countermodels (not displayed here) for non-theorems of , thus putting our encoding to the test. Our results coincide with the corresponding ones claimed (and in many cases proved) in van Benthem et al. [15], except for the claims encoded in lines 40-41 and 44-45, where countermodels are reported by Nitpick.
- Lines 25–47
- Some application-specific tests in preparation for the modelling of the legal DSL (including the value theory/ontology) are conducted.

Figure A5.
Experiments (continued): Testing the meta-theory of .

Figure A6.
Experiments (continued): Checking properties of strict preference relations.

Figure A7.
Experiments (continued): Checking properties of strict preference relations.
Appendix A.2. Encoding of the Legal DSL (Value Ontology)
The encoding of the legal DSL (value theory or ontology) is shown in Figure A8. The new theory is termed “ValueOntology”, and it imports theory “PreferenceLogicBasics” (and thus recursively also Isabelle/HOL’s internal theory “Main”).
As a preliminary, the legal parties plaintiff and defendant are introduced as an (extensible) two-valued datatype together with a function to obtain for a given party the other one () (Lines 4–5), and a predicate modelling the ruling for a party is also provided (Lines 7–8).
As regards the discoursive grammar value theory, a four-valued (parameterised) datatype is introduced (Line 10) as described in Section 2. Moreover, type aliases (Lines 11–12) and set-constructor operators for values (Lines 14–15) are introduced for ease of presentation. The legal principles from Section 2 are introduced as combinations of those basic values (Lines 17–28). As an illustration, the principle STABility is encoded as a set composed of the basic values SECURITY and UTILITY.
Next, the incidence relation I and operators ↑ and ↓, borrowed and adapted from formal concept analysis (FCA), are introduced (Lines 30–34).
We then define the aggregation operator ⊕ as , i.e., we select the second candidate as discussed in Section 2. And as our preference relation of choice, we select the relation (Line 38).
Figure A8.
Encoding of the legal DSL (value ontology).
Finally, we introduce the “Promotes” schema for encoding the promotion of value principles via legal decisions (Line 40), and we introduce a notion “” expressing a legal value conflict for a party x (Lines 42–43).
The consistency of the theory is confirmed by Nitpick (Line 45).
Tests on the modelling and encoding of the legal DSL are displayed in Figure A9.
Among others, we verify that the pair of operators for extension (↓) and intension (↑), cf. Formal Concept Analysis (Ganter and Wille [93]), indeed constitute a Galois connection (Lines 6–18), and we carry out some further tests on the value theory (extending the ones presented in Figure 6) concerning value aggregation and consistency (Lines 20ff.).

Figure A9.
Formally verifying/testing the legal DSL or value ontology.
Appendix A.3. Legal and World Knowledge
The encoding of the relevant legal and world knowledge (LWK) is shown in Figure A10. The defined Isabelle/HOL theory is termed “GeneralKowledge” and imports the “ValueOntology” (and thus recursively also “PreferenceLogicBasics”) theory.
- Lines 4–5
- Declaration of logical constant symbols that stand for kinds of legally relevant situations.
- Lines 8–11
- Meaning postulates for these kinds of legally relevant situations are introduced.
- Lines 14–16
- Preference relations for these kinds of legally relevant situations are introduced.
- Lines 18–26
- Some simple vocabulary is introduced and some taxonomic relations for wild and domestic animals are specified.
- Lines 28–36
- Some relevant situational factors are declared and subsequently constrained by meaning postulates.
- Line 39
- An example for a value preference conditioned on factors is specified.
- Lines 41–46
- The situational factors are related with values and with ruling outcomes according to the notion of value promotion.
- Line 48
- The model finder Nitpick is used to confirm the consistency of the introduced theory.
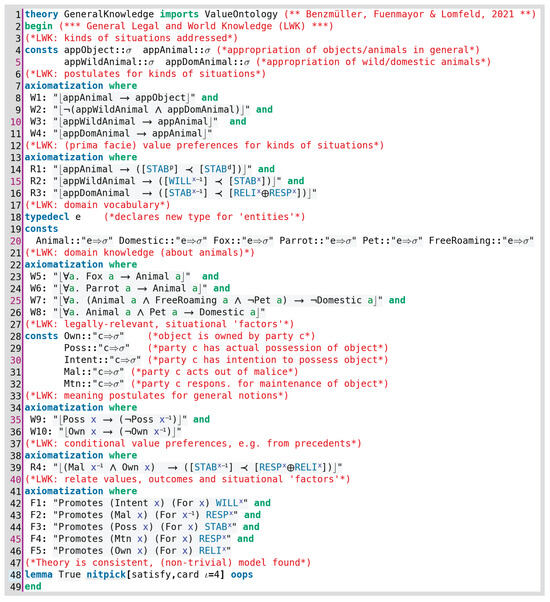
Figure A10.
Encoding of relevant legal and world knowledge.
Appendix A.4. Modelling Pierson v. Post
The Isabelle/HOL encoding of two scenarios in the Pierson v. Post case is presented in Figure A11 and Figure A12.
In Figure A11, which presents the initial ruling in favour of Pierson, the Isabelle/HOL theory is termed “Pierson” and imports the theory “GeneralKnowledge” (which recursively imports theories “ValueOntology” and “PreferenceLogicBasics”).
- Lines 5–19
- (Generic) theory and (contingent) facts suitable to the defendant (Pierson) are postulated.
- Lines 21–22
- Automated proof justifying the ruling for Pierson; the dependencies of the proof are shown.
- Lines 24–35
- Corresponding interactive proof (with the same dependencies as for the automated one) modelling the argument justifying the finding for Pierson.
- Lines 36–44
- Various checks for the consistency of the assumptions and the absence of value conflicts.

Figure A11.
Modelling the Pierson vs. Post case; ruling for Pierson.
As a further illustration, we present in Figure A12 a plausible counterargument by Post. The Isabelle/HOL theory is now termed “Post” and imports the theory “GeneralKnowledge” (which recursively imports theories “ValueOntology” and “PreferenceLogicBasics”).
- Lines 5–24
- Theory and facts suitable to the plaintiff (Post) are postulated.
- Lines 26–27
- Automated proof justifying the ruling for Post; the dependencies of the proof are shown.
- Lines 29–42
- Corresponding interactive proof (with the same dependencies as for the automated one) modelling the argument justifying the finding for Post.
- Lines 43–51
- Various checks for consistency of the assumptions and the absence of value conflicts.

Figure A12.
Modelling the Pierson v. Post case; ruling for Post.
Appendix A.5. Modelling Conti v. ASPCA
The reconstructed theory for the Conti v. ASPCA case is displayed in Figure A13. The Isabelle/HOL theory is termed “Conti” and imports the theory “GeneralKnowledge” (which recursively imports theories “ValueOntology” and “PreferenceLogicBasics”).

Figure A13.
Modelling of the Conti v. ASPCA case.
- Lines 5–20
- The theory and the facts of the pro-plaintiff (ASPCA) argument are formulated.
- Lines 22–23
- Automated proof justifying the ruling for ASPCA; the dependencies of the proof are shown.
- Lines 25–38
- Corresponding interactive proof (with the same dependencies as for the automated one) modelling the argument justifying the finding for ASPCA.
- Lines 39–47
- Various checks for consistency of the assumptions and the absence of value conflicts.
Appendix A.6. Complex (Counter-)Models
In Figure A14, we present an example of a model computed by model finder Nitpick for the statement in Line 41 in Figure A13. This non-trivial model features three possible worlds/states. It illustrates the richness of the information and the level of detail that is supported in the model (and countermodel) finding technology for HOL. This information is very helpful to support the knowledge engineer and user of the LogiKEy framework to gain insight about the modelled structures. We observe that the proof assistant Isabelle/HOL allows for the parallel execution of its integrated tools. We can thus execute, for a given candidate theorem, all three tasks in parallel (and in different modes): theorem proving, model finding, and countermodel finding. This is one reason for the very good response rates we have experienced in our work with the system—despite the general undecidability of HOL.

Figure A14.
Example of a (satisfying) model to the statement in Line 26 in Figure A13.
Notes
| 1 | In Section 6, these values will be assigned to particular parties/actors so that ruling in favour of different parties may promote different values. |
| 2 | All these taxonomies are pluralist frameworks that do encompass differences in global value patterns and cultural value evolution (Hofstede [47], Inglehart [48]). For an approach oriented at Maslow’s hierarchy of needs (Bench-Capon [49]). |
| 3 | Shallow semantical embeddings are different from deep embeddings of an object logic. In the latter case the syntax of the object logic is represented using an inductive data structure (e.g., following the definition of the language). The semantics of a formula is then evaluated by recursively traversing the data structure, and additionally a proof theory for the logic maybe be encoded. Deep embeddings typically require technical inductive proofs, which hinder proof automation, that can be avoided when shallow semantical embeddings are used instead. For more information on shallow and deep embeddings we refer to the literature (Gibbons and Wu [59], Svenningsson and Axelsson [60]). |
| 4 | In some cases, it can be convenient to split one or more layers into sublayers. For instance, in our case study (cf. Section 7), layer L3 has been further subdivided to allow for a more strict separation between general legal and world knowledge (legal concepts and norms), cf. Section 7.1, from its application to relevant facts in the process of deciding a case (factual/contextual knowledge), cf. Section 7.2. |
| 5 | The authors judiciously quote McCarty [62]: “The task for a lawyer or a judge in a ‘hard case’ is to construct a theory of the disputed rules that produces the desired legal result, and then to persuade the relevant audience that this theory is preferable to any theories offered by an opponent.” |
| 6 | In this article, we will actually associate type later on (cf. Section 5.2) with the domain of possible states/worlds. |
| 7 | Note that functions of more than one argument can be represented in HOL in terms of functions of one argument. In this case, the values of these one-argument function applications are themselves functions, which are subsequently applied to the next argument. This technique, introduced by Schönfinkel [72], is commonly called currying; cf. Benzmüller and Andrews [58]. |
| 8 | HOL formulas (layer L0) should not be confused with the object-logical formulas (layer L1); the latter will later be identified in Section 5.2 with HOL predicates of type . |
| 9 | For the purposes of the application scenarios studied later in Section 7, we have focused on ’s basic modal preference language, not yet employing ceteris paribus clauses. Nevertheless, we have provided a complete encoding and assessment of full in the associated Isabelle/HOL sources. |
| 10 | Von Wright’s proposal is discussed in some detail in van Benthem et al. [15]; cf. also Liu [80] for a discussion of further proposals. |
| 11 | This corresponds to the well-known standard translation to first-order logic. Observe, however, that the additional expressivity of HOL allows us to also encode and flexibly combine non-normal modal logics (conditional, deontic, etc.; cf. [81,82,83,84]) and we can elegantly add quantifiers (cf. Section 5.4). |
| 12 | In HOL (with Henkin semantics), sets are associated with their characteristic functions. |
| 13 | For many logics, our embedding technique allows such faithfulness results, and an example for a non-trivial dyadic deontic logic has been worked out in detail by Benzmüller et al. [84]. A key feature of LogiKEy is that these pen-and-paper faithfulness studies can be supported and complemented by experimentation and verification. This is illustrated in Figure 1.2 of Benzmüller et al. [84], where it is shown that both the standard inference rules and the axioms of the embedded dyadic deontic logic can be proven valid in our approach. For further related experiments and a discussion of the current limitations of the embedding approach, we refer the reader to Benzmüller and Reiche [85] and in particular to §4.5 of Parent and Benzmüller [86], which briefly discusses in this context the distinction between validity on frame structures versus validity on model structures for a frame. An example of a non-trivial and non-faithful, but practically very successful, embedding in HOL is presented in the PhD thesis of Kirchner [87], where it is shown how to provide an appropriate additional safety harness. |
| 14 | In fact, Halpern’s [79] variant corresponds to employing the preference relation discussed previously, augmented with an additional constraint to cope with infinite-sized countermodels to irreflexivity (building upon an approach by Lewis [89]). Thus, (read: is more likely than ) if and only if every -state has a more likely -state, say v, which dominates (i.e., no -state is more likely than v). Halpern [79] goes on to define a conditional operator as follows: . |
| 15 | Observe that in doing so, we are simplifying the legal theory (discoursive grammar) to the effect that, for example, STABility becomes identified with EFFIciency. This simplified model has proven sufficient for our modelling work in Section 7. A more granular encoding of principles is possible by adding a third axis to the value space in Figure 4, thus allocating each principle to its own octant |
| 16 | We recall that, from a modal logic perspective, a proposition is modelled as the set of ‘worlds’ (i.e., states or situations) in which it holds. Informally, we want to be able to express the fact that a given principle, say legal STABility, is being observed or respected in a particular situation, or, abusing modal logic jargon, that the principle is ‘satisfied’ in that ‘world’. This can become further interpreted as providing a justification for why that world or situation is desirable. |
| 17 | An old mathematician’s trick has been to employ—maybe unknowingly—Galois connections (respectively, adjunctions) to relate two universes of mathematical objects with each other in such a way that certain order structures become inverted (respectively, preserved). In doing so, insights and results can be transferred from a well-known universe towards a less-known one in order to gain information and help illuminate difficult problems; cf. the discussion in Erné [92]. |
| 18 | In particular, we want to highlight the potential of employing the powerful FCA methods, e.g., attribute exploration (Ganter et al. [94]), to prospective ‘legal value mining’ applications. |
| 19 | The terms extent and intent are reminiscent of the philosophical notions of extension and intension (comprehension) reaching back to the 17th century Logique de Port-Royal. |
| 20 | This result can be seamlessly stated for infinite meets and joins (infima and suprema) in the usual way. It corresponds to the first part of the so-called basic theorem on concept lattices (Ganter and Wille [93]). |
| 21 | In the presented modelling, we intentionally avoided connecting our formal contexts with the betterness relation. This approach allows us to study the extent of our progress without it initially. Establishing such a connection in future work is possible, and LogiKEy is particularly well suited to supporting such logical explorations. One reviewer suggested making such a connection, and along the same lines another recommended representing value principles by Kripke relations and associated modal operators, since considering values as distinct modalities could naturally lead to their aggregation, potentially negating the need to define a separate aggregation function. |
| 22 | Observe that this can be written semi-formally as: for all winwe have thatifthen, which can be interpreted as “P provides a reason for all those worlds that satisfy A”. |
| 23 | Employing discoursive grammar’s value theory, this corresponds to RELIance together with personal GAIN outweighing STABility. |
| 24 | Lacking any strong opinion regarding the correctness or adequacy of transitivity or the union property, we have nevertheless chosen this latter variant for our case study in Section 7, since it offers several benefits for our current modelling purposes: it can be faithfully encoded in the language of (van Benthem et al. [15]) and its behaviour is well documented in the literature; cf. Halpern [79], Liu [80] (Ch. 4). In fact, as mentioned in Section 5.4, drawing upon the strict variant we can even define a defeasible conditional ⇒ in . Our choice of thus strikes a good balance, it satisfies the desired properties, and it is used in related works (e.g., in preferential semantics for defeasible logics). |
| 25 | |
| 26 | We adopt the terminology of promoting (or advancing) a value from the literature (Bench-Capon and Sartor [5], Berman and Hafner [6], Prakken [51]) understanding it in a teleological sense: a decision promoting a value principle means taking that decision for the sake of observing the principle, thus seeing the value principle as a reason for making that decision. |
| 27 | We shall not be held responsible for damages resulting from sloppy Latin paraphrasings! |
| 28 | Recall our discussion in Section 6 (cf. note 15). In a future modelling of a (suitably enhanced) discoursive grammar (Section 2), we might take into account the order of combination of basic values in forming value principles, to the effect that, e.g., STABility can be properly distinguished from EFFIciency. |
| 29 | Nitpick (Blanchette and Nipkow [95]) searches for, or, respectively, enumerates finite models or countermodels to a conjectured statement/lemma. By default, Nitpick searches for countermodels, and model finding is enforced by stating the parameter keyword ‘satisfy’. These models are given as concrete interpretations of relevant terms in the given context so that the conjectured statement is satisfied or falsified. |
| 30 | Further related tests are reported in Figure A9 in Appendix A.2. |
| 31 | Cf. Berman and Hafner [6], Prakken [51], Bench-Capon [96], and also Gordon and Walton [97] for the significance of the Pierson v. Post case as a benchmark. |
| 32 | Isabelle documents are suggestively called “theories”. They correspond to top-level modules bundling together related definitions, theories, proofs, etc. |
| 33 | Remember that a defeasible conditional implication can be defined employing modal operators; cf. Section 5.4. Alternatively we may also opt for an SSE of a conditional logic in HOL using other approaches as in Benzmüller [99]. |
| 34 | We use of the term ‘default’ in the colloquial sense of ‘fallback’, noting however, that there exist in fact several (non-monotonic) logical systems aimed at modelling such a kind of defeasible, aka. “default”, behaviour for rules/conditionals (i.e., meaning that they can be ‘overruled’). One of them has been suggestively called “default logic”. We refer to Koons [100] for a discussion. In fact, and in the spirit of LogiKEy, we could have also employed, for encoding these rules, a -defined defeasible conditional as discussed in Section 5.4. For the illustrative purposes of the present paper, and in view of the good performance of our present modelling, we did not yet find this step necessary. |
| 35 | The introduction of legal factors is an established practice in the implementation of case-based legal systems (cf. Bench-Capon [56] for an overview). They can be conceived—as we do—as propositions abstracted from the facts of a case by the analyst/modeller in order to allow for assessing and comparing cases at a higher level of abstraction. Factors are typically either pro-plaintiff or pro-defendant, and their being true or false (respectively, present or absent) in a concrete case can serve to invoke relevant precedents or statutes. |
| 36 | We note that our normative assignment here is widely in accordance with classifications in the AI and Law literature (Berman and Hafner [6], Bench-Capon [52]). |
| 37 | The entire formalisation of this argument is presented in Figure A11 in Appendix A.4. |
| 38 | Also observe that the legal precedent rule R4 of Keeble v. Hickeringill (see Figure A10, Line 39) as appears in Section 7.1 does not apply to this case. |
| 39 | See the complete modelling in Figure A12 in Appendix A.4. |
| 40 | The full details of the encoding are presented in Figure A13 in Appendix A.5. |
| 41 | LogiKEy takes the position that expressive logics such as classical HOL (or possibly beyond, see Rothgang et al. [108]) are suited to serve as a universal meta-logic for knowledge representation and reasoning as motivated in Benzmüller [10] (regarding the choice of a meta-logic, we are thus in opposition to Quine [109], who advocated first-order logic for the task). This contrasts with the widespread view in the field of knowledge representation and reasoning in AI that decidability should be taken as a hard limiting criterion for the development of any logic tools and associated infrastructure. We strongly disagree with this latter view for the following reasons. (i) Although our metalogic HOL is not decidable in general, many of its fragments, such as the guarded fragment, are. For example, after unfolding the formula using our embedding from Section 5, we obtain a decidable first-order formula in the guarded fragment, which can be effectively decided by various specialised and non-specialised tools in our LogiKEy infrastructure (and more reasoners can easily be added). (ii) What counts in applications is practical performance, not theoretical pen-and-paper results that often do not even find their way into implemented code. Especially for non-experts, there is hardly any difference between a decision procedure timing out because a problem is still too hard to solve within a given time limit, and a HOL prover giving up for the same reasons. (Remark on the performance of our HOL-based LogiKEy approach: verifying all of our example files as presented and discussed in the Appendix takes only 62 s of wall clock time and 76 s of cpu time on a Apple MacBook Pro (2019) with a 2.6 GHz 6-core Intel Core i7 processor and 16 GB of 2667 MHz DDR4 memory, and proving the decisions for Pierson or Post under their respective assumptions with Sledgehammer, when no clues are given, takes much less than 10 s) (iii) For the metalogical exploration studies presented in this paper, the use of an expressive metalogic based on the simply typed lambda calculus has been crucial. The widespread rejection of the simply typed lambda calculus in the area of knowledge representation and reasoning in AI seems counterintuitive anyway, given that it serves as the very foundation of all functional programming. (iv) To solve really hard and interesting problems, e.g., in mathematics, expressiveness can be crucial. HOL can allow hyperexponentially shorter proofs than are achievable in its decidable fragments so that some really interesting proofs are generally inaccessible in traditional (decidable) knowledge representation and reasoning frameworks, while they are not in our HOL-based approach; this has been demonstrated in [110]. |
References
- Teubner, G. Substantive and Reflexive Elements in Modern Law. Law Soc. Rev. 1983, 17, 239–285. [Google Scholar] [CrossRef]
- Lomfeld, B. Vor den Fällen: Methoden soziologischer Jurisprudenz. In Die Fälle der Gesellschaft: Eine neue Praxis Soziologischer Jurisprudenz; Lomfeld, B., Ed.; Mohr Siebeck: Tübingen, Germany, 2017; pp. 1–16. [Google Scholar]
- Benzmüller, C.; Parent, X.; van der Torre, L. Designing Normative Theories for Ethical and Legal Reasoning: LogiKEy Framework, Methodology, and Tool Support. Artif. Intell. 2020, 287, 103348. [Google Scholar] [CrossRef]
- Lomfeld, B. Grammatik der Rechtfertigung: Eine kritische Rekonstruktion der Rechts(fort)bildung. Krit. Justiz 2019, 52, 516–527. [Google Scholar] [CrossRef]
- Bench-Capon, T.; Sartor, G. A model of legal reasoning with cases incorporating theories and value. Artif. Intell. 2003, 150, 97–143. [Google Scholar] [CrossRef]
- Berman, D.; Hafner, C. Representing teleological structure in case-based legal reasoning: The missing link. In Proceedings of the 4th International Conference on Artificial Intelligence and Law, Amsterdam The Netherlands, 15–18 June 1993; ACM Press: New York, NY, USA, 1993; pp. 50–59. [Google Scholar]
- Merrill, T.W.; Smith, H.E. Property: Principles and Policies; Foundation Press: Santa Barbara, CA, USA, 2017. [Google Scholar]
- Casanovas, P.; Palmirani, M.; Peroni, S.; van Engers, T.M.; Vitali, F. Semantic Web for the Legal Domain: The next step. Semant. Web 2016, 7, 213–227. [Google Scholar] [CrossRef]
- Hoekstra, R.; Breuker, J.; Bello, M.D.; Boer, A. LKIF Core: Principled Ontology Development for the Legal Domain. In Law, Ontologies and the Semantic Web—Channelling the Legal Information Flood; Frontiers in Artificial Intelligence and, Applications; Breuker, J., Casanovas, P., Klein, M.C.A., Francesconi, E., Eds.; IOS Press: Amsterdam, The Netherlands, 2009; Volume 188, pp. 21–52. [Google Scholar] [CrossRef]
- Benzmüller, C. Universal (Meta-)Logical Reasoning: Recent Successes. Sci. Comput. Program. 2019, 172, 48–62. [Google Scholar] [CrossRef]
- Moor, J. Four kinds of ethical robots. Philos. Now 2009, 72, 12–14. [Google Scholar]
- Scheutz, M. The Case for Explicit Ethical Agents. AI Mag. 2017, 38, 57–64. [Google Scholar] [CrossRef]
- Arkin, R.C.; Ulam, P.; Duncan, B.A. An Ethical Governor for Constraining Lethal Action in an Autonomous System; Technical Report GVU-09-02; Georgia Institute of Technology: Atlanta, GA, USA, 2009. [Google Scholar]
- Benzmüller, C.; Fuenmayor, D. Value-oriented Legal Argumentation in Isabelle/HOL. In International Conference on Interactive Theorem Proving (ITP), Proceedings; LIPIcs; Cohen, L., Kaliszyk, C., Eds.; Schloss Dagstuhl-Leibniz-Zentrum für Informatik: Wadern, Germany, 2021; Volume 193, pp. 23:1–23:18. [Google Scholar] [CrossRef]
- Van Benthem, J.; Girard, P.; Roy, O. Everything Else Being Equal: A Modal Logic for Ceteris Paribus Prefer. J. Philos. Log. 2009, 38, 83–125. [Google Scholar] [CrossRef]
- Prakken, H.; Sartor, G. Law and logic: A review from an argumentation perspective. Artif. Intell. 2015, 227, 214–225. [Google Scholar] [CrossRef]
- Alexy, R. (Ed.) Theorie der juristischen Argumentation; Suhrkamp: Frankfurt, Germany, 1978. [Google Scholar]
- Feteris, E. Fundamentals of Legal Argumentation; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Hage, J. Reasoning with Rules; Kluwer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Prakken, H. Logical Tools for Modelling Legal Argument; Springer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Modgil, S.; Prakken, H. Abstract Rule-Based Argumentation. In Handbook of Formal Argumentation; Baroni, P., Gabbay, D., Giacomin, M., van der Torre, L., Eds.; College Publications: Rickmansworth, UK, 2018; pp. 287–364. [Google Scholar]
- Ashley, K.D. Modelling Legal Argument: Reasoning with Cases and Hypotheticals; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Aleven, V. Teaching Case-Based Reasoning through a Model and Examples. Ph.D. Dissertation, University of Pittsburgh, Pittsburgh, PA, USA, 1997. [Google Scholar]
- Horty, J. Rules and reasons in the theory of precedent. Leg. Theory 2011, 17, 1–33. [Google Scholar] [CrossRef][Green Version]
- Bench-Capon, T.; Atkinson, K.; Chorley, A. Persuasion and value in legal argument. J. Log. Comput. 2005, 15, 1075–1097. [Google Scholar] [CrossRef][Green Version]
- Grabmair, M. Modeling Purposive Legal Argumentation and Case Outcome Prediction Using Argument Schemes in the Value Judgment Formalism. Ph.D. Dissertation, 2016. [Google Scholar]
- Maranhão, J.; Sartor, G. Value assessment and revision in legal interpretation. In Proceedings of the Seventeenth International Conference on Artificial Intelligence and Law, ICAIL 2019, Montreal, QC, Canada, 17–21 June 2019; pp. 219–223. [Google Scholar] [CrossRef]
- Lomfeld, B. Die Gründe des Vertrages: Eine Diskurstheorie der Vertragsrechte; Mohr Siebeck: Tübingen, Germany, 2015. [Google Scholar]
- Alexy, R. On Balancing and Subsumption: A Structural Comparison. Ratio Juris 2003, 16, 433–449. [Google Scholar] [CrossRef]
- Sartor, G. Doing justice to rights and values: Teleological reasoning and proportionality. Artif. Intell. Law 2010, 18, 175–215. [Google Scholar] [CrossRef]
- Sartor, G. A Quantitative Approach to Proportionality. In Handbook of Legal Reasoning and Argumentation; Bongiovanni, G., Postema, G., Rotolo, A., Sartor, G., Valentini, C., Walton, D., Eds.; Springer: Dordrecht, The Netherlands, 2018; pp. 613–636. [Google Scholar]
- Dworkin, R. Taking Rights Seriously; Harvard University Press: Cambridge, MA, USA, 1978; OCLC: 4313351. [Google Scholar]
- Alexy, R. On the Structure of Legal Principles. Ratio Juris 2000, 13, 294–304. [Google Scholar] [CrossRef]
- Raz, J. Legal Principles and the Limits of Law. Yale Law J. 1972, 81, 823–854. [Google Scholar] [CrossRef]
- Verheij, B.; Hage, J.C.; Van Den Herik, H.J. An integrated view on rules and principles. Artif. Intell. Law 1998, 6, 3–26. [Google Scholar] [CrossRef]
- Neves, M. Constitutionalism and the Paradox of Principles and Rules; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Barak, A. Proportionality; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Van der Weide, T.; Dignum, F.; Meyer, J.-J.C.; Prakken, H.; Vreeswijk, G. Practical Reasoning Using Values. In Argumentation in Multi-Agent Systems (ArgMAS); McBurney, P., Rahwan, I., Parsons, S., Maudet, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 79–93. [Google Scholar]
- Gruber, T. A Translation Approach to Portable Ontology Specifications. Knowl. Acquis. 1993, 5, 199–220. [Google Scholar] [CrossRef]
- Gruber, T. Ontology. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Smith, B. Ontology. In Blackwell Guide to the Philosophy of Computing and Information; Floridi, L., Ed.; Blackwell: Oxford, UK, 2003. [Google Scholar]
- Rokeach, M. The Nature of Human Values; Free Press Macmillan: New York, NY, USA, 1973. [Google Scholar]
- Schwartz, S. Universals in the Content and Structure of Values. Adv. Exp. Soc. Psychol. 1992, 25, 1–65. [Google Scholar]
- Eysenck, H. The Psychology of Politics; Routledge: London, UK, 1954. [Google Scholar]
- Mitchell, B. Eight Ways to Run the Country; Praeger: Westport, CT, USA, 2007. [Google Scholar]
- Clark, B. Political Economy: A Comparative Approach; Praeger: New York, NY, USA, 1991. [Google Scholar]
- Hofstede, G. Culture’s Consequences; Sage: Thousands Oaks, CA, USA, 2001. [Google Scholar]
- Inglehart, R. Cultural Evolution; Cambridge University Press: Cambridge, CA, USA, 2018. [Google Scholar]
- Bench-Capon, T. Ethical approaches and autonomous systems. Artif. Intell. 2020, 281, 103239. [Google Scholar] [CrossRef]
- Sartor, G. Teleological arguments and theory-based dialectics. Artif. Intell. Law 2002, 10, 95–112. [Google Scholar] [CrossRef]
- Prakken, H. An exercise in formalising teleological case-based reasoning. Artif. Intell. Law 2002, 10, 113–133. [Google Scholar] [CrossRef]
- Bench-Capon, T. Representing Popov v Hayashi with dimensions and factors. Artif. Intell. Law 2012, 20, 15–35. [Google Scholar] [CrossRef]
- Gordon, T.; Walton, D. A Carneades reconstruction of Popov v Hayashi. Artif. Intell. Law 2012, 20, 37–56. [Google Scholar] [CrossRef][Green Version]
- Bench-Capon, T.; Prakken, H. Using argument schemes for hypothetical reasoning in law. Artif. Intell. Law 2010, 18, 153–174. [Google Scholar] [CrossRef]
- Chorley, A.; Bench-Capon, T. An empirical investigation of reasoning with legal cases through theory construction and application. Artif. Intell. Law 2005, 13, 323–371. [Google Scholar] [CrossRef][Green Version]
- Bench-Capon, T. Hypo’s legacy: Introduction to the virtual special issue. Artif. Intell. Law 2017, 25, 205–250. [Google Scholar] [CrossRef]
- Verheij, B. Formalizing value-guided argumentation for ethical systems design. Artif. Intell. Law 2016, 24, 387–407. [Google Scholar] [CrossRef]
- Benzmüller, C.; Andrews, P. Church’s Type Theory. In The Stanford Encyclopedia of Philosophy, Summer 2019 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2019; pp. 1–62. [Google Scholar]
- Gibbons, J.; Wu, N. Folding domain-specific languages: Deep and shallow embeddings (functional Pearl). In Proceedings of the 19th ACM SIGPLAN International Conference on Functional Programming, Gothenburg, Sweden, 1–3 September 2014; Jeuring, J., Chakravarty, M.M.T., Eds.; ACM: New York, NY, USA, 2014; pp. 339–347. [Google Scholar] [CrossRef]
- Svenningsson, J.; Axelsson, E. Combining Deep and Shallow Embedding for EDSL. In Trends in Functional Programming; Loidl, H.W., Peña, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 21–36. [Google Scholar]
- Blanchette, J.C.; Kaliszyk, C.; Paulson, L.C.; Urban, J. Hammering towards QED. J. Formaliz. Reason. 2016, 9, 101–148. [Google Scholar]
- McCarty, L.T. An implementation of Eisner v. Macomber. In Proceedings of the 5th International Conference on Artificial Intelligence and Law, College Park, MD, USA, 21–24 May 1995; pp. 276–286. [Google Scholar]
- Fuenmayor, D.; Benzmüller, C. A Computational-Hermeneutic Approach for Conceptual Explicitation. In Model-Based Reasoning in Science and Technology. Inferential Models for Logic, Language, Cognition and Computation; SAPERE; Nepomuceno, A., Magnani, L., Salguero, F., Bares, C., Fontaine, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 49, pp. 441–469. [Google Scholar] [CrossRef]
- Daniels, N. Reflective Equilibrium. In The Stanford Encyclopedia of Philosophy, Summer 2020 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Rawls, J. A Theory of Justice; Harvard University Press: Cambridge, MA, USA, 1971; Revised edition 1999. [Google Scholar]
- Goodman, N. Fact, Fiction, and Forecast; Harvard University Press: Cambridge, MA, USA, 1955. [Google Scholar]
- Andrews, P.B. General Models, Descriptions, and Choice in Type Theory. J. Symb. Log. 1972, 37, 385–394. [Google Scholar] [CrossRef]
- Andrews, P.B. General Models and Extensionality. J. Symb. Log. 1972, 37, 395–397. [Google Scholar] [CrossRef]
- Benzmüller, C.; Brown, C.; Kohlhase, M. Higher-Order Semantics and Extensionality. J. Symb. Log. 2004, 69, 1027–1088. [Google Scholar] [CrossRef]
- Benzmüller, C.; Miller, D. Automation of Higher-Order Logic. In Handbook of the History of Logic, Volume 9—Computational Logic; Gabbay, D.M., Siekmann, J.H., Woods, J., Eds.; Elsevier: North Holland, The Netherlands, 2014; pp. 215–254. [Google Scholar] [CrossRef]
- Church, A. A Formulation of the Simple Theory of Types. J. Symb. Log. 1940, 5, 56–68. [Google Scholar] [CrossRef]
- Schönfinkel, M. Über die Bausteine der mathematischen Logik. Math. Ann. 1924, 92, 305–316. [Google Scholar] [CrossRef]
- Henkin, L. Completeness in the Theory of Types. J. Symb. Log. 1950, 15, 81–91. [Google Scholar] [CrossRef]
- Von Wright, G.H. The Logic of Preference; Edinburgh University Press: Edinburgh, UK, 1963. [Google Scholar]
- Benzmüller, C.; Paulson, L.C. Multimodal and Intuitionistic Logics in Simple Type Theory. Log. J. IGPL 2010, 18, 881–892. [Google Scholar] [CrossRef]
- Benzmüller, C.; Paulson, L.C. Quantified Multimodal Logics in Simple Type Theory. Log. Universalis 2013, 7, 7–20. [Google Scholar] [CrossRef]
- Carnielli, W.; Coniglio, M.E. Combining Logics. In The Stanford Encyclopedia of Philosophy, Fall 2020 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Carnielli, W.; Coniglio, M.; Gabbay, D.M.; Paula, G.; Sernadas, C. Analysis and Synthesis of Logics; Number 35 in Applied Logics Series; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Halpern, J.Y. Defining relative likelihood in partially-ordered preferential structures. J. Artif. Intell. Res. 1997, 7, 1–24. [Google Scholar] [CrossRef][Green Version]
- Liu, F. Changing for the Better: Preference Dynamics and Agent Diversity. Ph.D. Thesis, Institute for Logic, Language and Computation, Universiteit van Amsterdam, Amsterdam, The Netherlands, 2008. [Google Scholar]
- Benzmüller, C. Cut-Elimination for Quantified Conditional Logic. J. Philos. Log. 2017, 46, 333–353. [Google Scholar] [CrossRef]
- Benzmüller, C.; Farjami, A.; Meder, P.; Parent, X. I/O Logic in HOL. J. Appl. Logics—IfCoLoG J. Logics Their Appl. 2019, 6, 715–732. [Google Scholar]
- Benzmüller, C.; Farjami, A.; Parent, X. Åqvist’s Dyadic Deontic Logic E in HOL. J. Appl. Logics—IfCoLoG J. Logics Their Appl. 2019, 6, 733–755. [Google Scholar]
- Benzmüller, C.; Farjami, A.; Parent, X. Dyadic Deontic Logic in HOL: Faithful Embedding and Meta-Theoretical Experiments. In New Developments in Legal Reasoning and Logic: From Ancient Law to Modern Legal Systems; Logic, Argumentation & Reasoning; Rahman, S., Armgardt, M., Kvernenes, N., Christian, H., Eds.; Springer Nature: Cham, Switzerland, 2022; Volume 23. [Google Scholar] [CrossRef]
- Benzmüller, C.; Reiche, S. Automating Public Announcement Logic with Relativized Common Knowledge as a Fragment of HOL in LogiKEy. J. Log. Comput. 2022, 33, 1243–1269. [Google Scholar] [CrossRef]
- Parent, X.; Benzmüller, C. Normative conditional reasoning as a fragment of HOL. arXiv Preprint 2024, arXiv:2308.10686. [Google Scholar] [CrossRef]
- Kirchner, D. Computer-Verified Foundations of Metaphysics and an Ontology of Natural Numbers in Isabelle/HOL. Ph.D. Thesis, Freie Universität Berlin, Berlin, Germany, 2022. [Google Scholar] [CrossRef]
- Boutilier, C. Toward a logic for qualitative decision theory. In Principles of Knowledge Representation and Reasoning; Elsevier: Amsterdam, The Netherlands, 1994; pp. 75–86. [Google Scholar] [CrossRef]
- Lewis, D. Counterfactuals; Harvard University Press: Cambridge, MA, USA, 1973. [Google Scholar]
- Van Benthem, J. For Better or for Worse: Dynamic Logics of Preference. In Preference Change: Approaches from Philosophy, Economics and Psychology; Grüne-Yanoff, T., Hansson, S.O., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 57–84. [Google Scholar] [CrossRef]
- Liu, F. Reasoning about Preference Dynamics; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Erné, M. Adjunctions and Galois Connections: Origins, History and Development. In Galois Connections and Applications; Denecke, K., Erné, M., Wismath, S.L., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 1–138. [Google Scholar] [CrossRef]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ganter, B.; Obiedkov, S.; Rudolph, S.; Stumme, G. Conceptual Exploration; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Blanchette, J.C.; Nipkow, T. Nitpick: A Counterexample Generator for Higher-Order Logic Based on a Relational Model Finder. In Interactive Theorem Proving, Proceedings of the First International Conference, ITP 2010, Edinburgh, UK, 11–14 July 2010; LNCS; Kaufmann, M., Paulson, L.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6172, pp. 131–146. [Google Scholar]
- Bench-Capon, T. The missing link revisited: The role of teleology in representing legal argument. Artif. Intell. Law 2002, 10, 79–94. [Google Scholar] [CrossRef]
- Gordon, T.F.; Walton, D. Pierson vs. Post revisited. Front. Artif. Intell. Appl. 2006, 144, 208. [Google Scholar]
- Blanchette, J.C.; Böhme, S.; Paulson, L.C. Extending Sledgehammer with SMT Solvers. J. Autom. Reason. 2013, 51, 109–128. [Google Scholar] [CrossRef]
- Benzmüller, C. Automating Quantified Conditional Logics in HOL. In Proceedings of the 23rd International Joint Conference on Artificial Intelligence (IJCAI-13), Beijing, China, 3–9 August 2013; pp. 746–753. [Google Scholar]
- Koons, R. Defeasible Reasoning. In The Stanford Encyclopedia of Philosophy, Winter 2017 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2017. [Google Scholar]
- Wenzel, M. Isabelle/Isar—A generic framework for human-readable proof documents. Insight Proof-Festschr. Honour Andrzej Trybulec 2007, 10, 277–298. [Google Scholar]
- Rissland, E.L.; Ashley, K.D. A case-based system for trade secrets law. In Proceedings of the 1st International Conference on Artificial Intelligence and Law, Boston, MA, USA, 27 May 1997–29 May 1987; pp. 60–66. [Google Scholar]
- Krause, P.; Ambler, S.; Elvang-Goransson, M.; Fox, J. A Logic Of Argumentation for Reasoning under Uncertainty. Comput. Intell. 1995, 11, 113–131. [Google Scholar] [CrossRef]
- Carnielli, W.; Coniglio, M.E.; Fuenmayor, D. Logics of Formal Inconsistency Enriched with Replacement: An Algebraic and Modal Account. Rev. Symb. Log. 2021, 15, 771–806. [Google Scholar] [CrossRef]
- Fuenmayor, D. Topological Semantics for Paraconsistent and Paracomplete Logics. Archive of Formal Proofs. 2020. Available online: https://isa-afp.org/entries/Topological_Semantics.html (accessed on 12 December 2023).
- Benzmüller, C.; Lomfeld, B. Reasonable Machines: A Research Manifesto. In KI 2020: Advances in Artificial Intelligence, Proceedings of the 43rd German Conference on Artificial Intelligence, Bamberg, Germany, 21–25 September 2020; Lecture Notes in Artificial Intelligence; Schmid, U., Klügl, F., Wolter, D., Eds.; Springer: Cham, Switzerland, 2020; Volume 12352, pp. 251–258. [Google Scholar] [CrossRef]
- Fuenmayor, D.; Benzmüller, C. Normative Reasoning with Expressive Logic Combinations. In ECAI 2020, Proceedings of the 24th European Conference on Artificial Intelligence, Santiago de Compostela, Spain, 8–12 June 2020; Frontiers in Artificial Intelligence and Applications; De Giacomo, G., Catala, A., Dilkina, B., Milano, M., Barro, S., Bugarín, A., Lang, J., Eds.; IOS Press: Amsterdam, The Netherlands, 2020; Volume 325, pp. 2903–2904. [Google Scholar] [CrossRef]
- Rothgang, C.; Rabe, F.; Benzmüller, C. Theorem Proving in Dependently-Typed Higher-Order Logic. In Automated Deduction—CADE 29, Proceedings of the 29th International Conference on Automated Deduction, Rome, Italy, 1–4 July 2023; Lecture Notes in Artificial Intelligence; Pientka, B., Tinelli, C., Eds.; Springer: Cham, Switzerland, 2023; Volume 14132, pp. 438–455. [Google Scholar] [CrossRef]
- Hylton, P.; Kemp, G. Willard Van Orman Quine. In The Stanford Encyclopedia of Philosophy, Fall 2023 ed.; Zalta, E.N., Nodelman, U., Eds.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2023. [Google Scholar]
- Benzmüller, C.; Fuenmayor, D.; Steen, A.; Sutcliffe, G. Who Finds the Short Proof? Log. J. IGPL 2023. [Google Scholar] [CrossRef]
- Bench-Capon, T. The Need for Good Old-Fashioned AI and Law. In International Trends in Legal Informatics: A Festschrift for Erich Schweighofer; Hötzendorfer, W., Tschol, C., Kummer, F., Eds.; Weblaw: Bern, Switzerland, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).