Abstract
This paper briefly discusses the basic method that is the concept discovery & association and the Causal-Reasoning of Artificial cognition based on the framework of Universal factor space theory.
1. Introduction
In 2013, Yanke Bao studied the cognitive significance of factor operations in factor space theory, and in 2016, he proposed four cognitive ontological principles that artificial cognition must follow in the construction of mathematical language for concept expression, and based on these principles, he reconstructed the algebraic system of factor operations. At the same time, in 2016, Yanke Bao paid attention to the connotation of concept expression and extension expression based on multi-factor data, and in 2020, he drew the basic conclusion that factor algebra is a lattice in which complementary factors are not unique. This conclusion is different from classical factor space theory, which states that the algebraic system of factor operations is Boolean algebra.
This paper briefly introduces the basic methods of concept discovery & association and causal decision making from multifactor data in lattice algebraic factor systems.
2. The Universal Factor Space
Let the enumerable set be an ontological domain and be a family of factors (indicators) defined on . A strict mathematical definition of the factor and its generalized inverse (denoted as Recall) is given [1], and the composite factor is an equivalence relation on . The special elementary zero-factor and the full- factor in are defined. In turn, the basic concepts of equality (), less than (), the combination operation (), the decomposition operation (), and the complement operation () of two factors and are defined. The above concepts and properties of the operations are discussed more fully [1] and will not be repeated for the sake of space.
For the purposes of this paper, only the concept of the Universal Factor Space will be restated.
The equivalence relation is a division of , referred to as the -category of , and is denoted as the quotient set .
It can be proved that the algebraic system of set operations on the family of quotient sets is a lattice whose complementary elements are not unique, and this lattice is isomorphic to the algebraic system of factors on defined by the revision of [1].
So, we can know the Universal Factor Space is a representation space for data analysis and artificial concepts based on the lattice isomorphism between and .
3. Concept Discovery & Association
The implementation principle of the concept discovery & association and causal decision-making functions in the Universal Factor Space can be seen in Figure 1.
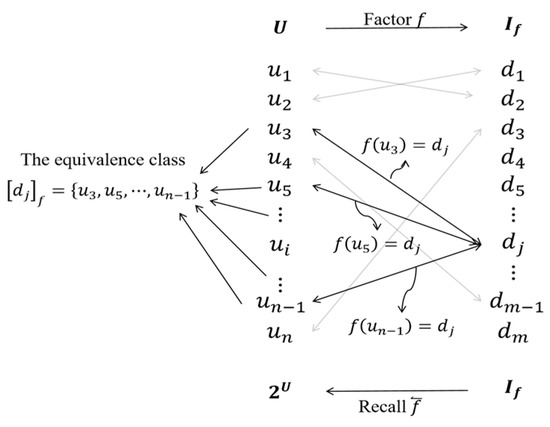
Figure 1.
The cognitive function of and .
3.1. Basic Theorem on Concept Discovery & Association
The expression of a concept in domain U is essentially determined by its connotative properties.
The connotative property is expressed as the phase state (value) of factor in factor frame , i.e., is the connotative expression of the concept.
The phase states sequence of determines a family of concepts, each of which is an element of the quotient set and constitutes an extension expression of the concept.
The association of concepts in domain that have been given factor frame is the process of generating new concepts from the relationships and operations of factors. The key techniques of this period are described by the following two theorems:
Disjunctive Operator Theorem 3.1
Conjunctive Operator Theorem 3.2
The conceptual Association’s function of these two theorems can be visualized in Figure 2.
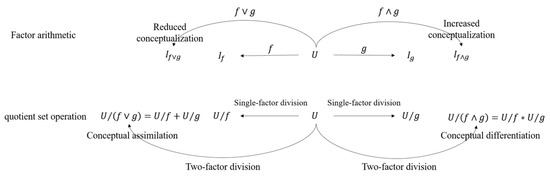
Figure 2.
The basic operator of Concept Association.
It is easy to understand from Figure 2 that the disjunctive operator of and makes more analytic, leading to the increase of connotation and the decrease in the extension of the new concept generated by the Concept Association. The Conjunctive operator makes more generalizable, leading to a reduction in the connotation and an increase in the extension of the new concept generated by the Concept Association. This change reflects the inverse relationship between connotation and extension of the concept.
3.2. Strength Measure of Concept Association
The correlation between factors and measures the strength of the conceptual association expressed by the combination of factors and .
Based on the principle of cognitive-ontology’ s moderate generalization, concepts are a dynamic balance of assimilation and differentiation in the process of concept formation. Therefore, the association of factors and should be measured in the context of the dynamic process in which and represent conceptual associations. The operation of results in an extension of the new concept that is greater than the individual extensions of the two unconnected concepts, thus weakening their correlation. Conversely, the operation of strengthens the correlation between the two concepts. Based on the above theoretical knowledge, the correlation q between factors and is defined by the quotient set.
where
This unique measure of correlation between variables in the Universal Factor Space e has excellent metric properties and relatively “moderate” results compared to familiar statistical measures.
For the effect and measure of conceptual association on sample similarity, [1] defines a discussion of the sample factor profile similarity measure formula (which embeds directed association information between adjacent factors) and the nature of its measure, which will not be repeated for the sake of space.
4. Causal Decision-Making Based on Concept Discovery & Association
The embedding of causal reasoning mechanisms is a key opportunity in the evolution of machine learning to artificial intelligence. The conceptual association function in the Universal Factor Space model implies a causal reasoning mechanism for decision-action problems.
Causal inference in domain relies on the existence of a correlation between the conditional factor as an antecedent and the consequent factor as a consequent, and the learning experience of causal inference is not transferable until a certain level of predictive correlation from to is reached.
4.1. Causal Reasoning and Decision-Making Mechanisms
In the literature [1], the following concepts are defined:
Representation The phase description of an ontological subset of the theoretical domain with respect to a factor f, denoted as .
Trace For two interrelated factors and , the equivalence class labelled by the phase state of is described on the phase space of the factor , denoted .
Deterministic-event The inclusion relation , where , , .
Determinant Directed correlation from factor to
Reasoning paradigm if , then .
Figure 3 illustrates the causal reasoning and decision-making mechanism based on the above concepts.
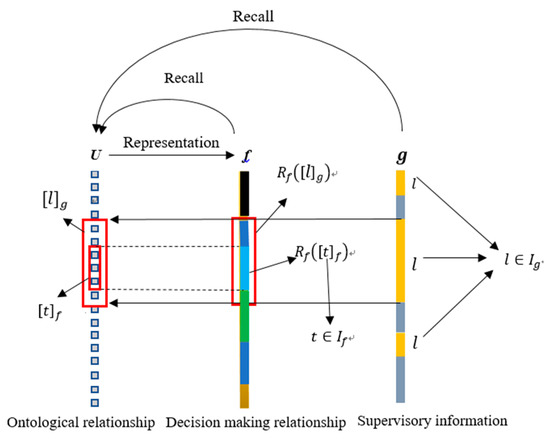
Figure 3.
Causal decision-making based on Concept discovery & Association.
From Figure 3, it is easy to understand that the causal reasoning mechanism in the Universal Factor Space is clearly different from the causal reasoning mechanism popular in the field of AI algorithm research today and has more symbolic reasoning characteristics of information processing theory.
The discussion of conceptual association and causal reasoning in the Universal Factor Space in [1] is limited by the application scenario of a “single-table database”. The way in which the human brain relates concepts and the patterns of causal reasoning are complex and multiform, even within the theoretical framework of [1], and still need to be explored.
4.2. Causal Decision-Making Algorithm
The Set Subtraction and Rotation calculation is a machine learning algorithm for data classification problems based on conceptual association and driven by factor analysis.
The algorithmic principles, algorithmic processes, information granularity transformation, application and validity evaluation of empirical inference systems, data discretization algorithms, and the integration of data discretization algorithms with the algorithmic processes of the Set Subtraction and Rotation calculation are discussed in the literature [1] and will not be repeated.
The next section describes the construction of the Set Subtraction and Rotation calculation for information only.
In 2013, Pei-Zhuang Wang proposed to replace the decision mechanism of decision trees driven by information entropy and information gain with causal judgments embedded in the inclusion relationship of equivalence classes based on the correlation of conditional and outcome factors.
The Set Subtraction and Rotation calculation aims to overcome the problems of premature convergence and low algorithm efficiency caused by the use of factor layering. The basic thought processes of the Set Subtraction and Rotation calculation are as follows:
- The main reason for the prematureness of the algorithm is the inadequacy of the factor set. That is, the given factors do not adequately characterize the object for the sample data set at hand. In addition, the large-determination decision-making mechanism may lead to conditional factors that “kidnap” the learning process.
- The concept of determinacy based on the strength of the association between two factors does not have the metaphor of a hierarchy of factors and is not subject to the logical constraint of “ordinal invariance” for the classification of factors.
- The data discretization algorithm must be integrated with the classification algorithm mechanism.
Limited algorithm testing and practical applications show that the Set Subtraction and Rotation calculation basically has the ability of self-learning and self-adaptation, and achieves better empirical knowledge of the algorithm than the decision tree algorithm.
Empirical studies have shown that increasing the capacity of a learning sample set does not necessarily improve the generalization effect of experiential knowledge. The key factor affecting the effectiveness of generalization of experiential knowledge is the representativeness and typicality of the learning sample. This is a characteristic of the non-statistical model of the Set Subtraction and Rotation calculation.
Author Contributions
Conceptualization, Y.B. and J.Z.; methodology, Y.B. and J.Z.; formal analysis, Y.B. and J.Z.; writing—original draft preparation, J.Z.; writing—review and editing, Y.B. and J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Department of Education of Guizhou Province (Qian Education and Technology [2022] No. 378), Foundations from department of education of Guizhou province ([2019]067), department of science and technology of Guizhou province, and under Grant, [2019]QNSYXM05 and Grant QNSY2018JS010.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Reference
- Bao, Y. Pan-Factor Space and Data Science Applications; Beijing University of Posts and Telecommunications Press: Beijing, China, 2021. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).