On an Optimal Interval Selection for the Regression of Molecular Frequency vs. Density Data Aimed at Determining Nonlinearity Parameters of Organic Liquids ^†

Abstract

Determining the isothermal and adiabatic nonlinearity parameters of liquids and soft matter is crucially important for a variety of engineering applications requiring operations under high pressures, nondestructive testing, exploring the propagation of finite amplitude and shock waves, etc. It has been shown recently that mathematically this problem can be reduced to the initial value problem for an ODE build based on the linear response theory for thermodynamic equalities. The required initial conditions should be determined from thermodynamic measurements at ambient pressure (or along the saturation curve). From the physical point of view, the required regression leading to the determining nonlinearity parameters originates from certain regularities in the response of molecular oscillations to the density changes. In this work, we explore how this regression procedure should be optimized computationally with respect to temperature ranges, which exclude anomalies affecting parameters of equations used for the required predictive calculations under high pressures. The validity of the proposed approach is tested by case studies of the propagation of weakly non-linear waves with finite amplitudes and density changes due to shock waves under the Rankine–Hugoniot jump conditions.

1. Introduction

The nonlinearity parameter in thermodynamic consideration of liquids is defined by the ratio between the coefficients determining the density-pressure response at the second and the first-order perturbations with respect to the equilibrium state $({\rho }_0,P_0)$:

$$P-P_0={\rho }_0{\left(\frac{\partial P}{\partial \rho }\right)}_{X,\rho ={\rho }_0}\left(\frac{\rho -{\rho }_0}{{\rho }_0}\right)+{\left(\frac{{\partial }^{2}P}{\partial {\rho }^2}\right)}_{X,\rho ={\rho }_0}{\left(\frac{\rho -{\rho }_0}{{\rho }_0}\right)}^2,$$

(1)

where $X=\{S,T\}$ means either adiabatic ($X\equiv S=\mathrm{const}$) or isothermal ($X\equiv T=\mathrm{const}$) compression.

The first case is realized by the finite amplitude sound waves [1] and leads to the so-called Beyer’s nonlinearity parameter [2], denoted as

$$\frac{B}{A}={\rho }_0{\left(\frac{{\partial }^{2}P}{\partial {\rho }^2}\right)}_{S,\rho ={\rho }_0}/{\left(\frac{\partial P}{\partial \rho }\right)}_{S,\rho ={\rho }_0}\equiv \frac{{\rho }_0}{c_0^2}{\left(\frac{{\partial }^{2}P}{\partial {\rho }^2}\right)}_{S,\rho ={\rho }_0}=2{\rho }_0{c}_0{\left(\frac{\partial c}{\partial P}\right)}_{S,{\rho }_0,P_0}.$$

(2)

Its value controls the unharmonic deformations of the spreading intensive sound wave, including the emergence of a shock wave, and also plays an important role in the modern applications of nonlinear acoustics to nondestructive sounding and biomedical diagnostics [3,4].

Simultaneously, knowledge of the isothermal nonlinearity parameter

$$k^{\prime }={\rho }_0{\left(\frac{{\partial }^{2}P}{\partial {\rho }^2}\right)}_{T,P=P_0}/{\left(\frac{\partial P}{\partial \rho }\right)}_{T,P=P_0}$$

(3)

allows an accurate prediction of the liquid density up to extremely high pressures [5] when considering the initial value problem for the ordinary differential equation along an isotherm obtained within the linear response theory

$${(-1)}^m{\rho }^n{\left(\frac{\partial P}{\partial \rho }\right)}_T={\left({\rho }_0{\kappa }_T^0\right)}^{-1}\left[1+k^{\prime }{\kappa }_T^0(P-P_0)\right],$$

(4)

where $(n,m)=\left\{\right(0,0),(1,0),(2,1\left)\right\}$ lead to the Fluctuation Theory-based Equation of State (FT-EoS), Murnaghan and Tait equations, respectively, when FT-EoS approximates Tait’s and Murnagan’s equations for not very high elevated pressures (less than about 100–150 MPa). For higher pressures, the best result can be achieved considering the half-sum of densities predicted by the Tait and Murnaghan equations with this parameter and ${\kappa }_T^0$ equal to the isothermal compressibility at the initial state $({\rho }_0,P_0)$.

It is worth noting that both nonlinearity parameters are not independent. The analysis of thermodynamic equalities given in the work H. Endo [6] provides the following expression (with some regrouping of its terms to be coordinated with Equation (4)):

$$\begin{array}{cc}\hfill \frac{B}{A}=k^{\prime }\gamma +& (\gamma -1)\left[k^{\prime }-\frac{2}{{\alpha }_P{\kappa }_T}{\left(\frac{\partial {\kappa }_T}{\partial T}\right)}_P\right]+\hfill \\ \hfill & {(\gamma -1)}^2\left[1+k^{\prime }+\frac{1}{{\alpha }_P^2}{\left(\frac{\partial {\alpha }_P}{\partial T}\right)}_P-\frac{2}{{\alpha }_P{\kappa }_T}{\left(\frac{\partial {\kappa }_T}{\partial T}\right)}_P\right]+\frac{2c_{0}T{\alpha }_P}{C_P}{\left(\frac{\partial c}{\partial T}\right)}_P,\hfill \end{array}$$

(5)

where $\gamma$, $C_P$, ${\alpha }_P$ are the heat capacity ratio, the isobaric heat capacity, and the isobaric coefficient of thermal expansion.

Note that except $k^{\prime }$ all terms in Equations (4) and (5) can be easily determined at ambient pressure (or along the liquid–vapor coexistence curve up to the normal boiling point) and one needs to obtain the value of $k^{\prime }$, which includes the pressure derivatives, at this condition. In the work [5], it has been shown, referring to the phonon theory of liquids [7,8], that

$$k^{\prime }={\left(\frac{\partial \left(c_0{\left(T\right)}^3{\rho }_0\left(T\right)\right)}{\partial \left({\rho }_0\left(T\right)\right)}\right)}_{P=P_0}\equiv 3{\left(\frac{\partial \ln {\nu }_{max}}{\partial \ln {\rho }_0}\right)}_{P=P_0}=3\Gamma ,$$

(6)

where $\Gamma$ is the microscopic (not thermodynamic) Grüneisen’s parameter and ${\nu }_{max}$ is the characteristic frequency of the highest phonon mode in Debye’s quasi-harmonic approximation.

In practice, this derivative is considered as the slope of a straight line fitting $\left(c_0{\left(T\right)}^3{\rho }_0\left(T\right)\right)$ vs. $\left({\rho }_0\left(T\right)\right)$ with rounding to the nearest integer or half-integer values. However, a range of temperatures, within which this regression is applied, can significantly affect the results. Thus, the principal goal of the present work is the exploration of this dependence and determining a criterion for the procedure’s optimization with the subsequent tests for real molecular liquid systems.

2. Materials and Methods

The thermodynamic data of liquids in the saturated and compressed state, which are used for studying the isothermal nonlinearity parameter as well as calculating the acoustic nonlinearity parameter via the thermodynamic route, were generated by the NIST REFPROP 10.0 (National Institute of Standards and Technology, Standard Reference Data Program, Gaithersburg, MD, USA) [9]. This program reports thermodynamic properties obtained using derivatives of the Helmholtz energy-based multiparametric fundamental equation of state with parameters accurately adjusted to the known comprehensive massive of existing experimental data and plays a role of an industrial standard. As a result, all thermodynamic quantities and their derivatives required for Equations (3) and (5) and combinations included in Equation (6) can be obtained directly.

The tests of the predictive capacity of the method based on the data determined at ambient pressure and the nonlinearity parameter use the scheme proposed in the work [5] when the target predicted density at high pressures is calculated as

$$\rho =\left({\rho }_{Tait}+{\rho }_{Murnaghan}\right)/2,$$

(7)

$${\rho }_{Tait}^{-1}={\rho }_0^{-1}\left(1-{k^{\prime }}^{-1}\ln \left[1+k^{\prime }{\kappa }_T^0(P-P_0)\right]\right);{\rho }_{Murnaghan}={\rho }_0{\left[1+k^{\prime }{\kappa }_T^0(P-P_0)\right]}^{1/k^{\prime }}.$$

3. Results

A number of examples of the density predictions from ambient pressure up to GPa range with the parameter $k^{\prime }$ fitted empirically within the room range of temperatures can be found in the work [5]. Here, we will consider two more complicated cases related to the predictive capacity of the discussed approach using two principal test substances considered above.

One of the principal questions is a possible variation of the parameter $k^{\prime }$ with temperature, which was determined in the work [5] as the slope of the linear fit of $\ln \left(c^3\rho \right)$ vs. $\ln \left(\rho \right)$ and may depend on the interval of the fitting. Instead, here we calculated it directly as the derivative (6) using the quantities given by the Span–Wagner fundamental equation of state by the REFPROP. Examples for methanol and toluene; the former is a typical substance with strong hydrogen bonding while the latter is the standard molecular liquid with dispersion forces only. Results are shown in Figure 1A. One can see that the case of methanol actually requires the consideration of a limited range of temperatures to consider $k^{\prime }$ (and $\Gamma$, see (6)) as approximately constant. For toluene, there is no such strong restriction of the interval, although linearity fulfills the best at the room range of temperatures that is well-coordinated with the Rao rule, see the more detailed discussion in [5].

Let us consider the application of Equation (7) with $k^{\prime }$ found within the determined optimized interval for the density prediction.

Figure 1B illustrates the case of methanol isothermally squeezed in the diamond anvil cell [10]. Under the conditions of the experiment, it keeps the normal liquid state up to $3.56\mathrm{GPa}$, then exists as a metastable liquid up to approximately $8.6\mathrm{GPa}$, after which the pressure transits to a glass state. As one can see from the course of markers, the density follows a rather smooth curve during this process and Equation (7), where we take $k^{\prime }=9$ and other parameters defined on the saturation curve only, reproduces this curve sufficiently accurately, always within the extended uncertainty range of the original experimental data. An absence of rounding to the nearest integer gives a curve, which goes even closer to the experimental points; however, the difference between these cases is negligible when taking into account the data uncertainty.

A more non-trivial example is the fast shock wave-based compression, which keeps a substance in the liquid state for pressures much higher than the freezing pressures at the isothermal process corresponding to the initial temperature of the shock compression. Naturally, the latter leads to heating of the liquid, but at very high pressures the adiabatic and isothermal compressibilities are close to each other as follows from the thermodynamic equality ${\kappa }_S^{-1}={\kappa }_T^{-1}+{\alpha }_P^{2}T/\left(\rho C_P\right),$ where the second term starts to be negligible due to the fast diminishing of ${\alpha }_P$. Whence, one can expect that the solutions to Equation (4) smoothly transfer from an isotherm to an adiabat.

Figure 1. (A) The isothermal nonlinerity parameters determined directly (dashed curve) as the derivative stated by Equation (6) and their constant values rounded to integer values within intervals of negligible temperature dependence (solid lines). (B) The experimental compression curve for methanol at $298\mathrm{K}$ [10] (circles) and the density predicted (solid line with whiskers denoting extended experimental uncertainty) as the half-sum of Tait’s (upper magenta curve) and Murnaghan’s (lower magenta curve) equations. (C) Experimental data for toluene initially taken at $295\mathrm{K}$: shock wave compression [11] (circles) and equilibrium isothermal compression from the REFPROP 10.0 [9] (squares); lines marked as for the subpanel (B) denote predictions.

Figure 1. (A) The isothermal nonlinerity parameters determined directly (dashed curve) as the derivative stated by Equation (6) and their constant values rounded to integer values within intervals of negligible temperature dependence (solid lines). (B) The experimental compression curve for methanol at $298\mathrm{K}$ [10] (circles) and the density predicted (solid line with whiskers denoting extended experimental uncertainty) as the half-sum of Tait’s (upper magenta curve) and Murnaghan’s (lower magenta curve) equations. (C) Experimental data for toluene initially taken at $295\mathrm{K}$: shock wave compression [11] (circles) and equilibrium isothermal compression from the REFPROP 10.0 [9] (squares); lines marked as for the subpanel (B) denote predictions.

Figure 1C, where circles denote the densities on the Hugoniot curve determined from the Rankine–Hugoniot conditions for the shock-wave compression of toluene. Taking into account their scattering, one can conclude that the density predicted isothermally with the temperature of initial conditions and $k^{\prime }=10$ reproduces them satisfactorily, especially at the region of $P>2\mathrm{GPa}$. To highlight the mentioned transition, the REFPROP data for this isotherm at lower pressures are shown as squares; their average relative absolute deviation from the predicted values is equal to 0.1%.

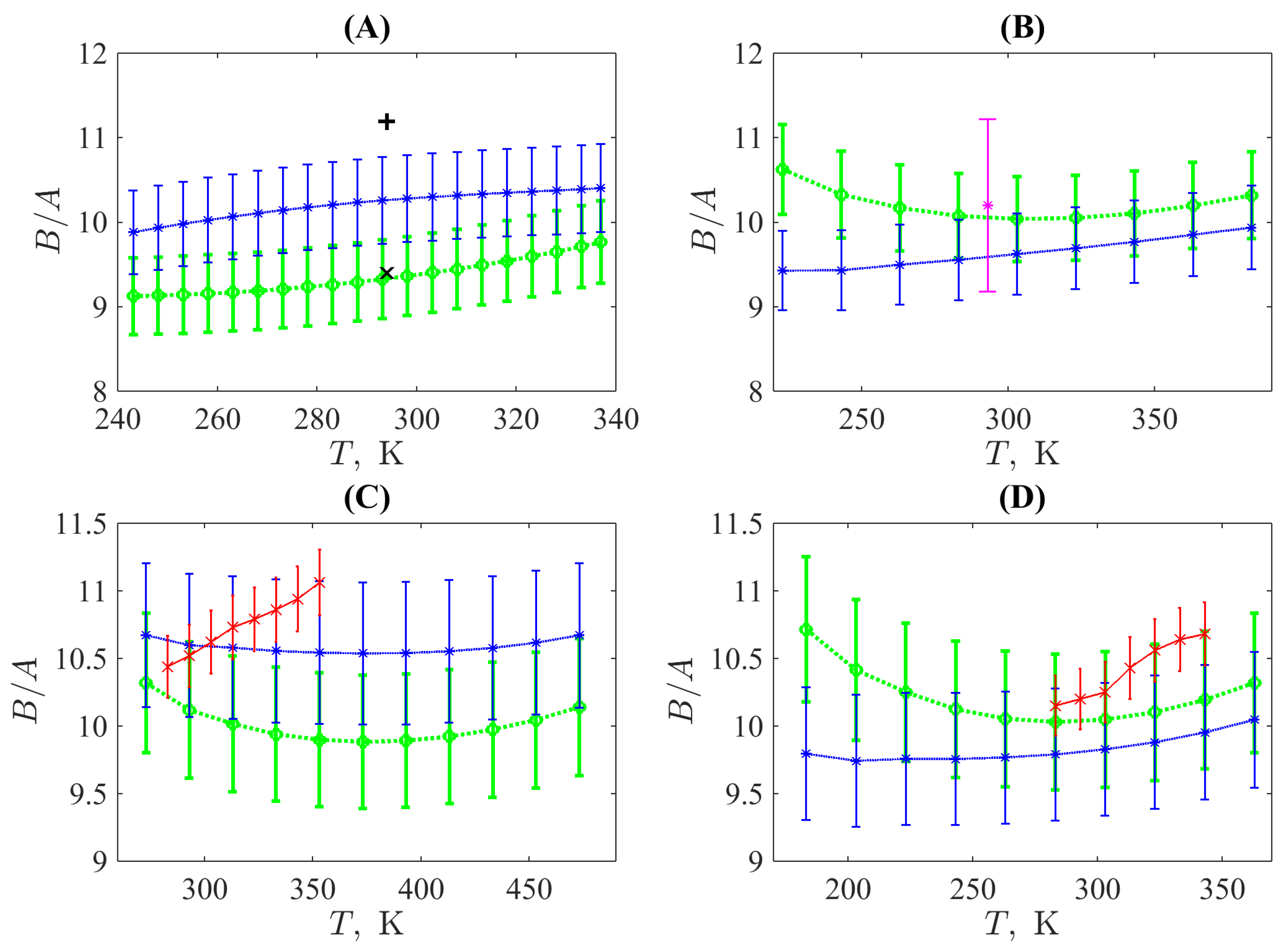
As another side of nonlinearity, let us consider the acoustic (adiabatic) nonlinearity parameter $B/A$, Equation (2) and the possibility to calculate it at atmospheric pressure using the considered model for the isothermal nonlinearity parameter (and other auxiliary thermodynamic data) substituted in Equation (5). Figure 2 illustrates these results in comparison with known experimental data and values obtained via the standard thermodynamic route [1] for methanol and toluene discussed above, and, additionally for two n-alkanes with different lengths of chain, n-dodecane and n-heptane. For all three non-polar liquids, $k^{\prime }=10$ was used, and $k^{\prime }=9$ for methanol.

It should be pointed out that the parameter $B/A$ when determined via higher derivatives of thermodynamic quantities is sensitive to the fitting curves and fundamental equation. As a result, its relative standard uncertainty, in this case, is not less than 5% (error bars in Figure 2 denote this interval). Taking into account this high uncertainty, one can see that the predictions based on the choosing interval of temperatures corresponding to the exhibition of effects of the phonon theory of liquid thermodynamics are reasonable.

4. Discussion and Conclusions

As it is seen in Figure 1, the isothermal nonlinearity parameter can be affected by the specificity of intermolecular interactions, especially hydrogen bonds. When approaching the freezing point, they lead to the string temperature dependence of $k^{\prime }$ if considering the quasi-harmonic Debye approximation. On the contrary, approaching the normal boiling point leads to destroying the microscopic oscillatory properties due to the more active diffusive movement of molecules as has been discussed within the frames of the phonon theory of liquid thermodynamics for simple liquids [7]. Thus, we can conclude that a warrant predictive approach to calculating nonlinear properties of compressed liquids requires an application of the date preprocessing based on Equation (6) aimed at revealing the temperature interval of the weak temperature dependence of the considered parameter. In addition, Figure 1 demonstrates that the method is also applicable for predicting density changes continued after the transition to the glass state as well as for the case of shock wave compressions that make it useful even beyond the pure field of classic thermodynamics of liquid.

As for the acoustic nonlinearity parameter $B/A$, this quantity has a more complicated behavior. These complications originate from the fact that the speed of sound can be considered as a thermodynamic quantity in the strict sense only for infinitesimally small amplitudes, which is not the exact case for the nonlinear waves of finite amplitudes. The difference in experimental values obtained by methods, which use the latter approach and the purely thermodynamic calculations seen in Figure 2, supports this. Nevertheless, the phonon-theory approach for calculating the acoustic nonlinearity parameter results in quite reasonable estimations, which are inside of the unavoidably wide range of the respective uncertainty. Moreover, its usage in Equation (5) reduces the origin of uncertainty to the last three terms, which considers only isobaric data while the validity of the only term, which replaces the unknown isothermal derivative, is confirmed independently due to the accuracy of the prediction of isothermal changes of density up to extremely high pressures. This reveals certain advantages of this approach over those that addressed the fluctuation theory [15] and revealed that improvements in results required the usage of the Rao rule connecting isobaric changes of the speed of sound and the density; it is shown in the work [5] that the origin of this empiric rule can be traced to Debye’s phonon theory leading to the results discussed above.

Finally, we can conclude that the relation of nonlinearity parameters to the Gruneisen parameter opens certain perspectives for studying microscopic properties of the latter in connection with the thermodynamically measurable quantities that is stated as one of the actual problems for high-pressure research [16].