The Odd Beta Prime-G Family of Probability Distributions: Properties and Applications to Engineering and Environmental Data ^†

Abstract

In this work, a novel generalized family of distributions called the odd beta prime is introduced. The linear representations of the proposed family are obtained. The expressions for the moments, the moment-generating function, and entropy are derived. A three-parameter special sub-model of the proposed family called the odd beta prime exponential distribution is proposed. Finally, two real data sets are used to illustrate the usefulness and flexibility of the proposed distribution.

1. Introduction

A popular research field is the construction of novel approaches for extending the existing distributions. The two interesting approaches to expanding a probability distribution are the T-X technique proposed by [1] and modified by [2]. The cumulative distribution function (cdf) for the generalizing family of distributions using this approach is given as:

$$F(x)={\displaystyle \underset{a}{\overset{W\left(G(x)\right)}{\int }}v(m)dm}=V\left\{W\left(G(x)\right)\right\},$$

(1)

where $v(m)$ is the pdf of the random variable $M\in \left[a,b\right]$, such that $-\infty \le a<b\le \infty$, and $W\left(G(x)\right)$ is a link function of any cdf of continuous distributions that take different forms. If we consider the odd function form, $W\left(G(x)\right)=\frac{G(x)}{1-G(x)}$, then the cdf of the T-X class will be:

$$F(x)={\displaystyle \underset{0}{\overset{\frac{G(x)}{1-G(x)}}{\int }}v(m)dm}=V\left\{\frac{G(x)}{1-G(x)}\right\}.$$

(2)

Many authors constructed extended generalized families by using the T-X approach. For example, see beta-G [3], Kw-G type-1 [4], gamma-X [5], exponentiated T-X [1], Weibull-G [6], generalized odd Lindley-G [7], and Maxwell–Weibull [8].

In this study, we consider the odd function form, $W\left(G(x)\right)=\frac{G(x)}{1-G(x)}$. Additionally, we considered the beta prime distribution for $v(m)=\frac{1}{B\left(c,d\right)}\frac{x^{c-1}}{{\left(1+x\right)}^{c+d}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x>0$.

Therefore, we now define the odd beta prime-G family with cdf given as:

$$F\left(x\right)=\frac{\hspace{0.17em}{B}_{\frac{G\left(x;\epsilon \right)}{1-G\left(x;\epsilon \right)}}\left(c,d\right)}{B\left(c,d\right)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\ge 0$$

(3)

.

The probability distribution function (pdf) of odd beta prime-G family is:

$$f(x)=\frac{g(x;\epsilon )}{B(c,d){\left[1-G(x;\epsilon )\right]}^2}\frac{{\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)}^{c-1}}{{\left[1+\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)\right]}^{c+d}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\in \Re ,$$

(4)

where $G(x;\epsilon )$ is a cdf of a baseline distribution with parameter $\epsilon$, $g\left(x;\epsilon \right)$ is the pdf of the baseline distribution, and $c>0$ and $d>0$ are the shape parameters.

Here, we are motivated to propose a new flexible family of distribution called the odd beta prime generalized (OBP-G) family, which provides greater accuracy and flexibility in fitting real-life data.

This article unfolds as follows. In Section 2, linear representations of the proposed family are derived. Some statistical properties are studied and obtained in Section 3. A special sub-model of the proposed family is introduced in Section 4. In Section 5, the performance of the proposed distribution is illustrated via two applications to real data sets. Finally, Section 6 concludes the article.

2. Linear Representations

This section presents important linear representations of the OBP-G family density function defined in (4).

Let us consider the generalized Binomial expansion as follows:

$${\left(1+m\right)}^{-\eta }={\displaystyle \sum _{i=0}^{\infty }\left(\underset{i}{\overset{-\eta }{}}\right)}{M}^i={\displaystyle \sum _{i=0}^{\infty }{\left(-1\right)}^i\left(\underset{i}{\overset{-\eta +i-1}{}}\right)}{M}^i.$$

(5)

Applying (5) into (4), we obtain:

$$\begin{array}{cc}f(x)& =\frac{g(x;\epsilon )}{B(c,d){\left[1-G(x;\epsilon )\right]}^2}{\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)}^{c-1}{\displaystyle \sum _{i=0}^{\infty }{\left(-1\right)}^i\left(\underset{i}{\overset{c+d+i-1}{}}\right)}{\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)}^i,\hspace{0.17em}\hspace{0.17em}\hfill \\ & =\frac{g(x;\epsilon )}{B(c,d)}{\displaystyle \sum _{i=0}^{\infty }{\left(-1\right)}^i\left(\underset{i}{\overset{c+d+i-1}{}}\right)}\frac{{\left(G(x;\epsilon )\right)}^{c+i-1}}{{\left(1-G(x;\epsilon )\right)}^{c+i+1}}.\hspace{0.17em}\hspace{0.17em}\hfill \end{array}$$

(6)

Using the generalized Binomial expansion for $\left|z\right|<1$ yields:

$${\left(1-m\right)}^{-n}={\displaystyle \sum _{j=0}^{\infty }\frac{\Gamma (n+j)}{j!\Gamma n}}\hspace{0.17em}{z}^i.$$

(7)

Substituting (7) into (6), we obtain:

$$\begin{array}{cc}f(x)& =\frac{g(x;\epsilon )}{B(c,d)}{\displaystyle \sum _{i=0}^{\infty }{\left(-1\right)}^i\left(\underset{i}{\overset{c+d+i-1}{}}\right)}{\left(G(x;\epsilon )\right)}^{c+i-1}{\displaystyle \sum _{j=0}^{\infty }\frac{\Gamma (c+i+j+1)}{j!\Gamma (c+i+1)}}\hspace{0.17em}{\left(G(x;\epsilon )\right)}^j,\hfill \\ & =\frac{g(x;\epsilon )}{B(c,d)}{\displaystyle \sum _{i,j=0}^{\infty }{\Psi }_{i,j}}{\left(G(x;\epsilon )\right)}^{c+i+j-1},\hfill \end{array}$$

(8)

where ${\Psi }_{i,j}={\left(-1\right)}^i\left(\underset{i}{\overset{c+d+i-1}{}}\right)\frac{\Gamma (c+i+j+1)}{j!\Gamma (c+i+1)}\hspace{0.17em}.$

3. Statistical Properties

This section provides some statistical properties of the OBP-G family of distributions, such as moments, the moment-generating function, and entropy.

3.1. Moments

Suppose that $X$ follows the OBP-G family, the rth moments of $X$ is obtained as:

$$E\left(X^r\right)=f(x)dx,$$

(9)

where $f(x)$ is defined in Equation (8).

Substituting (8) into (9) gives the moments of the OBP-G as:

$$E\left(X^r\right)=\frac{1}{B(c,d)}{\displaystyle \sum _{i,j=0}^{\infty }{\Psi }_{i,j}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{x}^{r}g(x;\epsilon )}{\left(G(x;\epsilon )\right)}^{c+i+j-1}dx.$$

(10)

3.2. Moment-Generating Function

Assuming that a random variable $X$ follows the OBP-G family, the moment-generating function of $X$ is given as:

$$M_X(t)=E\left(e^{tx}\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{tx}f(x)dx},$$

(11)

Inserting (8) into (11), we have:

$$M_X(t)=\frac{1}{B(c,d)}{\displaystyle \sum _{i,j=0}^{\infty }{\Psi }_{i,j}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{tx}g(x;\epsilon )}{\left(G(x;\epsilon )\right)}^{c+i+j-1}dx.$$

(12)

This can be expressed as:

$$M_X(t)={\displaystyle \sum _{k=0}^{\infty }\frac{{(-1)}^k}{k!}}E\left(X^r\right).$$

(13)

3.3. Entropy

Assuming that $X$ is a random variable that follows the OBP-G family, the Rényi entropy [9] of $X$ is expressed as:

$$R_{\alpha }(x)=\frac{1}{1-\alpha }\log \left[{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{f}^{\alpha }(x)dx}\right];\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\alpha >0,\hspace{0.17em}\alpha \ne 1,\hspace{0.17em}x\in \Re .$$

(14)

The integrand $f^{\alpha }(x)$ can be obtained as:

$$f^{\alpha }(x)={\left[f(x)\right]}^{\alpha }={\left\{\frac{g(x;\epsilon )}{B(c,d){\left[1-G(x;\epsilon )\right]}^2}\frac{{\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)}^{c-1}}{{\left[1+\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)\right]}^{c+d}}\right\}}^{\alpha }.$$

(15)

Therefore, (15) can be rewritten as:

$$f^{\alpha }(x)=\frac{g^{\alpha }(x;\epsilon )}{B^{\alpha }(c,d){\left[1-G(x;\epsilon )\right]}^{2\alpha }}\frac{{\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)}^{\alpha \left(c-1\right)}}{{\left[1+\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)\right]}^{\alpha \left(c+d\right)}}.$$

(16)

Substituting (5) into (16), we have:

$$f^{\alpha }(x)=\frac{g^{\alpha }(x;\epsilon )}{B^{\alpha }(c,d){\left[1-G(x;\epsilon )\right]}^{2\alpha }}{\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)}^{\alpha \left(c-1\right)}{\displaystyle \sum _{l=0}^{\infty }{\left(-1\right)}^l\left(\underset{l}{\overset{\alpha \left(c+d\right)+l-1}{}}\right)}{\left(\frac{G(x;\epsilon )}{1-G(x;\epsilon )}\right)}^l.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(17)

4. The Odd Beta Prime Exponential Distribution

This section develops a new probability distribution referred to as the odd beta prime exponential (OBPE) distribution as a sub-model of the proposed family.

Let $X$ be a random variable with exponential distribution; the cdf and pdf are, respectively, as follows:

$$G(x)=1-e^{-bx},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\ge 0,$$

(18)

$$g(x)=b{e}^{-bx},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\ge 0,$$

(19)

where $b>0$ is the rate parameter.

Hence, the cdf and pdf of the OBPE distribution can be obtained by inserting (18) and (19) into (3) and (4), respectively, as follows:

$$F\left(x\right)=\frac{\hspace{0.17em}{B}_{\frac{1-e^{-bx}}{e^{-bx}}}\left(c,d\right)}{B\left(c,d\right)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\ge 0.$$

(20)

$$f\left(x\right)=\frac{b{\left(1-e^{-bx}\right)}^{c-1}}{B\left(c,d\right)e^{-bcx}{\left[1+\left(\frac{1-e^{-bx}}{e^{-bx}}\right)\right]}^{c+d}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\ge 0.$$

(21)

5. Applications

In this section, we analyze two real data sets involving engineering and environment to evaluate the applicability of the OBPE distribution.

5.1. The Airborne Communications Transceiver Data

These engineering data were discussed in [10], and they represent the repair times of 46 failures (in hours) of an airborne communications transceiver.

Here, we will compare the fits of the OBPE with the gamma-exponentiated exponential (GEE) in [11] and the beta-exponential (BE) in [12].

We considered the following criteria to compare these distributions: the values of the negative log-likelihood $\left(-\widehat{\mathcal{l}}\right)$, Akaike information criteria (AIC), Bayesian information criteria (BIC), Cramer–von Mises (CM), and Anderson–Darling (AD). The smaller the values of these statistics, the better the fit to the data [13,14].

The maximum likelihood estimates (MLEs), standard errors (SEs), $-\widehat{\mathcal{l}}$, AIC, BIC, CM, and AD statistics for the OBPE, GEE, and BE are presented in Table 1. From the results in Table 1, it is clear that the OBPE distribution provides a better fit for the data, having smallest values of $-\widehat{\mathcal{l}}$, AIC, BIC, CM, and AD, and could be selected as a more appropriate model than other models. Figure 1 depicts the estimated pdfs and cdfs of the fitted distributions. It is clear from these plots that the OBPE describes the data in a more appropriate way than other competing models.

Table 1. MLEs with corresponding SEs (in parentheses), and some statistical measures of competing models for the airborne communications transceiver data.

Distribution	MLE and SE in ()			$-\widehat{\mathcal{l}}$	AIC	BIC	CM	AD
OBPE	c = 0.6583 (0.1625)	d = 1.1018 (0.1149)	b = 1.4863 (4.5831)	100.0163	204.032	207.689	0.054	0.337
GEE	α = 0.9323 (0.1701)	θ = 0.2585 (0.0615)	λ = 0.3685 (0.7650)	104.9309	213.861	217.519	0.175	1.103
BE	a = 2.6732 (0.4920)	b = 2.0190 (0.2613)	λ = 1.1455 (0.4016)	128.48	260.960	264.617	0.409	3.007

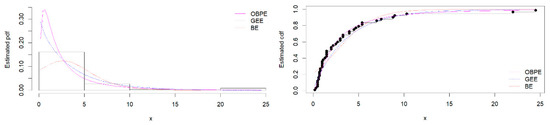
Figure 1. The estimated pdfs of the OBPE and other competing models for the airborne communications transceiver data.

5.2. Exceedances of Wheaton River Flood Data

These environmental data were analyzed by [15], and they represent the exceedances of flood peaks (in m³/s) of the Wheaton River near Carcross in Yukon Territory, Canada. The data consist of 72 exceedances for the years 1958–1984, rounded to one decimal place.

Additionally, it is clear from the results in Table 2 and the illustrations in Figure 2 that the OBPE provides a better fit for these data than other competing fitted models.

Table 2. MLEs with corresponding SEs (in parentheses), and some statistical measures of competing models for the exceedances of Wheaton River flood data.

Distribution	MLE and SE in ()			$-\widehat{\mathcal{l}}$	AIC	BIC	CM	AD
OBPE	c = 1.2126 (0.1166)	d = 6.7584 (1.1659)	b = 1.6077 (0.3743)	257.839	519.6782	524.231	0.232	1.472
GEE	α = 10.6378 (1.3609)	θ = 6.6058 (0.6475)	λ = 2.9650 (0.4475)	279.958	563.9169	568.470	0.330	2.478
BE	a = 12.2041 (1.4391)	b = 12.2115 (1.0176)	λ = 5.1753 (0.2352)	282.334	568.669	573.223	0.469	2.891

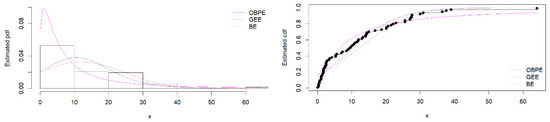
Figure 2. The estimated pdfs of the OBPE and other competing models for the exceedances of Wheaton River flood data.

6. Conclusions

A new family of life distributions called the odd beta prime-G family was introduced. Some statistical properties of the new family, including moments, the moment-generating function, and entropy, were derived. A special sub-model of the newly proposed family called the odd beta prime exponential distribution was developed, and two real applications were analyzed to demonstrate the flexibility of the new distribution. Empirically, it was proven that the proposed model can provide a better fit for modeling data than the other competing life distributions.