Abstract
The objective of this article is to present a simulation of quantum information. We take advantage of quantum entanglement to ensure the spontaneous transfer of a state from one qubit to another similar qubit. Similarly, the principle of quantum teleportation is conceived in the application; it is not about transfer of matter, but of information. Indeed, two systems already exist, and at the end of the teleportation, the process is destructive—the first system will no longer be in the same state as the initial state and the second system takes the state of the first, which does not contradict the no-cloning theorem.
1. Introduction
We adopt a computer approach using the Thread class of Java to represent two entangled qubits denoted (a) and (b), the first at Alice and the second at Bob. The simulation [1] is performed in the sense of teleporting the unknown state of a third qubit [2,3] (c) from Alice to qubit (b) from Bob. Alice couples to her partner qubit EPR [4,5] (a) the qubit (c); she performs a collective measurement on the set (a–c). This measurement has an immediate effect on Bob’s qubit (b) due to entanglement (a,b). The classic communication of the result to Bob allows him to reconstitute, thanks to a unitary transformation, the initial state of qubit (c) that is destroyed in Alice.
The rest of this paper is organized as follows: Section 2 offers a view of quantum information as a new field of research for which the avowed objective is to take advantage of the possibilities offered by quantum mechanics. Section 3 and Section 4 present a mathematical formulation used and explain the principle of quantum teleportation. The last section is reserved for simulation and analysis.
2. Quantum Information
2.1. Classic Bit
A classic bit has two states, 0 or 1 (for example, an open or closed switch). It can be read and copied without changing its value. It is always either in state 0 or in state 1.
2.2. Pbit and Qubit (Probabilistic Bit and Quantum Bit)
A pbit is similar to a classic bit, but introduces the probability distribution of a bit. This means that the pbit has a probability p of being in state 0 and 1-p of being in state 1 (piece of money thrown into space). The measurement result is reduced to a conventional bit without observing the intermediate result.
A qubit is the smallest unit of quantum information storage. It generalizes the notion of pbit because it operates in a multidimensional space. We can represent the state of a qubit by a vector traversing the Bloch sphere (Figure 1) [6] in which the two poles constitute the logical states represented by the two kets |0> and |1>.
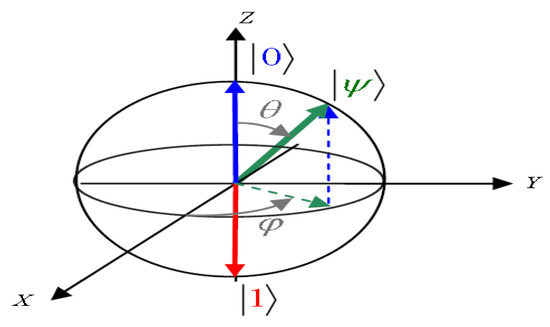
Figure 1.
Bloch’s sphere (Adapted from Ref. [7]).
A qubit can be represented in a two-dimensional Hilbert space by:
with and .
A qubit is in the general case in a superposition of the basic states |0> and |1>.
3. Quantum Entanglement
Einstein, Podolsky, and Rosen underlined the paradoxical nature of quantum entanglement. It is a correlation between the states of quantum particles despite their separation in space. Faced with this apparent paradoxical situation, the three scientists wondered if quantum mechanics was a complete and coherent description of physical reality.
3.1. Mathematical Formulation
We consider a system consisting of two photons (qubits) A and B for which the polarization state is described in a Hilbert space ; and each being a one-dimensional Hilbert space of state vector associated with the polarizations of photons A and B.
A state vector of is said to be factored if there exists and such as .
For such a state, each of the photons A and B is in a well-defined state; but for each state in , it is not factorizable as a product of two state in , in this case, the state is called entangled state.
3.2. Example of Entanglement State
The state of polarization of two photons A and B constituting the system {A, B} is entangled. Indeed, there is no qubit and such as .
This state leads to strong correlations between the two photons A and B: the measurement of the state of polarization of A instantly affects that of B. We can find the state of polarization of A and that of B both in the state with a probability of ½ or else always with the same probability in the state; certainly, one can never find them in the different states. This entanglement property is exploited in several quantum cryptography protocols.
Predictions of measurement results relating to only one of the two photons can no longer be expressed as a function of a vector |0> or |1>. We have to use the general formula , which gives the average value of the observable A in the state .
The experiment [7] of a nonlinear crystal producing two twin photons of the same energy is a typical example.
3.3. No-Cloning Theorem [8]
It is impossible to make clones of unknown quantum states. In another way, there does not exist a unitary operator U such that: .
3.4. Principle of Quantum Teleportation
Quantum teleportation uses entanglement [9] to transfer information from one system to another. Indeed, Alice and Bob share a pair of entangled qubits in the following “EPR” state:
Alice couples with her qubit another qubit of unknown state.
Via a classic public channel (Figure 2), Alice communicates to Bob the randomly chosen bases in his measurements, and according to the code fixed before, Bob applies a unitary transformation to his qubit that certainly takes Alice’s prior state.
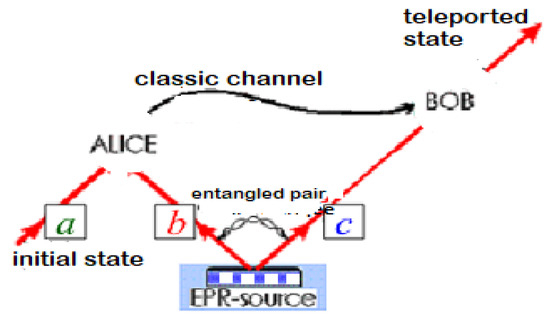
Figure 2.
Quantum teleportation (Adapted from Ref. [10]).
Thus, Bob’s measurement in the database publicly communicated by Alice has the same probability of finding the same information measured by Alice. This does not contradict the no-cloning theorem because the initial qubit state is projected to an eigenstate after the measurement.
3.5. Theoretical Realization
3.5.1. Walsh–Hadamard Gate
In quantum computing processing, the Hadamard transform (Figure 3), more often referred to as the “Hadamard gate: UwH” in this context, is a rotation of a qubit. It allows the transformation of the states |0> and |1> of the qubit in two superposed states with equal weight: |0> and |1>.
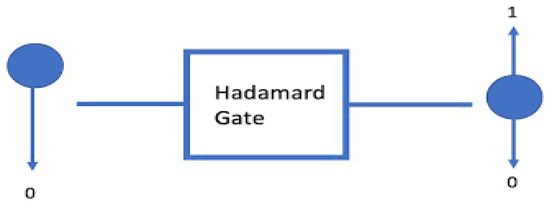
Figure 3.
Quantum circuit representing the Hadamard gate.
3.5.2. Controlled NOT
The CNOT gate (Figure 4) is two-qubit operation, where the first qubit is usually referred to as the control qubit and the second qubit as the target qubit. The Table 1 shows the truth table of CNOT gate.
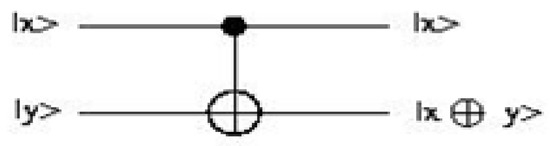
Figure 4.
Quantum circuit representing the controlled NOT gate.

Table 1.
Controlled NOT.
3.5.3. Measure Gate
The measure gate (Figure 5) is a non-reversible operation; the measurement actively modifies the observed variable. It takes a quantum state and projects it onto one of the basis vectors, with a probability equal to the square of the depth of the vectors along that basis vector.
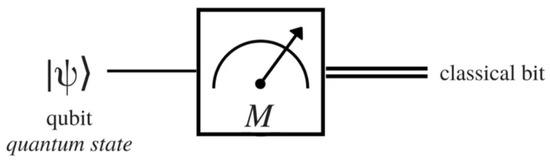
Figure 5.
Representation of the measurement. The two lines on the right side represent a classical bit; the single line on the left side represents a qubit (Adapted from Ref. [11]).
3.5.4. Teleport Circuit
The quantum circuit (Figure 6) below clearly shows the principle of quantum teleportation of an unknown qubit .
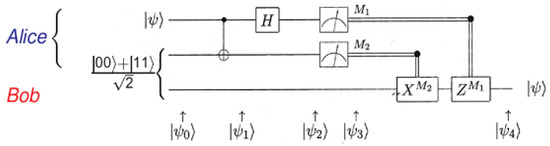
Figure 6.
Teleportation circuit (Adapted from Ref. [12]).
By applying the quantum transformations illustrated in the quantum circuit of Figure 4, the expressions of the qubits ps0, ps1, and ps2 are indicated in Equation (4).
is expressed in the Bell basis [13]; Alice communicates to Bob the values of the measures M1 and M2 and Bob finds by applying the necessary transformation as shown in Equation (5).
Alice’s qubit state is teleported in ¼ of cases. In other cases, she must transmit the result of her measurement to Bob so that the latter has the intuition of what transformation he must make to finalize the teleportation.
4. Comparison between Quantum Teleportation and BB84 Protocol
In article [14] we simulated the transmission on a quantum channel while building an intermediate system that plays the role of Eve, which intercepts Alice’s photons then sends them back to Bob, as “intercept and resend” [15]. The analysis of the estimated error defines the security zone of the transmission.
This time, our design does not support the quantum channel since there is nothing to transmit because the entanglement of photon pairs is enough to share a key between Alice and Bob. The spy no longer gains information. We admit that a classic and authenticated public channel allows Alice to communicate the basics of measuring the polarization of her photons. Moreover, unlike BB84, instead of throwing the qubits measured in the different bases into the trash, they are processed in order to ensure the degree of entanglement of the photons and finally the sharing of the key between Alice and Bob. The confirmation and purification steps are similar to those of the BB84 protocol.
5. Simulation and Analysis
5.1. Statistics
Imagine a spy who randomly chooses a qubit. The average number of common qubits between Alice and Bob on the one hand and between Bob and Eve (Spy) on the other hand, allows us to draw Figure 7.
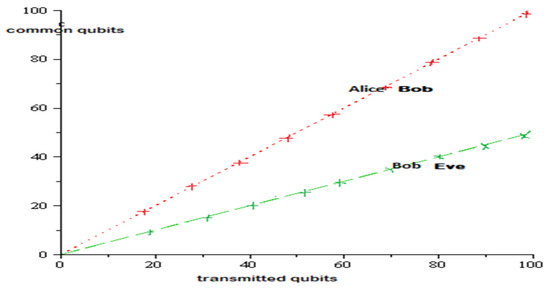
Figure 7.
Number of common qubits as a function of number of transmitted qubits.
5.2. Interpretation
The statistical analysis clearly shows that Eve can never spy on the shared key between Alice and Bob using this quantum transmission strategy based on entangled photon pairs. The secret shared in advance between Alice and Bob reinforces this protocol.
Alice and Bob almost share the polarization states of all transmitted photon pairs since they are entangled, whereas in the BB84 protocol, the number of common photons is reduced to half the number of transmitted photons (Figure 7).
6. Conclusions
Our work makes it possible to clarify the notion of quantum teleportation, which is a (quantum) communication protocol that consists of transferring the quantum state of a system to another similar and distant system without the need to physically transport the system itself. Our simulation responds well to the basic concept of quantum cryptography, with a secret message written in a random code remaining impossible to decipher by a spy. This could serve to make a secure communication network.
Despite the theoretical results obtained, a problem with quantum cryptography remains the gradual moving of technology from theoretical physics to application.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data have been presented in the main text.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cerf, N.J.; Adami, C.; Kwiat, P.G. Optical simulation of quantum logic. Phys. Rev. A 1998, 57, R1477–R1480. [Google Scholar] [CrossRef]
- Poyatos, J.F.; Cirac, J.I.; Zoller, P. Complete characterization of a quantum process: The two-bit quantum gate. Phys. Rev. Lett. 1997, 78, 390–393. [Google Scholar] [CrossRef]
- OXFORD QUANTUM. Available online: http://www.qubit.org (accessed on 10 January 2023).
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Podolskey, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Polarisation de la Lumière. Available online: http://gilbert.gastebois.pagesperso-orange.fr/java/birefringence/theorie_polarisation.htm (accessed on 10 January 2023).
- Nielsen, M.A.; Chuang, I.L.; Grover, L.K. Quantum Computation and Quantum Information. Am. J. Phys. 2002, 70, 558–559. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. arXiv 2020, arXiv:2003.06557. [Google Scholar] [CrossRef]
- Scarani, V. Initiation à la Physique Quantique; Vuibert: Paris, France, 2004. [Google Scholar]
- Bouwmeester, D.; Pan, J.-W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Understanding the Basics of Measurements in Quantum Computation. Available online: https://towardsdatascience.com/understanding-basics-of-measurements-in-quantum-computation-4c885879eba0 (accessed on 25 January 2023).
- Brassard, G. Teleportation as a quantum computation. arXiv 1996, arXiv:quant-ph/9605035. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A Single Quantum Cannot be Cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Ouchao, B.; El Kinani, E.H. Statistical analysis of common qubits between Alice and Bob in BB84 protocol. Contemp. Eng. Sci. 2011, 4, 363–370. [Google Scholar]
- Wootters, W.K. Entanglement of formation of an arbitraire state of two qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).