Mapping Petri Nets onto a Calculus of Context-Aware Ambients
Abstract
1. Introduction
- We propose an algorithm that transforms any Petri net into a CCA process (Section 2.3).
- We prove that a Petri net and its corresponding CCA process are behavioural equivalents (Section 2.3.3). This shows that CCA is at least as expressive as Petri nets, i.e., any system that can be specified in Petri nets can also be specified in CCA.
- We demonstrate that the proposed algorithm is efficient and scalable (Section 2.3.4). Indeed, the time complexity of the algorithm is quadratic (i.e., the execution time is in the order of the square of the size of the Petri net in input) and the size of the CCA process generated in output grows linearly with the size of the Petri net in input.
- The proposed algorithm is implemented in Python so a Petri net can be translated into a CCA process automatically at a click of a button (Section 2.3.4 and Appendix A).
- The proposed approach is illustrated using a case study of the dining cryptographers problem (Section 3).
2. Materials and Methods
2.1. Overview of Petri Nets
- P is a finite set of places.
- T is a finite set of transitions, such that and .
- is an input function. is the number of directed arcs from the place p to the transition t.
- is an output function. is the number of directed arcs from the transition t to the place p.
- is the initial marking, which defines the initial number of tokens in each place.
2.2. Overview of CCA
2.2.1. Processes
2.2.2. Capabilities
2.2.3. Context Model
2.2.4. Context Expressions
2.2.5. An Example
| Listing 1. The ambient representing the RFID tag. |
RFID_tag[ !@send(166).0 | in RFID_reader.0 ] |
| Listing 2. The ambient representing the RFID reader. |
RFID_reader[
!recv().#recv(id).server::send(RFID_reader, ac_service, id).
server::recv(status).send().0
| send().0
]
|
| Listing 3. The ambient representing the server. |
server[
proc ac_service(client, door, id) {
if
< (id>100) and (id<200) > client::send(valid).
door::send(open).send().0
else
client::send(invalid).door::send(close).send().0
fi
}
|
!recv().::recv(client, service, id).service(client, garage_door, id).0
| send().0
]
|
| Listing 4. The ambient representing the garage door. |
garage_door[
!recv().server::recv(x).
if
< x = close and state(opened) > del opened.send().closed[0]
< x = open and state(closed) > del closed.send().opened[0]
else
send().0
fi
| send().0
| closed[0] // initially the door is closed.
]
|
| Listing 5. The CCA process representing the access control system of Section 2.2.5. |
RFID_tag[
!@send(166).0
| in RFID_reader.0
]
|
RFID_reader[
!recv().#recv(id).server::send(RFID_reader, ac_service, id).
server::recv(status).send().0
| send().0
]
|
server[
proc ac_service(client, door, id) {
if
< (id>100) and (id<200) > client::send(valid).
door::send(open).send().0
else
client::send(invalid).door::send(close).send().0
fi
}
|
!recv().::recv(client, service, id).service(client, garage_door, id).0
| send().0
]
|
garage_door[
!recv().server::recv(x).
if
< x = close and state(opened) > del opened.send().closed[0]
< x = open and state(closed) > del closed.send().opened[0]
else
send().0
fi
| send().0
| closed[0] // initially the door is closed.
]
|
2.3. An Algorithm for Mapping a Petri Net onto a CCA Process
| Algorithm 1: Mapping a Petri net onto a CCA process. |
 |
| Listing 6. The ambient representing the semaphore . |
lock[
recv().::recv(t).{ on[0] | t::recv().del on.send().0 }
| send().0
]
|
2.3.1. Modelling Places
| Listing 7. General form of a place ambient. |
p[
send(x).0
| !recv(n).let zz=_+(1000+n) in ::recv(v).del zz.
let w=n+v, y=_+(1000+n+v) in send(w).::send().y[0]
| _(1000 + x)[0]
]
|
| Listing 8. Examples of the place ambients for the places red and black of Figure 1. |
red[
send(3).0
| !recv(n).let zz=_+(1000+n) in ::recv(v).del zz.
let w= n+v, y=_+(1000+n+v) in send(w).::send().y[0]
| _1003[0]
]
black[
send(2).0
| !recv(n).let zz=_+(1000+n) in ::recv(v).del zz.
let w= n+v, y=_+(1000+n+v) in send(w).::send().y[0]
| _1002[0]
]
|
- Base case:
- Induction case:
- If and , then , and . Let “” and “”, for some strings and . It follows that “” and “”. In string comparison, “” ≥ “” ⇔ “”≥ “”. We conclude that
- If and , then . Let “” and “” for some digits and strings and of equal length n. Since , “” ≥ “” is always true. Therefore, we conclude that
- If and , then let and , for some integers and , and digits and . There are two cases: or .
- -
- If , then .
- -
- If , let “ ” and “”, for some strings and . It follows that “” > “” .
2.3.2. Modelling Transitions
| Listing 9.General form of a transition ambient. |
1. t[
2. !< not lockOn() >lock::send(t).
3. find _M_p1: state(p1,_M_p1) for ...
find _M_pn: state(pn,_M_pn) for if
4. <_M_p1 >=_(1000 + I(p1,t)) and ... and _M_pn >=_(1000 + I(pn,t)) >
5. q1::send(-I(q1,t)+O(t,q1)).q1::recv(). ...
.qk::send(-I(qk,t)+O(t,qk)).qk::recv().
6. lock::send(end).0
7. else lock::send(not_enabled).0
8. fi.0
9. ]
|
| Listing 10.Example of the transition ambient for the transition rr of Figure 1. |
rr[
!< not lockOn() >lock::send(rr).
find _M_red: state(red,_M_red) for if
< _M_red>=_1002 > red::send(-2).red::recv().
black::send(1).black::recv().lock::send(end).0
else lock::send(not_enabled).0
fi.0
]
|
| Listing 11.Example of the CCA process generated by Algorithm 1 for the Petri net in Figure 1. |
BEGIN_DECLS
def lockOn() = { somewhere (lock[on[0] | true] | true) }
def state(p,x) = { somewhere (p[x[0] | true] | true) }
//display code
//display congruence
mode random
length=100
END_DECLS
lock[
! recv().::recv(t).{ on[0] | t::recv(x).del on.send().0 }
| send().0
]
|
red[
send(3).0
| !recv(n).let zz=_+(1000+n) in ::recv(v).del zz.let w= n+v,
y=_+(1000+n+v) in send(w).::send().y[0]
| _1003[0]
]
|
black[
send(2).0
| !recv(n).let zz=_+(1000+n) in ::recv(v).del zz.let w= n+v,
y=_+(1000+n+v) in send(w).::send().y[0]
| _1002[0]
]
|
rb[
!< not lockOn() >lock::send(rb).find _M_red: state(red,_M_red) for
find _M_black: state(black,_M_black) for if
< _M_red>=_1001 and _M_black>=_1001 > red::send(0).red::recv().
black::send(-1).black::recv().lock::send(end).0
else lock::send(not_enabled).0
fi.0
]
|
rr[
!< not lockOn() >lock::send(rr).find _M_red: state(red,_M_red) for if
< _M_red>=_1002 > red::send(-2).red::recv().black::send(1).
black::recv().lock::send(end).0
else lock::send(not_enabled).0
fi.0
]
|
bb[
!< not lockOn() >lock::send(bb).find _M_black: state(black,_M_black) for if
< _M_black>=_1002 > black::send(-1).black::recv().lock::send(end).0
else lock::send(not_enabled).0
fi.0
]
|
2.3.3. Behavioural Equivalence
- Each place and its corresponding place ambient have the same initial marking, i.e.,
- A transition is enabled if and only if its corresponding transition ambient is enabled, i.e.,
- For each transition , the execution of its corresponding transition ambient is atomic, i.e., two transition ambients cannot execute at the same time.
- For each transition , the execution of its corresponding transition ambient updates the markings of the place ambients, as in (2).
- ⇔
- , from Theorem 1.
- ⇔
- , from Lemma 1.
- ⇔
- , from Table 4 and Definition 2.
- ⇔
- , from predicate logic.
- ⇔
- .
- In Line 2 of Listing 9, the rules (R9) and (R12) are applied to obtain the semaphore lock.
- In Line 3, the rule (R5) is applied to find the name of the child ambient of each input place ambient.
- In Line 4, the condition of the if-statement is evaluated to be true, since the transition ambient is enabled (see (3)). Therefore, Line 5 is executed next, according to the semantic rule (R3).
- In line 5, for each input or output place ambient p of the transition ambient t, the process “p::send(-I(p,t)+O(t,p)).p::recv()” is executed to send (using the rule (R12)) to p the value , and then it must wait for the acknowledgement (using the rule (R13)) that p has successfully updated its marking. Note that the value is a constant for each pair .
- In Line 6, the transition ambient releases the semaphore lock using the semantic rule (R14).
- The rules (R9) and (R10) are applied to receive in the variable n the current marking of p.
- Rule (R6) is applied to calculate the name of the current child ambient of p in the variable .
- Rule (R12) is used to receive the value sent by the running transition ambient t in the variable v.
- Rule (R8) is applied to delete the current child ambient.
- Rule (R6) is applied to calculate the new value () of the marking of p in the variable w, as in (2), and to calculate (at the same time) the new name of the child ambient of p () in the variable y.
- Rules (R9) and (R10) are applied to set the new marking of the place ambient to w.
- Rule (R13) is used to tell the running transition ambient that the marking of p has been updated.
- Finally, the new child ambient named y is created.
2.3.4. Complexity of the Algorithm
3. Results
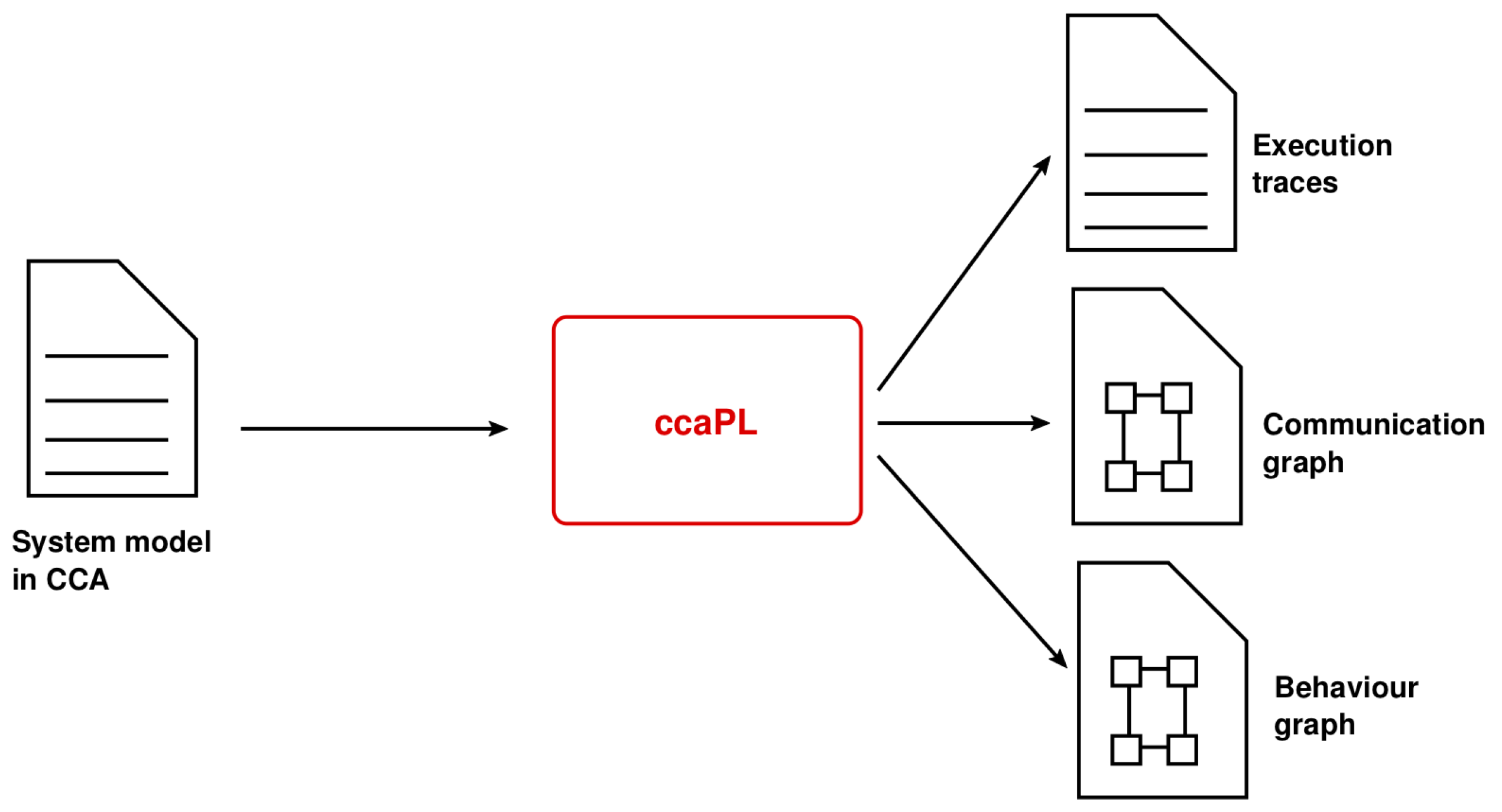
3.1. Overview of the CCA Simulator ccaPL
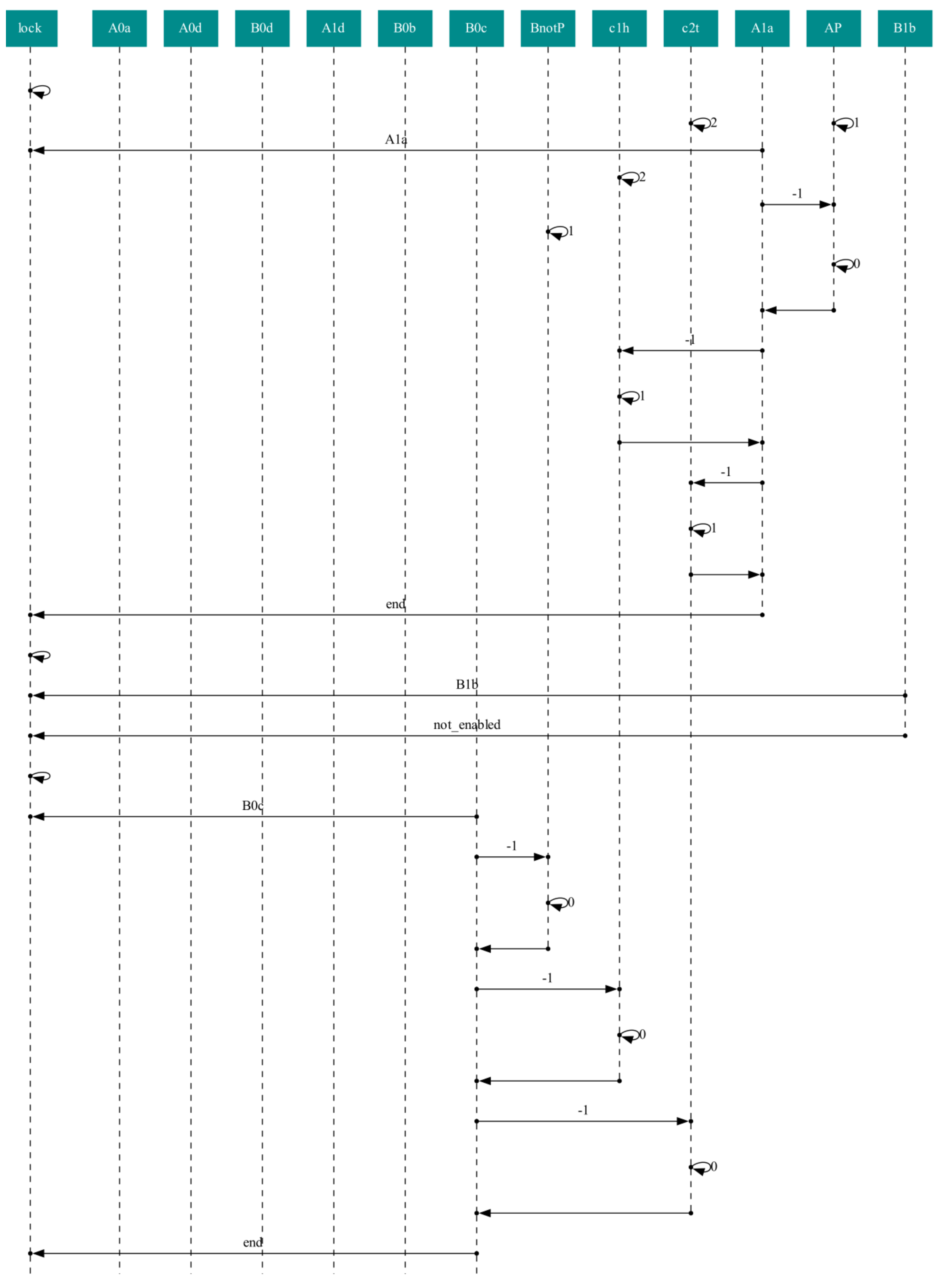
3.1.1. Textual Execution Trace
3.1.2. Communication Graph
3.1.3. Behaviour Graph
3.2. A Case Study: The Dining Cryptographers Problem
3.2.1. A Dining Cryptographers Protocol
3.2.2. Mapping the Petri Net of the Dining Cryptographers Protocol onto a CCA Process
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. An Implementation of Algorithm 1 in Python
# Mapping Petri net to CCA (March 2024, Python version 3.10.11)
# output file
PATH = "petrinet2cca.cca"
# Space: minim indentation
Space = " "
# P is a finite set of places names
P = ["red", "black"]
# T is a finite set of transitions names
T = ["rb", "rr", "bb"]
# I is the input function; I: PxT-->N.
# I = {place:{trans:nb_arcs, ...}, ...}
# nb_arcs: number of arcs from "place" to "trans"
I = {"red":{"rb":1, "rr":2}, "black":{"rb":1, "bb":2}}
# O is the output function; I: TxP-->N.
# O = {trans:{place:nb_arcs, ...}, ...}
# nb_arcs: number of arcs from "trans" to "place"
O = {"rb":{"red":1}, "rr":{"black":1}, "bb":{"black":1}}
# m0 is the initial marking. m0 = {place:nb_tokens, ...}
m0 = {"red":3, "black":2}
# Save output in a file
def display(cca_str):
F = open(PATH, "w")
i = 0; print(cca_str); F.write(cca_str)
F.close()
# Return the number of arcs from a place to a transition.
def inputs(place,trans):
if place in I.keys() and trans in I[place].keys():
return I[place][trans]
else:
return 0
# Return the number of arcs from a transition to a place.
def outputs(trans, place):
if trans in O.keys() and place in O[trans].keys():
return O[trans][place]
else:
return 0
# The mapping function
def mapping():
# cca_str: contain the CCA program generated
cca_str = "BEGIN_DECLS\n"+Space+\
"def lockOn() = { somewhere (lock[on[0] | true] | true) }\n"+\
Space+"def state(p,x) = { somewhere (p[x[0] | true] | true) }\n"+\
Space+"//display code\n"+Space+"//display congruence\n"+Space+\
"mode random\n"+Space+"length=200\nEND_DECLS\n"+ "lock[\n"+Space+\
"! recv().::recv(t).{ on[0] | t::recv(x).del on.send().0 }\n"+Space+\
"| send().0\n]\n"
# Create all the place ambients
for x in P:
cca_str += "|\n"; cca_str += x + "[\n"+Space+"send("+str(m0[x])+\
").0\n"+Space+"| !recv(n).let zz=_+(1000+n) in ::recv(v).del zz."+\
"let w= n+v, y=_+(1000+n+v) in send(w).::send().y[0] \n"
cca_str += Space+"| _"+str(1000+m0[x])+"[0]\n"; cca_str += "]\n"
# Create all the transitions ambients
for t in T:
var = ""; cond = ""; trouve = False;
for x in I.keys():
if t in I[x].keys():
if not trouve:
cond += "_M_"+x+">=_"+str(1000+I[x][t])
trouve = True
else:
cond += " and _M_"+x+">=_"+str(1000+I[x][t])
var += "find _M_"+x+": state("+x+",_M_"+x+") for "
cca_str += "|\n"
cca_str += t +"[\n"+Space+"!< not lockOn() >lock::send("+t+")."+\
var+"if \n"+Space+Space+"< "+cond+" > "
for x in P:
if (x in I.keys() and t in I[x].keys())\
or (t in O.keys() and x in O[t].keys()):
cca_str += x+"::send("+str(-inputs(x,t)+outputs(t,x))+\
")."+x+"::recv()."
cca_str += "lock::send(end).0\n"
cca_str += Space+Space+"else lock::send(not_enabled).0\n"+\
Space+Space+"fi.0\n]\n"
return cca_str;
# Display and save output
display(mapping())
|
References
- Petri, C.A. Kommunikation mit Automaten (Communication with Automata). Ph.D. Thesis, University of Bonn, Bonn, Germany, 1962. [Google Scholar]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Hoare, C. Communicating Sequential Processes; Prentice Hall: Hoboken, NJ, USA, 1985. [Google Scholar]
- Milner, R. A Calculus of Communicating Systems; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Milner, R. Communication and Mobile Systems: The π-Calculus; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Fournet, C.; Gonthier, G. The reflexive CHAM and the join-calculus. In Proceedings of the 23rd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, St. Petersburg Beach, FL, USA, 21–24 January 1996; pp. 372–385. [Google Scholar] [CrossRef]
- Siewe, F.; Zedan, H.; Cau, A. The Calculus of Context-aware Ambients. J. Comput. Syst. Sci. 2011, 77, 597–620. [Google Scholar] [CrossRef]
- Siewe, F. ccaPL: A CCA Programming Environment. Available online: https://fsiewe.afrilocode.net/CCA/index.html (accessed on 23 November 2023).
- Cardelli, L.; Gordon, A.D. Mobile Ambients. Theor. Comput. Sci. 2000, 240, 177–213. [Google Scholar] [CrossRef]
- Alfakeeh, A.S.; Al-Bayatti, A.H.; Siewe, F.; Baker, T. Agent-based negotiation approach for feature interactions in smart home systems using calculus of the context-aware ambient. Trans. Emerg. Telecommun. Technol. 2022, 33, e3808. [Google Scholar] [CrossRef]
- Mennicke, S. A Petri Net Semantics for the Join-Calculus; Technical Report; TU Braunschweig: Braunschweig, Germany, 2012; Available online: https://www.researchgate.net/profile/Stephan_Mennicke/publication/225026105_A_Petri_Net_Semantics_for_the_Join-Calculus/links/0c960531eab88c058c000000/A-Petri-Net-Semantics-for-the-Join-Calculus.pdf (accessed on 24 February 2024).
- Yao, W.; He, X. Mapping Petri nets to concurrent programs in CC++. Inf. Softw. Technol. 1997, 39, 485–495. [Google Scholar] [CrossRef]
- Korečko, T.; Sobota, B. Petri Nets to B-Language Transformation in Software Development. Acta Polytech. Hung. 2014, 11, 187–206. [Google Scholar]
- Boukelkoul, S.; Redjimi, M. Mapping between Petri nets and DEVS models. In Proceedings of the 2013 3rd International Conference on Information Technology and e-Services (ICITeS), Sousse, Tunisia, 24–26 March 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Marsan, M.A.; Balbo, G.; Conte, G.; Donatelli, S.; Franceschinis, G. Modelling with generalized stochastic Petri nets. ACM Sigmetr. Perform. Eval. Rev. 1998, 26, 2. [Google Scholar] [CrossRef]
- Van der Aalst, W.M.P. Putting high-level Petri nets to work in industry. Comput. Ind. 1994, 25, 45–54. [Google Scholar] [CrossRef]
- AT&T Labs-Research. Graphviz Distribution. Available online: http://www.research.att.com/sw/tools/graphviz/download.html (accessed on 23 November 2023).
- Chaum, D. The Dining Cryptographers Problem: Unconditional Sender and Recipient Untraceability. J. Cryptol. 1988, 1, 65–75. [Google Scholar] [CrossRef]
- Mazaré, L. Using unification for opacity properties. In Proceedings of the Workshop on Issues in the Theory of Security (WITS’04), Barcelona, Spain, 3–4 April 2004; pp. 165–176. [Google Scholar]
- Bryans, J.W.; Koutny, M.; Ryan, P.Y.A. Modelling Opacity Using Petri Nets. Electr. Notes Theor. Comput. Sci. 2005, 121, 101–115. [Google Scholar] [CrossRef]
- Best, E.; Devillers, R.; Hall, J.G. The box calculus: A new causal algebra with multi-label communication. In Advances in Petri Nets 1992; Rozenberg, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 21–69. [Google Scholar]
- Koutny, M.; Esparza, J.; Best, E. Operational Semantics for the Petri Box Calculus. In CONCUR ’94: Concurrency Theory; Jonsson, B., Parrow, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 210–225. [Google Scholar]
- Cerone, A. Implementing Condition/Event Nets in the Circal Process Algebra. In Proceedings of the 5th International Conference on Fundamental Approaches to Software Engineering, FASE ‘02, Grenoble, France, 8–12 April 2002; pp. 49–63. [Google Scholar]
- Milner, R. Bigraphs for Petri nets. In Advanced Course on Petri Nets; Springer: Berlin/Heidelberg, Germany, 2003; pp. 686–701. [Google Scholar]
- Sassone, V.; Sobociński, P. A congruence for Petri nets. Electron. Notes Theor. Comput. Sci. 2005, 127, 107–120. [Google Scholar] [CrossRef]
- Leifer, J.J.; Milner, R. Transition systems, link graphs and Petri nets. Math. Struct. Comput. Sci. 2006, 16, 989–1047. [Google Scholar] [CrossRef]
- Khomenko, V.; Meyer, R.; Hüchting, R. A polynomial translation of pi-calculus FCPs to safe Petri nets. Log. Methods Comput. Sci. 2013, 9, 1–36. [Google Scholar] [CrossRef]
- Khomenko, V.; Germanos, V. Modelling and Analysis Mobile Systems Using-calculus (EFCP). In Transactions on Petri Nets and Other Models of Concurrency X; Springer: Berlin/Heidelberg, Germany, 2015; pp. 153–175. [Google Scholar]
- Degano, P.; De Nicola, R.; Montanari, U. A distributed operational semantics for CCS based on condition/event systems. Acta Inform. 1988, 26, 59–91. [Google Scholar] [CrossRef]
- Goltz, U. CCS and Petri nets. In LITP Spring School on Theoretical Computer Science; Springer: Berlin/Heidelberg, Germany, 1990; pp. 334–357. [Google Scholar]
- Busi, N.; Gorrieri, R. Distributed semantics for the π-calculus based on Petri nets with inhibitor arcs. J. Log. Algebr. Program. 2009, 78, 138–162. [Google Scholar] [CrossRef][Green Version]
- Dam, M. Model Checking Mobile Processes. Inf. Comput. 1996, 129, 35–51. [Google Scholar] [CrossRef][Green Version]
- Sangiorgi, D.; Walker, D. The π-Calculus: A Theory of Mobile Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- van Glabbeek, R.; Vaandrager, F. Petri net models for algebraic theories of concurrency. In Proceedings of the PARLE Parallel Architectures and Languages Europe, Eindhoven, The Netherlands, 15–19 June 1987; pp. 224–242. [Google Scholar]
- Siewe, F.; Germanos, V.; Zeng, W. Analysing Petri Nets in a Calculus of Context-Aware Ambients. In Proceedings of the 2020 IEEE 44th Annual Computers, Software, and Applications Conference (COMPSAC), Madrid, Spain, 13–17 July 2020; pp. 1647–1652. [Google Scholar]
- Gorrieri, R.; Montanari, U. On the implementation of concurrent calculi in net calculi: Two case studies. Theor. Comput. Sci. 1995, 141, 195–252. [Google Scholar] [CrossRef][Green Version]
- Taubner, D.A. Finite Representations of CCS and TCSP Programs by Automata and Petri Nets; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]





| Processes | Context Expressions | ||||||
| inactivity | empty context | ||||||
| parallel composition | true | ||||||
| block | false | ||||||
| name restriction | name match | ||||||
| replication | hole | ||||||
| ambient | location context | ||||||
| context-guarded prefix | parallel composition | ||||||
| if-then | conjunction | ||||||
| … | disjunction | ||||||
| negation | |||||||
| if-then-else | spatial next modality | ||||||
| somewhere modality | |||||||
| arithmetic | |||||||
| search | |||||||
| process abstraction | |||||||
| M | Capabilities | Locations | |||||
| one transition | @ | any parent | |||||
| move into ambient n | specific parent n | ||||||
| move out of parent | # | any child | |||||
| delete ambient n | specific child n | ||||||
| receive data from | any sibling | ||||||
| send data to | specific sibling n | ||||||
| process abstraction call | locally |
| C |
| ⊧ | ||||
| C | ⊧ | iff | ||
| C | ⊧ | iff | ||
| C | ⊧ | iff | ||
| C | ⊧ | iff | ||
| C | ⊧ | iff | ||
| C | ⊧ | iff | ||
| C | ⊧ | iff | ||
| C | ⊧ | iff | ||
| C | ⊧ | iff | or |
| = | n is located at self. | ||
| = | self is located at n. | ||
| = | m is located at n. | ||
| = | self is with n. | ||
| = | n is with m. | ||
| = | the current state of p is x. | ||
| = | self current state is x. | ||
| = | the lock is on. |
| (R1) | if |
| (R2) | |
| , for some i, . | |
| (R3) | |
| (R4) | |
| if . | |
| (R5) | |
| if | |
| (R6) | |
| (R7) | |
| (R8) | |
| (R9) | |
| (R10) | , for |
| (R11) | |
| , for | |
| (R12) | |
| , for | |
| (R13) | |
| , for | |
| (R14) | |
| , for |
| Petri Net Concepts | CCA Concepts |
|---|---|
| a place | an ambient of the form in Listing 7, called place ambient . |
| a transition | an ambient of the form in Listing 9, called transition ambient. |
| the number of tokens (also known as marking) of a place | the name of the child ambient of a place ambient encodes the number of tokens of the place ambient, as in Definition 2. |
| a Petri net | the parallel composition of the semaphore ambient lock defined in Listing 6 with all the place ambients and all the transition ambients. An example is given in Listing 11 |
<Program> ::= <DeclarationBlock> P
<DeclarationBlock> ::= e | ‘‘BEGIN_DECLS’’ <DeclarationList> ‘‘END_DECLS’’
<DeclarationList> ::= e | <Declaration><DeclarationList>
<Declaration> ::= ‘‘def’’ <Id> ‘‘(’’ <ParamList> ‘‘) = {’’ k ‘‘}’’
| ‘‘mode random’’ | ‘‘display code’’ | ‘‘length = ’’ <Val>
| ‘‘display congruence’’
<ParamList> ::= e | <Id> <Params>
<Params> ::= e | ‘‘,’’ <Id> <Params>
|
| Inputs | Outputs | |||
|---|---|---|---|---|
| Coin | Cryptographer | Petri Net | CCA Process | |
| Markings | Markings | Enabled Transitions | Executed Ambients | # |
| , | A0a, B1c | 1 | ||
| , | A1c, B0a | 2 | ||
| , | A1c, B1c | 3 | ||
| , | A1a, B0c | 4 | ||
| , | A0c, B1a | 5 | ||
| , | A0c, B0c | 6 | ||
| , | A1b, B0b | 7 | ||
| , | A0d, B1b | 8 | ||
| , | A0d, B0d | 9 | ||
| , | A0b, B1d | 10 | ||
| , | A1d, B0b | 11 | ||
| , | A1d, B1d | 12 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siewe, F.; Germanos, V.; Zeng, W. Mapping Petri Nets onto a Calculus of Context-Aware Ambients. Software 2024, 3, 284-309. https://doi.org/10.3390/software3030015
Siewe F, Germanos V, Zeng W. Mapping Petri Nets onto a Calculus of Context-Aware Ambients. Software. 2024; 3(3):284-309. https://doi.org/10.3390/software3030015
Chicago/Turabian StyleSiewe, François, Vasileios Germanos, and Wen Zeng. 2024. "Mapping Petri Nets onto a Calculus of Context-Aware Ambients" Software 3, no. 3: 284-309. https://doi.org/10.3390/software3030015
APA StyleSiewe, F., Germanos, V., & Zeng, W. (2024). Mapping Petri Nets onto a Calculus of Context-Aware Ambients. Software, 3(3), 284-309. https://doi.org/10.3390/software3030015






