Are Infinite-Failure NHPP-Based Software Reliability Models Useful?
Abstract
:1. Introduction
2. Non-Homogeneous Poisson processes
2.1. Preliminary
- NHPP has independent increments, so the number of occurrences in a specific time interval depends on only the current time and not on the past history of the process, which is also known as the Markov property.
- The initial state of the process is given by .
- The occurrence probability of one event in a given time period for an NHPP is defined by . is an absolutely continuous function, and is named the intensity function of NHPP. is recognized as an infinitesimal period of time.
- NHPP has negligible probability for two or more events occurring in , i.e., , where and is the higher-order term of .
- As a typical Markov process, the Kolmogorov forward equations of NHPP can be written aswith where represents the free parameter vector in the transition rate function . By solving the above simultaneous equations, the steady-state transition probability is given by
2.2. NHPP-Based SRMs
2.2.1. Finite-Failure (Type-I) NHPP-Based SRMs
2.2.2. Infinite-Failure (Type-II) NHPP-Based SRMs
2.3. Parameter Estimation
2.3.1. Software Fault-Count Time-Domain Data
2.3.2. Software Fault-Count Time-Interval Data (Group Data)
3. Performance Comparison
3.1. Datasets
3.2. Goodness-of-Fit Performance
3.3. Predictive Performance
3.4. Software Reliability Assessment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kuo, L.; Yang, T.Y. Bayesian computation for nonhomogeneous Poisson processes in software reliability. J. Am. Stat. Associ. 1996, 91, 763–773. [Google Scholar] [CrossRef]
- Goel, A.L.; Okumoto, K. Time-Dependent Error-Detection Rate Model for Software Reliability and Other Performance Measures. IEEE Trans. Reliab. 1979, R-28, 206–211. [Google Scholar] [CrossRef]
- Okamura, H.; Dohi, T.; Osaki, S. Software reliability growth models with normal failure time distributions. Reliab. Eng. Syst. Saf. 2013, 116, 135–141. [Google Scholar] [CrossRef]
- Achcar, J.A.; Dey, D.K.; Niverthi, M. A Bayesian approach using nonhomogeneous Poisson processes for software reliability models. In Frontiers in Reliability; World Scientific: Hackensack, NJ, USA, 1998; pp. 1–18. [Google Scholar] [CrossRef] [Green Version]
- Ohba, M. Inflection S-Shaped Software Reliability Growth Model. In Stochastic Models in Reliability Theory; Springer: Berlin/Heidelberg, Germany, 1984; pp. 144–162. [Google Scholar] [CrossRef]
- Gokhale, S.S.; Trivedi, K.S. Log-logistic software reliability growth model. In Proceedings of the Third IEEE International High-Assurance Systems Engineering Symposium (Cat. No. 98EX231), Washington, DC, USA, 13–14 November 1998; pp. 34–41. [Google Scholar]
- Goel, A.L. Software reliability models: Assumptions, limitations, and applicability. IEEE Trans. Softw. Eng. 1985, SE-11, 1411–1423. [Google Scholar] [CrossRef]
- Ohishi, K.; Okamura, H.; Dohi, T. Gompertz software reliability model: Estimation algorithm and empirical validation. J. Syst. Softw. 2009, 82, 535–543. [Google Scholar] [CrossRef] [Green Version]
- Yamada, S.; Ohba, M.; Osaki, S. S-Shaped Reliability Growth Modeling for Software Error Detection. IEEE Trans. Reliab. 1983, R-32, 475–484. [Google Scholar] [CrossRef]
- Zhao, M.; Xie, M. On maximum likelihood estimation for a general non-homogeneous Poisson process. Scand. J. Stat. 1996, 23, 597–607. [Google Scholar]
- Abdel-Ghaly, A.A.; Chan, P.Y.; Littlewood, B. Evaluation of competing software reliability predictions. IEEE Trans. Softw. Eng. 1986, SE-12, 950–967. [Google Scholar] [CrossRef]
- Crétois, E.; Gaudoin, O. New Results on Goodness-of-Fit Tests for the Power-Law Process and Application to Software Reliability. Int. J. Reliab. Qual. Saf. Eng. 1998, 5, 249–267. [Google Scholar] [CrossRef]
- Duane, J.T. Learning Curve Approach to Reliability Monitoring. IEEE Trans. Aerosp. 1964, 2, 563–566. [Google Scholar] [CrossRef]
- Littlewood, B. Rationale for a modified Duane model. IEEE Trans. Reliab. 1984, R-33, 157–159. [Google Scholar] [CrossRef]
- Musa, J.D.; Okumoto, K. A logarithmic Poisson execution time model for software reliability measurement. In Proceedings of the 7th International Conference on Software Engineering, Orlando, FL, USA, 26–29 March 1984; pp. 230–238. [Google Scholar]
- Musa, J.D.; Iannino, A.; Okumoto, K. Software Reliability, Measurement, Prediction, Application; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Okamura, H.; Dohi, T. SRATS: Software reliability assessment tool on spreadsheet (Experience report). In Proceedings of the 2013 IEEE 24th International Symposium on Software Reliability Engineering (ISSRE), Pasadena, CA, USA, 4–7 November 2013; pp. 100–107. [Google Scholar]
- Lyu, M.R. Handbook of Software Reliability Engineering; IEEE Computer Society Press: Los Alamitos, CA, USA, 1996; Volume 222. [Google Scholar]
- Min, X. Software Reliability Modeling; World Scientific: Singapore, 1991. [Google Scholar]
- Jun, H.; Shigeru, Y.; Shunji, O. Reliability assessment measures based on software reliability growth model with normalized method. J. Inf. Process. 1991, 14, 178–183. [Google Scholar]
- Barlow, R.E.; Proschan, F. Mathematical Theory of Reliability, 1965; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Cox, D.; Lewis, P.A.W. The Statistical Analysis of Series of Events; Springer: Dordrecht, The Netherlands, 1966. [Google Scholar]
- Musa, J.D. Software Reliability Data; Technical Report in Rome Air Development Center; 1979. [Google Scholar]
- Vouk, M.A. Using reliability models during testing with non-operational profiles. In Proceedings of the 2nd Bellcore/Purdue Workshop on Issues in Software Reliability Estimation; IEEE: Manhattan, NY, USA, 1992; pp. 103–111. [Google Scholar]
- Okamura, H.; Etani, Y.; Dohi, T. Quantifying the effectiveness of testing efforts on software fault detection with a logit software reliability growth model. In Proceedings of the 2011 Joint Conference of the 21st International Workshop on Software Measurement and the 6th International Conference on Software Process and Product Measurement, Nara, Japan, 3–4 November 2011; pp. 62–68. [Google Scholar]
- Wood, A. Predicting software reliability. Computer 1996, 29, 69–77. [Google Scholar] [CrossRef]





| SRM & Time Distribution | ||
|---|---|---|
| Exp [2] (Exponential distribution) | ||
| Gamma [9,10] (Gamma distribution) | ||
| Pareto [11] (Pareto distribution) | ||
| Tnorm [3] (Truncated normal distribution) | ||
| Tlogist [5] (Truncated logistic distribution) | ||
| Txvmax [8] (Truncated extreme-value maximum distribution) | ||
| Txvmin [8] (Truncated extreme-value minimum distribution) | ||
| Lnorm [3,4] (Log-normal distribution) | ||
| Llogist [6] (Log-logistic distribution) | ||
| Lxvmax [8] (Log-extreme-value maximum distribution) | ||
| Lxvmin [7] (Log-extreme-value minimum distribution) |
| SRM & Time Distribution | ||
|---|---|---|
| Exp (HPP) (Exponential distribution) | ||
| Gamma (Gamma distribution) | ||
| Pareto (Musa-Okumoto) [15,16] (Pareto distribution) | ||
| Tnorm (Truncated normal distribution) | ||
| Tlogist (Truncated logistic distribution) | ||
| Txvmax (Truncated extreme-value maximum distribution) | ||
| Cox-Lewis [22] (Truncated extreme-value minimum distribution) | ||
| Lnorm (Log-normal distribution) | ||
| Llogist (Log-logistic distribution) | ||
| Lxvmax (Log-extreme-value maximum distribution) | ||
| Power-law [12,13,14] (Log-extreme-value minimum distribution) |
| Data Source | Nature of System | Testing Length (CPU Time) | Numbers of Detected Faults | |
|---|---|---|---|---|
| TDDS1 | SYS2 [23] | Real-time command and control system | 108708 | 54 |
| TDDS2 | S10 [23] | Real-time command and control system | 233700 | 38 |
| TDDS3 | SYS3 [23] | Military application | 67362 | 38 |
| TDDS4 | S27 [23] | Single-user workstation | 4312598 | 41 |
| TDDS5 | SYS4 [23] | Operating system | 52422 | 53 |
| TDDS6 | Project J5 [18] | Real-time command and control system | 5090 | 73 |
| TDDS7 | S17 [23] | Single-user workstation | 19572126 | 101 |
| TDDS8 | SYS1 [23] | Single-user workstation | 88682 | 136 |
| Data Source | Nature of System | Testing Length (Week) | Numbers of Detected Faults | |
|---|---|---|---|---|
| TIDS1 | SYS2 [23] | Real-time command and control system | 17 | 54 |
| TIDS2 | NASA-supported project [24] | Inertial navigating system | 14 | 9 |
| TIDS3 | SYS3 [23] | Military application | 14 | 38 |
| TIDS4 | DS3 [25] | Embedded application for printer | 30 | 52 |
| TIDS5 | DS2 [25] | Embedded application for printer | 33 | 58 |
| TIDS6 | Release 3 [26] | Tandem software system | 12 | 61 |
| TIDS7 | DS1 [25] | Embedded application for printer | 20 | 66 |
| TIDS8 | Release 2 [26] | Tandem software system | 19 | 120 |
| Type-I NHPP | Type-II NHPP | |||||
|---|---|---|---|---|---|---|
| Best SRM | AIC | MSE | Best SRM | AIC | MSE | |
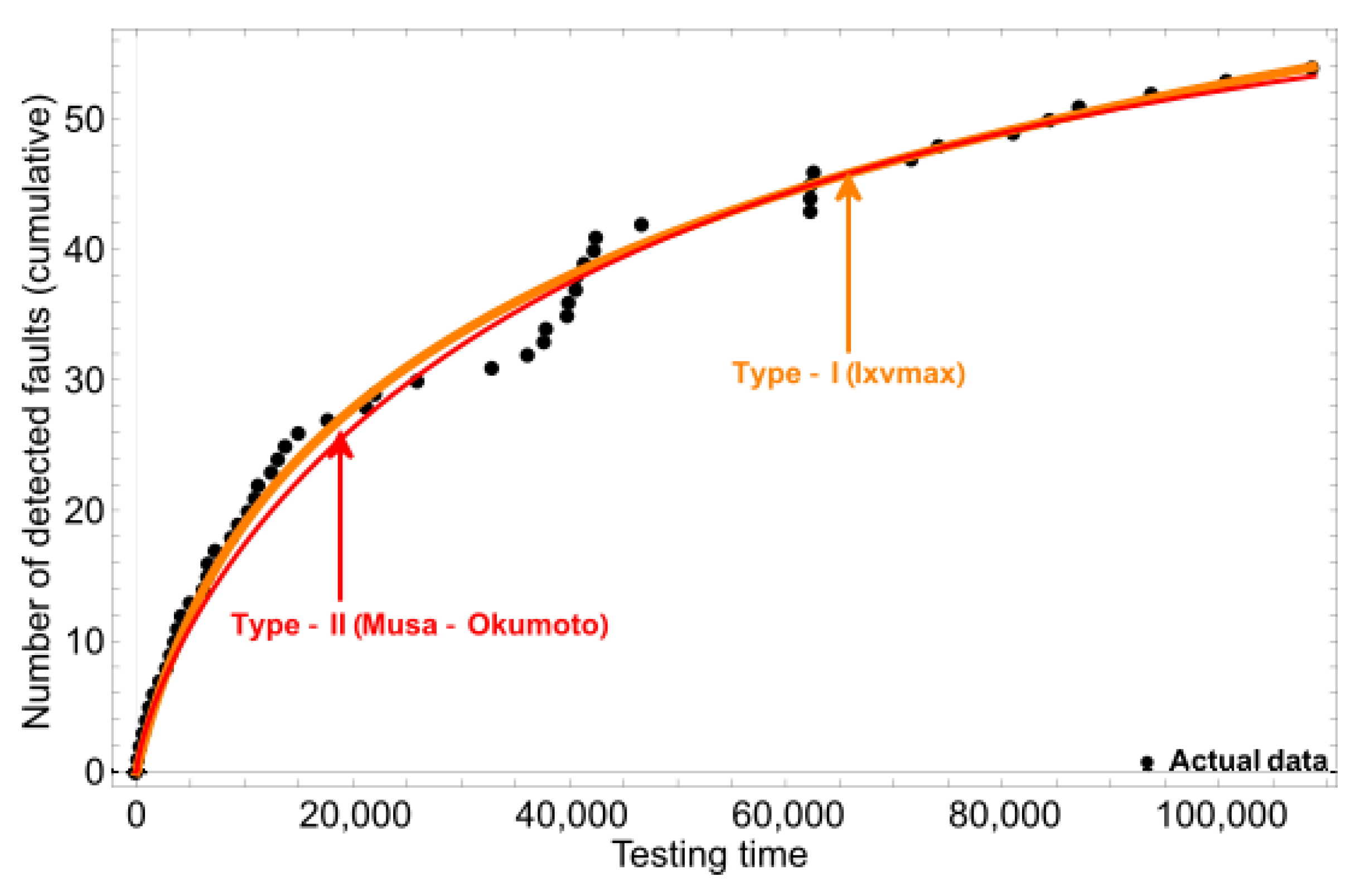
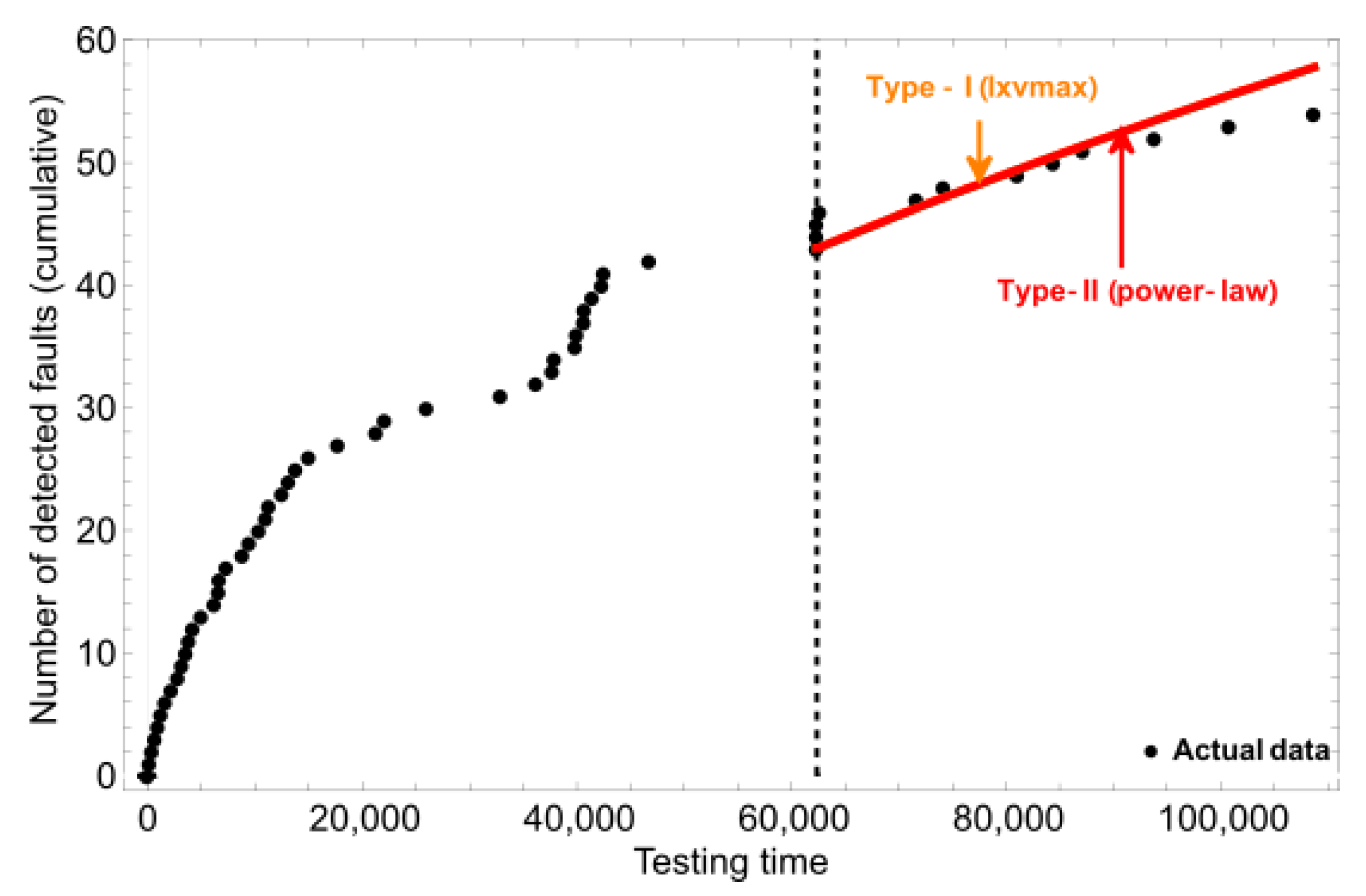
| TDDS1 | Lxvmax | 896.666 | 1.950 | Musa-Okumoto | 895.305 | 2.315 |
| TDDS2 | Lxvmax | 721.928 | 1.442 | Cox-Lewis | 726.052 | 2.803 |
| TDDS3 | Lxvmax | 598.131 | 1.705 | Musa-Okumoto | 596.501 | 1.809 |
| TDDS4 | Lxvmax | 1008.220 | 5.970 | Musa-Okumoto | 1007.100 | 7.039 |
| TDDS5 | Txvmin | 759.579 | 3.747 | Cox-Lewis | 759.948 | 5.509 |
| TDDS6 | Exp | 757.869 | 18.985 | Power-law | 757.031 | 19.315 |
| TDDS7 | Pareto | 2504.170 | 47.404 | Musa-Okumoto | 2503.370 | 63.699 |
| TDDS8 | Lxvmin | 1938.160 | 6.570 | Musa-Okumoto | 1939.600 | 8.052 |
| Type-I NHPP | Type-II NHPP | |||||
|---|---|---|---|---|---|---|
| Best SRM | AIC | MSE | Best SRM | AIC | MSE | |
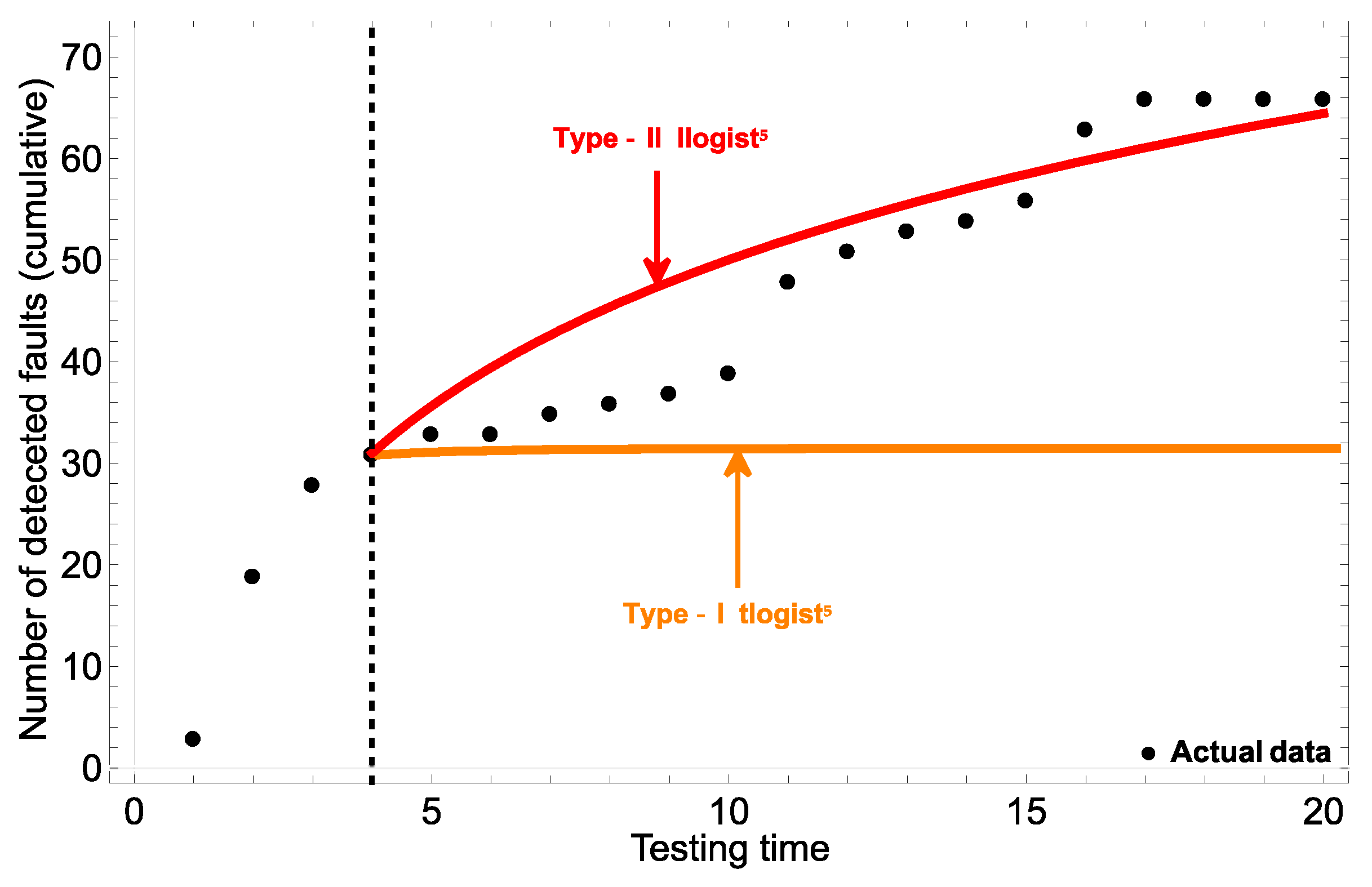
| TIDS1 | Llogist | 73.053 | 4.115 | Tlogist | 85.339 | 48.269 |
| TIDS2 | Exp | 29.911 | 0.118 | Exp | 27.753 | 0.186 |
| TIDS3 | Lxvmax | 61.694 | 3.239 | Llogist | 60.674 | 3.557 |
| TIDS4 | Llogist | 117.470 | 9.408 | Llogist | 148.438 | 45.178 |
| TIDS5 | Txvmin | 123.265 | 2.122 | Tlogist | 138.029 | 24.847 |
| TIDS6 | Tlogist | 51.052 | 1.968 | Cox-Lewis | 63.556 | 27.199 |
| TIDS7 | Lxvmax | 108.831 | 22.514 | Llogist | 107.211 | 24.394 |
| TIDS8 | Tnorm | 87.267 | 6.151 | Cox-Lewis | 91.919 | 31.232 |
| 20% Observation Point | ||||
|---|---|---|---|---|
| Type-I NHPP | Type-II NHPP | |||
| Best SRM | PMSE | Best SRM | PMSE | |
| TDDS1 | Lxvmax | 5.073 | Musa-Okumoto | 6.420 |
| TDDS2 | Txvmin | 83.964 | Llogist | 79.614 |
| TDDS3 | Tnorm | 42.104 | Musa-Okumoto | 145.648 |
| TDDS4 | Lxvmax | 32.217 | Llogist | 207.592 |
| TDDS5 | Lnorm | 56.477 | Musa-Okumoto | 198.490 |
| TDDS6 | Exp | 9177.670 | Tlogist | 467.320 |
| TDDS7 | Lxvmax | 1852.520 | Lnorm | 1474.020 |
| TDDS8 | Lxvmax | 32.131 | Power-law | 1417.110 |
| 50% Observation Point | ||||
| Type-I NHPP | Type-II NHPP | |||
| Best SRM | PMSE | Best SRM | PMSE | |
| TDDS1 | Pareto | 6.118 | Musa-Okumoto | 6.420 |
| TDDS2 | Lxvmax | 10.493 | Llogist | 30.944 |
| TDDS3 | Txvmin | 5.874 | Llogist | 11.747 |
| TDDS4 | Exp | 4480.620 | Llogist | 18.425 |
| TDDS5 | Tlogist | 103.504 | Cox-Lewis | 106.282 |
| TDDS6 | Llogist | 193.903 | Tlogist | 77.498 |
| TDDS7 | Txvmin | 3569.230 | Musa-Okumoto | 45.344 |
| TDDS8 | Pareto | 11.712 | Musa-Okumoto | 10.283 |
| 80% Observation Point | ||||
| Type-I NHPP | Type-II NHPP | |||
| Best SRM | PMSE | Best SRM | PMSE | |
| TDDS1 | Lxvmax | 5.772 | Power-law | 3.432 |
| TDDS2 | Lxvmax | 2.041 | Lxvmax | 3.697 |
| TDDS3 | Lxvmax | 0.588 | Musa-Okumoto | 0.819 |
| TDDS4 | Txvmin | 6.875 | Power-law | 4.291 |
| TDDS5 | Txvmin | 4.253 | Cox-Lewis | 4.258 |
| TDDS6 | Lxvmax | 21.715 | Power-law | 51.677 |
| TDDS7 | Lxvmax | 57.901 | Power-law | 9.268 |
| TDDS8 | Lxvmax | 9.419 | Power-law | 819.992 |
| 20% Observation Point | ||||
|---|---|---|---|---|
| Type-I NHPP | Type-II NHPP | |||
| Best SRM | PMSE | Best SRM | PMSE | |
| TIDS1 | Gamma | 220.732 | Power-law | 218.763 |
| TIDS2 | Pareto | 2.628 | Musa-Okumoto | 2.625 |
| TIDS3 | Lxvmax | 29.244 | Llogist | 47.377 |
| TIDS4 | Txvmin | 448.935 | Cox-Lewis | 423.360 |
| TIDS5 | Exp | 387.694 | Cox-Lewis | 67.730 |
| TIDS6 | Exp | 142.854 | Tlogist | 86.083 |
| TIDS7 | Tlogist | 98.903 | Llogist | 25.613 |
| TIDS8 | Gamma | 820.049 | Gamma | 171.702 |
| 50% Observation Point | ||||
| Type-I NHPP | Type-II NHPP | |||
| Best SRM | PMSE | Best SRM | PMSE | |
| TIDS1 | Txvmin | 96.992 | Musa-Okumoto | 159.545 |
| TIDS2 | Exp | 0.344 | Musa-Okumoto | 0.347 |
| TIDS3 | Txvmin | 30.786 | Power-law | 3.722 |
| TIDS4 | Txvmin | 29.097 | Llogist | 156.329 |
| TIDS5 | Lxvmax | 22.894 | Gamma | 27.045 |
| TIDS6 | Exp | 101.303 | Musa-Okumoto | 101.258 |
| TIDS7 | Pareto | 365.493 | Gamma | 18.825 |
| TIDS8 | Lxvmax | 564.782 | Gamma | 849.736 |
| 80% Observation Point | ||||
| Type-I NHPP | Type-II NHPP | |||
| Best SRM | PMSE | Best SRM | PMSE | |
| TIDS1 | Lnorm | 1.762 | Llogist | 8.736 |
| TIDS2 | Tnorm | 0.224 | Lxvmax | 0.090 |
| TIDS3 | Exp | 0.464 | Cox-Lewis | 0.464 |
| TIDS4 | Tnorm | 0.864 | Llogist | 6.333 |
| TIDS5 | Txvmin | 6.118 | Llogist | 17.300 |
| TIDS6 | Lxvmax | 1.850 | Llogist | 18.985 |
| TIDS7 | Lnorm | 3.432 | Llogist | 6.144 |
| TIDS8 | Tnorm | 0.331 | Cox-Lewis | 41.228 |
| Type-I NHPP | Type-II NHPP | |||
|---|---|---|---|---|
| Best SRM | Reliability | Best SRM | Reliability | |
| TDDS1 | Lxvmax | Musa-Okumoto | ||
| TDDS2 | Lxvmax | Cox-Lewis | ||
| TDDS3 | Lxvmax | Musa-Okumoto | ||
| TDDS4 | Lxvmax | Musa-Okumoto | ||
| TDDS5 | Txvmin | Cox-Lewis | ||
| TDDS6 | Exp | Power-law | ||
| TDDS7 | Pareto | Musa-Okumoto | ||
| TDDS8 | Lxvmin | Musa-Okumoto | ||
| Type-I NHPP | Type-II NHPP | |||
|---|---|---|---|---|
| Best SRM | Reliability | Best SRM | Reliability | |
| TIDS1 | Llogist | Tlogist | ||
| TIDS2 | Exp | Exp | ||
| TIDS3 | Lxvmax | Llogist | ||
| TIDS4 | Llogist | Llogist | ||
| TIDS5 | Txvmin | Tlogist | ||
| TIDS6 | Tlogist | Cox-Lewis | ||
| TIDS7 | Lxvmax | Llogist | ||
| TIDS8 | Tnorm | Cox-Lewis | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Dohi, T.; Okamura, H. Are Infinite-Failure NHPP-Based Software Reliability Models Useful? Software 2023, 2, 1-18. https://doi.org/10.3390/software2010001
Li S, Dohi T, Okamura H. Are Infinite-Failure NHPP-Based Software Reliability Models Useful? Software. 2023; 2(1):1-18. https://doi.org/10.3390/software2010001
Chicago/Turabian StyleLi, Siqiao, Tadashi Dohi, and Hiroyuki Okamura. 2023. "Are Infinite-Failure NHPP-Based Software Reliability Models Useful?" Software 2, no. 1: 1-18. https://doi.org/10.3390/software2010001
APA StyleLi, S., Dohi, T., & Okamura, H. (2023). Are Infinite-Failure NHPP-Based Software Reliability Models Useful? Software, 2(1), 1-18. https://doi.org/10.3390/software2010001








