Fluidized Bed Co-Melt Granulation: New Insights in the Influence of Process Variables and Validation of Regime Map Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Granulation
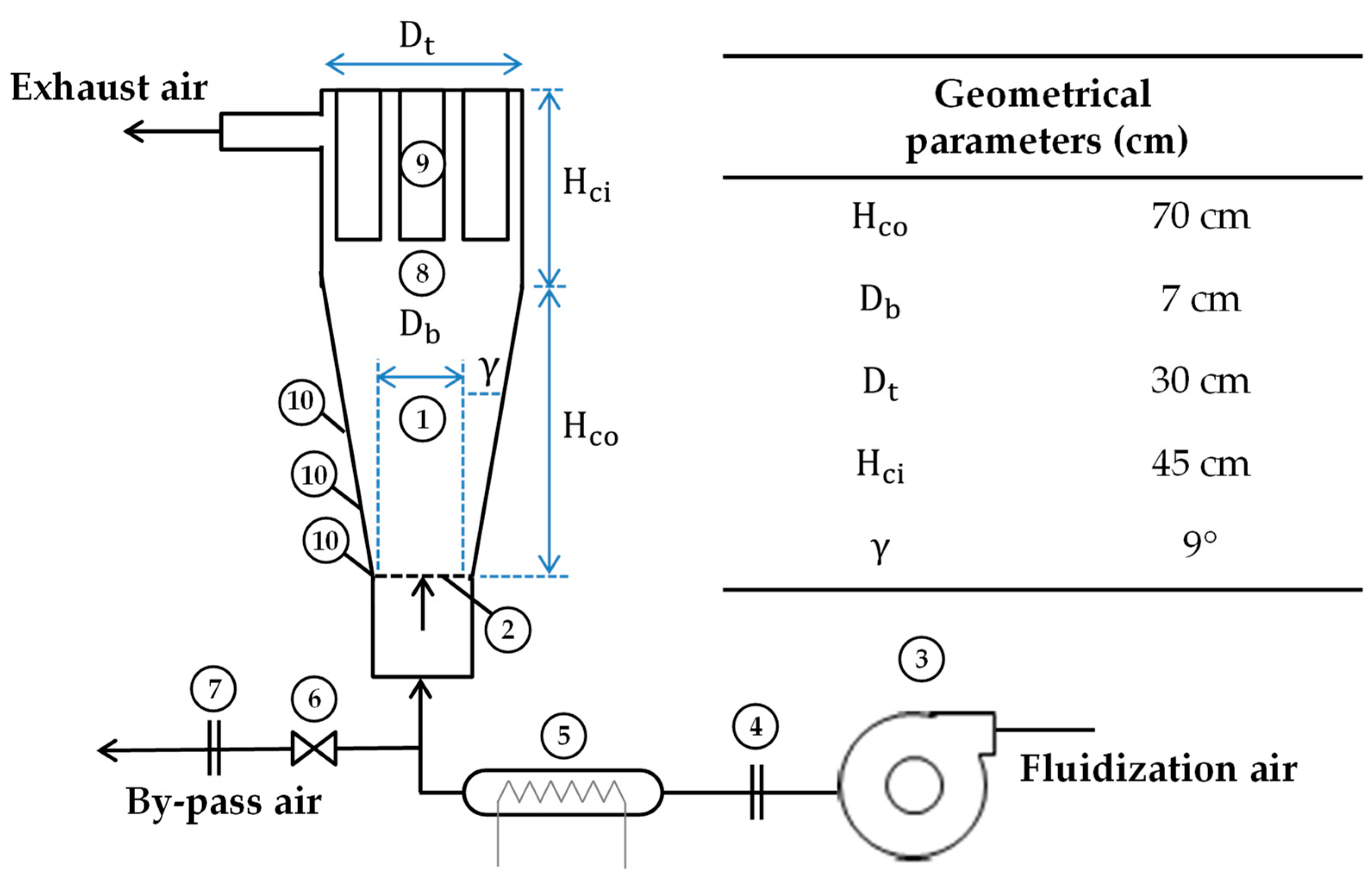
2.2.1. Equipment
2.2.2. Experimental Procedure
2.3. Experimental Design
2.4. Characterization of the Granules
2.4.1. Particle Size Distribution
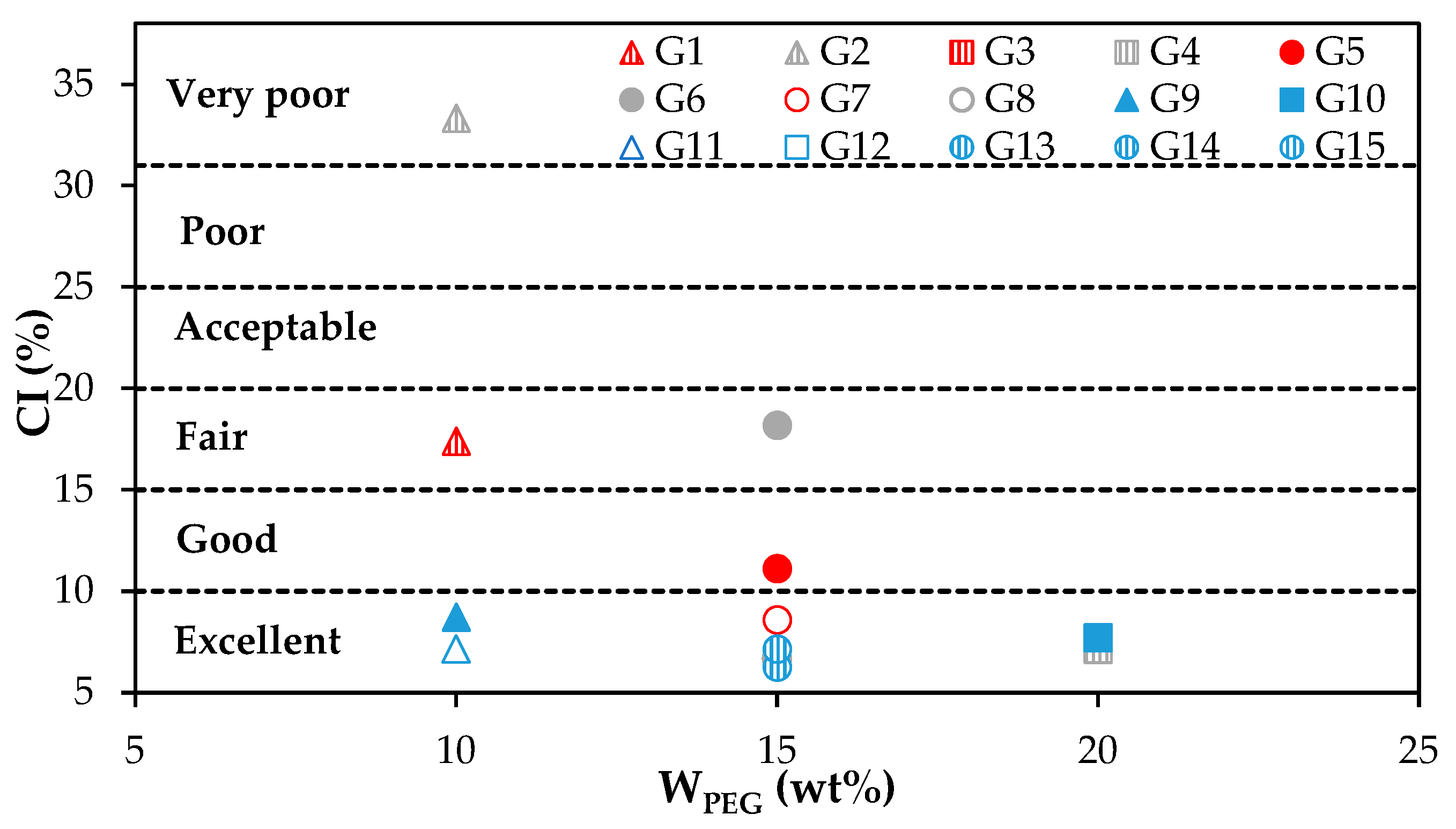
2.4.2. Bulk and Tapped Densities. Carr Index. Angle of Repose
2.4.3. Granule Porosity
2.5. Granulation Performance
2.6. Regime Map
3. Results and Discussion
3.1. Experimental Design
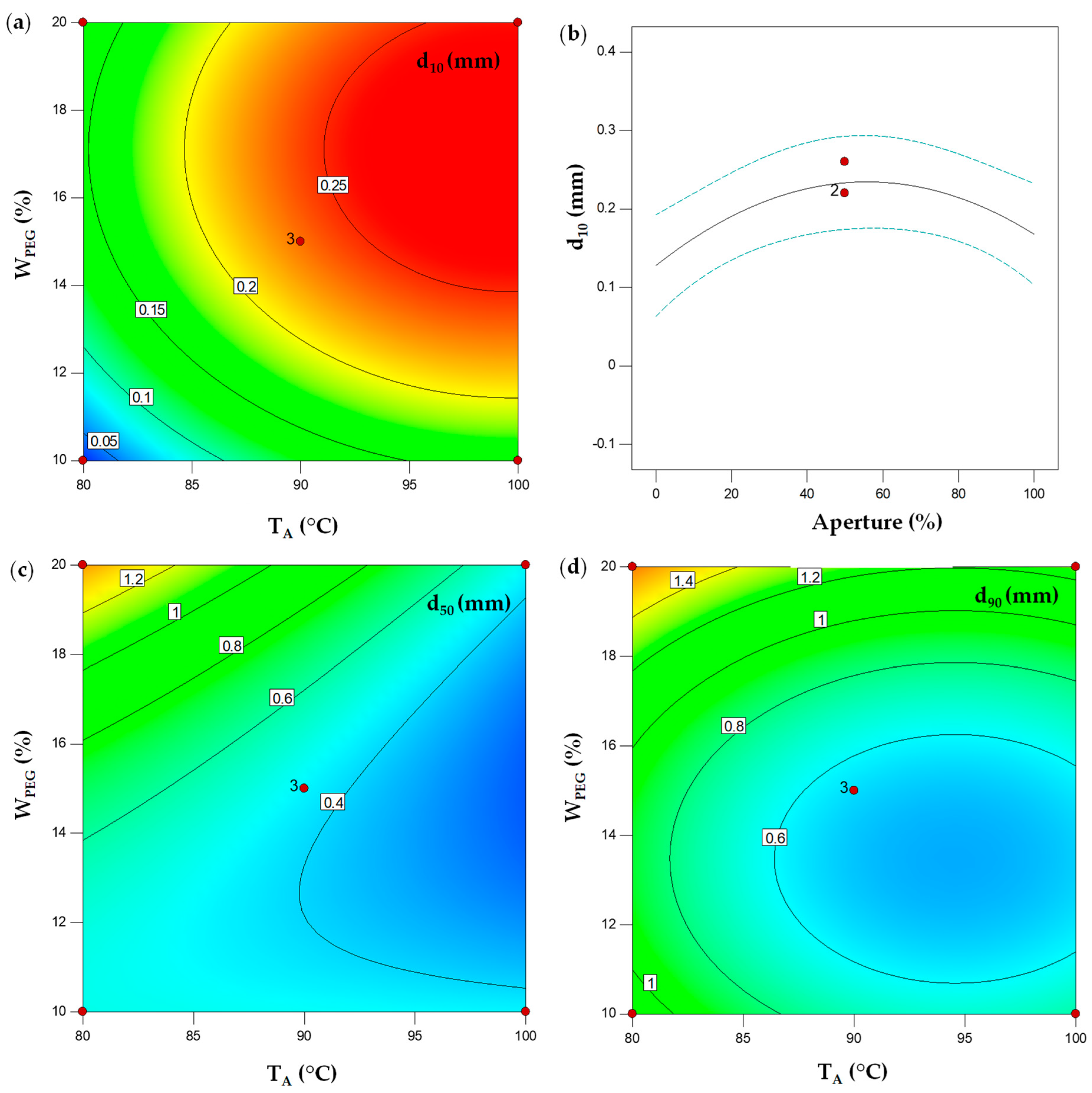
3.1.1. Characterization of the Granules: Particle Size Distribution and Flow Properties
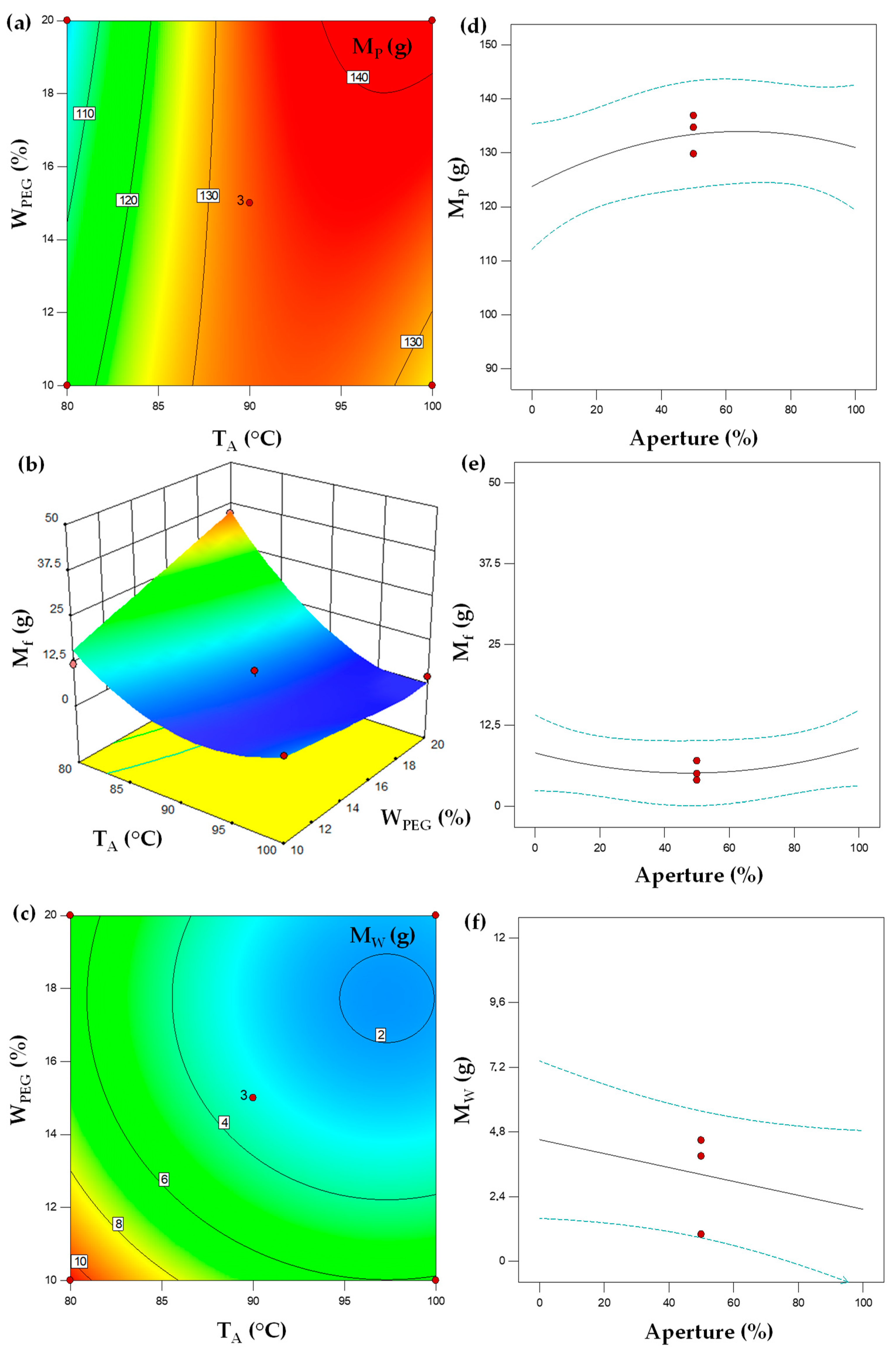
3.1.2. Granulation Performance
3.2. Regime Map
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Meng, W.; Rao, K.S.; Snee, R.D.; Ramachandran, R.; Muzzio, F.J. A comprehensive analysis and optimization of continuous twin-screw granulation processes via sequential experimentation strategy. Int. J. Pharm. 2019, 556, 349–362. [Google Scholar] [CrossRef] [PubMed]
- Barrasso, D.; Ramachandran, R. Multi-scale modeling of granulation processes: Bi-directional coupling of PBM with DEM via collision frequencies. Chem. Eng. Res. Des. 2015, 93, 304–317. [Google Scholar] [CrossRef]
- Bertín, D.; Cotabarren, I.M.; Moraga, S.V.; Piña, J.; Bucalá, V. The effect of binder concentration in fluidized-bed granulation: Transition between wet and melt granulation. Chem. Eng. Res. Des. 2018, 132, 162–169. [Google Scholar] [CrossRef]
- Moraga, S.V.; Villa, M.P.; Bertín, D.E.; Cotabarren, I.M.; Piña, J.; Pedernera, M.; Bucalá, V. Fluidized-bed melt granulation: The effect of operating variables on process performance and granule properties. Powder Technol. 2015, 286, 654–667. [Google Scholar] [CrossRef]
- Pohl, S.; Kleinebudde, P. A review of regime maps for granulation. Int. J. Pharm. 2020, 587, 119660. [Google Scholar] [CrossRef]
- Korteby, Y.; Kristó, K.; Sovány, T.; Regdon, G. Use of machine learning tool to elucidate and characterize the growth mechanism of an in-situ fluid bed melt granulation. Powder Technol. 2018, 331, 286–295. [Google Scholar] [CrossRef]
- Kukec, S.; Vrečer, F.; Dreu, R. A study of in situ fluid bed melt granulation using response surface methodology. Acta Pharm. 2012, 62, 497–513. [Google Scholar] [CrossRef]
- Walker, G.; Andrews, G.; Jones, D. Effect of process parameters on the melt granulation of pharmaceutical powders. Powder Technol. 2006, 165, 161–166. [Google Scholar] [CrossRef]
- Walker, G.M.; Holland, C.R.; Ahmad, M.M.; Craig, D.Q. Influence of process parameters on fluidised hot-melt granulation and tablet pressing of pharmaceutical powders. Chem. Eng. Sci. 2005, 60, 3867–3877. [Google Scholar] [CrossRef]
- Walker, G.; Bell, S.; Andrews, G.; Jones, D. Co-melt fluidised bed granulation of pharmaceutical powders: Improvements in drug bioavailability. Chem. Eng. Sci. 2007, 62, 451–462. [Google Scholar] [CrossRef]
- Zhai, H.; Li, S.; Jones, D.; Walker, G.; Andrews, G. The effect of the binder size and viscosity on agglomerate growth in fluidised hot melt granulation. Chem. Eng. J. 2010, 164, 275–284. [Google Scholar] [CrossRef]
- Zhai, H.; Li, S.; Andrews, G.; Jones, D.; Bell, S.; Walker, G. Nucleation and growth in fluidised hot melt granulation. Powder Technol. 2009, 189, 230–237. [Google Scholar] [CrossRef]
- Mangwandi, C.; Zainal, N.; JiangTao, L.; Glocheux, Y.; Albadarin, A.B. Investigation of influence of process variables on mechanical strength, size and homogeneity of pharmaceutical granules produced by fluidised hot melt granulation. Powder Technol. 2015, 272, 173–180. [Google Scholar] [CrossRef]
- Ansari, M.A.; Stepanek, F. Formation of hollow core granules by fluid bed in situ melt granulation: Modelling and experiments. Int. J. Pharm. 2006, 321, 108–116. [Google Scholar] [CrossRef] [PubMed]
- Kidokoro, M.; Haramiishi, Y.; Sagasaki, S.; Shimizu, T.; Yamamoto, Y. Application of fluidized hot-melt granulation (fhmg) for the preparation of granules for tableting; properties of granules and tablets prepared by fhmg. Drug Dev. Ind. Pharm. 2002, 28, 67–76. [Google Scholar] [CrossRef]
- Passerini, N.; Calogerà, G.; Albertini, B.; Rodriguez, L. Melt granulation of pharmaceutical powders: A comparison of high-shear mixer and fluidised bed processes. Int. J. Pharm. 2010, 391, 177–186. [Google Scholar] [CrossRef]
- Prado, H.J.; Bonelli, P.R.; Cukierman, A.L. In situ fluidized hot melt granulation using a novel meltable binder: Effect of formulation variables on granule characteristics and controlled release tablets. Powder Technol. 2014, 264, 498–506. [Google Scholar] [CrossRef]
- Pauli-Bruns, A.; Knop, K.; Lippold, B.C. Preparation of sustained release matrix pellets by melt agglomeration in the fluidized bed: Influence of formulation variables and modelling of agglomerate growth. Eur. J. Pharm. Biopharm. 2010, 74, 503–512. [Google Scholar] [CrossRef]
- Mašić, I.; Ilić, I.; Dreu, R.; Ibrić, S.; Parojčić, J.; Đurić, Z. An investigation into the effect of formulation variables and process parameters on characteristics of granules obtained by in situ fluidized hot melt granulation. Int. J. Pharm. 2012, 423, 202–212. [Google Scholar] [CrossRef]
- Mašić, I.; Ilić, I.; Dreu, R.; Ibrić, S.; Parojčić, J.; Srčič, S. Melt granulation in fluidized bed: A comparative study of spray-on versusin situprocedure. Drug Dev. Ind. Pharm. 2014, 40, 23–32. [Google Scholar] [CrossRef]
- Aleksić, I.; Đuriš, J.; Ilić, I.; Ibrić, S.; Parojčić, J.; Srčič, S. In silico modeling of in situ fluidized bed melt granulation. Int. J. Pharm. 2014, 466, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Iveson, S.M.; Litster, J.D. Growth regime map for liquid-bound granules. AIChE J. 1998, 44, 1510–1518. [Google Scholar] [CrossRef]
- Iveson, S.M.; Wauters, P.A.; Forrest, S.; Litster, J.D.; Meesters, G.M.; Scarlett, B. Growth regime map for liquid-bound granules: Further development and experimental validation. Powder Technol. 2001, 117, 83–97. [Google Scholar] [CrossRef]
- Walker, G.; Bell, S.; Vann, M.; Zhai, H.; Jones, D.; Andrews, G. Pharmaceutically Engineering Powders Using FHMG: The effects of process parameters and formulation variables. Chem. Eng. Res. Des. 2007, 85, 981–986. [Google Scholar] [CrossRef]
- Desai, U.S.; Chaudhari, P.; Bhavsar, D.B.; Chavan, R.P. Melt granulation: An alternative to traditional granulation techniques. Indian Drugs 2013, 50, 5–13. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Rattes, A.L.R.; Oliveira, W.P. Spray drying conditions and encapsulating composition effects on formulation and properties of sodium diclofenac microparticles. Powder Technol. 2007, 171, 7–14. [Google Scholar] [CrossRef]
- Schüssele, A.; Bauer-Brandl, A. Note on the measurement of flowability according to the European Pharmacopoeia. Int. J. Pharm. 2003, 257, 301–304. [Google Scholar] [CrossRef]
- United States Pharmacopeia and National Formulary; USP 30-NF; United States Pharmacopeial Conv.: Rockville, MD, USA, 2007.
- Abberger, T.; Seo, A.; Schæfer, T. The effect of droplet size and powder particle size on the mechanisms of nucleation and growth in fluid bed melt agglomeration. Int. J. Pharm. 2002, 249, 185–197. [Google Scholar] [CrossRef]



| Property | Value |
|---|---|
| d10 (mm) | 0.0093 |
| d50 (mm) | 0.038 |
| d90 (mm) | 0.096 |
| (g/mL) | 1.512 |
| (g/mL) | 0.517 |
| (g/mL) | 0.805 |
| IC (%) | 35.71 |
| AR (°) | 35.40 |
| Run | X1 (%) | X2 (wt%) | X3 (°C) | d10 (mm) | d50 (mm) | d90 (mm) | AR (°) | MP (g) | MF (g) | MW (g) |
|---|---|---|---|---|---|---|---|---|---|---|
| G1 | 0 | 10 | 90 | 0.03 | 0.31 | 0.72 | 20.6 | 109 | 11 | 11 |
| G2 | 100 | 10 | 90 | 0.02 | 0.22 | 0.74 | 33.4 | 134 | 4 | 3 |
| G3 | 0 | 20 | 90 | 0.07 | 0.71 | 0.97 | 13.9 | 128 | 11 | 6 |
| G4 | 100 | 20 | 90 | 0.24 | 0.72 | 1.45 | 13.1 | 137 | 8 | 0 |
| G5 | 0 | 15 | 80 | 0.03 | 0.75 | 1.50 | 18.4 | 110 | 24 | 6 |
| G6 | 100 | 15 | 80 | 0.02 | 0.07 | 0.19 | 20.3 | 93 | 39 | 6 |
| G7 | 0 | 15 | 100 | 0.20 | 0.29 | 0.71 | 18.3 | 125 | 5 | 2 |
| G8 | 100 | 15 | 100 | 0.21 | 0.28 | 0.55 | 16.4 | 136 | 3 | 5 |
| G9 | 50 | 10 | 80 | 0.09 | 0.72 | 1.08 | 10.4 | 122 | 12 | 11 |
| G10 | 50 | 20 | 80 | 0.12 | 1.63 | 1.83 | 9.2 | 100 | 35 | 8 |
| G11 | 50 | 15 | 100 | 0.13 | 0.32 | 0.73 | 15.6 | 130 | 7 | 5 |
| G12 | 50 | 20 | 100 | 0.23 | 0.35 | 1.14 | 14.5 | 135 | 2 | 1 |
| G13 | 50 | 15 | 90 | 0.22 | 0.31 | 0.42 | 19.9 | 130 | 7 | 4 |
| G14 | 50 | 15 | 90 | 0.22 | 0.31 | 0.48 | 18.9 | 135 | 5 | 1 |
| G15 | 50 | 15 | 90 | 0.26 | 0.51 | 0.79 | 15.2 | 137 | 4 | 4 |
| Source a | d10 (mm) R2 (0.88) | d50 (mm) R2 (0.81) | d90 (mm) R2 (0.75) | AR R2 (0.62) | ||||
|---|---|---|---|---|---|---|---|---|
| Coeff. | p-Value | Coeff | p-Value | Coeff | p-Value | Coeff | p-Value | |
| b | 0.23 | 0.45 | 0.55 | 16.87 | ||||
| X1 | 0.02 | 0.2342 | −0.0962 | 0.2825 | −0.1212 | 0.2796 | - | |
| X2 | 0.0487 | 0.0156 | 0.23 | 0.0272 | 0.265 | 0.0350 | −3.660 | 0.0317 |
| X3 | 0.0637 | 0.0043 | −0.2412 | 0.0224 | −0.1837 | 0.1169 | - | - |
| X1X2 | 0.045 | 0.0771 | - | - | - | - | −3.394 | 0.1328 |
| X1X3 | - | - | 0.1675 | 0.1951 | 0.2875 | 0.0878 | - | - |
| X2X3 | - | - | −0.22 | 0.1019 | - | - | - | - |
| X12 | −0.0854 | 0.0069 | −0.1561 | 0.2390 | - | - | 4.231 | 0.0777 |
| X22 | −0.0579 | 0.0375 | 0.2513 | 0.0771 | 0.4340 | 0.0222 | - | - |
| X32 | −0.0329 | 0.1888 | - | - | 0.2015 | 0.2254 | −3.599 | 0.1254 |
| AP | 7.524 | 8.263 | 6.102 | 7.742 | ||||
| LOF | 0.1897 | 0.1651 | 0.3015 | 0.2559 | ||||
| Model p | 0.0076 | 0.0383 | 0.0381 | 0.0339 | ||||
| Source a | MP (g) R2 (0.85) | Mf (g) R2 (0.93) | MW (g) R2 (0.71) | |||
|---|---|---|---|---|---|---|
| Coeff. | p-Value | Coeff | p-Value | Coeff | p-Value | |
| b | 133.45 | 5.15 | 3.23 | |||
| X1 | 3.6 | 0.2719 | 0.37 | 0.8166 | −1.29 | 0.1257 |
| X2 | 0.59 | 0.8499 | 2.75 | 0.1207 | −1.89 | 0.0359 |
| X3 | 12.6 | 0.0055 | −11.63 | 0.0001 | −2.23 | 0.0172 |
| X1X2 | −4 | 0.3785 | - | - | - | - |
| X1X3 | 7.06 | 0.1447 | −4.25 | 0.0949 | - | - |
| X2X3 | 7.09 | 0.1433 | −7 | 0.0155 | - | - |
| X12 | −6.06 | 0.2151 | 3.48 | 0.1715 | - | - |
| X22 | - | - | 1.73 | 0.1588 | ||
| X32 | −11.51 | 0.0389 | 8.98 | 0.0057 | 1.52 | 0.2081 |
| AP | 6.496 | 11.583 | 6.839 | |||
| LOF | 0.1203 | 0.0838 | 0.4694 | |||
| Model p | 0.0464 | 0.0016 | 0.0288 | |||
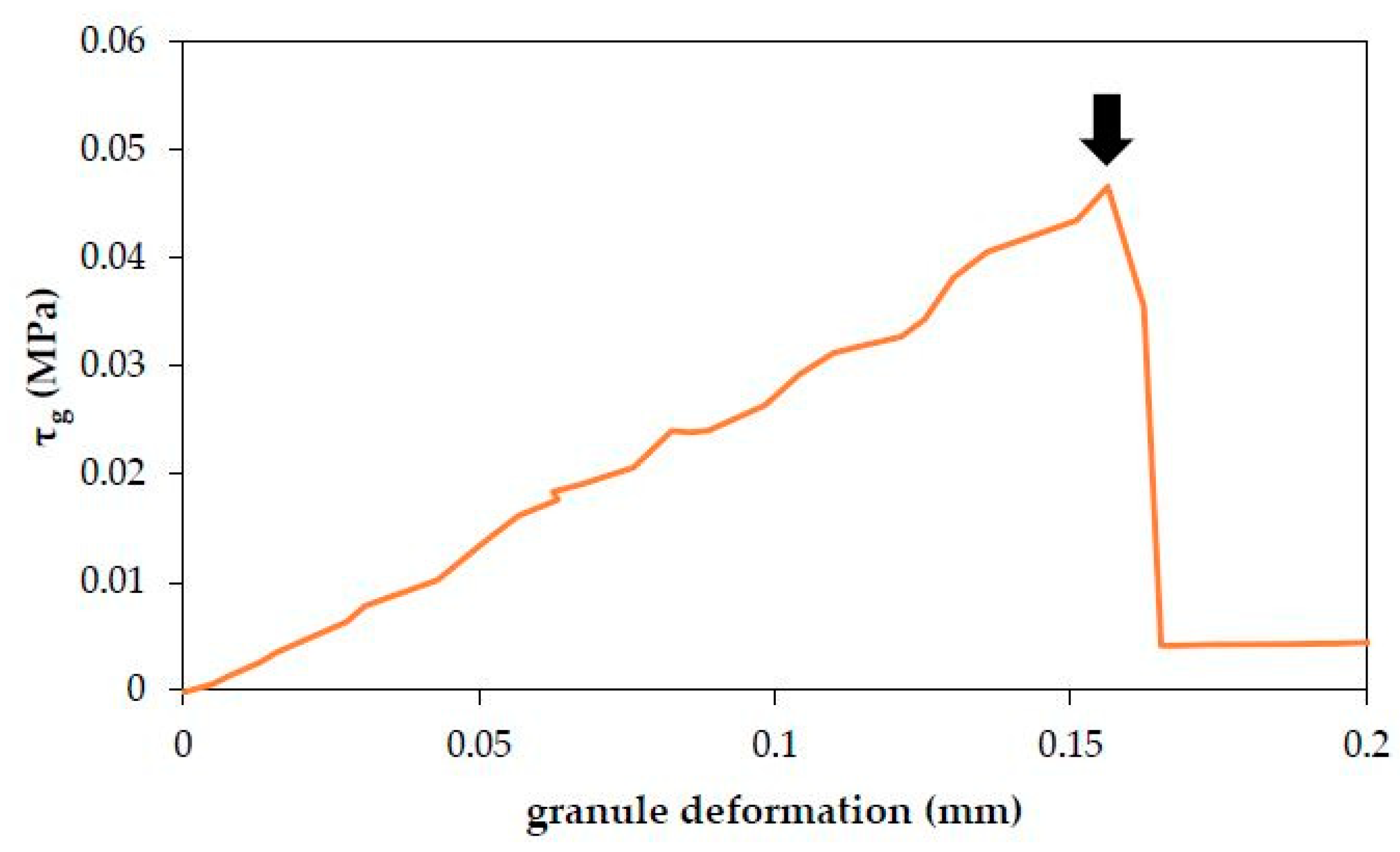
| Run | X1 (%) | X2 (wt%) | X3 (°C) | (MPa) | Σ (MPa) | TTEST (°C) |
|---|---|---|---|---|---|---|
| G1 | 0 | 10 | 90 | 0.045 | 0.022 | 74 |
| G3 | 0 | 20 | 90 | 0.035 | 0.015 | 78 |
| G5 | 0 | 15 | 80 | 0.076 | 0.010 | 70 |
| G8 | 100 | 15 | 100 | 0.026 | 0.013 | 70 |
| Average | 0.045 |
| Run | (g/mL) | (g/mL) | (-) | (-) | (-) |
|---|---|---|---|---|---|
| G1 | 1.28 | 1.48 | 0.134 | 1.24 | 0.0583 |
| G2 | 1.24 | 1.48 | 0.162 | 0.99 | 0.0187 |
| G3 | 1.16 | 1.44 | 0.196 | 1.76 | 0.0565 |
| G4 | 1.28 | 1.44 | 0.111 | 3.45 | 0.0195 |
| G5 | 1.30 | 1.46 | 0.107 | 2.53 | 0.0625 |
| G6 | 1.17 | 1.46 | 0.199 | 1.22 | 0.0187 |
| G7 | 1.43 | 1.46 | 0.018 | 16.77 | 0.0726 |
| G8 | 1.37 | 1.46 | 0.060 | 4.72 | 0.0216 |
| G9 | 1.35 | 1.48 | 0.086 | 2.04 | 0.0356 |
| G10 | 1.13 | 1.44 | 0.216 | 1.56 | 0.0298 |
| G11 | 1.42 | 1.48 | 0.037 | 5.02 | 0.0444 |
| G12 | 1.32 | 1.44 | 0.086 | 4.57 | 0.0279 |
| G13 | 1.36 | 1.46 | 0.070 | 4.00 | 0.0346 |
| G14 | 1.37 | 1.46 | 0.064 | 4.45 | 0.0395 |
| G15 | 1.38 | 1.46 | 0.057 | 5.02 | 0.0420 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobos de Ponga, J.C.; Piña, J.; Cotabarren, I.M. Fluidized Bed Co-Melt Granulation: New Insights in the Influence of Process Variables and Validation of Regime Map Theory. Powders 2023, 2, 639-658. https://doi.org/10.3390/powders2030040
Lobos de Ponga JC, Piña J, Cotabarren IM. Fluidized Bed Co-Melt Granulation: New Insights in the Influence of Process Variables and Validation of Regime Map Theory. Powders. 2023; 2(3):639-658. https://doi.org/10.3390/powders2030040
Chicago/Turabian StyleLobos de Ponga, Jacquelina C., Juliana Piña, and Ivana M. Cotabarren. 2023. "Fluidized Bed Co-Melt Granulation: New Insights in the Influence of Process Variables and Validation of Regime Map Theory" Powders 2, no. 3: 639-658. https://doi.org/10.3390/powders2030040
APA StyleLobos de Ponga, J. C., Piña, J., & Cotabarren, I. M. (2023). Fluidized Bed Co-Melt Granulation: New Insights in the Influence of Process Variables and Validation of Regime Map Theory. Powders, 2(3), 639-658. https://doi.org/10.3390/powders2030040







