LUME 2D: A Linear Upslope Model for Orographic and Convective Rainfall Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Two-Dimensional Data Preprocessing
2.1.1. WMO Data
2.1.2. Interpolation Techniques
- ▪
- For each piece of radiosonde data, the temporal interpolation of each variable for each reference pressure layer was designed using a 1D “spline” technique. Firstly, an average state was computed by roughly describing the 6:00 am (averaging the previous 00:00 am and the subsequent 12:00 pm) and the 18:00 pm (averaging the previous 12:00 pm and the subsequent 00:00 am) atmosphere state for every day of the simulation. This method can double the amount of available data for the temporal interpolation, giving the spline further degrees of freedom to better reconstruct the continuous polynomial function. Several tests (not reported here) have verified the errors of the interpolation with respect to the reference data, indicating a very good data-series reproduction (absolute and relative errors < 10%). After that, the interpolator was sampled with a 1h timestep and the new interpolated temporal series were saved as a table in a .csv file.
- ▪
- For the 2D enlarged domain, the spatial interpolation was performed using the 2D polynomial “spline”. Since a spline requires several spatially and uniformly distributed points across the interpolation domain, the procedure has been partitioned into 2 different steps. Firstly, a “nearest-neighbour” interpolator has been evaluated within the 2D enlarged domain for the selected atmospheric variable. The obtained 2D field was then spatially sampled using a regular grid scheme where each sample point’s relative distance was about 100 km. These points were then passed to a 2D spline algorithm, obtaining the final spatial data reconstruction across the enlarged domain. Several tests (not reported here) have verified the accuracy and the good reproduction of the interpolated field with respect to the reference radiosonde station, showing rather small errors (absolute and relative errors <10%). Since spatial interpolation was initialised by the .csv dataset provided after the temporal interpolation, the obtained data were saved in a stack of matrices (distinguishing the reference layer and the atmospheric variable) within a .netcd file format.
2.2. LUME 2D Core
2.2.1. Boundary Conditions and Key Parameters
- ▪
- Atmospheric variables: Tref, , , , , , U and D.
- ▪
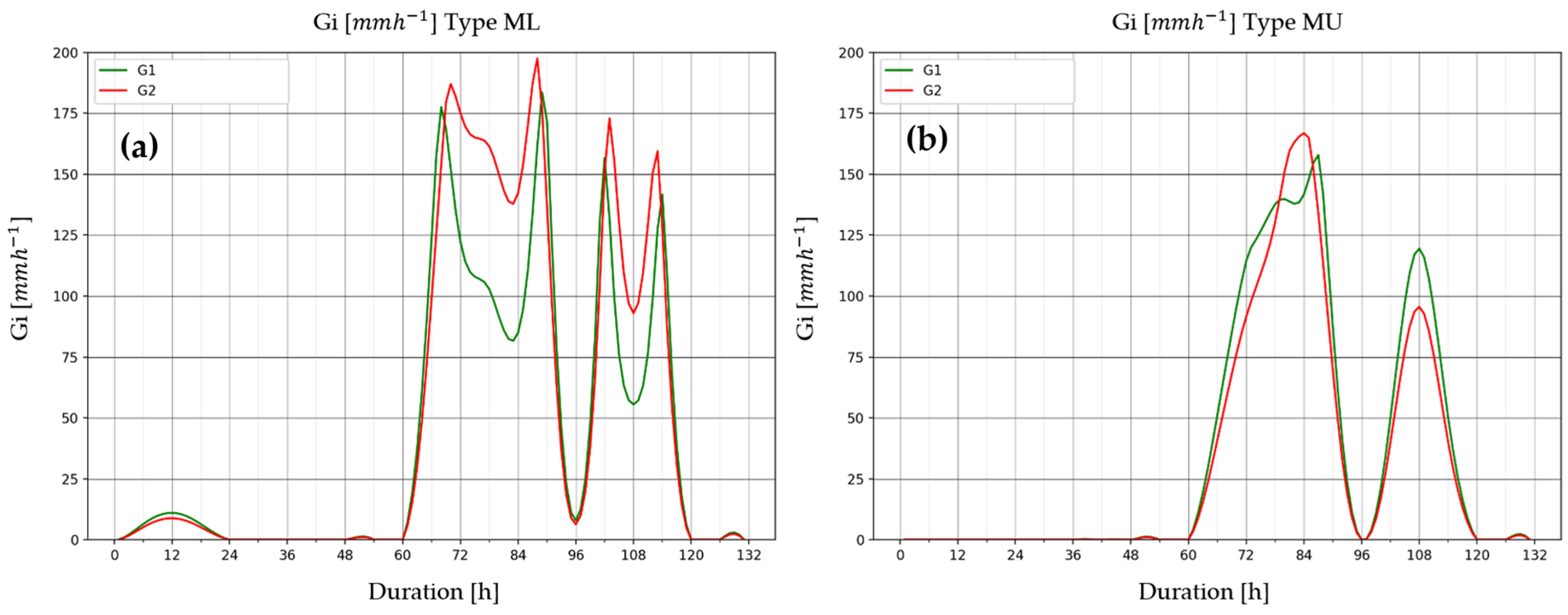
- Convective parameters: CAPE, CIN, LCL, LFC, EL, PW, PE, G1 and G2.
- ▪
- Boundary-layer height.
2.2.2. Microphysical Routines
- ▪
- In the warm-rain scheme, only 3 microphysical categories are allowed: qv, qc, and qr. They are the same as those proposed in the previous version of LUME, but with a different microphysical parameterisation of the source terms, suggested by the COSMO model.
- ▪
- In the cold-rain scheme, two “cold” categories are added to the system: qh (hail) and qs (snow). The former is a simplification of the full cold scheme proposed in COSMO, where the qi (ice) category has been neglected. This choice was motivated by the fact that the microphysics of ice is highly non-linear and it is difficult to implement straightforwardly, assuring the numerical stability of the code [30].
Warm-Rain Model
Cold-Rain Model
Numerical Integration
2.3. Atmospheric Convection
- ▪
- When: The triggering functions to determine when the convection may activate during a storm are available in the literature [49]. Using the convective parameters or a combination of them, these functions can detect when moist convection may develop. These functions could be continuous or discrete, but generally are represented as a critical value (threshold) of a specific convective index (CI). If |CI|< threshold, moist convection does not occur, while if |CI| ≥ threshold, it is likely to start. In Table 3, the convective indices are specified (CAPE, CIN, LI, KI, SI and DCI) and the relative thresholds are applied in this study according to the indications in the literature [49].
- ▪
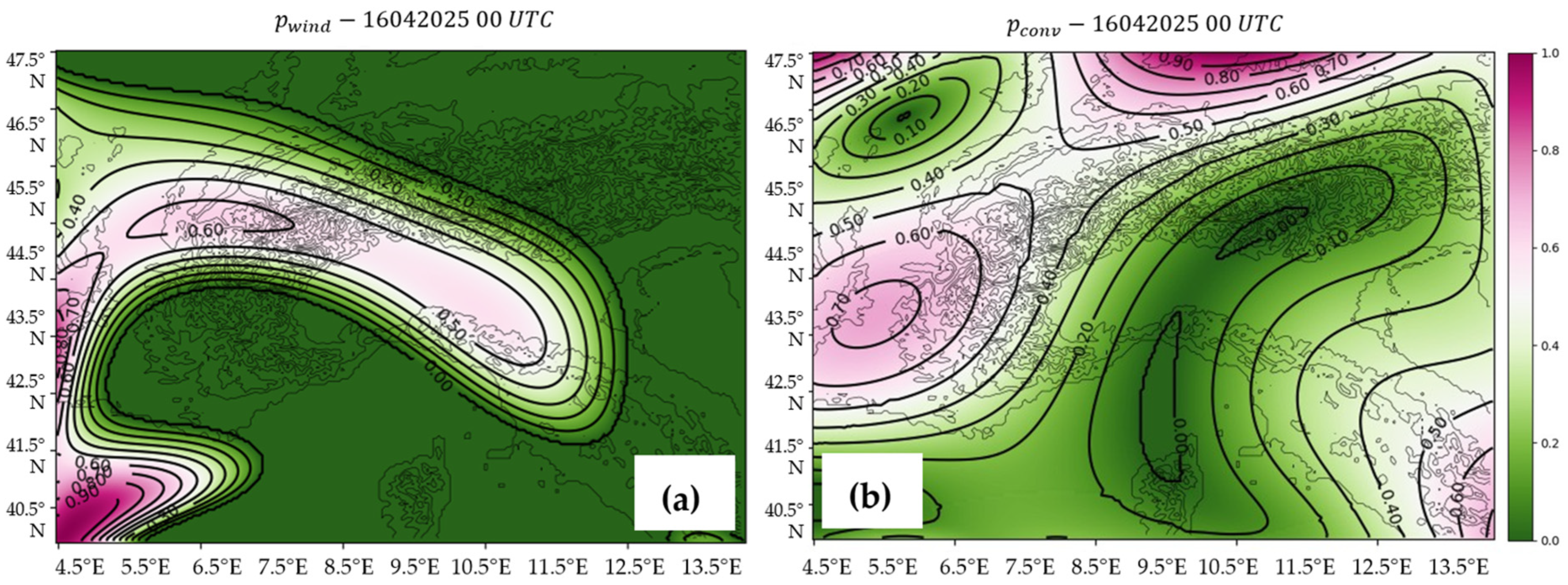
- Where: Triggering functions can be applied at each radiosonde location simply by considering the local estimation of the convective indices. However, due to the significant spatial variability of CI (stations may lie several hundred kilometres apart, experiencing different convective environments), it is advisable to carry out the study considering a spatial interpolation of the convective parameters. This could help determine the location where moist convection is more likely to occur, i.e., when the CIs overcome the triggering thresholds.
2.4. Data Analysis
2.4.1. Global Statistics of the Total Rainfall Field
2.4.2. Local Statistics on a Single Rain Gauge
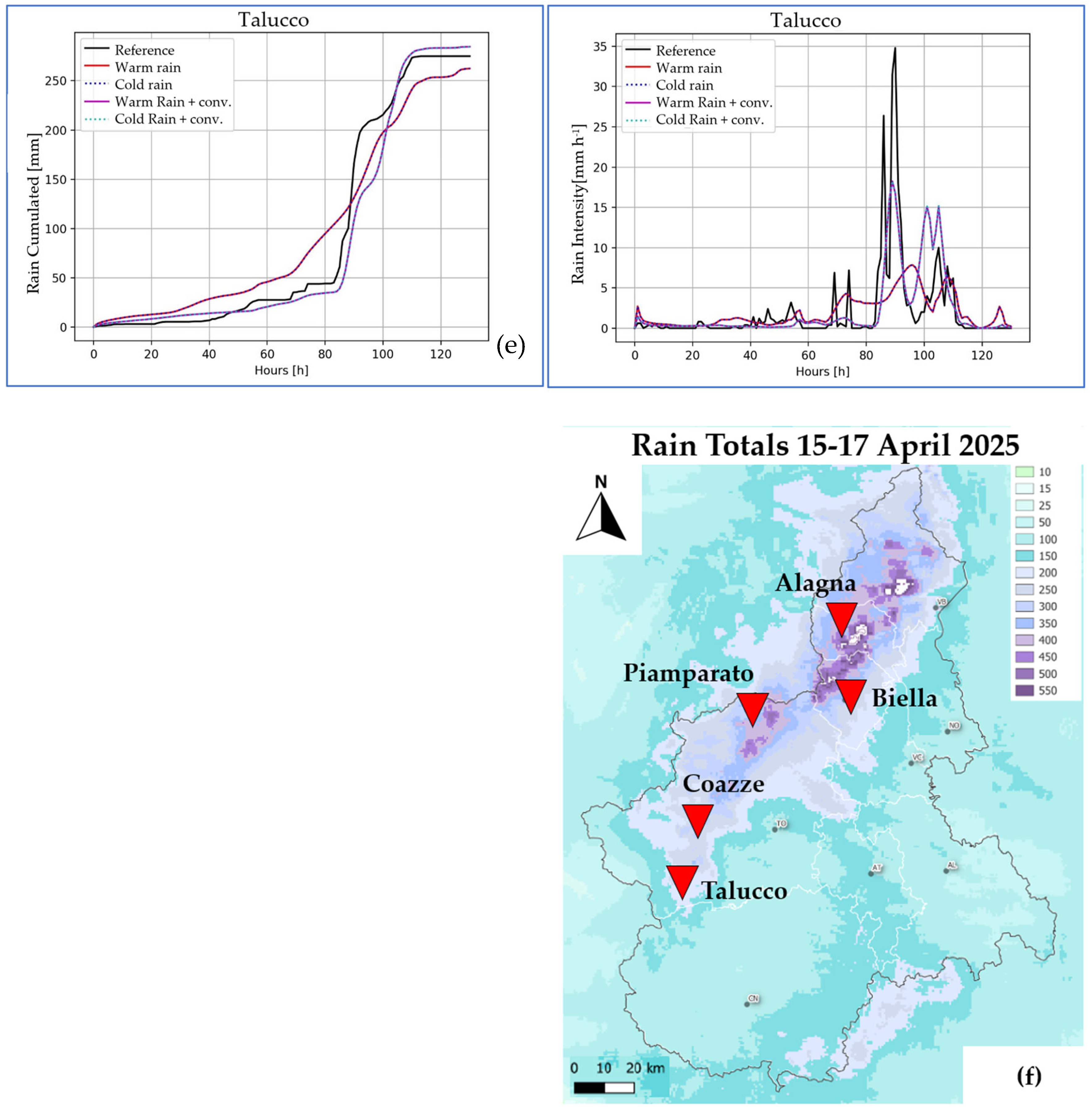
2.5. Case-Study Description
3. Results
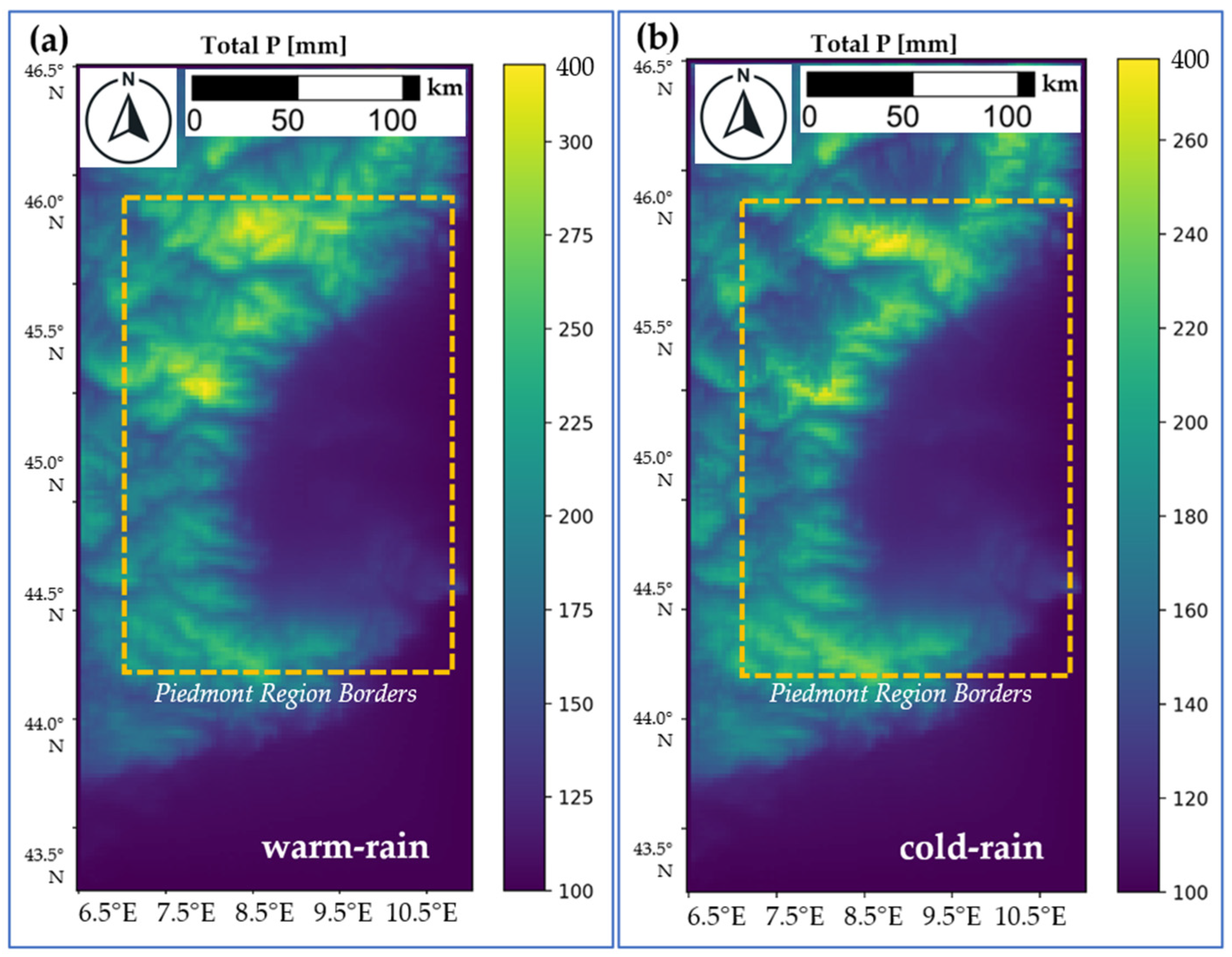
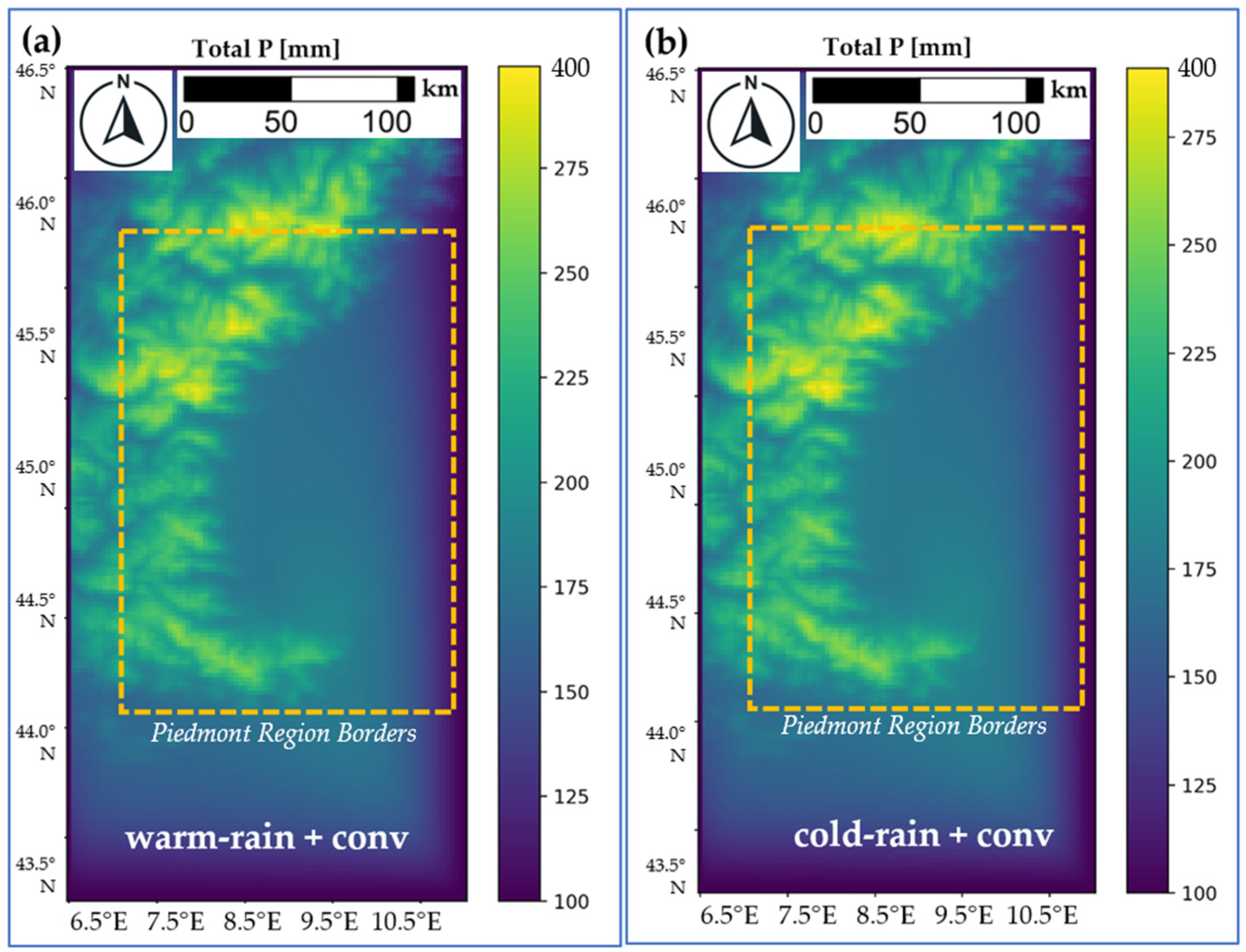
3.1. Two-Dimensional Data: The Wind Influences the Event Strength
3.2. Synoptic and Convective Data: Probability and Magnitude
3.3. Initial Conditions
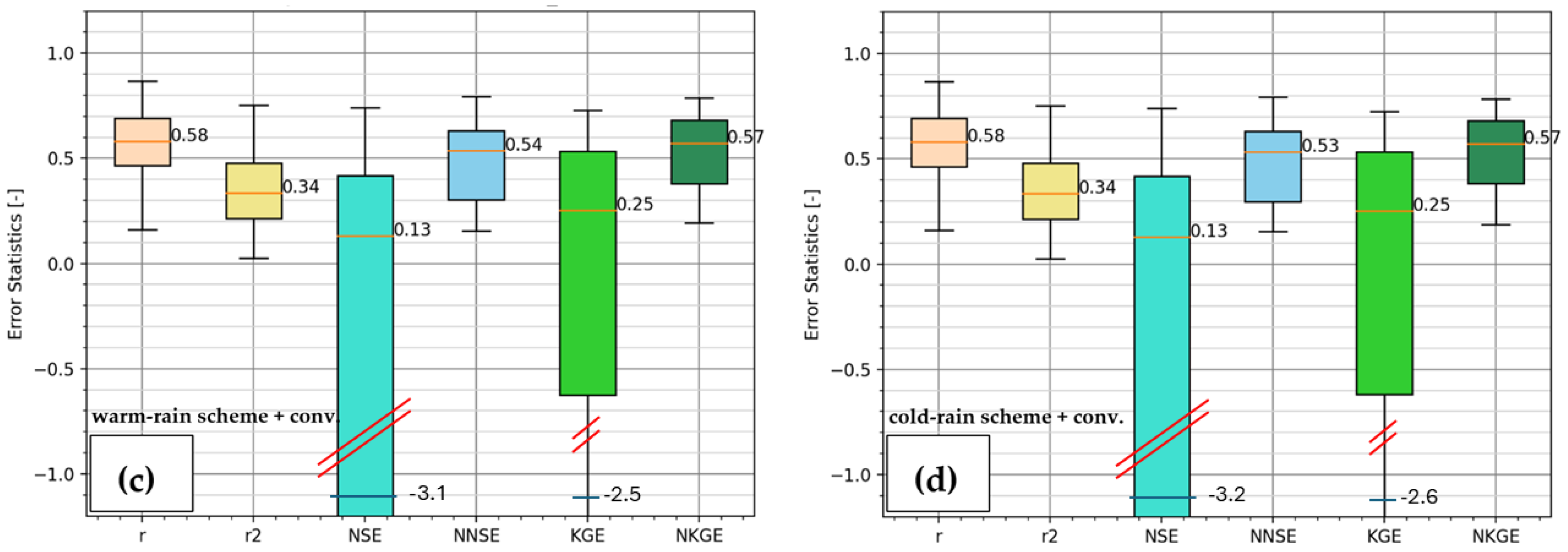
3.4. Global Error Analysis: Total Rainfall Fields Comparison
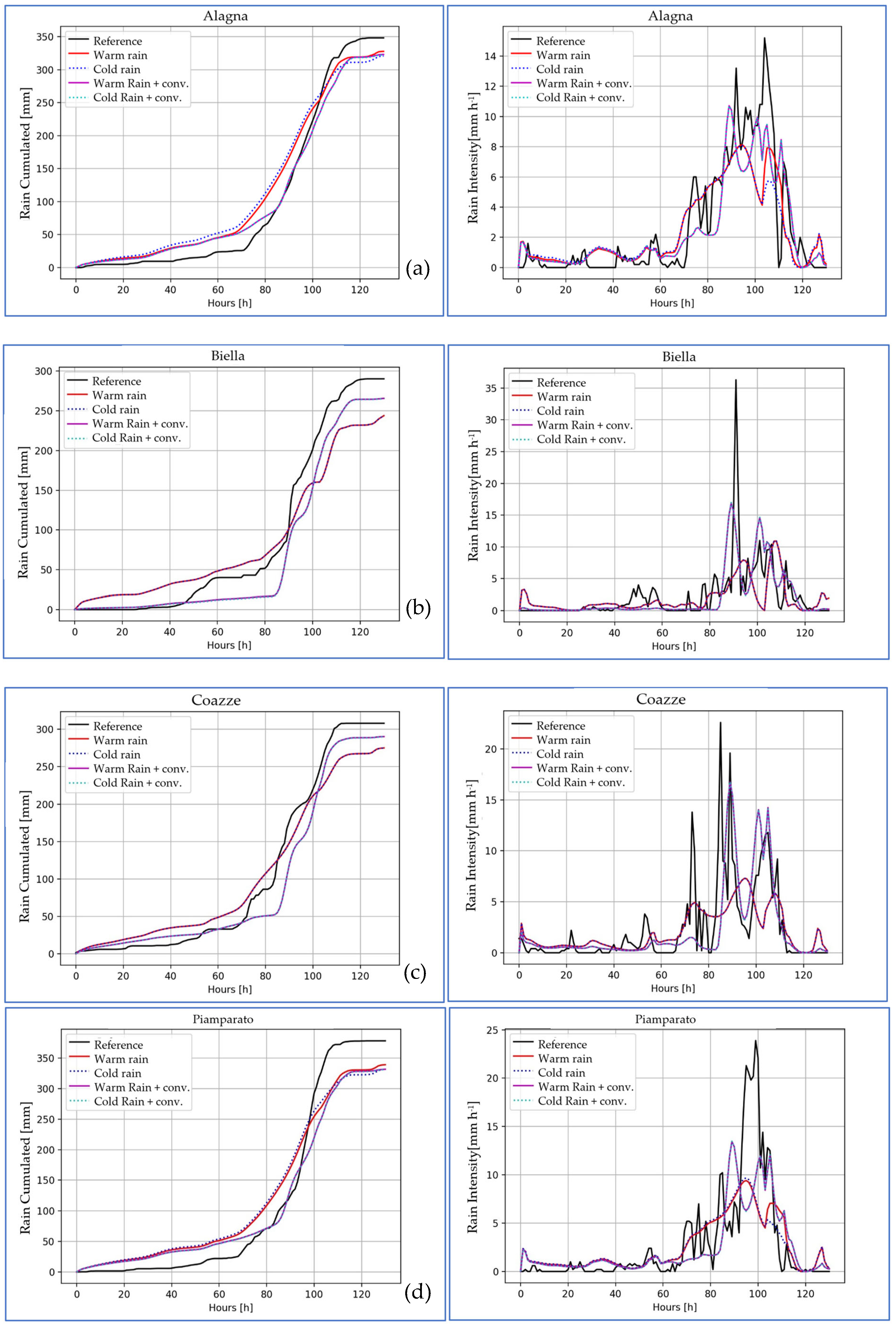
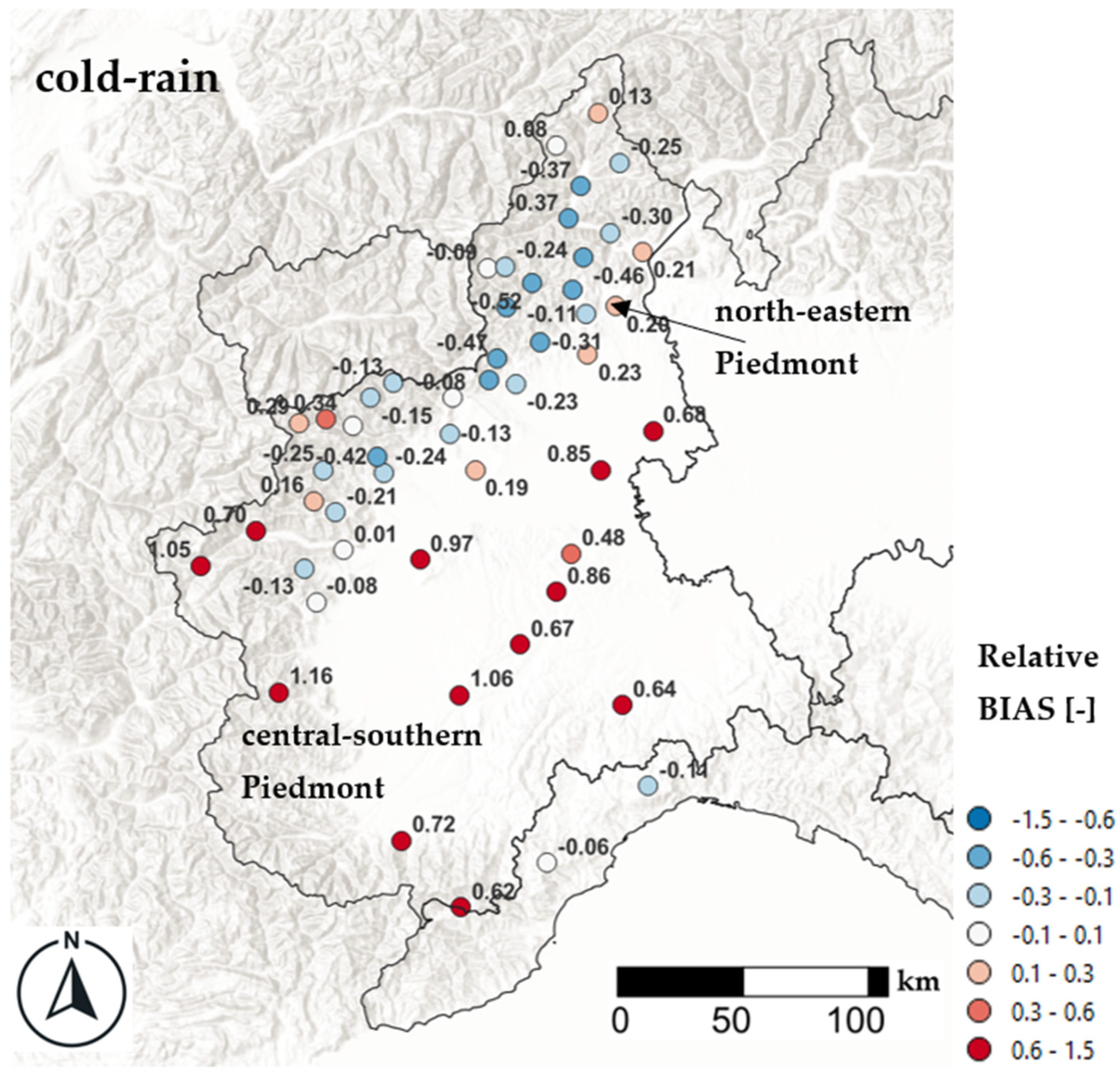
3.5. Local Error Analysis: Single Rain-Gauge Comparison
- ▪
- Cumulated precipitation evolution generally follows the reference data, with “no-convection” routines slightly anticipating the “enabled-convection” versions. Moreover, the total amounts recorded at the end of the simulated event are comparable (with BIAS lower than 50 mm), confirming the results of the error analysis previously conducted.
- ▪
- The intensity pattern is rather interesting since the simulated rainfall is able to follow the reference data, giving a correct depiction of the rain rate pattern and highlighting the most intense phase of the event (between 15th and 17th of April). Again, “no-convection” models produce lower rain rates with respect to the “enabled-convection” routines. This is physically consistent, since convective rainfalls are reported to be most intense with respect to the stratiform ones. On the contrary, the high spikes recorded by reference rain-gauges are not always reproduced due to the numerical smoothing introduced by model time integration.
BIAS and NSE Evaluations Across the Investigated Area
4. Discussion
4.1. A 2.5D Model Perspective
4.2. Sensitivity Analysis on Microphysical Parameters
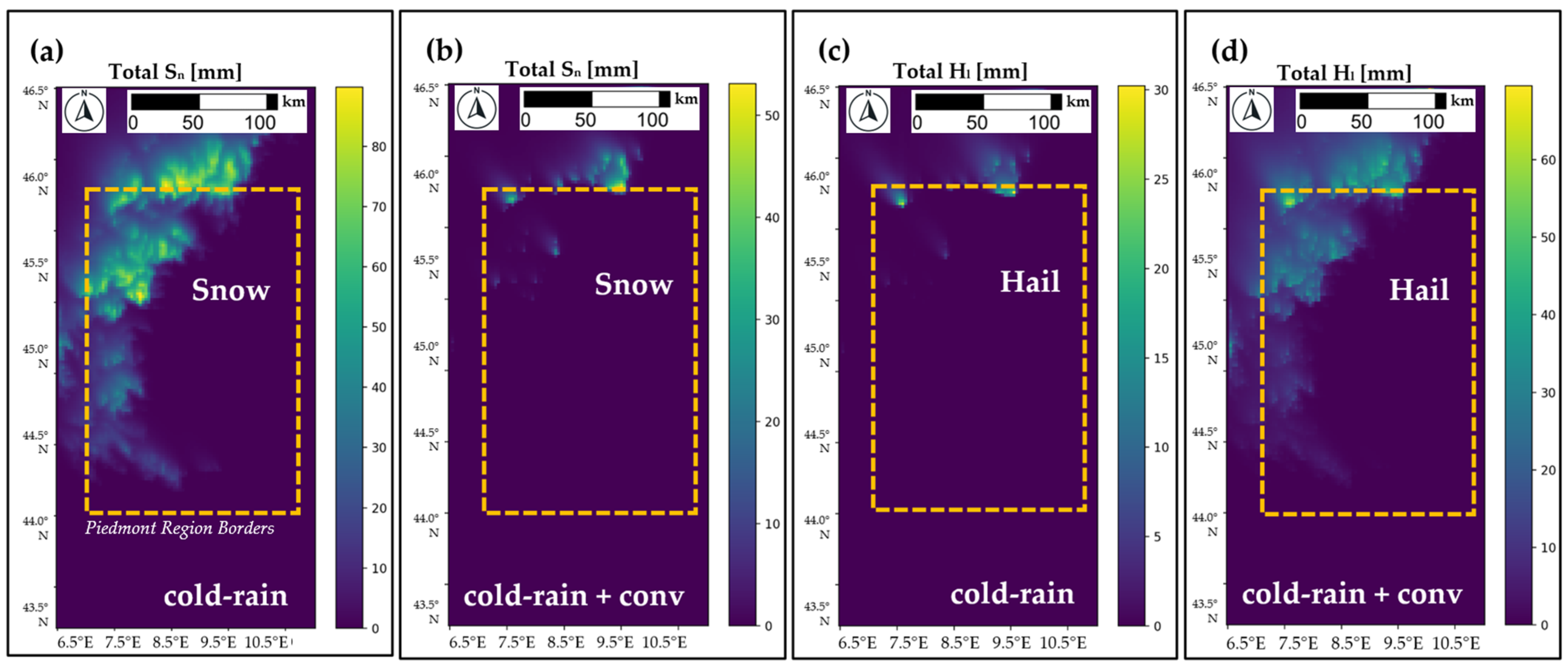
4.3. Cold-Rain Dynamics
4.4. Moist Convection Contribution to Extreme Precipitation
4.5. Non-Orographic Areas and Pbase Estimation
4.6. Practical Indication for Model Implementation
- ▪
- The choice of ICs and BCs in function of WVF;
- ▪
- The reanalysis and forecast modes;
- ▪
- The effect of DEM resolution;
- ▪
- The spatial extension of the computational domain.
4.7. Open Issues and Further Developments
- ▪
- BC uncertainties and domain nesting;
- ▪
- Radiosonde parameter inaccuracies and variabilities;
- ▪
- Cold-rain microphysical schemes and their parametrisation;
- ▪
- Moist convection activation in space and time and its magnitude;
- ▪
- Pbase evaluation across non-orographic areas.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LUME | Linear Upslope Model Extension |
| RMSE | Root Mean Square Error |
| AIS | All Indicator Scores |
| SMAPE | Symmetric Mean Absolute Percentage Error |
| CC | Correlation Coefficient |
| NSE | Nash–Sutcliffe Efficiency |
| KGE | Kling–Gupta Efficiency |
| PE | Precipitation Efficiency |
| BL | Boundary Layer |
| EL | Equilibrium Layer |
| LFC | Layer of Free Convection |
| LCL | Lifting Condensation Level |
| GLM | General Linear Model |
| CRM | Cloud Resolving Models |
| LAM | Local Area Model |
Appendix A
- ▪
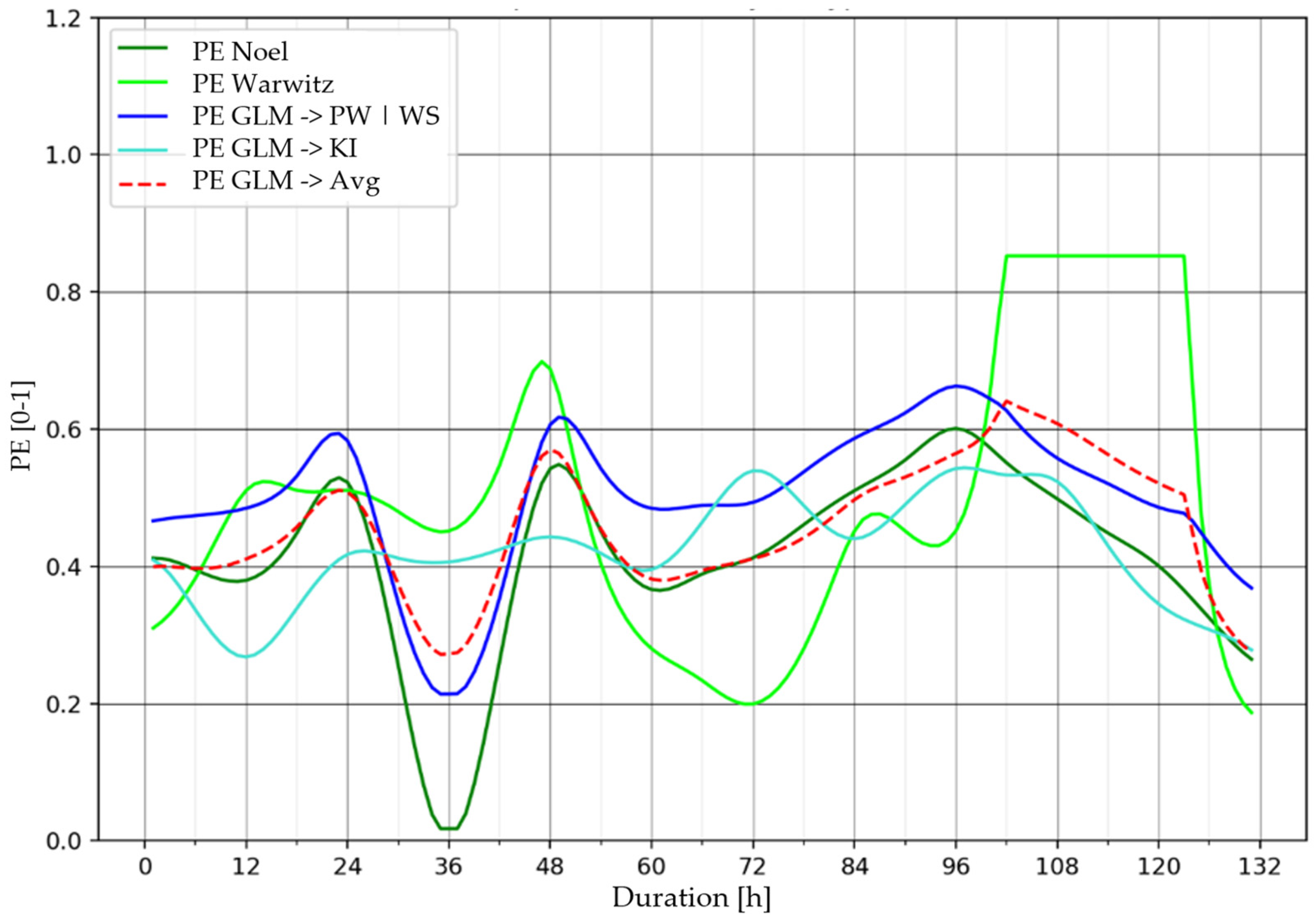
- PENoel [66] is a formulation that simply correlates PE with the PW and RH parameters (A5). It is a straight equation generally adopted by meteorologists for roughly forecasting PE over a spatial domain.
- ▪
- PEMarwitz [67] was already adopted in precedent studies considering the storms in the USA. It comes from a regression study where the PE is correlated to WS (wind shear, expressed in ms−1 (A6)) evaluated from radiosonde or aircraft campaign.
- ▪
- PELIN was calculated applying a GLM (General Linear Model) algorithm [83] to the historical radiosonde data provided by the Milano Linate station (A7). The regression was carried out on a series of 30 years (from 1990 to 2020) to explain the PE calculated in the proximity of the station with the radiosonde indexes. PE was calculated simply by considering the ratio between rainfall records [68,69] and the corresponding total available cloud moisture for each day (A1). For the rainfall records, a spatial average among stations located in the surrounding area of the radiosonde (a circle of 100 km was considered) was evaluated (A2), while was retrieved simply by applying the moisture advection Equations (A3) and (A4):If it is assumed that evaporation E is small in areas of intense precipitation and saturation, and that local changes in water vapour content are primarily those owing to advection in synoptic-scale systems, the precipitation amount is proportional to the vertically integrated product of specific humidity and horizontal mass convergence through the depth of the atmosphere. The regression has shown a dependence of PE on PW and WS, confirming the studies of [66,67]. In particular, the PE increases with PW ( is >0) while it decreases with WS ( is <0).
- ▪
- GLM algorithms were also applied, considering convective indices (the ones listed in the text), finding a significant correlation (r2 = 0.68) with the KI [44], obtaining PEKI (A8). The K-Index (KI) is a meteorological index used to assess the potential for convection and thunderstorms. It combines temperature and moisture information from different atmospheric levels to estimate the likelihood of unstable conditions conducive to thunderstorm development. The KI ranges from 15 to 45 (generally) and is positively correlated to the PE (with increasing KI, PE also increases).
Appendix B
- ▪
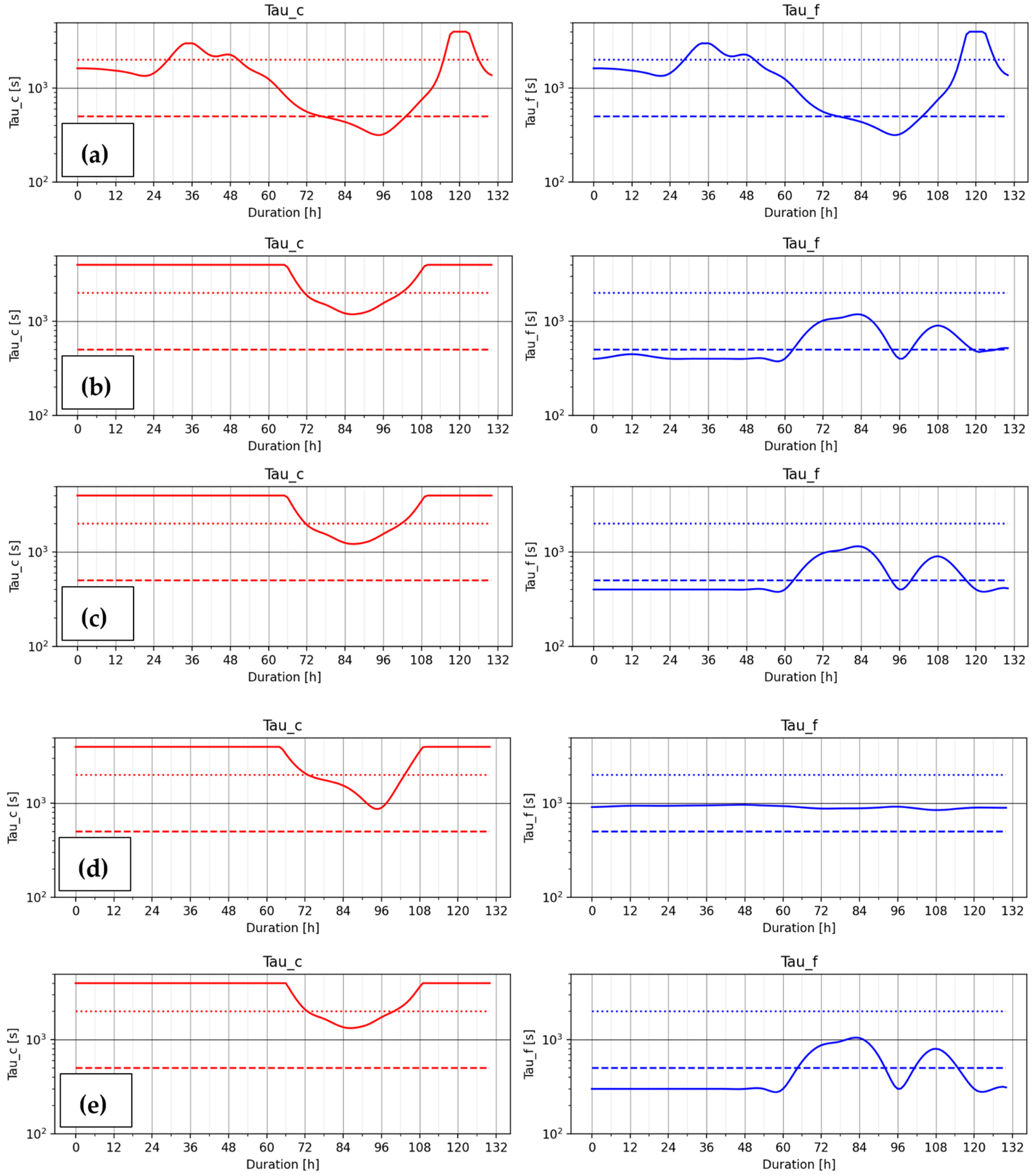
- For τf1, the “rain height” considered representative of the droplet’s fallout start was selected, equal to the EL divided by 2 (A10). The fallout is supposed to start in the middle of the cloud, which is roughly represented by EL/2.
- ▪
- For τf2, the “rain height” considered as representative of the droplet’s start was selected equal (A11), considering a combination of the EL and LFC height levels.
- ▪
- For τf3, the “rain height” considered as representative of the droplet’s fallout starts height was selected equal (A12), considering a combination of the EL and LCL height levels.
- ▪
- For τf4, the “rain height” considered as representative of the droplet’s fallout start was selected equal to (A13), considering the sum of the reference DEM height. Hdem and the water vapour scale Hw. This expression was already proposed by [27] and slightly adapted to consider the local topography.
Appendix C
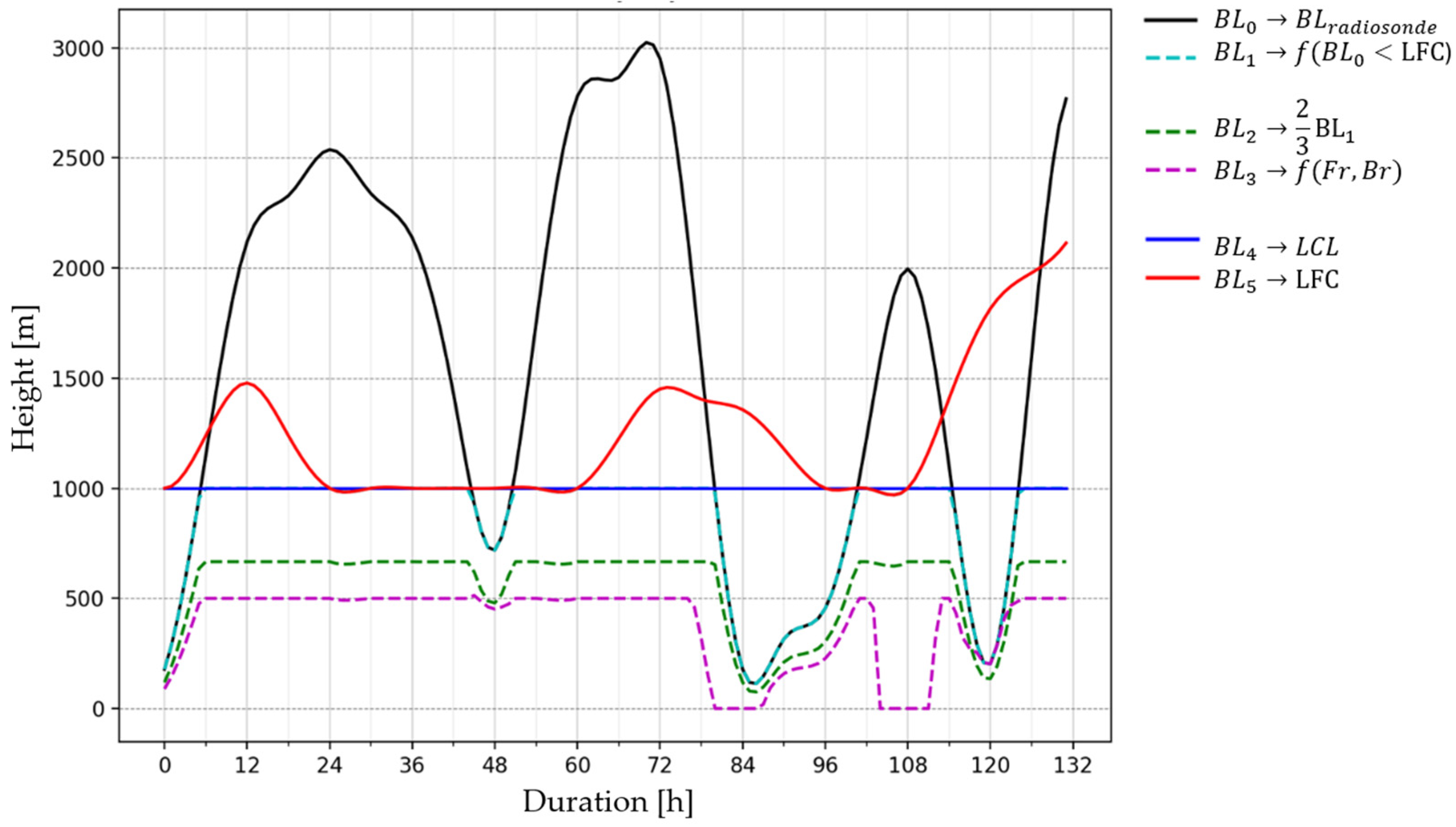
- ▪
- The Equation (A19) shows how BL0 is superiorly bounded by the LFC. In fact, especially when moist convection is triggered, the BL is located quite near to LFC or LCL; therefore, they have been considered as representative layers.
- ▪
- The Equations (A20)–(A26) show two possible solutions to eventually reduce the BL0 when intense rainfall events are approaching. From the evidence, BL is progressively depleted when precipitation starts, since the rainfall process triggers airflow mixing that may dissolve it completely. Therefore, a reduction in BL0 is expected. The BL2 Formula (A20) considers an empirical reduction of about 2/3 of the BL1, while the BL3 applies a more physical BL correction which considers Froude and Burger numbers [85,86]. The Froude (A21) and the Burger numbers (A22) are dimensionless quantities used in fluid dynamics to characterise flow behaviour. The Froude number is particularly relevant for open-channel flow (it depends on U, Nmoist and Hdem, the average elevation of the mountain range), while the Burger number is used in stratified flows (it depends on Hdem, Nmoist, fc, and awidth, the average width of the mountain range in the direction of the impinging airflow. They can be combined in order to evaluate the condition of “blocked”, “not-blocked” airflow. These conditions are significantly important for rain generation. A “blocked” humid airflow may not have sufficient energy to overpass the mountain range, causing persistent and prolonged rainfall in the upslope flank that may trigger extensive floods. Conversely, a “not-blocked” humid airflow can pass over the mountain range more easily, causing less intense and uniformly spatially distributed rainfalls. Therefore, “blocked” conditions are more critical and happen when Fr < 0.8 and Br > 1.2, while for “not-blocked” situations Fr > 1.2 and Br < 0.8 and the intermediate cases, the flow experiences a transition. From the BL perspective, when the airflow is “blocked”, the BL is depleted much faster than in a “not-blocked” situation. The flow is in a “transitional” phase when 0.8 < Fr < 1.2 and 0.8 < Br < 1.2.
- ▪
- The empirical formulation reported in Equation (A23) permits correcting the BL1 through aFr and aBr weights (comprised between 0 and 1), taking into account not only the thermodynamic state but also the airflow dynamics.
- ▪
- Equations (A24) and (A25) evaluate BL as a function of convective heights, while in (A26) the contribution of BL is neglected.
References
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New High-Resolution Climate Change Projections for European Impact Research. Reg. Environ. Change 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Allen, M.; Babiker, M.; Chen, Y.; de Coninck, H.; Connors, S.; van Diemen, R.; Dube, O.; Ebi, K.; Engelbrecht, F.; IPCC; et al. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2018; pp. 3–24. [Google Scholar] [CrossRef]
- Stull, R.B. Practical Meteorology: An Algebra-Based Survey of Atmospheric Science.; University of British Columbia: Vancouver, BC, Canada, 2017. [Google Scholar]
- Martel, J.-L.; Brissette, F.P.; Lucas-Picher, P.; Troin, M.; Arsenault, R. Climate Change and Rainfall Intensity–Duration–Frequency Curves: Overview of Science and Guidelines for Adaptation. J. Hydrol. Eng. 2021, 26, 03121001. [Google Scholar] [CrossRef]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Emanuel, K.A. Atmospheric Convection; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Smith, R.B. 100 Years of Progress on Mountain Meteorology Research. Meteorol. Monogr. 2018, 59, 20.1–20.73. [Google Scholar] [CrossRef]
- Abbate, A.; Longoni, L.; Papini, M. Extreme Rainfall over Complex Terrain: An Application of the Linear Model of Orographic Precipitation to a Case Study in the Italian Pre-Alps. Geosciences 2021, 11, 18. [Google Scholar] [CrossRef]
- Herman, G.R.; Schumacher, R.S. Extreme Precipitation in Models: An Evaluation. Weather Forecast. 2016, 31, 1853–1879. [Google Scholar] [CrossRef]
- Davolio, S.; Della Fera, S.; Laviola, S.; Miglietta, M.M.; Levizzani, V. Heavy Precipitation over Italy from the Mediterranean Storm “Vaia” in October 2018: Assessing the Role of an Atmospheric River. Mon. Weather Rev. 2020, 148, 3571–3588. [Google Scholar] [CrossRef]
- Baartman, J.; Jetten, V.G.; Ritsema, C.; de Vente, J. Exploring Effects of Rainfall Intensity and Duration on Soil Erosion at the Catchment Scale Using openLISEM: Prado Catchment, SE Spain. Hydrol. Process. 2012, 26, 1034–1049. [Google Scholar] [CrossRef]
- Ceriani, M.; Lauzi, S.; Padovan, M. Rainfall Thresholds Triggering Debris-Flow in the Alpine Area of Lombardia Region, Central Alps—Italy. In Proceedings of the Man and Mountain’94, Ponte di Legno, Italy, 20 June 1994. [Google Scholar]
- Crosta, G.; Frattini, P. Rainfall Thresholds for Triggering Soil Slips and Debris Flow. In Proceedings of the 2nd EGS Plinius Conference on Mediterranean Storms, Siena, Italy, 16–18 October 2001; pp. 463–487. [Google Scholar]
- Longoni, L.; Ivanov, V.I.; Brambilla, D.; Radice, A.; Papini, M. Analysis of the Temporal and Spatial Scales of Soil Erosion and Transport in a Mountain Basin. Ital. J. Eng. Geol. Environ. 2016, 16, 17–30. [Google Scholar] [CrossRef]
- Abbate, A.; Papini, M.; Longoni, L. Analysis of Meteorological Parameters Triggering Rainfall-Induced Landslide: A Review of 70 Years in Valtellina. Nat. Hazards Earth Syst. Sci. 2021, 21, 2041–2058. [Google Scholar] [CrossRef]
- Ivanov, V.; Arosio, D.; Tresoldi, G.; Hojat, A.; Zanzi, L.; Papini, M.; Longoni, L. Investigation on the Role of Water for the Stability of Shallow Landslides-Insights from Experimental Tests. Water 2020, 12, 1203. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a Changing Climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Alvioli, M.; Melillo, M.; Guzzetti, F.; Rossi, M.; Palazzi, E.; von Hardenberg, J.; Brunetti, M.T.; Peruccacci, S. Implications of Climate Change on Landslide Hazard in Central Italy. Sci. Total Environ. 2018, 630, 1528–1543. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall Thresholds for Possible Landslide Occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Luino, F. Sequence of Instability Processes Triggered by Heavy Rainfall in the Northern Italy. Geomorphology 2005, 66, 13–39. [Google Scholar] [CrossRef]
- Michael, D. Ozturk Ugur A Flood of Disaster Response Challenges. Science 2021, 373, 1317–1318. [Google Scholar] [CrossRef]
- Anip, M.; Market, P. Dominant Factors Influencing Precipitation Efficiency in a Continental Mid-Latitude Location. Tellus A 2007, 59, 122–126. [Google Scholar] [CrossRef]
- Abbate, A.; Papini, M.; Longoni, L. Orographic Precipitation Extremes: An Application of LUME (Linear Upslope Model Extension) over the Alps and Apennines in Italy. Water 2022, 14, 2218. [Google Scholar] [CrossRef]
- Kirshbaum, D.; Adler, B.; Kalthoff, N.; Barthlott, C.; Serafin, S. Moist Orographic Convection: Physical Mechanisms and Links to Surface-Exchange Processes. Atmosphere 2018, 9, 80. [Google Scholar] [CrossRef]
- Smith, R.B. The Influence of Mountains on the Atmosphere. In Advances in Geophysics; Saltzman, B., Ed.; Elsevier: Amsterdam, The Netherlands, 1979; Volume 21, pp. 87–230. ISBN 0065-2687. [Google Scholar]
- Smith, R.B.; Barstad, I. A Linear Theory of Orographic Precipitation. J. Atmos. Sci. 2004, 61, 1377–1391. Available online: https://journals.ametsoc.org/view/journals/atsc/61/12/1520-0469_2004_061_1377_altoop_2.0.co_2.xml (accessed on 1 August 2025). [CrossRef]
- Caroletti, G.; Barstad, I. An Assessment of Future Extreme Precipitation in Western Norway Using a Linear Model. Hydrol. Earth Syst. Sci. 2010, 14, 2329–2341. [Google Scholar] [CrossRef]
- Barstad, I.; Schüller, F. An Extension of Smith’s Linear Theory of Orographic Precipitation: Introduction of Vertical Layers. J. Atmos. Sci. 2011, 68, 2695–2709. [Google Scholar] [CrossRef]
- Smith, R. A Linear Time-Delay Model of Orographic Precipitation. J. Hydrol. 2003, 282, 2–9. [Google Scholar] [CrossRef]
- Doms, G.; Vogel, G.; Förstner, J.; Heise, E.; Herzog, H.; Mironov, D.; Raschendorfer, M.; Reinhardt, T.; Ritter, B.; Schrodin, R.; et al. COSMO-Model Version 6.00: A Description of the Nonhydrostatic Regional COSMO-Model. In Part II: Physical Parametrizations; Deutscher Wetterdienst: Offenbach, Germany, 2021; p. 173. [Google Scholar]
- ARPA Piemonte Rapporto Evento 15–17 Aprile 2025; p. 70. Available online: https://www.arpa.piemonte.it/notizia/rapporto-sullevento-15-17-aprile-2025-piemonte (accessed on 1 August 2025).
- Cat Berro, D.; Acordon, V.; Castellano, C. Metà Aprile 2025: Alluvioni e Dissesti in Piemonte e Valle D’aosta, Straordinari per la Stagione; Nimbus: Torino, Italy, 2025. [Google Scholar]
- Pruppacher, H.R.; Klett, J. Microphysics of Clouds and Precipitation; Springer Nature: New York, NY, USA, 2010; Volume 18, ISBN 978-0-7923-4211-3. [Google Scholar]
- Kessler, E. Model of Precipitation and Vertical Air Currents1. Tellus 1974, 26, 519–542. [Google Scholar] [CrossRef]
- Kessler, E. On the Condensed Water Mass in Rising Air. Pure Appl. Geophys. 1975, 113, 971–981. [Google Scholar] [CrossRef]
- Kessler, E. On the Continuity and Distribution of Water Substance in Atmospheric Circulations. Atmos. Res. 1995, 38, 109–145. [Google Scholar] [CrossRef]
- Department of Atmospheric Science, University of Wyoming Airport Radiosonde. Available online: https://weather.uwyo.edu/upperair/sounding.shtml (accessed on 15 September 2025).
- Hutchinson, M.F. Interpolating Mean Rainfall Using Thin Plate Smoothing Splines. Int. J. Geogr. Inf. Syst. 1995, 9, 385–403. [Google Scholar] [CrossRef]
- Patane, G.; Cerri, A.; Skytt, V.; Pittaluga, S.; Biasotti, S.; Sobrero, D.; Dokken, T.; Spagnuolo, M. Comparing Methods for the Approximation of Rainfall Fields in Environmental Applications. ISPRS J. Photogramm. Remote Sens. 2017, 127, 57–72. [Google Scholar] [CrossRef]
- Daly, C.; Taylor, G.; Gibson, W. The PRISM Approach to Mapping Precipitation and Temperature; Oregon State University: Corvallis, OR, USA, 1997. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Nelson, E.L.; L’Ecuyer, T.S.; Saleeby, S.M.; Berg, W.; Herbener, S.R.; Van Den Heever, S.C. Toward an Algorithm for Estimating Latent Heat Release in Warm Rain Systems. J. Atmos. Ocean. Technol. 2016, 33, 1309–1329. [Google Scholar] [CrossRef]
- Bocchiola, D.; Rosso, R. The Distribution of Daily Snow Water Equivalent in the Central Italian Alps. Adv. Water Resour. 2007, 30, 135–147. [Google Scholar] [CrossRef]
- Cotton, W.R.; Bryan, G.H.; Van Den Heever, S.C. Cumulonimbus Clouds and Severe Convective Storms. In Storm and Cloud Dynamics; Elsevier: London, UK, 2011. [Google Scholar]
- Quarteroni, A.; Valli, A. Numerical Approximation of Partial Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 23, ISBN 3-540-85267-0. [Google Scholar]
- Courant, E.D.; Ruth, R.D.; Weng, W.T. Stability in Dynamical Systems I; Brookhaven National Lab.: Upton, NY, USA, 1984. [Google Scholar]
- Quarteroni, A. Modellistica Numerica per Problemi Differenziali; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 88-470-2748-9. [Google Scholar]
- Ćurić, M. Numerical Modeling of Thunderstorm. Theor. Appl. Climatol. 1989, 40, 227–235. [Google Scholar] [CrossRef]
- Suhas, E.; Zhang, G. Evaluation of Trigger Functions for Convective Parameterization Schemes Using Observations. J. Clim. 2014, 27, 7647–7666. [Google Scholar] [CrossRef]
- Arakawa, A.; Cheng, M.-D. The Arakawa-Schubert Cumulus Parameterization. In The Representation of Cumulus Convection in Numerical Models; Springer: Berlin/Heidelberg, Germany, 1993; pp. 123–136. [Google Scholar]
- Doswell, C.A., III. Severe Convective Storms—An Overview. Sev. Convect. Storms 2001, 28, 1–26. [Google Scholar]
- Kuo, H.-L. On Formation and Intensification of Tropical Cyclones through Latent Heat Release by Cumulus Convection. J. Atmos. Sci. 1965, 22, 40–63. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling Errors in Daily Precipitation Measurements: Additive or Multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef]
- Brownlees, C.; Cipollini, F.; Gallo, G. Multiplicative Error Models. In Handbook of Volatility Models and Their Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Yang, R.; Xing, B. A Comparison of the Performance of Different Interpolation Methods in Replicating Rainfall Magnitudes under Different Climatic Conditions in Chongqing Province (China). Atmosphere 2021, 12, 1318. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New Global Hydrography Derived From Spaceborne Elevation Data. Eos Trans. Am. Geophys. Union 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, X.; Zhao, J.; Cao, J.; Wang, X.; Li, D. Effect of DEM Interpolation Neighbourhood on Terrain Factors. ISPRS Int. J. Geo-Inf. 2019, 8, 30. [Google Scholar] [CrossRef]
- GDAL/OGR contributors. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation: Beaverton, OR, USA, 2020. [Google Scholar]
- McMillan, H.; Jackson, B.; Clark, M.; Kavetski, D.; Woods, R. Rainfall Uncertainty in Hydrological Modelling: An Evaluation of Multiplicative Error Models. J. Hydrol. 2011, 400, 83–94. [Google Scholar] [CrossRef]
- McClung, T. Technical Implementation Notice 16-11 Amended; Nation Weather Service: Silver Spring, MD, USA, 2016. [Google Scholar]
- Cogan, J.L. Change in Weather Research and Forecasting (WRF) Model Accuracy with Age of Input Data from the Global Forecast System (GFS). 2016. Available online: https://apps.dtic.mil/sti/tr/pdf/AD1016607.pdf (accessed on 15 September 2025).
- Chen, T.; Ren, L.; Yuan, F.; Yang, X.; Jiang, S.; Tang, T.; Liu, Y.; Zhao, C.; Zhang, L. Comparison of Spatial Interpolation Schemes for Rainfall Data and Application in Hydrological Modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Giorgi, F. Simulation of Regional Climate Using a Limited Area Model Nested in a General Circulation Model. J. Clim. 1990, 3, 941–963. [Google Scholar] [CrossRef]
- de Elía, R.; Laprise, R.; Denis, B. Forecasting Skill Limits of Nested, Limited-Area Models: A Perfect-Model Approach. Mon. Weather Rev. 2002, 130, 2006–2023. [Google Scholar] [CrossRef]
- Noel, J.; Dobur, J.C. A Pilot Study Examining Model-Derived Precipitation Efficiency for Use in Precipitation Forecasting in the Eastern United States. Natl. Weather Dig. 2002, 26, 3–8. [Google Scholar]
- Marwitz, J.D. Precipitation Efficiency of Thunderstorms on the High Plains. J. Rech. Atmos. 1972, 6, 367–370. [Google Scholar]
- Sui, C.-H.; Li, X.; Yang, M.-J. On the Definition of Precipitation Efficiency. J. Atmos. Sci. 2007, 64, 4506–4513. [Google Scholar] [CrossRef]
- Robinson, P.J.; Lutz, J.T. Precipitation Efficiency of Cyclonic Storms. Ann. Assoc. Am. Geogr. 1978, 68, 81–88. [Google Scholar] [CrossRef]
- Jiang, Q.; Smith, R.B. Cloud Timescales and Orographic Precipitation. J. Atmos. Sci. 2003, 60, 1543–1559. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 13, ISBN 94-009-3027-5. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988; ISBN 0-07-010810-2. [Google Scholar]
- Abbate, A.; Mancusi, L.; Apadula, F.; Frigerio, A.; Papini, M.; Longoni, L. CRHyME (Climatic Rainfall Hydrogeological Modelling Experiment): A New Model for Geo-Hydrological Hazard Assessment at the Basin Scale. Nat. Hazards Earth Syst. Sci. 2024, 24, 501–537. [Google Scholar] [CrossRef]
- Kim, M.H.; Lee, J.; Lee, S.-J. Hail: Mechanisms, Monitoring, Forecasting, Damages, Financial Compensation Systems, and Prevention. Atmosphere 2023, 14, 1642. [Google Scholar] [CrossRef]
- Rädler, A.; Groenemeijer, P.; Pistotnik, G.; Sausen, R.; Faust, E. Identification of Favorable Environments for Thunderstorms in Reanalysis Data. Meteorol. Z. 2015, 26, 59–70. [Google Scholar] [CrossRef]
- Taszarek, M.; Allen, J.T.; Marchio, M.; Brooks, H.E. Global Climatology and Trends in Convective Environments from ERA5 and Rawinsonde Data. NPJ Clim. Atmos. Sci. 2021, 4, 35. [Google Scholar] [CrossRef]
- Wang, W. Forecasting Convection with a “Scale-Aware” Tiedtke Cumulus Parameterization Scheme at Kilometer Scales. Weather Forecast 2022, 37, 1491–1507. [Google Scholar] [CrossRef]
- Tiedtke, M. A Comprehensive Mass Flux Scheme for Cumulus Parameterization in Large-Scale Models. Mon. Weather Rev. 1989, 117, 1779–1800. Available online: https://journals.ametsoc.org/configurable/content/journals$002fmwre$002f117$002f8$002f1520-0493_1989_117_1779_acmfsf_2_0_co_2.xml?t:ac=journals%24002fmwre%24002f117%24002f8%24002f1520-0493_1989_117_1779_acmfsf_2_0_co_2.xml (accessed on 1 August 2025). [CrossRef]
- Krishnamurti, T.N.; Moxim, W.J. On Parametrization of Convective and Nonconvective Latent Heat Release. J. Appl. Meteorol. 1971, 10, 3–13. [Google Scholar] [CrossRef]
- Houze, R.A., Jr.; Hobbs, P.V.; Biswas, K.R.; Davis, W.M. Mesoscale Rainbands in Extratropical Cyclones. Mon. Weather Rev. 1976, 104, 868–878. [Google Scholar] [CrossRef]
- Rotunno, R.; Houze, R. Lessons on Orographic Precipitation for the Mesoscale Alpine Programme. Q. J. R. Meteorol. Soc. 2007, 133, 811–830. [Google Scholar] [CrossRef]
- Bechtold, P.; Bazile, E.; Guichard, F.; Mascart, P.; Richard, E. A Mass-flux Convection Scheme for Regional and Global Models. Q. J. R. Meteorol. Soc. 2001, 127, 869–886. [Google Scholar] [CrossRef]
- McCullagh, P. Generalized Linear Models; Routledge: Oxfordshire, UK, 2019; ISBN 0-203-75373-9. [Google Scholar]
- Serafin, S.; Zardi, D. Structure of the Atmospheric Boundary Layer in the Vicinity of a Developing Upslope Flow System: A Numerical Model Study. J. Atmos. Sci. 2010, 67, 1171–1185. [Google Scholar] [CrossRef]
- Baines, P. Upstream Blocking and Airflow over Mountains. Annu. Rev. Fluid Mech. 1987, 19, 75–95. [Google Scholar] [CrossRef]
- Baines, P.G.; Manins, P.C. The Principles of Laboratory Modeling of Stratified Atmospheric Flows over Complex Terrain. J. Appl. Meteorol. Climatol. 1989, 28, 1213–1225. [Google Scholar] [CrossRef]


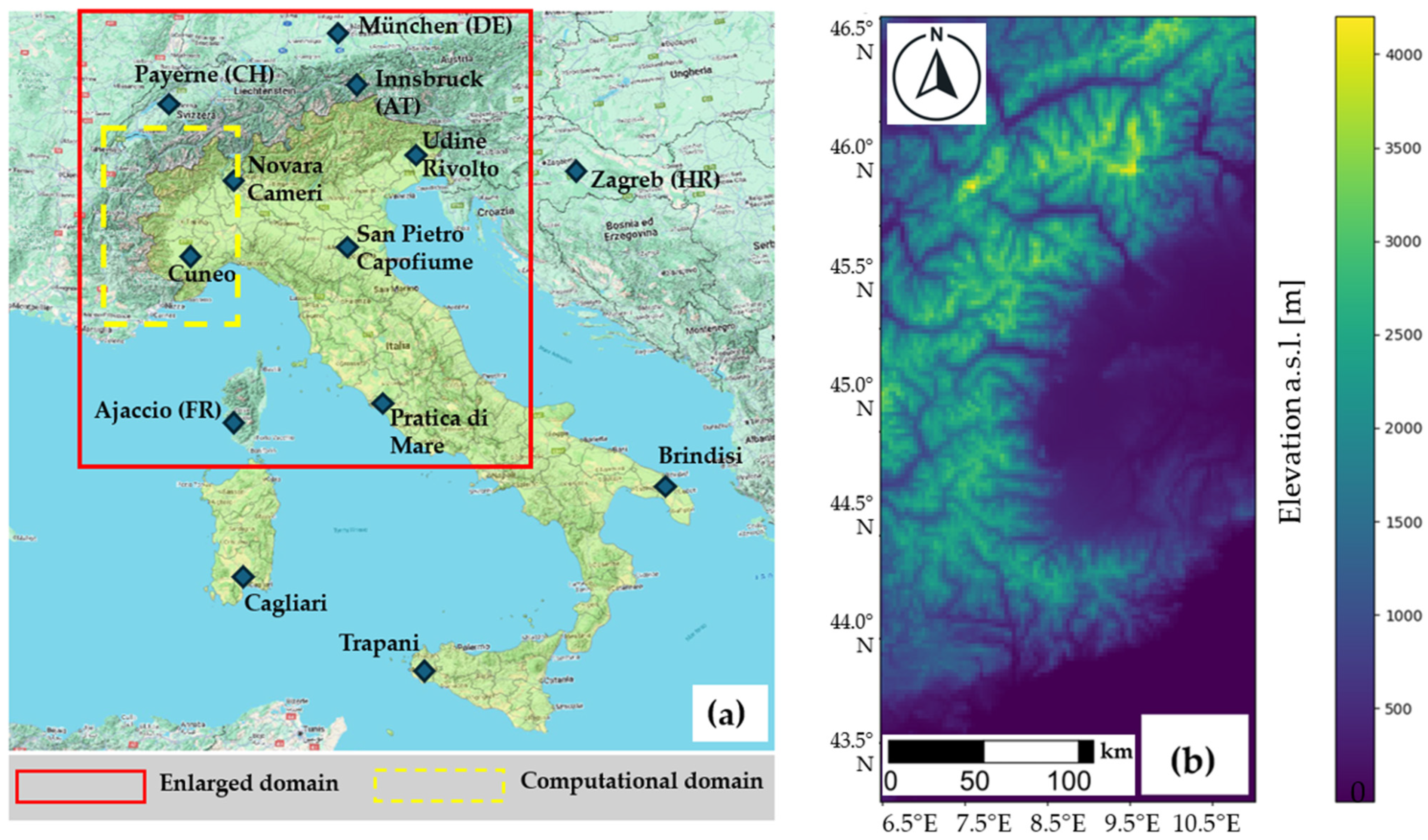
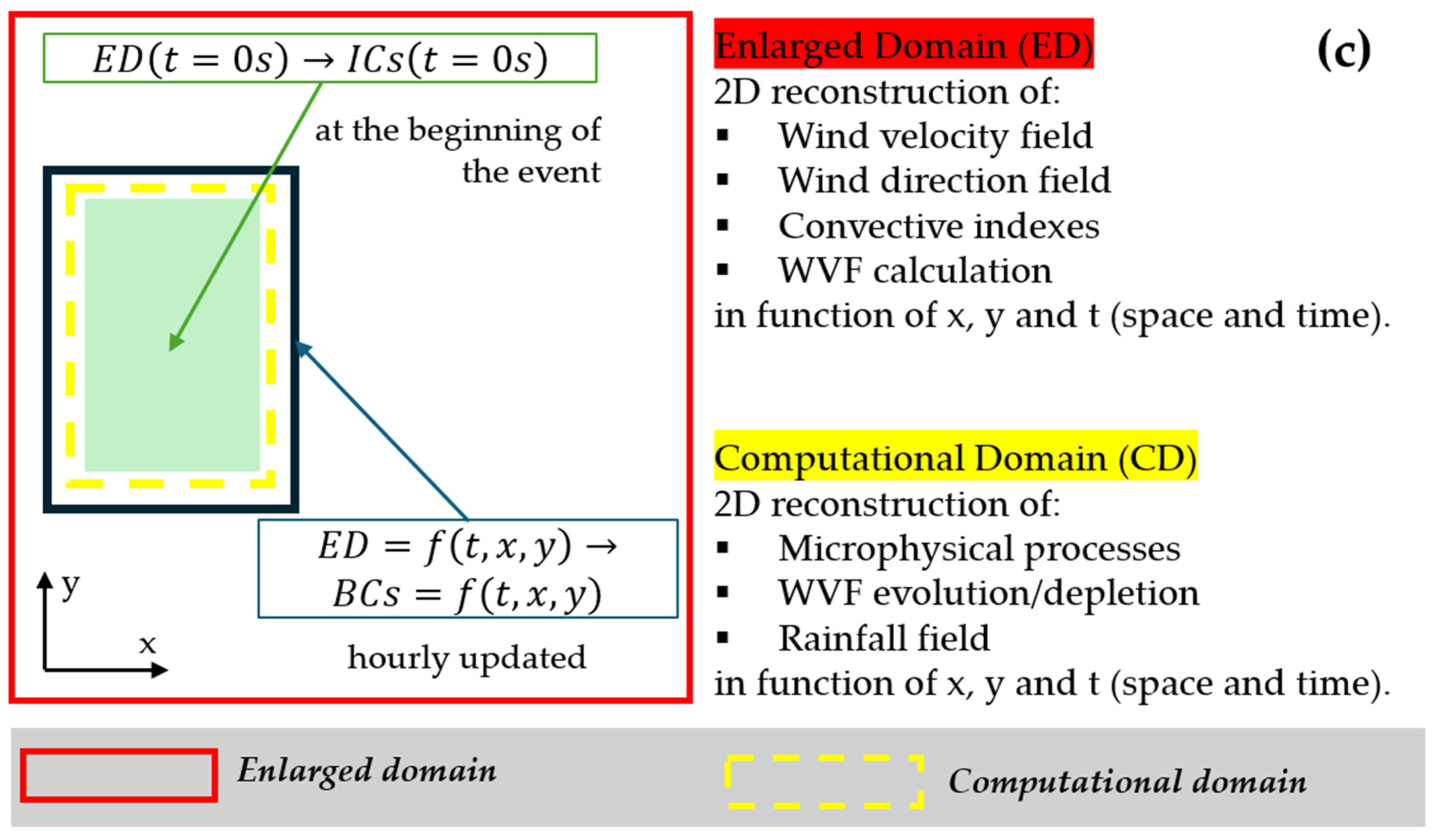
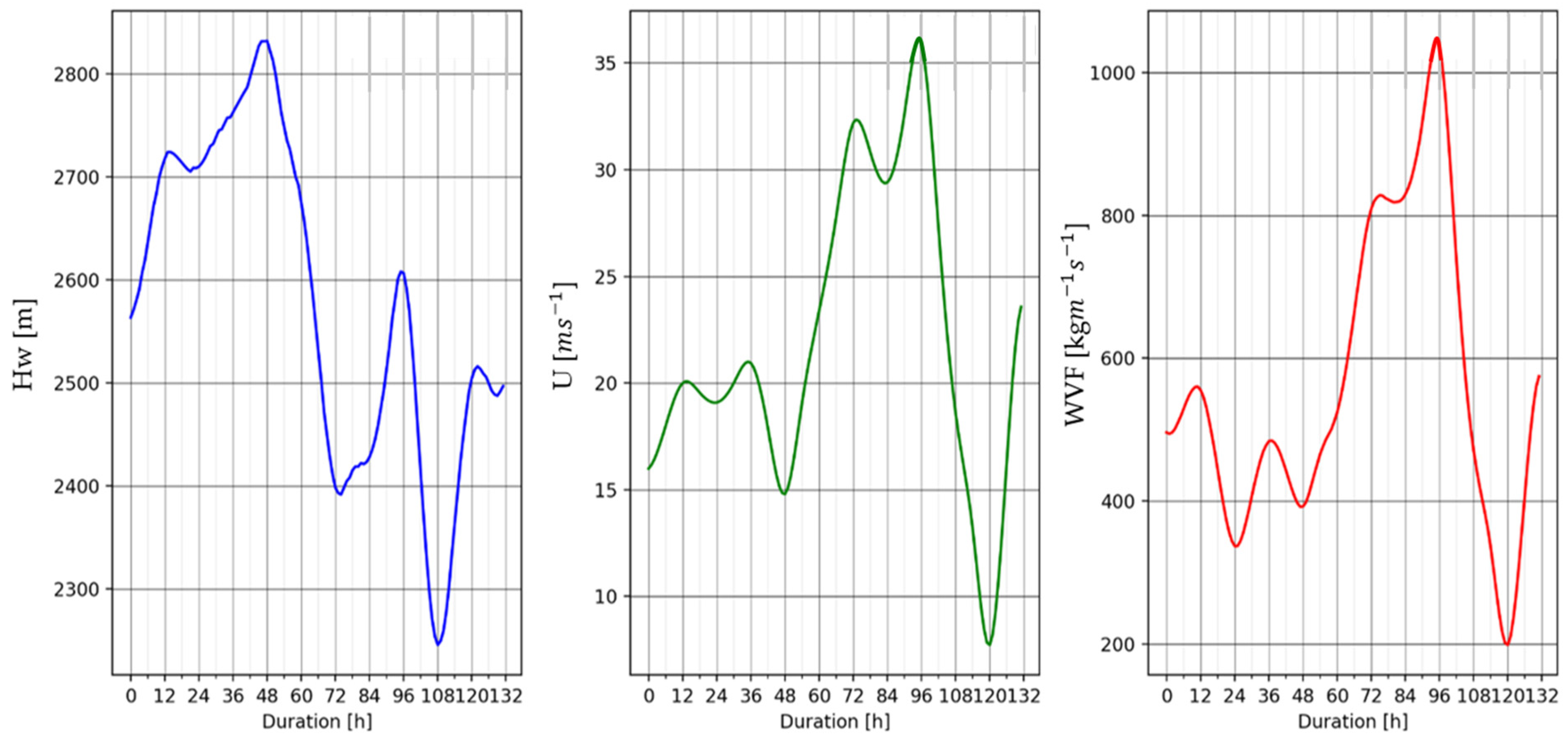
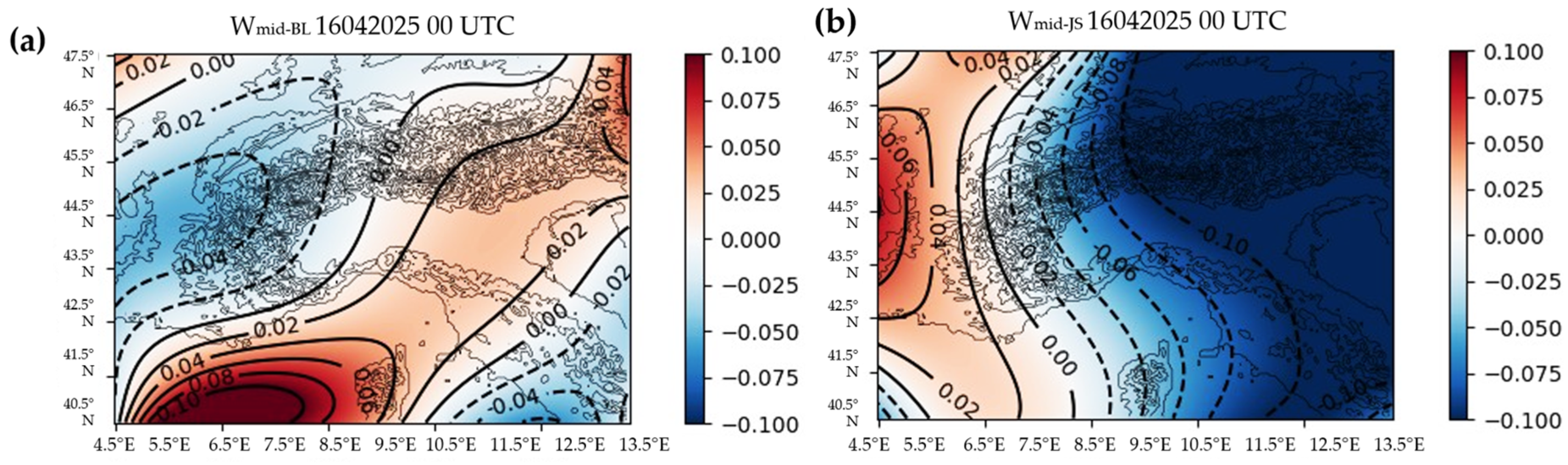





| Radiosonde Name | Location | Nation | WMO Code |
|---|---|---|---|
| Novara Cameri | Novara | Italy | 16064 |
| Cuneo Levaldigi | Cuneo | Italy | 16117 |
| San Pietro Capofiume | Bologna | Italy | 16144 |
| Pratica di Mare | Roma | Italy | 16245 |
| Udine | Udine | Italy | 16045 |
| Payerne | Payerne | Switzerland | 06610 |
| Ajaccio | Ajaccio | France | 07761 |
| Innsbruck | Innsbruck | Austria | 11120 |
| Muenchen | Muenchen | Germany | 10410 |
| Variable or Parameter | Symbol | Unit of Measure |
|---|---|---|
| Reference Temperature (z = 0 m) | [°C] | |
| Environmental Lapse Rate | [°C m−1] | |
| Moist Lapse Rate | [°C m−1] | |
| Brunt Vaisala Frequency | [s−1] | |
| Reference Air Density | [kg m−3] | |
| Reference Humidity | [-] | |
| Wind Velocity | [m s−1] | |
| Wind Direction | [°] | |
| Convective Available Potential Energy | [J kg−1] | |
| Convective Inhibition | [J kg−1] | |
| Low Convective Layer | [m] | |
| Level of Free Convection | [m] | |
| Equilibrium Layer | [m] | |
| Precipitable Water | [mm] | |
| Precipitation Efficiency | [-] | |
| Convective Generator term | and | [mm h−1] |
| Boundary Layer Height | [m] | |
| Wind Vapour Flux | [kg s−1 m−1] | |
| Water-Scale Height | [m] | |
| Conversion and Fallout time-scale terms | and | [s] |
| CI | Name | Min Value | Max Value | Threshold |
|---|---|---|---|---|
| CAPE-CAPEv [J kg−1] | Convective Available Potential Energy (using T and virtual T) | 0 | 4000 | >1000 |
| CIN-CINv [J kg−1] | Convective Inhibition (using T and virtual T) | −100 | 0 | >−50 |
| LI-Liv [-] | Lifted Index (using T and virtual T) | −7 | 3 | <−3 |
| TT [-] | Total Totals | 40 | 60 | >50 |
| KI [-] | K-Index | 10 | 50 | >26 |
| SI [-] | Showalter Index | −7 | 4 | <−2 |
| DCI [-] | Deep Convective Index | 10 | 50 | >30 |
| Rain-Gauge Stations—ARPA Piemonte | Total Rainfall [mm] | ID |
|---|---|---|
| Gressoney-St-Jean–Lago Seebna (Valle del Lys, Aosta) | 643.3 | 1 |
| Trivero-Camparient (Val Sessera, Biella) | 570.6 | 2 |
| Lillianes-Granges (Valle del Lys, Aosta) | 567.2 | 3 |
| Boccioleto (Val Sesia, Vercelli) | 565.0 | 4 |
| Santuario di Oropa (Biella) | 509.5 | 5 |
| Carcoforo (Val Sesia, Vercelli) | 473.4 | 6 |
| Corio-Pian Audi (Val Malone, Torino) | 465.9 | 7 |
| Valstrona-Sambughetto (VCO) | 462.2 | 8 |
| Andrate-Alpe Pinalba (between Ivrea e Biella) | 460.4 | 9 |
| Montecrestese-Lago Larecchio (Valle Isorno, VCO) | 458.4 | 10 |
| N_Sim | Code | Type | MEANs | MEANr | SQMs | SQMr | BIAS_add | BIAS_mul | RMSE_add | RMSE_mul | AIS | SMAPE | CC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [-] | [-] |
| 1 | RaML_Sv0_Mt0_Co0_Sr0_Ta0_Bl0 | A | 190.21 | 263.38 | 66.07 | 125.77 | 73.18 | 11.05 | 138.43 | 23.38 | 246.04 | 0.45 | 0.907 |
| 2 | RaML_Sv0_Mt0_Co0_Sr0_Ta0_Bl1 | A | 226.23 | 263.38 | 94.89 | 125.77 | 37.15 | 4.99 | 131.48 | 24.06 | 197.68 | 0.44 | 0.894 |
| 3 | RaML_Sv0_Mt0_Co0_Sr0_Ta1_Bl1 | A | 244.25 | 263.38 | 33.53 | 125.77 | 19.13 | −1.86 | 121.03 | 23.22 | 165.24 | 0.4 | 0.912 |
| 4 | RaML_Sv0_Mt0_Co0_Sr0_Ta1_Bl3 | A | 259.42 | 263.38 | 38.33 | 125.77 | 3.96 | −4.76 | 114 | 23.31 | 146.03 | 0.38 | 0.921 |
| 5 | RaML_Sv0_Mt0_Co0_Sr0_Ta1_Bl5 | A | 228.47 | 263.38 | 25.6 | 125.77 | 34.91 | 0.9 | 129.05 | 23.52 | 188.38 | 0.43 | 0.905 |
| 6 | RaML_Sv0_Mt0_Co0_Sr0_Ta4_Bl3 | A | 259.6 | 263.38 | 38.31 | 125.77 | 3.78 | −4.76 | 117.37 | 23.79 | 149.7 | 0.39 | 0.916 |
| 7 | RaML_Sv0_Mt0_Co0_Sr1_Ta4_Bl3 | M | 410.71 | 263.38 | 133.32 | 125.77 | −147.33 | −30.49 | 204.67 | 41.63 | 424.12 | 0.5 | 0.912 |
| 8 | RaML_Sv0_Mt0_Co0_Sr1_Ta4_Bl1 | M | 362.72 | 263.38 | 123.74 | 125.77 | −99.33 | −21.55 | 181.11 | 36.47 | 338.46 | 0.46 | 0.891 |
| 9 | RaML_Sv0_Mt0_Co0_Sr0_Ta0_Bl3 | M | 361.89 | 263.38 | 105.08 | 125.77 | −98.51 | −22.05 | 152.57 | 33.08 | 306.21 | 0.43 | 0.927 |
| 10 | RaML_Sv0_Mt0_Co0_Sr0_Ta0_Bl5 | M | 280.82 | 263.38 | 76.19 | 125.77 | −17.43 | −7.88 | 136.16 | 27.57 | 189.04 | 0.43 | 0.891 |
| 11 | RaML_Sv0_Mt0_Co0_Sr0_Ta0_Bl11 | M | 411.28 | 263.38 | 125.88 | 125.77 | −147.9 | −30.49 | 190.34 | 39.87 | 408.6 | 0.5 | 0.932 |
| 12 | RaML_Sv0_Mt0_Co0_Sr0_Ta0_Bl12 | M | 370.35 | 263.38 | 103.15 | 125.77 | −106.97 | −23.95 | 155.51 | 33.98 | 320.41 | 0.44 | 0.93 |
| 13 | RaML_Sv0_Mt0_Co0_Sr0_Ta0_Bl13 | A | 255.12 | 263.38 | 28.98 | 125.77 | 8.26 | −4.25 | 119.93 | 24.09 | 156.53 | 0.4 | 0.912 |
| N_Sim | Code | Sim | Type | MEANs | MEANr | BIAS_add | BIAS_mul | RMSE_add | RMSE_mul | AIS | SMAPE | CC_2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [-] | [-] |
| 1 | RaML_Sv0_Mt0_Co0_Sr0_Ta1_Bl3 | warm_no_c | A | 259.42 | 263.38 | 3.96 | −4.76 | 114 | 23.31 | 146.03 | 0.38 | 0.921 |
| 2 | RaML_Sv0_Mt1_Co0_Sr0_Ta1_Bl3 | cold_no_c | A | 258.26 | 263.38 | 5.12 | −4.75 | 113.2 | 22.79 | 145.86 | 0.38 | 0.922 |
| 3 | RaML_Sv0_Mt0_Co1_Sr0_Ta1_Bl5 | warm_c | M | 270.33 | 263.38 | −6.95 | −7.25 | 127.27 | 26.59 | 168.06 | 0.42 | 0.9 |
| 4 | RaML_Sv0_Mt1_Co1_Sr0_Ta1_Bl5 | cold_c | M | 269.94 | 263.38 | −6.56 | −7.25 | 127.18 | 26.58 | 167.57 | 0.42 | 0.901 |
| Rain-Gauge Stations—ARPA Piemonte | Total Rainfall [mm] | Total Rainfall LUME 2D [mm] | BIAS [mm] | Relative BIAS [-] |
|---|---|---|---|---|
| Gressoney-St-Jean–Lago Seebna (Valle del Lys, Aosta) | 643.3 | 410 | −233.3 | −0.36 |
| Trivero-Camparient (Val Sessera, Biella) | 570.6 | 400 | −170.6 | −0.29 |
| Lillianes-Granges (Valle del Lys, Aosta) | 567.2 | 396 | −171.2 | −0.30 |
| Boccioleto (Val Sesia, Vercelli) | 565 | 310 (*) | −255 | −0.45 |
| Santuario di Oropa (Biella) | 509.5 | 290 (**) | −219.5 | −0.43 |
| Carcoforo (Val Sesia, Vercelli) | 473.4 | 345 | −128.4 | −0.27 |
| Corio-Pian Audi (Val Malone, Torino): | 465.9 | 320 | −145.9 | −0.31 |
| Valstrona-Sambughetto (VCO): | 462.2 | 275 | −187.2 | −0.39 |
| Andrate-Alpe Pinalba (between Ivrea e Biella) | 460.4 | 340 | −120.4 | −0.26 |
| Montecrestese-Lago Larecchio (Valle Isorno, VCO) | 458.4 | 323 | −135.4 | −0.29 |
| Topic | LUME 2D Implementation Strategies |
|---|---|
| IC and BC setup | Specified from the enlarged domain, BC functions of WVF; updated hourly. |
| Reanalysis and forecast modes setup | Reanalysis (using recorded RAOBS) and forecast (using forecasted RAOBS from global forecasting models). |
| Effect of DEM resolution on computations | Influence upslope–downslope flux; suggested resolution ≈ 1–2 km. |
| Spatial Extension of Computational Domain | Any, but the suggested regional scale is recommended (≈100,000 km2). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbate, A.; Apadula, F. LUME 2D: A Linear Upslope Model for Orographic and Convective Rainfall Simulation. Meteorology 2025, 4, 28. https://doi.org/10.3390/meteorology4040028
Abbate A, Apadula F. LUME 2D: A Linear Upslope Model for Orographic and Convective Rainfall Simulation. Meteorology. 2025; 4(4):28. https://doi.org/10.3390/meteorology4040028
Chicago/Turabian StyleAbbate, Andrea, and Francesco Apadula. 2025. "LUME 2D: A Linear Upslope Model for Orographic and Convective Rainfall Simulation" Meteorology 4, no. 4: 28. https://doi.org/10.3390/meteorology4040028
APA StyleAbbate, A., & Apadula, F. (2025). LUME 2D: A Linear Upslope Model for Orographic and Convective Rainfall Simulation. Meteorology, 4(4), 28. https://doi.org/10.3390/meteorology4040028







