Abstract
The twin problems of closure and dissipation have been barriers to the analytical solution of the Navier–Stokes equation for fluid flow by top-down methods for two centuries. Here, the statistical multifractal analysis of airborne observations is used to argue that bottom-up approaches based on the dynamic behaviour of the basic constituent particles are necessary. Contrasts among differing systems will yield scale invariant turbulence, but not with universal analytical solutions to the Navier–Stokes equation. The small number of publications regarding a molecular origin for turbulence are briefly considered. Research approaches using suitable observations are recommended.
1. Introduction
Turbulence has been used to describe motion in many systems where a fluid flow is evident. Water and air were historically the most apparent, but it has been applied to systems as large as giant astronomical molecular clouds, to galaxies, to stars, to magnetohydrodynamic systems such as solar winds, to the atmosphere, to the ocean, to rivers and to smaller systems such as those that exist in industrial facilities and in laboratories, in superconducting fluids and in biological cells.
The basic argument used here is that rather than taking a top-down approach, a bottom-up approach should be adopted. That implies knowing what the basic constituent particles are and using their dynamics to transition upscale to a flow.
Although Leonardo da Vinci employed the word ‘turbulenza’ to describe the flow of water in a stream, the initial successful attempt at the mathematical formulation of fluid flow was made by Navier [1]. Stokes later amended the formulation to produce the well-known Navier–Stokes equation [2]. At the time, the existence and behaviour of atoms and molecules was not known, so a top-down approach was unavoidable. Since we are concerned with meteorology, we concentrate on air, a gas composed of molecules, noting that the hydrogen-bonded structures in liquid water make the ocean different than the atmosphere, although both are turbulent.
The format of this article will be a text with embedded references, but introducing a small number of key equations, equivalences and figures located in the Discussion section below. This perspective can be short because few authors have considered a bottom-up approach to turbulence, particularly in the atmosphere.
2. Brief Historical Progression
The experiments of Reynolds [3] showed a transition from a laminar to a turbulent flow in viscous liquids forced down a pipe by a pressure gradient. That transition was the subject of much research, including the thesis work of Heisenberg [4]. Heisenberg’s theory supervisor, Sommerfeld, gave him the highest grade, while his experimental supervisor Wien gave him the lowest. A compromise gave Heisenberg a mediocre pass, whereupon he left to work for Born in Göttingen, remarking that turbulence was too difficult, a fortunate circumstance for the development of quantum theory. Chapman and Enskog approached the transport properties of gases from an atomic and molecular standpoint [5,6]. Their work did not extend to fluid flow. The fourth edition of Lamb’s book [7] introduced the term ‘vorticity’ to specify the spin of a local fluid element about its axis, a concept originated by Helmholtz [8]. Research starting with the Navier–Stokes equation continued for half a century, but even with numerical simulation, twin difficulties arose, from dissipation and from the closure problem, and the fact that the expression for the nth moment of a variable involves its (n + 1)th power. Chapman and Cowling [9] utilized the solution of the Maxwell–Boltzmann equations to derive transport functions for non-uniform gases. Alder and Wainwright [10] initiated the study of fluids via the computer integration of the motion of hard, elastic spheres, molecular dynamics. In the J. G. Kirkwood memorial issue of The Journal of Chemical Physics, Grad [11] considered the need for a molecular approach to gas dynamics. Alder and Wainwright continued their work [12,13] and showed, in a crucial development, that hydrodynamic behaviour emerged, as ‘ring currents’, in a thermalized population subject to a symmetry-breaking flux of energetic ‘molecules’ represented as hard elastic spheres. Vorticity was generated nonlinearly at the smallest possible scale and could propagate upscale in a self-sustaining manner.
The development of statistical multifractality for application to the atmosphere by Schertzer and Lovejoy was a significant event [14,15,16]. Their formulation of generalized scale invariance demonstrated that the formal equivalence between equilibrium statistical thermodynamic variables and their scaling equivalents in the Hamiltonian flux dynamics by a Legendre transform was more than a mathematical coincidence, it was a mapping [16]. When applied to the largely ‘horizontal’ airborne data collected in the lower stratosphere between 1987 and 2004, and the ‘vertical’ data collected via a dropsonde through the winter troposphere over the northeastern Pacific Ocean 2004, 2005 and 2006 [17], it vindicated the theory and yielded new results about atmospheric dimensionality and scaling [18,19].
Muriel [20,21] argued for a molecular origin of turbulence, even claiming an exact solution for the Navier–Stokes equation [22], a claim that did not find favour with the Clay Institute. The final sentence of the abstract reads “No turbulence is obtained from the solution”. Abramov [23] has argued that the rotational motion of molecules can cause turbulence in gases via the effect on intermolecular potentials. There have been calls to measure the rotational state of O2 and N2 in the atmosphere [17,18,19].
3. A Mechanism
We pursue the view that hydrodynamics has to be formulated from the bottom scales up, which means that the basic constituent particles, which are the photons, atoms, molecules, electrons, ions, or nucleons, are the starting point. In turn, that may imply there is no unique formulation of turbulence. One size does not fit all, the basic particles and their interaction with boundary conditions offer differing possibilities for different systems. Scale invariance is a feature common to many differing turbulent systems.
The application of Lovejoy and Schertzer’s statistical multifractal approach [16] to airborne observations [24,25] led to the conclusion that the correlation of the intermittency of temperature with the ozone photodissociation rate implied that local thermodynamic equilibrium was not attained in the lower stratosphere. An explanation was sought in Alder and Wainwright’s molecular dynamics calculations that hydrodynamic behaviours (‘ring currents’) emerged on very short timescales in a thermalized population of Maxwellian hard spheres subjected to a symmetry-breaking flux of such high-speed particles [13]. The statistical multifractal approach also offers scaling versions of entropy and Gibbs free energy [25], and when combined with the Langevin equation, points to a mechanism for turbulence in the air [18,19]. The persistence of molecular velocity after collision prevents instantaneous thermalization and breaks the continuous translational symmetry of a Maxwell–Boltzmann equilibrated gas. Rotational symmetries in real molecules [23,26], N2 and O2, will also break the continuous translational symmetry of any thermalized air. This view of the generation of turbulence implies effects on radiative transfer via spectral line shapes and, hence, dissipation via radiation to space. It implies that turbulence is associated with the operation of the Second Law of Thermodynamics. The Gibbs free energy enables the work that allows the emergent turbulence to propagate nonlinearly upscale. It will possess the directional variation that is observed in the turbulent structure and that is expected from the nature of molecular rotation and collisions. Laminar flow is unlikely to emerge from such conditions. The real atmosphere has more energy than numerical models which assume local thermodynamic equilibrium, as illustrated in Figure 3 of reference [19].
An unexpected result arising from the application of statistical multifractality to airborne data was the correlation between the intermittency of temperature with the ozone photodissociation rate and with temperature itself [24,25]. The excited photofragments were not thermalized immediately, but instead, the persistence of their velocity after collision [9] induced vorticity via the Alder–Wainwright mechanism [13], the nonlinearity of which enabled its propagation upscale in the form of turbulence.
The importance of the boundary conditions is evidenced by comparing the atmosphere’s turbulence with that in giant molecular clouds, which are vastly larger, much colder, much more dilute and in which gravity plays a different role [27,28]. Nevertheless, fractality is evident and characterizes the observed turbulence. Its intermittency, the concentration of energy in local structures, is evident both astronomically and in Earth’s atmosphere [29,30]. The scaling exponents in the two milieux show that the contrasting physical processes produce different manifestations of turbulence. It is unrealistic to expect the integration of the Navier–Stokes equation for fluid motion to produce a universal solution for turbulence, given the differing mechanisms of dissipation.
The Langevin equation has been used to interpret the molecular dynamical approach to atmospheric turbulence [18]. The emergent hydrodynamic behaviour exhibited by Alder and Wainwright [13] is viewed as organization sustained by the most energetic molecules, while the maintenance of an operational temperature by the majority of the near-average molecules is dissipation. That is the reverse of the meteorological convention that means are organized while eddies are dissipative. The most energetic molecules in the probability distribution carry the Gibbs free energy that provides the work that sustains the flow, while the more numerous, average molecules define an operational temperature, which does not, however, equal the theoretical temperature of the equilibrium of the Maxwell–Boltzmann distribution [18,19].
Symmetry breaking is an important factor in the mechanism of turbulence and its generation [18,19,31]. Symmetry is also involved in the effect of boundary conditions. When studying laminar flow in a cylindrical pipe, Couette flow in a channel, the flow over an aerofoil, or over the planetary surface the solid boundaries impose a symmetry on the fluid that it does not naturally have. The transition from a laminar to a turbulent flow is a manifestation of that, and of the lack of sensitivity and resolution in the examining instruments. All angles occur in the scattering from molecular collisions, but are rarely considered in experimental or theoretical studies of turbulence. The numerical modelling and diagnostic approaches that employ such techniques as Fourier analysis and large eddy simulation seek to impose symmetries on the air that it does not have, respectively, sine waves and cubes.
4. Discussion
The discussion will centre around two equations, a table and three key figures which have been generated in analysing atmospheric observations [9,13,18,24,25].
Chapman and Cowling [5] formulated an equation describing the persistence of molecular velocity after collision:
The persistence ratio ϖ12 is the ratio of the mean velocity after collision to what it was prior to the collision between molecules of masses m1 and m2. If m1 = m2, then ϖ12 = 0.406, but in the general case for m1 ≠ m2, the more massive molecule will be decelerated less than the lighter one.
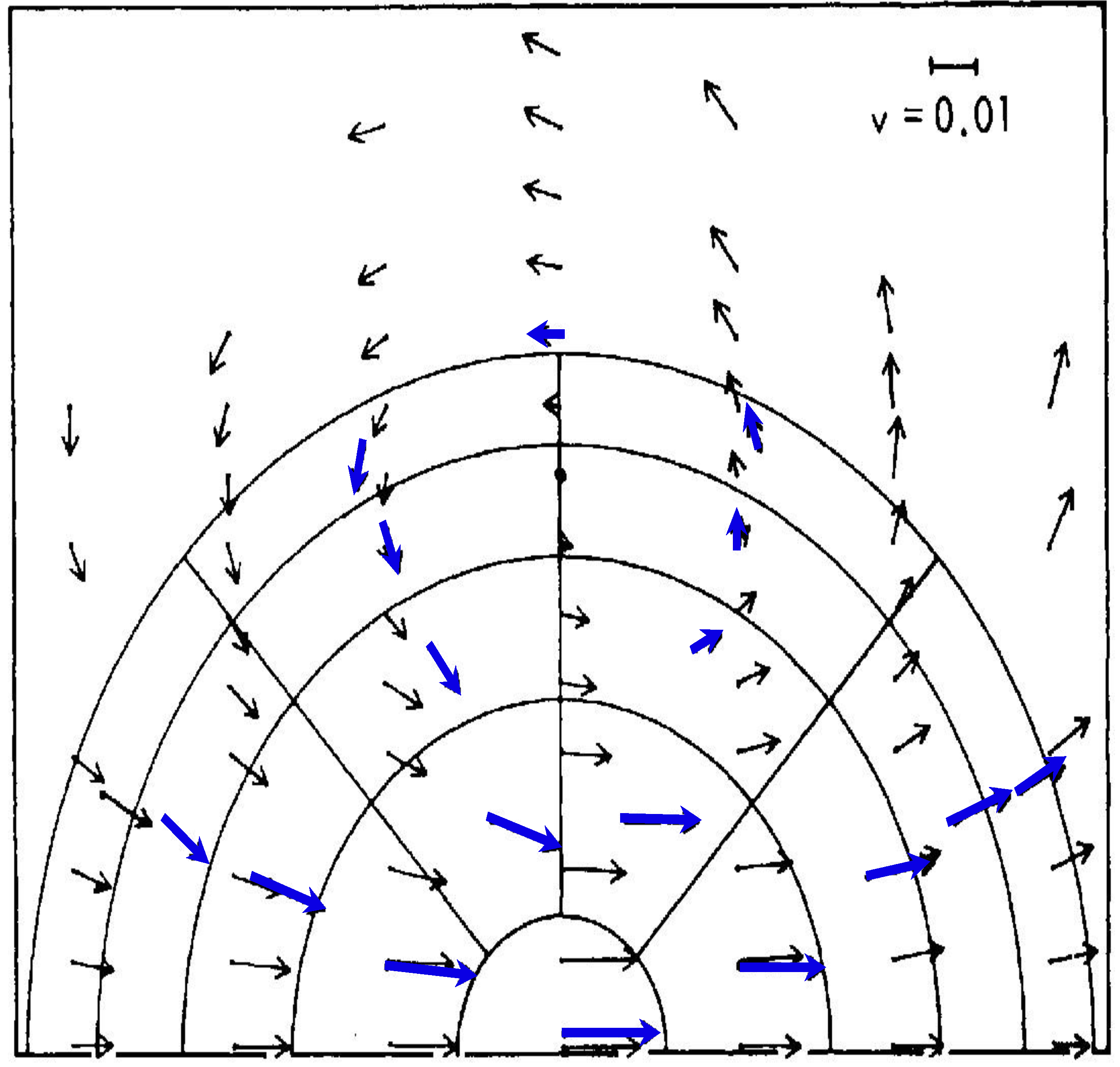
This process, when applied to the Alder and Wainwright mechanism [13], will break the continuous translational symmetry of a sample of an equilibrated Maxwell–Boltzmann gas, especially that of an inhomogeneous gas like air, which is never isotropic or at equilibrium. Alder and Wainwright discovered, via a molecular dynamics calculation, that hydrodynamic behaviour was induced in an equilibrated population of ‘billiards’ on very short time and space scales when subjected to a symmetry-breaking energetic flux of such elastic spheres. See Figure 1. These ‘ring currents’ are what a meteorologist would call vortices; the generation of vorticity thus occurs on the smallest scales and exhibits scaling behaviour [32]—it is emergent turbulence. By virtue of the nonlinearity of the mechanism, it can propagate upscale. The closure problem is automatically avoided. Dissipation is automatically included via the action of the energetically near-average molecules in defining an operational temperature, which, in the atmosphere, provide dissipation via radiation to space. It is why large-scale global models can successfully integrate the Navier–Stokes equation for weather forecasting—provided they are continually fed with observations. In free-running mode, they will have difficulties [19]. The absence of local thermodynamic equilibrium also affects, in principle, the line shapes of the infrared active molecules—carbon dioxide, water vapour and its dimer, nitrous oxide, methane, ozone, CFCs, HCFCs—via collisional effects.
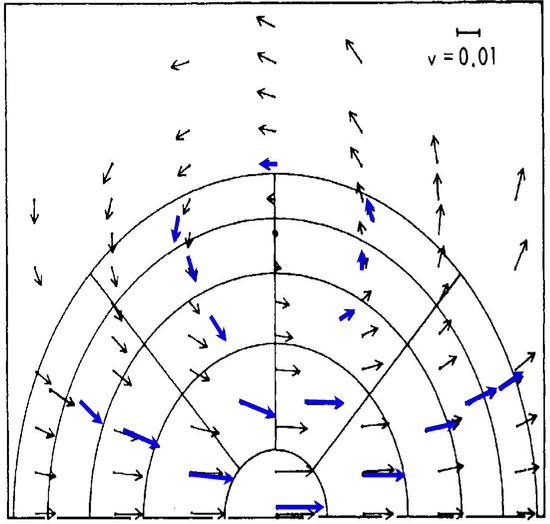
Figure 1.
The emergence of ring currents, vortices, in a thermalized population of 220 Maxwellian elastic atomic spheres subjected to a symmetry–breaking flux of energetic atoms. The molecular dynamics simulation was originally performed by Alder and Wainwright [13]. The blue arrows are averages of the atom vectors after 9.9 collisions, the black arrows are from a Navier–Stokes equation integration. Later simulations showed disagreements between the two approaches.
The fluctuating variability in atmospheric observations [17,18,19] led to the application of the generalized scale invariance pioneered by Schertzer and Lovejoy [14,15] and the statistical multifractality of Lovejoy and Schertzer’s work [16]. The results are summarized in Table 1. The equivalences between statistical thermodynamical and scale invariant quantities are not merely formal but are mappings via a Legendre transform between the energy in the former and its Hamiltonian flux dynamics in the latter.

Table 1.
The equivalence between statistical thermodynamic and scaling variables.
The variables are obtained as follows. q defines the qth order structure function of the observed quantity. The scaling exponent K(q) is derived from the slope of a log–log plot [25]. Equation (2) expresses the relation of the Hurst exponent H to the Gibbs free energy equivalent.
The examination of energy E in terms of a scale ratio produces an expression for the fractal co-dimension c(γ). C1 is the co-dimension of the mean, characterizing the intensity of the intermittency. The Lévy exponent α characterizes the generator of the intermittency, which is the logarithm of the turbulent flux; for a real system, its value may not be confined to the theoretical range. Means converge but the variance does not, a result expressed as 2.0 > α >1.5.
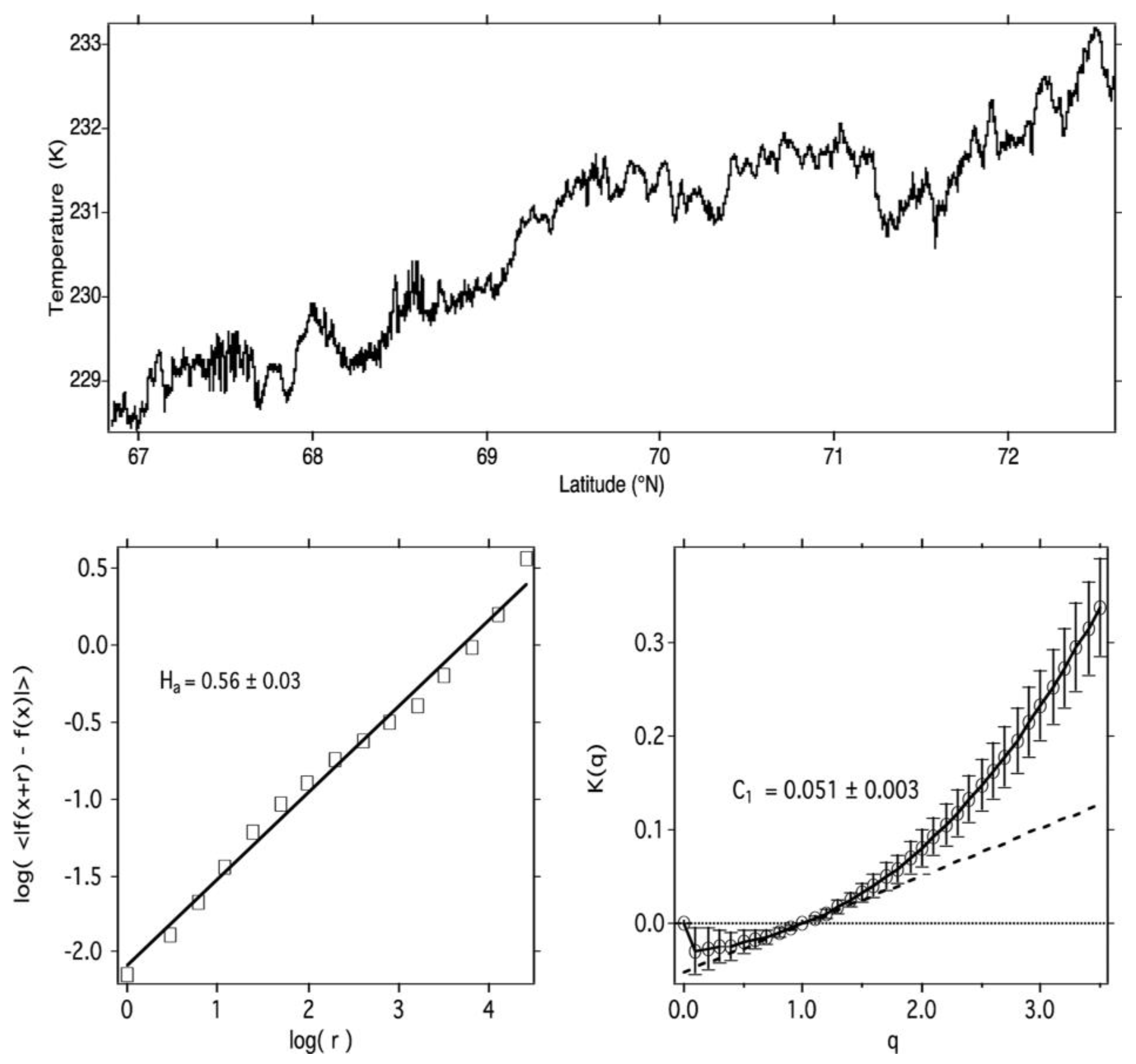
The calculation of the intermittency of temperature C1(T) is exemplified in Figure 2. The implication is that local thermodynamic equilibrium is not obtained in the lower stratosphere, possibly extending to the entire atmosphere above and below [19]. The correlation between the intermittency of temperature C1(T) with both ozone photodissociation rate J[O3] and with the temperature itself is shown in Figure 3. The scale invariance associated with turbulence is revealed and enables that condition [14,15,16,17,18,19]. Note that any change in dynamical phase, say, between the lower stratosphere and the troposphere below or the mesosphere above, would show up as a change in the slope of the log–log plot.
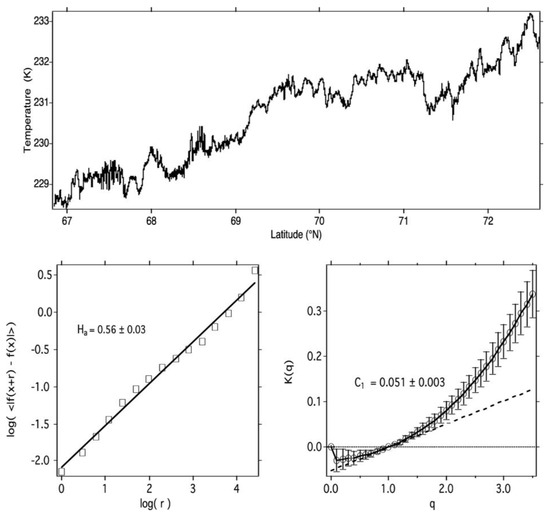
Figure 2.
(Upper): The temperature record observed from the ER-2 during POLARIS at approximately 55 mbar, 19970506 (yyyymmdd format) in low wind speed conditions. (Lower left): The log–log graph from which H(T) was calculated, corresponding with the 5/9 theoretical value of statistical multifractality. (Lower right): The graph from which C1(T), the intermittency of temperature, was calculated using scaling variables K(q) and q, see Equation (2).
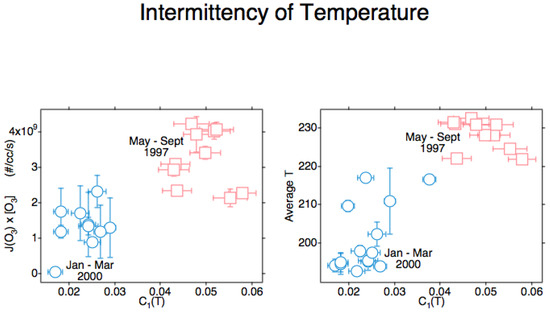
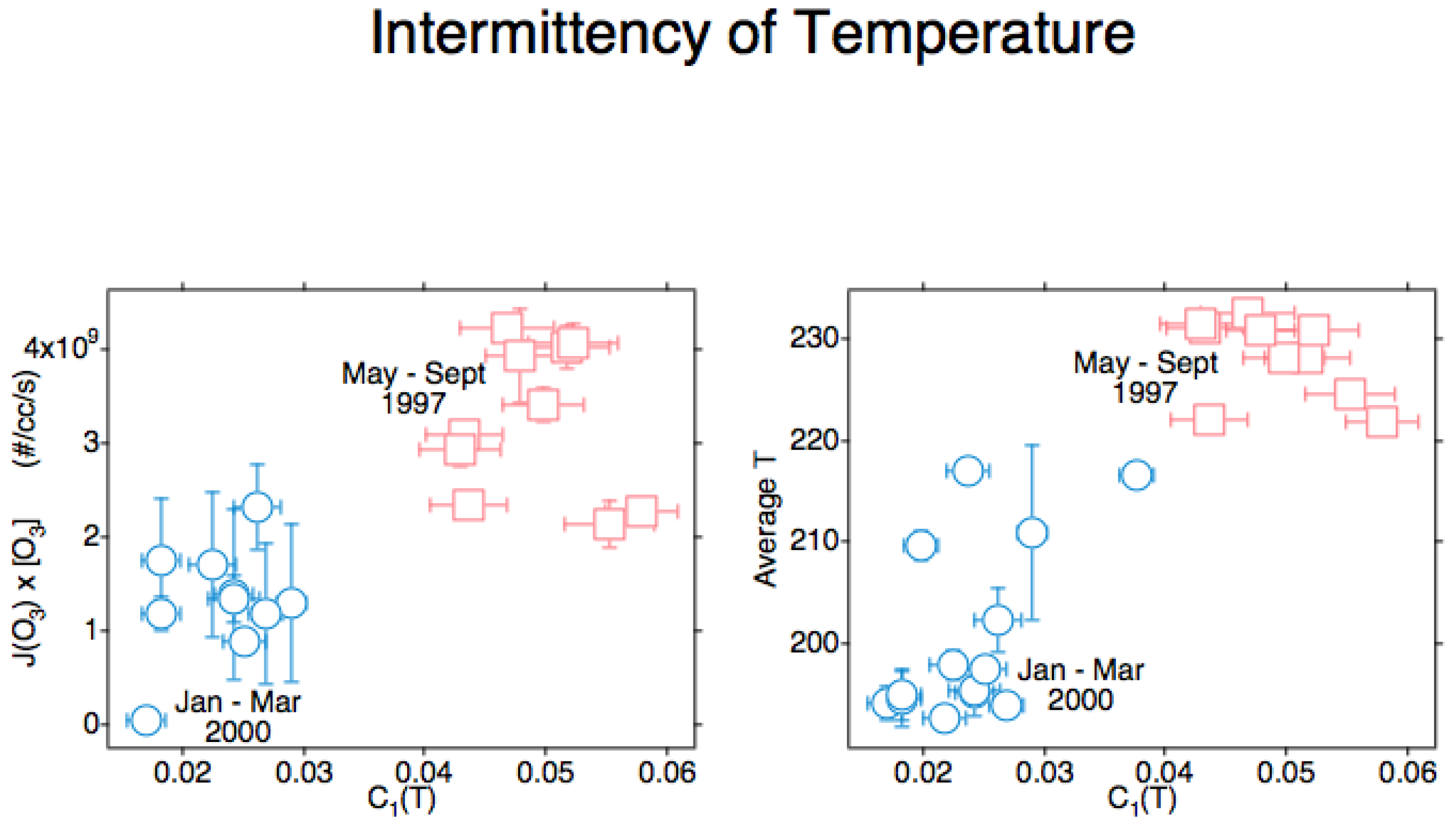
Figure 3.
These results are from Arctic flights [19]. J[O3] is averaged along the flight segment concerned and is shown on the ordinate of the left plot, with T averaged in the same way and displayed on the right plot. The abscissa on both shows the intermittency of T, calculated from the relevant lower right graph in Figure 2. The vertical and horizontal bars are standard deviations. The nonconvergence of variance and the changes of air mass within the time periods account for the scatter; nevertheless, the effect is clear and makes physical sense [17,18,19,24].
The way this mechanism is envisaged in the stratosphere is that the translationally hot molecules created by ozone photodissociation pile up a higher-number density ahead of themselves, leaving lower-velocity molecules at lower number density behind. The average molecules move to eradicate the gradient, creating ring currents as they do so. The higher-number density ahead of the fast molecules will experience higher ozone photodissociation rates, so enabling the acceleration and propagation of the emergent hydrodynamic flow. This accounts for the correlation seen in Figure 3. At the same time, the action of the more numerous, average molecules ensures thermodynamic behaviour by establishing an operational temperature. Those average molecules will emit infrared radiation appropriate to their state and, in doing so, ensure that the Second Law of Thermodynamics is obeyed by the atmosphere.
The statistical multifractal analysis also applies to atmospheric aerosols as well as to air molecules [33]. Such particles span the mesoscale gap between microscopic and macroscopic scales [34]. Turbulent flow is probably manifested both two-dimensionally in the surface film and three-dimensionally in the interior.
Future research should address the translational and rotational state of the N2 and O2 molecules, from the surface to the mesosphere. In situ observations over the same range would assess whether statistical multifractal analysis would provide scaling exponents capable of addressing the cold bias evident in many free-running models of the atmosphere. If N2 and O2 are not instantly equilibrated, their rotation will ensure that the directionality of the emergent hydrodynamic flow will vary through the whole 360o, as frequently observed in turbulence. The real atmosphere will have more energy than models that assume local thermodynamic equilibrium.
The thermodynamic form of multifractality is discussed in [16], Chapter 5.1, and the scaling from atomic scale-up is examined in [32]. A recent perspective can be found in [35], and for hydromagnetic systems, in [36]. An examination of Stokes’s Law at different molecular scales has appeared very recently [37].
5. Conclusions
Turbulence is a state arising from the dynamics of the basic constituent particles of a fluid medium. In the atmosphere, that is nitrogen and oxygen molecules subject to an influx of solar photons. In other systems composed differently and where gravity and temperature interact differently, scale invariant turbulence is still manifested, but not with the same scaling exponents. The turbulence characterized in this way is argued to be consistent with the statistical multifractal formulation of energy, entropy and Gibbs free energy and, hence, is involved in the action of the Second Law of Thermodynamics. In principle, the Navier–Stokes equation can be solved from the bottom up, but not from the top down. The problems of closure and dissipation are automatically avoided.
Funding
This research received no external funding.
Data Availability Statement
The data used are available on the NASA Airborne Database https://earthdata.nasa.gov/esds/impact/admg/theairborne-inventory (accessed on 5 June 2021).
Acknowledgments
Many scientists, engineers, technicians and aircrew contributed to the observations underlying this paper. Acknowledgements can be found in references [17,18,19,25,31,33].
Conflicts of Interest
The author declares no conflicts of interest.
References
- Navier, C.l.M.H. Mémoire sur les lois du mouvement des fluides. Mém. Acad. R. Sci. 1823, 6, 389–440. [Google Scholar]
- Stokes, G.G. On some cases of fluid motion. Trans. Camb. Phil. Soc. 1843, 8, 105–137. [Google Scholar]
- Reynolds, O. On the dynamical theory of turbulent incompressible viscous fluids and the determination of the criterion. Philos. Trans. R. Soc. Lond. A 1894, 186, 123–161. [Google Scholar]
- Heisenberg, W. On the Stability and Turbulence of Liquid Currents. Ph.D. Thesis, Munich University, Munich, Germany, 1923. [Google Scholar]
- Chapman, S. On the law of distribution of velocities, and on the theory of viscosity and conduction, in a non-uniform simple monatomic gas. Philos. Trans. R. Soc. Lond. 1916, 216, 279–348. [Google Scholar]
- Enskog, D. Inaugural Dissertation. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 1917. [Google Scholar]
- Lamb, H.H. Hydrodynamics, 4th ed.; Cambridge University Press: Cambridge, UK, 1916; 708p. [Google Scholar]
- Von Helmholtz, H. On integrals of the hydrodynamical equations, which express vortex-motion. Philos. Mag. 1867, 33, 485–512, Translation by P. G. Tait of 1858 German original. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases, 3rd ed.; Cambridge University Press: Cambridge, UK, 1970; pp. 93–96+327, 1st edition 1939. [Google Scholar]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Grad, H. On molecular chaos and the Kirkwood superposition. J. Chem. Phys. 1960, 33, 1342–1348. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Studies on molecular dynamics. II. Behaviour of a small number of elastic spheres. J. Chem. Phys. 1960, 33, 1439–1451. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Decay of the velocity autocorrelation function. Phys. Rev. A 1970, 1, 18–21. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Generalized scale invariance in turbulent phenomena. Physicochem. Hydrodyn. 1985, 6, 623–635. [Google Scholar]
- Schertzer, D.; Lovejoy, S. Physical modeling and analysis of rain and clouds by anisotropic scaling multiplicative processes. J. Geophys. Res. D 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. The Weather and Climate: Emergent Laws and Multifractal Cascades; Cambridge University Press: Cambridge, UK, 2013; Chapter 5.1; pp. 127–128. [Google Scholar]
- Tuck, A.F. Atmospheric Turbulence: A Molecular Dynamics Perspective; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Tuck, A.F. Scaling up: Molecular to meteorological via symmetry breaking and statistical multifractality. Meteorology 2022, 1, 4–28. [Google Scholar] [CrossRef]
- Tuck, A.F. Air temperature intermittency and photofragment excitation. Meteorology 2023, 2, 445–463. [Google Scholar] [CrossRef]
- Muriel, A.; Jirkovsky, L.; Dresden, M. A quantum model for the onset of turbulence. Phys. D Nonlinear Phenom. 1996, 94, 103–115. [Google Scholar] [CrossRef]
- Muriel, A. A molecular basis for the onset of turbulence. J. Vac. Sci. Technol. A 2009, 27, 315–320. [Google Scholar] [CrossRef]
- Muriel, A. An exact solution of the 3-D Navier-Stokes equation. Results Phys. 2011, 1, 2–18. [Google Scholar] [CrossRef]
- Abramov, R. Turbulence via intermolecular potential: Uncovering the origin. Commun. Nonlinear Sci. 2023, 130, 224–226. [Google Scholar] [CrossRef]
- Tuck, A.F.; Hovde, S.J.; Richard, E.C.; Gao, R.-S.; Bui, T.P.; Swartz, W.H.; Lloyd, S.A. Molecular velocity distributions and generalized scale invariance in the turbulent atmosphere. Faraday Discuss 2005, 130, 181–193. [Google Scholar] [CrossRef]
- Tuck, A.F. Proposed empirical entropy and Gibbs energy based on observations of scale invariance in open nonequilibrium systems. J. Phys. Chem. A 2017, 121, 6620–6629. [Google Scholar] [CrossRef]
- Frank, S.A. Common probability patterns arise from simple invariances. Entropy 2016, 18, 192. [Google Scholar] [CrossRef]
- Falgarone, E.; Hily-Blant, P.; Pety, J. Small-scale intermittency of the dissipation of interstellar turbulence. In Proceedings of the Submillimeter Astrophysics and Technology: A Symposium Honoring Thomas G. Phillips, ASP Conference Series, Pasadena, CA, USA, 23–24 February 2009; Volume 417. [Google Scholar]
- Lesaffre, P.; Falgarone, E.; Hily-Blant, P. Intermittency of turbulence in magneto-hydrodynamical simulations and in the cosmos. Atmosphere 2024, 15, 211. [Google Scholar] [CrossRef]
- Lovejoy, S.; Tuck, A.F.; Hovde, S.J.; Schertzer, D. Is isotropic turbulence relevant in the atmosphere? Geophys. Res. Lett. 2007, 34, L15802. [Google Scholar] [CrossRef]
- Lovejoy, S.; Tuck, A.F.; Hovde, S.J.; Schertzer, D. Do stable atmospheric layers exist? Geophys. Res. Lett. 2008, 35, L01802. [Google Scholar] [CrossRef]
- Tuck, A.F. Theoretical chemistry and the calculation of the atmospheric state. Atmosphere 2021, 12, 727. [Google Scholar] [CrossRef]
- Kadau, K.; Barber, J.L.; Germann, T.C.; Holian, B.L.; Alder, B.J. Atomistic methods in fluid simulation. Philos. Trans. R. Soc. A 2012, 368, 1547–1560. [Google Scholar] [CrossRef]
- Tuck, A.F. Gibbs free energy and reaction rate acceleration in and on microdroplets. Entropy 2019, 21, 1044. [Google Scholar] [CrossRef]
- Laughlin, R.B.; Pines, D.; Schmalian, J.; Stojkovic, B.P.; Wolynes, P. The middle way. Proc. Natl. Acad. Sci. USA 2000, 97, 32–37. [Google Scholar] [CrossRef] [PubMed]
- Alberti, T.; Benzi, R.; Carbone, V. Why (still) studying turbulence in fluids and plasmas? Perspect. Earth Space Sci. 2023, 4, e2023CN000215. [Google Scholar] [CrossRef]
- Carbone, V.; Sorriso-Valvo, L.; Veltri, P. Evidence of extended self-similarity in hydromagnetic turbulence. Europhys. Lett. 2009, 88, 25001. [Google Scholar] [CrossRef]
- Acharya, S.; Bagchi, B. Exploration of Stokes hydrodynamic law at molecular length scales. J. Chem. Phys. 2024, 160, 174502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).