A Library of 77 Multibody Solar and Extrasolar Subsystems—A Review of Their Dynamical Properties, Global Mean-Motion Resonances, and the Landau-Damped Mean Tidal Fields
Abstract
1. Introduction
- (a)
- Six Laplace resonances, including the famous Galilean LR (Section 3.1, Figures 1–5).
- (b)
- Seven global solar-system MMRs and our local terrestrial MMR (Section 3.2, Figures 6–10).
- (c)
- Sixty-three extrasolar non-LR MMRs with 2–9 orbiting planets (Section 3.3,Figures 11–18).
- 1.
- Classical Laplace resonances.
- 2.
- Solar-system: Gaseous giant planets.
- 3.
- Solar-system: Terrestrial planets.
- 4.
- Solar-system: Satellite systems.
- 5.
- Exosystems with 2–9 planets and no classical LRs.
- 6.
- Commonly-occurring triple MMR chains.
- 7.
- Tidal-field wavelengths and theoretical Landau wavelengths [16].
- 8.
- Extrasolar dwarf planets with surface gravities m [35].
- 9.
- Bodies on or near the so-called “critical orbital period” of each system [16].
- 10.
- Summary of the longest global MMR chains and the geometric sequences [24].
- 11.
- Beyond the classical LRs: Summary of important groups of triple MMR chains.
- 12.
- A criterion for the absence of librations in triple MMR chains.
2. Modeling Assumptions and Adopted Constraints
- 1.
- The most massive (and most inert) body is assigned to the 1:1 MMR at the “center” of the MMR chain.
- 2.
- In the few cases where the most massive body is too distant from the group of the other bodies, the most massive body of the group is assigned to the 1:1 MMR for a better look at the resonant chain (e.g., K-90, K-176, K-254).
- 3.
- If the masses of the bodies are not known, then the largest body is assigned to the 1:1 MMR. When mass information will be obtained, the adopted global MMR chain can be easily rescaled if necessary.
- 4.
- Distant outer bodies (say, beyond the 5:1 MMR) are assigned only to principal exterior MMRs of the form k:1, where is an integer.
- 5.
- Inner bodies orbiting near the host (say, inward of the 1:5 MMR) are also assigned only to principal interior MMRs of the form 1:k, where is an integer.
- 6.
- Rational secondary MMRs of the form k:ℓ with integer are limited, as much as possible, to single-digit values of k and ℓ, i.e., . Important exceptions in this case are some geometric MMR sequences (e.g., K-444) and some distant MMRs disconnected from the inner compact chains (e.g., 14:5 for K2-268 f and HD 191939 g that are obviously displaced inward from 3:1 for some unknown reason).
- 7.
- When peculiar fractions appear to be necessary in long MMR chains, the MMRs are fitted by a single denominator, if possible (see, e.g., the MMR chain (1:3:13:40: in GJ 163).
- 1.
- 2.
- 3.
- The nearest neighbors of the most massive body should be separated from it by a distance of at least . Low-mass bodies may, however, be separated by a distance of only .
- 4.
- The local Landau wavelength of each body i (, where is the body’s Hill radius) should not overlap with the wavelengths of its nearest neighbors.
- 5.
- 6.
- The mean tidal field is expected to show a minimum at the location of the central host. In some systems, this precise condition is not achieved (e.g., the Galilean moons and TRAPPIST-1 (TR-1) shown below); then, the actual wavelength is expected to be somewhat different than our best-fit value, and the orbiting bodies are by all means displaced off of the actual minima of their tidal potential troughs.
3. Library Setup and Details
- 1.
- Central host mass , radius , and surface gravity .
- 2.
- Orbiting-body periods , semimajor axes , masses , radii , and surface gravities .
- 3.
- Orbiting-body period ratios , nearest global MMRs, and their relative deviations.
- 4.
- Subsystem critical orbital period [16] and whether a body is orbiting to within <8%.
- 5.
- Theoretical Landau wavelength and empirical wavelength of the mean tidal field [16].
- 6.
- Orbiting-body Hill radii and local Landau wavelengths .
- 7.
- For each pair of adjacent orbiting bodies i and , a comparison between and . It is generally expected that the adjacent local Landau wavelengths should not overlap (certainly not substantially), viz.
- 8.
- Pairs of bodies in which condition (2) is violated (marginally or decidedly) are noted by *** in the Output.txt files. The systems that show clear violations should be revisited in future studies. The systems that show “marginal” overlaps are not considered as cause for concern.
- 9.
- Certain issues and peculiarities encountered during modeling are noted under the heading “Needs more work” in the following 21 Output.txt files of the library: 55 Cnc, GJ 163, HD 20781, HD 108236, HD 158259, HR 8799, K-11, K-33, K-36, K-55, K-80, K-102, K-150, K-238, K-254, K-292, K-363, K-1542, K2-384, TOI-270, Teegarden’s Star (TS).
- 10.
- In particular, peculiar, or at least unusual, MMR chains are found in the following 18 systems (see the corresponding files System_Name.m and System_Name.eps): 12 also found in the preceding list, GJ 163, HD 108236, K-11, K-33, K-36, K-80, K-238, K-292, K-363, K-1542, TOI-270, TS; and additionally, HD 191939, K-32, K-154, K2-38, K2-268, TOI-700.
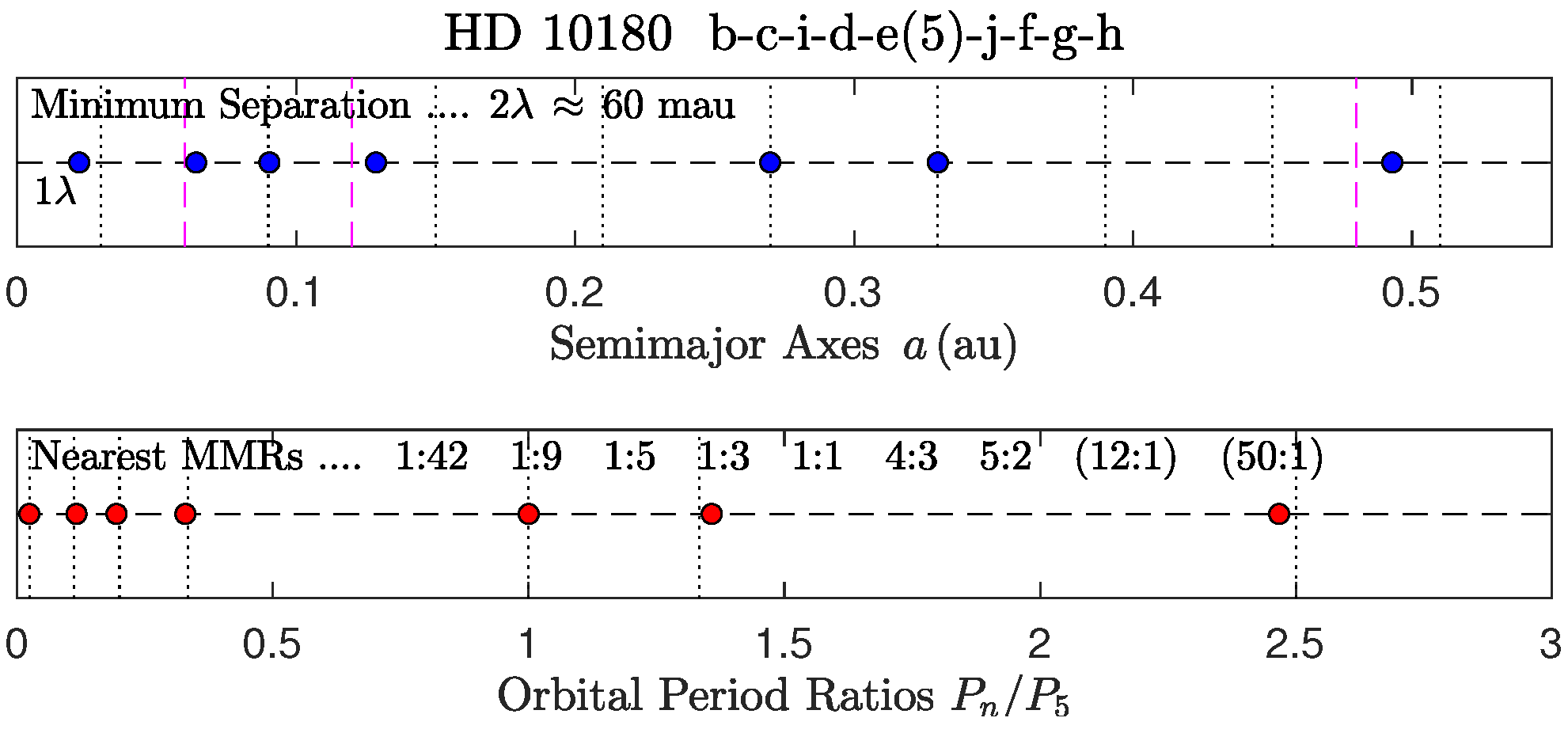
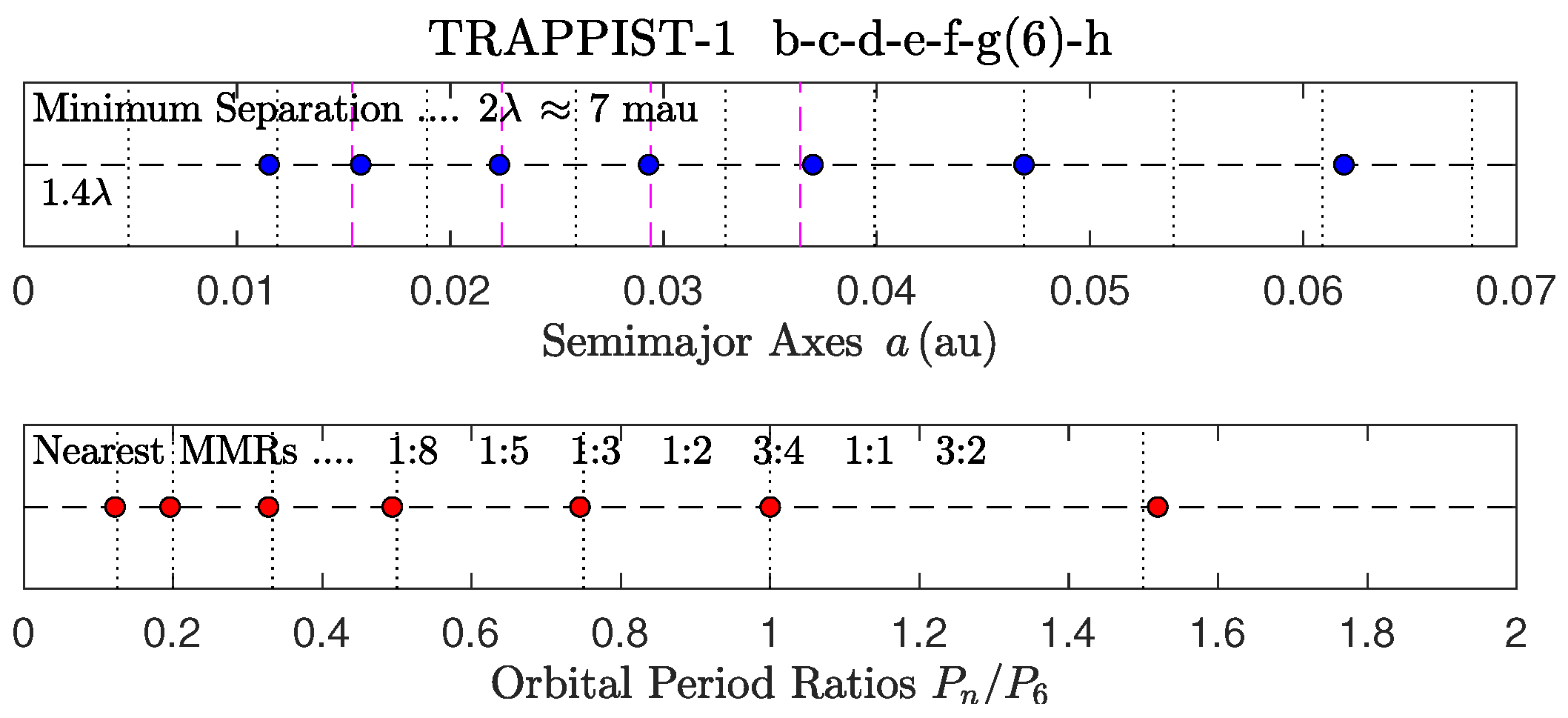
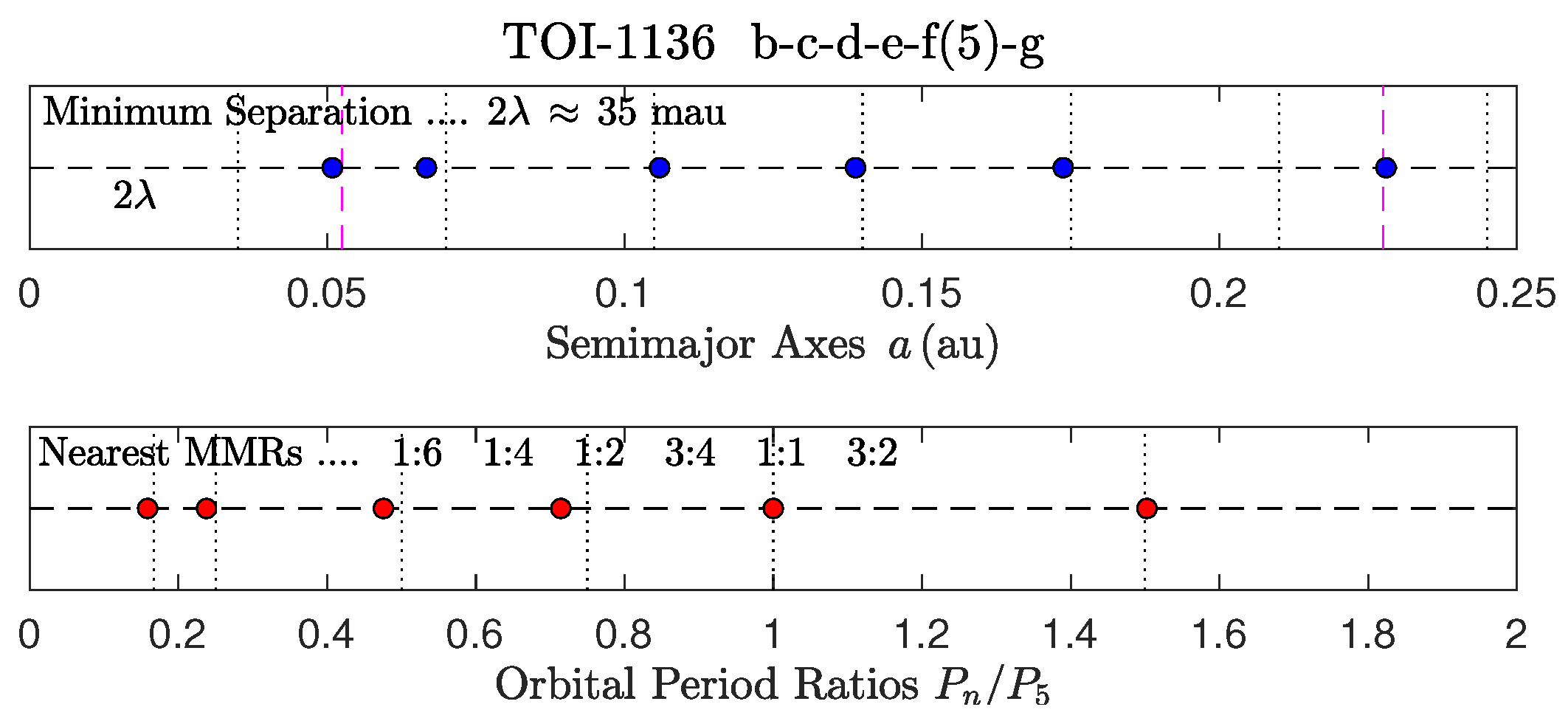
- 1.
- The title displays the names of the orbiting bodies.
- a.
- A number in parentheses denotes the radial location (n) of the most massive body.
- b.
- The names of solar-system bodies are abbreviated by their initials.
- c.
- Names of bodies not shown in the plots are enclosed in parentheses.
- 2.
- The top frame shows the spatial distribution of semimajor axes.
- a.
- The empirically determined value of “Minimum Separation” is displayed.
- b.
- The value of is determined from the most massive body and its neighbors [16].
- c.
- Vertical dotted lines are drawn in intervals of .
- d.
- Vertical dashed lines are midlines of the corresponding intervals.
- e.
- Blue circles denote the semimajor axes of the orbits.
- 3.
- The bottom frame shows the distribution of orbital-period ratios.
- a.
- The nearest global MMRs are displayed in k:ℓ form.
- b.
- Nearest MMRs to bodies not shown in the plots are enclosed in parentheses.
- c.
- Presence of a Laplace resonance in the MMR chain is indicated by the symbol (LR).
- d.
- Vertical dotted lines denote the precise locations of the nearest MMRs.
- e.
- Red circles denote the normalized orbital periods .
- f.
- The normalizing period is , where n is specified in item 1a above.
3.1. Laplace Resonances: The Galilean LR and the 5 Extrasolar LRs
- 1.
- These 6 LRs have also been discussed extensively in Ref. [23].
- 2.
- 3.
- 4.
- In K-176, the most massive planet of the LR (planet d) is assigned to the 1:1 MMR.
- 5.
- SI units of Mm ( m) and Gm ( m) are used for the Galilean-moon subsystem.
- 6.
- Units of au and mau ( au) are used for the extrasolar systems.
- 7.

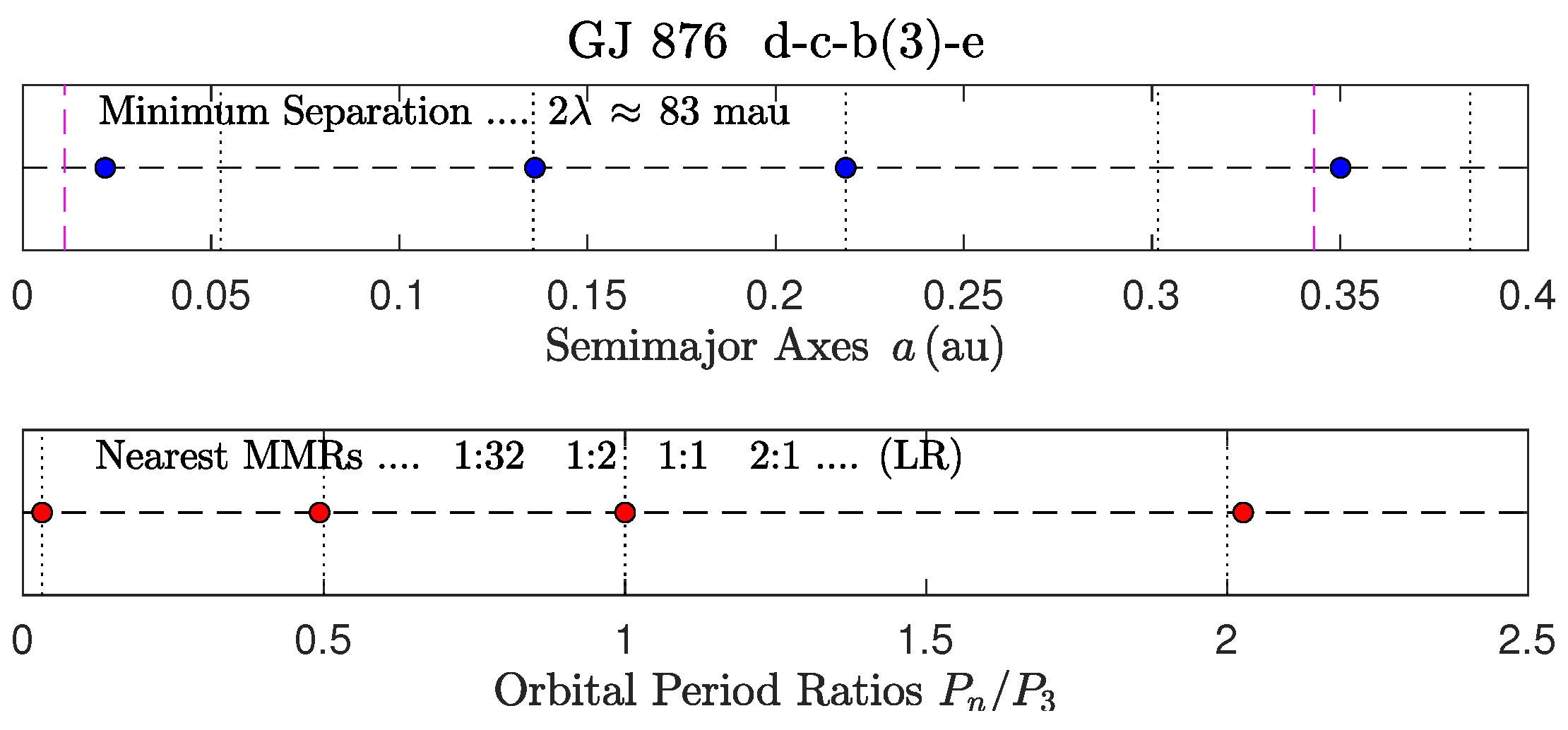
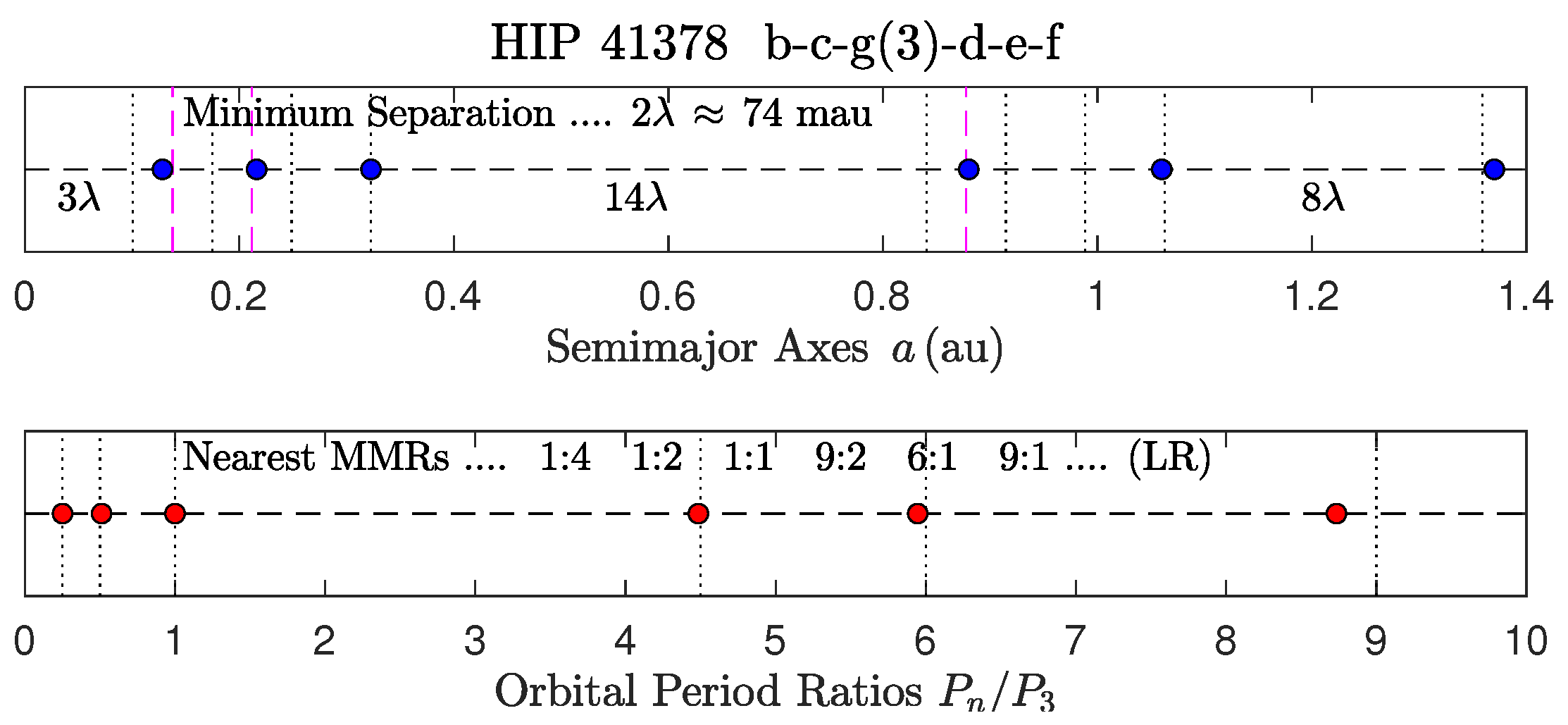
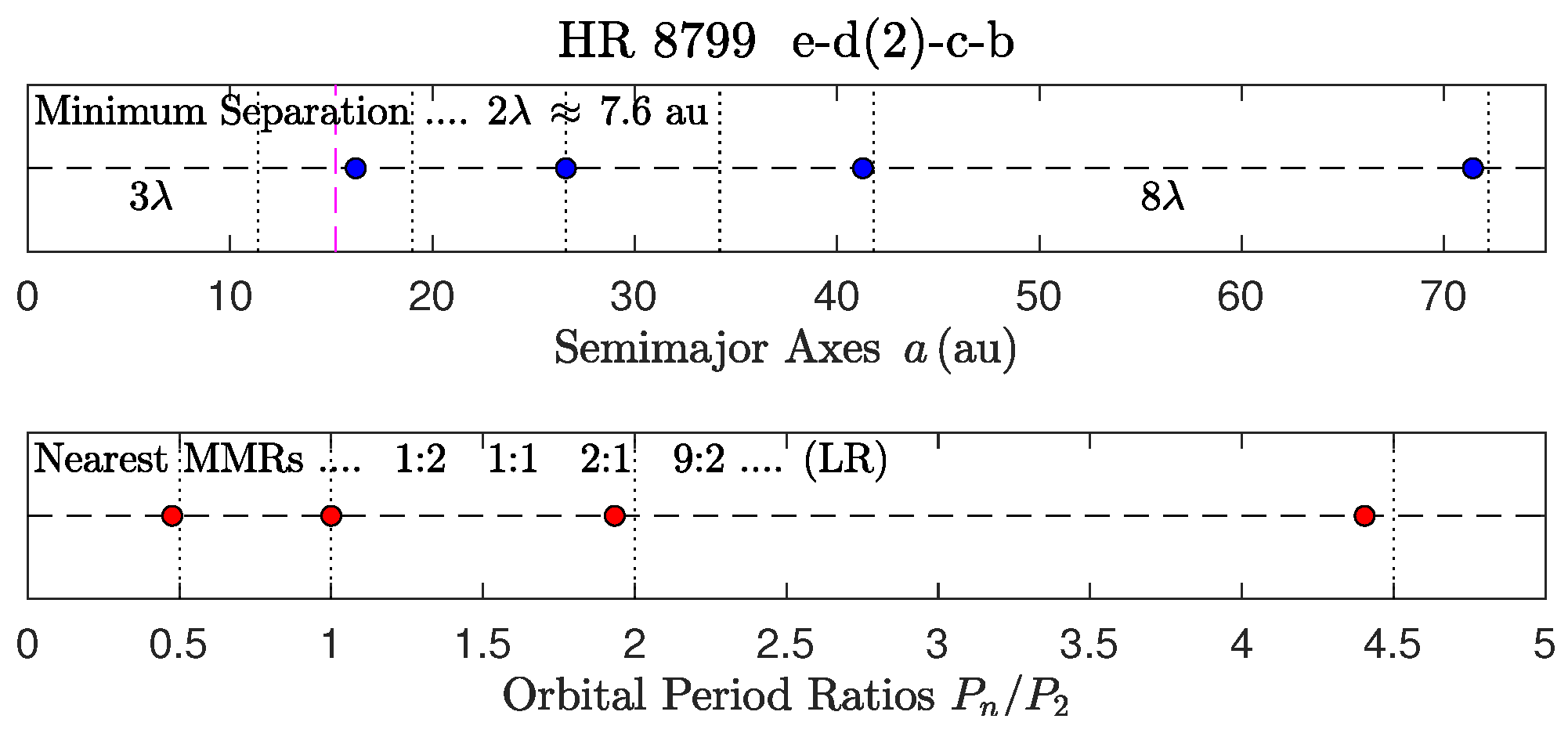
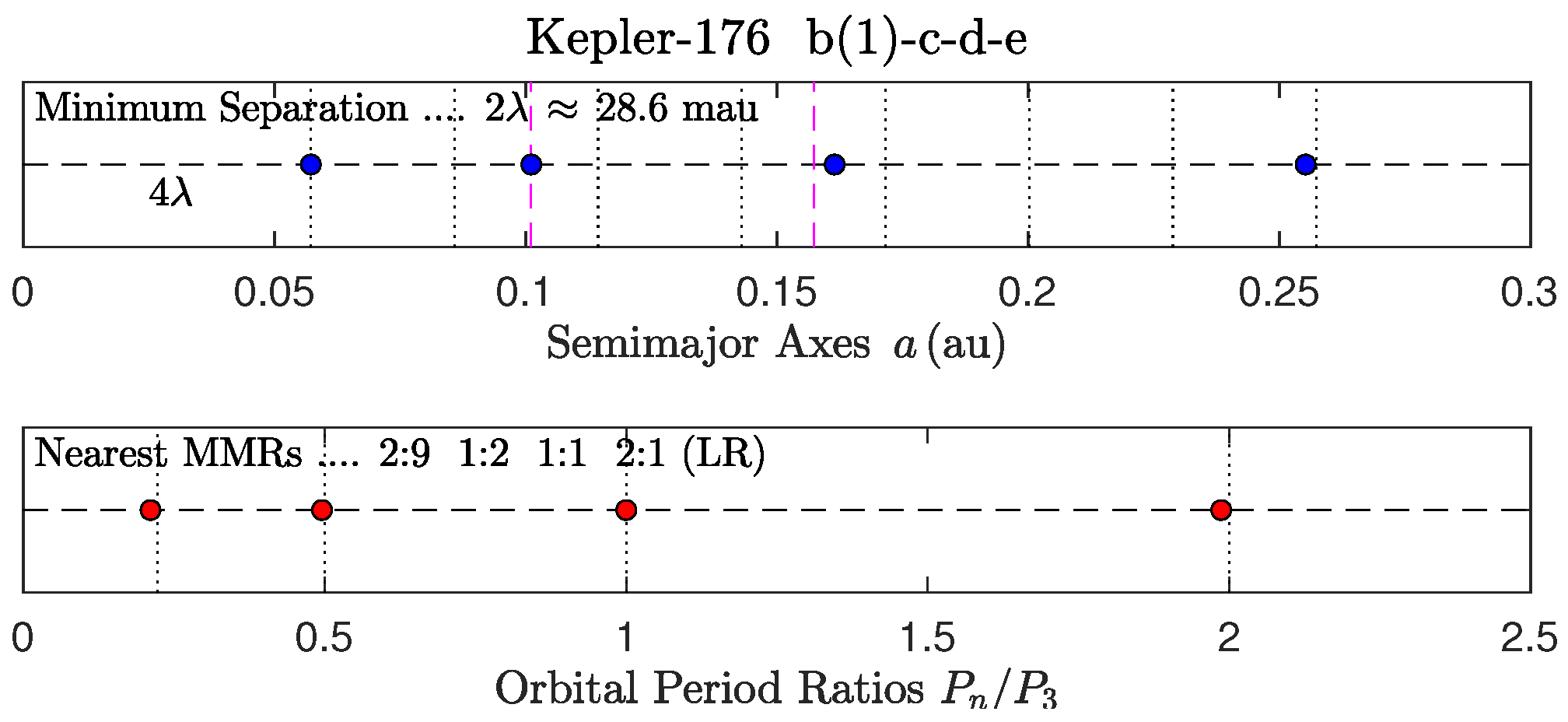
3.2. Solar Subsystems: The Terrestrial Local MMR and the 7 Global Non-LR MMRs
- 1.
- Units of au are used for the planetary subsystems.
- 2.
- SI units of Mm are used for the satellite subsystems.
- 3.
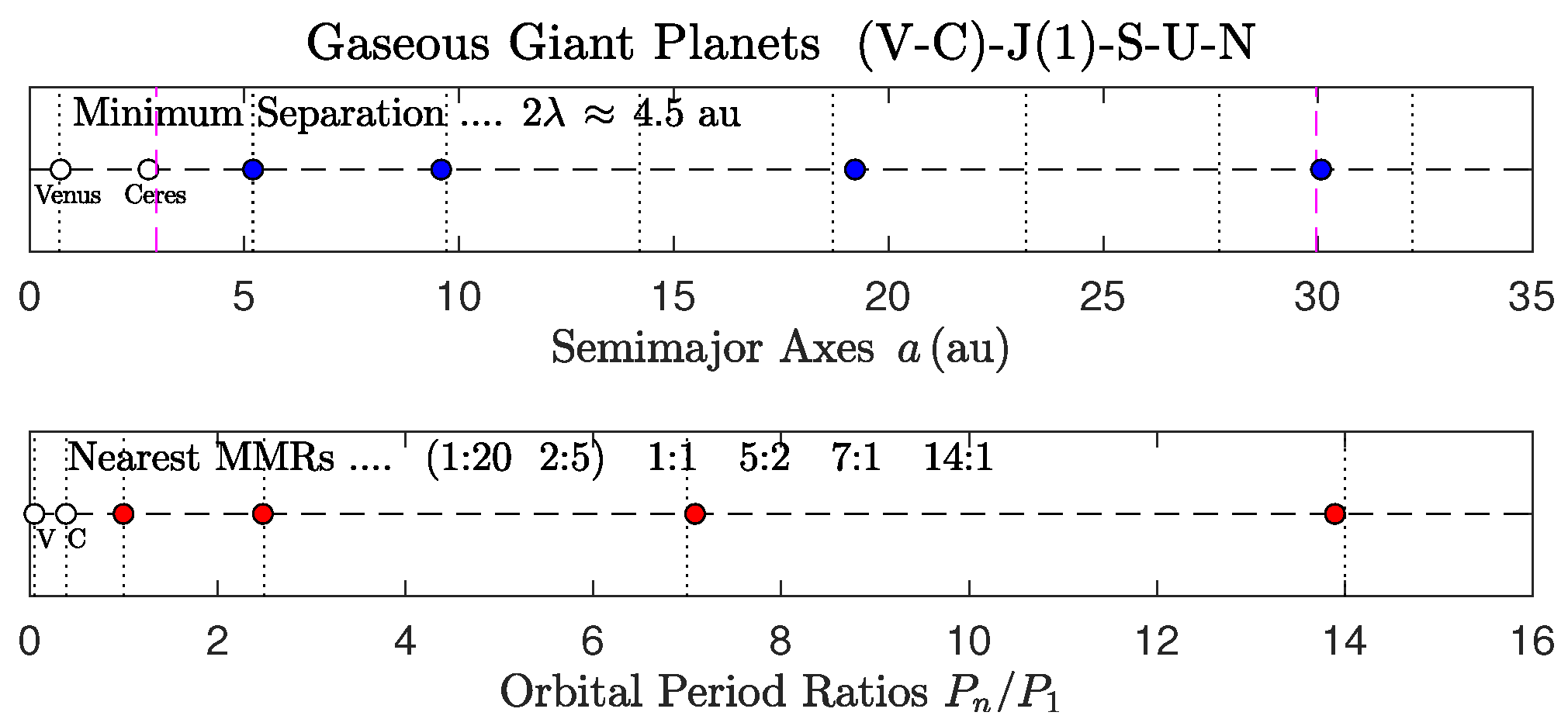
- Venus and Ceres are shown with the gaseous giants, but they are not included in the fit.
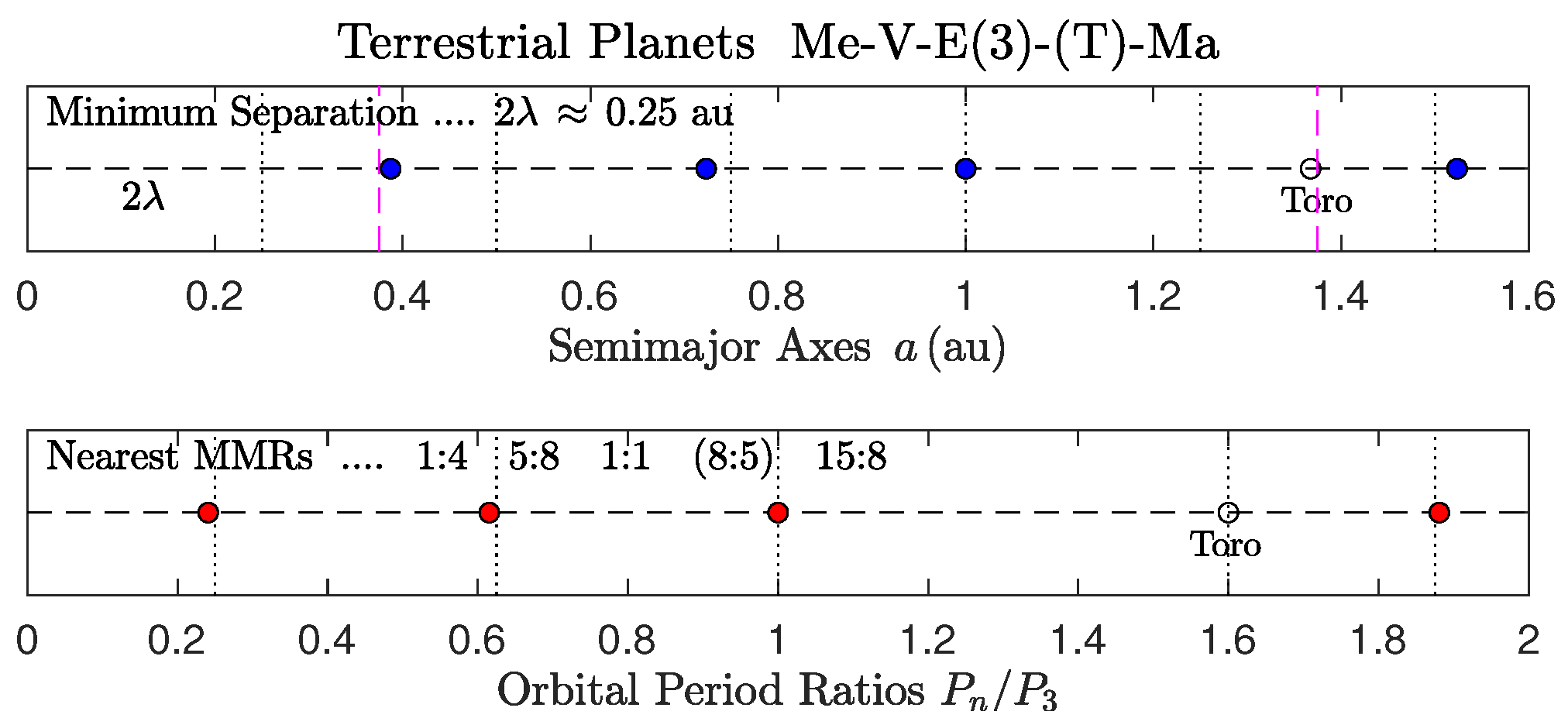
- 4.
- Asteroid Toro [43] is shown with the terrestrial planets, but it is not included in the fit.
- 5.
- The five inner moons of Neptune with semimajor axes Mm [36] are also plotted separately for clarity (file Solar_8/Neptune_moons_9s/Neptune_Inner.m in the library).
- 6.

3.3. Extrasolar Planetary Systems: The 63 Global Non-LR MMRs
- 1.
- Units of au and mau ( au) are used for the extrasolar systems.
- 2.
- 3.
- 4.
- 5.
- 6.


4. Comparisons of Results
4.1. Classical Laplace Resonances
- (a)
- The Galilean-moon subsystem has been analyzed in Ref. [16].
- (b)
- The LR of HIP 41378 is the only one that has the same layout as the famous Galilean LR.
- (c)
- No LR has been found with the most massive body at radial position (viz. 1:2:4).
- (d)
- The 9:2/2:9 MMRs are not too uncommon in LR-systems (or in non-LR systems; e.g., K-48, K-332, HD 23472).
- (e)
- Callisto’s 7:3 MMR is unique in LR-systems, and the 3:7 interior MMR does not occur—although these resonances are quite common in non-LR systems.3
4.2. Solar System: Gaseous Giant Planets
- (a)
- This subsystem has been analyzed in Ref. [16].
- (b)
- Beyond Jupiter, the semimajor axes of the gaseous planets form approximately an arithmetic progression with common difference au, in which dwarf Pluto also participates. This type of layout also occurs in the Mercury–Venus–Earth subsystem ( au), and these two arithmetic progressions are sufficient to invalidate the empirical Titius–Bode rule [67] on both ends of the solar planetary sequence.
- (c)
- Pluto is orbiting near the 21:1 MMR, and together with Uranus (7:1) and Neptune (14:1), the bodies form a triple MMR of the reduced ratio 1:2:3. This reduced ratio is quite common in exosystems, but the actual integer 1:2:3 MMR does not occur in multibody systems, thus supporting the vacancy of the 2:1 MMR.4
- (d)
- The 2:1 global MMR of Jupiter is vacant (see also Refs. [15,68]). Saturn could not occupy this MMR because then the local Landau wavelengths would overlap substantially. Nonetheless, Saturn (presently at 5:2) seems to violate marginally the no-overlap condition (2): au, whereas au, an overlap width of 0.6 au (13.7% of the separation ).
- (e)
- Saturn’s orbital period ( yr) is close to the critical orbital period ( yr) of the subsystem ( is actually longer by 34 days) [16].
4.3. Solar System: Terrestrial Planets
- (a)
- The MMR chain is local with the Earth taken at the 1:1 MMR.
- (b)
- It is obvious that Mars did not settle anywhere near the 2:1 local MMR of the subsystem.
- (c)
- The empirical tidal wavelength is mau, but the local Landau wavelength set by the Earth is only mau. For consistency, the empirical value has to be halved, so that the actual wavelength will be set to 62.5 mau in close agreement with . This subdivision of -values has to be implemented in a number of other systems as well (see below).
- (d)
- The planets fit within a single potential trough of the global mean tidal field ( au), yet pairs of adjacent orbits do not violate the no-overlap condition (2) since the largest -sum, viz. au, does not exceed the smallest (V-E) separation of 0.27 au.
- (e)
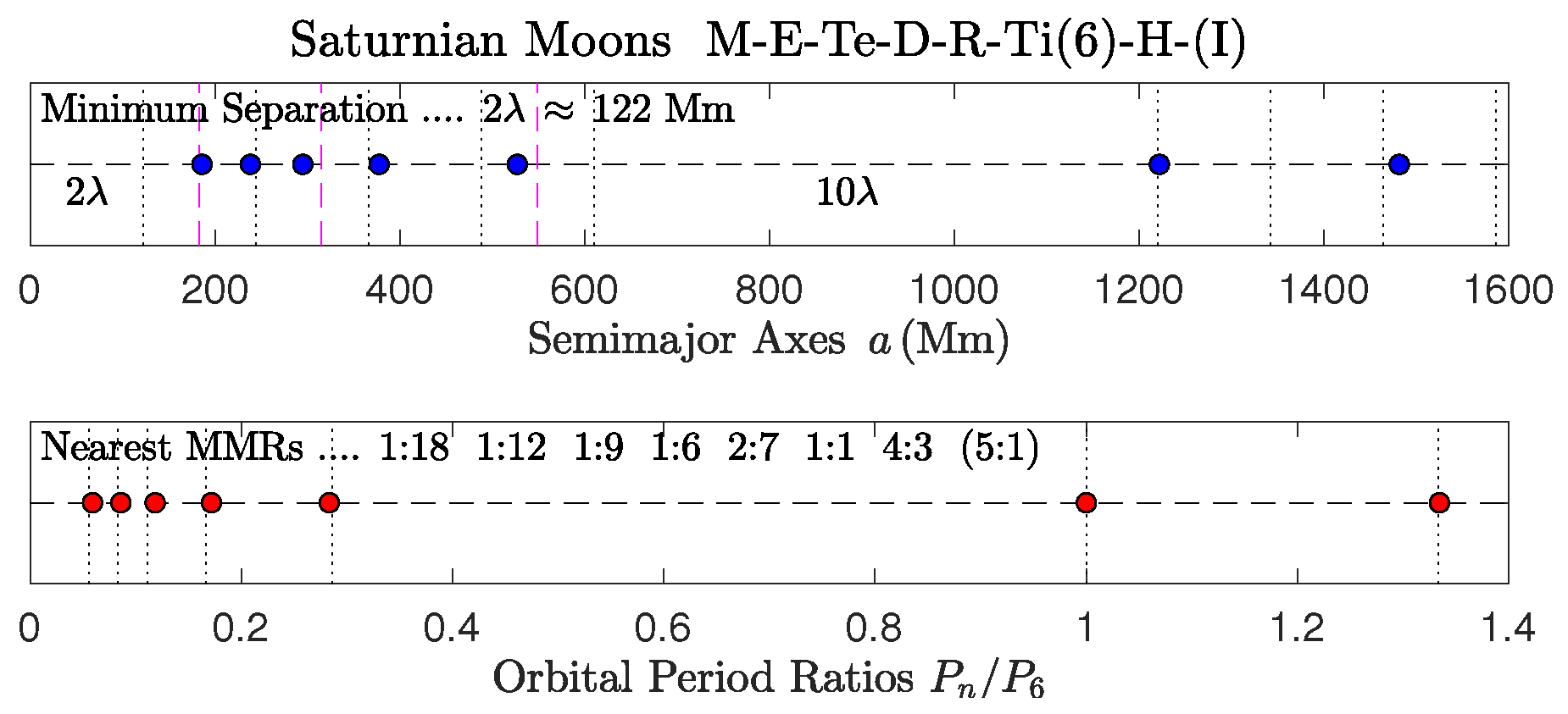
4.4. Solar System: Satellite Systems
- (a)
- The disturbed inner satellite system of Neptune [36] is also included in the library (section Solar_8/Neptune_moons_9s).
- (b)
- (c)
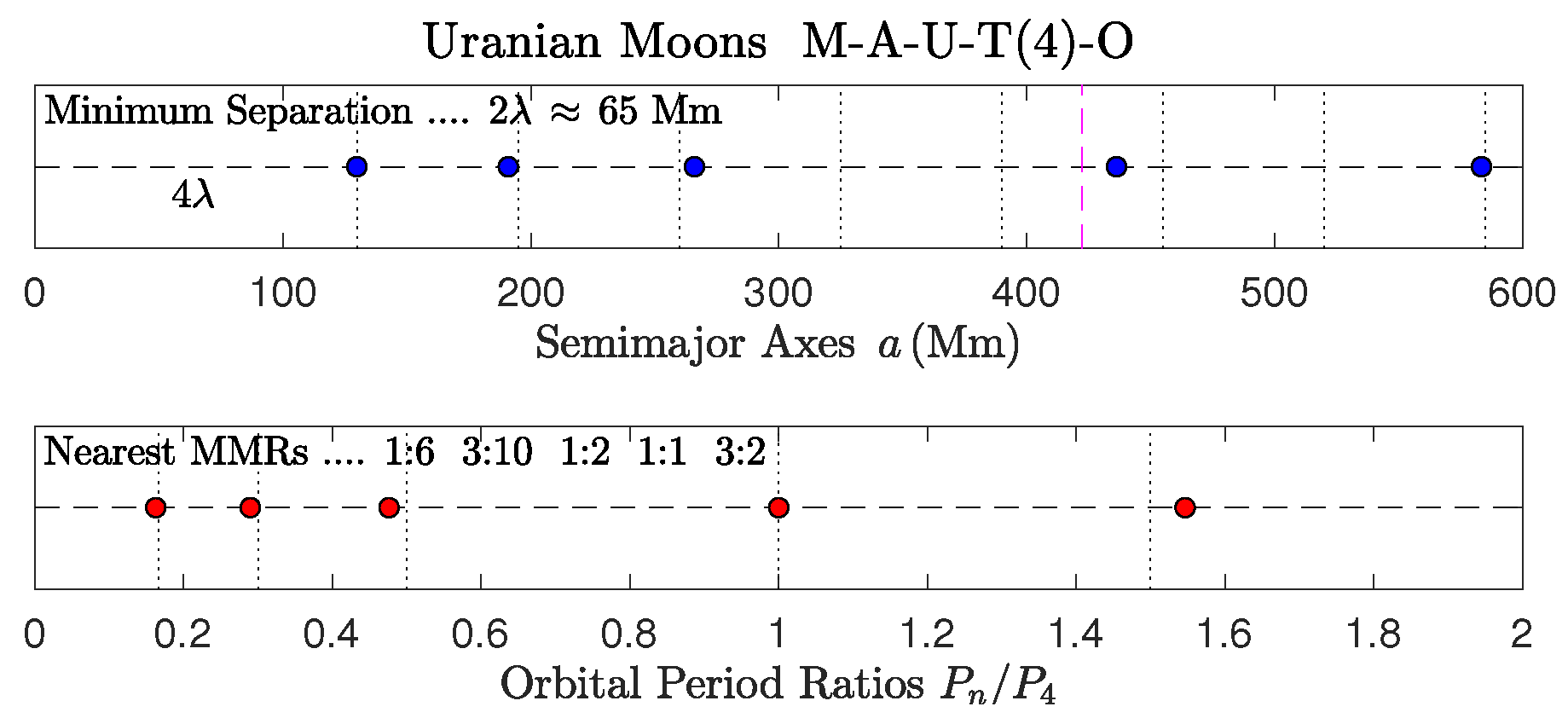
- In Uranus, the adjacent small moons Ariel and Umbriel are presumed to be in a 5:3 local MMR [69], which produces a reduced integer MMR chain of 3:5:10 with Titania (Figure 9). The same layout occurs in TOI-270 (i.e., :1:2), where the occupied 2:1 MMR proved to be a major concern in a recent study [23].
- (d)
- However, a more accurate solution for the MMR of Ariel is 2:7 leading to the unusual reduced chain of 6:10:21:33 (or the global MMR ::1:) with Titania. This model makes it clear that Umbriel is displaced off of the 1:2 MMR by about % and Oberon lies off of the 3:2 MMR by +3% (library file Uranus_alt.m in folder Solar_8/Uranus_moons_5s).
- (e)
- The group of the five Plutonian satellites is the prototypical example of a regular multibody system with an obviously vacant 2:1 MMR (Figure 10).
- (f)
- The satellites are organized in three subsets by surface gravity g [35]:
- (i)
- The largest of the large satellites with m : Earth’s moon, Jupiter’s Galilean moons, and Saturn’s Titan.
- (ii)
- The 10 large satellites with m : Tethys, Dione, Rhea, Iapetus (Saturn); Ariel, Umbriel, Titania, Oberon (Uranus); Neptune’s Triton; and Pluto’s Charon.
- (iii)
- The small satellites with m .
4.5. Exosystems with 2–9 Planets and No Classical LRs
- (a)
- (b)
- Ref. [24] also contains a detailed study of three-body and four-body MMRs occurring in many exosystems.
- (c)
- Few body systems are usually not compact (or `closely-packed’), and the empirically determined wavelength is too long to satisfy the Landau condition (1), in which case has to be subdivided to match (see below). But, as far as we can tell, these systems appear to satisfy the no-overlap condition (2) quite comfortably.
- (d)
- (e)
- (f)
- Some of the 63 exoplanetary systems show peculiarities and/or unique properties that are noted in the Output.txt files of the library (see also items 9, 10 at the top of Section 3).
4.6. Commonly-Occurring Triple MMR Chains
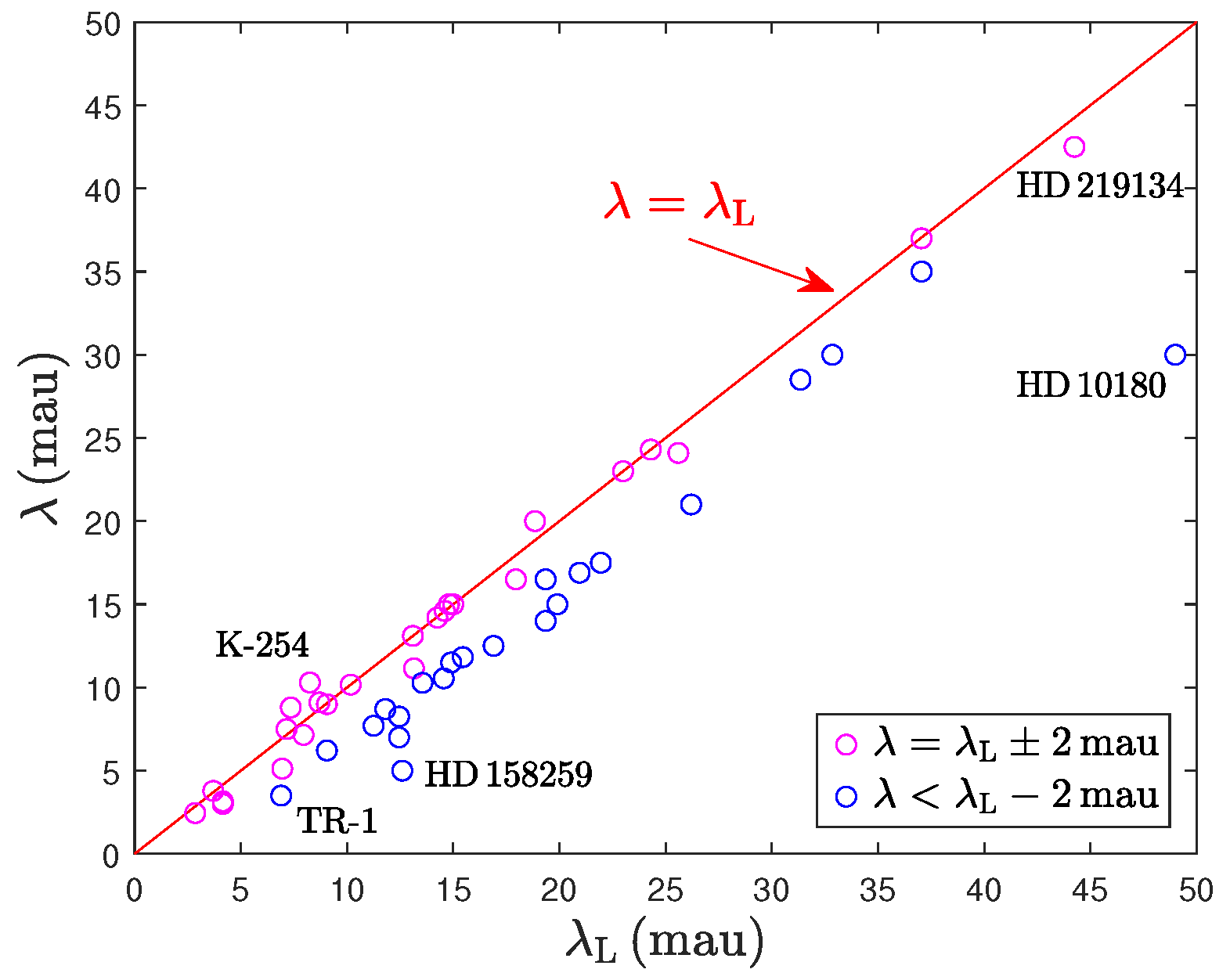
4.7. Tidal-Field Wavelengths
- (a)
- (b)
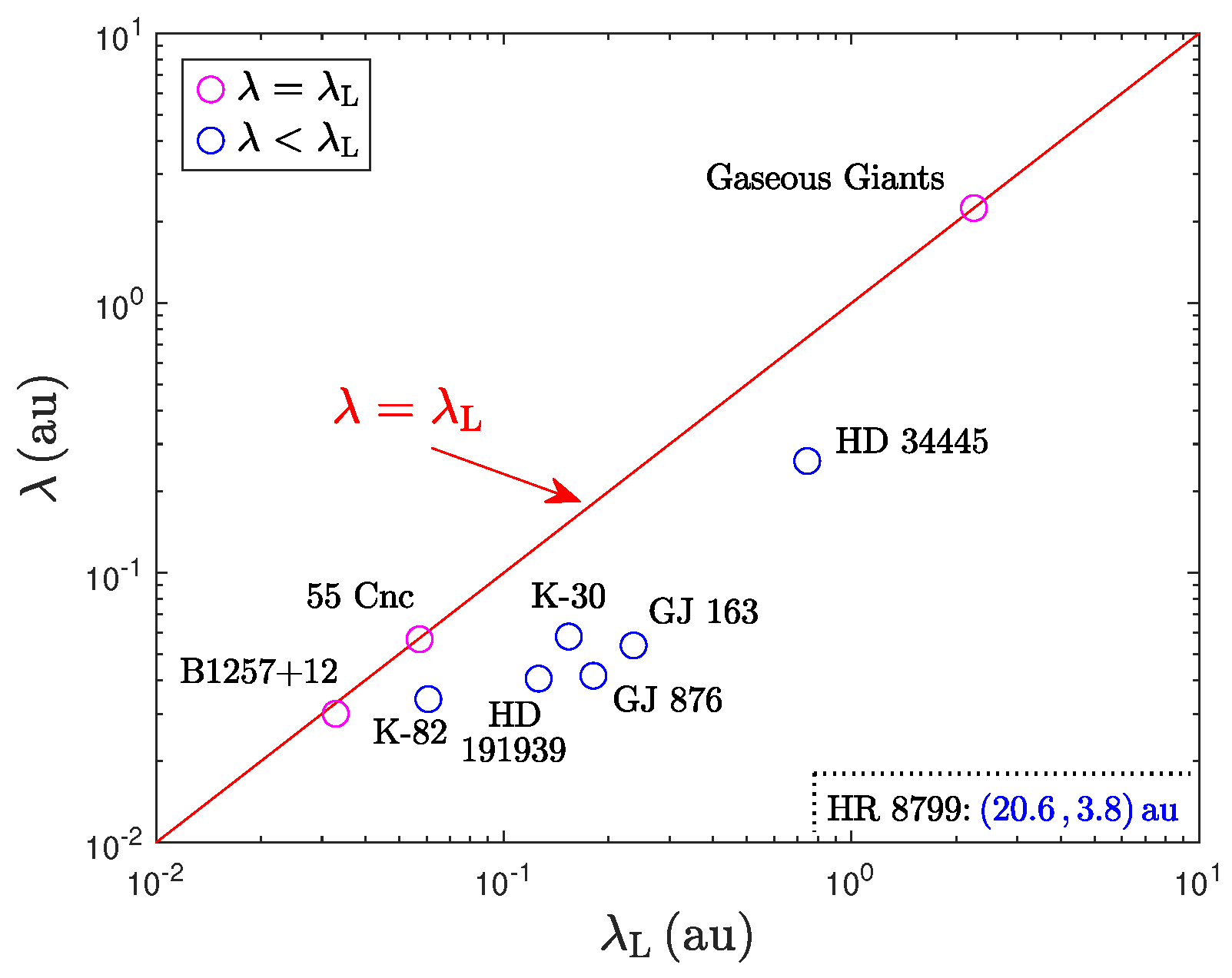
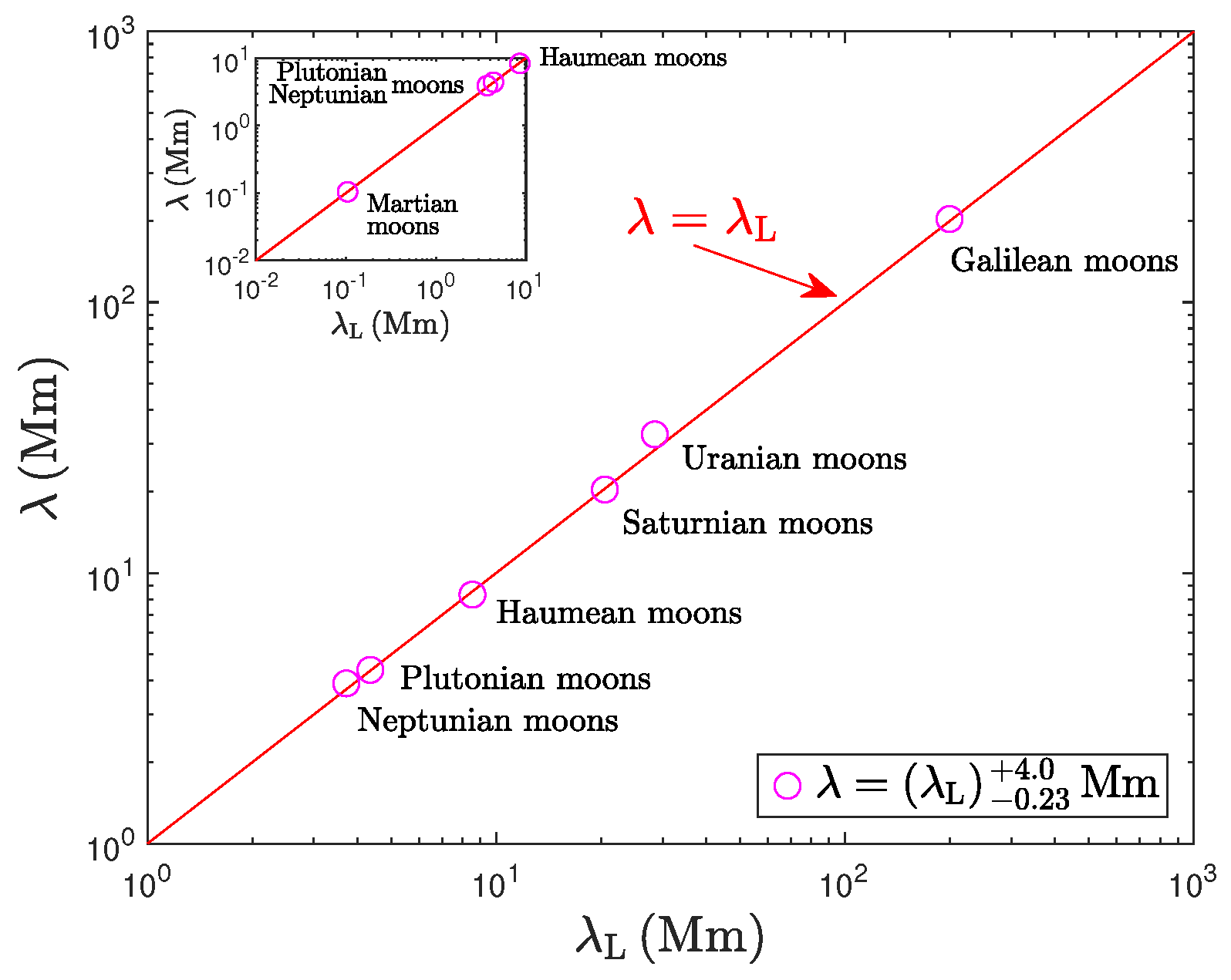
- Planetary systems at au scales are shown separately and named individually in Figure 20. The gaseous giants of our solar system appear in this plot on the line. HR 8799 is off-scale (), as noted at the bottom right of the figure.
- (c)
- (d)
- The Martian satellite system is shown in the inset of Figure 21, and it also fits the condition well. With only two moons present in the system, the empirical -value had to be divided by 45 (row 7 of Table 9) to match the Landau wavelength of km derived theoretically for the inner and more massive moon Phobos.
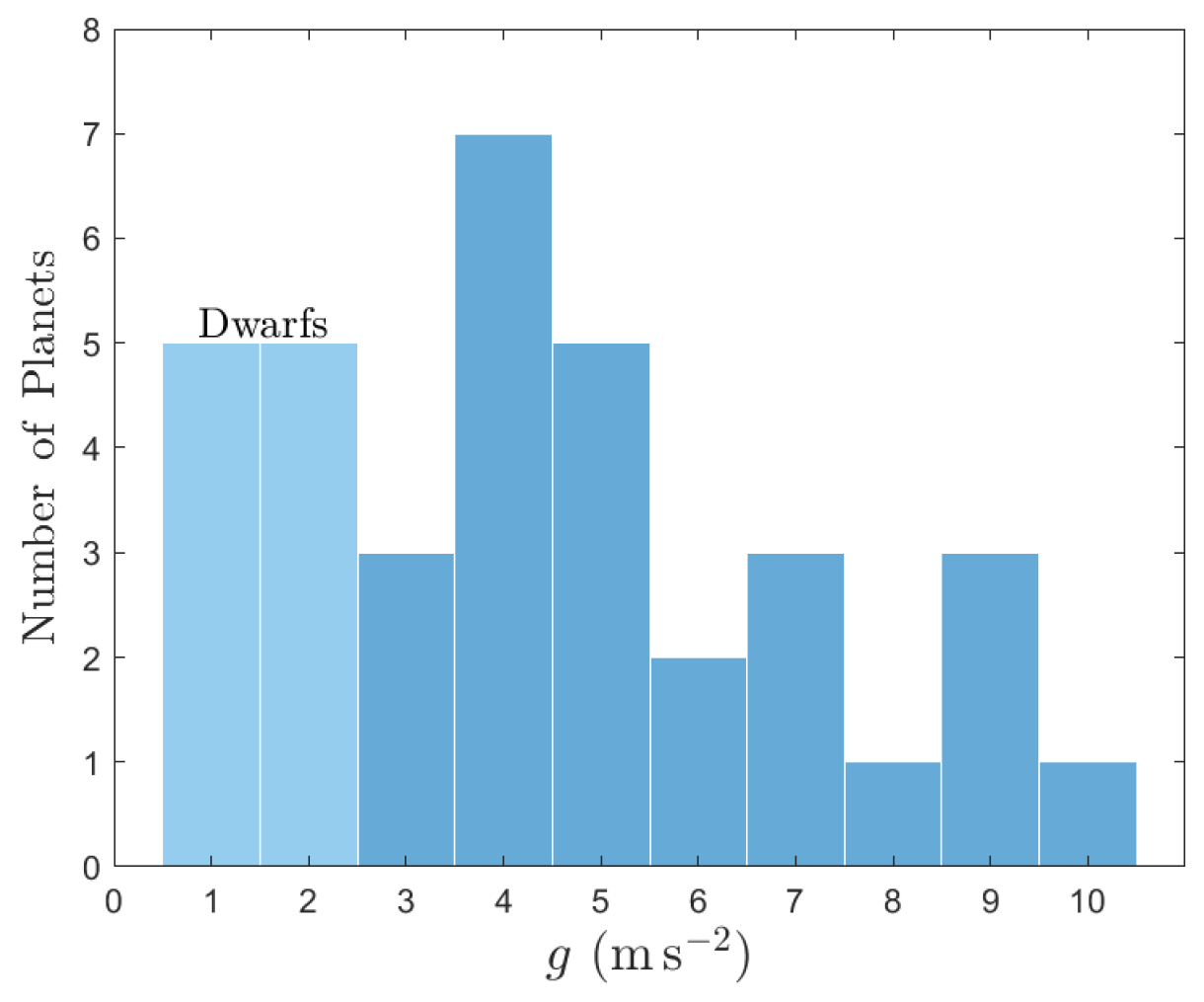
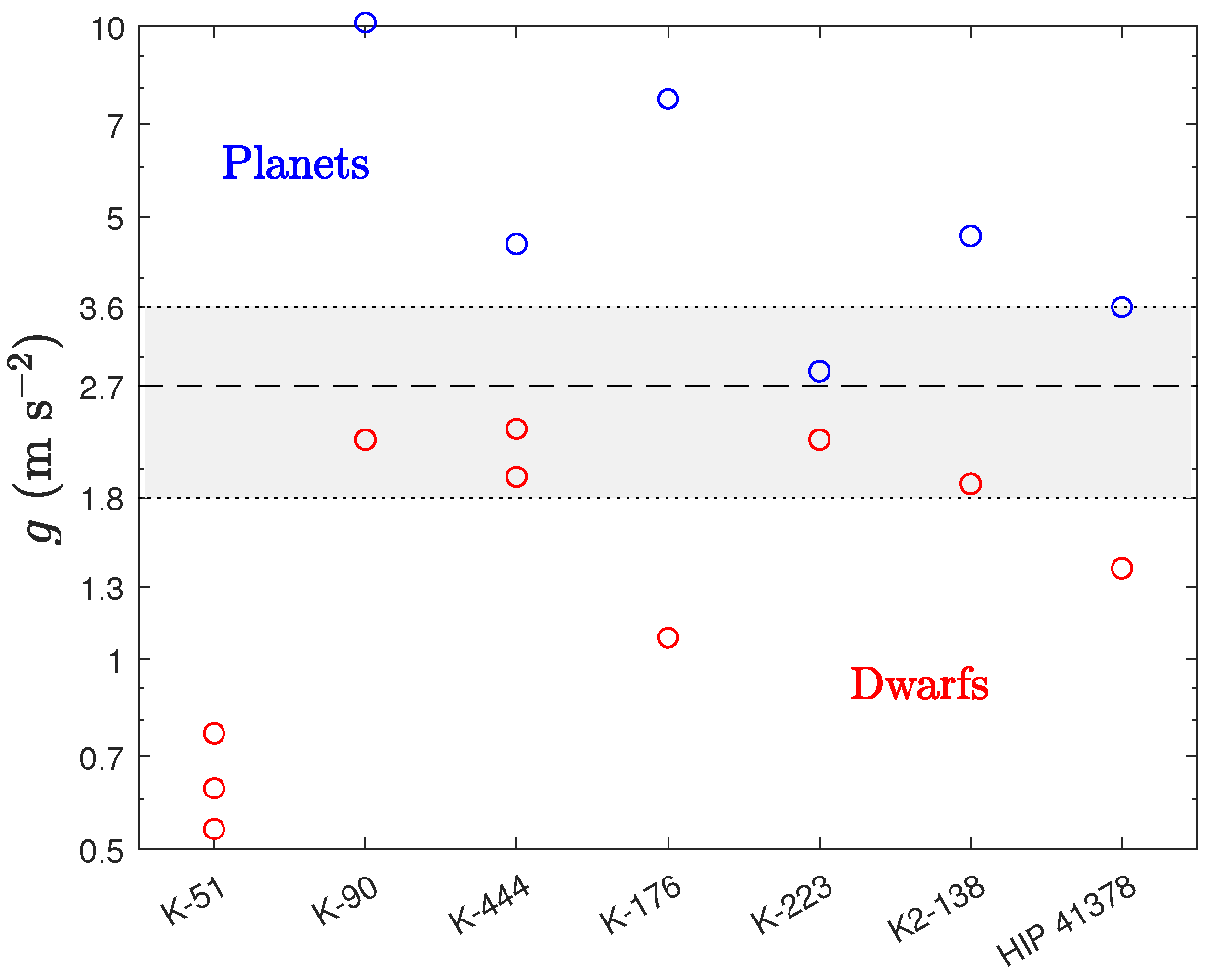
4.8. Extrasolar Dwarf Planets by Their Surface Gravities
- (a)
- Dwarf planets appear in 7 of 27 exosystems (i.e., 26% of the tabulated systems).
- (b)
- All 3 planets of K-51 with m are certainly dwarfs.
- (c)
- Two of 5 planets of K-444 (d and e) are likely dwarfs.
- (d)
- K-444 d ( m ), K-223 e, and K-90 g ( m ) are marginally identified as dwarfs (Figure 23).
- (e)
- The three bodies named d in HD 191939, K-30, and K-223, all with m , are marginally identified as planets.
4.9. Bodies on or near the Critical Orbital Period of Each System
- (a)
- The top group of 15 bodies includes the satellites of the 3 gaseous giants except Uranus. All other entries represent well-known exoplanets.
- (b)
- Neptune’s satellite system was severely disturbed by the capture of Triton, so it is remarkable that Larissa (L) managed to settle so close to the critical orbit; its period ( min) is shorter by only 18 min, whereas it is longer than the nearest assigned 1:11 MMR by 30.5 min. The critical orbit of the system and the moons of Neptune interior to the orbit of Triton are shown in Figure 24.
- (c)
- The bottom group of 11 pairs includes Ariel–Umbriel whose orbital periods nearly form an arithmetic progression with as well. All other entries represent well-known exoplanet pairs with periods symmetrically located about the values of their systems.
- (d)
- Planets b and c of pulsar B1257+12 are also included in the bottom group. This is also a remarkable symmetry because the innermost planet b is less massive than its neighbors (), and it appears to be unimportant for the overall layout of this unique pulsar planetary system. Of course, this particular orbital symmetry indicates the opposite (see also Ref. [16], Appendix A).
- (1)
- (2)
- HR 8799 d is also notable. It is orbiting close to the critical orbit of the system of 4 exoplanets, and its long orbital period ( yr) is shorter by only 4.5 yr (). The planetary system of HR 8799 is depicted in Figure 4 above.
4.10. Summary of the Longest Global MMR Chains and the Geometric Sequences
- (a)
- Triple geometric sequences are denoted by the acronym GS and their common ratio . All triple GSs found in exosystems have been summarized in Ref. [24].
- (b)
- There exist three types of triple GSs with , viz. ::, :1:, and ::1.
- (c)
- (d)
- (e)
- The entire quintuple MMR chain in K2-138 and HD 158259 is approximately geometric with a common ratio of . This raises the issue of whether this chain could actually be precisely geometric:
- (i)
- The unusual resonances 2/7 and 3/7 were chosen for the inner planets because these values are very close (to within <1%) to the measured orbital period ratios of 0.285 and 0.430, respectively; but the corresponding geometric resonances () are also nearby (to within <4%).
- (ii)
- If we assume that the MMR chains of K2-138 and HD 158259 (including the additional planets not listed in Table 13) may be precise GSs, then their MMRs are all powers of the ratio 2/3 as follows:
- ✩
- K2-138 MMR sequence (6 confirmed planets): , where for planets b–c–d–e(4)–f–g, respectively.
- ✩
- HD 158259 MMR sequence (5 confirmed planets plus a strong candidate, planet g): , where for planets b–c–d–e–f(5)–g, respectively.
- (iii)
- Similar issues of difficult choices between nearby MMRs are raised in another two cases listed in Table 13:
- ①
- Instead of the best-fitting 5:9 MMR, K-186 and K-296 may have a 4:7 MMR.
- ②
- Instead of the adopted 3:4 MMR, TOI-1136 and K2-384 may have a 5:7 MMR. However, no such issue exists in the case of the 3:4 MMRs identified in K-90, K-226, and TR-1 (relative deviations of <2% from 3/4).
- (iv)
- A summary of 4 markedly similar global MMR chains is listed at the bottom of Table 13. The prototypical sequence occurs in TR-1 and in TOI-1136:
- ➣
- The 1:5 and 1:4 inner MMRs (blue color) occur sufficiently far away from the 1:1 MMR (where the density of consecutive principal MMRs is too high), so failure to match the nearby 1:6 and 1:3 MMRs, respectively, is not a cause for concern.
- ➣
- The unusual 4:9 and 2:3 MMRs in HD 110067 cannot be overlooked in the same way because these resonances are not far away from 1:1, but their appearance is understood: these MMRs are exact elements of the GS with .
- ➣
- It is interesting that the 3:2 MMR in K2-384 is the only 3:2 MMR that is vacant in the markedly similar systems listed at the bottom of Table 13. We searched for another planet at d, but we did not find a signal in the archival Kepler data.
- ➣
- On the other hand, the 2:1 MMR in HD 110067 is not vacant. This resonance has drawn much attention recently [14,15,16,23,24]. It turns out that the pristine 6 triple MMR 1::2 observed in HD 110067 [14] represents a stable `Laplace-like resonance’ [23] whose double Laplace phase angle () most likely librates near (based on the results of Ref. [13]).7
- ➣
- (v)
- The issues highlighted in items (i)–(iv) above will have to be addressed by future studies.
- (f)
- Summary of recently studied global MMRs and the librations of their phase angles:
- (i)
- (ii)
- Three-body and four-body resonances of the 6 planets in HD 110067 have been extensively studied in Ref. [24].
- (iii)
- The geometric sequences, the four-body MMRs of K-223 and HD 110067, and the unusual LR encountered in K-176 (that does not include the most massive planet) have been extensively studied in Ref. [24].
- (iv)
- (v)
| A Chain of 5 MMRs | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2/7 | 3/7 | 2/3 | 1 | 3/2 | HD 158259, K2-138 (GS: 2/3:1:3/2, ) | ||||
| Chains of 4 MMRs | |||||||||
| 1/3 | 1/2 | 3/4 | 1 | TR-1, K2-384 (GS: 1/3:1/2:3/4, ) | |||||
| 1/2 | 3/4 | 1 | 3/2 | TR-1, TOI-1136 | |||||
| 4/9 | 2/3 | 1 | 3/2 | HD 110067 (Quadruple GS: ) | |||||
| 2/7 | 5/9 | 1 | 5/3 | K-186, K-296 | |||||
| Commonly-occurring Chains of 3 MMRs | |||||||||
| 3/4 | 1 | 3/2 | TR-1, TOI-1136, K-226 | ||||||
| 2/3 | 1 | 3/2 | HD 110067, HD 158259, K-11, K2-138 (GS: ) | ||||||
| 4/9 | 2/3 | 1 | HD 110067, HD 23472 (GS: ) | ||||||
| 1/2 | 3/4 | 1 | TR-1, TOI-1136, K-90, K2-384 | ||||||
| 1/3 | 1/2 | 3/4 | TR-1, K2-384 (GS: ) | ||||||
| Summary: Markedly Similar Long MMR Chains | |||||||||
| 1/6 | 1/3 | 1/2 | 3/4 | 1 | K2-384 | ||||
| 1/8 | 1/5 | 1/3 | 1/2 | 3/4 | 1 | 3/2 | TR-1 | ||
| 1/6 | 1/4 | 1/2 | 3/4 | 1 | 3/2 | TOI-1136 | |||
| 4/9 | 2/3 | 1 | 3/2 | 2 | 8/3 | HD 110067 | |||
4.11. Beyond the Classical LRs: Summary of Important Groups of Triple MMR Chains
- (a)
- All triple MMRs are combinations of local pairs chosen from the set {2:1, 3:2, 4:3}. Of the 9 possible combinations, three pairs do not appear in the tables:
- (i)
- The pair 4:3 and 4:3—This GS occurs in HD 110067 (:2: [14]), but it is not otherwise common (which may be surprising).
- (ii)
- The pair 2:1 and 4:3—This :1: MMR does not occur in real systems, probably because it is too close to the dominant Laplace-like resonance :1: (the MMRs mostly overlap).
- (iii)
- The pair 4:3 and 2:1—This MMR of type :1:2 does not occur in real systems either, although it is not close to the dominant LR :1:2. If it can be formed in exosystems, it is expected to not show librations because of the unique composition of its phase (, where () are the mean longitudes of the orbits [24]), the only one among the 9 combinations from set in which . More details are given in Section 4.12 below.
- (iv)
- We note that the pair 3:2 and 2:1, which is closer to the LR than the 4:3 and 2:1 pair, does occur in real systems, but its phase angle ( is defined in the notes to Table 15) does not librate either (see also group (6) in item (3) below).
- (b)
- (c)
- Group (2): These are the most common GSs, and they have a common ratio of [24].
- (d)
- Group (3): These are the 3 types of Laplace-like resonances (::1, :1:, and 1::2) with phase angle and libration centers in the vicinity of (see Table 15).
- (1)
- (2)
- Groups (4) and (5): The trailing local MMR is 3:2, the same in both groups. Other than that, these groups are very different, although the global MMRs may both show LCs located at ∼180°. These MMRs have not been explored in the past. They are also listed in Table 2 of Ref. [24].
- (3)
- Group (6): These MMRs are not locked in librations. The reason appears to be the trailing 2:1 local MMR, which is not viable outside of the classical LR and the Laplace-like resonances (see Endnote 7). As mentioned above, a single puzzling exception occurs in TOI-270, which shows a trailing 2:1 MMR and an unusual phase angle [23]:
- •
- In TOI-270, the MMR chain :1:2 has the same phase () as the uncommon first-order MMR pair 4:3 and 4:3, the GS described in item (a)–(i) above. In this case, (); therefore, phase librations are feasible in principle.
- •
- This phase is expected to librate about a center in the vicinity of , but N-body simulations have not been carried out for long enough to check the results [72].
- •
- The MMR chain :1:2 is closer to the dominant LR :1:2 than the MMR pairs listed in items (a)-(iii, iv) above. The two chains mostly overlap. Yet, the TOI-270 MMR survives intact, unlike the 2:1 and 4:3 pair of MMRs discussed in items (a)–(ii) above.
- •
- Thus, the pair 2:1 and 4:3 is suppressed by the Laplace-like pair 3:2 and 4:3, whereas the pair 5:3 and 2:1 is unaffected by the LR pair 2:1 and 2:1. This disparity could characterize a fundamental difference between LRs and Laplace-like MMRs, with the latter being dominant over the range of their resonances and the former being incapable of suppressing nearly overlapping MMRs.
- •
- For the above reasons, the stability of the :1:2 MMR of TOI-270 remains a mystery, and the problem needs to be studied in more detail in the future.8
- (4)
- Groups (7)–(10): These are 14 global MMRs that appear rarely in individual exosystems:
- (i)
- They are unusual (they show large “integer gaps” between their MMRs), and it remains to be seen whether the same types of reduced MMR chains will be discovered in exosystems in the future.
- (ii)
- The set is dominated by the pristine principal MMR chain of Plutonian moons (1:3:4:5:6), whose triple MMRs appear in the list in all possible consecutive combinations (despite the striking vacancy of the 2:1 global MMR).
- (iii)
- The unusual chain :1: (huge gap beyond 1:1) appears in both K-48 and HIP 41378.
- (iv)
- The unusual chain :1: (gap at 4:3 – 3:2) appears in both HD 23472 and K-102.
- (v)
- Two very different MMRs of the 2:4:9 form appear in two very different exosystems (K-332 and HR 8799).
- (vi)
- Notable MMRs of future interest are ::1 (HD 20781), :1: (HD 10180, gap at 2:3), :1: (K-80, gaps at 2:3 and at 4:3), and :: (K2-268, gap at 1:3).
4.12. A Criterion for the Absence of Librations in Triple MMR Chains
5. Summary of Contents and Cross-References
| Description of Contents and Cross-References | ||||
| Section 2 | ||||
| Items 1–7 | Assumptions on modeling the nearest MMRs | |||
| Items 1–6 | Conditions on modeling the spacings of the orbits | |||
| Section 3 | ||||
| Items 1–10 | Notes on the dynamical parameters listed in the library | |||
| Items 1–3 | Notes on the EPS file figures included in the library | |||
| Section 3.1 | ||||
| Items 1–7 | Notes on Laplace resonances | |||
| Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 | Figures of 5 LR systems | |||
| Section 3.2 | ||||
| Items 1–6 | Notes on solar subsystems | |||
| Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 | Figures of 5 solar subsystems | |||
| Section 3.3 | ||||
| Items 1–6 | Notes on extrasolar planetary systems | |||
| Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 | Figures of 8 extrasolar planetary systems | |||
| Section 4 | ||||
| Section 4.1 | Items (a)–(e) | Classical Laplace resonances (Table 1) | ||
| Section 4.2 | Items (a)–(e) | Gaseous giant planets (Figure 6) | ||
| Section 4.3 | Items (a)–(e) | Terrestrial planets (Figure 7) | ||
| Section 4.4 | Items (a)–(f) | Satellite systems (Figure 8, Figure 9 and Figure 10 and Figure 24) | ||
| Section 4.5 | Items (a)–(f) | Exosystems (Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 and Figure 25) | ||
| Section 4.6 | Items (a)–(c) | Triple MMR chains (Table 2, Table 3, Table 4, Table 5 and Table 6) | ||
| Section 4.7 | Items (a)–(d) | Tidal-field wavelengths (Table 7, Table 8 and Table 9, Figure 19 and Figure 21) | ||
| Section 4.8 | Items (a)–(e) | Extrasolar dwarf planets (Table 10, Figure 22 and Figure 23) | ||
| Section 4.9 | Items (a)–(d) | Critical orbital periods (Table 11) | ||
| Items (1)–(2) | Bodies with yr (Table 12) | |||
| Section 4.10 | Items (a)–(f) | Longest MMRs and geometric sequences (Table 13) | ||
| Section 4.11 | Items (a)–(d) | Characteristics of the 6 main groups of triple MMRs | ||
| Items (1)–(4) | Properties of 10 groups of triple MMRs (Table 14 and Table 15) | |||
| Section 4.12 | Equations (3)–(6) | Criterion for the absence of librations (Equation (6)) | ||
| Tables | ||||
| Table 1 | Section 4.1 | The 6 classical Laplace resonances | ||
| Table 2, Table 3, Table 4, Table 5 and Table 6 | Section 4.6 | Common and uncommon triple MMRs | ||
| Table 7, Table 8 and Table 9 | Section 4.7 | Tidal-field wavelengths and Landau wavelengths | ||
| Table 10 | Section 4.8 | Dwarf planets by surface gravity g | ||
| Table 11 and Table 12 | Section 4.9 | Bodies on/near the critical orbital periods | ||
| Table 13 | Section 4.10 | The longest global MMR chains | ||
| Table 14 and Table 15 | Section 4.11 | Groups of triple integer MMR chains | ||
| Figures | ||||
| Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 | LR systems | Galilean moons, GJ 876, HIP 41378, HR 8799, K-176 | ||
| Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 | Solar subsystems | Planets: Gas giants, Terrestrial; Moons: Saturn, Uranus, Pluto | ||
| Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 | Extrasolar planets | HD 10180, K-90, TR-1, TOI-1136, K-444, K2-32, K-60, K-51 | ||
| Figure 19 | Table 7 exosystems | Landau tidal-field wavelengths | ||
| Figure 20 | -au-scale systems | Landau tidal-field wavelengths | ||
| Figure 21 | Inner-moon systems | Landau tidal-field wavelengths | ||
| Figure 22 | Table 10 exoplanets | Distribution of surface gravities m | ||
| Figure 23 | Table 10 exodwarfs | Surface gravities m | ||
| Figure 24 | Neptunian moons | MMRs and semimajor axes | ||
| Figure 25 | K2-138 | MMRs and semimajor axes | ||
| Endnotes | ||||
| Note 1 | Section 1 | Citation guide to previous analyses | ||
| Note 2 | Section 1 and Section 3.1(5–6) | SI unit multiples and milli-au (mau) unit | ||
| Note 3 | Section 4.1(e) | The 7:3 exterior MMR | ||
| Note 4 | Section 4.1(e) | The 3:7 interior MMR | ||
| Note 5 | Section 4.2(c) | The reduced 1:2:3 MMR ratio | ||
| Note 6 | Table 8 | Long Landau wavelengths | ||
| Note 7 | Section 4.10(e)–(iv) | The 1::2 MMR in HD 110067 | ||
| Note 8 | Section 4.10(e)–(iv) | Four-planet resonant angles in HD 110067 | ||
| Note 9 | Table 15 | No librations for the 3:2 and 2:1 MMR pair | ||
| Note 10 | Table 15 | The unobserved 4:3 and 5:4 MMR pair | ||
| Note 11 | Section 4.11(3) | Beyond the LRs: The global 2:1 MMR in K-9 | ||
| Note 12 | Section 4.11(3) | Summary of occupied 2:1 non-LR MMRs | ||
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOI | Digital Object Identifier |
| DP | Dwarf Planet (Table 10) |
| EPS | Encapsulated PostScript |
| GS | Geometric Sequence |
| K- | Kepler- |
| K2- | Kepler2- |
| LC | Libration Center |
| LR | Laplace Resonance |
| MMR | Mean-Motion Resonance |
| P | Planet (Table 10) |
| Portable Document Format | |
| SI | Système International d’unités |
| TR-1 | TRAPPIST-1 |
| TS | Teegarden’s Star [76,77,78] |
| 1 | |
| 2 | In the SI system of units, m and m. Furthermore, we use au, where au is the astronomical unit. |
| 3 | The 7:3 exterior MMR occurs in K-30, K-80, K2-32, TOI-700, Teegarden’s system, and the Galilean moons. The 3:7 interior MMR occurs in K2-138, TOI-178, and HD 158259. |
| 4 | The reduced 1:2:3 MMR ratio does not occur in this precise form (so the 2:1 MMR remains vacant), but its rational scalings occur in Uranus (Umbriel–Titania–Oberon), K-32, K-51, K-62, K-82, K-84, K2-384, TOI-1136, and HD 23472. |
| 5 | An extreme ratio of (such as those at the bottom of Table 8) implies that the most massive planet is orbiting at the outer end of the MMR chain while the less massive inner planets are in a compact configuration characterized by . Additional solar-system examples are the Uranian and Neptunian moon systems, respectively. |
| 6 | In the 1::2 MMR section of HD 110067, the planets are orbiting to within <0.05% of their respective MMRs. Outside this section, the planets continue to exhibit tiny relative deviations of ≤0.093% from the corresponding MMRs. The relative deviations from the empirically determined MMRs in the HD 110067 system (viz. [ 0.0 4.4 4.7 9.3]) are the smallest ones among all systems in the library. |
| 7 | Furthermore, two four-planet resonant phase angles were calculated for HD 110067 in Ref. [24]. |
| 8 | We note that planet K-9 c was also found to be near the 2:1 MMR of the three-planet system K-9 d–b–c [106,107,108], but we do not consider it a mystery. Planet d is too distant to participate in a triple MMR, and the two massive planets b and c form a single pair that is kept off of the exact 2:1 MMR, which was shown to be unstable [109]. It was also shown in Ref. [109] that the long-term stability of the pair is maintained by the libration of the difference of apsidal angles about ∼180° with amplitude . A summary of chains with an occupied non-LR 2:1 MMR follows: 1::2 in HD 110067 d–e–f, a Laplace-like resonance [24]; :1:2 in TOI-270 b–c–d, unexplained [23]; :1:2 in K-9 d-b-c, apsidal difference librates about ∼180° maintaining long-term stability [109]. |
References
- Goldreich, P. An explanation of the frequent occurrence of commensurable mean motions in the solar system. Mon. Not. R. Astron. Soc. 1965, 130, 159. [Google Scholar] [CrossRef]
- Lissauer, J.J.; Ragozzine, D.; Fabrycky, D.C.; Steffen, J.H.; Ford, E.B.; Jenkins, J.M.; Shporer, A.; Holman, M.J.; Rowe, J.F.; Quintana, E.V.; et al. Architecture and dynamics of Kepler’s candidate multiple transiting planet systems. Astrophys. J. Suppl. 2011, 197, 8. [Google Scholar] [CrossRef]
- Papaloizou, J.C.B. Three body resonances in close orbiting planetary systems: Tidal dissipation and orbital evolution. Int. J. Astrobiol. 2015, 14, 291. [Google Scholar] [CrossRef]
- Mills, S.M.; Fabrycky, D.C.; Migaszewski, C.; Ford, E.B.; Petigura, E.; Isaacson, H. A resonant chain of four transiting, sub-Neptune planets. Nature 2016, 533, 509. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Ragozzine, D.; Fabrycky, D.C.; Ford, E.B.; Holman, M.J.; Isaacson, H.T.; Lissauer, J.J.; Lopez, E.D.; Mazeh, T.; Rogers, L.; et al. A dyamical analysis of the Kepler-80 system of five transiting planets. Astron. J. 2016, 152, 105. [Google Scholar] [CrossRef]
- Luger, R.; Sestovic, M.; Kruse, E.; Grimm, S.L.; Demory, B.-O.; Agol, E.; Bolmont, E.; Fabrycky, D.; Fernandes, C.S.; Van Grootel, V.; et al. A seven-planet resonant chain in TRAPPIST-1. Nat. Astron. 2017, 1, 0129. [Google Scholar] [CrossRef]
- Delisle, J.B. Analytical model of multi-planetary resonant chains and constraints on migration scenarios. Astron. Astrophys. 2017, 605, A96. [Google Scholar] [CrossRef]
- Christiansen, J.L.; Crossfield, I.J.M.; Barentsen, G.; Lintott, C.J.; Barclay, T.; Simmons, B.D.; Petigura, E.; Schlieder, J.E.; Dressing, C.D.; Vanderburg, A.; et al. The K2-138 System: A near-resonant chain of five sub-Neptune planets discovered by Citizen Scientists. Astron. J. 2018, 155, 57. [Google Scholar] [CrossRef]
- Millholland, S.; Laughlin, G.; Teske, J.; Butler, R.P.; Burt, J.; Holden, B.; Vogt, S.; Crane, J.; Shectman, S.; Thompson, I. New constraints on Gliese 876—Exemplar of mean-motion resonance. Astron. J. 2018, 155, 106. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Dawson, R.I. Three pathways for observed resonant chains. Astron. J. 2018, 156, 228. [Google Scholar] [CrossRef]
- Lopez, T.A.; Barros, S.C.C.; Santerne, A.; Deleuil, M.; Adibekyan, V.; Almenara, J.-M.; Armstrong, D.J.; Brugger, B.; Barrado, D.; Bayliss, D.; et al. Exoplanet characterisation in the longest known resonant chain: The K2-138 system seen by HARPS. Astron. Astrophys. 2019, 631, A90. [Google Scholar] [CrossRef]
- Morrison, S.J.; Dawson, R.I.; MacDonald, M. Chains of planets in mean motion resonances arising from oligarchic growth. Astrophys. J. 2020, 904, 157. [Google Scholar] [CrossRef]
- Siegel, J.C.; Fabrycky, D. Resonant chains of exoplanets: Libration centers for three-body angles. Astron. J. 2021, 161, 290. [Google Scholar] [CrossRef]
- Luque, R.; Osborn, H.P.; Leleu, A.; Pallé, E.; Bonfanti, A.; Barragán, O.; Wilson, T.G.; Broeg, C.; Collier Cameron, A.; Lendl, M.; et al. A resonant sextuplet of sub-Neptunes transiting the bright star HD 110067. Nature 2023, 623, 932. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Laycock, S.G.T.; Kazanas, D. The global 2:1 mean-motion resonance in HD 110067 is not vacant! Res. Not. AAS 2023, 7, 275. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D. Landau tidal damping and major-body clustering in solar and extrasolar subsystems. Astronomy 2024, 3, 139. [Google Scholar] [CrossRef]
- Rivera, E.J.; Laughlin, G.; Butler, R.P.; Vogt, S.S.; Haghighipour, N.; Meschiari, S. The Lick-Carnegie exoplanet survey: A Uranus-mass fourth planet for GJ 876 in an extrasolar Laplace configuration. Astrophys. J. 2010, 719, 890. [Google Scholar] [CrossRef]
- Goździewski, K.; Migaszewski, C.; Panichi, F.; Szuszkiewicz, E. The Laplace resonance in the Kepler-60 planetary system. Mon. Not. R. Astron. Soc. 2016, 455, L104. [Google Scholar] [CrossRef]
- Charalambous, C.; Martí, J.G.; Beaugé, C.; Ramos, X.S. Resonance capture and dynamics of three-planet systems. Mon. Not. R. Astron. Soc. 2018, 477, 1414. [Google Scholar] [CrossRef]
- Goździewski, K.; Migaszewski, C. An exact, generalized Laplace resonance in the HR 8799 planetary system. Astrophys. J. Lett. 2020, 902, L40. [Google Scholar] [CrossRef]
- Celletti, A.; Karampotsiou, E.; Lhotka, C.; Pucacco, G.; Volpi, M. Laplace-like resonances with tidal effects. Astron. Astrophys. 2021, 655, A94. [Google Scholar] [CrossRef]
- Zurlo, A.; Goździewski, K.; Lazzoni, C.; Mesa, D.; Nogueira, D.; Desidera, S.; Gratton, R.; Marzari, F.; Langlois, M.; Pinna, E.; et al. Orbital and dynamical analysis of the system around HR8799. New astrometric epochs from VLT/SPHERE and LBT/LUCI. Astron. Astrophys. 2022, 666, A133. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Sorabella, N.M.; Bhattacharya, S.; Laycock, S.G.T.; Kazanas, D. Global mean-motion resonances: Part I—An exceptional multiplanetary resonant chain in TOI-270 and an exact Laplace-like resonance in HD 110067. Galaxies 2025, 13, 42. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Sorabella, N.M.; Bhattacharya, S.; Laycock, S.G.T.; Kazanas, D. Global mean-motion resonances: Part II—Laplace-like phase angles to facilitate libration searches in multiplanetary N-body simulations. Galaxies 2025, 13, 41. [Google Scholar] [CrossRef]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 1999; pp. 364–371, 396–399. [Google Scholar]
- Lieske, J.H. Galilean satellite ephemerides E5. Astron. Astrophys. Suppl. Ser. 1998, 129, 205. [Google Scholar] [CrossRef]
- Musotto, S.; Varadi, F.; Moore, W.; Schubert, G. Numerical simulations of the orbits of the Galilean satellites. Icarus 2002, 159, 500. [Google Scholar] [CrossRef]
- Lainey, V.; Duriez, L.; Vienne, A. Synthetic representation of the Galilean satellites’ orbital motions from L1 ephemerides. Astron. Astrophys. 2006, 456, 783. [Google Scholar] [CrossRef]
- Landau, L. Oscillations of an electron plasma. J. Phys. 1946, 10, 25, (English Translation). [Google Scholar]
- Lynden-Bell, D. The stability and vibrations of a gas of stars. Mon. Not. R. Astron. Soc. 1962, 124, 279. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987; pp. 347, 412, 437–439, 677. [Google Scholar]
- Kandrup, H.E. Violent relaxation, phase mixing, and gravitational Landau damping. Astrophys. J. 1998, 500, 120. [Google Scholar] [CrossRef]
- Vandervoort, P.O. On stationary oscillations of galaxies. Mon. Not. R. Astron. Soc. 2003, 339, 537. [Google Scholar] [CrossRef]
- Trigger, S.A.; Ershkovich, A.I.; van Heijst, G.J.F.; Schram, P.P.J.M. Kinetic theory of Jeans instability. Phys. Rev. E 2004, 69, 066403. [Google Scholar] [CrossRef] [PubMed]
- Christodoulou, D.M.; Laycock, S.G.T.; Kazanas, D. An objective classification scheme for solar-system bodies based on surface gravity. Galaxies 2024, 12, 74. [Google Scholar] [CrossRef]
- Showalter, M.R.; de Pater, I.; Lissauer, J.J.; French, R.S. The seventh inner moon of Neptune. Nature 2019, 566, 350. [Google Scholar] [CrossRef]
- Cabrera, J.; Csizmadia, S.Z.; Lehmann, H.; Dvorak, R.; Gandolfi, D.; Rauer, H.; Erikson, A.; Dreyer, C.; Eigmüller, P.H.; Hatzes, A.; et al. The planetary system to KIC 11442793: A compact analogue to the solar system. Astrophys. J. 2015, 781, 18. [Google Scholar] [CrossRef]
- Shallue, C.J.; Vanderburg, A. Identifying exoplanets with deep learning: A five-planet resonant chain around Kepler-80 and an eighth planet around Kepler-90. Astron. J. 2018, 155, 94. [Google Scholar] [CrossRef]
- Fulton, B.J.; Petigura, E.A. The California-Kepler Survey. VII. Precise planet radii leveraging Gaia DR2 reveal the stellar mass dependence of the planet radius gap. Astron. J. 2018, 156, 264. [Google Scholar] [CrossRef]
- Vogt, S.S.; Burt, J.; Meschiari, S.; Butler, R.P.; Henry, G.W.; Wang, S.; Holden, B.; Gapp, C.; Hanson, R.; Arriagada, P. Six planets orbiting HD 219134. Astrophys. J. 2015, 814, 12. [Google Scholar] [CrossRef]
- Rosenthal, L.J.; Fulton, B.J.; Hirsch, L.A.; Isaacson, H.T.; Howard, A.W.; Dedrick, C.M.; Sherstyuk, I.A.; Blunt, S.C.; Petigura, E.A.; Knutson, H.A.; et al. The California Legacy Survey. I. A catalog of 178 planets from precision radial velocity monitoring of 719 nearby stars over three decades. Astrophys. J. Suppl. 2021, 255, 8. [Google Scholar] [CrossRef]
- Judkovsky, Y.; Ofir, A.; Aharonson, O. Kepler multitransiting system physical properties and impact parameter variations. Astron. J. 2024, 167, 103. [Google Scholar] [CrossRef]
- Danielsson, L. The orbital resonances between the asteroid Toro and the Earth and Venus. Moon Planets 1978, 18, 265. [Google Scholar] [CrossRef]
- Jacobson, R.A. The orbits of the main Saturnian satellites, the Saturnian system gravity field, and the orientation of Saturn’s pole. Astron. J. 2022, 164, 199. [Google Scholar] [CrossRef]
- Jacobson, R.A. The orbits of the Uranian satellites and rings, the gravity field of the Uranian system, and the orientation of the pole of Uranus. Astron. J. 2014, 148, 76. [Google Scholar] [CrossRef]
- Showalter, M.R.; Hamilton, D.P. Resonant interactions and chaotic rotation of Pluto’s small moons. Nature 2015, 522, 45. [Google Scholar] [CrossRef]
- Stern, S.A.; Grundy, W.M.; McKinnon, W.B.; Weaver, H.A.; Young, L.A. The Pluto system after New Horizons. Ann. Rev. Astron. Astrophys. 2018, 56, 357. [Google Scholar] [CrossRef]
- Lovis, C.; Ségransan, D.; Mayor, M.; Udry, S.; Benz, W.; Bertaux, J.-L.; Bouchy, F.; Correia, A.C.M.; Laskar, J.; Lo Cuorto, G.; et al. The HARPS search for southern extra-solar planets XXVIII. Up to seven planets orbiting HD 10180: Probing the architecture of low-mass planetary systems. Astron. Astrophys. 2011, 528, A112. [Google Scholar] [CrossRef]
- Tuomi, M. Evidence for nine planets in the HD10180 system. Astron. Astrophys. 2012, 543, A52. [Google Scholar] [CrossRef]
- Kiefer, F.; Hébrard, G.; Etangs, A.L.d.; Martioli, E.; Dalal, S.; Vidal-Madjar, A. Determining the true mass of radial-velocity exoplanets with Gaia. Astron. Astrophys. 2021, 645, A7. [Google Scholar] [CrossRef]
- Mills, S.M.; Fabrycky, D.C. Mass, density, and formation constraints in the compact, sub-Earth Kepler-444 system including two Mars-mass planets. Astrophys. J. Lett. 2017, 838, L11. [Google Scholar] [CrossRef]
- Buldgen, G.; Farnir, M.; Pezzotti, C.; Eggenberger, P.; Salmon, S.J.A.J.; Montalban, J.; Ferguson, J.W.; Khan, S.; Bourrier, V.; Rendle, B.M.; et al. Revisiting Kepler-444, Astron. Astrophys. 2019, 630, A126. [Google Scholar]
- Weiss, L.M.; Isaacson, H.; Howard, A.W.; Fulton, B.J.; Petigura, E.A.; Fabrycky, D.; Jontof-Hutter, D.; Steffen, J.H.; Schlichting, H.E.; Wright, J.T.; et al. The Kepler Giant Planet Search. I. A decade of Kepler planet-host radial velocities from W. M. Keck Observatory. Astrophys. J. Suppl. 2024, 270, 8. [Google Scholar] [CrossRef]
- Rowe, J.F.; Coughlin, J.L.; Antoci, V.; Barclay, T.; Batalha, N.M.; Borucki, W.J.; Burke, C.J.; Bryson, S.T.; Caldwell, D.A.; Campbell, J.R.; et al. Planetary candidates observed by Kepler. V. Planet sample from Q1-Q12 (36 months). Astrophys. J. Suppl. 2015, 217, 16. [Google Scholar] [CrossRef]
- Jontof-Hutter, D.; Ford, E.B.; Rowe, J.F.; Lissauer, J.J.; Fabrycky, D.C.; Van Laerhoven, C.; Agol, E.; Deck, K.M.; Holczer, T.; Mazeh, T. Erratum: “Secure mass measurements from transit timing: 10 Kepler exoplanets between 3 and 8 M⊕ with diverse densities and incident fluxes”. Astrophys. J. 2021, 911, 154. [Google Scholar] [CrossRef]
- Leleu, A.; Deslisle, J.-B.; Udry, S.; Mardling, R.; Turbet, M.; Egger, J.A.; Alibert, Y.; Chatel, G.; Eggenberger, P.; Stalport, M. Removing biases on the density of sub-Neptunes characterised via transit timing variations. Astron. Astrophys. 2023, 669, A117. [Google Scholar] [CrossRef]
- Wolszczan, A.; Frail, D.A. A planetary system around the millisecond pulsar PSR1257+12. Nature 1992, 355, 145. [Google Scholar] [CrossRef]
- Konacki, M.; Wolszczan, A. Masses and orbital inclinations of planets in the PSR B1257+12 system. Astrophys. J. Lett. 2003, 591, L147. [Google Scholar] [CrossRef]
- Goździewski, K.; Konacki, M.; Wolszczan, A. Long-term stability and dynamical environment of the PSR 1257+12 planetary system. Astrophys. J. 2005, 619, 1084. [Google Scholar] [CrossRef]
- Wolszczan, A. Discovery of pulsar planets. New Astron. Rev. 2012, 56, 2. [Google Scholar] [CrossRef]
- Heller, R.; Rodenbeck, K.; Hippke, M. Transit least-squares survey. I. Discovery and validation of an Earth-sized planet in the four-planet system K2-32 near the 1:2:5:7 resonance. Astron. Astrophys. 2019, 625, A31. [Google Scholar] [CrossRef]
- Lillo-Box, J.; Lopez, T.A.; Santerne, A.; Nielsen, L.D.; Barros, S.C.C.; Deleuil, M.; Acuña, L.; Mousis, O.; Sousa, S.G.; Adibekyan, V.; et al. Masses for the seven planets in K2-32 and K2-233. Astron. Astrophys. 2020, 640, A48. [Google Scholar] [CrossRef]
- Rowe, J.F.; Bryson, S.T.; Marcy, G.W.; Lissauer, J.J.; Jontof-Hutter, D.; Mullally, F.; Gilliland, R.L.; Issacson, H.; Ford, E.; Howell, S.B.; et al. Validation of Kepler’s multiple planet candidates. III. Light curve analysis and announcement of hundreds of new multi-planet systems. Astrophys. J. 2014, 784, 45. [Google Scholar] [CrossRef]
- Steffen, J.H.; Fabrycky, D.C.; Agol, E.; Ford, E.B.; Morehead, R.C.; Cochran, W.D.; Lissauer, J.J.; Adams, E.R.; Borucki, W.J.; Bryson, S.; et al. Transit timing observations from Kepler—VII. Confirmation of 27 planets in 13 multiplanet systems via transit timing variations and orbital stability. Mon. Not. R. Astron. Soc. 2013, 428, 1077. [Google Scholar] [CrossRef]
- Masuda, K. Very low density planets around Kepler-51 revealed with transit timing variations and an anomaly similar to a planet-planet eclipse event, Astrophys. J. 2014, 783, 53. [Google Scholar] [CrossRef]
- Libby-Roberts, J.E.; Berta-Thompson, Z.K.; Désert, J.-M.; Masuda, K.; Morley, C.V.; Lopez, E.D.; Deck, K.M.; Fabrycky, D.; Fortney, J.J.; Line, M.R.; et al. The featureless transmission spectra of two super-puff planets. Astron. J. 2020, 159, 57. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D. A physical interpretation of the Titius-Bode rule and its connection to the closed orbits of Bertrand’s theorem. Res. Astron. Astrophys. 2017, 17, 129. [Google Scholar] [CrossRef]
- Steffen, J.H. Kepler’ s missing planets. Mon. Not. R. Astron. Soc. 2013, 433, 3246. [Google Scholar] [CrossRef]
- Ćuk, M.; El Moutamid, M.; Tiscareno, M.S. Dynamical history of the Uranian system. Planet. Sci. J. 2020, 1, 22. [Google Scholar] [CrossRef]
- Günther, M.N.; Pozuelos, F.J.; Dittman, J.A.; Dragomir, D.; Kane, S.R.; Daylan, T.; Feinstein, A.D.; Huang, C.X.; Morton, T.D.; Bonfanti, A.; et al. A super-Earth and two sub-Neptunes transiting the nearby and quiet M dwarf TOI-270. Nat. Astron. 2019, 3, 1099. [Google Scholar] [CrossRef]
- Van Eylen, V.; Astudillo-Defru, N.; Bonfils, X.; Livingston, J.; Hirano, T.; Luque, R.; Lam, K.W.F.; Justesen, A.B.; Winn, J.N.; Gandolfi, D.; et al. Masses and compositions of three small planets orbiting the nearby M dwarf L231-32 (TOI-270) and the M dwarf radius valley. Mon. Not. R. Astron. Soc. 2021, 507, 2154. [Google Scholar] [CrossRef]
- Kaye, L.; Vissapragada, S.; Günther, M.N.; Aigrain, S.; Mikal-Evans, T.; Jensen, E.L.N.; Parviainen, H.; Pozuelos, F.J.; Abe, L.; Acton, J.S.; et al. Transit timings variations in the three-planet system: TOI-270. Mon. Not. R. Astron. Soc. 2022, 510, 5464. [Google Scholar] [CrossRef]
- Mikal-Evans, T.; Madhusudhan, N.; Dittman, J.; Günther, M.N.; Welbanks, L.; Van Eylen, V.; Crossfield, I.J.M.; Daylan, T.; Kreidberg, L. Hubble Space Telescope transmission spectroscopy for the temperate sub-Neptune TOI-270 d: A possible hydrogen-rich atmosphere containing water vapor. Astron. J. 2023, 165, 84. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Polania Vivas, M.S.; D’Angiolillo, S.; Fernandez, A.N.; Quinn, T. exoMMR: A new python package to confirm and characterize mean motion resonances. Astron. J. 2023, 166, 94. [Google Scholar] [CrossRef]
- Borucki, W.J.; Koch, D.G.; Basri, G.; Batalha, N.; Brown, T.M.; Bryson, S.T.; Caldwell, D.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; et al. Characteristics of planetary candidates observed by Kepler II. Analysis of the first four months of data. Astrophys. J. 2011, 736, 19. [Google Scholar] [CrossRef]
- Teegarden, B.J.; Pravdo, S.H.; Hicks, M.; Lawrence, K.; Shaklan, S.B.; Covey, K.; Fraser, O.; Hawley, S.L.; McGlynn, T.; Reid, I.N. Discovery of a new nearby star. Astrophys. J. Lett. 2003, 589, L51. [Google Scholar] [CrossRef][Green Version]
- Zechmeister, M.; Dreizler, S.; Ribas, I.; Reiners, A.; Caballero, J.A.; Bauer, F.F.; Béhar, V.J.S.; González-Cuesta, L.; Herrero, E.; Lalitha, S.; et al. The CARMENES search for exoplanets around M dwarfs. Astron. Astrophys. 2019, 627, A49. [Google Scholar] [CrossRef]
- Dreizler, S.; Luque, R.; Ribas, I.; Koseleva, V.; Ruh, H.L.; Nagel, E.; Pozuelos, F.J.; Zechmeister, M.; Reiners, A.; Caballero, J.A.; et al. Teegarden’s star revisited. Astron. Astrophys. 2024, 684, A117. [Google Scholar] [CrossRef]
- Gillon, M.; Triaud, A.H.M.J.; Demory, B.-O.; Jehin, E.; Agol, E.; Deck, K.M.; Lederer, S.M.; de Wit, J.; Burdanov, A.; Ingalls, J.G.; et al. Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1. Nature 2017, 542, 456. [Google Scholar] [CrossRef]
- Agol, E.; Dorn, C.; Grimm, S.L.; Turbet, M.; Ducrot, E.; Delrez, L.; Gillon, M.; Demory, B.-O.; Burdanov, A.; Barkaoui, K.; et al. Refining the transit-timing and photometric analysis of TRAPPIST-1: Masses, radii, densities, dynamics, and ephemerides. Planet. Sci. J. 2021, 2, 1. [Google Scholar] [CrossRef]
- Mah, J. Formation and Dynamics of the Resonant Chain in the TRAPPIST-1 Exoplanet System. Master’s Thesis, The University of Hong Kong, Hong Kong, 2018. [Google Scholar]
- Ducrot, E.; Gillon, M.; Delrez, L.; Agol, E.; Rimmer, P.; Turbet, M.; Günther, M.N.; Demory, B.-O.; Triaud, A.H.M.J.; Bolmont, E.; et al. TRAPPIST-1: Global results of the Spitzer exploration science program Red Worlds. Astron. Astrophys. 2020, 640, A112. [Google Scholar] [CrossRef]
- Hirano, T.; Gaidos, E.; Winn, J.N.; Dai, F.; Fukui, A.; Kuzuhara, M.; Kotani, T.; Tamura, M.; Hjorth, M.; Albrecht, S.; et al. Evidence for spin-orbit alignment in the TRAPPIST-1 system. Astrophys. J. Lett. 2020, 890, L27. [Google Scholar] [CrossRef]
- Pichierri, G.; Morbidelli, A.; Batygin, K.; Brasser, R. The formation of the TRAPPIST-1 system in two steps during the recession of the disk inner edge. Nat. Astron. 2024, 8, 1408. [Google Scholar] [CrossRef]
- Dai, F.; Masuda, K.; Beard, C.; Robertson, P.; Goldberg, M.; Batygin, K.; Bouma, L.; Lissauer, J.J.; Knudstrup, E.; Albrecht, S.; et al. TOI-1136 is a young, coplanar, aligned planetary system in a pristine resonant chain. Astron. J. 2023, 165, 33. [Google Scholar] [CrossRef]
- Beard, C.; Robertson, P.; Dai, F.; Holcomb, R.; Lubin, J.; Akana Murphy, J.M.; Batalha, N.M.; Blunt, S.; Crossfield, I.; Dressing, C.; et al. The TESS-Keck Survey. XVII. Precise mass measurements in a young, high-multiplicity transiting planet system using radial velocities and transit timing variations. Astron. J. 2024, 167, 70. [Google Scholar] [CrossRef]
- Polanski, A.S.; Lubin, J.; Beard, C.; Akana Murphy, J.M.; Rubenzahl, R.; Hill, M.L.; Crossfield, I.J.M.; Chontos, A.; Robertson, P.; Isaacson, H.; et al. The TESS-Keck Survey. XX. 15 new TESS planets and a uniform RV analysis of all survey targets. Astrophys. J. Suppl. 2024, 272, 32. [Google Scholar] [CrossRef]
- Hardegree-Ullman, K.K.; Christiansen, J.L.; Ciardi, D.R.; Crossfield, I.J.M.; Dressing, C.D.; Livingston, J.H.; Volk, K.; Agol, E.; Barclay, T.; Barentsen, G.; et al. K2-138 g: Spitzer spots a sixth planet for the Citizen Science System. Astron. J. 2021, 161, 219. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Feil, L.; Quinn, T.; Rice, D. Confirming the 3:2 resonance chain of K2-138. Astron. J. 2022, 163, 162. [Google Scholar] [CrossRef]
- Hara, N.C.; Bouchy, F.; Stalport, M.; Boisse, I.; Rodrigues, J.; Delisle, J.-B.; Santerne, A.; Henry, G.W.; Arnold, L.; Astudillo-Defru, N.; et al. The SOPHIE search for northern extrasolar planets. XVI. HD 158259: A compact planetary system in a near-3:2 mean motion resonance chain. Astron. Astrophys. 2020, 636, L6. [Google Scholar] [CrossRef]
- Vallenari, A.; Brown, A.G.A.; Prusti, T.; de Bruijne, J.H.J.; Arenou, F.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Ducourant, C.; Evans, D.W.; et al. (Gaia Collaboration) Gaia Data Release 3. Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar]
- Barros, S.C.C.; Demangeon, O.D.S.; Alibert, Y.; Leleu, A.; Adibekyan, V.; Lovis, C.; Bossini, D.; Sousa, S.G.; Hara, N.; Bouchy, F.; et al. HD 23472: A multi-planetary system with three super-Earths and two potential super-Mercuries. Astron. Astrophys. 2022, 665, A154. [Google Scholar] [CrossRef]
- Christiansen, J.L.; Bhure, S.; Zink, J.K.; Hardegree-Ullman, K.K.; Adkins, B.D.; Hedges, C.; Morton, T.D.; Bieryla, A.; Ciardi, D.R.; Cochran, W.D.; et al. Scaling K2. V. Statistical validation of 60 new exoplanets from K2 campaigns 2–18. Astron. J. 2022, 163, 244. [Google Scholar] [CrossRef]
- Lissauer, J.J.; Jontof-Hutter, D.; Rowe, J.F.; Fabrycky, D.C.; Lopez, E.D.; Agol, E.; Marcy, G.W.; Deck, K.M.; Fischer, D.A.; Fortney, J.J.; et al. All six planets known to orbit Kepler-11 have low densities. Astrophys. J. 2013, 770, 131. [Google Scholar] [CrossRef]
- Bedell, M.; Bean, J.L.; Meléndez, J.; Mills, S.M.; Fabrycky, D.C.; Freitas, F.C.; Ramírez, I.; Asplund, M.; Liu, F.; Yong, D. Kepler-11 is a solar twin: Revising the masses and radii of benchmark planets via precise stellar characterization. Astrophys. J. 2017, 839, 94. [Google Scholar] [CrossRef]
- Quintana, E.V.; Barclay, T.; Raymond, S.N.; Rowe, J.F.; Bolmont, E.; Caldwell, D.A.; Howell, S.B.; Kane, S.R.; Huber, D.; Crepp, J.R.; et al. An Earth-sized planet in the habitable zone of a cool star. Science 2014, 344, 277. [Google Scholar] [CrossRef] [PubMed]
- Berger, T.A.; Huber, D.; Gaidos, E.; van Saders, J.L. Revised radii of Kepler stars and planets using Gaia Data Release 2. Astrophys. J. 2018, 866, 99. [Google Scholar] [CrossRef]
- Thompson, S.E.; Coughlin, J.L.; Hoffman, K.; Mullally, F.; Christiansen, J.L.; Burke, C.J.; Bryson, S.; Batalha, N.; Haas, M.R.; Catanzarite, J.; et al. Planetary candidates observed by Kepler. VIII. A fully automated catalog with measured completeness and reliability based on Data Release 25. Astrophys. J. Suppl. 2018, 235, 38. [Google Scholar] [CrossRef]
- Quinn, T.; MacDonald, M.G. Confirming resonance in three transiting systems. Astron. J. 2023, 166, 58. [Google Scholar] [CrossRef]
- Barclay, T.; Quintana, E.V.; Adams, F.C.; Ciardi, D.R.; Huber, D.; Foreman-Mackey, D.; Montet, B.T.; Caldwell, D. The five planets in the Kepler-296 binary system all orbit the primary: A statistical and analytical analysis. Astrophys. J. 2015, 809, 7. [Google Scholar] [CrossRef]
- Becker, J.C.; Adams, F.C. Effects of unseen additional planetary perturbers on compact extrasolar planetary systems. Mon. Not. R. Astron. Soc. 2017, 468, 549. [Google Scholar] [CrossRef]
- Lari, G.; Saillenfest, M. The nature of the Laplace resonance between the Galilean moons. Celest. Mech. Dyn. Astr. 2024, 136, 19. [Google Scholar] [CrossRef]
- Henrard, J.; Lemaitre, A. A second fundamental model for resonance. Celest. Mech. 1983, 30, 197. [Google Scholar] [CrossRef]
- Delisle, J.-B.; Laskar, J.; Correia, A.C.M.; Boué, G. Dissipation in planar resonant planetary systems. Astron. Astrophys. 2012, 546, A71. [Google Scholar] [CrossRef]
- Batygin, K.; Morbidelli, A. Analytical treatment of planetary resonances. Astron. Astrophys. 2013, 556, A28. [Google Scholar] [CrossRef]
- Torres, G.; Fressin, F.; Batalha, N.M.; Borucki, W.J.; Brown, T.M.; Bryson, S.T.; Buchhave, L.A.; Charbonneau, D.; Ciardi, D.R.; Dunham, E.W.; et al. Modeling Kepler light curves as false positives: Rejection of blend scenarios for Kepler-9, and validation of Kepler-9 d, a super-Earth-size planet in a multiple system. Astrophys. J. 2011, 727, 24. [Google Scholar] [CrossRef]
- Borsato, L.; Malavolta, L.; Piotto, G.; Buchhave, L.A.; Mortier, A.; Rice, K.; Cameron, A.C.; Coffinet, A.; Sozzetti, A.; Charbonneau, D.; et al. HARPS-N radial velocities confirm the low densities of the Kepler-9 planets. Mon. Not. R. Astron. Soc. 2019, 484, 3233. [Google Scholar] [CrossRef]
- Faridani, T.H.; Naoz, S.; Li, G.; Rice, M.; Inzunza, N. More likely than you think: Inclination-driving secular resonances are common in known exoplanet systems. Astrophys. J. 2025, 978, 18. [Google Scholar] [CrossRef]
- Antoniadou, K.I.; Libert, A.-S. Exploiting periodic orbits as dynamical clues for Kepler and K2 systems. Astron. Astrophys. 2020, 640, A55. [Google Scholar] [CrossRef]

| System | Global MMR chains with LRs | ||||||
|---|---|---|---|---|---|---|---|
| Radial position in LR: | |||||||
| Galilean moons | 1:4 | 1:2 | 1:1 | 7:3 | |||
| HIP 41378 | 1:4 | 1:2 | 1:1 | 9:2 | 6:1 | 9:1 | |
| Radial position in LR: | |||||||
| GJ 876 | 1:32 | 1:2 | 1:1 | 2:1 | |||
| HR 8799 | 1:2 | 1:1 | 2:1 | 9:2 | |||
| K-176 | 2:9 | 1:2 | 1:1 | 2:1 | |||
| HD | 1:15 | 1:7 | 1:2 | 1:1 | 2:1 | 48:1 | |
| 1/9 | 1/6 | 1/3 | K-20 |
| 1/5 | 1/3 | HD 10180 | |
| 2/3 | HD 34445 | ||
| 1/4 | 2/3 | K-55 | |
| 1/8 | 1/5 | 1/3 | TR-1 |
| 3/7 | TOI-178 | ||
| 1/6 | 1/3 | 5/9 | K-20 |
| 1/2 | K2-384 | ||
| 1/4 | 1/2 | TOI-1136 | |
| 1/4 | 1/2 | 2/3 | K2-268 |
| 3/4 | TOI-1136 | ||
| 1/3 | 1/2 | 3/4 | TR-1, K2-384 (GSs) |
| 2/7 | 3/7 | 2/3 | K2-138, HD 158259 |
| 1/2 | 3/4 | 1 | TR-1, K-90, K2-384, TOI-1136 |
| 2/3 | K-223, K2-268 [K-1542] | ||
| 1/3 | 2/3 | 1 | K-51, K-62, K-82 [K-11] |
| 5/9 | K-20 | ||
| 1/4 | 3/5 | 1 | K-33 |
| 1/2 | HIP 41378 (LR) | ||
| 2/3 | K-55 | ||
| 1/5 | 1/3 | 1 | HD 10180 |
| 1/2 | HD 40307, K-154 | ||
| 2/3 | HD 34445 | ||
| 2/5 | 2/3 | 1 | K-11 |
| 2/7 | 2/5 | 1 | HD 191939 |
| 4/7 | K-238 | ||
| 5/9 | K-186, K-296 | ||
| 3/7 | 2/3 | 1 | K2-138, HD 158259, TOI-178 |
| 4/9 | HD 110067, HD 23472, K-102 (GSs) |
| 3/2 | K-32, K-84 [TR-1, TOI-1136] | ||
| 5/3 | HD 40307, TOI-2076, K-150 [K-90] | ||
| 1/2 | 1 | 2 | GJ 876, HR 8799, K-176, HD 219134 (LRs) |
| 7/3 | K-30, K2-32 | ||
| 8/5 | K-154 | ||
| 4/3 | HD 10180 | ||
| 1/3 | 1 | 3/2 | K-80 [K-11] |
| 7 | HD 20781 | ||
| 5/3 | HD 23472, K-102 | ||
| 4/3 | TOI-178, K-223 | ||
| 2/3 | 1 | 3/2 | K-11, K2-138, HD 158259, HD 110067 (GSs) |
| 14/5 | K2-268 | ||
| 5 | HD 34445 | ||
| 2/5 | 1 | 3/2 | B1257+12 |
| 14/5 | HD 191939 | ||
| 3/2 | K-33, K-305 | ||
| 7/4 | K-292 | ||
| 3/5 | 1 | 2 | TOI-270 |
| 9/4 | HD 108236 | ||
| 6 | K-169 | ||
| 3/4 | 1 | 3/2 | TR-1, TOI-1136, K-226 |
| 5/3 | K-90 |
| 1 | 3/2 | 2 | HD 110067 |
| 7/3 | K-80 | ||
| 5 | K2-138 | ||
| 3 | K-84, K-305 | ||
| 8/5 | 3 | K-154 | |
| 1 | 5/3 | 8/3 | K-90 |
| 5/2 | HD 40307 | ||
| 4/3 | 5/2 | HD 10180 |
| 16/25 | 4/5 | 1 | K-444 (GS) | |
| 4/5 | 1 | 4/3 | K-60 | |
| 1 | 7/4 | 7/3 | TOI-700 | |
| 1 | 7/3 | 7/2 | K2-32 | |
| 3/7 | 2/3 | TOI-178 | ||
| 1/5 | 1/3 | 1/2 | TR-1 | |
| 3/10 | 3/5 | K-292 | ||
| Unique principal MMR chains: | ||||
| 1/6 | 1/3 | 1 | HD 20781 | |
| 1/8 | 1/2 | 1 | K-32 | |
| Obviously empty 2:1 MMRs: | ||||
| 3/2 | 3 | 5 | K-84 | |
| 3/2 | 7/3 | 3 | K-80 | |
| 1 | 8/5 | 3 | K-154 | |
| A detached 2:9 MMR and a unique 5:6 MMR: | ||||
| 2/9 | 4/9 | 2/3 | 1 | HD 23472 (GS) |
| 1/2 | 2/3 | 5/6 | 1 | K-1542 |
| Exosystem | ||
|---|---|---|
| Name | (mau) | (mau) |
| Exosystems with adjusted values of | ||
| HD 40307 | 38.7 | |
| K-48 | 24.9 | |
| K-51 | 112.9 | |
| K-62 | 39.8 | |
| K-80 | 08.3 | |
| K-176 | 15.9 | |
| K-186 | 18.1 | |
| K-332 | 30.9 | |
| K-363 | 22.5 | |
| K-444 | 05.7 | |
| B1257+12 | 65.7 | |
| 07.4 | ||
| Exosystems with | ||
| HD 110067 | 40.0 | 37.7 |
| K-223 | 30.0 | 29.6 |
| K-254 | 20.6 | 16.5 |
| K-292 | 17.6 | 14.7 |
| K-305 | 18.2 | 17.4 |
| TOI-270 | 15.0 | 14.3 |
| Exosystems with | ||
| HD 20781 | 48.2 | 51.2 |
| HD 108236 | 28.4 | 28.5 |
| HD 219134 | 85.0 | 88.5 |
| K-20 | 70.0 | 74.1 |
| K-84 | 33.0 | 35.9 |
| K-102 | 22.3 | 26.3 |
| K-226 | 10.2 | 13.9 |
| K-1542 | 6.3 | 8.3 |
| HIP 41378 | 74.0 | 74.1 |
| 55 Cnc | 113.4 | 114.5 |
| Exosystems with unknown (set to ) | ||
| K-150 | 29.2 | (29.2) |
| K-154 | 48.6 | (48.6) |
| K-169 | 30.0 | (30.0) |
| K-296 | 26.2 | (26.2) |
| K2-268 | 20.3 | (20.3) |
| TOI-700 | 46.0 | (46.0) |
| Exosystem | ||||
|---|---|---|---|---|
| Name | (mau) | (mau) | (mau) | Scale |
| K-9 | 57.0 | 62.7 | 5.7 | 1.10 |
| K-33 | 33.0 | 38.7 | 5.7 | 1.17 |
| K2-233 | 33.8 | 41.9 | 8.1 | 1.24 |
| TOI-1136 | 35.0 | 43.9 | 8.9 | 1.25 |
| K-11 | 42.0 | 52.4 | 10.4 | 1.25 |
| TOI-178 | 23.0 | 29.8 | 6.8 | 1.30 |
| K2-32 | 20.6 | 27.1 | 6.5 | 1.32 |
| HD 23472 | 25.0 | 33.8 | 8.8 | 1.35 |
| K2-138 | 17.4 | 23.6 | 6.2 | 1.36 |
| GJ 806 | 21.1 | 29.1 | 8.0 | 1.38 |
| K-60 | 12.4 | 18.1 | 5.7 | 1.46 |
| HD | 60.0 | 98.0 | 38.0 | 1.63 |
| HD 134606 | 50.0 | 83.6 | 33.6 | 1.67 |
| K-82 | 68.0 | 121.3 | 53.3 | 1.78 |
| K2-384 | 14.0 | 24.9 | 10.9 | 1.78 |
| GJ 357 | 37.1 | 67.0 | 29.9 | 1.81 |
| K-90 | 60.0 | 116.6 | 56.6 | 1.94 |
| TR-1 | 7.0 | 13.8 | 6.8 | 1.97 |
| HD | 10.0 | 25.2 | 15.2 | 2.52 |
| K-238 | 33.0 | 112.3 | 79.3 | 3.40 |
| K-55 | 32.4 | 122.7 | 90.3 | 3.79 |
| K-32 | 20.0 | 82.3 | 62.3 | 4.12 |
| Row | Satellite | Inner | ||
|---|---|---|---|---|
| No. | System | Moon | (Mm) | (Mm) |
| 1 | Galilean | Ganymede | 406.0 | 398.6 |
| 2 | Uranian | Umbriel | 65.0 | 57.0 |
| 3 | Saturnian | Dione | 41.0 | |
| 4 | Haumean | Namaka | 16.6 | 17.1 |
| 5 | Plutonian | Hydra | 8.8 | 8.7 |
| 6 | Neptunian | Proteus | 7.4 | |
| 7 | Martian | Phobos | 0.2 |
| Exoplanet Name (s) | g (m s−2) | Identification |
|---|---|---|
| K-51 b,d,c | 0.762, 0.624, 0.538 | DP, DP, DP |
| K-90 g | 2.22 | DP |
| K-444 f,d,e | 4.53, 2.31, 1.94 | P, DP, DP |
| K-176 d,e | 7.68, 1.08 | P, DP |
| K-223 d,e | 2.85, 2.22 | P, DP |
| K2-138 g,f | 4.66, 1.89 | P, DP |
| HIP 41378 d,f | 3.60, 1.39 | P, DP |
| TR-1 d | 4.71 | P |
| HIP 9618 b | 6.44 | P |
| TOI-178 d | 4.46 | P |
| TOI-270 b | 8.85 | P |
| TOI-1136 d | 3.66 | P |
| HD 23472 f | 5.84 | P |
| HD 108236 e | 8.76 | P |
| HD 110067 f | 7.30 | P |
| HD 191939 d | 3.06 | P |
| K-9 c | 4.49 | P |
| K-11 f | 3.64 | P |
| K-20 e | 9.02 | P |
| K-30 d | 3.01 | P |
| K-32 f | 7.12 | P |
| K-33 d | 3.68 | P |
| K-36 c | 5.16 | P |
| K-80 b | 4.20 | P |
| K-82 c | 4.78 | P |
| K-102 e | 9.78 | P |
| K2-32 b | 6.57 | P |
| Body | P | ||
|---|---|---|---|
| Name | (d) | (d) | (%) |
| TR-1 d | 4.050 | 4.050 | 0.01 |
| K-60 c | 8.918 | 8.919 | 0.01 |
| K2-138 d | 5.405 | 5.385 | 0.37 |
| K-226 c | 5.350 | 5.319 | 0.58 |
| Larissa a | 0.556 | 0.568 | 2.11 |
| K-176 c | 12.759 | 12.469 | 2.33 |
| Dione b | 2.737 | 2.641 | 3.64 |
| K-238 c | 6.156 | 6.424 | 4.17 |
| K-80 d | 3.072 | 3.210 | 4.30 |
| HD 158259 d | 5.198 | 4.962 | 4.76 |
| HD 110067 d | 20.520 | 19.564 | 4.89 |
| K-1542 b | 3.951 | 4.159 | 5.00 |
| K2-32 b | 8.992 | 9.499 | 5.34 |
| Europa c | 3.551 | 3.822 | 7.09 |
| K-305 b | 5.487 | 5.930 | 7.47 |
| Body | |||
| Name | (d) | (d) | (%) |
| HD 34445 d,c | 166.270 | 166.311 | 0.02 |
| K-292 c,d | 5.386 | 5.377 | 0.17 |
| B1257+12 b,c | 45.902 | 46.300 | 0.86 |
| K-62 c,d | 15.303 | 15.512 | 1.35 |
| K-169 c,d | 7.272 | 7.430 | 2.13 |
| TOI-178 c,d | 4.898 | 5.009 | 2.22 |
| Ariel, d Umbriel d | 3.333 | 3.259 | 2.27 |
| K-444 c,d | 5.368 | 5.611 | 4.33 |
| K-84 b,c | 10.804 | 10.249 | 5.41 |
| HD 10180 c,i | 7.707 | 7.302 | 5.55 |
| K2-268 d,e | 5.330 | 5.030 | 5.96 |
| Body | P | ||
|---|---|---|---|
| Name | (yr) | (yr) | (%) |
| Saturn a | 29.457 | 29.364 | 0.32 |
| HR 8799 d | 111.092 | 115.580 | 3.88 |
| Group | Actual MMR Chains | System | Integer | Local | |||||
|---|---|---|---|---|---|---|---|---|---|
| No. | (Common MMRs) | Names | Ratios | MMR Pairs | |||||
| (1) | 1/2 | 1 | 2 | GJ 876, HR 8799, HD 219134, K-176 | 1:2:4 (LRs) | ||||
| 1/4 | 1/2 | 1 | HIP 41378, Galilean LR | (2 types [23]) | |||||
| (2) | 4/9 | 2/3 | 1 | HD 110067, HD 23472, K-102 | 4:6:9 | ||||
| 2/3 | 1 | 3/2 | HD 110067, HD 158259, K-11, K2-138 | (GSs) | |||||
| 1/3 | 1/2 | 3/4 | TR-1, K2-384 | ( [24]) | |||||
| (3) | 1 | 3/2 | 2 | HD 110067 | 2:3:4 | ||||
| 2/3 | 1 | 4/3 | TOI-178, K-223 | (Laplace-like) | |||||
| 1/2 | 3/4 | 1 | TR-1, TOI-1136, K-90, K2-384 | (3 types [23]) | |||||
| 1/18 | 1/12 | 1/9 | Saturn | ||||||
| (4) | 3/4 | 1 | 3/2 | TR-1, TOI-1136, K-226 | 3:4:6 | ||||
| 1/2 | 2/3 | 1 | K-223, K2-268 | ||||||
| 1/3 | 4/9 | 2/3 | K-102 | ||||||
| 1/12 | 1/9 | 1/6 | Saturn | ||||||
| (5) | 1/4 | 1/2 | 3/4 | TOI-1136 | 1:2:3 | ||||
| 1/6 | 1/3 | 1/2 | K2-384 | ||||||
| 1/3 | 2/3 | 1 | K-51, K-62, K-82 | ||||||
| 1/2 | 1 | 3/2 | K-32, K-84, Uranus | ||||||
| (6) | 1/9 | 1/6 | 1/3 | K-20 | 2:3:6 | ||||
| 1/6 | 1/4 | 1/2 | TOI-1136 | ||||||
| 1/5 | 3/10 | 3/5 | K-292 | ||||||
| 1 | 3/2 | 3 | K-84, K-305 | ||||||
| (7) | 1/6 | 1/3 | 1 | HD 20781 | 1:2:6 | ||||
| 1/2 | 1 | 9/2 | K-48, HIP 41378 | 1:2:9 | |||||
| 1/3 | 1 | 4/3 | HD 10180 | 1:3:4 (Pluto) | |||||
| 1/8 | 1/2 | 1 | K-32 | 1:4:8 | |||||
| (8) | 2/3 | 1 | 5/3 | HD 23472, K-102 | 2:3:5 | ||||
| 2/9 | 4/9 | 2/3 | HD 23472 | 2:4:6 | |||||
| 2/7 | 4/7 | 1 | K-238 | 2:4:7 | |||||
| 2/9 | 4/9 | 1 | K-332 | 2:4:9 | |||||
| 2 | 9/2 | HR 8799 | |||||||
| 1/3 | 1 | 3/2 | K-80 | 2:6:9 | |||||
| (9) | 1/2 | 2/3 | 5/6 | K-1542 | 3:4:5 (Pluto) | ||||
| 1 | 5/3 | 8/3 | K-90 | 3:5:8 | |||||
| 1 | 5/3 | 3 | K-296 | 3:5:9 | |||||
| 1/4 | 1/2 | 2/3 | K2-268 | 3:6:8 | |||||
| (10) | 2/3 | 5/6 | 1 | K-1542 | 4:5:6 (Pluto) | ||||
| Group | System | Integer | Local | Coefficients | Phase | Likely | |
|---|---|---|---|---|---|---|---|
| No. | Names | Ratios | MMR Pairs | LCs | |||
| (1) | GJ 876, HR 8799, HD 219134, K-176 | 1:2:4 (LRs) | 1 | 2 | |||
| HIP 41378, Galilean LR | (2 types [23]) | ||||||
| (2) | HD 110067, HD 23472, K-102 | 4:6:9 | 2 | 3 | |||
| HD 110067, HD 158259, K-11, K2-138 | (GSs) | ||||||
| TR-1, K2-384 | ( [24]) | [13,19,21] | |||||
| (3) | HD 110067 | 2:3:4 | 2 | 4 | |||
| TOI-178, K-223 | (Laplace-like) | ||||||
| TR-1, TOI-1136, K-90, K2-384 | (3 types [23]) | ||||||
| Saturn | |||||||
| (4) | TR-1, TOI-1136, K-226 | 3:4:6 | 3 | 3 | |||
| K-223, K2-268 | or | ||||||
| K-102 | |||||||
| Saturn | |||||||
| (5) | TOI-1136 | 1:2:3 | 1 | 3 | |||
| K2-384 | |||||||
| K-51, K-62, K-82 | [13,19,21] | ||||||
| K-32, K-84, Uranus | |||||||
| (6) | K-20 | 2:3:6 | 2 | 2 | |||
| TOI-1136 | No | ||||||
| K-292 | Librationsa,b | ||||||
| K-84, K-305 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christodoulou, D.M.; Laycock, S.G.T.; Kazanas, D. A Library of 77 Multibody Solar and Extrasolar Subsystems—A Review of Their Dynamical Properties, Global Mean-Motion Resonances, and the Landau-Damped Mean Tidal Fields. Astronomy 2025, 4, 11. https://doi.org/10.3390/astronomy4030011
Christodoulou DM, Laycock SGT, Kazanas D. A Library of 77 Multibody Solar and Extrasolar Subsystems—A Review of Their Dynamical Properties, Global Mean-Motion Resonances, and the Landau-Damped Mean Tidal Fields. Astronomy. 2025; 4(3):11. https://doi.org/10.3390/astronomy4030011
Chicago/Turabian StyleChristodoulou, Dimitris M., Silas G. T. Laycock, and Demosthenes Kazanas. 2025. "A Library of 77 Multibody Solar and Extrasolar Subsystems—A Review of Their Dynamical Properties, Global Mean-Motion Resonances, and the Landau-Damped Mean Tidal Fields" Astronomy 4, no. 3: 11. https://doi.org/10.3390/astronomy4030011
APA StyleChristodoulou, D. M., Laycock, S. G. T., & Kazanas, D. (2025). A Library of 77 Multibody Solar and Extrasolar Subsystems—A Review of Their Dynamical Properties, Global Mean-Motion Resonances, and the Landau-Damped Mean Tidal Fields. Astronomy, 4(3), 11. https://doi.org/10.3390/astronomy4030011










