Shell Universe: Reducing Cosmological Tensions with the Relativistic Ni Solutions

Abstract

Recent discoveries of massive galaxies existing in the early universe, as well as apparent anomalies in Ω_m and H₀ at high redshift, have raised sharp new concerns for the ΛCDM model of cosmology. Here, we address these problems by using new solutions for the Einstein field equations of relativistic compact objects originally found by Ni. Applied to the universe, the new solutions imply that the universe’s mass is relatively concentrated in a thick outer shell. The interior space would not have a flat, Minkowski metric, but rather a repulsive gravitational field centered on the origin. This field would induce a gravitational redshift in light waves moving inward from the cosmic shell and a corresponding blueshift in waves approaching the shell. Assuming the Milky Way lies near the origin, within the KBC Void, this redshift would make H₀ appear to diminish at high redshifts and could thus relieve the Hubble tension. The Ni redshift could also reduce or eliminate the requirement for dark energy in the ΛCDM model. The relative dimness of distant objects would instead arise because the Ni redshift makes them appear closer to us than they really are. To account for the CMB temperature–redshift relation and for the absence of a systematic blueshift in stars closer to the origin than the Milky Way, it is proposed that the Ni redshift and blueshift involve exchanges of photon energy with a photonic spacetime. These exchanges in turn form the basis for a cosmic CMB cycle, which gives rise to gravity and an Einsteinian cosmological constant, Λ. Black holes are suggested to have analogous Ni structures and gravity/Λ cycles.

1. Introduction

The ΛCDM model of cosmology, featuring dark matter, dark energy and cosmological expansion, continues to enjoy wide acceptance by cosmologists. In recent years, however, it has encountered significant new challenges. Observations with the JWST have revealed massive, bright galaxies existing when the universe was only ~500 Myr old, far earlier than galaxy formation models allow [1]. The cosmological principle, a cornerstone of modern cosmology, is also increasingly open to question, with numerous indications that the universe is not so homogeneous after all [2,3]. Vast structures such as the Keenan–Barger–Cowie (KBC) Void, within which the Milky Way resides, have been difficult to explain [4]. At the same time, older problems of the ΛCDM model persist with no resolution in sight. Despite much effort, it has not been possible to resolve the Hubble tension, for example, or to identify plausible candidates for either dark matter or dark energy. The hypothesis of cosmic inflation remains unsubstantiated.

An additional recent challenge has been an apparent evolution at increasing redshifts in the matter density Ω_m (from lower to higher) and the Hubble constant H₀ (from higher to lower) within the flat ΛCDM framework. In quasars, an empirical relation between the x-ray and ultraviolet luminosities has allowed them to be used as effective standard candles across a wide range of redshifts and luminosities [5]. The quasar data are consistent with an increase in Ω_m values towards 1 at higher redshifts, suggesting a transition at z ≈ 1 from a dark energy-dominated universe to a matter-dominated one [6]. Similar redshift-dependent trends in Ω_m and H₀ have also been seen in Type Ia SN data [6,7]. The trend in Ω_m also leads to differing S₈ values when comparing early and late universe measurements.

In this paper, we suggest that the route to relieving these cosmological tensions lies in a different morphology of the universe. Recent findings in general relativity suggest that the universe’s mass may not be distributed homogeneously but rather in a shell-like configuration. A new class of solutions for the equations of state of neutron stars was found in 2011 by Jun Ni [8]. Neslušan [9,10,11] subsequently modified Ni’s solutions and then applied them to relativistic compact objects (RCOs) (e.g., white dwarfs, black holes) and larger objects, such as quasars. Recently, deLyra et al. [12] put these modified solutions into a more general form.

The Ni solutions are characterized by the presence of a central matter void and a singularity also centered on the origin. The singularity represents the center of an outwardly acting, repulsive gravitational field. One consequence of this field is that the interior metric of a spherical shell would no longer be flat and Minkowski, as is generally assumed in general relativity. Photons moving inwardly from the shell towards the origin accordingly acquire a redshift in the Ni metric, their energy lost to the gravitational field, while photons moving from the interior towards the shell are blue-shifted [12].

Applying the Ni solutions on the cosmic scale would imply an analogous shell structure for the observable universe. A rough comparison with the solutions for RCOs suggests that the outer surface of this shell could be situated at or beyond the Hubble radius and the inner surface at perhaps one-third to one-half this distance, possibly in the redshift range z~0.5–1. Supposing the Milky Way lies very close to the origin of the shell, within the KBC Void, the observed flows of matter away from the void could be consistent with the repulsive Ni field. A Ni shell configuration would also be consistent with the findings of massive galaxies and a superabundance of neutral hydrogen in the early universe.

The shell morphology, if real, could conceivably have evolved slowly over time or have existed as a quasi-permanent feature from the earliest days. Within the ΛCDM framework, the latter possibility could imply a shell or series of shells expanding outwards from a point coinciding with the origins event. The persistent shell morphology in this case might be incorporated as a ‘static’ term in the expanding metric. On the other hand, the anomalies could also be consistent with the cosmic mass density having always been concentrated in a relatively static outer shell. In either case, the presence of the KBC Void and other anomalies suggest that such a primordial organization persists to some degree in the universe today.

Significantly, the Ni solutions would also imply that the Hubble redshift can no longer be uniquely attributed to the expansion of the universe. Instead, it would arise at least partly from the Ni redshift. A hybrid approach involving a Ni redshift and an expansion redshift is not unfeasible. Gupta [13] showed that a tired light (TL) redshift combined with the cosmological redshift could potentially extend the universe’s age, thus alleviating the problem of too massive galaxies in the early universe. The Ni redshift could replace Gupta’s TL redshift in this approach while avoiding the problems of TL models with respect to the CMB temperature distribution and SN time dilation [14]. The time dilation seen in remote SNe would arise from the gravitational redshift induced by the Ni metric. This same gravitational redshift would also induce a redshift of CMB photons moving inwardly from the shell, while a matching blueshift would be seen in CMB photons going back toward the shell. As will be shown, this would create a spatial pattern in CMB temperature (T_CMB) similar to the one observed. In this case, measurements of remote T_CMB could reflect CMB temperatures not only as they existed at those distances long ago, but also to some extent as they exist at those same distances today.

The Ni shell model nonetheless encounters a serious problem not shared with TL models. Unless the Milky Way was positioned at the very center of the shell universe, there should be CMB temperatures cooler than 2.73 K found in zones closer to the center than we are. This possibility could be tested for since those nearby regions have not been systematically investigated for directional anomalies in T_CMB. However, in those same regions of space, there should also be stars that, under the Ni approach, would exhibit a systematic blueshift at our position. No such blueshift signature has ever been observed.

Our proposed solution to this problem will involve a different conceptualization of spacetime. Adapting earlier proposals, we suggest that the energy lost from photons in the Ni redshift is absorbed in a photonic spacetime. The stored energy is later released by spacetime to photons moving toward the shell in the Ni blueshift. As described herein, the energy gap between starlight photons, CMB photons and the photonic spacetime would then ensure that starlight photons experience a one-way Ni redshift.

With this refinement, it will be shown that the Ni approach could potentially relieve some of the major tensions in cosmology. Not only could it address the anomalies in Ω_m, H₀ and S₈, but in doing so could also reduce or eliminate the requirement for dark energy to account for cosmic acceleration. The SN observations that suggest cosmic acceleration would instead be explained with distant galaxies being further away from us than currently estimated.

The aims of this paper are thus to resolve the theoretical problems of the Ni approach concerning the CMB and the unobserved stellar blueshifts and thus demonstrate its internal consistency. Some significant possible roles of the Ni approach in cosmology and physics will also be highlighted. To this end, we will employ a simple toy model that maximizes the shell factor and the static (nonexpanding) component. In this model, the CMB near the shell will be shown to have T_CMB~29 K and energy density u = 5.3 × 10⁻⁹ erg cm⁻³~Λ. We will show that the static Ni component can mimic the expansion-only component with respect to Hubble redshift, T_CMB and Λ. From there, following Gupta’s approach, the path forward would be to integrate the two components to various degrees and temporal sequences in various models.

The paper is organized as follows. In Section 2, the Ni approach to solving the equations of state in relativistic compact objects is reviewed and then applied to the universe. In Section 3, the stellar blueshift problem is examined in connection with the Hubble redshift, the T_CMB-redshift relationship and SN time dilation. Our proposed solution is then given that spacetime is photonic in nature and that the Hubble redshift is actually a multiphotonic process, in which the CMB attempts to reach thermal equilibrium with spacetime. In Section 4, the toy model of the Ni approach is presented and used to describe a possible CMB cycle for gravity and Λ. In Section 5, we discuss some possible cosmological tests of the model. The Ni shell model is then used to reexamine the structures of black holes and other RCOs in Section 6. Some general conclusions are made in Section 7.

2. Ni Shell Universe with Repulsive Gravitational Field

We begin with a discussion of the Ni solutions of the Einstein field equations (EFEs) of relativistic compact objects and their application to a shell universe. Our descriptions are drawn from Neslušan [9,10,11] and deLyra et al. [12]. Historically, the first kinds of solutions of these equations to be found for spherically symmetrical neutron stars were the Tolman–Oppenheimer–Volkoff (TOV) solutions. In these solutions, the energy density and pressure invariably reach their maximum values at the center of the object. The TOV solutions have largely remained the central basis for our understanding of these objects today. In 2011, however, Jun Ni [8] found that the TOV solutions are just a small subclass of a much larger superclass of possible solutions.

In Ni’s new solutions, matter is not concentrated at the object’s center as with the TOV solutions. Instead, a void appears at the center, such that the object has both an exterior and an interior surface. Ni found the solutions by using a novel integration technique. Whereas Oppenheimer and Volkoff started the integration of the EFEs at the center of the object, Ni started at a finite distance from the star’s center and performed the integration in two parts, moving inward and outward. Ni’s solutions were subsequently modified by Neslušan to take into account the interface boundary conditions of the two surfaces [9,10,11]. These modified solutions were recently put into a general form by deLyra et al. [12] to describe liquid and gaseous spherical shells. The general solutions can thus be termed the Ni–Neslušan–deLyra (NND) solutions or, more simply, the Ni solutions.

In general, for a spherical matter shell with inner radius r₁, outer radius r₂ and an energy density between these boundaries that is constant with r, the solution of the EFEs in the inner vacuum region, where r < r₁, leads to an integration constant, r_μ. This constant determines the singularities in the inner vacuum region. Singularities are avoided only if r_μ = 0, and r_μ by convention is thus often set to 0. The Ni approach is to start in the outer vacuum region (r > r₂), where the exterior Schwarzschild solution holds, and use the continuity of the solution in the two boundaries of the shell to determine the constant r_μ. Imposition of the surface boundary conditions leads to the result that r_μ > 0 and, consequently, that the solutions do contain a singularity at the origin. This singularity is not related to a concentration of matter at the origin, however, but rather to a repulsive gravitational field centered on the origin.

This repulsive gravitational field imparts spacetime curvature to the interior space of a spherical shell. In GR, the standard description of the metric in this space is that it is flat and Minkowski, such that the gravitational forces on a test particle cancel out everywhere inside. Here, GR follows Newtonian gravity with its familiar shell theorem. With the Ni solutions, however, there arises a relativistic contraction of radial lengths in the interior space compared to the exterior. The true physical volume of the interior space is thus smaller than its apparent coordinate volume. The gravitational field associated with this curvature can then be interpreted as repulsive with respect to the origin. Unless at the very center, a test particle in the interior region (r < r₁) will thus be attracted towards the shell, while a test particle in the exterior space of the shell (r > r₂) is attracted inwardly towards the shell. At the point of maximum pressure inside the matter region of the shell, the inwardly and outwardly acting forces cancel out. The repulsive gravitational field thus tends to stabilize the shell. A Newtonian analogy for this unexpected situation depicts the gravitational force behaving as 1/r^2+ε, with ε << 1 [12]. Under these conditions, a test particle is attracted more strongly to the side of the shell nearest to it than the more distant side. The repulsive field also tends to drive matter away from the origin.

Many astrophysical implications could arise from this. In RCOs, for example, the suggestion by Oppenheimer and Volkoff that in the absence of an internal energy source a star having a mass above a certain limit (later the Oppenheimer–Volkoff limit) would collapse below its event horizon would no longer hold. Alternative models of neutron stars, other RCOs and quasars have been proposed which incorporate a central void and repulsive interior field [9,10,11].

Most critically, were the universe to have an analogous Ni shell structure, the repulsive gravitational field would affect masses and photons in the interior region, where r < r₁ [12]. The flows of matter away from the KBC Void, for example, could be consistent with this repulsive Ni field. Photons traveling inward from the shell would be redshifted and lose energy to the gravitational field. This could account for a portion of the Hubble redshift. Conversely, photons traveling outward towards the shell would be blue-shifted and therefore gain energy from the gravitational field.

A Ni shell universe is shown schematically in Figure 1. It is patterned after Ni shell structures given by deLyra et al. [12]. On the far left, at position 1, is the presumed location of the Milky Way near the origin. The repulsive gravitational field and Ni redshift are seen to be at their maximum near the origin, as indicated by the derivative of the EFE function ν(r). The higher Ni redshift in this region could account for the higher values of the Hubble redshift (72–75 km s^–1 Mpc^–1) measured using Cepheid variables in this region. Near position 2, however, the derivative ν’(r) starts to diminish and then drops to zero inside the shell (position 3). The lower values found for the Hubble constant measured in the Planck and other studies use ΛCDM model assumptions regarding the CMB and expansion rate. The value for H₀ found in this way (67–68 km s^–1 Mpc^–1) could reflect a value for ν’(r) weighted over the entire interior space and so be much lower than the one obtained locally through the Cepheids. This could resolve the Hubble tension.

The Ni approach to dark energy would be similar. Dark energy is needed in the ΛCDM model to explain the unexpected dimness of remote Type 1a SNe compared to nearby ones. This is explained by dark energy dominating the late universe, thereby allowing galaxies to recede from each other at faster rates. Within the Ni universe, however, the Hubble redshift distance for an object at position 2 would falsely place that object at position 2′. The underestimated distance could account for its diminished apparent luminosity. The amount of cosmic acceleration and dark energy needed to explain it could therefore be reduced or even eliminated entirely in a Ni model. In addition to the elusiveness of dark energy, other theoretical difficulties remain with it. For example, its energy density is far below the amount predicted to exist from quantum field theory.

As already noted, the Ni approach introduces a static component to ΛCDM models similar to the TL component used by Gupta in his hybrid model [13]. This inclusion permits the universe to have an age greater than 13.8 Gyr, thus potentially addressing the early galaxy formation problem. The matter distribution would no longer be homogeneous but instead would generally increase from a minimum value near the origin to a maximum in the midpoint of the shell (Figure 1). The relative void at the origin may have originated in the early or late universe and shifted in magnitude and width over time. Detailed models would combine individual contributions of the Ni metric and expanding FLRW (or other) metric in various weightings and scenarios.

Black Hole Universe

A shell universe patterned on Ni’s solutions for neutron stars might be expected to share other properties with RCOs. With a huge reservoir of baryonic or dark matter potentially existing in the outer shell, the observable universe could have the critical density $\rho$_c needed to form a black hole universe (BHU). Many models of a black hole universe have previously been proposed [15,16,17,18,19,20,21], but the premise of an external Schwarzschild metric enclosing an expanding Friedmann–Lemaître–Robertson–Walker (FLRW) interior metric has been considered problematic [22,23]. In addition, the many mechanisms suggested for avoiding a singularity in black holes and other compact objects, e.g., [24,25,26,27,28,29,30,31,32,33,34], do not appear readily applicable to a BHU.

By contrast, in a Ni shell BHU, the exterior and interior metrics would be continuous at both the inner and outer shell boundaries. It would also have a built-in mechanism for avoiding collapse into a singularity. The interior repulsive gravitational field would act to push matter and radiation away from the origin and towards the shell, thus stabilizing it against collapse. Lacking a mass singularity, the observable universe would not be a true black hole, but perhaps an analogue of one of the relativistic structures already suggested as alternatives to black holes. These include thin spherical shells [29,30,31]; black shells [32]; dark energy stars [33] and gravastars [34]. By comparison with Ni shell models [9,10,12], the cosmic shell of baryonic and/or dark matter could have a considerable thickness, perhaps as much as 0.3–0.5 R_U.

The Ni shell in the BHU could consist simply of massive galaxies or gas clouds having large amounts of hydrogen and/or dark matter. If this hydrogen has enough mass to account for the CMB perturbations alone, then the necessity of including dark matter in this case could also be reduced. Neslušan [11] suggested that large objects like quasars could have a Ni shell structure, with the repulsive field perhaps mimicking the gravitational effects of dark matter halos.

3. Photonic Spacetime

We next address the stellar blueshift problem that arises in a Ni shell universe. As mentioned earlier, unless the Milky Way were positioned at the exact origin of the shell universe, there should be some stars closer to the origin than we are that would exhibit a Ni blueshift as seen by us. Since such a pattern has not been observed, this presents a serious obstacle to a Ni shell universe which must first be resolved.

Our suggested solution to this problem involves a specific conceptualization of spacetime. Within the Ni framework, deLyra et al. [12] suggested that photons moving inwards from the shell lose energy to the gravitational field, while photons moving outwardly towards the shell conversely gain energy from this field. The question that arises is where and how is this energy stored in the gravitational field? One possibility is to have a spacetime that is photonic in character. In this case, the energy that is lost to the gravitational field by inwardly moving CMB photons could be absorbed by this photonic spacetime. This stored energy could later be returned to outwardly moving CMB photons in the corresponding Ni blueshift. In Section 4, it will be suggested that the Ni redshift and blueshift form the basis for a cosmic CMB cycle for gravity and Λ.

Let us first review the T_CMB problem in TL models [14] (for a general discussion of the historical roles of the CMB in cosmology, see [35]). In the ΛCDM model, the CMB temperature, T_z, at a redshift z increases according to the relationship,

$$T_z=T_0\left(1+z\right),$$

(1)

where T₀ = 2.726 K is the average CMB temperature today [36]. Here, the CMB photons originate from the surface of last scattering at the time of recombination, with T_z ≈ 3000 K and redshift z ≈ 1100. Evidence in favor of Equation (1) is found with the presumed CMB heating of atoms and molecules in remote gas clouds [37]; in the Sunyaev–Zeldovich (SZ) effect [38] and with water molecules at the very high redshift of 6.34 [39].

The temperature–redshift relationship for the CMB follows from some basic relations for a photon gas:

$$u={\displaystyle \frac{U}{V}}={\displaystyle \frac{4\sigma }{c}}{T}^4,$$

(2)

$$P={\displaystyle \frac{1}{3}}{\displaystyle \frac{U}{V}}={\displaystyle \frac{4\sigma }{3c}}{T}^4,$$

(3)

$$n={rT}^3,$$

(4)

where $U$ is the total energy, V the volume, u the energy density, P the pressure, T the temperature, n the photon number density, r a constant and σ the Stefan–Boltzmann constant (see, e.g., [40]). In a laboratory system, a photon gas is in constant contact with matter, such that equilibration between photons and baryons maintains the blackbody spectrum appropriate for the system. In the ΛCDM model, the CMB photons after leaving the surface of last scattering are only able to retain their blackbody spectrum by virtue of cosmological expansion. This allows the energy density and photon number of the CMB to diminish in the correct manner.

Significant deviations from Equation (1) would be possible indications of other processes at work, such as a decaying vacuum energy density [41]. A net photon production or destruction over time would give T_CMB(z) $\propto$(1 + z)^{(1 − β)}, with β ≠ 0. A positive β would be consistent with net photon production until today, while β < 0 would imply photon destruction. With no clear evidence thus far for a non-zero β, however, a basic challenge for the Ni shell universe is how to retain the CMB blackbody signature over time. The CMB photon energy would vary as (1 + z)⁻¹, but the photon number density would remain constant.

3.1. Paired-Photon Vacuum

With a photonic model of spacetime, the Ni approach can address the T_CMB and supernova time dilation problems in TL models, as well as the stellar blueshift problem. In models of gravity and astro/geophysics, spacetime has previously been modeled as a network of graviton filaments linking all the particles of the observable universe, with the graviton subunits being photonic in nature [42,43]. The photonic energy in the graviton filaments connecting any two masses was assumed to be equal in magnitude to their mutual gravitational potential energy. This arrangement allows spacetime to be continuously updated at each point in space by the masses embedded within it, as required in general relativity. Information concerning a particle’s velocity or spin, for example, would be continuously encoded and carried away from it by gravitons. In this picture, particles act essentially as reprocessing centers for gravitons, converting gravitons with older, outdated information originating from remote masses into newer ones carrying updated information about local particles.

The paired-photon vacuum (PPV) model of Annila and coworkers can also be integrated with this scheme (Figure 2) [44,45,46]. In the PPV model, the vacuum likewise consists of filaments of spin-2 gravitons, but with the latter occurring as overlapping pairs of in-phase and antiphase spin-1 photons. In their overlapping, double-stranded state, the photons do not exert electromagnetic forces but still have energy density. When pushed into hotter states, however, the photon pairs unwind and the now single-stranded, non-overlapping photons (e.g., CMB photons) do exert electromagnetic forces. The spectral density of the paired-photon vacuum in their model has the same form as blackbody radiation.

From these considerations, it is evident that such a photonic spacetime can be treated as a quasi-photon gas. Like the CMB, it would have analogous values for energy density u_s, pressure p_s, temperature T_s and photon number n_s (where the subscripts ‘s’ denote spacetime). Since the CMB contributes the largest energy component to electromagnetic radiation fields, even in the local universe, the CMB and spacetime pools at all locations would thus exchange energy primarily with each other. This would tend to bring these two photon gases into thermal equilibrium at each point in space, such that everywhere T_s = T_CMB. From Equation (2), we would then also have u_s = u at each point. A laboratory model for such a spacetime could even exist. Recent work has shown that light pulses propagating in optical fibers organize themselves in the manner of ordinary gases [47].

A spacetime with variable photon content could account for the energy transfers in the Ni redshift and blueshift. Spacetime at all points in space would be capable of exchanging energy with the CMB or other electromagnetic waves directly, mediating their photon number in the process.

3.2. Hubble Redshift of CMB versus Stellar Photons

We can now finally address the question of why CMB photons can be either red-shifted or blue-shifted in the Ni approach, whereas starlight photons are invariably red-shifted. Using the photonic spacetime model, the Ni redshift can be viewed as a multiphotonic process operating on wave trains of photons. Stellar surfaces have effective temperatures thousands of degrees higher than that of the CMB at any point in the universe. This gives rise to a critical difference in how the Ni redshift would operate on CMB photons versus ordinary starlight.

Consider first the CMB photons. As will be shown in Section 4, the CMB at its peak strength in the shell would have T_CMB = T_shell~29 K and u~5 × 10⁻⁹ erg cm⁻³. At its weakest position, possibly near our location, the respective values are 2.7 K and 4 × 10⁻¹³ erg cm⁻³. As it moves from the shell toward the interior, an array of CMB photons would transfer energy to spacetime packets it encounters along the way. The photon wavelengths in the array would thus increase, while its values for u and n would decrease: the Ni redshift. Conversely, an array of ‘cooler’ CMB photons moving from the interior back towards the shell encounters regions of progressively ‘hotter’ and denser spacetime, with higher T_CMB and T_s. With energy equipartition the CMB wavelengths would accordingly diminish, while the values for u and n would increase: the Ni blueshift.

In the case of starlight, however, there would only be a Ni redshift. A sunlike star has T_Eff~6000 K. Its photon energies thus vastly exceed those of CMB photons at any point within the universe. With the assumption that T_s = T_CMB at each point in space, the equipartition of energy between starlight, spacetime and the CMB would invariably result in a one-way redshift for starlight photons.

As discussed in Section 4, mechanisms for gravity and Λ can then potentially exploit the difference between the energies of CMB photons entering or leaving a specific zone of space with those of CMB photons that are characteristic of that zone. In each zone, the decrease in T_CMB due to the Ni redshift is balanced by an increase arising from the analogous Ni blueshift. In a sense, there would be two equal and opposite β terms in operation, such that overall β = 0.

3.3. Supernova Time Dilation

The Ni approach must also be able to account for the observed time dilation in supernovae. As noted earlier, this is a problem for TL models generally [14]. In the ΛCDM model, time dilation arises due to expansion of spacetime since the time of the stellar explosion. The light curve of the distant supernova is stretched in the observer’s frame by a factor (1 + z) compared to the SN rest frame [48].

Since the Ni redshift in a shell universe is a gravitational redshift, however, time intervals in events recorded in the light from these sources would also be stretched by a factor of (1 + z), just as in other situations where the gravitational redshift arises. At the same time, regions of space closer to the origin than the Milky Way would be at higher points in the Ni gravitational well. Observations of a slight time contraction in events in these regions could thus be indicative of a Ni metric in action.

4. CMB Cycle for Gravity and Λ

We next consider some possible wider implications of the Ni approach in physics and cosmology, specifically with respect to gravity and the cosmological constant, Λ. As the Ni solutions are based on general relativity, there is in a sense no need to prescribe special mechanisms for gravity and Λ in a Ni universe. It is generally conceptualized in GR that gravity is already fully described without adding such mechanisms. In a similar fashion, shell stability is already guaranteed in the Ni solutions without further modifications (Neslušan, personal communication). On the other hand, the goal of unifying gravity with the other forces requires that gravity be described in a more physical, quantum form. In this sense, the CMB cycle now proposed could be seen as the quantum manifestation of the Ni solutions in action. In this context, it should be noted that Carnot cycles for the CMB have previously been discussed within the ΛCDM framework [40,49,50,51].

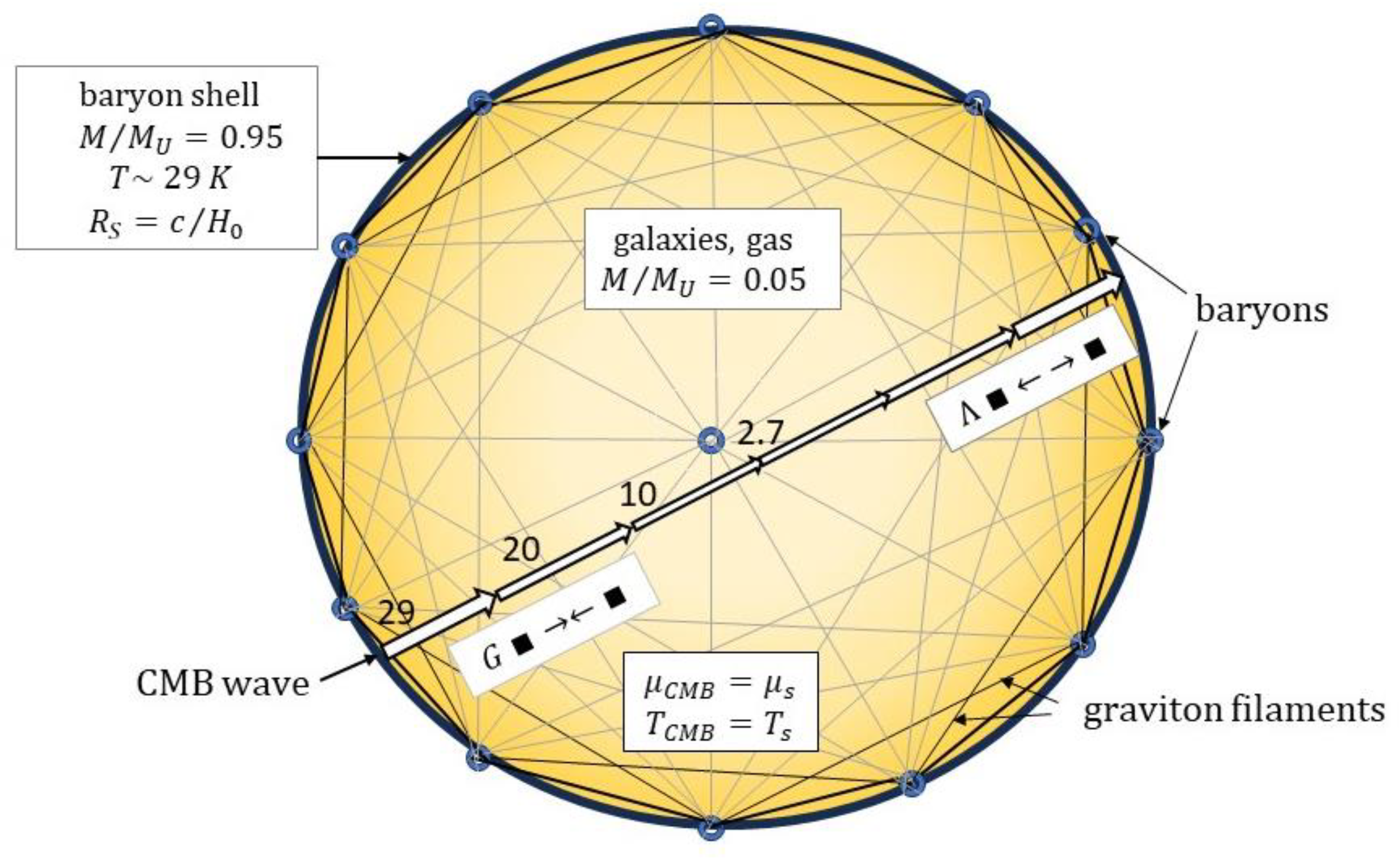
To examine the CMB cycle, we employ a simple toy model in which the static Ni component is maximized (Figure 3). For simplicity, we take the matter of the universe here to be entirely baryonic and concentrated in an ultrathin rather than a thick shell positioned near the Hubble radius, R_U. We suppose this thin shell essentially holds all the universe’s mass, the small effects due to galaxies, gas and dust in the interior region being neglected for now. The network of graviton (paired photon) filaments is then seen to have its highest density nearest the shell and its lowest density near the center, which is assumed to be close to the Milky Way. It is assumed that the CMB does not substantially leak out to an exterior space. Such a space would not exist anyway in the ΛCDM model, but possibly could in the Ni approach with a reduced expansion component (Figure 1). In this case, the provision that the universe has BHU properties might then be necessary to constrain the CMB.

The gradients in spacetime density and T_CMB then form the basis for the CMB cycle. CMB photons originating at the shell are redshifted as they move towards the interior space. The lost photon momentum is transferred to the graviton filaments connecting masses and then to the masses themselves, pushing them together. Increasing spacetime curvature at one position, through the gravitation of masses, would necessarily be balanced by spacetime relaxation—and thus mass separation—elsewhere in the universe. By symmetry, the energy released by spacetime in this process would be transferred back to photons. As discussed below, abundant evidence already exists for such an energy release in a variety of masses and mass systems [42,43,52,53,54].

In Figure 3, the universe is shown as having concentric zones of space each having a uniform CMB temperature. The outermost zone near the shell is estimated below to have T_CMB~29 K and thus u~5.3 × 10⁻⁹ erg cm⁻³. This is 10⁴ times that of the zone nearest our position, where T_CMB = 2.73 K and u = 4.2 × 10⁻¹³ erg cm⁻³. As the CMB photons move inwards from the shell they would lose energy and momentum to spacetime filaments. As discussed below, this could lead to gravitational work being done, in the unconventional sense of masses being pushed together. During this cooling phase, the CMB photon number and energy density in these inwardly moving waves would diminish.

After reaching the innermost points on their trajectories, the energy-depleted CMB photons then proceed onwards toward the shell. During this phase, the photons pass through regions of progressively higher spacetime density and thus regain energy due to equilibration with spacetime. As discussed below, the rate of energy gain here on the cosmic level yields the Hubble luminosity output, c⁵/4G. With this release of energy, spacetime curvature is relaxed and masses are pushed apart.

4.1. Hubble Luminosity

The CMB in this scheme could have key possible roles both in forming the Ni shell structure and in maintaining its stability thereafter. The shell would be stabilized against gravitational collapse by blue-shifted CMB photons. The CMB would thus be the placeholder for a positive cosmological constant Λ in the Einsteinian sense. It would not have a uniform value at each point in space, but instead would increase from its minimum at the center of the universe to its maximum value at the shell, tracking the CMB energy density (Figure 3).

This novel form of Λ would be closely connected to gravitation. Since the energy of the graviton filaments of spacetime consists of real energy quanta, the sum of their total energies within a shell universe of essentially fixed mass and radius must have a finite value. This implies that the total quantity $\left|U\right|$ is fixed also. When two particles approach each other in gravitation, increasing their share of the total $\left|U\right|$, other spacetime filaments must diminish in energy by amounts which offset this energy increase. To have symmetry with the Hubble redshift, wherein photon energy is absorbed into spacetime filaments, the reverse process would be a transfer of photon energy from spacetime to other photons, leading to a blueshift of the latter.

The Ni blueshift of graviton filaments in each mass or system of masses would then give rise to an effective ‘Hubble luminosity’, given by

$$L_{\mathrm{H}}=-U{H}_0,$$

(5)

where $U$ is the internal gravitational potential energy (conventionally negative). Evidence for such a process can be found in the excess energy releases seen in planets, white dwarfs, neutron stars and supermassive black holes (SMBHs) (Figure 4) [52,53]. In geophysics, it also forms the basis for a different model of plate tectonics, in which the release of core energy drives a slow expansion of the mantle [54].

The Hubble luminosity of the universe would stabilize the universe against gravitational collapse via the CMB blueshift and Λ. The gravitational and Λ forces can be shown to balance at the shell, where r = R_U = c/H₀. The gravitational potential energy of the baryonic Ni shell is

$$U=-{\displaystyle \frac{G{M}^2}{R_U}}.$$

(6)

Since H₀ = c/R_U, the Hubble luminosity from Equation (5) is then

$$L_{\mathrm{H}}={\displaystyle \frac{G{M}^2{H}_0}{R_U}}={\displaystyle \frac{G{M}^{2}c}{R_U^2}}.$$

(7)

Using the black hole mass–radius relationship, we have R_S = R_U = 2GM/c². Substituting for R_U in Equation (7), we have

$$L_{\mathrm{H}}={\displaystyle \frac{c^5}{4G}}=9.1\times {10}^{58}erg{s}^{-1}.$$

(8)

Since a photon of energy E has momentum E/c, the sum of the forces associated with this power is then

$$F={\displaystyle \frac{c^4}{4G}}=3.0\times {10}^{48}dynes.$$

(9)

By comparison, the sum of all the inwardly acting forces on the particles of the shell, in the Newtonian approximation, is

$$F_g=-{\displaystyle \frac{G{M}^2}{R_U^2}}.$$

(10)

Once again, making the substitution for R_U, the magnitude in Equation (10) becomes equal to that of Equation (9). The inward forces of attraction thus precisely balance the outward forces of repulsion at the shell. The Hubble luminosity can thus ensure stability of the baryon shell against gravitation. As noted in Section 2, the Ni solutions for a spherical shell imply that any particles leaving the shell tend to be pushed back towards the shell.

The power c⁵/4G and force c⁴/4G have long attracted interest as a possible maximum power and maximum force in the universe, possibly even reflected in the field equations of general relativity [31,55,56,57,58]. The so-called ‘Dyson luminosity’ would be just the Hubble luminosity of the observable universe. In Section 6, it will be suggested that similar values for the Hubble luminosity occur in all black hole-like objects.

4.2. CMB as Λ

We next consider how the CMB can be associated with Λ. The shell T_CMB can first be estimated using the Hubble luminosity. Since we have assumed that electromagnetic radiation is trapped within the shell, any radiation emitted from the shell must be redirected inwards towards the origin. The CMB temperature in the shell is then effectively determined by the shell baryon temperature. Under equilibrium conditions, the rate at which CMB radiation leaves the shell, expressed as a redirected bolometric luminosity, must be equal to the rate at which radiation returns to the shell as blue-shifted CMB waves. The effective shell temperature in this case can then be estimated as

$$T_{\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{l}}={\left({\displaystyle \frac{L_{\mathrm{H}}}{4\pi R_U^2\sigma }}\right)}^{{\displaystyle \frac{1}{4}}},$$

(11)

where σ is the Stefan–Boltzmann constant = 5.67 × 10⁻⁵ erg cm⁻² s⁻¹ K⁻⁴. With L_H = c⁵/4G from Equation (5) and R_U = c/H₀, we find T_shell = 29 K.

In and near the shell the CMB would thus have T_CMB $\cong$ 29 K and a corresponding energy density u $\cong$ 5.3 × 10⁻⁹ erg cm⁻³. By comparison, recent measurements from the Planck Collaboration for the ΛCDM model give a strikingly similar vacuum energy density ρ_vac = 5.36 × 10⁻⁹ erg cm⁻³. Despite the different assumptions used, this is consistent with the CMB energy functioning as the cosmological constant Λ in the static Einsteinian sense.

T_CMB near the shell can also be estimated using broad assumptions of cosmic evolution and energy balance. The proto-CMB in a Ni universe would presumably have arisen from gravitational energy released by a collapsing baryon cloud, this energy being captured within the Schwarzschild radius (see [59] for a similar scenario in the ΛCDM model). With its shell structure, the total gravitational potential energy of the universe is given by Equation (6). The density of this gravitational energy would then be u_g = −$U$/V = GM²/(4/3πR_U⁴). From the black hole mass–radius relationship R_S = 2GM/c² and with R_S = R_U we then obtain a gravitational energy density of

$$u_g={\displaystyle \frac{3c^2{H}_0^2}{16\pi G}}.$$

(12)

This density, expressed in terms of mass, corresponds to half the cosmic critical density of the ΛCDM model, ρ_c = 3H₀²/8πG. For H₀ = 67 km s⁻¹ Mpc⁻¹ = 2.2 × 10⁻¹⁸ s⁻¹ gm⁻¹, we find u_g = 3.9 × 10⁻⁹ erg cm⁻³. This would match the density of a uniform CMB throughout the universe with T_CMB = 27 K. If T_CMB values in the model range from ~0 at the center to ~29 at the shell, then this value for u would not be unreasonable. Its similarity to the value for Λ in the ΛCDM model is again suggestive of a link between the CMB and Λ.

As a further check on our general approach, the rate of energy loss by spacetime via the Hubble luminosity should equal the rate at which energy is absorbed by it from CMB photons in the Ni redshift. For the Ni universe this equality can be written as uVH₀ = c⁵/4G. This condition is once again satisfied for u = 3.9 × 10⁻⁹ erg cm⁻³ and for a uniform T_CMB~27 K, consistent with the other estimates given above.

4.3. Gravity from CMB Photons

The other half of the suggested CMB cycle is the process whereby the Ni redshift drives gravity. A detailed treatment of gravity employing the Ni solutions will be deferred to a future paper. Here a preliminary framework for gravity is briefly given based on our earlier work.

The basic premise of an optical material spacetime—as filaments of photonic gravitons interlinking all masses—was used in earlier models of ‘optical gravity’ [42,43]. These models were based on a subtheme in general relativity which treats relativistic light deflection as refraction of light in an optical medium with a varying density gradient [60,61,62,63,64,65,66,67]. This optical analogy has been used in numerous studies of gravitational lensing and simulation of black holes [68,69,70] and in gravity models featuring spacetime as a material medium [71,72,73,74]. Within this context, the possibility that gravity arises from the absorption of CMB photon energy in a photonic spacetime was previously considered [42]. The local CMB of 2.7 K was found to have insufficient energy to drive gravity, however, and so, in a later proposal, gravity was powered instead by photons released in the Hubble luminosity [43].

The two approaches can be unified, however, with the provision that the Hubble luminosity reenergizes redshifted CMB photons and the recognition that the hotter CMB in remote regions closer to the shell does have enough energy to drive gravity. Under the Ni redshift, energy from inwardly moving, ‘hotter’ CMB photons would be transferred to the optical filaments of spacetime, inducing gravity in the masses to which they are fixed.

If the Hubble luminosity converts graviton energy, expressed as $\left|U\right|$, to photon energy, then, for reasons of symmetry, gravity must simply result from the reverse process of converting photon energy to graviton energy. In this process, the quantity $\left|U\right|$ between gravitating masses is increased. The Ni redshift could then be considered once again as a spacetime absorption effect raising the cosmic values for $\left|U\right|$.

The linear absorption coefficient and mass absorption coefficient of light can then be estimated and used to derive a classical gravitational force as previously [42,43]. For ordinary matter, this pressure is conventionally given as p = u/3, which includes terms for the incident and emitted radiation. Since the CMB photon energy absorbed by graviton filaments is only reradiated later, where it generates Λ, the effective pressure arising on graviton filaments through absorption would be just one-half this, i.e., p = u/6. Adjusting the value found in [42] accordingly, we find a suitable value for G is obtained if u = 5.5 × 10⁻⁹ erg cm⁻³. This corresponds to a uniform CMB with T_CMB~29 K, which is once again consistent with other values given above for the outermost regions of the shell universe.

4.4. Conservation of Energy and Entropy

The static Ni component could also have major implications regarding energy and entropy conservation in the observable universe. To the extent that the Ni component dominates the Hubble redshift, the latter would not endlessly deplete electromagnetic energy. At each point in space the energy density of CMB radiation u would be equal to that of the photonic spacetime at that point and thus also to the gravitational energy density there, i.e., u = u_s ≡ u_g. These equalities would also hold for the observable universe. Energy would be conserved under the Ni redshift, since the lost photon energy would be converted to spacetime energy, i.e., du/dt = −du_s/dt. With the action of the Hubble luminosity, spacetime energy reenergizes CMB photons, such that on the cosmic scale the two pools of energy would be equal. The gradual conversion of all the universe’s mechanical energy to thermal energy, ultimately culminating in a ‘heat death’ of the universe, would be avoided. Nor would matter fall into one heap as a singularity, since the energy stored in spacetime is returned to CMB photons, in the process restoring Λ. Regarding the Ni contribution alone, the universe would function as a perpetuum mobile, with all its energy forms being interconvertible at rates proportional to H₀.

4.5. Evolutionary Processes

As discussed in Section 4.2, a Ni shell universe could have arisen by the initial collapse of a baryon cloud. Simultaneous capture of the radiation released in the gravitational infall in this case could then have given rise to the nascent CMB (Equation (12)). A similar process had earlier been invoked for the origin of the CMB within the ΛCDM framework [59]. Due to the mass-radius relationship of black holes, a proto-universe of fixed mass could not have increased in size through cosmological expansion while at the same time remaining a black hole. Just as in ordinary black holes, however, it could have grown by accretion, capturing dust and gas at the rim until reaching its current size. Inside the proto-universe, smaller black holes could also have formed at any time and likewise have grown through accretion. The youngest of these would presumably be out at the expanding rim. In this case, observations of stars and galaxies near the Hubble radius could match predictions of the ΛCDM model, as they would similarly have a younger look. The general pattern might then be one of successive waves of black hole-like structures emanating from interior regions of the observable universe, engulfing extant structures encountered. Voids would arise with the counterbalancing of the Hubble luminosity and gravity, in a manner perhaps akin to the forces operating in soap bubbles.

5. Cosmological Tests of the Ni Model

As we have emphasized, the Ni relativistic solutions potentially open a new window onto some of the perplexing problems of the ΛCDM model. Following Gupta’s hybrid TL + expansion approach, these solutions can in principle be combined with various expansion metrics to reshape the observable cosmos. To the extent that the ΛCDM components of expansion, dark energy and dark matter predominate, the tests of this hybrid approach would reduce to those of the ΛCDM model, albeit modified to incorporate certain Ni effects. Apart from the recent cosmological tensions highlighted above, the ΛCDM model has passed numerous cosmological tests. On the other hand, to the extent that the Ni component predominates in a hybrid model, the Ni model must then be shown to pass these same tests or at least the ones that do not presuppose cosmological expansion. The easiest way to achieve this is once again to isolate the Ni contributions in a static model (Figure 3).

5.1. CMB Tests

As mentioned earlier, measuring T_CMB at different points in space potentially affords a method of testing for a Ni contribution to the Hubble redshift. The validity of the temperature-distance relationship for the CMB is only well established for redshifts less than z~3. Such measurements may not be feasible in the regions deep within the shell. Recent observations from the JSWT have up to this point not found galaxies with spectroscopically confirmed redshifts larger than z~14. If these were the galaxies closest to the shell midpoint, then simply applying the relationship from Equation (1) would yield T_CMB~41 K at this position. However, as can be seen in Figure 1, the Hubble constant decreases towards the shell and falls to 0 at the midpoint. In this case, T_CMB would not increase linearly with distance in the remote range. Moreover, as discussed in Section 4, other considerations favor a cooler shell with T_shell~29 K. Measurements of T_CMB at high redshifts could thus afford a means of testing for a Ni shell effect.

A potentially better testing ground for the Ni approach could be in the central regions closer to us. If the origin of the Ni universe roughly coincides with the center of the KBC Void, as suggested above, the Milky Way would be just slightly off-center with respect to the shell. In this case, T_CMB might drop further than 2.7 K in regions closer to the origin than we are. However, searching for nearby anisotropies in T_CMB could be problematic. A CMB with T_CMB = 1 K, for example, would have an energy density of only 2% of that of the 2.7 K CMB. Its peak wavelength could thus be obscured by other radiation known to exist in that range. A further possibility is that T_CMB cools to a minimal but non-zero temperature in the central region incorporating our position. This could arise, for example, through the Hubble luminosity that is specific to galaxies and galaxy filaments, which we have not considered here. Possessing only 5% of the universe’s mass, the Hubble luminosity of this component would be lower than the cosmic value by a factor of ~2.5 × 10⁻³. Yet this small luminosity could still be enough to generate a temperature of a few degrees K at the center. This energy output could have a role in preventing bulk aggregation of galactic matter, analogous to the role of the CMB in generating Λ.

More detailed tests of the Ni shell model would involve reinterpretation of CMB anisotropy data from Planck, COBE, WMAP and other studies to search for signatures of a cold hydrogen shell. Just as this data was used to characterize the primordial mass configuration in the ΛCDM model, it might likewise allow structural details of a Ni shell to be revealed, such as its thickness and whether it has a dual or composite structure. As noted above, the observed anomalies in Ω_m and S₈ already lend support to a shell morphology. In a Ni shell universe, the many problems connected to inflation in the ΛCDM model are notably avoided, as the cool glow of a spherical baryonic shell alone could suffice to account for the extreme smoothness of the CMB. The concentration of the universe’s mass in the shell moreover reduces or even eliminates the need for dark matter to explain the CMB data.

The situation is similar with respect to the baryonic acoustic oscillations (BAOs). Interpretation of these fluctuations in the density of visible baryonic matter are framed specifically within the ΛCDM model and its assumptions concerning the cooling of plasma, recombination and other factors. Gupta [75] showed in a later study that his hybrid model combing TL and ΛCDM features was compatible with the BAO data. A similar study would be needed to show how the BAO data can fit with a hybrid Ni model. On the other hand, in a static Ni model without ΛCDM inputs, the BAO problem would in a sense disappear. The starting assumptions would no longer the same. The data used in BAO analyses would then need reinterpretation in the Ni context, similarly as with the CMB perturbation data.

5.2. Light Element Abundances

The explanation for the light element abundance in the universe would likewise have a dual nature in the Ni approach. If the ΛCDM inputs to the model are predominant, then the predictions of these abundances simply follow those of the ΛCDM model. The situation again becomes more complex in a model with a strong Ni component. Processes would then be necessary whereby helium and other elements produced in stellar fusion are converted back to hydrogen. In this context, it has long been speculated that the high-energy environments of quasars could facilitate the destruction of elements through processes like photodisintegration and high-energy collisions (e.g., [76]). As discussed in Section 6, the Hubble luminosity of SMBHs would play the major role in generating high temperatures within these objects. The containment and ejection mechanisms in quasar outflows and jets would then distribute the synthesized hydrogen into the interstellar and intergalactic medium.

6. Black Holes

The Ni solutions, which form the basis for our shell universe model, were initially used to study neutron stars and other RCOs. In this section, we now consider whether the shell universe can be reverse engineered to describe objects that have previously been named black holes, but which in Ni’s approach could be more akin to gravastars, dark energy stars or other postulated alternative structures [29,30,31,32,33,34]. For simplicity, we will use the term black holes to refer generically to these structures.

We first consider non-rotating black holes. Drawing from the basic relationship H₀ = c/R_U, it can immediately be seen that the Hubble constant would no longer be a true constant in these objects. Instead, we would have in each case

$$H_{bh}={\displaystyle \frac{c}{R_S}}.$$

(13)

Since $\rho$_bh = M_bh/(4/3πR_S³) and R_S = 2GM_bh/c², we would then have

$${\rho }_{bh}={\displaystyle \frac{3c^2}{8\pi G{R}_S^2}}.$$

(14)

We thus have $\rho$_bh $\propto$ 1/R_S². Inserting Equation (13) in Equation (14), we find that the expression for the black hole density then becomes analogous to that of the cosmic critical density, i.e.,

$${\rho }_{bh}={\displaystyle \frac{3H_{bh}^2}{8\pi G}}.$$

(15)

Using the analyses in [42,43], the expression for G is, moreover, seen to be invariant in black holes, even though H_bh varies hugely.

The same sequence of steps used in Section 4.1 to determine the cosmic Hubble luminosity can be used to find the respective values for black holes. Remarkably, it is found that all black holes would have L_H = c⁵/4G, regardless of the black hole mass. They would thus all feature the ‘maximum luminosity’ or ‘Dyson luminosity’ [31,55,56,57,58]. The larger Hubble constant of a black hole could here reflect the greater rate of energy recycling needed to prevent gravitational collapse into a singularity.

The Ni shell model can also be roughly applied to estimate the characteristics of the internal radiation of black holes. The equivalent blackbody radiation inside a non-rotating shell SMBH, for example, would have a much higher energy density than the CMB at any point in the universe, since u $\propto$ 1/R_S². Using the same sequence of steps as in the Ni model for Sagittarius A*, where R_S ≈ 10¹² cm, we would find T_shell ≈ 10⁹ K. Its peak blackbody wavelength would therefore be ~1 pm, in the gamma-ray band. This radiation would ordinarily be confined within the shell, but in certain situations could conceivably give rise to the GRB-type phenomena that have been observed.

However, the situation would be quite different in rapidly rotating SMBHs. Photographic evidence and theoretical considerations related to the Kerr metric suggest that the spherical shell in this case collapses to a torus, as reflected in the dark energy star model [33].

On a larger scale, supposing that the Ni shell universe itself resides in a still larger analogous structure, the Hubble constant of the latter would be much smaller than H_0, and its internal blackbody radiation much cooler than the CMB. Yet, from the above considerations, it can be inferred that G, and presumably the other fundamental constants, would be unchanged.

7. Concluding Remarks

Until quite recently, solutions for the equations of the state of neutron stars and other spherical compact objects generally featured an energy density and pressure increasing to maximum values at the center of these objects. A larger class of solutions was then found by Ni featuring a material void and repulsive gravitational field centered on the origin. Neslušan subsequently modified Ni’s solutions in developing models of RCOs and other astrophysical objects. Much more work is needed to substantiate the Ni–Neslušan–deLyra solutions and to demonstrate their applicability in describing real-world objects.

As one possibility, we have proposed that the observable universe could have a shell-like matter configuration consistent with the Ni solutions. A Ni shell model could potentially account for numerous observations that are problematic in the ΛCDM model. Since the gravitational redshift would be lower in and near the thick shell, the Hubble constant at high redshifts would be lower than in the local universe. This could reduce the Hubble tension and simultaneously allow for a reinterpretation of the evidence taken as proof of cosmic acceleration in a way that does not involve dark energy.

In analogy with Gupta’s ‘CCC + TL’ model, the Ni solutions could be incorporated in hybrid ‘Ni + ΛCDM’ models to varying degrees. At the same time, an extreme Ni model with zero ΛCDM inputs can possibly be envisaged possessing neither dark matter nor dark energy and expanding only by accretion of mass. Removing dark matter would require a separate theory such as MOND to fully explain galactic rotation curves, the speeds of galaxies in clusters and other phenomena connected to dark matter.

Due to a serious theoretical problem concerning stellar blueshifts, relativistic solutions for a Ni shell universe were not presented at this time. This must be the focus of future work. Our more limited aim was instead to tackle the issue of unobserved stellar blueshifts using the premise that spacetime is photonic in nature and thus able to exchange energy with photons. These energy exchanges could then account for the absence of general stellar blueshifts and for the observed T_CMB-redshift relation. The premise of photonic spacetime itself requires additional theoretical and experimental support.

Assuming photonic spacetime, however, the Ni shell model was further linked to gravity and Λ. As the Hubble luminosity is central to these processes, there is a pressing need to study and confirm its existence in masses and mass systems on all scales. In this effort, promising candidates for study include such objects as brown dwarfs and planetary moons—especially icy ones—which might be relatively free of other sources of internal heating. Theoretical support for a fundamental gravitational decay process might come from further geophysical evidence of expansion-related tectonic processes [54] or astrophysical evidence of a general secular increase in the orbits of moons and planets, as highlighted in some recent studies [77,78].

A general consistency in our approach can be seen with two estimates for a shell temperature and outermost T_CMB of ~29 K, one based on the Hubble luminosity and one from the density of gravitational energy. There is also an energy density requirement consistent with T_CMB~29 K in this region to induce gravity, a density which remarkably matches the required value for Λ in the ΛCDM model.

One objection to a Ni shell universe is that it violates the Cosmological Principle and even imposes a geo-centric view. Yet the increasing discoveries of anisotropies and nonuniformities, such as in quasar counts, CMB polarization and mass distribution, including the KBC Void, collectively imply that this principle is no longer a valid assumption. In any case, the Milky Way in a Ni universe would not be at the very center but displaced from it by a factor of ~0.1 R_U. It would be in mapping out our precise position relative to the origin that the Ni model could most effectively establish itself.

While Ni shell structures were initially proposed to describe neutron stars and other RCOs, the preliminary Ni shell universe developed herein might potentially be used to reverse engineer these dense objects and assist in finding relativistic solutions for them. In this respect, future efforts to model the Ni shell universe and RCOs would go hand in hand.

Lastly, we note that the Ni approach combined with photonic spacetime could form a basis for quantum physics generally. A photonic spacetime would be well-suited to incorporate quantum entanglement, for example, since all particles within the observable universe would be physically interconnected by filaments of photon-like gravitons. The problem of the origins of inertia could also find a resolution since the Ni shell would seemingly establish a universal rest frame.