Cosmography of the Minimally Extended Varying Speed-of-Light Model
Abstract
1. Introduction
2. Brief Review of the Minimally Extended Varying Speed-of-Light (meVSL) Model
2.1. Cosmological Redshift
2.2. The Possibility of Varying Speed-of-Light Theory in the Robertson–Walker Metric
2.3. The Modification of Einstein’s Field Equations
3. Cosmolography of Varying Speed-of-Light Models
4. Observation
5. Parameters
6. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harrison, E.R. Observational tests in cosmology. Nature 1976, 260, 591–592. [Google Scholar] [CrossRef]
- Visser, M. Jerk, snap and the cosmological equation of state. Class. Quantum Gravity 2004, 21, 2603–2616. [Google Scholar] [CrossRef]
- Visser, M. Cosmography: Cosmology without the Einstein equations. Gen. Relativ. Gravit. 2005, 37, 1541–1548. [Google Scholar] [CrossRef]
- Cattoen, C.; Visser, M. Cosmography: Extracting the Hubble series from the supernova data. arXiv 2007, arXiv:gr-qc/0703122. [Google Scholar]
- Cattoen, C.; Visser, M. The Hubble series: Convergence properties and redshift variables. Class. Quantum Gravity 2007, 24, 5985–5998. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Y. Cosmography: Supernovae Union2, Baryon Acoustic Oscillation, Observational Hubble Data and Gamma Ray Bursts. Phys. Lett B 2011, 702, 114–120. [Google Scholar] [CrossRef]
- Luongo, O. Cosmography with the Hubble parameter. Mod. Phys. Lett. A 2011, 26, 1459–1466. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Updated constraints on f(R) gravity from cosmography. Phys. Rev. D 2013, 87, 044012. [Google Scholar] [CrossRef]
- Busti, V.C.; Cruz-Dombriz, ḋ.; Dunsby, P.K.S.; Sáez-Gómez, D. Is cosmography a useful tool for testing cosmology? Phys. Rev. D 2015, 92, 123512. [Google Scholar] [CrossRef]
- Dunsby, P.K.S.; Luongo, O. On the theory and applications of modern cosmography. Int. J. Geom. Meth. Mod. Phys. 2016, 13, 1630002. [Google Scholar] [CrossRef]
- Luongo, O.; Pisani, G.B.; Troisi, A. Cosmological degeneracy versus cosmography: A cosmographic dark energy model. Int. J. Mod. Phys. D 2016, 26, 1750015. [Google Scholar] [CrossRef]
- Zhou, Y.N.; Liu, D.Z.; Zou, X.B.; Wei, H. New generalizations of cosmography inspired by the Padé approximant. Eur. Phys. J. C 2016, 76, 281. [Google Scholar] [CrossRef]
- de la Cruz-Dombriz, A. Limitations of cosmography in extended theories of gravity. arXiv 2016, arXiv:1604.07355. [Google Scholar]
- Bolotin, Y.L.; Konchtnyi, M.I.; Lemets, O.A.; Zazunov, L.G. Cosmography of Cardassian model. arXiv 2017, arXiv:1706.09710. [Google Scholar]
- de la Cruz Dombriz, Á. Towards New Constraints in Extended Theories of Gravity: Cosmography and Gravitational-Wave Signals from Neutron Stars. Galaxies 2018, 6, 28. [Google Scholar] [CrossRef]
- Pannia, F.A.T.; Bergliaffa, S.E.P.; Manske, N. Cosmography and the redshift drift in Palatini theories. Eur. Phys. J. C 2019, 79, 267. [Google Scholar] [CrossRef]
- Bolotin, Y.L.; Cherkaskiy, V.A.; Ivashtenko, O.Y.; Konchatnyi, M.I.; Zazunov, L.G. Applied Cosmography: A Pedagogical Review. arXiv 2018, arXiv:1812.02394. [Google Scholar]
- Yin, Z.Y.; Wei, H. Observational Constraints on Growth Index with Cosmography. Eur. Phys. J. C 2019, 79, 698. [Google Scholar] [CrossRef]
- Li, E.K.; Du, M.; Xu, L. General Cosmography Model with Spatial Curvature. Mon. Not. R. Astron. Soc. 2020, 491, 4960–4972. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended Gravity Cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. High-redshift cosmography: Auxiliary variables versus Padé polynomials. Mon. Not. R. Astron. Soc. 2020, 494, 2576–2590. [Google Scholar] [CrossRef]
- Lizardo, A.; Amante, M.H.; García-Aspeitia, M.A.; Magaña, J.; Motta, V. Cosmography using strong-lensing systems and cosmic chronometers. Mon. Not. R. Astron. Soc. 2021, 507, 5720–5731. [Google Scholar] [CrossRef]
- Hu, J.P.; Wang, F.Y. High-redshift cosmography: Application and comparison with different methods. Astron. Astrophys. 2022, 661, A71. [Google Scholar] [CrossRef]
- Martins, C.J.A.P.; Ferreira, F.P.S.A.; Marto, P.V. Varying fine-structure constant cosmography. Phys. Lett. B 2022, 827, 137002. [Google Scholar] [CrossRef]
- Rocha, B.A.R.; Martins, C.J.A.P. Redshift drift cosmography with ELT and SKAO measurements. Mon. Not. R. Astron. Soc. 2022, 518, 2853–2869. [Google Scholar] [CrossRef]
- Gao, J.; Zhou, Z.; Du, M.; Zou, R.; Hu, J.; Xu, L. A Measurement of Hubble Constant Using Cosmographic Approach from Fast Radio Bursts and SNe Ia. arXiv 2023, arXiv:2307.08285. [Google Scholar]
- Petreca, A.T.; Benetti, M.; Capozziello, S. Beyond ΛCDM with f(z)CDM: Criticalities and solutions of Padé Cosmography. Phys. Dark Universe 2023, 44, 101453. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, T.; Xu, B.; Huang, Q.; Yuan, Y. Joint Constraints on the Hubble Constant, Spatial Curvature, and Sound Horizon from the Late-time Universe with Cosmography. Astrophys. J. 2023, 957, 5. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.R.; Halpern1, M.; Hill, R.S.; Odegard, N.; et al. Nine-yearwilkinson microwave anisotropy probe (WMAP) observations: Cosmological parameter results. Astrophys. J. Suppl. Ser. 2013, 208, 20. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A1. [Google Scholar] [CrossRef]
- Guzzo, L.; Bel, J.; Bianchi, D.; Carbone, C.; Granett, B.R.; Hawken, A.J.; Mohammad, F.G.; Pezzotta, A.; Rota, S.; Zennaro, M. Measuring the Universe with galaxy redshift surveys. In Toward a Science Campus in Milan: A Snapshot of Current Research at the Physics Department Aldo Pontremoli; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–16. [Google Scholar] [CrossRef]
- Cawthon, R.; Elvin-Poole, J.; Porredon, A.; Crocce, M.; Giannini, G.; Gatti, M.; Ross, A.J.; Rykoff, E.S.; Rosell, A.C.; DeRose, J.; et al. Dark Energy Survey Year 3 Results: Calibration of Lens Sample Redshift Distributions using Clustering Redshifts with BOSS/eBOSS. Mon. Not. R. Astron. Soc. 2022, 513, 5517. [Google Scholar] [CrossRef]
- Robertson, H.P. On the Foundations of Relativistic Cosmology. Proc. Natl. Acad. Sci. USA 1929, 15, 822–829. [Google Scholar] [CrossRef] [PubMed]
- Robertson, H.P. Relativistic Cosmology. Rev. Mod. Phys. 1933, 5, 62. [Google Scholar] [CrossRef]
- Walker, A.G.; Milne, E.A. On the Formal Comparison of Milne’s Kinematical System with the Systems of General Relativity. Mon. Not. R. Astron. Soc. 1935, 95, 263. [Google Scholar] [CrossRef]
- Walker, A.G. On Milne’s theory of world-structure. Proc. Lond. Math. Soc. 1937, 42, 90–127. [Google Scholar] [CrossRef]
- Morin, D. Introduction to Classical Mechanics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Weyl, H. Republication of: On the general relativity theory. Gen. Relativ. Gravit. 2009, 41, 1661. [Google Scholar] [CrossRef]
- Islam, J.N. An Introduction to Mathematical Cosmology; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Narlikar, J.V. An Introduction to Cosmology, 3rd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Hobson, M.P.; Efstathiou, G.P.; Lasenby, A.N. General Relativity: An Introduction for Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Grøn, Ø.; Hervik, S. Einstein’s General Theory of Relativity; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ryder, L. Introduction to General Relativity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Choquet-Bruhat, Y. Introduction to General Relativity, Black Holes and Cosmology; Oxford University Press: Cambridge, UK, 2015. [Google Scholar]
- Roos, M. Introduction to Cosmology; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Guidry, M. Modern General Relativity: Black Holes, Gravitational Waves, and Cosmology; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Ferrari, V.; Gualtieri, L.; Pani, P. General Relativity and its Applications: Black Holes, Compact Stars and Gravitational Waves; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Das, A. The Special Theory of Relativity, A Mathematical Exposition; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Schutz, J. Independent Axioms for Minkowski Spacetime; Addison Wesley Longman Limited: London, UK, 1997. [Google Scholar]
- Lee, S. The minimally extended Varying Speed of Light (meVSL). J. Cosmol. Astropart. Phys. 2021, 8, 54. [Google Scholar] [CrossRef]
- Barrow, J.D. Cosmologies with varying light speed. Phy. Rev. D 1988, 59, 043515. [Google Scholar] [CrossRef]
- Einstein, A. Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. Annalen der Physik 1911, 35, 898–906. [Google Scholar] [CrossRef]
- Dicke, R. Gravitation without a Principle of Equivalence. Rev. Mod. Phys. 1957, 29, 363–376. [Google Scholar] [CrossRef]
- Petit, J.P. An interpretation of cosmological model with variable light velocity. Mod. Phys. Lett. A 1988, 3, 1527–1532. [Google Scholar] [CrossRef]
- Petit, J.P. Cosmological model with variable light velocity: The interpretation of red shifts. Mod. Phys. Lett. A 1988, 3, 1733–1744. [Google Scholar] [CrossRef]
- Petit, J.P.; Viton, M. Gauge cosmological model with variable light velocity. Comparizon with QSO observational data. Mod. Phys. Lett. A 1989, 4, 2201–2210. [Google Scholar] [CrossRef]
- Midy, P.; Petit, J.P. Scale invariant cosmology. Int. J. Mod. Phys. D 1989, 8, 271–280. [Google Scholar] [CrossRef]
- Moffat, J.W. Superluminary universe: A Possible solution to the initial value problem in cosmology. Int. J. Mod. Phys. D 1993, 2, 351–366. [Google Scholar] [CrossRef]
- Petit, J.P. Twin Universe Cosmology. Astrophys. Space Sci. 1995, 226, 273. [Google Scholar] [CrossRef]
- Albrecht, A.; Magueijo, J. A Time varying speed of light as a solution to cosmological puzzles. Phys. Rev. D 1999, 59, 043516. [Google Scholar] [CrossRef]
- Barrow, J.D.; Magueijo, J. Solutions to the quasi-flatness and quasilambda problems. Phys. Lett. B 1999, 447, 246. [Google Scholar] [CrossRef]
- Clayton, M.A.; Moffat, J.W. Dynamical mechanism for varying light velocity as a solution to cosmological problems. Phys. Lett. B 1999, 460, 263–270. [Google Scholar] [CrossRef]
- Barrow, J.D.; Magueijo, J. Solving the flatness and quasiflatness problems in Brans-Dicke cosmologies with a varying light speed. Class. Quantum Gravity 1999, 16, 1435–1454. [Google Scholar] [CrossRef]
- Clayton, M.A.; Moffat, J.W. Scalar tensor gravity theory for dynamical light velocity. Phys. Lett. B 2000, 477, 269–275. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Magueijo, J. Imaginative cosmology. In Large Scale Structure Formation; Springer: Dordrecht, The Netherlands, 2000; pp. 331–371. [Google Scholar]
- Bassett, B.A.; Liberati, S.; Molina-Paris, C.; Visser, M. Geometrodynamics of variable speed of light cosmologies. Phys. Rev. D 2000, 62, 103518. [Google Scholar] [CrossRef]
- Gopakumar, P.; Vijayagovindan, G.V. Solutions to cosmological problems with energy conservation and varying c, G and Lambda. Mod. Phys. Lett. A 2001, 16, 957–962. [Google Scholar] [CrossRef]
- Magueijo, J. Covariant and locally Lorentz invariant varying speed of light theories. Phys. Rev. D 2000, 62, 103521. [Google Scholar] [CrossRef]
- Magueijo, J. Stars and black holes in varying speed of light theories. Phys. Rev. D 2001, 63, 043502. [Google Scholar] [CrossRef]
- Magueijo, J. New varying speed of light theories. Rep. Prog. Phys. 2003, 66, 2025. [Google Scholar] [CrossRef]
- Magueijo, J.; Moffat, J.W. Comments on ‘Note on varying speed of light theories’. Gen. Relativ. Gravit. 2008, 40, 1797–1806. [Google Scholar] [CrossRef]
- Petit, J.P.; d’Agostini, G. Bigravity: A Bimetric model of the Universe with variable constants, inluding VSL (variable speed of light). arXiv 2008, arXiv:0803.1362. [Google Scholar]
- Roshan, M.; Nouri, M.; Shojai, F. Cosmological solutions of time varying speed of light theories. Phys. Lett. B 2009, 672, 197–202. [Google Scholar] [CrossRef]
- Sanejouand, Y.H. About some possible empirical evidences in favor of a cosmological time variation of the speed of light. Europhys. Lett. 2009, 88, 59002. [Google Scholar] [CrossRef]
- Nassif, C.; de Faria, A.C.A. Variation of the speed of light with temperature of the expanding universe. Phys. Rev. D 2012, 86, 027703. [Google Scholar] [CrossRef]
- Moffat, J.W. Variable Speed of Light Cosmology, Primordial Fluctuations and Gravitational Waves. Eur. Phys. J. C 2016, 76, 130. [Google Scholar] [CrossRef]
- Ravanpak, A.; Farajollahi, H.; Fadakar, G.F. Normal DGP in varying speed of light cosmology. Res. Astron. Astrophys. 2017, 17, 26. [Google Scholar] [CrossRef]
- Costa, R.; Cuzinatto, R.R.; Ferreira, E.M.G.; Franzmann, G. Covariant c-flation: A variational approach. Int. J. Mod. Phys. D 2019, 28, 1950119. [Google Scholar] [CrossRef]
- Nassif, C.; Silva, F.A. Variation of the speed of light and a minimum speed in the scenario of an inflationary universe with accelerated expansion. Phys. Dark Universe 2018, 22, 127. [Google Scholar]
- Lee, S. Constraining minimally extended varying speed of light by cosmological chronometers. Mon. Not. R. Astron. Soc. 2023, 522, 3248–3255. [Google Scholar] [CrossRef]
- Lee, S. Constraint on the minimally extended varying speed of light using time dilations in Type Ia supernovae. Mon. Not. R. Astron. Soc. 2023, 524, 4019–4023. [Google Scholar] [CrossRef]
- Lee, S. A Viable Varying Speed of Light Model in the RW Metric. Found. Phys. 2023, 53, 40. [Google Scholar] [CrossRef]
- Lee, S. Review on the Minimally Extended Varying Speed of Light Model. Preprints 2024, 2024030236. [Google Scholar] [CrossRef]
- Lee, S. The cosmological evolution condition of the Planck constant in the varying speed of light models through adiabatic expansion. Phys. Dark Universe 2023, 42, 101286. [Google Scholar] [CrossRef]
- Leibundgut, B. Time dilation in the light curve of the distant type ia supernovae sn 1995 k. Astrophys. J. Lett. 1996, 466, L21. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Leonard, D.C.; Schmidt, B.P.; Suntzeff, N.; Phillips, M.M.; Schommer, R.; Clocchiatti, A.; Kirshner, R.P.; Garnavich, P.; et al. Time dilation from spectral feature age measurements of type ia supernovae. Astron. J. 1997, 114, 722. [Google Scholar] [CrossRef]
- Foley, R.J.; Filippenko, A.V.; Leonard, D.C.; Riess, A.G.; Nugent, P.; Perlmutter, S. A Definitive measurement of time dilation in the spectral evolution of the moderate-redshift Type Ia supernova 1997 ex. Astrophys. J. Lett. 2005, 626, L11–L14. [Google Scholar] [CrossRef]
- Blondin, S.; Tonry, J.L. Determining the Type, Redshift, and Age of a Supernova Spectrum. Astrophys. J. 2007, 666, 1024–1047. [Google Scholar] [CrossRef]
- Blondin, S.; Davis, T.M.; Krisciunas, K.; Schmidt, B.P.; Sollerman, J.; Wood-Vasey, W.M.; Becker, A.C.; Challis, P.; Clocchiatti, A.; Damke, G.; et al. Time Dilation in Type Ia Supernova Spectra at High Redshift. Astrophys. J. 2008, 682, 724–736. [Google Scholar] [CrossRef]
- Norris, J.P.; Nemiroff, R.J.; Scargle, J.D.; Kouveliotou, C.; Fishman, G.J.; Meegan, C.A.; Paciesas, W.S.; Bonnell, J.T. Detection of signature consistent with cosmological time dilation in gamma-ray bursts. Astrophys. J. 1994, 424, 540. [Google Scholar] [CrossRef]
- Wijers, R.A.M.J.; Paczynski, B. On the nature of gamma-ray burst time dilations. Astrophys. J. Lett. 1994, 437, L107. [Google Scholar] [CrossRef]
- Band, D. Cosmological time dilation in gamma-ray bursts? Astrophys. J. Lett. 1994, 432, L23. [Google Scholar] [CrossRef]
- Meszaros, A.; Meszaros, P. Cosmological evolution and luminosity function effects on number counts, redshift and time dilation of bursting sources. Astrophys. J. 1996, 466, 29. [Google Scholar] [CrossRef]
- Lee, T.T.; Petrosian, V. Time dilation of batse gamma-ray bursts. Astrophys. J. 1997, 474, 37. [Google Scholar] [CrossRef]
- Chang, H.Y. Fourier analysis of gamma-ray burst light curves: Searching for direct signature of cosmological time dilation. Astrophys. J. Lett. 2001, 557, L85. [Google Scholar] [CrossRef]
- Crawford, D.F. No Evidence of Time Dilation in Gamma-Ray Burst Data. arXiv 2009, arXiv:0901.4169. [Google Scholar]
- Zhang, F.W.; Fan, Y.Z.; Shao, L.; Wei, D.M. Cosmological Time Dilation in Durations of Swift Long Gamma-Ray Bursts. Astrophys. J. Lett. 2013, 778, L11. [Google Scholar] [CrossRef]
- Singh, A.; Desai, S. Search for cosmological time dilation from gamma-ray bursts—A 2021 status update. J. Cosmol. Astropart. Phys. 2022, 2, 10. [Google Scholar] [CrossRef]
- Hawkins, M.R.S. Time dilation and quasar variability. Astrophys. J. Lett. 2001, 553, L97. [Google Scholar] [CrossRef]
- Dai, D.C.; Starkman, G.D.; Stojkovic, B.; Stojkovic, D.; Weltman, A. Using quasars as standard clocks for measuring cosmological redshift. Phys. Rev. Lett. 2012, 108, 231302. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Lewis, G.F.; Brewer, B.J. Detection of the cosmological time dilation of high-redshift quasars. Nat. Astron. 2023, 7, 1265–1269. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Capozziello, S.; Lazkoz, R.; Salzano, V. Comprehensive cosmographic analysis by Markov Chain Method. Phys. Rev. D 2011, 84, 124061. [Google Scholar] [CrossRef]
- Muthukrishna, D.; Parkinson, D. A cosmographic analysis of the transition to acceleration using SN-Ia and BAO. J. Cosmol. Astropart. Phys. 2016, 11, 052. [Google Scholar] [CrossRef]
- Birrer, S.; Treu, T.; Rusu, C.E.; Bonvin, V.; Fassnacht, C.D.; Chan, J.H.H.; Agnello, A.; Shajib, A.J.; Chen, G.C.F.; Auger, M.; et al. H0LiCOW–IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206 + 4332 and a new measurement of the Hubble constant. Mon. Not. R. Astron. Soc. 2019, 484, 4726. [Google Scholar] [CrossRef]
- Rezaei, M.; Pour-Ojaghi, S.; Malekjani, M. A Cosmography Approach to Dark Energy Cosmologies: New Constraints Using the Hubble Diagrams of Supernovae, Quasars, and Gamma-Ray Bursts. Astrophys. J. 2020, 900, 70. [Google Scholar] [CrossRef]
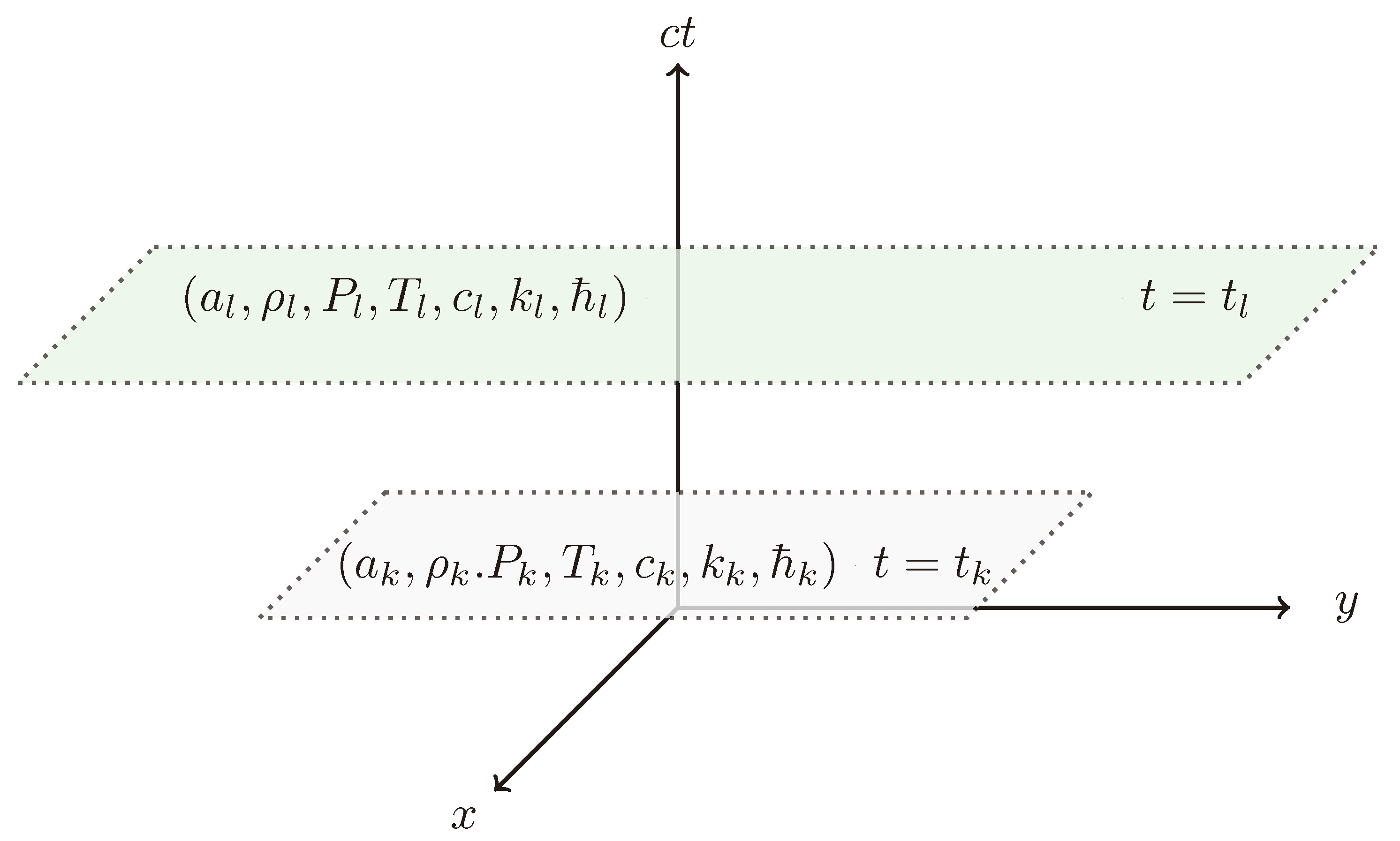
| Local Physics Laws | Special Relativity | Electromagnetism | Thermodynamics |
|---|---|---|---|
| quantities | |||
| constants | |||
| energies |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S. Cosmography of the Minimally Extended Varying Speed-of-Light Model. Astronomy 2024, 3, 100-113. https://doi.org/10.3390/astronomy3020007
Lee S. Cosmography of the Minimally Extended Varying Speed-of-Light Model. Astronomy. 2024; 3(2):100-113. https://doi.org/10.3390/astronomy3020007
Chicago/Turabian StyleLee, Seokcheon. 2024. "Cosmography of the Minimally Extended Varying Speed-of-Light Model" Astronomy 3, no. 2: 100-113. https://doi.org/10.3390/astronomy3020007
APA StyleLee, S. (2024). Cosmography of the Minimally Extended Varying Speed-of-Light Model. Astronomy, 3(2), 100-113. https://doi.org/10.3390/astronomy3020007





