(No) Eternal Inflation in the Starobinsky Inflation Corrected by Higher Curvature Invariants
Abstract
1. Introduction
2. Mechanism of Eternal Inflation
3. Eternal Inflation in Starobinsky-Like Models
3.1. Starobinsky Inflation
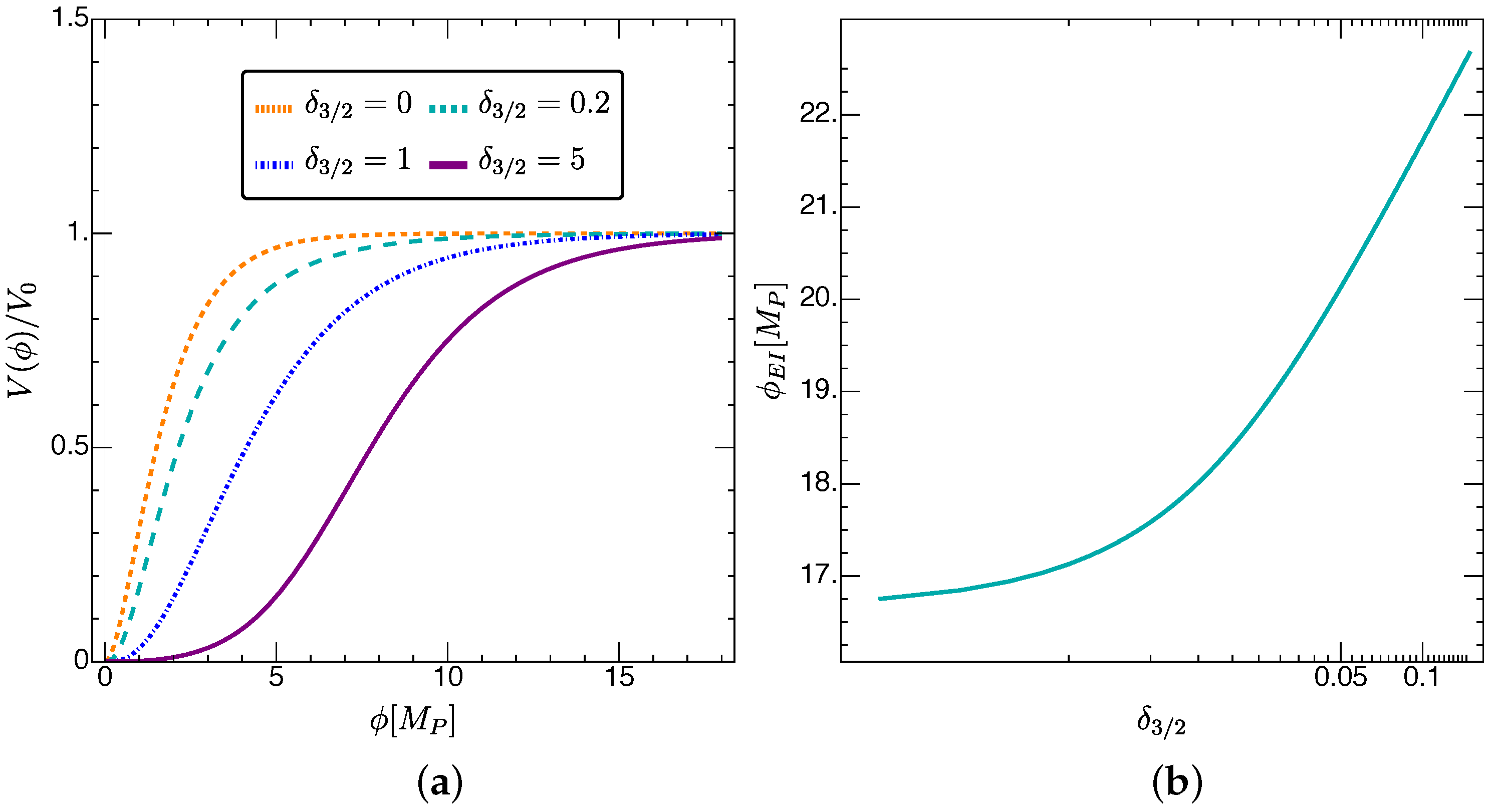
3.2. Eternal Inflation for Correction
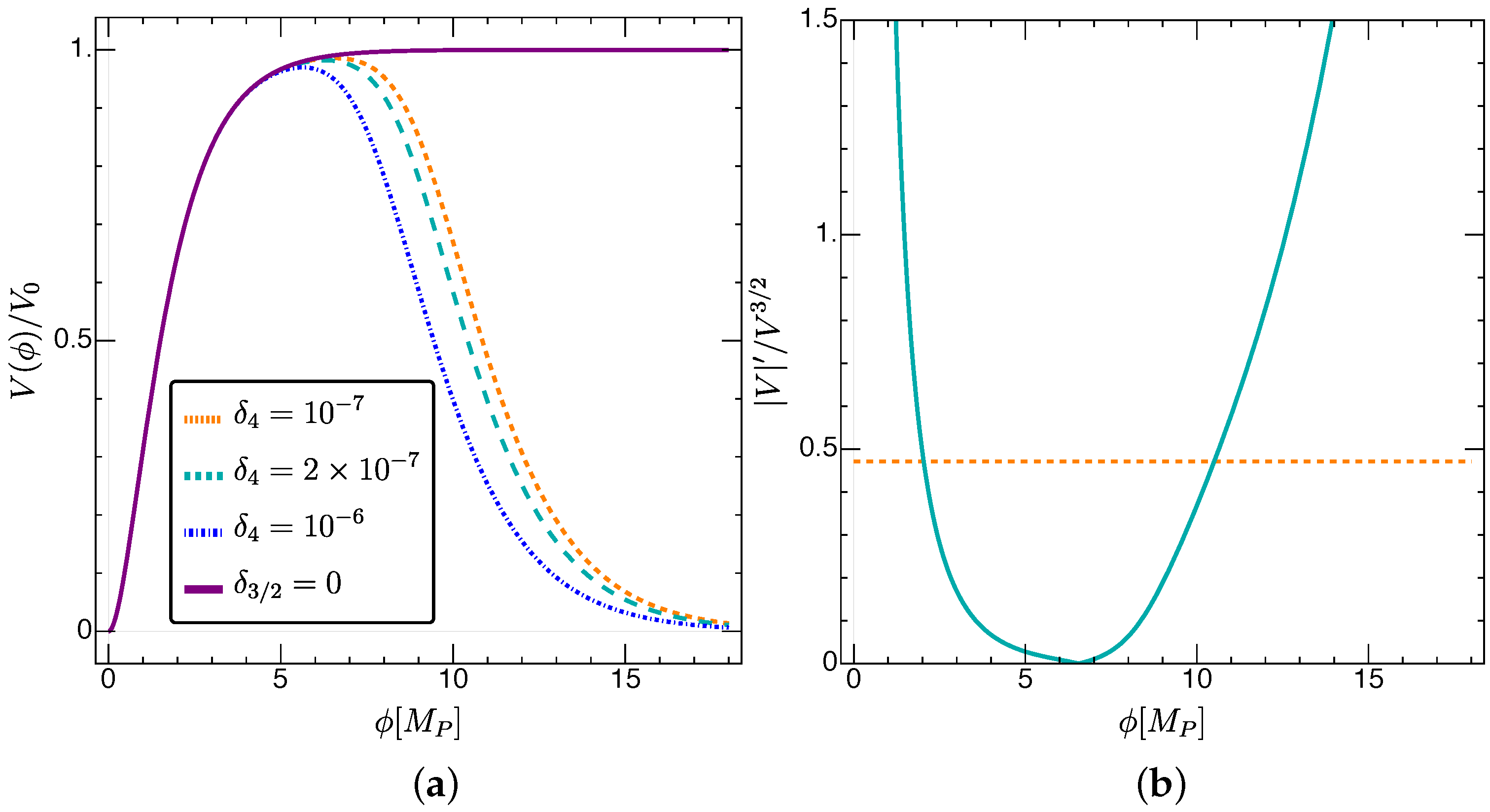
3.3. Eternal Inflation for the Correction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vafa, C. The String Landscape and the Swampland. arXiv 2005, arXiv:hep-th/0509212. [Google Scholar]
- Brennan, T.D.; Carta, F.; Vafa, C. The String Landscape, the Swampland, and the Missing Corner. arXiv 2017, arXiv:1711.00864. [Google Scholar]
- Palti, E. The Swampland: Introduction and Review. Fortsch. Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- Meissner, K.A.; Veneziano, G. Symmetries of cosmological superstring vacua. Phys. Lett. B 1991, 267, 33–36. [Google Scholar] [CrossRef]
- Meissner, K.A.; Veneziano, G. Manifestly O(d,d) invariant approach to space-time dependent string vacua. Mod. Phys. Lett. A 1991, 6, 3397–3404. [Google Scholar] [CrossRef]
- Meissner, K.A. Symmetries of higher order string gravity actions. Phys. Lett. B 1997, 392, 298–304. [Google Scholar] [CrossRef]
- Hohm, O.; Zwiebach, B. Non-perturbative de Sitter vacua via α′ corrections. Int. J. Mod. Phys. D 2019, 28, 1943002. [Google Scholar] [CrossRef]
- Hohm, O.; Zwiebach, B. Duality invariant cosmology to all orders in α’. Phys. Rev. D 2019, 100, 126011. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J.; Loeb, A. Inflationary paradigm in trouble after Planck 2013. Phys. Lett. B 2013, 723, 261–266. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J.; Loeb, A. Inflationary schism. Phys. Lett. B 2014, 736, 142–146. [Google Scholar] [CrossRef]
- Guth, A.H.; Kaiser, D.I.; Nomura, Y. Inflationary paradigm after Planck 2013. Phys. Lett. B 2014, 733, 112–119. [Google Scholar] [CrossRef]
- Rudelius, T. Conditions for (no) eternal inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 009. [Google Scholar] [CrossRef]
- Chojnacki, J.; Krajecka, J.; Kwapisz, J.; Slowik, O.; Strag, A. Is asymptotically safe inflation eternal? J. Cosmol. Astropart. Phys. 2021, 2021, 076. [Google Scholar] [CrossRef]
- Bonanno, A.; Platania, A. Asymptotically safe inflation from quadratic gravity. Phys. Lett. B 2015, 750, 638–642. [Google Scholar] [CrossRef]
- Platania, A. From renormalization group flows to cosmology. Front. Phys. 2020, 8, 188. [Google Scholar] [CrossRef]
- Nielsen, N.G.; Sannino, F.; Svendsen, O. Inflation from Asymptotically Safe Theories. Phys. Rev. D 2015, 91, 103521. [Google Scholar] [CrossRef]
- Svendsen, O.; Bazrafshan Moghaddam, H.; Brandenberger, R. Preheating in an Asymptotically Safe Quantum Field Theory. Phys. Rev. D 2016, 94, 083527. [Google Scholar] [CrossRef]
- Kaiser, D.I. Conformal Transformations with Multiple Scalar Fields. Phys. Rev. D 2010, 81, 084044. [Google Scholar] [CrossRef]
- Liddle, A.R.; Parsons, P.; Barrow, J.D. Formalizing the slow-roll approximation in inflation. Phys. Rev. D 1994, 50, 7222–7232. [Google Scholar] [CrossRef]
- Linde, A.D. Hard art of the Universe creation (stochastic approach to tunneling and baby Universe formation). Nucl. Phys. B 1992, 372, 421–442. [Google Scholar] [CrossRef]
- Linde, A. Stochastic approach to tunneling and baby Universe formation. Nucl. Phys. B 1992, 372, 421–442. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Ivanov, V.R.; Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. Analytic extensions of Starobinsky model of inflation. arXiv 2021, arXiv:2111.09058. [Google Scholar] [CrossRef]
| 1 | |
| 2 | We thank Astrid Eichhorn for pointing this out. |
| 3 | The model with the correction leads to a similar shape of the potential. Its agreement with the CMB, however, is restricted to a much narrower range of the coupling values. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chojnacki, J.; Kwapisz, J.H. (No) Eternal Inflation in the Starobinsky Inflation Corrected by Higher Curvature Invariants. Astronomy 2023, 2, 15-21. https://doi.org/10.3390/astronomy2010003
Chojnacki J, Kwapisz JH. (No) Eternal Inflation in the Starobinsky Inflation Corrected by Higher Curvature Invariants. Astronomy. 2023; 2(1):15-21. https://doi.org/10.3390/astronomy2010003
Chicago/Turabian StyleChojnacki, Jan, and Jan Henryk Kwapisz. 2023. "(No) Eternal Inflation in the Starobinsky Inflation Corrected by Higher Curvature Invariants" Astronomy 2, no. 1: 15-21. https://doi.org/10.3390/astronomy2010003
APA StyleChojnacki, J., & Kwapisz, J. H. (2023). (No) Eternal Inflation in the Starobinsky Inflation Corrected by Higher Curvature Invariants. Astronomy, 2(1), 15-21. https://doi.org/10.3390/astronomy2010003




