Scaling Challenges for Conical Plain Bearings as Wind Turbine Main Bearings
Abstract
:1. Introduction
2. Approach
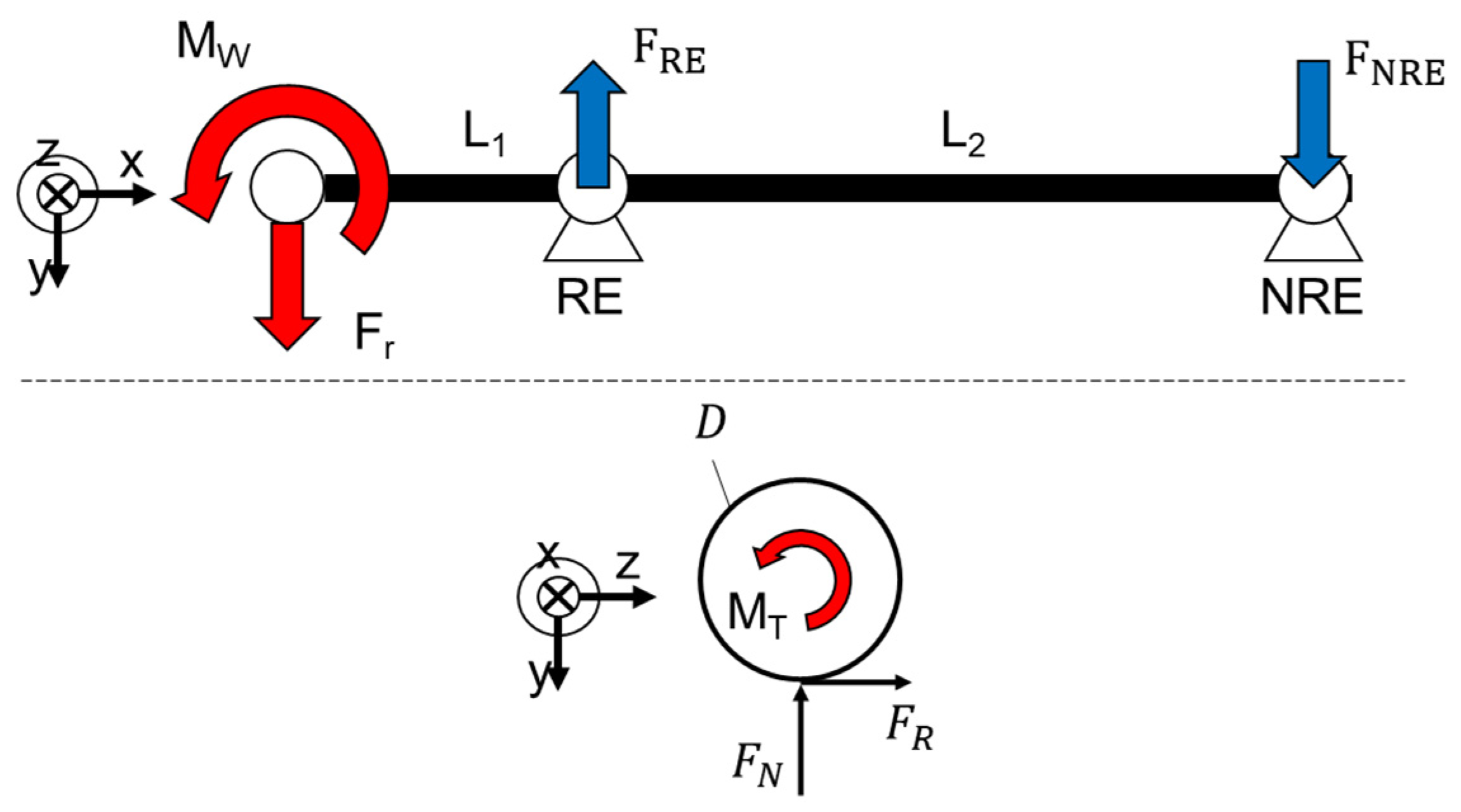
2.1. Load Scaling
2.2. Simulative Approach
2.3. Scaled FlexPad Design
3. Results
3.1. Segment Weight Increase and Restricted Servviceability
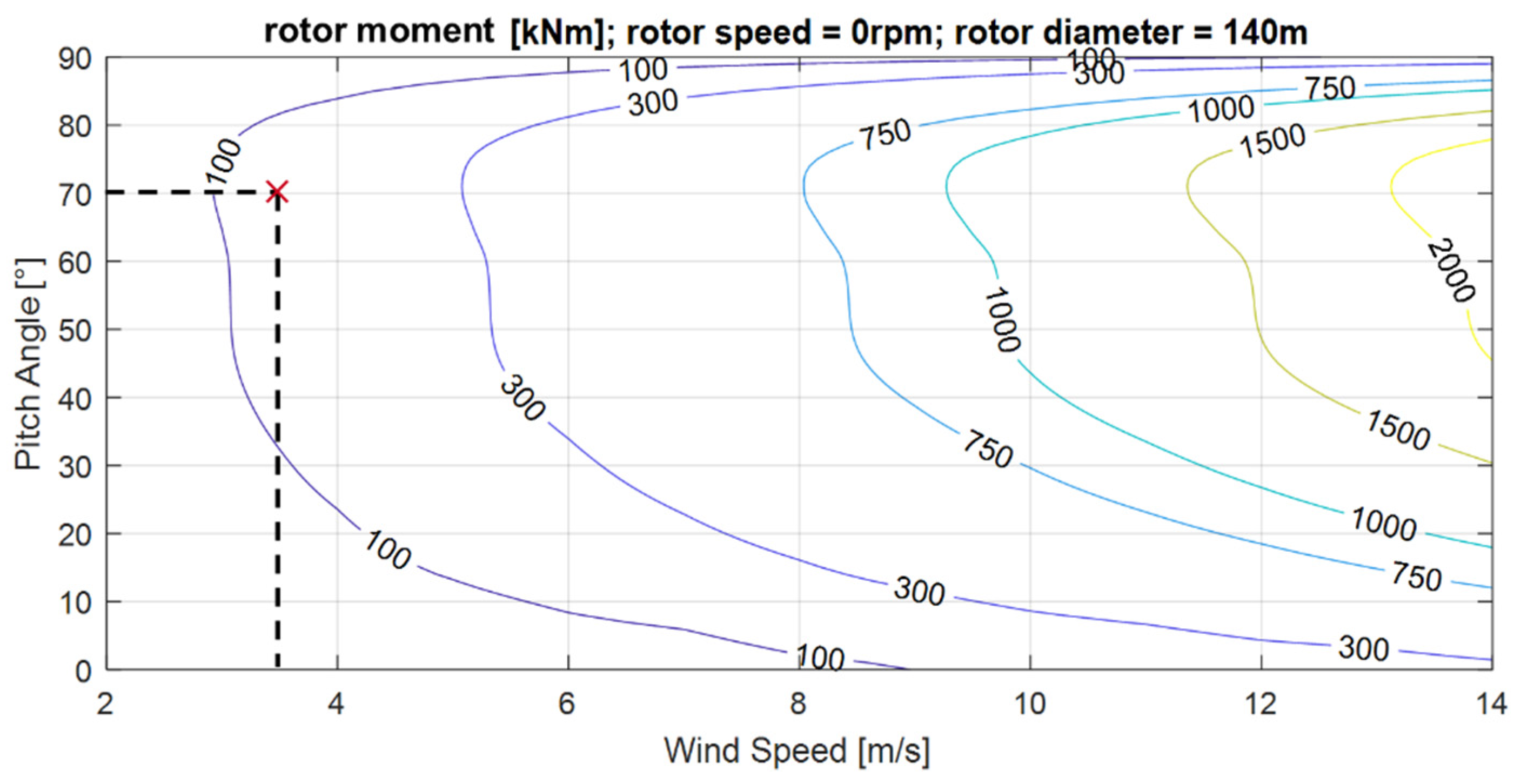
3.2. Higher Starting Loads and Resulting Breakaway Torque
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Parliament: Amendments Adopted by the European Parliament on the Renewable Energy Directive; European Parliament: Brussels, Belgium, 2022.
- German Bundestag: Gesetz für den Ausbau Erneuerbarer Energien (Erneuerbare Energien-Gesetz—EEG 2023); German BundesTAg: Berlin, Germany, 2023.
- Stehly, T.; Duffy, P. 2021 Cost of Wind Energy Review; National Renewable Energy Lab.: Golden, CO, USA, 2023. [Google Scholar]
- Windeurope: Offshore Wind in Europe Key Trends and Statistics. 2019. Available online: https://windeurope.org/wp-content/uploads/files/about-wind/statistics/WindEurope-Annual-Offshore-Statistics-2019.pdf (accessed on 24 October 2023).
- Windeurope: Wind Energy in Europe Trends and Statistics. 2019. Available online: https://windeurope.org/wp-content/uploads/files/about-wind/statistics/WindEurope-Annual-Statistics-2019.pdf (accessed on 24 October 2023).
- Fraunhofer: Turbine Size. Available online: https://windmonitor.iee.fraunhofer.de/windmonitor_en/3_Onshore/2_technik/4_anlagengroesse/ (accessed on 11 January 2023).
- Wiser, R.; Bolinger, M.; Barbose, G.; Darghouth, N.; Hoen, B.; Mills, A.; Rand, J.; Millstein, D.; Jeong, S.; Mills, A.; et al. 2018 Wind Technologies Market Report; U.S. Department of Energy: Washington, DC, USA, 2018.
- Costanzo, G.; Bindley, G.; Cole, P. Wind Energy in Europe: 2022 Statistics and the Outlook for 2023–2027; Wind Europe: Brussels, Belgium, 2022. [Google Scholar]
- Edward, H.; Turnbull, A.; Feuchtwang, J.; Mcmillan, D.; Golysheva, E.; Elliott, R. Wind turbine main-bearing loading and wind field characteristics. In Wind Energy; Wiley: Hoboken, NJ, USA, 2019; Volume 22, pp. 1534–1547. [Google Scholar]
- Hart, E.; Clarke, B.; Nicholas, G.; Amiri, A.K.; Stirling, J.; Carroll, J.; Dwyer-Joyce, R.; McDonald, A.; Long, H. A review of wind turbine main bearings: Design, operation, modelling, damage mechanisms and fault detection. In Wind Energy Science; EAWE: Oldenburg, Germany, 2020; Volume 5, pp. 105–124. [Google Scholar]
- Hau, E. Windkraftanlagen; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Heier, S. Windkraftanlagen; Springer Fachmedien: Wiesbaden, Germany, 2018. [Google Scholar]
- Manwell, J.F. Wind Energy Explained: Theory, Design and Application; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Nejad, A.R.; Keller, J.; Guo, Y.; Sheng, S.; Polinder, H.; Watson, S.; Dong, J.; Qin, Z.; Ebrahimi, A.; Schelenz, R. Wind turbine drivetrains: State-of-the-art technologies and future development trends. In Wind Energy Science; Wiley: Hoboken, NJ, USA, 2022; Volume 7, pp. 387–411. [Google Scholar]
- Liu, Z.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Meas. J. Int. Meas. Confed. 2020, 149, 107002. [Google Scholar] [CrossRef]
- Torsvik, J.; Nejad, A.R.; Pedersen, E. Main bearings in large offshore wind turbines: Development trends, design and analysis requirements. J. Phys. Conf. Ser. 2018, 1037, 42020. [Google Scholar] [CrossRef]
- Steffen, B.; Beuse, M.; Tautorat, P.; Schmidt, T.S. Experience Curves for Operations and Maintenance Costs of Renewable Energy Technologies. Joule 2020, 4, 359–375. [Google Scholar] [CrossRef]
- Mcgowan, E. Giant, turbine-installing ship is Dominion Energy’s $500M bet on U.S. offshore wind. Energy News Netw. 2022. [Google Scholar]
- Walgern, J.; Peters, L.; Madlener, R. Economic Evaluation of Maintenance Strategies for Offshore Wind Turbines Based on Condition Monitoring Systems. FCN Work. Pap. 2017. [Google Scholar] [CrossRef]
- Buck, B.H.; Langan, R. Aquaculture Perspective of Multi-Use Sites in the Open Ocean: The Untapped Potential for Marine Resources in the Anthropocene, 1st ed.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Stehly, T.; Beiter, P.; Duffy, P. 2019 Cost of Wind Energy Review; National Renewable Energy Laboratory: Golden, CO, USA, 2019. [Google Scholar]
- Abschlussbericht: Thermisch Gespritzte Gleitlagerbeschichtungen für Hauptlager von Windenergieanlagen (WEA)—WEA Triebstrang und Oberflächentechnik, eng.: Final Report, WEA-GliTS; Technische Informationsbibliothek Hannover: Hannover, Germany, 2016.
- Schröder, T.; Jacobs, G.; Rolink, A.; Bosse, D. “FlexPad”—Innovative conical sliding bearing for the main shaft of wind turbines. J. Phys. Conf. Ser. 2019, 1222, 12026. [Google Scholar] [CrossRef]
- Rolink, A.; Jacobs, G.; Schröder, T.; Keller, D.; Jakobs, T.; Bosse, D.; Lang, J.; Knoll, G. Methodology for the systematic design of conical plain bearings for use as main bearings in wind turbines. Forsch. Im Ingenieurwesen 2021, 85, 629–637. [Google Scholar] [CrossRef]
- Schröder, T.N. Konisches Gleitlager für die Rotorlagerung einer Windenergieanlage, eng: Conical Sliding Bearing for the Rotor Main Bearing of a Wind Turbine; University Library RWTH Aachen: Aachen, Germany, 2021. [Google Scholar]
- Rolink, A.; Jacobs, G.; Pérez, A.; Bosse, D.; Jakobs, T. Sensitivity analysis of geometrical design parameters on the performance of conical plain bearings for use as main bearings in wind turbines. J. Phys. Conf. Ser. 2022, 2265, 32010. [Google Scholar] [CrossRef]
- Loriemi, A.; Jacobs, G.; Bosse, D. Estimation of Rotor and Main Bearing Loads Using Artificial Neural Networks; IOP Publishing Ltd.: Bristol, UK, 2022. [Google Scholar]
- Wind Turbines Database. Available online: https://en.wind-turbine-models.com/turbines?kwrange=4410%2C7110 (accessed on 4 May 2023).
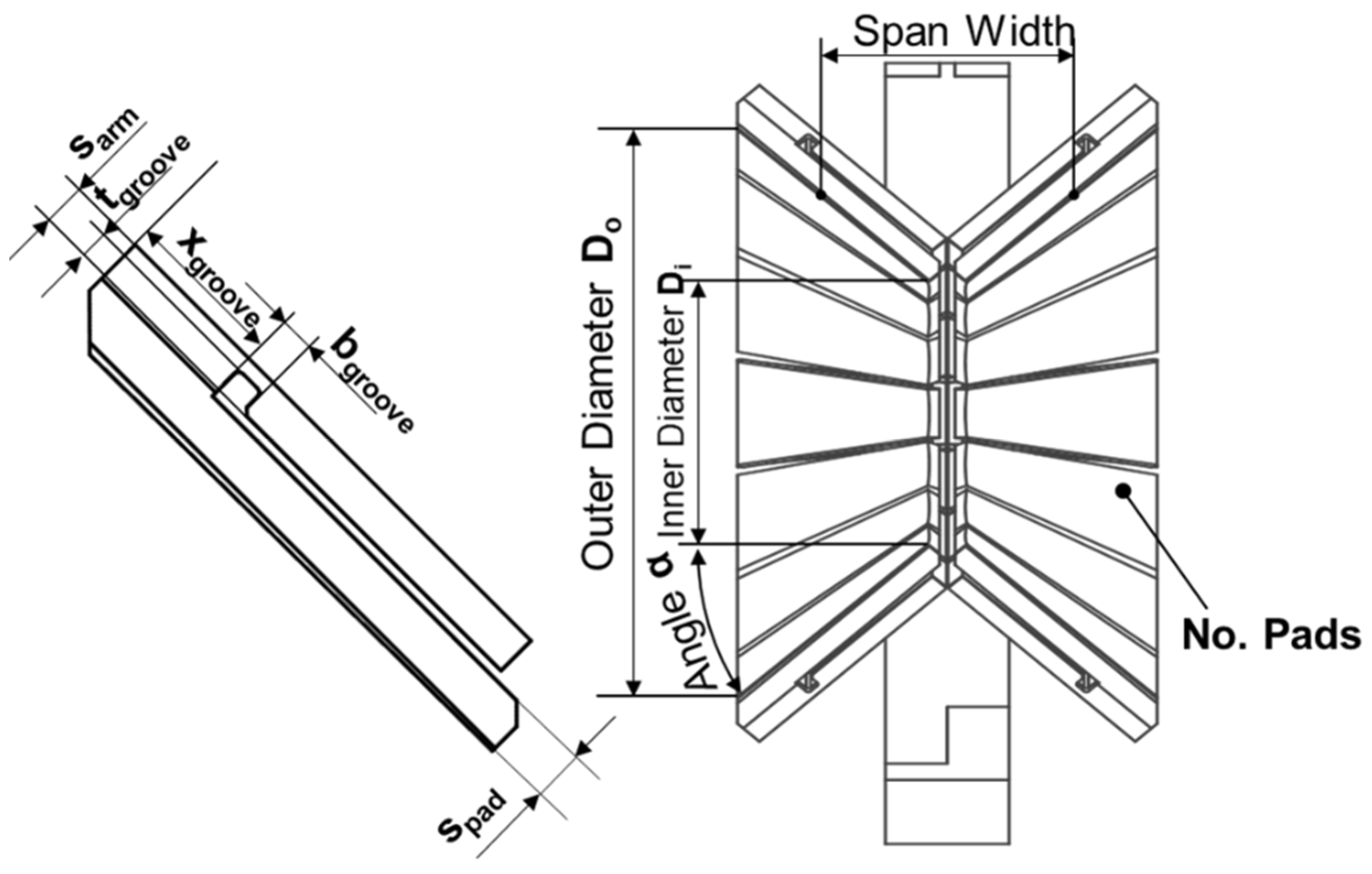
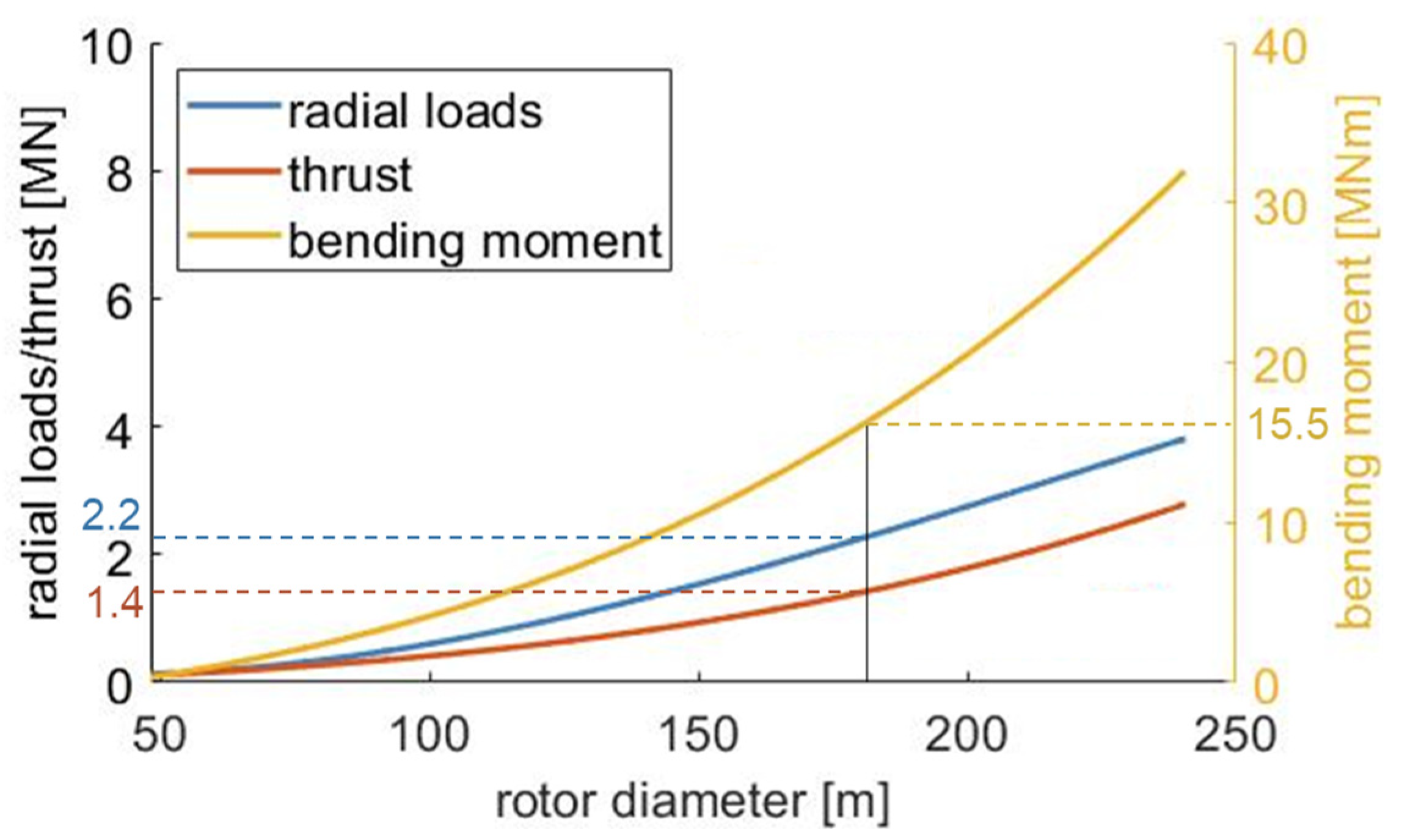
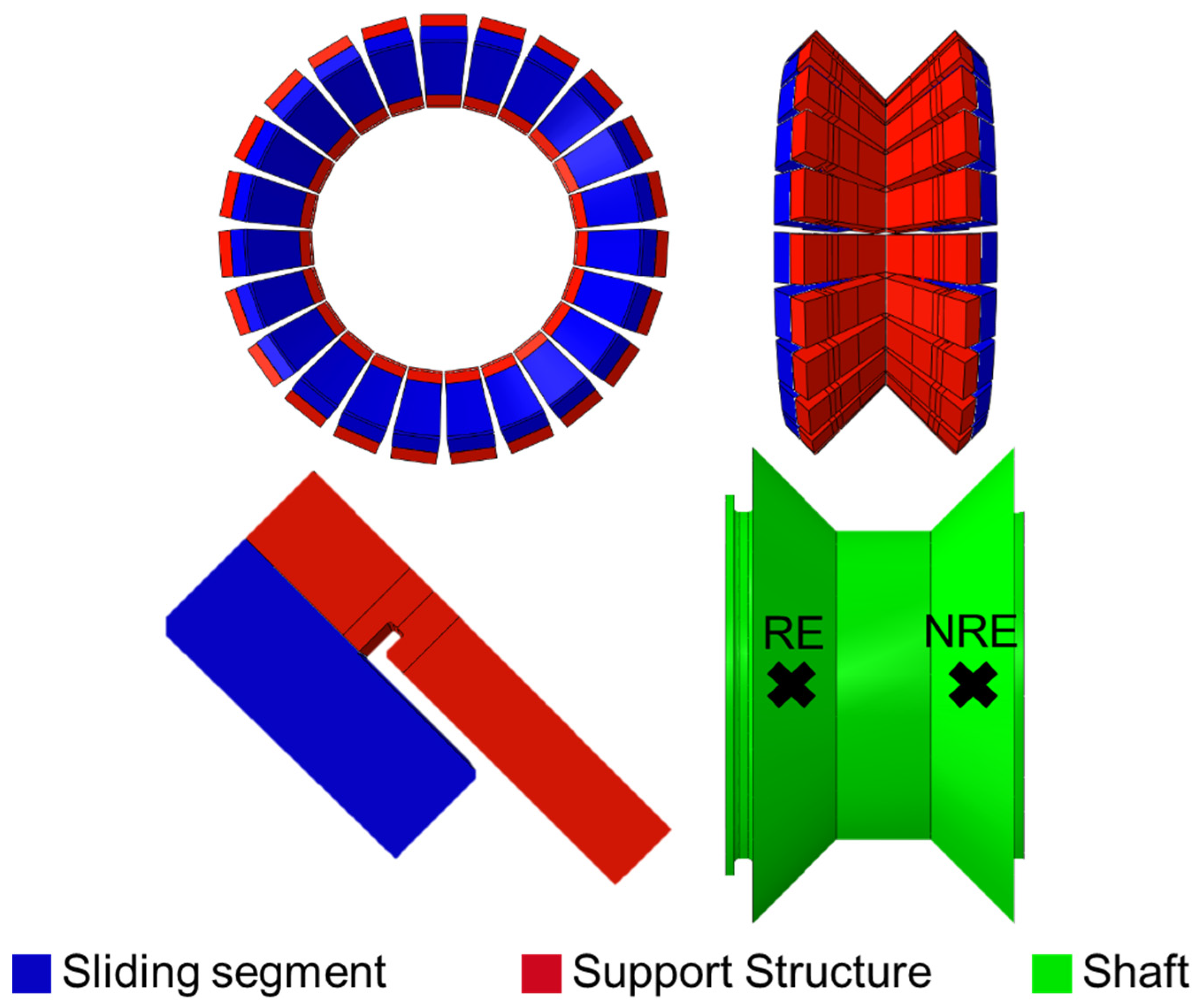
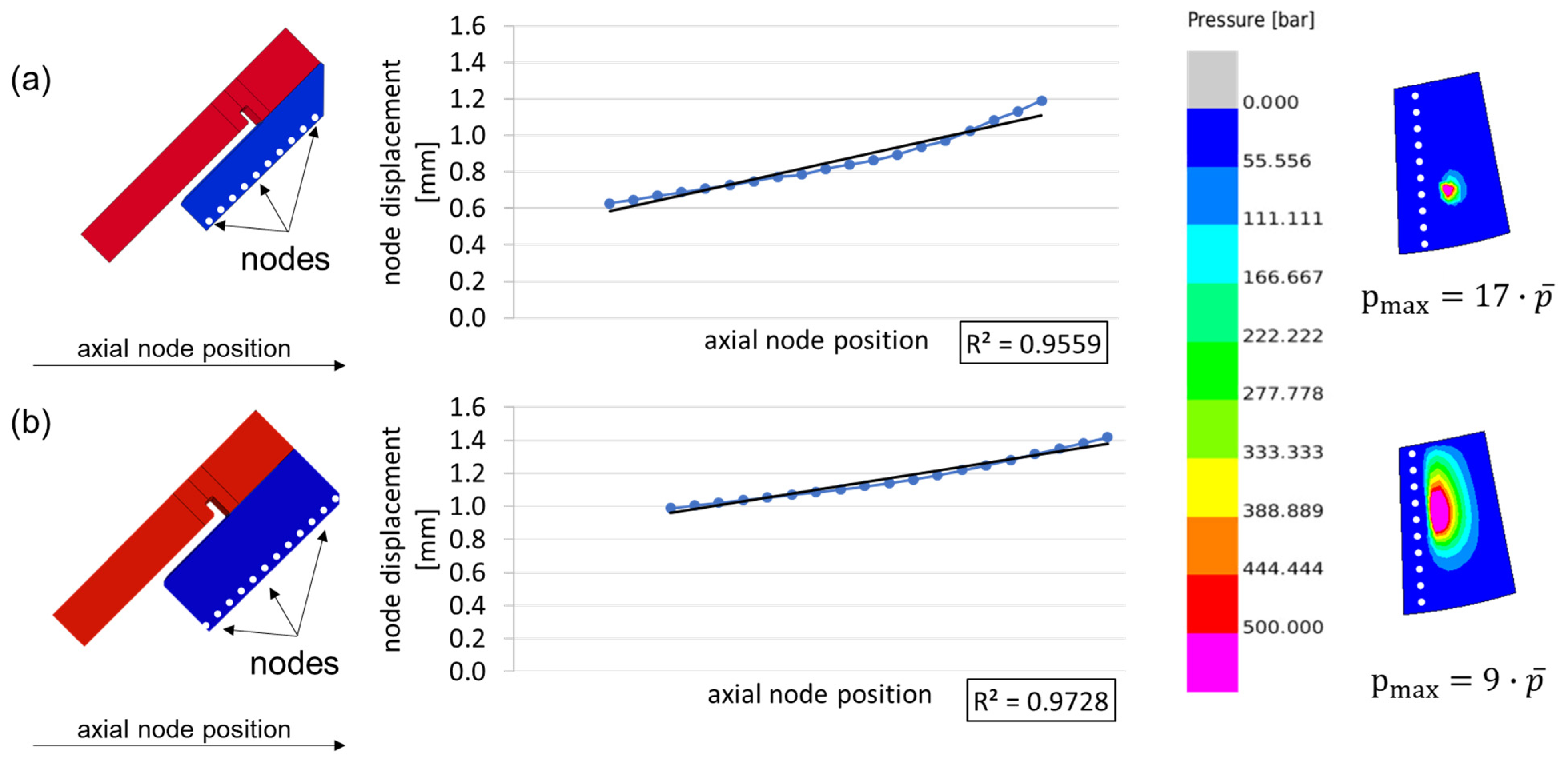
| Power [MW] | 8.5 |
| D [m] | 175 |
| Fx [kN] | 1400 |
| Fr [kN] | 2200 |
| Mw [kNm] | 15,500 |
| Moment Bearing 0.75 MW WEAGLiTS | Moment Bearing 8.5 MW NextMBU | |
|---|---|---|
| α | 45° | 45° |
| Do | 926.6 mm | 2400 mm |
| Di | 424.52 mm | 1822 mm |
| Span Width | 298.3 mm | 987 mm |
| No. Segments | 32 | 48 |
| sarm | 30 mm | 120 mm |
| bgroove | 20 mm | 25 mm |
| tgroove | 17 mm | 35 mm |
| xgroove | 105 mm | 205 mm |
| spad | 33 mm | 150 mm |
| Material Threshold | ||
|---|---|---|
| Hydrodynamic load bearing [%] | 100 | - |
| Friction torque [kNm] | 24.2 | - |
| Friction power [kW] | 29.9 | - |
| Maximum specific segment pressure [MPa] | 16.0 | 30 |
| Pressure area [%] | 41.0 | - |
| Maximum pressure [MPa] | 251.4 | 180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Euler, J.; Jacobs, G.; Loriemi, A.; Jakobs, T.; Rolink, A.; Röder, J. Scaling Challenges for Conical Plain Bearings as Wind Turbine Main Bearings. Wind 2023, 3, 485-495. https://doi.org/10.3390/wind3040027
Euler J, Jacobs G, Loriemi A, Jakobs T, Rolink A, Röder J. Scaling Challenges for Conical Plain Bearings as Wind Turbine Main Bearings. Wind. 2023; 3(4):485-495. https://doi.org/10.3390/wind3040027
Chicago/Turabian StyleEuler, Jan, Georg Jacobs, Amin Loriemi, Timm Jakobs, Amadeus Rolink, and Julian Röder. 2023. "Scaling Challenges for Conical Plain Bearings as Wind Turbine Main Bearings" Wind 3, no. 4: 485-495. https://doi.org/10.3390/wind3040027
APA StyleEuler, J., Jacobs, G., Loriemi, A., Jakobs, T., Rolink, A., & Röder, J. (2023). Scaling Challenges for Conical Plain Bearings as Wind Turbine Main Bearings. Wind, 3(4), 485-495. https://doi.org/10.3390/wind3040027






