Application of a Numerical Simulation to the Estimation of Wind Loads on Photovoltaic Panels Installed Parallel to Sloped Roofs of Residential Houses
Abstract
1. Introduction
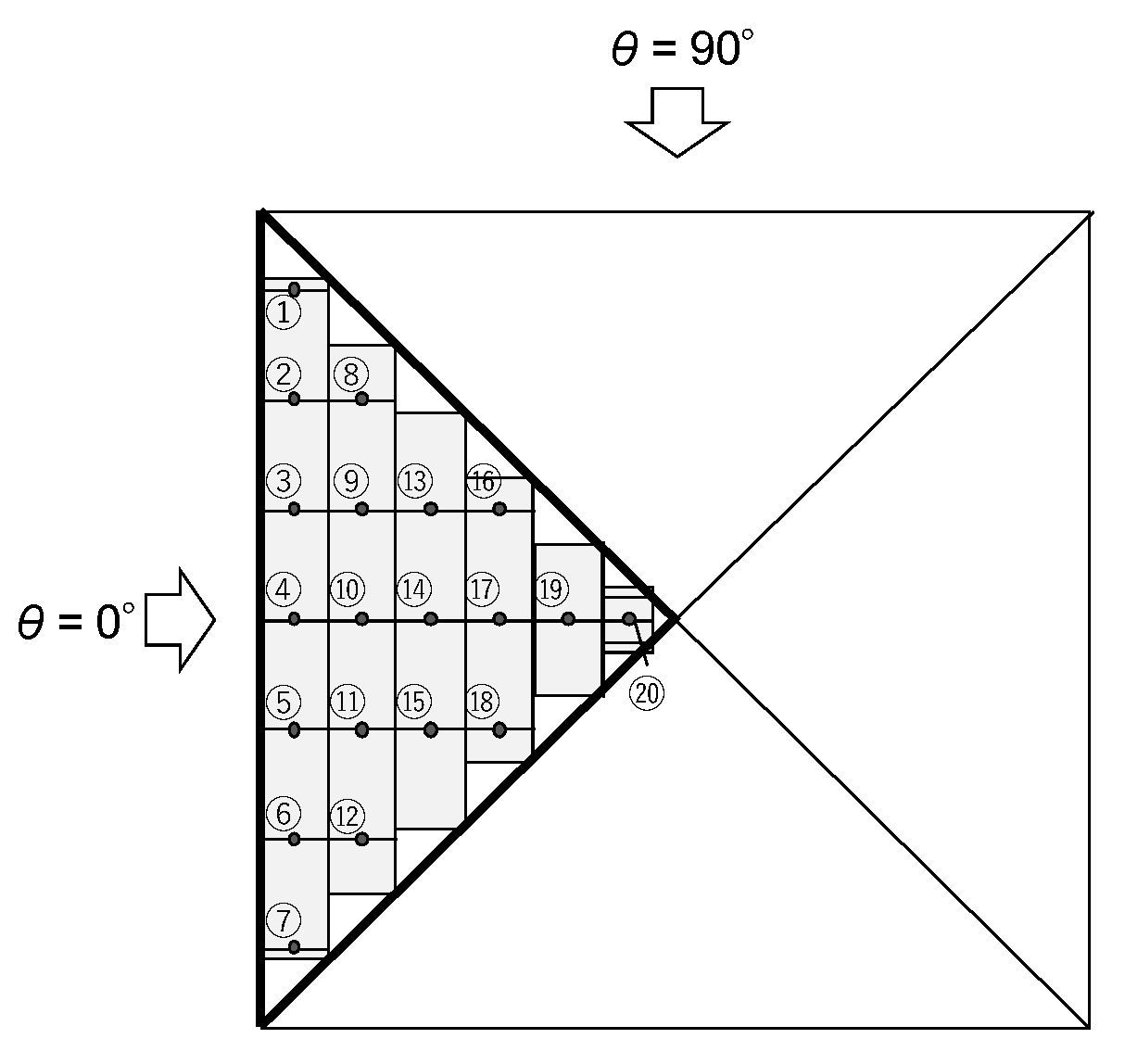
2. Wind Tunnel Experiment
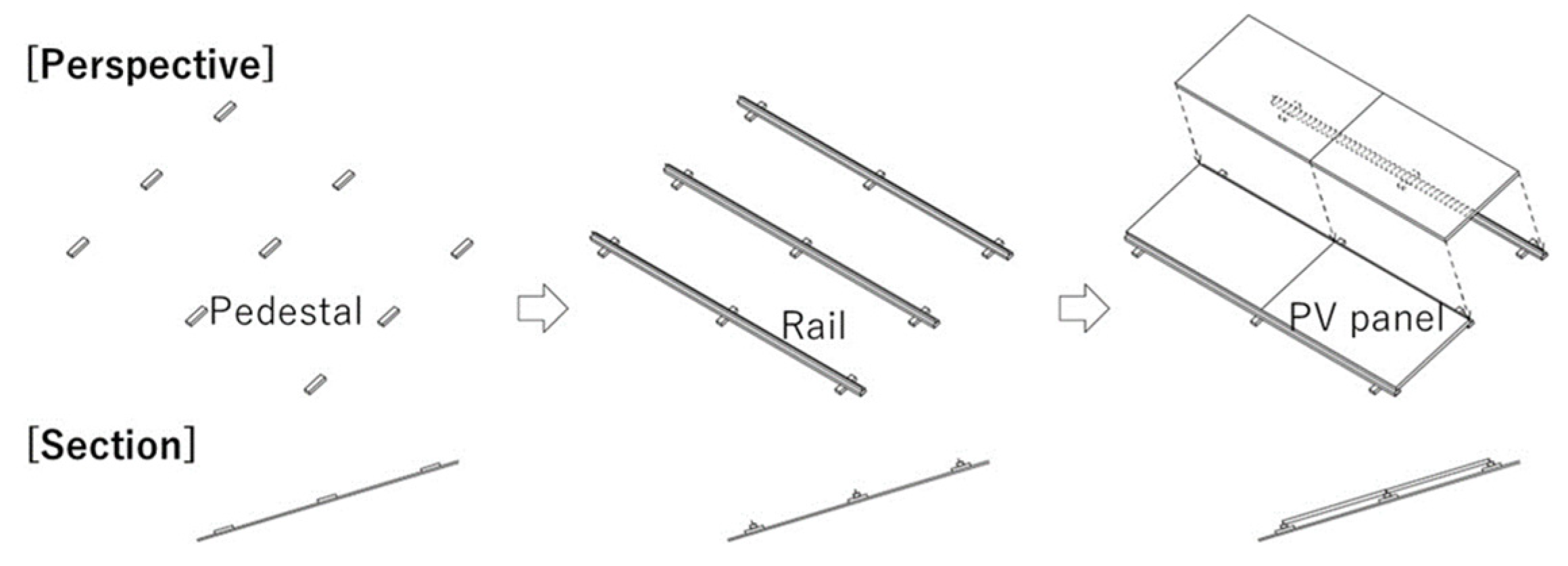
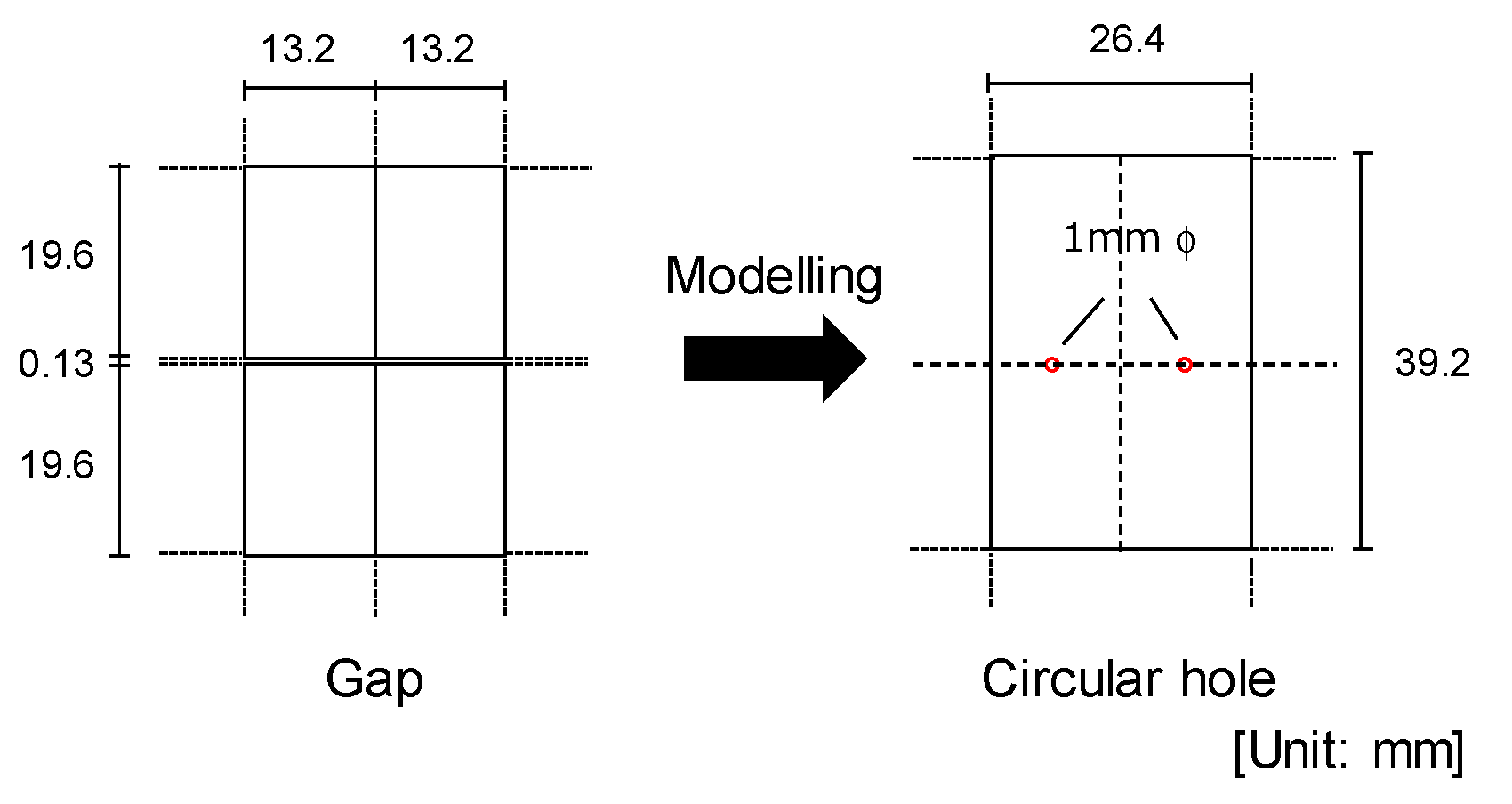
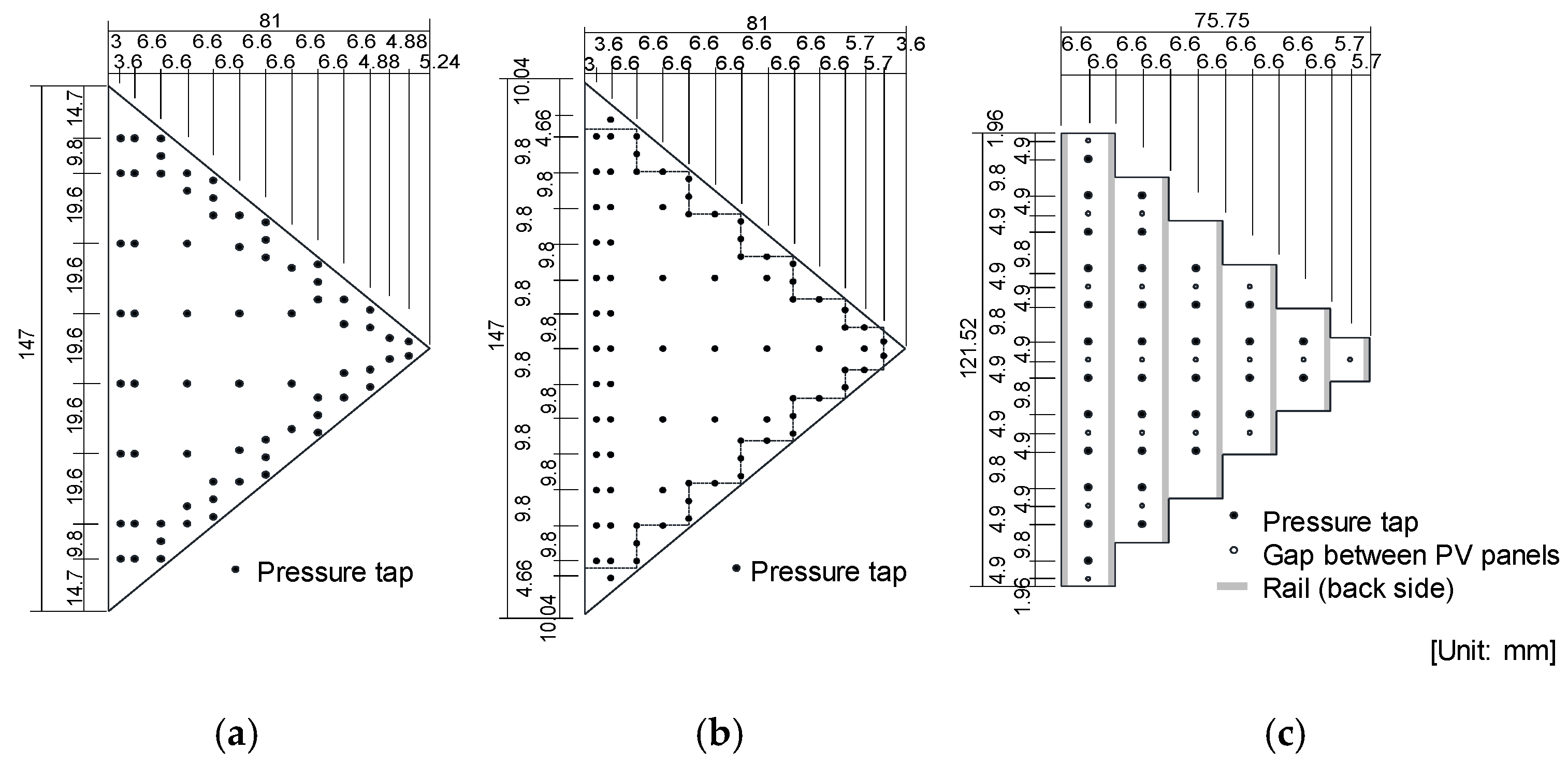
2.1. Wind Tunnel Model
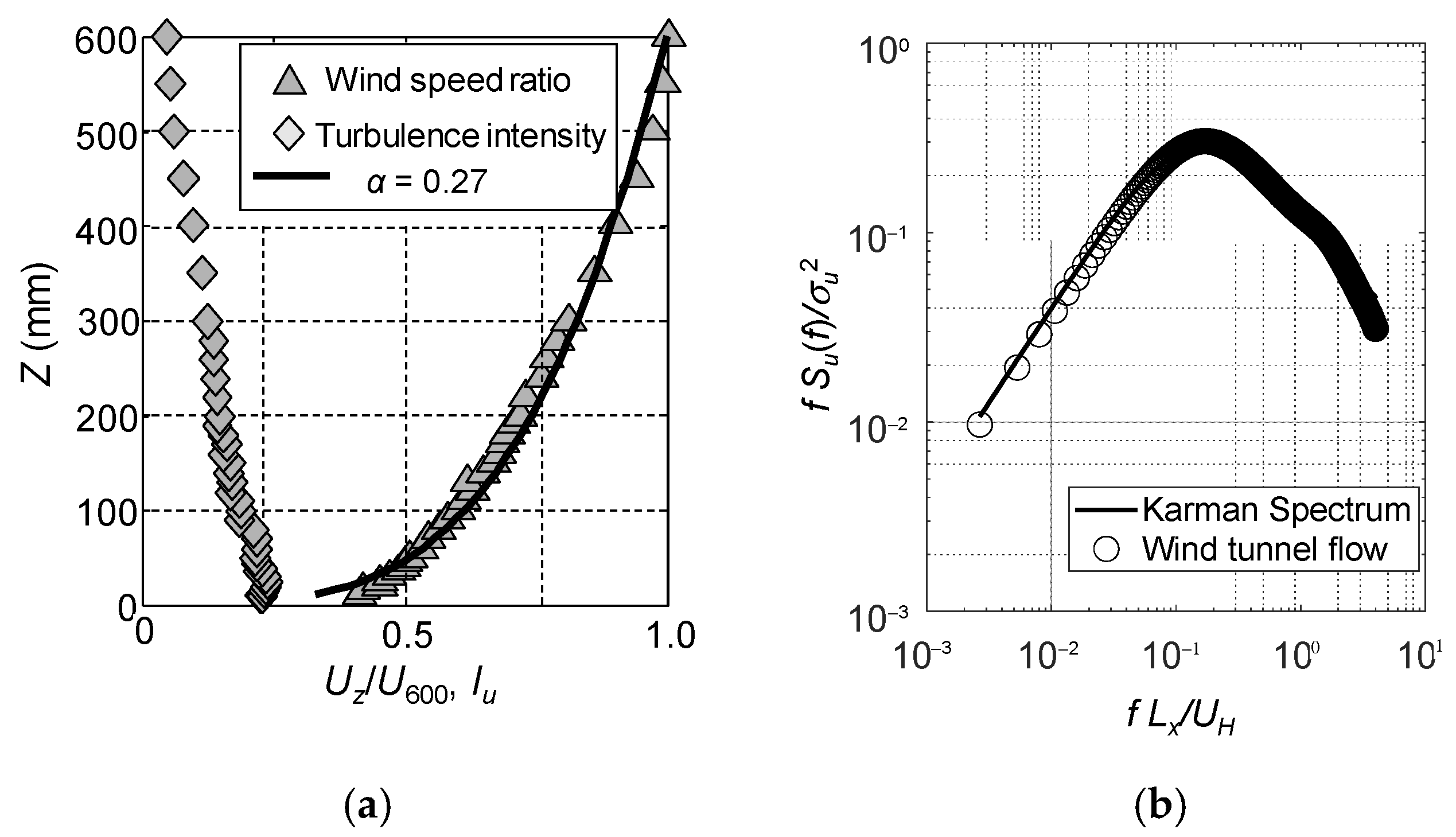
2.2. Wind Tunnel Flow
2.3. Experimental Procedure
2.4. Experimental Results
2.4.1. Wind Pressures on the Roof without PV Panels
2.4.2. Wind Pressures and Forces on PV Panels
2.4.3. Effect of PV Panels on the Roof Pressures
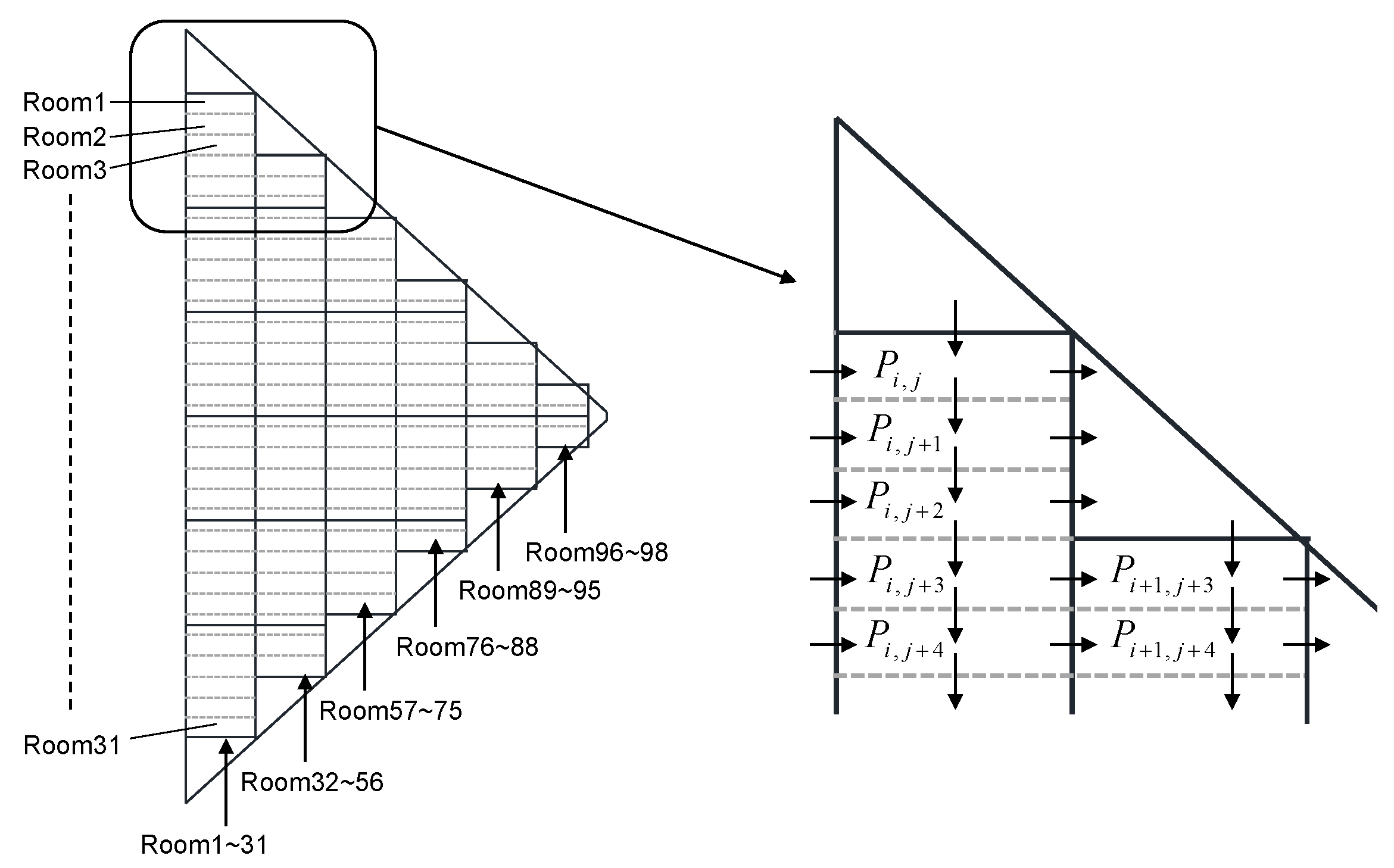
3. Numerical Simulation of Layer Pressures
3.1. Method of Simulation
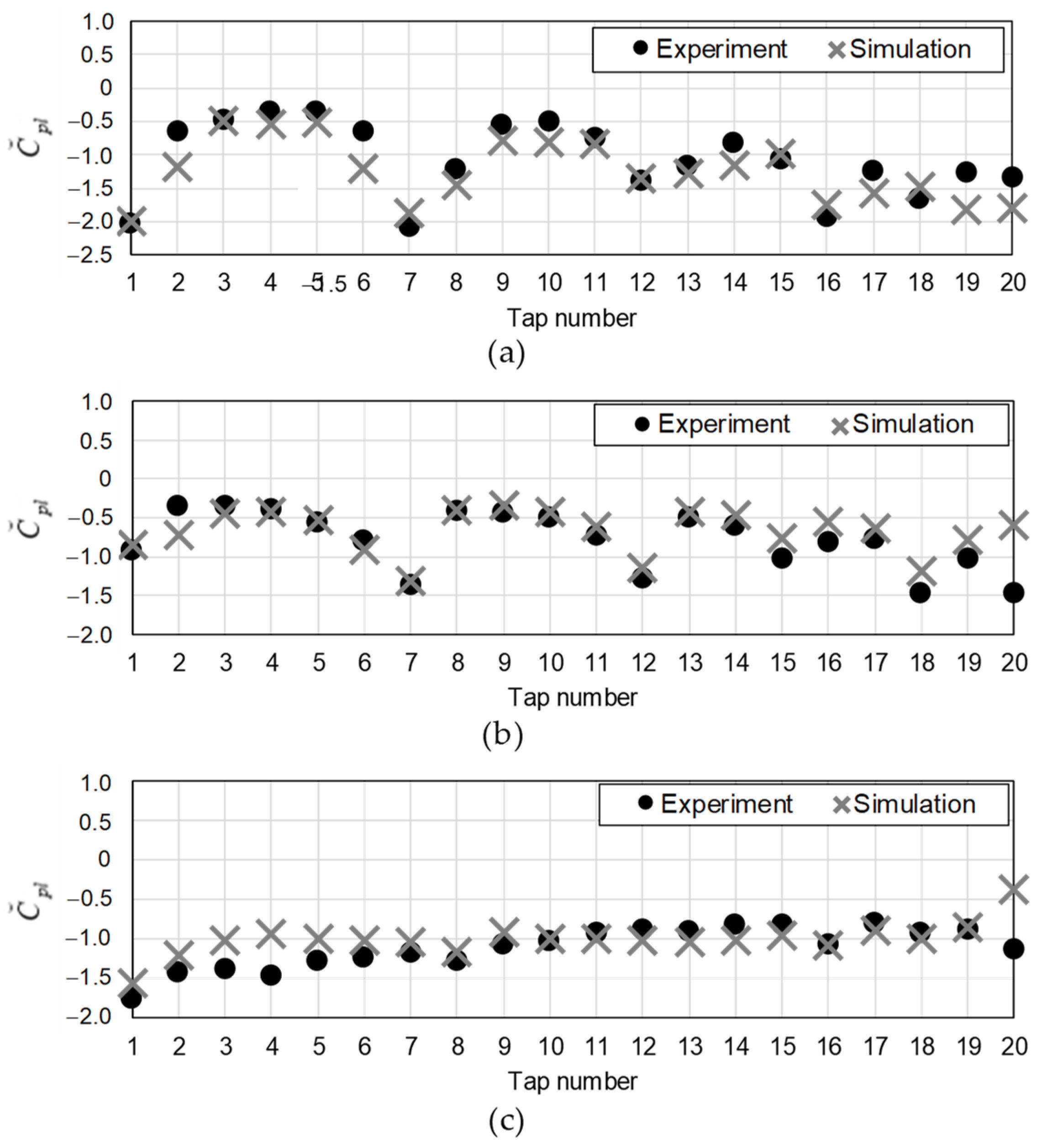
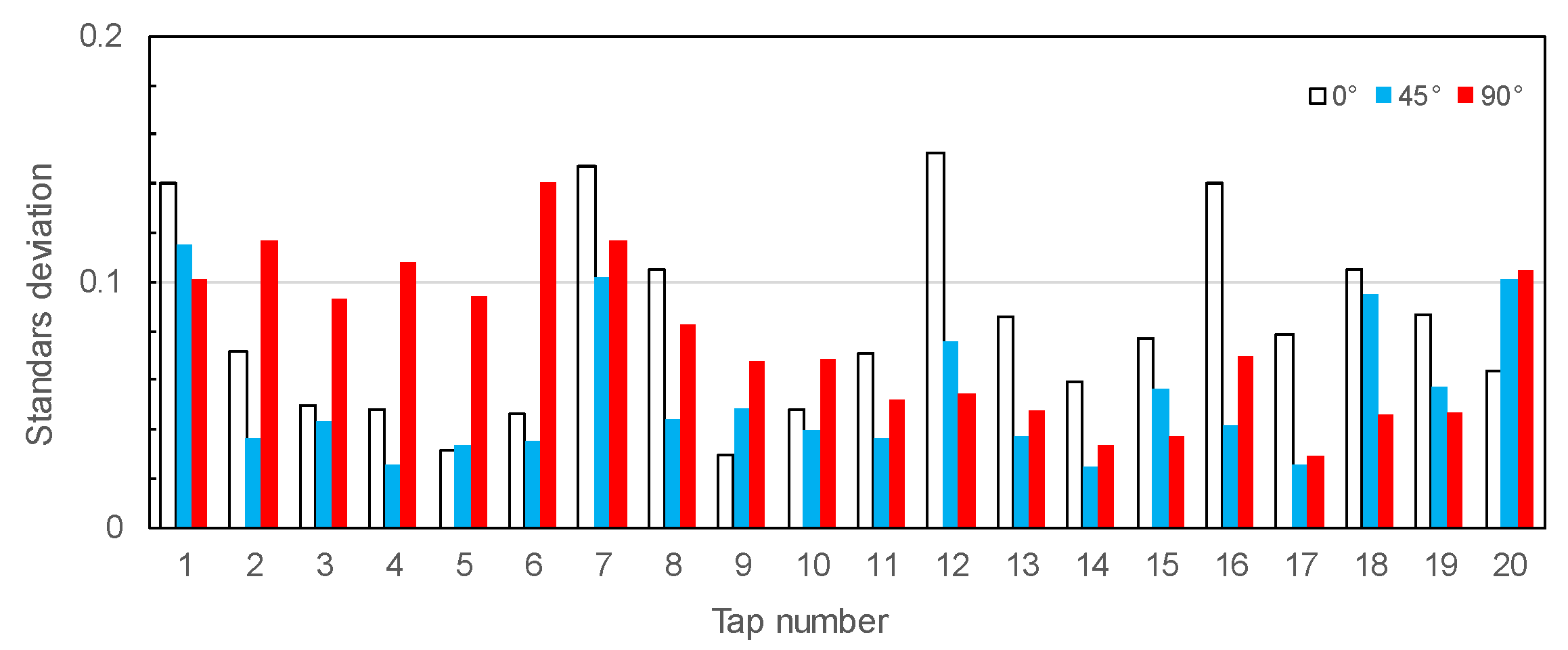
3.2. Comparison with the Experimental Results
4. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Japan Association for Wind Engineering, Tokyo Polytechnic University. Manual of Wind Resistant Design for Photovoltaic System; Japan Association for Wind Engineering: Tokyo, Japan, 2017. (In Japanese) [Google Scholar]
- Aly, A.M.; Bitsuamlak, G. Aerodynamics of ground-mounted solar panels: Test model scale effects. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 250–260. [Google Scholar] [CrossRef]
- Strobel, K.; Banks, D. Effects of vortex shedding in arrays of long inclined flat plates and ramifications for ground-mounted photovoltaic arrays. J. Wind. Eng. Ind. Aerodyn. 2014, 133, 146–149. [Google Scholar] [CrossRef]
- Jubayer, C.M.; Hangan, H. Numerical simulation of wind effects on a stand-alone ground mounted photovoltaic (PV) system. J. Wind. Eng. Ind. Aerodyn. 2014, 134, 56–64. [Google Scholar] [CrossRef]
- Jubayer, C.M.; Hangan, H. A numerical approach to the investigation of wind loading on an array of ground mounted solar photovoltaic (PV) panels. J. Wind. Eng. Ind. Aerodyn. 2016, 153, 60–70. [Google Scholar] [CrossRef]
- Ginger, J.D.; Bodhinayake, G.G.; Ingham, S. Wind loads for designing ground-mounted solar-panel arrays. Aust. J. Struct. Eng. 2019, 20, 204–218. [Google Scholar] [CrossRef]
- Browne, M.T.L.; Taylor, Z.J.; Li, S.; Gamble, S. A wind load design method for ground-mounted multi-row solar arrays based on a compilation of wind tunnel experiments. J. Wind. Eng. Ind. Aerodyn. 2020, 205, 104. [Google Scholar] [CrossRef]
- Yemenici, O.; Aksoy, M.O. An experimental and numerical study of wind effects on a ground-mounted solar panel at different panel tilt angles and wind directions. J. Wind. Eng. Ind. Aerodyn. 2021, 213, 104630. [Google Scholar] [CrossRef]
- Güemes, A.; Fajardo, P.; Raiola, M. Experimental assessment of RANS models for wind load estimation over solar-panel arrays. Appl. Sci. 2021, 11, 2496. [Google Scholar] [CrossRef]
- Wood, G.S.; Denoon, R.O.; Kwok, K.C.S. Wind loads on industrial solar panel arrays and supporting roof structure. Wind. Struct. 2001, 4, 481–494. [Google Scholar] [CrossRef]
- Kopp, G.A.; Farquhar, S.; Morrison, M.J. Aerodynamic mechanisms for wind loads on tilted, roof-mounted, solar arrays. J. Wind. Eng. Ind. Aerodyn. 2012, 111, 40–52. [Google Scholar] [CrossRef]
- Kopp, G.A.; Banks, D. Use of the wind tunnel test method for obtaining design wind loads on roof-mounted solar arrays. J. Struct. Eng. ASCE 2013, 139, 284–287. [Google Scholar] [CrossRef]
- Banks, D. The role of corner vortices in dictating peak wind loads on tilted flat solar panels mounted on large, flat roofs. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 192–201. [Google Scholar] [CrossRef]
- Browne, M.T.L.; Gibbons, M.P.M.; Gamble, S.; Galsworthy, J. Wind loading on tilted roof-top solar arrays: The parapet effect. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 202–213. [Google Scholar] [CrossRef]
- Cao, J.; Yoshida, A.; Saha, P.K.; Tamura, Y. Wind loading characteristics of solar arrays mounted on flat roofs. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 214–225. [Google Scholar] [CrossRef]
- Kopp, G.A. Wind loads on low-profile, tilted, solar arrays placed on large, flat, low-rise building roofs. J. Struct. Eng. ASCE 2014, 140, 04013057. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Zisis, I.; Xypnitou, E. Local and overall wind pressure and force coefficients for solar panels. J. Wind. Eng. Ind. Aerodyn. 2014, 125, 195–206. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Q.; Tamura, Y. Effects of building parameters on wind loads on flat-roof-mounted solar arrays. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 210–224. [Google Scholar] [CrossRef]
- Wang, J.; Phuc, P.V.; Yang, Q.; Tamura, Y. LES study of wind pressure and flow characteristics of flat-roof-mounted solar arrays. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104096. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Q.; Phuc, P.V.; Tamura, Y. Characteristics of conical vortices and their effects on wind pressures on flat-roof-mounted solar arrays by LES. J. Wind. Eng. Ind. Aerodyn. 2020, 200, 104146. [Google Scholar] [CrossRef]
- Alrawashdeh, H.; Stathopoulos, T. Wind loads on solar panels mounted on flat roofs: Effect of geometric scale. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104339. [Google Scholar] [CrossRef]
- Geurts, C.; Blackmore, P. Wind loads on stand-off photovoltaic systems on pitched roofs. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 239–249. [Google Scholar] [CrossRef]
- Aly, A.M.; Bitsuamlak, G.T. Wind-induced pressures on solar panels mounted on residential homes. J. Archit. Eng. ASCE 2014, 20, 04013003. [Google Scholar] [CrossRef]
- Stenabaugh, S.E.; Iida, Y.; Kopp, G.A.; Karava, P. Wind loads on photovoltaic arrays mounted parallel to sloped roofs on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 2015, 139, 16–26. [Google Scholar] [CrossRef]
- Naeiji, A.; Raji, F.; Zisis, I. Wind loads on residential scale rooftop photovoltaic panels. J. Wind. Eng. Ind. Aerodyn. 2017, 168, 228–246. [Google Scholar] [CrossRef]
- Takamori, K.; Nakagawa, N.; Yamamoto, M.; Okuda, Y.; Taniguchi, T.; Nakamura, O. Study on design wind force coefficients for photovoltaic modules installed on low-rise building. AIJ J. Technol. Des. 2015, 21, 67–70. (In Japanese) [Google Scholar] [CrossRef]
- JIS C 8955:2017; Japanese Industrial Standard. Load Design Guide on Structures for Photovoltaic Array. Japanese Standards Association: Tokyo, Japan, 2017.
- Uematsu, Y.; Isyumov, N. Review Wind pressures acting on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 1999, 82, 1–25. [Google Scholar] [CrossRef]
- Uematsu, Y. Peak gust pressures acting on low-rise building roofs. In Proceedings of the Eighth East Asia-Pacific Conference on Structural Engineering and Construction 2001, Singapore, 5–7 December 2001. [Google Scholar]
- Amano, T.; Fujii, K.; Tazaki, S. Wind loads on permeable roof-blocks in roof insulation systems. J. Wind. Eng. Ind. Aerodyn. 1988, 29, 39–48. [Google Scholar] [CrossRef]
- Okada, H.; Ohkuma, T.; Katagiri, J. Study on estimation of wind pressure under roof tiles. J. Struct. Constr. Eng. Archit. Inst. Jpn. 2008, 73, 1943–1950. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Oh, J.H.; Kopp, G.A. Modeling of spatially and temporary-varying cavity pressures in air-permeable, double-layer roof systems. Build. Environ. 2014, 82, 135–150. [Google Scholar] [CrossRef]
- Uematsu, Y.; Shimizu, Y.; Miyake, Y.; Kanegae, Y. Wind-induced scattering of permeable unit flooring decks loosely laid on rooftops and balconies of high-rise buildings. Tech. Trans. Civ. Eng. 2015, 2-B, 191–213. [Google Scholar]
- Watanabe, K.; Uematsu, Y. Evaluation of wind loads on ventilated exterior wall systems. J. Wind. Eng. Jpn. Assoc. Wind. Eng. 2019, 44, 23–32. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Oh, J.H.; Kopp, G.A. An experimental study of pressure equalization on double-layered roof system of low-rise buildings. In Proceedings of the 6th International Conference on Computational Wind Engineering, Hamburg, Germany, 8–12 June 2014. [Google Scholar]
- Oh, J.H.; Kopp, G.A.; Inculet, D.R. The UWO contribution to the NIST aerodynamic database for wind loads on low buildings: Part 3. Internal pressures. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 755–779. [Google Scholar] [CrossRef]
- Architectural Institute of Japan. Recommendations for Loads on Buildings; Architectural Institute of Japan: Tokyo, Japan, 2015. [Google Scholar]
- Tieleman, H.W.; Reinhold, T.A.; Marshall, R.D. On the wind-tunnel simulation of the atmospheric surface layer for the study of wind loads on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 1978, 3, 21–38. [Google Scholar] [CrossRef]
- Tieleman, H.W. Pressures on surface-mounted prisms: The effects of incident turbulence. J. Wind. Eng. Ind. Aerodyn. 1993, 49, 289–299. [Google Scholar] [CrossRef]
- Tieleman, H.W.; Hajj, M.R.; Reinhold, T.A. Wind tunnel simulation requirements to assess wind loads on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 1998, 74–76, 675–686. [Google Scholar] [CrossRef]
- ASCE/SEI 49-12; Wind Tunnel Testing for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2012.
- Meecham, D.; Surry, D.; Davenport, A.G. The magnitude and distribution of wind-induced pressures on hip and gable roofs. J. Wind. Eng. Ind. Aerodyn. 1991, 38, 257–272. [Google Scholar] [CrossRef]
- Xu, Y.L.; Reardon, G.F. Variations of wind pressure on hip roofs with roof pitch. J. Wind. Eng. Ind. Aerodyn. 1998, 73, 267–284. [Google Scholar] [CrossRef]
- Ahmad, S.; Kumar, K. Effect of geometry on wind pressures on low-rise hip roof buildings. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 755–779. [Google Scholar] [CrossRef]
- Ahmad, S.; Kumar, K. Wind pressures on low-rise hip roof buildings. Wind. Struct. 2002, 5, 493–514. [Google Scholar] [CrossRef]
- Takamori, K.; Nishimura, H.; Asami, R.; Somekawa, D.; Aihara, T. Wind pressures on hip roofs of a low-rise building–Case of square plan. In Proceedings of the 20th National Symposium on Wind Engineering 2008, Tokyo, Japan, 3–5 December 2008; pp. 463–466. (In Japanese). [Google Scholar]
- Aihara, T.; Asami, Y.; Nishimura, H.; Takamori, K.; Asami, R.; Somekawa, D. An area correct factor for the wind pressure coefficient for cladding of hip roof–The case of square plan hip roof with roof pitch of 20 degrees. In Proceedings of the 20th National Symposium on Wind Engineering 2008, Tokyo, Japan, 3–5 December 2008; pp. 463–466. (In Japanese). [Google Scholar]
- Shao, S.; Tian, Y.; Yang, Q.; Stathopoulos, T. Wind-induced cladding and structural loads on low-rise buildings with 4:12-splped hip roofs. J. Wind. Eng. Ind. Aerodyn. 2019, 193, 103948. [Google Scholar] [CrossRef]
- Uematsu, Y.; Yambe, T.; Watanabe, T.; Ikeda, H. The benefit of horizontal photovoltaic panels in reducing wind loads on a membrane roofing system on a flat roof. Wind 2020, 1, 44–62. [Google Scholar] [CrossRef]
- Yambe, T.; Uematsu, Y.; Sato, K.; Watanabe, T. Wind loads on photovoltaic systems installed parallel to the roof of flat-roofed building and its wind load reduction effect on the roofing system. AIJ J. Technol. Des. 2020, 26, 461–466. (In Japanese) [Google Scholar] [CrossRef]
- Yambe, T.; Yamamoto, A.; Uematsu, Y. Wind loads of photovoltaic panels mounted on a hip roof to the edge and their wind-load reduction effect on roof cladding. J. Struct. Constr. Eng. Archit. Inst. Jpn. 2021, 86, 1581–1588. (In Japanese) [Google Scholar] [CrossRef]





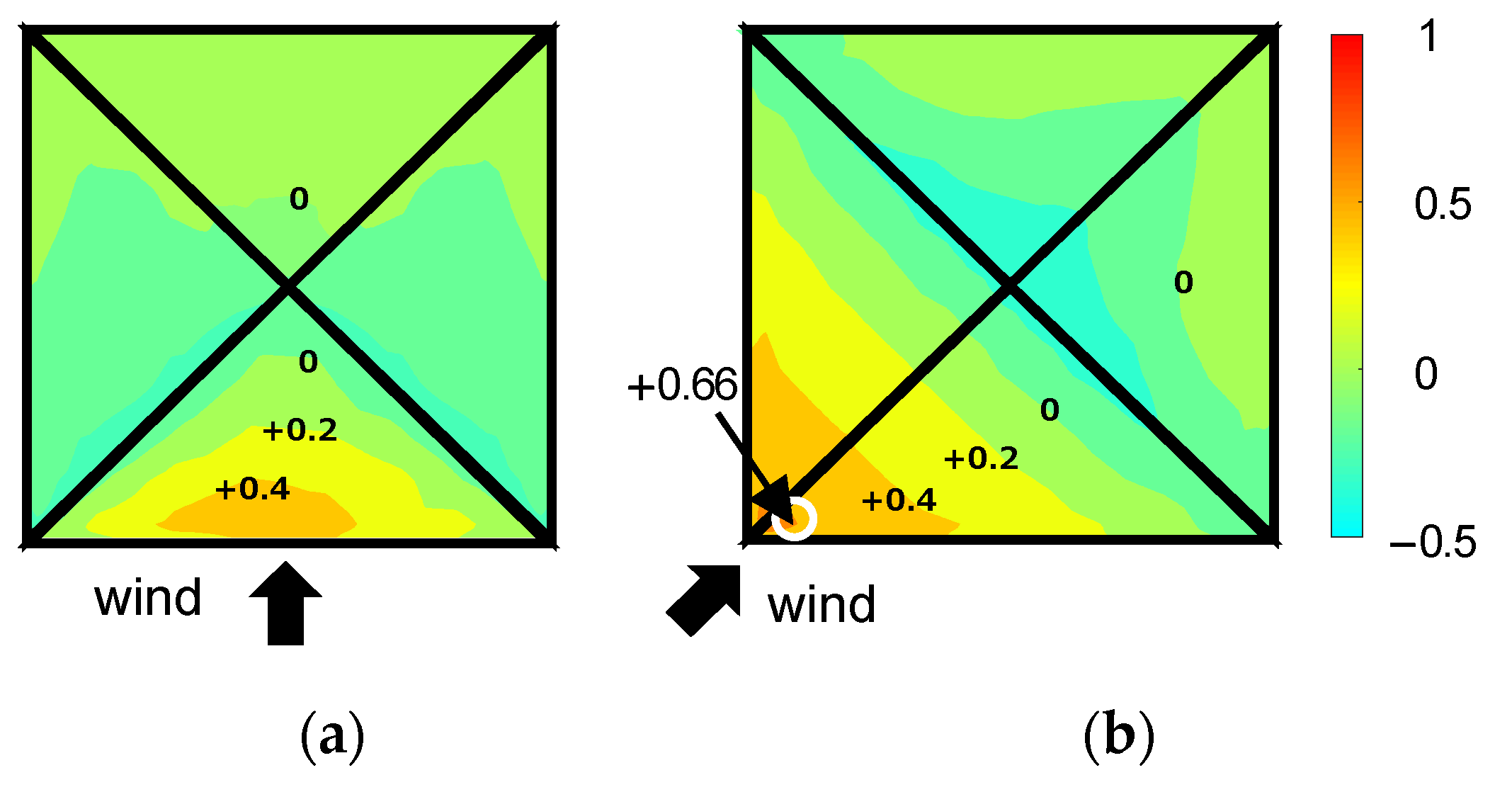
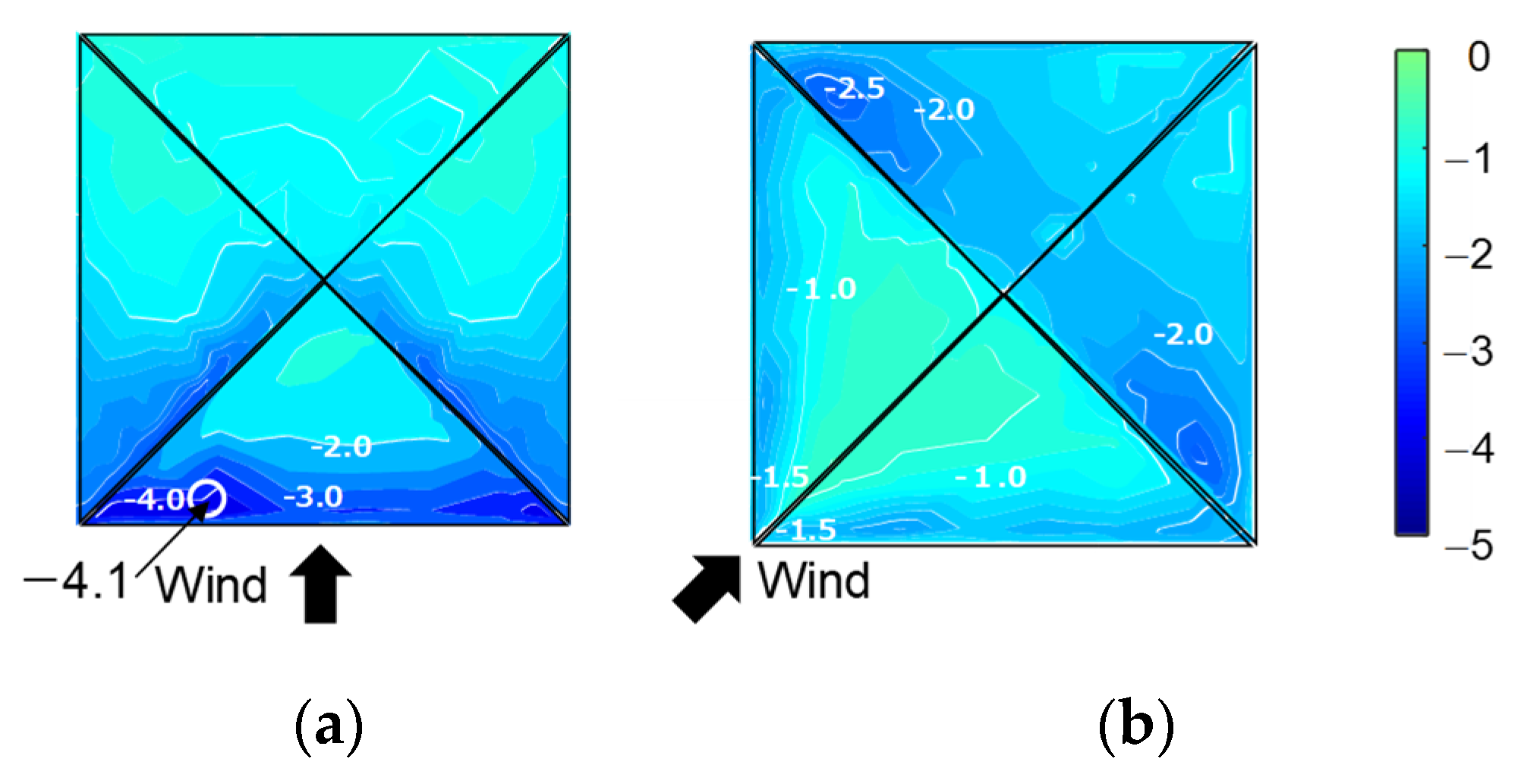
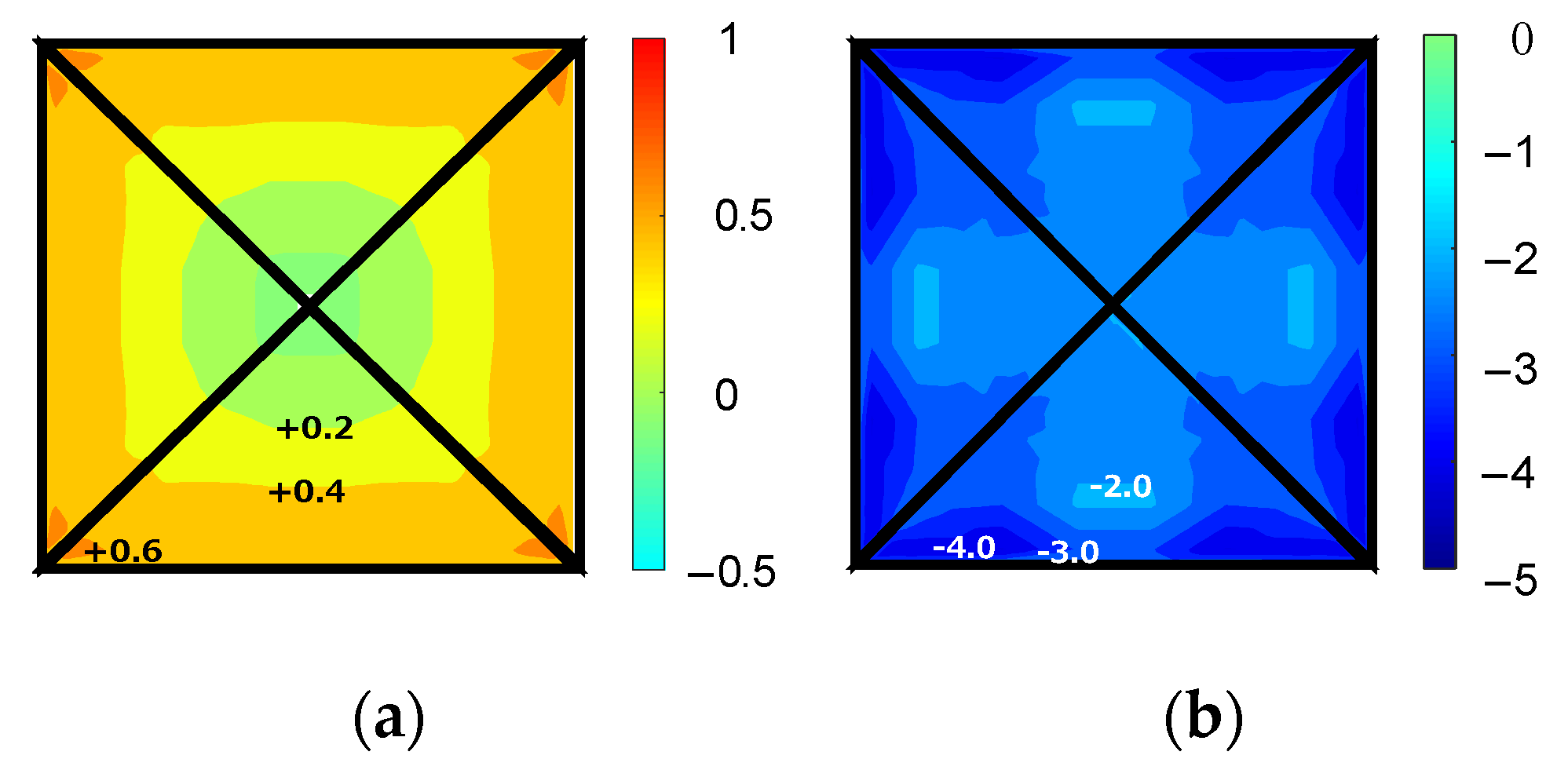
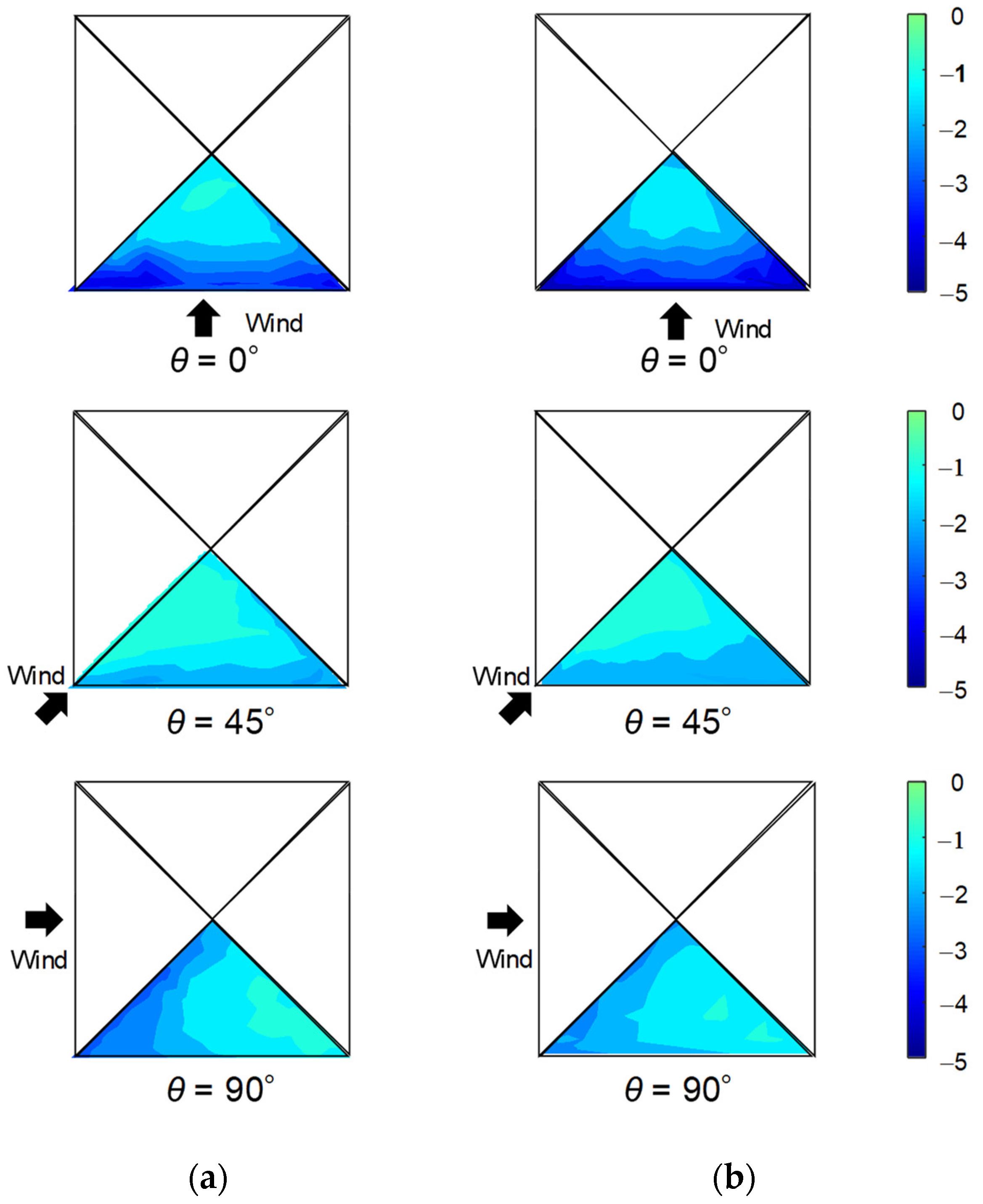
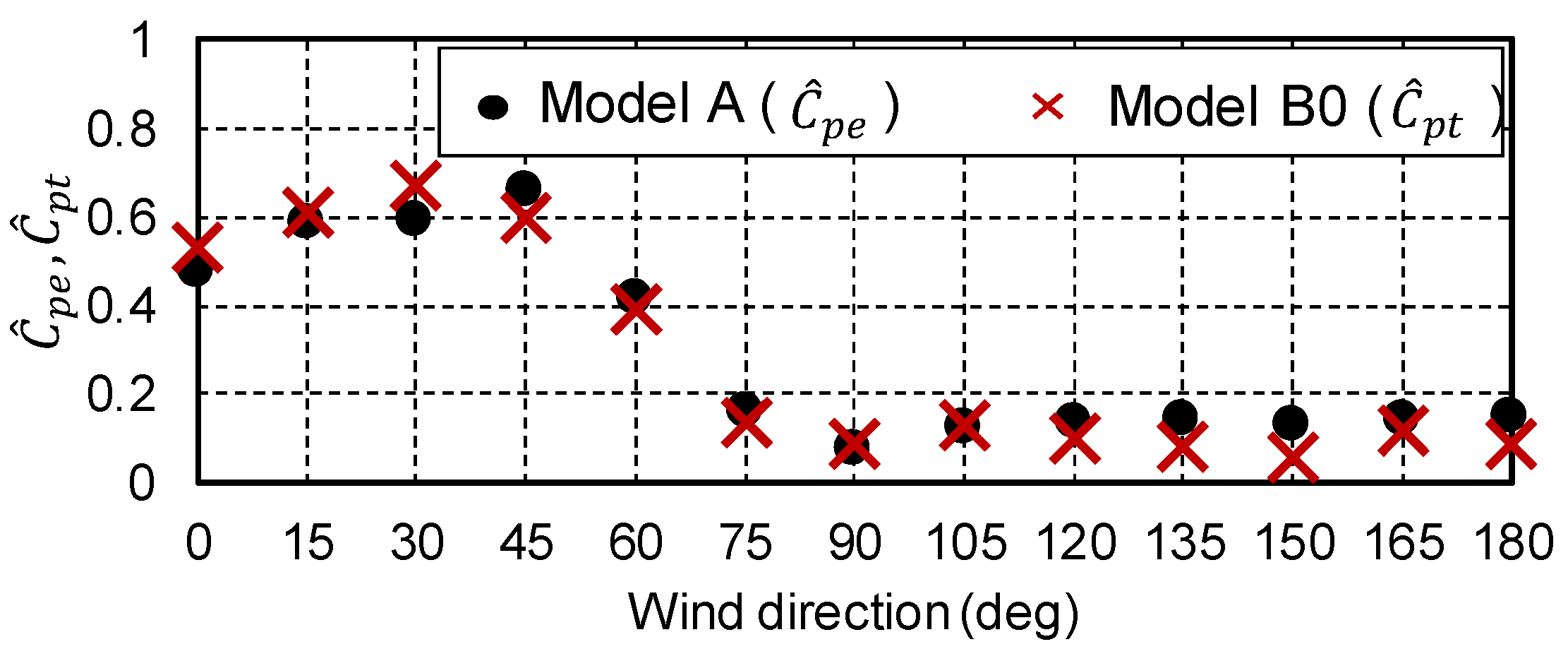

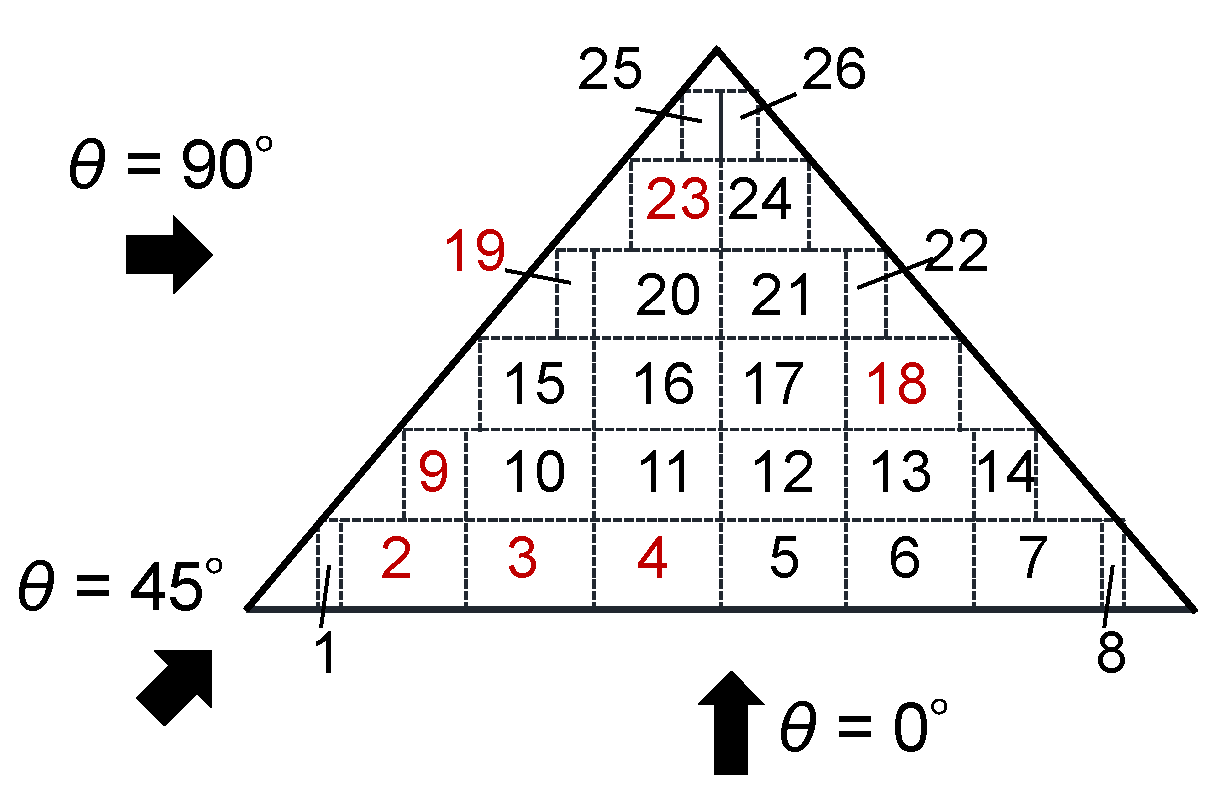

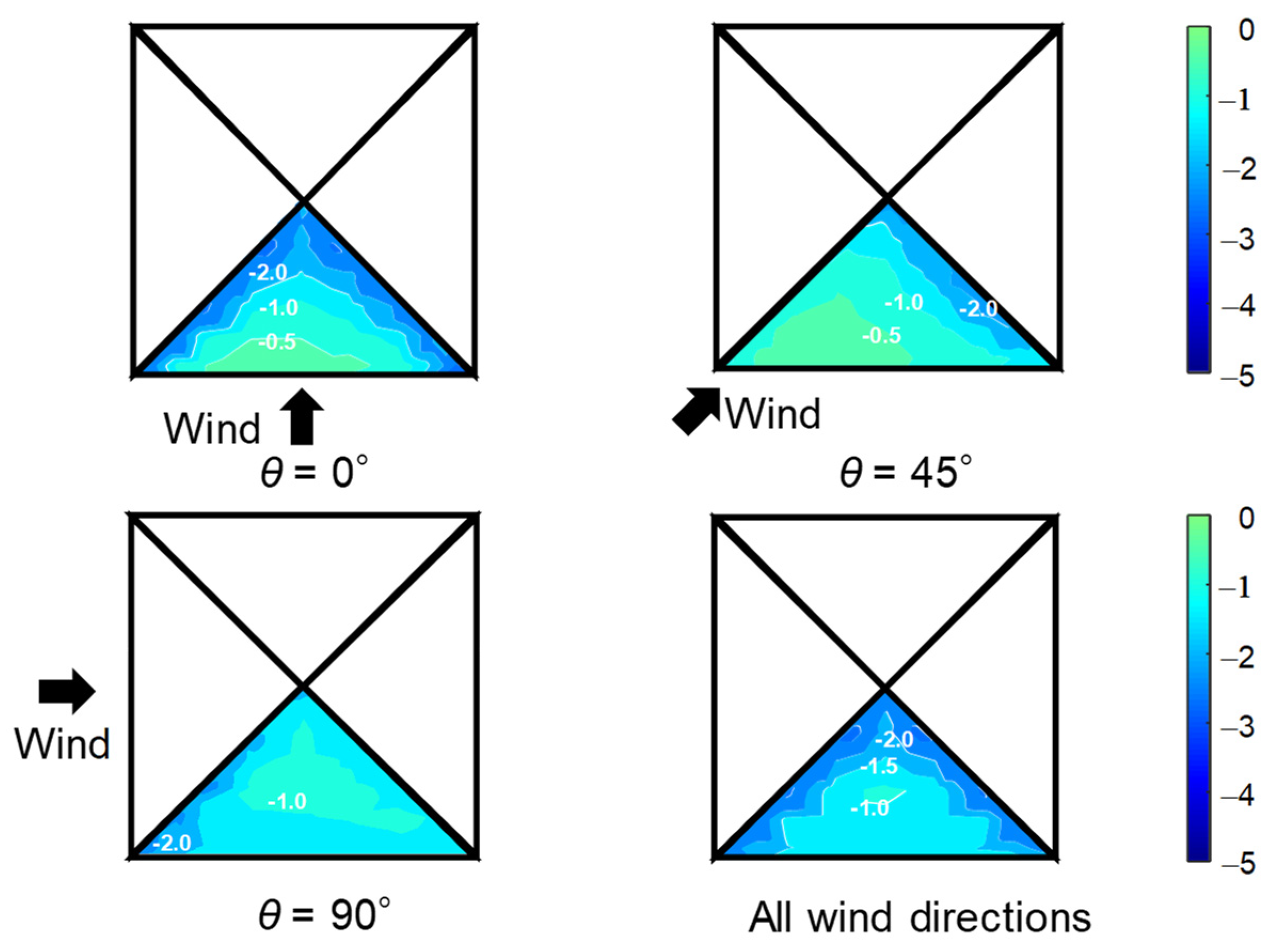
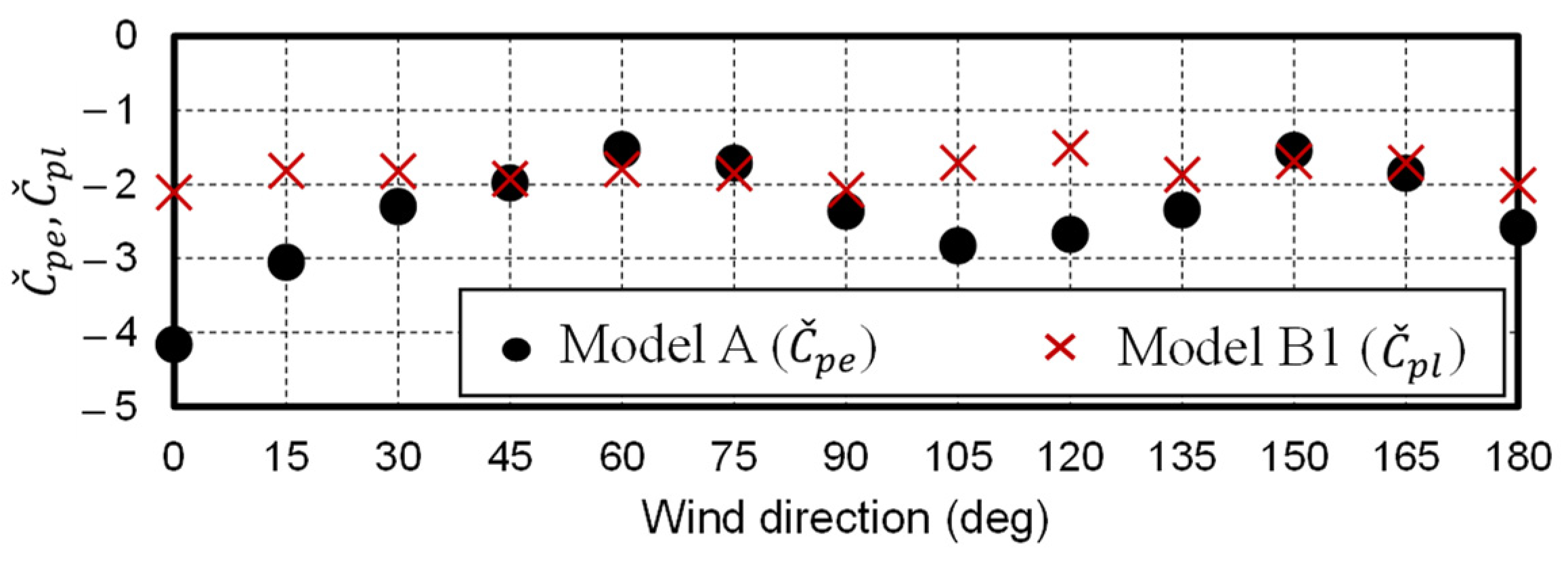


| θ (deg) | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 |
| Panel | 4 | 3 | 2 | 3 | 3 | 23 | 9 | 23 | 19 | 19 | 9 | 19 | 18 |
| Data Source | Positive Value | Negative Value | ||
|---|---|---|---|---|
| Edge Zone | Internal Zone | Edge Zone | Internal Zone | |
| JIS C 8955 (, ) | – | +2.85 | – | −2.81 |
| Experiment & simulation (, ) | +2.34 | +1.84 | −3.70 | −2.58 |
| Prediction from the Cp distribution | +1.79 | +1.65 | −4.18 | −2.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uematsu, Y.; Yambe, T.; Yamamoto, A. Application of a Numerical Simulation to the Estimation of Wind Loads on Photovoltaic Panels Installed Parallel to Sloped Roofs of Residential Houses. Wind 2022, 2, 129-149. https://doi.org/10.3390/wind2010008
Uematsu Y, Yambe T, Yamamoto A. Application of a Numerical Simulation to the Estimation of Wind Loads on Photovoltaic Panels Installed Parallel to Sloped Roofs of Residential Houses. Wind. 2022; 2(1):129-149. https://doi.org/10.3390/wind2010008
Chicago/Turabian StyleUematsu, Yasushi, Tetsuo Yambe, and Atsushi Yamamoto. 2022. "Application of a Numerical Simulation to the Estimation of Wind Loads on Photovoltaic Panels Installed Parallel to Sloped Roofs of Residential Houses" Wind 2, no. 1: 129-149. https://doi.org/10.3390/wind2010008
APA StyleUematsu, Y., Yambe, T., & Yamamoto, A. (2022). Application of a Numerical Simulation to the Estimation of Wind Loads on Photovoltaic Panels Installed Parallel to Sloped Roofs of Residential Houses. Wind, 2(1), 129-149. https://doi.org/10.3390/wind2010008






